Electromigration dispersion in a capillary in the presence of electro-osmotic flow

Abstract

The differential migration of ions in an applied electric field is the basis for separation of chemical species by capillary electrophoresis. Axial diffusion of the concentration peak limits the separation efficiency. Electromigration dispersion is observed when the concentration of sample ions is comparable to that of the background ions. Under such conditions, the local electrical conductivity is significantly altered in the sample zone making the electric field, and therefore, the ion migration velocity concentration dependent. The resulting nonlinear wave exhibits shock like features, and, under certain simplifying assumptions, is described by Burgers’ equation (S. Ghosal and Z. Chen Bull. Math. Biol. 2010 72, pg. 2047). In this paper, we consider the more general situation where the walls of the separation channel may have a non-zero zeta potential and are therefore able to sustain an electro-osmotic bulk flow. The main result is a one dimensional nonlinear advection diffusion equation for the area averaged concentration. This homogenized equation accounts for the Taylor-Aris dispersion resulting from the variation in the electro-osmotic slip velocity along the wall. It is shown that in a certain range of parameters, the electro-osmotic flow can actually reduce the total dispersion by delaying the formation of a concentration shock. However, if the electro-osmotic flow is sufficiently high, the total dispersion is increased because of the Taylor-Aris contribution.

1. Introduction

Macromolecules such as DNA and proteins carry an electrical charge in aqueous solution because of ionic dissociation of molecular groups on their surface. The amount and sign of the charge depends on various factors such as the pH of the solution. If an external electric field is applied, these macro-ions migrate along the field with a velocity that depends on its charge, size and shape as well as on the ionic composition of the background electrolyte. Electrophoresis is a technique of analytical chemistry for separating a mixture of chemical compounds by exploiting their differing migration velocities in an applied electric field. It is a widely used laboratory technique in areas such as molecular biology, forensics and medicine.

The most common format is “gel electrophoresis,” where the electrolyte is suspended in a porous gel. The technique of capillary electrophoresis (CE) has developed rapidly in recent years, partly because of the possibility of integrating CE channels on to micro-fluidic chips. In CE, the sample and suspending electrolyte are contained in a micro-fluidic channel with width in the range of tens of microns. CE can proceed in several modes, the simplest of which is “zone electrophoresis”. Here a sample zone or band is injected into a micro-channel, which then moves by electrophoresis towards the detector at the opposite end under an applied electric field. Different components arrive at different times and their arrival is marked by a peak in some solute property (usually the UV absorbance) at the detector window (Landers 1996; Camilleri 1998). The walls of the capillary, which are most commonly made of fused silica, has an electrostatic charge that is characterized by its zeta potential. Therefore, the applied electric field results in an electro-osmotic flow along the capillary (Probstein 1994). This flow is normally advantageous in CE because it sweeps both positive and negative ions past a single detector near the outlet and also reduces the transit time from inlet to detector. However, it can, under certain circumstances adversely affect the separation by causing “anomalous dispersion” of the sample peak (Ghosal 2006).

The physical process of separation in CE is the result of the mutually opposed and competing processes of differential migration of ions and diffusive spreading along the axis of separation. The resolution depends on the strength of the applied electric field. In practice, the applied voltage is often very large, in the range of kilo volts. The highest voltage that can be applied is limited by the ability to dissipate the considerable Joule heat that is produced in the buffer by the electrolytic current. This is the reason why the channel width may not exceed some tens of microns. It is clearly advantageous to have an electrolytic buffer of low conductivity in order to minimize heating. It is also advantageous to have a relatively high concentration of sample ions, since one of the limitations of CE is the high demand placed on the sensitivity of the detector, which must be sensitive to light attenuation over an optical path length of only a few tens of microns. However, the ratio of sample to background ion concentration cannot be increased indefinitely; distortions due to “electromigration dispersion” or the “sample overloading effect” limits the highest ratio of sample to background ion concentration that may be used in CE.

The underlying physical mechanism of electromigration dispersion was elucidated by Mikkers et al. (1979) and may be roughly explained as follows: when the concentration of sample ions is comparable to that of the carrier electrolyte, the local electrical conductivity is altered in the vicinity of the sample peak. On the other hand, since the current through the capillary must be the same at all points along the axis, the electric field must change locally. This follows since the product of the conductivity and electric field is the current (according to Ohm’s law, neglecting for the time being the diffusion current due to ionic concentration gradients). This varying electric field alters the effective migration speed of the sample ions, which, in turn, alters its concentration distribution. Thus, we have a nonlinear transport problem that must be solved in a self consistent manner. Electromigration dispersion causes highly asymmetric concentration profiles, high rates of dispersion and shock like structures that are reminiscent of nonlinear waves seen in many other physical systems. These effects have been widely reported in the literature on electrophoresis (Boušková et al. 2004).

Simple one dimensional mathematical models of electromigration dispersion have been studied by Mikkers et al. (1979); Mikkers (1999); Babskii et al. (1989) by invoking the assumption of vanishing diffusivity which results in a single nonlinear hyperbolic equation for the concentration of sample ions. Solutions describe the observed steepening of an intitially smooth profile leading to subsequent shock formation. Two recent reviews by Gaš (2009) and Thormann et al. (2009) provide more extensive references to this early work. The restriction of zero diffusivity was removed by Ghosal & Chen (2010) (henceforth referred to as GC) who considered a three ion system – the sample ion, co-ion and counter-ion – where the diffusivities of the three ionic species were equal but not necessarily zero. The sample concentration was shown to obey a one dimensional nonlinear advection diffusion equation which reduced to Burgers’ equation if the sample concentration was not too high relative to that of the background ions. Since the initial value problem for Burgers’ equation may be exactly solved, useful insight into the nature of electromigration dispersion could be gained in the limits of small as well as large Péclet numbers. A generalization of this model to the situation where the buffer is a weak electrolyte has recently been presented (Chen & Ghosal 2011). It was found that the evolution of the peak shape may still be described by the Burgers’ equation with a slight re-interpretation of a certain model parameter. If this parameter is taken as a fitting parameter, excellent quantitative agreement is obtained with measured values of the peak variance in experiments. A similar nonlinear advection diffusion equation was derived by Zangle et al. (2009) in order to describe “desalination shocks” near constrictions in micro channels. However, in their problem the physical origin of the nonlinearity is related to surface conduction effects.

In this paper, we extend the earlier work of GC by taking into account the fact that the channel wall generally has a non-zero zeta potential which creates a bulk fluid flow in the capillary due to electro-osmosis. The electro-osmotic flow affects the transport process in the following way: the axial variation of the electric field created by the conductivity changes results in a variable electro-osmotic slip velocity on the channel walls. This in turn results in an induced pressure gradient and the concomitant appearance of a shear in the velocity profile across the channel due to a well known mechanism (Herr et al. 2000; Ghosal 2002a,b,c). The shear then enhances axial dispersion due to the Taylor-Aris effect (Taylor 1953; Aris 1956). Our principal result is equation (3.23), which is a one dimensional nonlinear advection diffusion equation for the sample concentration averaged over the channel cross-section.

The rest of the paper is organized as follows. In § 2 the complete mathematical statement of the flow and electro-diffusion problem is presented. In § 3 a systematic reduction of the full equations leading to equation (3.23) is achieved by introducing a number of physical approximations. The consequences of this equation are discussed in § 4, where it is shown that there is a peak in the efficiency of separation at an intermediate value of the electro-osmotic flow strength. The broad implications of the analysis to separation efficiency in CE are discussed in § 5.

2. Mathematical Formulation

We consider (see Figure 1) a uniform, long capillary of arbitrary cross-sectional shape connected to infinite reservoirs at either end. The length of the capillary is much greater than the width; the capillary may, for most purposes, be assumed infinitely long. The capillary contains a solute and N strong (i.e. completely dissociated) electrolytes of concentration c_i(x, y, z, t) where i = 1 to N. These concentrations then obey the conservation equations based on the Nernst-Planck model for ion flux (Probstein 1994)

Figure 1.

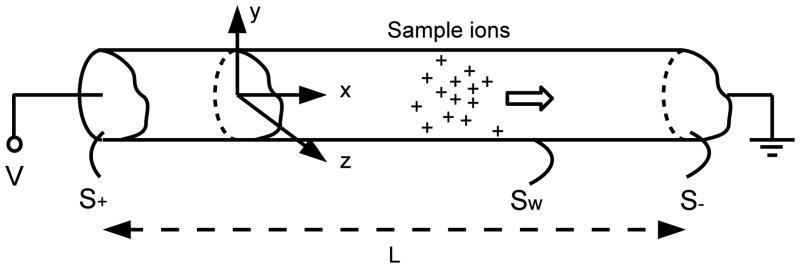
Schematic diagram (not to scale) illustrating the mathematical problem of electro-migration dispersion of a sample in CE. In addition to the sample ions shown, the capillary also contains a carrier electrolyte consisting of co- and counter- ions.

$$\frac{\partial c_i}{\partial t}+\mathbf{\nabla }·(\mathbf{u}{c}_i-z_{i}e{\nu }_i{c}_i\mathbf{\nabla }{\phi }_e-D_i\mathbf{\nabla }{c}_i)=0,$$ (2.1)

where z_i, ν_i and D_i are the valence, mobility and diffusivity of species i, the electronic charge is e, φ_e is the electric potential and u(x, y, z, t) is the fluid flow velocity. The potential φ_e obeys the Poisson equation (in CGS units)

$$\epsilon {\nabla }^2{\phi }_e=-4\pi {\rho }_e=-4\pi \sum _{i=1}^N{z}_i{ec}_i(x,y,z,t)$$ (2.2)

where ε is the permittivity of the solvent and ρ_e is the density of free charges in the solvent. Since the Reynolds number is small for flow in micro-capillaries, the fluid flow is described by Stokes equation

$$-\mathbf{\nabla }p+\eta {\nabla }^2\mathbf{u}-{\rho }_e\mathbf{\nabla }{\phi }_e=0,$$ (2.3)

together with the incompressibility constraint

$$\mathbf{\nabla }·\mathbf{u}=0,$$ (2.4)

where p is the pressure and η is the dynamic viscosity of the solvent.

These equations are associated with a number of boundary conditions that describe our situation. The concentrations c_i reduce to their equilibrium distributions in a uniform capillary very far away from the sample zone

$$c_i(x,y,z)\sim c_i^{eq}(y,z)\text{if}\mid x\mid \to \infty .$$ (2.5)

Clearly $c_i^{eq}(y,z)=0$ when i corresponds to the sample and is given by solutions of the two dimensional Poisson-Boltzmann model for the other species (background electrolytes). The potential φ_e obeys Dirichlet boundary conditions

$${\phi }_e(x,y,z)=\{\begin{array}{ll}{\phi }_e^w\hfill & \text{if}(x,y,z)\epsilon S_w\hfill \\ V\hfill & \text{if}(x,y,z)\epsilon S_{+}\hfill \\ 0\hfill & \text{if}(x,y,z)\epsilon S_{-}\hfill \end{array}$$ (2.6)

where ${\phi }_e^w$ is the value of the potential at the wall, V is the applied voltage, and, S_w, S₊ and S₋ are the parts of the bounding surface of the capillary that correspond to the walls, the inlet and the outlet respectively (Figure 1). The inlet and the outlet sections are separated by a distance L and we are interested in the limit where V and L approach infinity but V/L = E₀ remains finite. The hydrodynamic flow satisfies the no-slip conditions at the wall

$$\mathbf{u}(x,y,z,t)=0\text{if}(x,y,z)\epsilon S_w,$$ (2.7)

and,

$$\mathbf{u}(x,y,z,t)\sim {\mathbf{u}}^{eq}(y,z)\text{if}\mid x\mid \to \infty ,$$ (2.8)

where u^eq(y, z) is the electro-osmotic flow in the uniform capillary when no sample is present, and, when L is infinite. Finally, the ion fluxes are zero at the capillary walls (S_w)

$$(z_{i}e{\nu }_i{c}_i\mathbf{\nabla }{\phi }_e+D_i\mathbf{\nabla }{c}_i)·\widehat{\mathbf{n}}=0\text{if}(x,y,z)\epsilon S_w$$ (2.9)

where n̂ is the unit normal at the wall directed into the fluid.

These equations and boundary conditions form a well posed system of equations that may be integrated numerically for given initial conditions. Such a description would, however, be unnecessarily complex. Our objective is to introduce a series of approximations that enable a reduced description in terms of a single one dimensional evolution equation for the cross-sectionally averaged concentrations c̄_i(x, t), since this is the quantity that is essentially measured by the detector. Henceforth, a bar above a field variable will always denote its average over the cross-section of the capillary.

3. One dimensional homogenized equations

We now introduce a number of approximations that simplify the description and lead up to the one dimensional homogenized equation for the sample ion concentration that we seek. The developments closely follow GC except for the important difference that the possibility of a hydrodynamic flow field u is admitted.

3.1. Thin Debye layers

The fixed charges on the wall are shielded by a cloud of counter-ions over a length scale of the order of the Debye length (λ_D) which is related to the equilibrium ionic concentrations (Probstein 1994). The Debye length is typically of the order of nanometers; much smaller than the characteristic width of the micro-channel which is in the range of tens of microns. Under such conditions, the left hand side of (2.2) may be set to zero (Planck 1890), and, as a consequence, the last term in (2.3), representing the density of electric forces also vanish.^† Thus, Poisson’s equation is replaced by the constraint of local electro-neutrality. The loss of the equation for φ_e is however not catastrophic, because φ_e can be determined from the equation of current conservation

$$\mathbf{\nabla }·{\mathbf{J}}_e=0$$ (3.1)

where the current density

$${\mathbf{J}}_e=-\left(\sum _{i=1}^N{z}_i^2{e}^2{\nu }_i{c}_i\right)\mathbf{\nabla }{\phi }_e-\sum _{i=1}^N{z}_i{eD}_i\mathbf{\nabla }{c}_i$$ (3.2)

is the sum of the Ohmic conduction (first term) and a contribution due to differential diffusion (second term). Equation (3.1) follows from the constraint of local electro-neutrality on summing (2.1) after multiplying by z_ie. The loss of the electrical forcing term in (2.3) is mitigated by replacing the no-slip boundary condition (2.7) with the Helmholtz-Smoluchowski slip boundary condition (Probstein 1994)

$$\mathbf{u}(x,y,z)=\frac{\epsilon \zeta \mathbf{\nabla }{\phi }_e}{4\pi \eta }\text{if}(x,y,z)\epsilon S_w$$ (3.3)

that takes into account the presence of a boundary layer of non-vanishing charge next to the capillary wall. Here ζ, the so called “zeta-potential” is the difference in the values of φ_e between a point at the outer edge of the Debye layer and the corresponding point on the wall. It is a material property that will be assumed constant. The boundary conditions (2.6) are replaced by

$${\mathbf{J}}_e·\widehat{\mathbf{n}}=0$$ (3.4)

which follows from (2.9) and is the condition of zero current flow into capillary walls. At large distances from the sample zone we have a uniform field (E₀) and a uniform flow (u_eo), thus,

$${\phi }_e(x,y,z,t)\sim -E_{0}x\text{if}\mid x\mid \to \infty$$ (3.5)

and

$$\mathbf{u}(x,y,z,t)\sim {\mathbf{u}}^{eq}(y,z)=-\frac{\epsilon \zeta E_0}{4\pi \eta }\widehat{\mathbf{x}}=u_{eo}\widehat{\mathbf{x}}\text{if}\mid x\mid \to \infty$$ (3.6)

where x̂ is the unit vector in the axial direction.

3.2. Three ion model

We introduce the Kohlrausch (Kohlrausch 1897) function

$$K(x,y,z,t)=\sum _{i=1}^N\frac{1}{{\nu }_i}{c}_i(x,y,z,t).$$ (3.7)

Then (2.1) together with the constraint of local electro-neutrality yields the following equation for K:

$$\frac{\partial K}{\partial t}+\mathbf{\nabla }·(\mathbf{u}K)={\nabla }^2\left(\sum _{i=1}^N{D}_i\frac{c_i}{{\nu }_i}\right).$$ (3.8)

For a two ion system, equation (3.8) together with the condition of local electro-neutrality leads to the Ohmic model (Melcher & Taylor 1969; Chen et al. 2005) where the local electrical conductivity evolves as a passive scalar with an effective diffusivity D_e = 2D₊D₋/(D₊ + D₋); D₊ and D₋ denotes the diffusivities of the cation and anion. In our problem, we have more than two ionic species and the Ohmic model is not applicable. However, if we assume that the ions all have the same mobilities, ν_i = ν, and therefore, on account of the Einstein relation D_i/ν_i = k_BT, the same diffusivities, D_i = D, then the function K, rather than the conductivity, is found to evolve as a passive scalar:

$$\frac{\partial K}{\partial t}+\mathbf{\nabla }·(\mathbf{u}K)=D{\nabla }^{2}K.$$ (3.9)

We restrict ourselves to a minimal model consisting of a system of just three ions (N = 3). We will drop the index i and instead use the suffix p and n to denote the positive ion and negative ion respectively, in the background electrolyte. The absence of a suffix will indicate the sample ion. For example, c_p, c_n and c are the concentrations of positive ions, negative ions and sample ions respectively. Then from the local electro-neutrality constraint and the definition of K we have

$$c_n-c_n^{(\infty )}=\frac{z-z_p}{z_p-z_n}c+\frac{\nu z_p}{z_p-z_n}\delta K,$$ (3.10)

$$c_p+\frac{z_n}{z_p}{c}_n^{(\infty )}=-\frac{z-z_n}{z_p-z_n}c-\frac{\nu z_n}{z_p-z_n}\delta K,$$ (3.11)

where $c_n^{(\infty )}$ is the concentration of negative ions in the background electrolyte far from the sample zone. If K_∞ denotes the value of K in the far field, then the perturbation δK = K − K_∞ is advected by the flow and spreads diffusively from the injection region. Therefore (GC), after an initial transient that is small compared to the total analysis time, the sample peak, which moves by electrophoresis in addition to being advected by the flow, migrates into a region of space where δK is effectively zero. Thus, in the vicinity of the sample peak, we may assume that δK = 0, so that, the background ion concentrations c_p and c_n may be expressed as linear functions of the sample ion concentration c.

The diffusion current represented by the second term in (3.2) vanishes when D_i = D on account of local electro-neutrality, so that it reduces to Ohm’s law for a homogeneous electrolyte: J_e = −σ_e∇φ_e, where

$${\sigma }_e=\sum _{i=1}^N{z}_i^2{e}^2{\nu }_i{c}_i={\sigma }_{\infty }(1-\alpha \phi )$$ (3.12)

is the local electrolyte conductivity. The expression on the right is obtained on eliminating c_p and c_n using (3.10) and (3.11) with δK = 0. Here σ_∞ is the bulk electrolyte conductivity, $\phi =c/c_n^{(\infty )}$ is the sample concentration relative to the background and α is the parameter

$$\alpha =\frac{(z-z_n)(z-z_p)}{z_n(z_p-z_n)}$$ (3.13)

introduced in GC to characterize the nature of the nonlinearity.

3.3. The lubrication limit

The subsequent development is based on the premise of “slow axial variations” on account of the inlet to detector separation, L, being much larger than the characteristic channel width, w₀. In practice, L is of the order of tens of cm whereas w₀ ~ 10 − 100 μm. Thus, L/w₀ ~ 10³ − 10⁴. Therefore, as the sample moves down the micro-channel, the sample concentration and all other quantities controlled by this concentration vary on an axial length scale L_x ≫ w₀. To see this, suppose that the initial sample concentration was a delta function in the axial direction. Then it would spread over a distance of the order of the channel width in time ${\tau }_d\sim w_0^2/D$. The total analysis time is τ_a ~ L/v₀, where v₀ is a characteristic migration velocity. Thus, τ_a/τ_d ~ (L/w₀)Pe⁻¹ where Pe = v₀w₀/D is the Péclet number. Since typically Pe ~ 10 − 100, τ_a/τ_d ≫ 1 so that concentrations are homogenized across the channel and the fluid flow and transport problems both become quasi one dimensional a short time (~ τ_d) after sample injection.

The equation of current conservation, (3.1), may then be integrated using the boundary condition (3.4) to give

$$\mathbf{E}=\widehat{\mathbf{x}}{E}_0/(1-\alpha \overline{\phi })+\cdots ,$$ (3.14)

where E = −∇φ_e is the electric field and the neglected terms are asymptotically small in the lubrication limit. Thus, the field is predominantly in the axial direction and depends on the local sample concentration. The axial variability of the electric field affects the evolution of the sample concentration in two ways. First, it results in a variable electrophoretic migration velocity v₀/(1 − αφ̄) for the sample ions, where v₀ = zeνE₀ is the migration velocity of an isolated sample ion. Second, it results in a variable slip velocity for the electro-osmotic flow through the boundary condition (3.3).

The hydrodynamic flow field due to such a variable slip velocity may be written down using lubrication theory (Ghosal 2002c). The velocity is predominantly in the axial direction, u = ux̂ + ··· and the axial component u may be written as the sum of a mean ū and a fluctuation about the mean, Δu, due to the induced pressure gradient. The mean flow ū is a constant given by

$$\overline{u}=\underset{L\to \infty }{lim}\frac{1}{L}{\int }_0^L{u}_s(x,t)dx=u_{eo}$$ (3.15)

where u_s(x, t) is the slip velocity^† at the wall

$$u_s(x,t)=u_{eo}/(1-\alpha \overline{\phi })+\cdots ,$$ (3.16)

and,

$$\mathrm{\Delta }u\equiv u-\overline{u}=(u_s-u_{eo})\left(1-\frac{u_p}{{\overline{u}}_p}\right)=\frac{\alpha \overline{\phi }{u}_{eo}}{1-\alpha \overline{\phi }}\left(1-\frac{u_p}{{\overline{u}}_p}\right)+\cdots$$ (3.17)

to leading order in the lubrication approximation. Here u_p is a function that depends solely on the cross-sectional shape and represents the flow profile due to a unit pressure gradient. It is defined by the solution of the equation

$$\frac{{\partial }^2{u}_p}{\partial y^2}+\frac{{\partial }^2{u}_p}{\partial z^2}=-1$$ (3.18)

with the boundary condition

$$u_p(y,z)=0\text{if}(x,y,z)\epsilon S_w.$$ (3.19)

The function u_p admits analytical representation for several cross-sectional shapes.

3.4. Taylor-Aris limit and macrotransport

The time evolution of the concentration field of an advected scalar in the limit τ_a/τ_d ≫ 1 was first described by Taylor and Aris (Taylor 1953; Aris 1956) and later applied to a wide variety of problems involving shear induced dispersion (Brenner & Edwards 1993) including dispersion problems in CE (Ghosal 2006). In this limit, lateral inhomogeneities in the scalar concentration are small c(x, y, z, t) = c̄(x, t)+···, so that the cross-sectionally averaged concentration c̄ is advected by the mean flow ū and undergoes axial diffusion with an effective diffusivity (Datta & Ghosal 2008)

$$D_e=D-\frac{\overline{Gu}}{D}$$ (3.20)

where G satisfies

$$\frac{{\partial }^{2}G}{\partial y^2}+\frac{{\partial }^{2}G}{\partial z^2}=\mathrm{\Delta }u=u-\overline{u}$$ (3.21)

and the conditions

$$\mathbf{\nabla }G·\widehat{\mathbf{n}}=0\text{if}(x,y,z)\epsilon S_w.$$ (3.22)

To remove the indeterminacy of G up to a constant, we further impose the condition Ḡ = 0. Furthermore, the sample ions are advected with a concentration dependent velocity v₀/(1 − αφ̄). Thus, the equation satisfied by φ̄ is

$$\frac{\partial \overline{\phi }}{\partial t}+\frac{\partial }{\partial x}\left[\left(u_{eo}+\frac{v_0}{1-\alpha \overline{\phi }}\right)\overline{\phi }\right]=\frac{\partial }{\partial x}\left[\left\{D+\frac{{ku}_{eo}^2{w}_0^2}{D}{\left(\frac{\alpha \overline{\phi }}{1-\alpha \overline{\phi }}\right)}^2\right\}\frac{\partial \overline{\phi }}{\partial x}\right]$$ (3.23)

where k is a numerical constant depending solely on the cross-sectional shape and w₀ is a characteristic channel width. The expression for the effective diffusivity D_e appearing on the right hand side of (3.23) follows on evaluating (3.20) using (3.17). In particular, for a planar channel of half-width w₀, a simple calculation shows that $u_p=(w_0^2-y^2)/2$, which leads to k = 2/105. Equation (3.23) is the generalization of the evolution equation derived in GC to the situation where the channel has a non-zero electro-osmotic slip velocity. An alternative derivation of (3.23) using the method of multiple scales is sketched in the Appendix.

If |α|φ̄ ≪ 1, the nonlinear terms in (3.23) may be expanded in Taylor series: (1 − αφ̄)⁻¹ = 1 + αφ̄ + α²φ̄² + ···, so that, in place of Burgers’ equation arrived at in GC we get the following equation

$$\frac{\partial \overline{\phi }}{\partial t}+(v_0+u_{eo}+2\alpha v_0\overline{\phi }+3{\alpha }^2{v}_0{\overline{\phi }}^2)\frac{\partial \overline{\phi }}{\partial x}=\frac{\partial }{\partial x}\left\{\left(D+\frac{k{\alpha }^2{u}_{eo}^2{w}_0^2}{D}{\overline{\phi }}^2\right)\frac{\partial \overline{\phi }}{\partial x}\right\}$$ (3.24)

which shows an amplitude dependent contribution to the diffusivity in addition to a correction to the term 2αv₀φ̄(∂φ̄/∂x) representing nonlinear wave steepening. Equation (3.23), or, its weakly nonlinear version (3.24), is our principal result.

Equation (3.23) has a singularity at φ̄ = 1/α when α is positive. However, (3.23) ceases to be valid even before this singularity is reached (GC), because, the requirement that c_p and c_n must be non-negative, imposes the constraint φ < φ_c where φ_c = (z_p − z_n)/(z_p − z) when z < 0 and φ_c = −[z_n(z_p − z_n)/[z_p(z − z_n)] when z > 0. If α > 0, then it may be shown that φ_c < 1/α. The physical reason for the breakdown of (3.23) when φ > φ_c is the following: under those conditions the conductivity in the sample zone is so high as to reduce the electric field to very small values. Then the electrophoretic motion of the sample ions become very small and there is little relative motion between the sample peak and δK. Thus, the assumption that δK may be set to zero in the sample zone can no longer be employed and (3.23) is no longer valid. However, after sufficient time has passed and axial diffusion has caused the peak value of φ̄ to fall below φ_c, the time evolution once again proceeds in accordance with (3.23). Numerical simulations of the full electrohydrodynamic equations described in § 3.1 confirm this behavior (Chen & Ghosal, unpublished). For the purpose of numerical integration, (3.24) is a little more convenient than (3.23) since it does not exhibit the singularity at φ̄ = 1/α. Nevertheless, even though solutions to (3.24) may be formally calculated even for φ > φ̄_c, the solution in this regime is devoid of physical significance, and indeed, will yield negative concentrations of background electrolytes in parts of the domain if (3.10) and (3.11) with δK = 0 are employed to calculate the concentrations of the background ions.

4. Dispersion

Equation (3.23) or (3.24) provide a compact description of electromigration dispersion that is helpful for gaining a qualitative understanding of the underlying mechanisms. Furthermore, it is much more amenable to numerical integration than the full three dimensional coupled problem involving fluid flow and transport. By way of example, in this section, we use numerical integration to illustrate a point that at first sight may appear counter-intuitive, but, is clarified by an analysis of (3.23).

Since the presence of a zeta-potential results in cross-channel variations in the flow velocity due to induced pressure gradients, one would expect the efficiency of separation to be adversely affected. However, in certain ranges of parameters the reverse may actually be true. To understand this, one needs to examine the roles of the different terms in (3.24). The nonlinear term on the left hand side causes wave steepening leading to the formation of shock like structures. This is the dominant mechanism that contributes to electromigration dispersion (GC). Taylor dispersion can actually mitigate this tendency by increasing the effective axial diffusivity that serves to diffuse the electrokinetic shock. However, on the other hand, if the Taylor dispersion is too large, its contribution to the axial dispersion dominates with a consequent loss of separation efficiency. Thus, there is an intermediate value of the wall zeta potential that corresponds to the lowest peak dispersion.

Equation (3.23) was integrated numerically using a finite volume method that allows for adaptive grid refinement and variable time steps^†. The geometry chosen was that of a planar channel of width 2w₀. A “moving window” that is advected with the mean migration velocity v₀ + u_eo was used to optimize the number of grid points needed. The size of the window was chosen large enough that φ̄ can be set to zero at the domain boundaries with negligible loss in accuracy. The initial concentration profile φ̄(x, 0) was chosen as a Gaussian of standard deviation w₀ centered on x = 0 and with different peak strengths. The “sample loading” is characterized (GC) by a Péclet number P = v₀Γ/D based on the length scale

$$\mathrm{\Gamma }\equiv {\int }_{-\infty }^{+\infty }\overline{\phi }dx,$$ (4.1)

which is an integral of motion. A second Péclet number that characterizes the diffusion, Pe = v₀w₀/D is held fixed at the value 200. The parameter α was set to 0.5. These conditions are fairly typical for laboratory experiments.

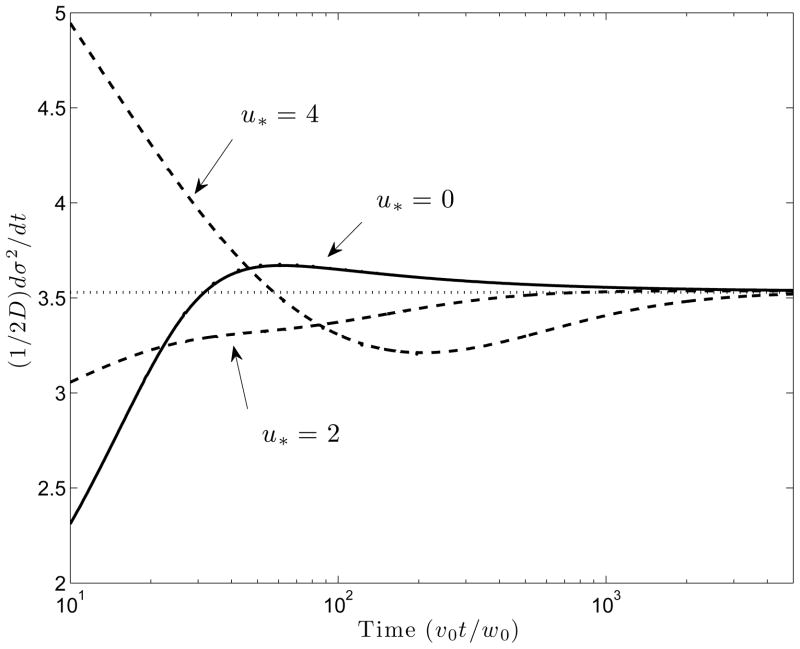
Figure 2 shows the evolution of the quantity D_t = (2D)⁻¹dσ²/dt, where σ² is the variance of φ̄(x, t), as a function of the dimensionless time v₀t/w₀. At late times, when φ̄ is sufficiently small, (3.23) may be replaced by (3.24). At even larger times, the quadratic terms in φ̄ become vanishingly small, so that, the equation describing the evolution of φ̄ essentially reduces to Burgers’ equation as discussed in GC with the minor difference that the constant part of the advection velocity is v₀ + u_eo and not v₀. Therefore, one would expect that D_t, which is like an “instantaneous” diffusivity, should asymptote to the value given by equation (35) in GC. Figure 2 shows that indeed, this is the case for all values of the flow strength, u_* = u_eo/v₀. However, the evolution of D_t to the common asymptotic value follows different trajectories depending on the strength of the electro-osmotic flow. For larger values of u_*, D_t is initially relatively large because of the contribution of the quadratic (and higher order) terms in φ̄ to the effective diffusivity in (3.23). This is because of Taylor dispersion. At intermediate times, D_t is lower than the asymptotic value predicted by equation (35) in GC, a consequence of the fact that a larger effective axial diffusivity delays the formation of shock like structures that result from nonlinear wave steepening. The total variance^† is the initial variance ( $w_0^2$) plus the area under the curve D_t from t = 0 to some time t = t_f when the peak arrives at a detector located at x = L.

Figure 2.

Time evolution of the normalized rate of increase of variance for three different values of the dimensionless electro-osmotic flow strength u_* = u_eo/v₀. Horizontal dotted line is the effective diffusivity predicted by equation (35) in GC.

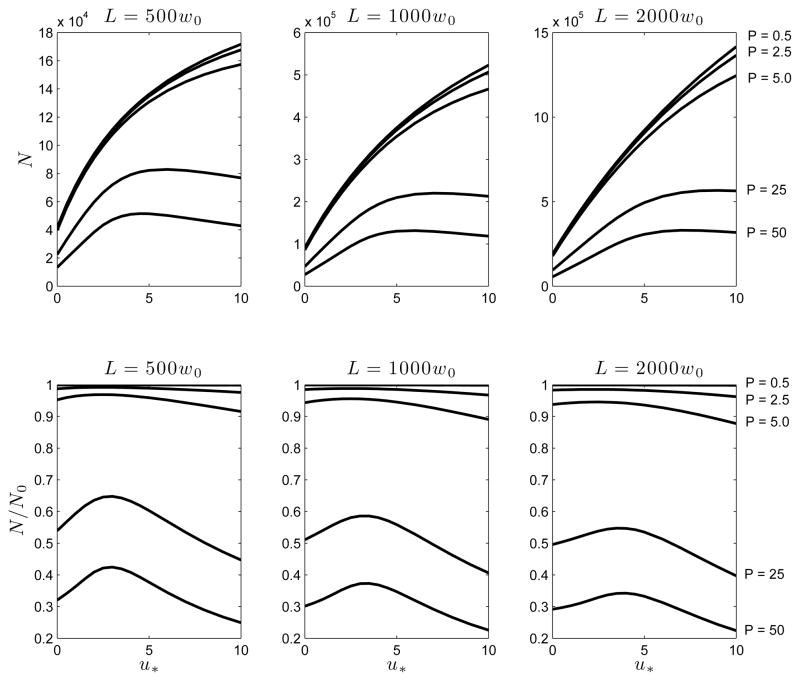
The efficiency of separation in CE is often characterized by the “number of theoretical plates” N = L²/σ² which is a dimensionless measure of the peak width. In the top panel of Figure 3, we plot N as a function of u_* for a number of downstream detector positions and for sample loading ranging from P = 0.5 (weak) to P = 50 (strong). It is clear that increasing P reduces N due to electromigration dispersion. However, the dependance on u_* is non-monotonic with N increasing at first with u_* but then decreasing or leveling off to a plateau depending on the location of the detector. Increasing the electro-osmotic flow u_eo generally increases N due to an obvious and quite trivial reason. If the detector position is fixed, the peak reaches it faster for higher electro-osmotic flow speeds and the accumulated variance is less simply because the peak has evolved for a shorter time period. In fact, in the absence of the nonlinearities induced by electromigration dispersion, ${\sigma }^2\equiv {\sigma }_0^2=w_0^2+2{Dt}_f=w_0^2+2DL/(u_{eo}+v_0)$. In this ideal limit $N\equiv N_0=L^2/{\sigma }_0^2$. In order to eliminate this obvious effect that electro-osmotic flow has on peak dispersion, we plot N/N₀ as a function of u_* in the lower panel of Figure 3, which clearly shows, that the degradation of separation efficiency by electromigration dispersion is minimized at an intermediate value of the electro-osmotic flow u_*. The dependence of N on L at different values of P is shown in Figure 4 of the Supplementary Material included in the online version.

Figure 3.

The number of theoretical plates N = L²/σ² as a function of dimensionless electro-osmotic velocity u_* = u_eo/v₀ for three different detector to injection point distances (L) and a range of sample loading characterized by the Péclet number P = v₀Γ/D. Here N₀ is the “ideal” value of N in the absence of electromigration dispersion.

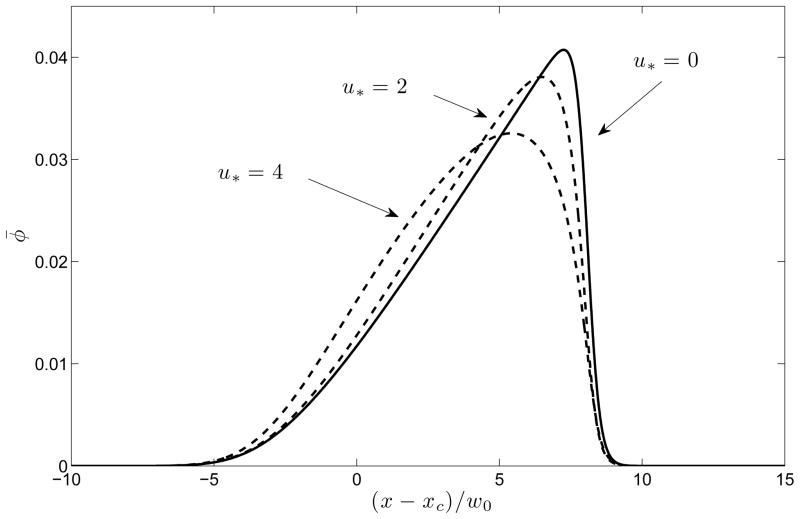
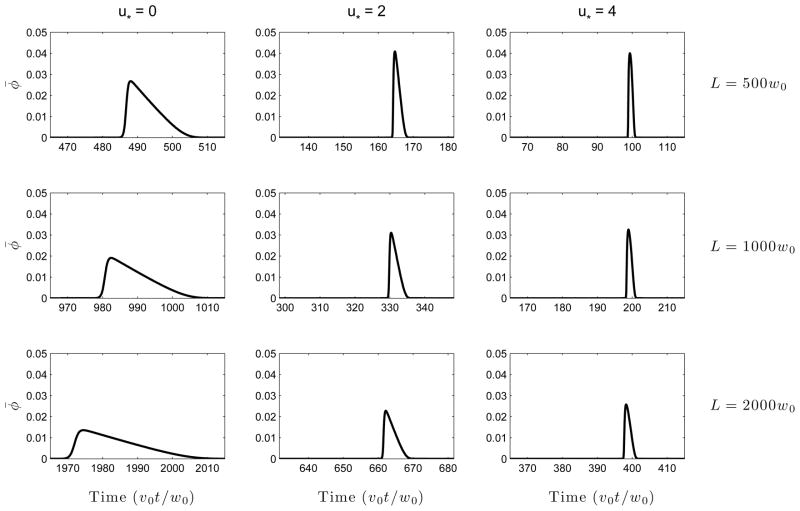
The mechanism of this reduction in total variance when u_* is sufficiently small is evident from Figure 4 depicting peak shapes at a fixed time v₀t/w₀ = 200 for a number of values of u_*. It is seen that the increase in the effective axial diffusivity due to Taylor dispersion “softens” the electrokinetic shock that results from nonlinear wave steepening due to electromigration. Thus, electro-osmotic flow has three competing effects (a) reduction in the time available for diffusion (b) reduction in the nonlinear wave steepening on account of enhanced effective diffusivity (c) increase in axial diffusion due to the Taylor-Aris effect. The total dispersion is determined by the relative contribution of each of (a), (b) and (c). At low values of u_*, (a) and (b) dominate, but at higher values, (c) is more important. In laboratory systems, u_* could have either sign and a magnitude that could vary between zero (e.g. in a coated capillary where electro-osmosis is suppressed) to some number of order unity, since the electro-osmotic velocity is similar in magnitude to the electrophoretic velocity. Figure 5 provides an alternate viewpoint that has a closer correspondence with experiments: the signal intensity φ̄(L, t) is plotted as a function of the time of arrival at a fixed detector position at distance L from the injection point. It is seen that introduction of an electro-osmotic flow at first results in a significant reduction in peak width, but with diminishing returns as the flow strength is increased. A similar plot is shown as Figure 6 in the Supplementary Material except there φ̄(x, t) is plotted as a function of x at fixed times.

Figure 4.

Concentration profiles φ̄(x, t) at a fixed instant of time (v₀t/w₀ = 200) for several values of the electro-osmotic flow strength, u_* = u_eo/v₀. The increased effective axial diffusivity due to Taylor dispersion “softens” the electromigration shock that tends to form at the leading edge. Here P = 50 and x = x_c is the location of the centroid of the peak.

Figure 5.

Concentration φ̄(L, t) as a function of time of arrival (t) at a fixed detector location (x = L) for several values of electro-osmotic flow strength, u_* = u_eo/v₀. It is seen that though electro-osmotic flow improves the resolution, the degree of improvement “saturates” as the flow rate is increased, as one might expect from Figure 3. Here P = 50.

5. Conclusions

In conclusion, we would like to make a few remarks about the relevance of the analysis presented here to laboratory practice. The model studied here is clearly oversimplified and (3.23) cannot be expected to predict in detail the peak shapes in a real laboratory experiment. In particular, real electrophoresis buffers contain many more than three ions including one or more weak acids or bases that are added to maintain a stable pH. Nevertheless, it is important to understand the qualitative effects predicted by the simplified model considered here, since the actual dispersion in a real laboratory experiment is likely to be due to a multiplicity of causes, of which, the mechanism discussed here would be one.

In this paper, we have described the effects of electromigration dispersion by means of a small set of dimensionless parameters: the Péclet numbers Pe = vw₀/D, P = vΓ/D, α, and, the dimensionless electro-osmotic flow speed u_* = u_eo/v₀. A rough idea of typical values of these parameters in laboratory experiments is helpful. If we take v₀ ~ 1 mm/s, w₀ ~ 10μm, D ~ 10⁻⁵ cm²/s as fairly typical, we have Pe ~ 10. For large molecules, D could be an order of magnitude smaller, so that Pe could be in the hundreds. If the sample concentration is of the same order as the background electrolyte concentration and the peak width is of the order of the channel width, then Γ ~ w₀. However, such sample concentrations would be considered extremely high in CE and would show very strong peak distortion. We may therefore take this as an upper limit for Γ. Thus, P could range from essentially zero (the linear regime) to P = vΓ/D ~ vw₀/D = Pe. Since electrophoresis and electro-osmosis are generally of comparable magnitudes, u_eo ~ v. Thus, u_* ~ 1, though u_* could be close to zero if the channel walls have a low zeta potential (as in a coated capillary). The magnitude of the parameter α is of order unity if the sample valence and the valence of the background electrolytes are similar. However, for macro-ions |z| ~ 10 or larger. For such large value of z, α ~ z² could be in the hundreds, and, nonlinear effects of the kind considered in this paper would be very pronounced.

Electro-osmotic flow is generally desirable in the context of CE as it shortens the transit time from inlet to detector and as a consequence also reduces the peak variance. The effect of electro-osmotic flow on separation efficiency is however complicated in the presence of electromigration dispersion since a number of competing effects are simultaneously present. This paper generalizes the analysis presented in an earlier paper (GC) where the effect of electromigration dispersion in the absence of any bulk flow was considered. However, capillary electrophoresis channels are usually made of fused silica which has a large negative zeta potential and sustains strong electro-osmotic flow. Thus, the theory presented here broadens the scope of the earlier paper making it more relevant to practical systems.

In summary, a homogenized equation for the cross-sectionally averaged concentration of sample ions was derived by exploiting the approximations outlined in § 3, which are: (a) the Debye length is much smaller than the typical channel width (b) the electrolyte contains only three ionic species of equal diffusivity which are also strong electrolytes (c) the time between injection and detection is much longer than characteristic transport times across the capillary. The outcome of the analysis is the replacement of the molecular diffusion coefficient in the one dimensional transport equation derived in GC by an effective axial diffusivity which is a nonlinear function of the concentration. If the concentration is not too high, this effective diffusivity is a quadratic function of the concentration.

The reduced one-dimensional equation (3.23) provides a compact description of electromigration dispersion that is much more amenable to numerical integration than the full coupled three dimensional problem involving fluid flow and transport in the capillary. In fact, since both the length to width aspect ratio of the capillary as well as the Péclet number (Pe) are usually large in experiments, such three dimensional simulations can be computationally intensive. The loss of accuracy in replacing the full equations by the one dimensional model is minimal because the requirements for its validity are well satisfied and the asymptotic convergence of the thin Debye layer and long length scale approximations have been shown to be rapid (Ghosal 2006; Datta & Ghosal 2009, 2008).

The effect of a wall zeta potential may be explained qualitatively in the following way: alteration of the ionic composition of the solute in the sample zone results in a change of the electrical conductivity and therefore in the axial electric field. Thus, the electro-osmotic slip velocity now has an axial variation which induces pressure gradients along the channel. This in turn induces shear in the electro-osmotic velocity profile. The consequent shear induced (Taylor-Aris) dispersion results in a concentration dependent axial diffusivity. Numerical integration of the homogenized equation (3.23) provided some qualitative insights into the effect of this nonlinear diffusion on separation efficiency. It is seen that the total variance for a fixed detector position actually decreases with the strength of the electro-osmotic flow as long as the flow is not too strong. This is due to the fact that an increase in the effective diffusivity for axial transport counteracts the wave steepening resulting from electromigration dispersion, and, furthermore, the transit time from injection to detection is reduced. However, if the flow is much stronger, the dispersion caused by the enhanced axial diffusivity itself is dominant, and this degrades any gain in resolution due to the aforemetioned causes. Thus, if all other parameters are invariant, the peak variance is a non-monotonic function of the electro-osmotic flow strength and is optimal at a certain intermediate value of the flow velocity.

Appendix A. Derivation of (3.23) by the method of multiple scales

It is advantageous to work with dimensionless variables. This is achieved by using w₀ as the unit of length and w₀/v₀ as the unit of time. The governing equations are therefore those presented in § 2 and § 3 but with w₀ and v₀ set to one. These equations are

$${[(1-\alpha \phi )X]}_x+{[(1-\alpha \phi )Y]}_y+{[(1-\alpha \phi )Z]}_z=0$$ (A1)

$${\phi }_t+{[(u+X)\phi ]}_x+{[(v+Y)\phi ]}_y+{[(w+Z)\phi ]}_z={Pe}^{-1}[{\phi }_{xx}+{\phi }_{yy}+{\phi }_{zz}]$$ (A2)

$$-p_x+u_{xx}+u_{yy}+u_{zz}=0$$ (A3)

$$-p_y+v_{xx}+v_{yy}+v_{zz}=0$$ (A4)

$$-p_z+w_{xx}+w_{yy}+w_{zz}=0$$ (A5)

where (X, Y, Z) is the electric field vector (normalized by E₀), u = (u, v, w), φ is the normalized sample concentration, Pe = v₀w₀/D (Péclet number) and suffixes denote partial derivatives. The flow is solenoidal:

$$u_x+v_y+w_z=0$$ (A6)

and the electric field is irrotational:

$$X_y=Y_x{X}_z=Z_x{Y}_z=Z_y$$ (A7)

The boundary conditions at the wall are

$$u=u_{\ast }Xv=0w=0$$ (A8)

and

$$m{\phi }_y+n{\phi }_z=0$$ (A9)

$$mY+nZ=0$$ (A10)

where (0, m, n) is the unit normal on the wall and u_* = u_eo/v₀. At points far upstream and downstream of the sample peak

$$X\sim 1u\sim u_{\ast }v\sim 0w\sim 0\phi \sim 0.$$ (A11)

This description presumes infinitely thin Debye layers (§ 3.1) and constancy of the Kohlrausch function in a three ion system (§ 3.2).

We now assume that all axial variations happen on a slow spatial scale for which we introduce the slow variable ξ = εx and the corresponding slow times τ = εt and T = ε²t, where ε is a small parameter. The physical origin of the two times is due to the existence of the time-scale w₀/v₀ which is the advective time over a channel diameter and the diffusion time-scale $w_0^2/D$ for diffusion across the channel diameter. Since the flow and fields are predominantly axial, we introduce

$$\stackrel{\sim }{Y}=Y/\epsilon \stackrel{\sim }{Z}=Z/\epsilon \stackrel{\sim }{v}=v/\epsilon \stackrel{\sim }{w}=w/\epsilon \stackrel{\sim }{p}=\epsilon p$$ (A12)

where the pressure scaling is designed to retain the pressure gradient term at leading order. Next we re-write (A 1)–(A 5) in terms of the scaled variables using the transformations ∂_t = ε∂_τ + ε²∂_T and ∂_x = ε∂_ξ and expand all dependent variables f in asymptotic series f = f⁽⁰⁾ + εf⁽¹⁾ + ε²f⁽²⁾ + ··· Equating like powers of ε on either side of the governing equations we get a series of successive problems to solve.

A.1. Zeroth Order

From (A 1) and (A 7)

$${[(1-\alpha {\phi }^{(0)})X^{(0)}]}_{\xi }+{[(1-\alpha {\phi }^{(0)}){\stackrel{\sim }{Y}}^{(0)}]}_y+{[(1-\alpha {\phi }^{(0)}){\stackrel{\sim }{Z}}^{(0)}]}_z=0,$$ (A13)

$$X_y^{(0)}=X_z^{(0)}=0.$$ (A14)

Thus, X⁽⁰⁾ is independent of y and z. Integrating (A 13) over the channel cross-section and using the boundary condition (A 10) we get

$${[(1-\alpha {\overline{\phi }}^{(0)})X^{(0)}]}_{\xi }=0,$$ (A15)

and thus, on account of the far field conditions (A 11)

$$X^{(0)}=1/(1-\alpha {\overline{\phi }}^{(0)}).$$ (A16)

Equation (A 2) gives at lowest order

$${\phi }_{yy}^{(0)}+{\phi }_{zz}^{(0)}=0,$$ (A17)

which, with the Neuman boundary condition (A 9) implies that φ ⁽⁰⁾ is independent of y and z, thus,

$${\phi }^{(0)}={\overline{\phi }}^{(0)}(\xi ,\tau ,T).$$ (A18)

Finally, the flow equations (A 3)–(A 5) give

$$-{\stackrel{\sim }{p}}_{\xi }^{(0)}+u_{yy}^{(0)}+u_{zz}^{(0)}=0,$$ (A19)

$$-{\stackrel{\sim }{p}}_y^{(0)}=-{\stackrel{\sim }{p}}_z^{(0)}=0.$$ (A20)

Thus, p̃⁽⁰⁾ is independent of y and z. Now (A 19) with boundary condition derived from (A 8) may be readily integrated,

$$u^{(0)}=-{\stackrel{\sim }{p}}_{\xi }^{(0)}{u}_p+u_{\ast }{X}^{(0)}=-{\stackrel{\sim }{p}}_{\xi }^{(0)}{u}_p+u_{\ast }/(1-\alpha {\overline{\phi }}^{(0)}).$$ (A21)

where u_p is the solution of (u_p)_yy + (u_p)_zz = −1 that vanishes at the wall. To determine the unknown function p̃⁽⁰⁾ we use (A 6). Integrating over the cross-section and using (A 8) we get

$${\overline{u}}^{(0)}=-{\stackrel{\sim }{p}}_{\xi }^{(0)}{\overline{u}}_p+u_{\ast }/(1-\alpha {\overline{\phi }}^{(0)})=u_{\ast },$$ (A22)

which determines ${\stackrel{\sim }{p}}_{\xi }^{(0)}$. Substituting this in (A 21) we obtain the axial flow velocity which is identical to the lubrication theory solution (Ghosal 2002c) applied to the case of an axially varying slip velocity u_*/(1 − αφ̄⁽⁰⁾) along the channel wall:

$$u^{(0)}=\frac{u_{\ast }}{1-\alpha {\overline{\phi }}^{(0)}}\left[1-\frac{\alpha {\overline{\phi }}^{(0)}}{{\overline{u}}_p}{u}_p(y,z)\right].$$ (A23)

Since φ ⁽⁰⁾ = φ̄⁽⁰⁾, (A 7) and (A 13) show that the two dimensional vector (Ỹ⁽⁰⁾, Z̃⁽⁰⁾) is both solenoidal and irrotational in the y – z plane, and, on account of the zero flux condition, must within the domain. Therefore,

$${\stackrel{\sim }{Y}}^{(0)}={\stackrel{\sim }{Z}}^{(0)}=0.$$ (A24)

A.2. First Order

From (A 2)

$${Pe}^{-1}[{\phi }_{yy}^{(1)}+{\phi }_{zz}^{(1)}]={\phi }_{\tau }^{(0)}+{[(u^{(0)}+X^{(0)}){\phi }^{(0)}]}_{\xi }+{[({\stackrel{\sim }{v}}^{(0)}+{\stackrel{\sim }{Y}}^{(0)}){\phi }^{(0)}]}_y+{[({\stackrel{\sim }{w}}^{(0)}+{\stackrel{\sim }{Z}}^{(0)}){\phi }^{(0)}]}_z.$$ (A25)

Integrating (A 25) over the cross-section of the capillary and using the boundary conditions (A 8) and (A 10) we get a solvability condition for (A 25)

$${\overline{\phi }}_{\tau }^{(0)}+[{(\overline{u^{(0)}+X^{(0)}){\phi }^{(0)}}]}_{\xi }=0$$ (A26)

which reduces to

$${\overline{\phi }}_{\tau }^{(0)}+{[\{u_{\ast }+{(1-\alpha {\overline{\phi }}^{(0)})}^{-1}\}{\overline{\phi }}^{(0)}]}_{\xi }=0$$ (A27)

on using (A 16) and (A 23). On using the solvability equation (A 27) in (A 25) we get

$${Pe}^{-1}[{\phi }_{yy}^{(1)}+{\phi }_{zz}^{(1)}]={[(u^{(0)}+X^{(0)}-{\overline{u}}^{(0)}-{\overline{X}}^{(0)}){\overline{\phi }}^{(0)}]}_{\xi }-u_{\xi }^{(0)}{\overline{\phi }}^{(0)}$$ (A28)

where we have used the continuity equation (A 6) to replace ${\stackrel{\sim }{v}}_y^{(0)}+{\stackrel{\sim }{w}}_z^{(0)}$ with $-u_{\xi }^{(0)}$. Equation (A 28) is readily integrated. If the constant of integration is expressed in terms of φ̄⁽¹⁾ we get

$${\phi }^{(1)}={\overline{\phi }}^{(1)}-\alpha Pe{u}_{\ast }G{\overline{\phi }}^{(0)}{\overline{\phi }}_{\xi }^{(0)}/[{\overline{u}}_p(1-\alpha {\overline{\phi }}^{(0)})]$$ (A29)

where G is defined by the equation G_yy + G_zz = u_p − ū_p with the condition that G has zero flux at the walls and is normalized so that Ḡ = 0. From (A 1)

$${[(1-\alpha {\phi }^{(0)}){\stackrel{\sim }{Y}}^{(1)}]}_y+{[(1-\alpha {\phi }^{(0)}){\stackrel{\sim }{Z}}^{(1)}]}_z=\alpha {[{\phi }^{(1)}{X}^{(0)}]}_{\xi }-{[(1-\alpha {\phi }^{(0)})X^{(1)}]}_{\xi }$$ (A30)

where we have used (A 24). Integrating over the cross-section and using the boundary condition gives the solvability condition

$$\alpha {[{\overline{\phi }}^{(1)}{\overline{X}}^{(0)}]}_{\xi }-{[(1-\alpha {\overline{\phi }}^{(0)}){\overline{X}}^{(1)}]}_{\xi }=0,$$ (A31)

which may be integrated with the far field boundary conditions to give

$${\overline{X}}^{(1)}=\frac{\alpha {\overline{\phi }}^{(1)}}{{(1-\alpha {\overline{\phi }}^{(0)})}^2}$$ (A32)

A.3. Second Order

From (A 2)

$$\begin{array}{l}{Pe}^{-1}[{\phi }_{yy}^{(2)}+{\phi }_{zz}^{(2)}]-{[({\stackrel{\sim }{v}}^{(0)}+{\stackrel{\sim }{Y}}^{(0)}){\phi }^{(1)}]}_y-{[({\stackrel{\sim }{v}}^{(1)}+{\stackrel{\sim }{Y}}^{(1)}){\phi }^{(0)}]}_y\\ -{[({\stackrel{\sim }{w}}^{(0)}+{\stackrel{\sim }{Z}}^{(0)}){\phi }^{(1)}]}_z-{[({\stackrel{\sim }{w}}^{(1)}+{\stackrel{\sim }{Z}}^{(1)}){\phi }^{(0)}]}_z=-{Pe}^{-1}{\phi }_{\xi \xi }^{(0)}\\ +{\phi }_{\tau }^{(1)}+{\phi }_T^{(0)}+{[(u^{(0)}+X^{(0)}){\phi }^{(1)}]}_{\xi }+{[(u^{(1)}+X^{(1)}){\phi }^{(0)}]}_{\xi }\end{array}$$ (A33)

Integrating over the cross-section and using the boundary conditions we derive

$${\overline{\phi }}_{\tau }^{(1)}+{\overline{\phi }}_T^{(0)}+{[\overline{u^{(0)}{\phi }^{(1)}}+\overline{X^{(0)}{\phi }^{(1)}}+\overline{X^{(1)}{\phi }^{(0)}}]}_{\xi }={Pe}^{-1}{\overline{\phi }}_{\xi \xi }^{(0)}.$$ (A34)

A.4. Reconstitution

On combining (A 34) with (A 27) after substituting for the lower order terms from (A 16), (A 23) and (A 32) we get

$$\epsilon {\overline{\phi }}_{\tau }^{(0)}+{\epsilon }^2{\overline{\phi }}_{\tau }^{(1)}+{\epsilon }^2{\overline{\phi }}_T^{(0)}+\epsilon {[\left(u_{\ast }+\frac{1}{(1-\alpha {\overline{\phi }}^{(0)})}\right){\overline{\phi }}^{(0)}+\epsilon {\alpha }^2\mathit{kPe}{u}_{\ast }^2\frac{{({\overline{\phi }}^{(0)})}^2{\overline{\phi }}_{\xi }^{(0)}}{{(1-\alpha {\overline{\phi }}^{(0)})}^2}+\epsilon u_{\ast }{\overline{\phi }}^{(1)}+\epsilon \frac{{\overline{\phi }}^{(1)}}{1-\alpha {\overline{\phi }}^{(0)}}+\epsilon \alpha \frac{{\overline{\phi }}^{(0)}{\phi }^{(1)}}{{(1-\alpha {\overline{\phi }}^{(0)})}^2}]}_{\xi }-{\epsilon }^2{Pe}^{-1}{\overline{\phi }}_{\xi \xi }^{(0)}=0,$$ (A35)

which may be put in an alternate form that is asymptotically equivalent to it for all terms up to order ε²:

$${\overline{\phi }}_t+{\left[\left(u_{\ast }+\frac{1}{1-\alpha \overline{\phi }}\right)\overline{\phi }-{\alpha }^2\mathit{kPe}{u}_{\ast }^2\frac{{\overline{\phi }}^2{\overline{\phi }}_x}{{(1-\alpha \overline{\phi })}^2}\right]}_x-{Pe}^{-1}{\overline{\phi }}_{xx}+O({\epsilon }^3)=0.$$ (A36)

Here $k=-\overline{{Gu}_p}/{\overline{u}}_p^2$ is a constant that depends solely on the geometry of the channel cross-section. On transforming back to dimensional variables (3.23) follows.