Abstract
The rate of consumption of dithiothreitol (DTT) is increasingly used to measure the oxidative potential of particulate matter (PM), which has been linked to the adverse health effects of PM. While several quinones are known to be very reactive in the DTT assay, it is unclear what other chemical species might contribute to the loss of DTT in PM extracts. To address this question, we quantify the rate of DTT loss from individual redox-active species that are common in ambient particulate matter. While most past research has indicated that the DTT assay is not sensitive to metals, our results show that seven out of the ten transition metals tested do oxidize DTT, as do three out of the five quinones tested. While metals are less efficient at oxidizing DTT compared to the most reactive quinones, concentrations of soluble transition metals in fine particulate matter are generally much higher than those of quinones. The net result is that metals appear to dominate the DTT response for typical ambient PM2.5 samples. Based on particulate concentrations of quinones and soluble metals from the literature, and our measured DTT responses for these species, we estimate that for typical PM2.5 samples approximately 80 % of DTT loss is from transition metals (especially copper and manganese), while quinones account for approximately 20 %. We find a similar result for DTT loss measured in a small set of PM2.5 samples from the San Joaquin Valley of California. Because of the important contribution from metals, we also tested how the DTT assay is affected by EDTA, a chelator that is sometimes used in the assay. EDTA significantly suppresses the response from both metals and quinones; we therefore recommend that EDTA should not be included in the DTT assay.
1 Introduction
Dithiothreitol (DTT, HSCH2(CH(OH))2CH2SH) is commonly used as a cell-free measure of the oxidative potential of particles (e.g., Cho et al., 2005; Shima et al., 2006; Sauvain et al., 2008; Li et al., 2009a; McWhinney et al., 2011; Verma et al., 2011). In this assay, redox-active chemicals in particulate matter (PM) oxidize added DTT to its disulfide form and the linear rate of DTT loss is used as a measure of the oxidative capacity of the PM. Redox-active species in PM then donate an electron to dissolved molecular oxygen, forming superoxide (Kumagai et al., 2002), which can form other reactive oxygen species (ROS) such as hydrogen peroxide (HOOH) and, in the presence of metals, hydroxyl radical (OH). All three ROS species have been measured from the oxidation of DTT (Kumagai et al., 2002; Park et al., 2005; Chung et al., 2006; Wang et al., 2010). While the DTT assay provides a quantitative measure of oxidation, it does not measure the production of specific ROS, which is significant since the different ROS have very different reactivities.
Though the DTT assay is widely used, there is little information on the particulate species that oxidize DTT. The particulate species responsible for DTT oxidation are typically examined by correlating DTT activity with PM composition. These analyses most often identify carbonaceous species, i.e., elemental carbon, water soluble organic carbon and/or polycyclic aromatic hydrocarbons (PAHs), as most strongly correlated with DTT loss (Li et al., 2003; Cho et al., 2005; Ntziachristos et al., 2007; Hu et al., 2008; Verma et al., 2009b). However, correlations do not show causation, especially since particulate species are often highly covariate. For example, PAHs levels often strongly correlate with DTT loss from particles, but PAHs are not redox active. It is thought that their correlation with DTT loss is due to a correlation between PAHs and quinones (Cho et al., 2005), some of which can oxidize DTT. For example, phenanthrenequinone (PQN) and 1,4-naphthoquinone (1,4-NQN) oxidize DTT, while 1,4-benzoquinone (1,4-BQN) does not (Kumagai et al., 2002; Li et al., 2009a).
Metals, on the other hand, are generally not thought to be active in the DTT assay, although particulate metals can cause oxidative damage both in vitro and in vivo (Leonard et al., 2004; Ghio et al., 2012). In the original application of the DTT assay to atmospheric particles, the addition of a low concentration (50 nM) of iron (Fe) or copper (Cu) to an unspecified concentration of PQN did not increase the rate of DTT oxidation, leading to the conclusion that the DTT assay is insensitive to metals (Cho et al., 2005). Some later studies found correlations between DTT loss and the metal content of ambient PM, but these relationships were attributed to covariance between metals and carbonaceous redox-active organic species, which were thought to be responsible for DTT oxidation (Ntziachristos et al., 2007; Hu et al., 2008). Recent studies have found that heating diesel or ambient ultrafine particles reduces their DTT response by 40 to 100 percent, but does not change their soluble metal content, indicating that semi-volatile organics dominate the DTT response for these particle types, which are likely enriched in organics (Biswas et al., 2009; Verma et al., 2011). Very recently, Lin and Yu (2011) found DTT loss in laboratory solutions of Cu(II) and Zn(II), but not from Fe. While most of the current literature indicates that DTT assay responds strongly to certain organic species, other measures of oxidative potential from ambient PM indicate that metals are most important for ROS production. For example, specific measurements of HOOH and OH production from ambient PM largely attribute ROS production to the metal content of PM, especially iron and copper (DiStefano et al., 2009; Vidrio et al., 2009; Wang et al., 2010; Shen and Anastasio, 2011; Shen et al., 2011; Shen and Anastasio, 2012). In addition, the depletion of ascorbate and glutathione by PM in acellular assays has also been linked to metals, especially copper (Ayres et al., 2008). These results suggest there is a fundamental difference between the DTT assay and other measurements of the oxidative potential of PM, although the assays should be measuring similar properties of PM.
Our goal in this work is to better understand the chemical species in ambient PM that oxidize DTT, with a focus on the possible roles of metals. Towards this end, we measure DTT oxidation rates from PAHs, quinones and metals at a range of environmentally relevant concentrations. We then use these results to quantify the contributions of metals and quinones to the DTT response, both for a hypothetical, typical particle composition as well as for six ambient PM2.5 samples from the San Joaquin Valley of California.
2 Methods
2.1 Chemicals
9,10-phenanthrenequinone (99 %), 1,2-naphthoquinone (97 %), 1,4-naphthoquinone (97 %), 1,4-benzoquinone (98 %), acenaphthenequinone (ACS), pyrene (98 %), fluoranthene (99 %), phenanthrene (98 %), and iron(III) chloride (ACS) were from Sigma-Aldrich. Copper(II) sulfate (98 %), cobalt(II) chloride (analytical grade), vanadium(V) oxide (99.999 %), chromium(III) potassium sulfate (ACS), 10 % trichloroacetic acid, sodium phosphate (NaH2PO4, ACS), potassium phosphate (KHPO4, HPLC grade), Tris base (Mol Bio grade), acetonitrile (HPLC grade), and disodium EDTA (ACS) were from Fisher Scientific. Manganese(II) Chloride (ACS) was from EM Science. Nickel(II) sulfate (ACS) and cadmium(II) nitrate (99.999 %) were from Alfa Aesar. Lead(II) nitrate (analytical grade) and zinc(II) sulfate (analytical grade) were from Mallinckrodt. Dithiothreitol (99 %), vanadium(III) chloride (97 %) and iron(II) sulfate (99.5 %) were from Arcos Organics. Dithiobisnitrobenzoic acid (DTNB) was from Bio Synth and Tris-HCl (Mol Bio grade) was from Promega.
2.2 Stock solutions
Quinone and PAH stock solutions were made in acetonitrile and stored in parafilm-wrapped amber glass vials in the dark at −20 °C. Figure 1 shows the chemical structures and abbreviations of the quinones and PAHs we examined. The absorbance spectrum of each stock solution was measured periodically to check stability. All metal stock solutions were made in Milli-Q water (without adjusting pH) on the day of the experiment.
Fig. 1.
Chemical structures and abbreviations for the quinones and polycyclic aromatic hydrocarbons tested for DTT activity.
2.3 DTT assay
We followed the procedure of Cho et al. (2005) for DTT experiments, but with the additional step of treating our phosphate solutions with Chelex 100 resin to remove transition metals (see Sect. 2.4). Briefly, the loss of 100 μM of DTT in 0.10 M phosphate buffer (77.8 mM NaH2PO4 and 22.2 mM KHPO4; pH 7.4) was measured over time at 37 °C. At time zero a small volume (< 0.10 mL) of the material of interest (e.g., quinone or dissolved metal stock solution) was added to 3.0 mL of DTT/phosphate solution in an 8.0-mL amber glass vial that was shaken continuously on a shake table (setting “4”). Temperature was maintained at 37 °C using a dry bath (Fisher Scientific, M-110033) on low setting 6. At known times, a 0.50 mL aliquot of the reaction mixture was removed and added to 0.50 mL of 10 % trichloroacetic acid to stop the reaction. When all time points were quenched, 50 μL of 10.0 mM DTNB (made in 0.10 M phosphate buffer; pH 7.4) was added, mixed well, and allowed to react for 5 minutes, then 2.0 mL of 0.40 M Tris-Base (pH 8.9) with 20 mM of EDTA was added. Though the reaction of DTT and DTNB is fast, we found it important to add the DTNB before the Tris-Base to ensure the sample remains quenched (i.e., at low pH) until DTT has reacted with DTNB. The reaction of DTT and DTNB forms 2-nitro-5-thiobenzoic acid (TNB), which is stable in the final solution for at least 2 h at room temperature. TNB was quantified using a 1-cm path length quartz cell in a Shimadzu UV-2501PC UV/VIS spectrophotometer. The absorption at 412 nm was measured and TNB was quantified using a molar absorptivity of 14 150 M−1 cm−1 (Eyer et al., 2003; Li et al., 2009a).
Because both DTT and TNB are sensitive to light (Damodaran, 1985; Eyer et al., 2003), we excluded light as much as possible by working in a dark hood with the room lights off and covering the amber reaction vials with aluminum foil when not in use. Blanks and positive controls (0.050 μM PQN) were initially run in triplicate. Because positive controls proved to be very reproducible, we ran a single positive control and duplicate blank each day in later experiments, while samples were run in duplicate or triplicate.
2.4 Chelex treatment to remove trace metals
When initially using the DTT assay we found a high rate of DTT loss in the blank, which made it difficult to accurately measure rates of DTT loss in samples. To reduce this background oxidation we started treating the phosphate buffer with Chelex 100 resin (sodium form, Biorad), a cation exchange resin that removes trace metals, as described below. The high affinity of Chelex 100 for iron and copper makes it an ideal material to remove trace metals from phosphate buffer solutions (Biorad, 1991). This treatment significantly improved the reproducibility and stability of the assay. We later found that the Cho group also treats their phosphate buffer with Chelex resin (Debra Schmitz, personal communication).
New Chelex is basic and must be washed until the pH of the effluent is between 7 and 8; this can require up to 20 liters of Milli-Q water. After this, phosphate buffer was treated for transition metals by first adding 100 g of Chelex 100 Resin to approximately 150 mL of Milli-Q water to make a slurry, which was poured into a large, acid-rinsed glass chromatography column (5 cm diameter, 33 cm height) that had a permanent glass frit to contain the Chelex resin. The Chelex in the column was first washed with two column volumes of phosphate buffer, which were discarded. The remaining phosphate solution was allowed to drip through the resin at a rate of approximately one drop per second and the resulting treated phosphate buffer was collected into a clean, acid washed, Teflon (PFA) bottle. Unlike metal chelators such as EDTA, the Chelex 100 resin is not permanently added to the phosphate buffer, so it does not reduce the reactivity of metals in the DTT assay. The Chelex resin is stored at +4 °C as a phosphate buffer slurry. We find one 100 g bottle of Chelex 100 resin is effective for multiple years under these conditions, though the lifetime depends on the amount of solution treated with the Chelex resin. Removal of metals becomes less efficient as the Chelex metal binding sites are occupied, which can be identified by a systematically increasing rate of DTT loss in the blank.
2.5 Ambient particulate matter
Ambient PM2.5 was collected onto Teflon (or Teflon-coated glass fiber) filters by collaborators from one urban (Fresno) and one rural (Westside) site in the San Joaquin Valley of California between 2006 and 2009. Each sample was collected over ten days during the hours of 10:00 a.m. to 4:00 p.m. Additional information about sampling can be found in Shen et al. (2011).
Our lab has previously reported the concentrations of soluble metals, as well as the production of hydrogen peroxide (HOOH) and hydroxyl radical (OH), from these samples (Shen and Anastasio, 2011; Shen et al., 2011) and the same PM was also used for on-site rat exposures (Wilson et al., 2010). The PM2.5 samples on filters were stored at −20 °C in the dark prior to use. In our experiments, we added a filter punch with a known mass of PM2.5 (Shen et al., 2011) to the DTT vial and monitored the rate of DTT loss over time.
2.6 Data analysis and statistics
Rates of DTT loss were determined from a linear regression of four points of DTT concentration versus time, as illustrated in Fig. 2. The blank consists of 100 μM DTT with no added redox-active species; each time point shown is the average ± σ of three individual blank runs. The colored symbols in Fig. 2 show the results for triplicate sample vials, each containing 100 μM of initial DTT plus 0.050 μM of PQN. The rate of DTT loss in each replicate sample was calculated from the slope of the linear regression and then blank-corrected by subtracting the average blank rate on a given day. The average and standard deviation of the resulting blank-corrected rates of DTT loss were then calculated from the replicate measurements.
Fig. 2.
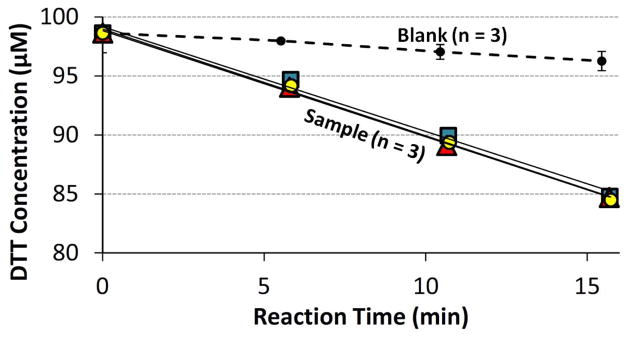
Example of raw DTT data. Each sample initially contains 100 μM of DTT with 0.050 μM of PQN, while the blank initially contains 100 μM DTT with no PQN. The rate of DTT loss for each sample vial is determined as the slope of its sample regression line (the three lines are shown, but are hard to distinguish because of their similarities) minus the daily blank slope. The blank slope is determined from the average (±1 σ) linear regression from triplicate blank vials.
In almost all cases we limited DTT loss to no more than 20 % of the initial 100 μM over the course of an experiment; in a few cases we used points with greater DTT loss if the rate of loss was linear over the entire experiment. Blanks and samples were typically run in triplicate, though sometimes in duplicate, on each day. We ran a positive control with every experiment to ensure consistency of the assay. Our positive control consisted of 0.050 μM PQN in the DTT solution, made by adding 16.1 μl of a 9.34 μM PQN stock in acetonitrile to 3.0 mL of DTT solution. This positive control is simple, inexpensive, and quite reproducible, with an average (± 1 σ ) blank-corrected rate of 0.71 ± 0.09 μM DTT min−1 (n = 74 over a period of 11 months). The blank was fairly reproducible, with an average (± 1 σ ) value of 0.24 ± 0.09 μM DTT min−1 (n = 93). Individual data points (i.e., not rates) in a DTT run were identified as outliers by constructing a 95 % confidence interval around the triplicate data point regression line using the statistical package “R”. Rates for a given sample were identified as outliers using the Student’s T-test with a two-tailed p value of 0.05.
3 Results and discussion
3.1 DTT response from individual organic species and transition metals
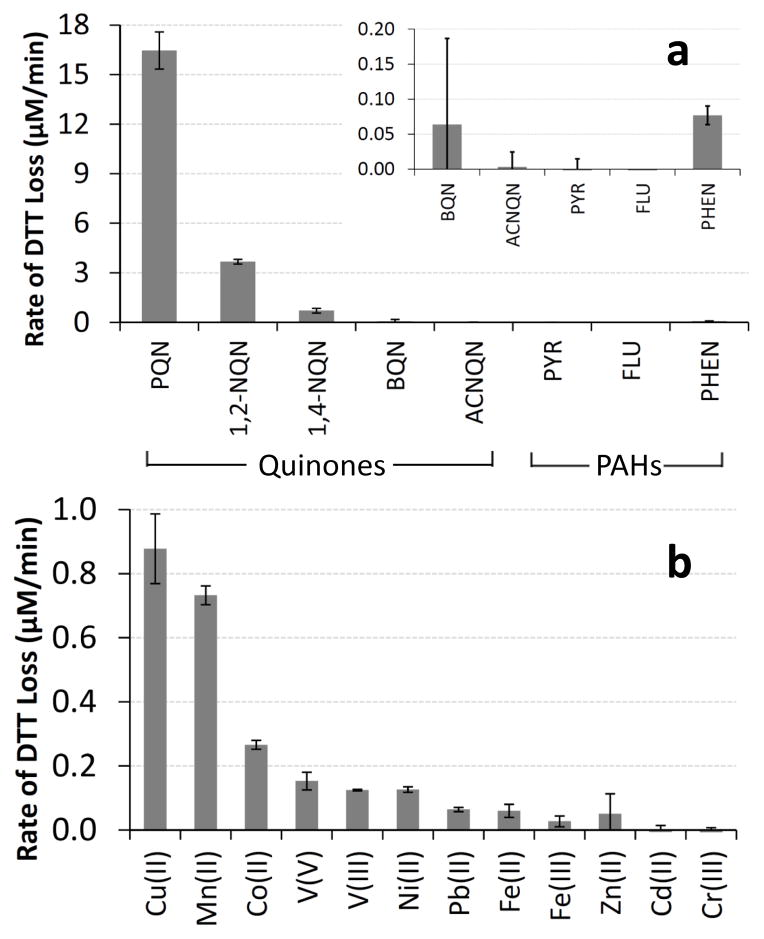
To identify species that might contribute to DTT loss in PM samples we measured the rate of DTT consumption in the presence of 18 individual quinones, PAHs, and dissolved transition metals, all of which are commonly present in ambient PM (Connell et al., 2006; Shinyashiki et al., 2009; Vidrio et al., 2009; Walgraeve et al., 2010). As shown in Fig. 3, of the five quinones tested PQN is the most reactive while 1,2-NQN and 1,4-NQN also oxidize DTT. In contrast, BQN and ACNQN (at 1.2 and 1.0 μM, respectively) do not degrade DTT. This agrees with measurements of HOOH production from 12 quinones in the presence of 100 μM DTT (Chung et al., 2006): HOOH generation occurred from PQN, 1,2-NQN, and 1,4-NQN, but not from the other 9 quinones, a set which included ACNQN but not BQN. Other researchers have also observed DTT loss from PQN and 1,4-NQN (Kumagai et al., 2002; Li et al., 2009a).
Fig. 3.
Blank-corrected rates of DTT loss from five quinones and three PAHs (a) and from 12 transition metals (b). The concentration of each species was 1 μM, except for BQN which was 0.93 μM, 1,4-NQN which was 1.21 μM and Cd(II), which was 5 μM.
Of the three PAHs we tested, PYR and FLU caused no loss of DTT, while PHEN showed a very small DTT response (Fig. 3a, inset). However, since PAHs are not redox active, they should not oxidize DTT (Cho et al., 2005). We believe that the DTT response in the PHEN solution is from a small amount of PQN contaminant, since this is an oxidation product of PHEN that could form over time in the solid (and is the most DTT-active compound we tested). Our observed response for PHEN would be explained by a contaminant level of just 0.2 % PQN in our PHEN solid. Even if PQN is not the responsible species and PHEN itself is oxidizing DTT, the reactivity is small enough that PHEN would make an insignificant contribution to DTT loss compared to other chemical components of PM, as we discuss below.
Although most published reports indicate that the DTT assay is insensitive to metals, we also tested ten soluble transition metals, as well as two different oxidation states for V and Fe (Fig. 3b). We find that seven of the metals do oxidize DTT, with Cu(II) and Mn(II) being the most reactive. The next most reactive metals (on a concentration-normalized basis) are Co(II), V(V) and V(III), Ni(II), and Pb(II). DTT oxidation by Fe(II) and Fe(III) is slow, but ambient concentrations of Fe are often high and thus soluble Fe might still be important for DTT loss. In contrast, 1.0 μM of Cr(III), Cd(II), or Zn(II) does not cause measurable DTT oxidation. Within error, in 1.0 μM metal solutions there was no statistical difference (p > 0.05) between the reactivity of the different oxidation states for vanadium (V(V) and V(III)), or for iron (Fe(II) and Fe(III)), although the latter gives different responses when compared across a wide range of metal concentrations (Sect. 3.2). Lin and Yu (2011) also found that Cu(II) caused DTT loss, but did not observe DTT loss from Fe, which is consistent with our finding of low DTT reactivity by iron. Oxidation of DTT by metals is a catalytic process, as it is for quinones (Kumagai et al., 2002). For example, in our experiments 1.0 μM of Cu(II) oxidizes 13.2 μM of DTT in 15 min. Cu(II) likely accepts an electron from DTT, forming Cu(I), which rapidly donates an electron to dissolved oxygen to form superoxide and reform Cu(II).
As we describe in the introduction, the oxidation of DTT by redox-active species forms ROS (superoxide, HOOH, and OH), which can subsequently oxidize DTT (e.g., Kumagai et al., 2002). To investigate the extent of this secondary, ROS-mediated oxidation of DTT we measured the rate of DTT loss in solutions containing 5–35 μM HOOH, which is the range of concentrations that we measured in our blank and 0.10 μM PQN DTT solutions after 15 min. As described in the Supplement Sect. S5, our results indicate that degradation of DTT by HOOH may account for up to 20 % of the DTT loss in blanks and PQN samples.
3.2 DTT loss from various concentrations of quinones and metals
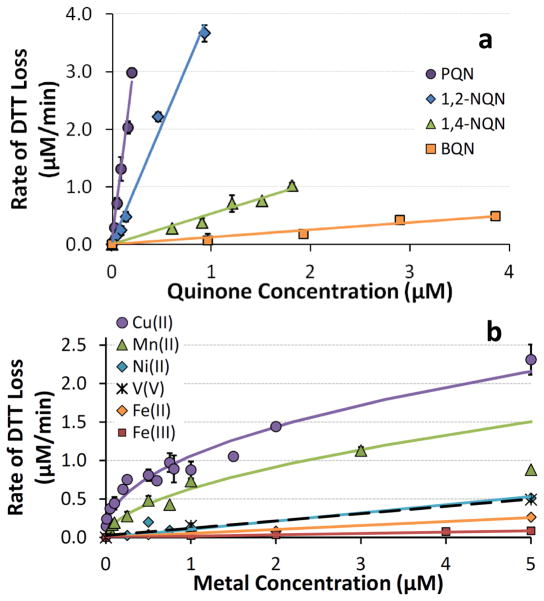
While Fig. 3 is a useful screening of the reactivities of quinones and metals in the DTT assay, the concentration used for each species (around 1.0 μM) is relatively high for typical DTT solutions containing ambient particles or particle extracts. To more fully understand the DTT responses we also measured the rate of DTT loss as a function of the concentration of the reactive metals and quinones; regression equations for the quinones (and metals) are compiled in Table 1. As shown in Fig. 4a, the rate of DTT loss from quinones is proportional to the concentration of quinone, i.e., the reaction is first-order in quinone. The slope of each of the Fig. 4a regression lines is the pseudo first-order rate constant for DTT oxidation in units of (μmol DTT oxidized/μmol of quinone/minute), which is a measure of the reactivity of a quinone with DTT. Based on our results (Table 1), the relative reactivities of the redox-active quinones are 111:32:4:1 for PQN:1,2-NQN:1,4-NQN:BQN (i.e., PQN is 111 times more reactive towards DTT than is BQN).
Table 1.
Regression equations for DTT loss from individual metals and quinonesa.
| Species | Range of Concentrations Tested (μM) | Regression Equation | R2 | Nb |
|---|---|---|---|---|
| PQN | 0.025–0.2 | y = 14.1x | 0.99 | 6 |
| 1,2-NQN | 0.01–1 | y = 4.09x | 0.99 | 5 |
| 1,4-NQN | 0.5–1.5 | y = 0.533x | 0.97 | 6 |
| BQN | 1–4 | y = 0.127x | 0.94 | 4 |
| Cu(II) | 0.005–5 | y = 1.06x0.442 | 0.96 | 14 |
| Mn(II) | 0.05–3 | y = 0.633x0.538 | 0.98 | 8 |
| Co(II)c | 1 | y = 0.27x | n/a | 1 |
| Ni(II) | 0.1–5 | y = 0.106x | 0.88 | 6 |
| V(V) | 1–5 | y = 0.101x | 0.98 | 2 |
| Pb(II)c | 1 | y = 0.064x | n/a | 1 |
| Fe(II) | 0.5–5 | y = 0.052x | 0.98 | 4 |
| Fe(III) | 0.5–10 | y = 0.017x | 0.96 | 7 |
For each equation, y represents the rate of DTT loss (units of μM-DTT min−1) and x is the concentration of metal or quinone (units of μM) in the DTT solution.
Number of different concentrations used in regression; for each concentration we measured at least two independent rate determinations and used the resulting average rate in the regression.
The regression equation was calculated from the 1 μM data point assuming the response was linear and went through the origin. A more complete concentration response was not measured because Co(II) and Pb(II) will not contribute significantly to the overall DTT response.
Fig. 4.
Blank-corrected rates of DTT loss as a function of concentration of redox-active species. (a) shows results for the four quinones that oxidized DTT, while (b) shows results for the six DTT-reactive metals. Each point represents the average (± σ ) of multiple individual rate determinations. Lines represent regression fits to the experimental data; the corresponding equations are listed in Table 1. The regression for Mn(II) does not include the 5.0 μM point.
The concentration response for most metals is also linear, with the exception of Cu(II) and Mn(II), which have a response that is well fit by a power relationship (Fig. 4b; Table 1). Cu(II) and Mn(II) are the most DTT-active metals across the entire range of concentrations tested. Co is the third most reactive metal (Fig. 3), but since atmospheric PM2.5 concentrations of Co are very low (Connell et al., 2006; Verma et al., 2009a) and would not cause significant DTT loss, we did not measure responses over a range of Co concentrations. V and Ni(II), the next most reactive metals, have very similar concentration responses. While the concentration responses of Fe(II) and Fe(III) are similar in 1 μM iron solutions (Fig. 3b), these responses are more clearly different at higher concentrations (Fig. 4b), though the responses from both iron oxidation states are small compared to Cu(II) and Mn(II).
The reactivity of the transition metals is Cu(II) > Mn(II) > Co(II) > V(V) ~ V(III) ~ Ni(II) > Pb(II) ~ Fe(II) > Fe(III). It is difficult to quantify the relative reactivities of Cu(II) and Mn(II) towards DTT (as we did for quinones) because of their non-linear concentration responses (Fig. 4b). For example, as shown in Fig. S1, the relative reactivities of Cu and Mn depend on their concentrations in solution. At 10 nM, Cu and Mn oxidize DTT 300 and 100 times faster than Fe(II), respectively, but these relative reactivities decrease with increasing metal concentration. If we use typical environmental concentrations of each water-soluble PM2.5 metal from the literature (see Sect. 3.3), the DTT reactivities of each metal (i.e., rate of DTT loss/metal concentration) relative to Fe(II) are 38:19:5.1:2.0:1.9:1.2:1:0.3 for Cu:Mn:Co:Ni:V:Pb:Fe(II):Fe(III). While these concentration-normalized values quantify the relative reactivities of the metals, the importance in the DTT assay for a PM sample also depends upon the absolute concentration of each metal, as we describe in section 3.3.
It is not clear why the oxidation of DTT by Cu(II) and Mn(II) is nonlinear, i.e., becomes less efficient at higher metal concentrations (Fig. 4b). However, we have seen similar nonlinear concentration-response curves for HOOH and OH formation from dissolved Cu and Fe (Charrier and Anastasio, 2011; Shen and Anastasio, 2012). Past work has shown that metals can bind to DTT (Kachur et al., 1997; Krezel et al., 2001; Xiao et al., 2011) and of the five metals tested (Cu(I), Ni(II), Cd(II), Pb(II), and Zn(II)) copper has the strongest binding constant (Krezel et al., 2001). This is consistent with the observation that adding high concentrations of Cu(II) reduces initial DTT levels by a stoichiometric amount, likely due to binding (Kachur et al., 1997). In our solutions removal of DTT by metal binding is insignificant compared to oxidation of DTT by redox-cycling of metals since our metal concentrations are much lower than the DTT concentration. The practical consequence of the nonlinear Cu(II) and Mn(II) concentration responses is that DTT is more efficiently oxidized by these metals at low concentrations.
3.3 Identifying the redox-active species responsible for DTT loss from ambient PM
As described earlier, past efforts at identifying the species responsible for the oxidation of DTT by ambient or source particles have relied on correlations of DTT response versus the measured chemical components of the samples (e.g., Hu et al., 2008; Verma et al., 2009a). As an alternative, here we apply a quantitative, mechanistic approach, which is analogous to what we have developed for identifying the species responsible for OH and HOOH production in ambient PM extracts (Vidrio et al., 2009; Charrier and Anastasio, 2011; Shen and Anastasio, 2011; Shen et al., 2011); a similar approach has been used by Chung et al. (2006) to identify the contributions of quinones to HOOH production in the presence of DTT. By combining the concentration responses for DTT-active species (Table 1) with reported concentrations of metals and quinones in ambient PM, we can calculate the expected DTT response from each chemical species in the PM sample and apportion the overall DTT response to individual species.
To understand the relative importance of metals and organics towards DTT loss from ambient particles, we first calculate the DTT responses expected for a hypothetical urban PM2.5 sample. As described in Sect. S2 of the Supplement, we use median concentrations of individual quinones in urban PM2.5 reported in the review by Walgraeve et al. (2010), and median soluble PM2.5 metal concentrations from several studies (Connell et al., 2006; Verma et al., 2009a; Vidrio et al., 2009). Because the oxidation state of soluble Fe was not provided in these articles, we assume soluble Fe is 80 % Fe(II) and 20 % Fe(III), based on measurements of urban particles from Majestic et al. (2007).
The median particle-phase concentration of each DTT-active species is listed in Table 2, along with the resulting concentration in the DTT solution, details of this calculation can be found in the supplemental section S2. While the species listed in Table 2 are all minor contributors to the total PM2.5 mass, Fe is the most abundant soluble metal, followed by Pb, Mn, and Cu. Concentrations of V, Ni and especially Co are quite low. Of the quinones, BQN is generally the most abundant particle-phase species, followed by PQN, while 1,2-NQN and 1,4-NQN are less abundant. The median literature concentrations normalized to PQN are listed in Table 2 and show that mass concentrations of water-soluble Fe, Cu and Mn are typically 6 to 24 times larger than the value for PQN. Since our DTT reactivities in Table 1 are normalized to species concentrations in mole (and not mass) units, we also show the mole-based concentration ratios of each redox-active species relative to PQN in our typical fine PM sample in Table 2. These are up to 4 times greater than the corresponding mass-based concentration ratios because of the high molecular weight of PQN relative to the metals; for example, mole-based concentrations of Fe, Mn, and Cu are, respectively, 84, 24, and 20 times higher than that of PQN.
Table 2.
Median concentrations of water-soluble metals and total organics in ambient fine particles and their corresponding DTT solution concentrations and DTT responses.
| Species | Median Particulate Concentration (ng m−3-air) | Concentration Relative to PQNa | Concentration Referenceb | Median Concentration in DTT solution (μM) | DTT Response (μM min−1) | |
|---|---|---|---|---|---|---|
| Mass Basis | Mole Basis | |||||
| Water-Soluble Metals
| ||||||
| Fe | 7.0 | 23 | 84 | c | 1.37 | 0.062 |
| Mn | 2.0 | 6.5 | 24 | c | 0.40 | 0.39 |
| Cu | 1.9 | 6.1 | 20 | c | 0.33 | 0.65 |
| V | 0.55 | 1.8 | 7.2 | c | 0.12 | 0.012 |
| Ni | 0.50 | 1.6 | 5.7 | c | 0.093 | 0.010 |
| Pb | 3.8 | 12 | 12 | c | 0.20 | 0.013 |
| Co | 0.035 | 0.1 | 0.4 | c | 0.0065 | 0.0017 |
|
| ||||||
| Quinones and PHEN
| ||||||
| BQN | 0.63 | 2.0 | 3.9 | d | 0.064 | 0.0081 |
| PQN | 0.31 | 1 | 1 | e | 0.017 | 0.23 |
| 1,4-NQN | 0.11 | 0.4 | 0.5 | e | 0.0077 | 0.0041 |
| 1,2-NQN | 0.02 | 0.1 | 0.08 | e | 0.0012 | 0.0049 |
| PHEN | 0.7 | 2.3 | 2.6 | f | 0.043 | 0.0033 |
Each concentration was divided by the concentration of PQN, either on a mass basis (ng m−3-air) or a mole basis (nmol m−3-air). The mole basis relative concentrations are most relevant here since our DTT results are expressed using species concentrations on a molar basis (e.g., Table 1).
As described in Sect. S2 of the Supplement, we examined multiple studies to determine typical particulate concentrations of each species. The reference listed in this column is the study that contained the median average value for a given species. Concentrations in the DTT solution were determined assuming that 32.8 m3 of air was sampled onto a filter and the whole filter PM mass was added to 3.0 mL of DTT reaction solution.
Connell et al. (2006) for PM2.5 collected in Steubenville, Ohio during 2000–2002.
Delhomme et al. (2008) for PM2.5 collected in Tempe, Arizona during 2005.
Cho et al. (2004) for PM2.5 collected in Riverside, California in May through July 2001.
The maximum PHEN concentration reported for PM2.5 (range: 0.043 to 0.7 ng m−3) in Atlanta, GA and Missoula, MT during January to April (Ward et al., 2005; Li et al., 2009b).
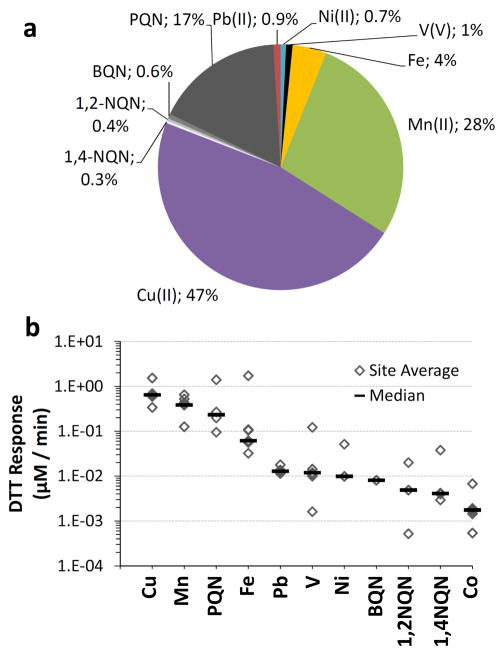
The final column of Table 2 shows the calculated rate of DTT loss from each redox-active species in our hypothetical PM2.5 extract. These are expressed in Fig. 5a as the percent of total DTT response in the sample. In these calculations we assume that the DTT responses of complex mixtures of metals and quinones are additive, which is essentially what we find in several tests of simple binary mixtures (Supplement Sect. S6).
Fig. 5.
(a) Calculated contributions of soluble metals and quinones to DTT loss in a hypothetical typical PM2.5 sample. The aerosol concentration for each metal and quinone, and the corresponding rate of DTT loss from each component, was estimated based on median concentrations in ambient PM2.5 (see Sect. S2 in the Supplement for more details). The total rate of DTT loss in this hypothetical sample is 1.4 μM min−1. (b) Calculated rates of DTT loss from individual species in hypothetical extracts of PM2.5 based on reported particulate concentrations. Each diamond represents the DTT response for the average concentration of DTT-active species from a given site. Each horizontal line is the response from the median concentration of the site averages. Using the median values for all of the DTT-active species gives the DTT reactivity distribution shown in panel (a).
Figure 5a shows that the majority of DTT loss is from transition metals, while quinones make a modest, though significant, contribution. Even though quinones, especially PQN, can be much more reactive than metals on a concentration-normalized basis (Fig. 3), metals dominate the DTT response because their concentrations are generally much higher than quinones (Table 2). For this hypothetical aerosol, metals account for 82 % of DTT loss while quinones account for the remaining 18 %. Cu(II) is the most important species for DTT loss, accounting for 47 % of DTT loss, followed by Mn(II) at 28 %. PQN is by far the most reactive quinone, accounting for 17 % of the DTT loss, while the other quinones together account for only 1 %. Even though the rate of DTT loss from Fe is slow relative to other chemicals (Figs. 3 and 4), ambient concentrations of Fe are large and Fe accounts for 4 % of DTT loss under these typical conditions. While we believe the PHEN reactivity observed in Fig. 3 is due to PQN contamination we included PHEN in Table 2 to investigate its possible reactivity. Even if PHEN is able to oxidize DTT, the contribution to total DTT loss is insignificant (Table 2). Of course these results apply to a hypothetical “typical” ambient PM2.5 sample and the relative contribution of any given species to DTT loss will depend on the actual concentrations of soluble metals and quinones in the PM. This is an especially important caveat since ambient particulate concentrations of soluble metals and quinones vary by one to two orders of magnitude (Figs. S2 and S3). We have been unable to find measurements of both soluble metals and quinones from the same ambient PM samples so it is unclear whether these redox-active species are covariant, as noted for soluble metals and PAHs in ambient PM samples at four urban sites in California (Ntziachristos et al., 2007). As shown in Fig. 5b, the large variations in reported concentrations suggest that Cu, Mn, PQN, or Fe could be the dominant DTT-active species in any given ambient PM2.5 sample, although we expect the typical case to be Cu > Mn > PQN > Fe (Fig. 5a).
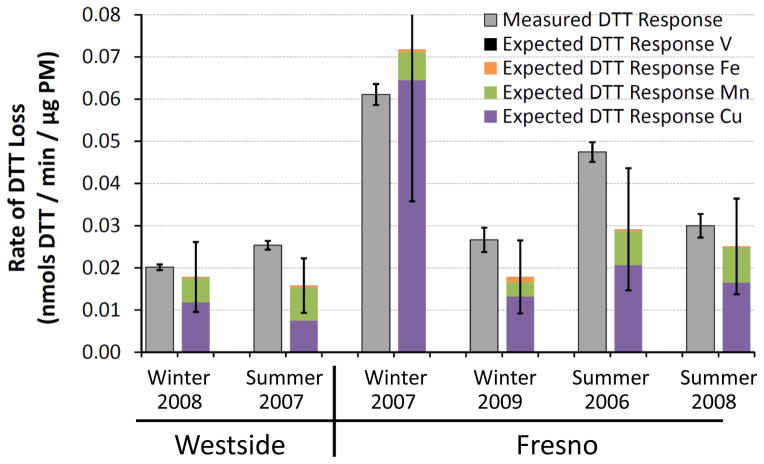
It is possible that there are other, unidentified, DTT-active species in ambient PM that we are not accounting for in this bottom-up approach. To investigate this, we measured rates of DTT loss from six ambient PM2.5 samples collected from an urban (Fresno) and rural (Westside) site in the San Joaquin Valley of California between 2006 and 2009. We have previously reported the soluble metal composition of these samples (Shen et al., 2011), but have not measured the concentrations of any organic species. Based on this data we can calculate the expected DTT response from the metals in each PM extract and compare that to the measured DTT loss to quantify the contributions of metals to DTT loss.
Figure 6 shows the measured DTT losses from the ambient PM2.5 samples (grey bars) compared to the calculated DTT losses from individual soluble metals (colored stacked bars). On average (± 1 σ), soluble metals can explain (80 ± 27) % of the observed DTT loss, mostly due to Cu and Mn, which account for (57 ± 26) % and (21 ± 8.9) % of the observed DTT response, respectively (Fig. S4). This measured result agrees well with the hypothetical PM2.5 result in Fig. 5 and indicates that metals are major contributors to DTT loss in ambient PM2.5. The remaining 20 % of DTT loss not explained by soluble metals in Fig. 6 is likely from quinones, insoluble metals, or other redox-active species that we did not investigate. Based on our results in Fig. 5, PQN likely accounts for a large portion of this “unknown” DTT loss.
Fig. 6.
Measured rates of DTT loss from ambient PM2.5 collected from the San Joaquin Valley of California. For each sample the left gray bar represents the rate of DTT loss measured for the particles (average ± 1 σ, n = 2 to 4 for each sample), while the right colored bar represents the expected rate of DTT loss from metals based on measured metal concentrations in each sample (Shen et al., 2011) and our DTT response for each metal (Table 1). Error bars for the expected DTT responses represent 1 σ, propagated from uncertainties in each metal concentration.
One weakness of this analysis is that the PM samples were stored in the freezer for two to five years prior to our DTT measurements, so it is possible that semi-volatile and reactive species such as quinones were lost during storage, which would artificially inflate the contribution of metals to DTT loss. However, if we are missing important contributions from organic species that degraded during storage, our measured rates of DTT loss should be much lower than those previously reported in the literature. As shown in Table 3, this is not the case: our rates of DTT loss are well within the ranges observed by other researchers using the same DTT method, and our median DTT loss rate is also similar. This suggests that we are not missing a significant fraction of DTT activity in our Fresno and Westside samples; however, additional research is needed to support these results and further examine the role of metals in DTT oxidation by PM.
Table 3.
Reported rates of DTT loss from ambient particulate matter.a
| Source | PM Size Fraction (μm) | Rate of DTT Loss (pmol min−1 μg−1) | Location | Location Type | Number of Samples | |
|---|---|---|---|---|---|---|
| Range | Median | |||||
| Verma et al. (2009b) | ≤ 2.5 | 5.0–24 | 14 | Los Angeles CA | Urban | 6 |
| Verma et al. (2009a) | 0.18–2.5 | 20–120 | 70 | Los Angeles CA | Urban | 8 |
| De Vizcaya-Ruiz et al. (2006) | ≤ 2.5 | 15–40 | 25 | Mexico City | Urban | 18 |
| Ntziachristos et al. (2007) | ≤ 0.15 | 42–170 | 61 | Los Angeles Basin and Caldecott Tunnel CA | Urban | 7 |
| ≤ 2.5 | 21–75 | 27 | 8 | |||
| Hu et al. (2008) | ≤ 0.25 | 31–55 | 34 | Los Angeles Port CA | Urban | 6 |
| 0.25–2.5 | 14–24 | 19 | 6 | |||
| This work | ≤ 2.5 | 27–61 | 39 | Fresno CA | Urban | 4 |
| ≤ 2.5 | 20–25 | 23 | Westside CA | Rural | 2 | |
The table only includes studies that used a similar DTT method to what we have used in this work (i.e., 37 °C, pH ≈ 7.3, 100 μM DTT in 0.1 M phosphate buffer) and that provided results in units of mol-DTT time−1 PM-mass−1 or give sufficient information to convert results to comparable units.
3.4 Previous evidence for a significant role of metals in the DTT assay
Our results indicate that a number of transition metals can oxidize DTT and that metals account for the majority of DTT loss from typical ambient PM2.5 where the concentrations of DTT-active metals are generally much higher than those of quinones (Fig. 5b). This is a relatively new finding in the DTT literature and is in contrast to several past studies that have stated that the DTT assay is insensitive to metals. However, our results showing DTT oxidation by metals (e.g., Figs. 3 and 4) are not unique: both Cu and Fe have been shown to oxidize DTT, forming ROS such as HOOH and OH in the process (Held and Biaglow, 1993; Netto and Stadtman, 1996; Kachur et al., 1997). In addition, Zn also consumes DTT, but via strong binding rather than redox-cycling (Lin and Yu, 2011). The DTT response of Fe and Cu have been examined in the past (Cho et al., 2005) but only at a concentration of 0.05 μM, which is too low to cause significant DTT loss based on our data (Fig. 4b) and significantly lower than expected for extracts of ambient PM2.5 samples (Table 2). Higher concentrations of Cu, Zn and Fe showed that Cu and Zn consume DTT while Fe does not (Lin and Yu, 2011).
While a majority of past reports have concluded that DTT loss in particle extracts is due to organic species, there is some evidence that metals are significant for DTT loss. Eiguren-Fernandez et al. (2010) examined the DTT activity of ambient PM2.5 that was collected in Riverside, CA and extracted using two methods. In the first method, filters were extracted with dichloromethane then the extracts were filtered, removing the particles and leaving only the dichloromethane-soluble fraction of the PM (which should include quinones and organics but not metals). In the second method the PM was extracted in water (which should dissolve the soluble metals efficiently, but not quinones); these samples were not filtered, so water-insoluble PM components such as non-polar organics were also retained. The aqueous PM extracts were nearly an order of magnitude more reactive than the dichloromethane extracts, indicating that dichloromethane-soluble species – e.g. quinones – were not responsible for much of the total DTT response. Lin and Yu (2011) provided convincing evidence that metals were an important sink for DTT in the hydrophilic fraction of their ambient particle extracts. They also found that nearly all DTT loss in their PM water extracts was removed by adding the metal chelator DTPA. While this suggests that metals dominated the DTT response, it is unclear whether DTPA might also reduce the reactivities of redox-active organics and thus not be specific for metals; as described in the next section, we have found this to be the case for EDTA.
There is additional, though more circumstantial, evidence from past reports that metals are important for DTT loss. For example, Ntziachristos et al. (2007) observed good correlations (R2 > 0.8) between DTT loss from ambient PM and their Fe, Cu, Mn, and Zn content, while Hu et al. (2008) found correlations between DTT response and two metals (V and Ni) in ambient PM. Geller (2006) also saw correlations between DTT loss and the Ni and Zn content of PM emitted by vehicles. However, in all cases these correlations were considered specious because the metals also correlated with PAHs and/or organic carbon, which were thought to be the true sources of DTT loss.
There are several possible reasons why much past work has not found a correlation between the metal content of PM and DTT loss. First, soluble metal concentrations are not always measured and therefore cannot be used in correlation analysis. Second, much of the current literature has examined ambient ultrafine PM or diesel exhaust, which may be enriched in organics and quinones compared to metals, causing organics to dominate the DTT response in these cases. Finally, Cu(II) and Mn(II) are the two most DTT-reactive metals and can account for a majority of DTT loss based on our work here. However, since they both have a non-linear concentration response with DTT (Fig. 4), linear correlation analysis is less likely to identify these species as being significant.
3.5 Effect of EDTA on the rate of DTT loss from metals and quinones
The DTT procedure used here was developed by Kumagai et al. (2002) and Cho et al. (2005). More recently, some researchers have added 1 mM EDTA to the DTT reaction mixture (Li et al., 2009a; Rattanavaraha et al., 2011), most likely because EDTA reduces the variability and rate of DTT oxidation in the blank. Since the DTT assay has been reported not to respond to metals (e.g., Cho et al., 2005), it would be natural to assume that EDTA would not change the overall DTT response. However, because we find that the DTT assay is sensitive to metals, we tested the effect of EDTA on the DTT response from metals and quinones.
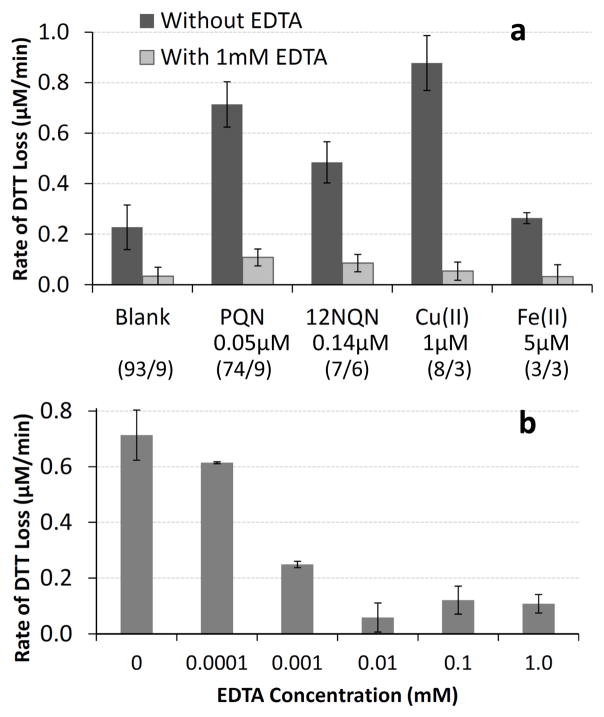
As expected, addition of 1.0 mM EDTA significantly reduces the rate of DTT loss from 1.0 μM Cu(II) or 5.0 μM Fe(II), by 94 % and 88 %, respectively (Fig. 7a). For both of these metals, the DTT response in the presence of EDTA is not statistically different from the response in the blank with EDTA. Surprisingly, we find that 1.0 mM of EDTA also decreases DTT loss from quinones, by 85 % and 82 % for PQN and 1,2-NQN, respectively (Fig. 7a). As with the metals, the quinone responses in the presence of EDTA are also not statistically different from the response in the blank with EDTA. Because these quinone results are unexpected, we repeated them multiple times on several days: our results are reproducible between experimental days. To further confirm our quinone results, we measured the rate of DTT loss from 0.050 μM PQN with varying concentrations of EDTA (Fig. 7b). Even the addition of 0.10 μM EDTA causes a slight (15 %), though not statistically significant, reduction in the rate of DTT loss from PQN. At higher EDTA concentrations the rate of DTT loss by 0.050 μM PQN is further suppressed. The rate of DTT loss in the blank is also reduced by EDTA (Supplemental Fig. S5), likely because EDTA chelates trace levels of metals that are not completely removed by Chelex treatment of the phosphate buffer. (Note that this effect on the blank is not responsible for our PQN or metal results in Fig. 7a and b, since we correct our sample results with a blank containing the same concentration of EDTA.)
Fig. 7.
Effect of EDTA on DTT loss from quinones and metals. (a) shows the average rate of DTT loss in the blank and for several compounds (at the concentrations listed) with and without 1.0 mM EDTA. The rates for the quinones and metals are blank-corrected using a blank containing the same concentration of EDTA as the corresponding sample. Error bars represent ± 1 σ from replicate measurements. Numbers in parentheses indicate the number of experiments performed without/with EDTA that are included in each average. For each sample the rate with and without EDTA are statistically different at the 95 % confidence limit. (b) shows the rate of DTT loss in a 0.050 μM PQN solution as a function of EDTA concentration. Each bar in (b) has been corrected using a blank with the same amount of EDTA as the sample.
Based on these results, the addition of EDTA suppresses DTT response from both metals and quinones. For this reason we do not advise the use of EDTA in the DTT assay, though the assay may still provide sufficient response in the presence of a high concentration of PM (or redox-active species). EDTA does markedly improve the background loss of DTT in the assay (i.e., in the blank), but removal of trace metals by Chelex 100 resin is a better option. Additionally, these results indicate that EDTA cannot be used to identify the contribution of metals to DTT loss, as both metals and organics are affected by the chelator. It is not clear if other metal chelators, such as desferoxamine or DTPA, have a similar effect on quinone response in the DTT assay, or if the reactivities of quinones are reduced by chelators in other assays (e.g., HOOH production). More research in this area is clearly needed.
4 Conclusions
We have measured the rate of DTT loss from individual dissolved metals, quinones, and PAHs to identify which species contribute to DTT loss from ambient PM. Of the ten metals tested at a concentration of 1.0 μM, seven cause DTT loss, as do three of the five quinones tested. On a concentration-normalized basis, phenanthrenequinone is by far the most DTT-active compound we tested, followed by 1,2-naphthoquinone, copper(II), manganese(II), 1,4-naphthoquinone, cobalt(II), and vanadium (III or V). The three PAHs tested do not cause significant DTT loss. Because we find that the DTT assay is sensitive to metals, we tested the effect of EDTA on DTT response. While the addition of EDTA improves loss of DTT in the blank, it significantly suppresses the response of both quinones and metals. Therefore, we do not recommend the use of EDTA in the DTT assay.
As a first step in determining which chemical species are responsible for DTT loss in ambient PM extracts, we measured the rate of DTT loss as a function of species concentration. Using this information with median ambient PM2.5 concentrations of each species from the literature, we calculate that metals should dominate DTT response in ambient fine particles, while quinones are typically a modest contributor to DTT loss. In this calculation for a hypothetical, typical PM2.5, Cu is responsible for nearly half of the total DTT loss, while Mn accounts for nearly one third. We find a similar result in six ambient PM2.5 samples where we measured rates of DTT loss: the soluble metals of the PM2.5 accounted for an average (± 1 σ) of (80 ± 27) % of DTT oxidation, with copper and manganese being the most important components. The remaining (20 ± 22) % of DTT loss in these samples is likely due to quinones or other redox-active species not specifically measured here. All of our results indicate that metals play a major role in oxidative potential as measured by the DTT assay, which has not been previously recognized. While this suggests that the DTT assay is a more representative measure of oxidative potential (compared to the case if it did not respond to metals), additional research is needed to understand how the assay compares to other (acellular and cellular) measures of oxidative potential and how well it represents the in vitro and in vivo oxidative stress that can be caused by particles.
Supplementary Material
Acknowledgments
This research was made possible by an EPA STAR Graduate Fellowship to J.G.C. (no. FP-91718101-0). This work has not been formally reviewed by the EPA. The views expressed in this article are solely those of the authors, and the EPA does not endorse any products or commercial services mentioned in this article. Additional support was provided by grant no. P42ES004699 from the National Institute of Environmental Health Sciences (NIEHS). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIEHS or NIH. We thank Debra Schmitz and Arthur Cho for sharing details of their DTT procedure; Norman Kado, Robert Rice, Sanjai Parikh and William Horwath for metal salts and quinones; Timothy Doane for discussions on the preparation of metal solutions; Yongjing Zhao, Walter Ham, Mike Kleeman, Chris Ruehl, Yuee Pan and Norman Kado for PM2.5 sample collection; the UC Davis ICP-MS facility for soluble metals measurements; and Mengfan Lei and Alex McFall for assistance with data collection.
Footnotes
Supplementary material related to this article is available online at: http://www.atmos-chem-phys.net/12/9321/2012/acp-12-9321-2012-supplement.zip.
References
- Ayres JG, Borm P, Cassee FR, Castranova V, Donaldson K, Ghio A, Harrison RM, Hider R, Kelly F, Kooter IM, Marano F, Maynard RL, Mudway I, Nel A, Sioutas C, Smith S, Baeza-Squiban A, Cho A, Duggan S, Froines J. Evaluating the toxicity of airborne particulate matter and nanoparticles by measuring oxidative stress potential - a workshop report and consensus statement. Inhal Tox. 2008;20:75–99. doi: 10.1080/08958370701665517. [DOI] [PubMed] [Google Scholar]
- Biorad: Chelex 100 and Chelex 20 chelating ion exchange resin instruction manual. 1991 http://www.bio-rad.com/webmaster/pdfs/9184Chelex.PDF.
- Biswas S, Verma V, Schauer JJ, Cassee FR, Cho AK, Sioutas C. Oxidative Potential of Semi-Volatile and Non Volatile Particulate Matter (PM) from Heavy-Duty Vehicles Retrofitted with Emission Control Technologies. Env Sci Technol. 2009;43:3905–3912. doi: 10.1021/es9000592. [DOI] [PubMed] [Google Scholar]
- Charrier JG, Anastasio C. Impacts of antioxidants on hydroxyl radical production from individual and mixed transition metals in a surrogate lung fluid. Atmos Environ. 2011;45:7555–7562. doi: 10.1016/j.atmosenv.2010.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho AK, Di Stefano E, You Y, Rodriguez CE, Schmitz DA, Kumagai Y, Miguel AH, Eiguren-Fernandez A, Kobayashi T, Avol E, Froines JR. Determination of four quinones in diesel exhaust particles, SRM 1649a, an atmospheric PM2.5. Aerosol Sci Technol. 2004;38:68–81. [Google Scholar]
- Cho AK, Sioutas C, Miguel AH, Kumagai Y, Schmitz DA, Singh M, Eiguren-Fernandez A, Froines JR. Redox activity of airborne particulate matter at different sites in the Los Angeles Basin. Environ Res. 2005;99:40–47. doi: 10.1016/j.envres.2005.01.003. [DOI] [PubMed] [Google Scholar]
- Chung MY, Lazaro RA, Lim D, Jackson J, Lyon J, Rendulic D, Hasson AS. Aerosol-borne quinones and reactive oxygen species generation by particulate matter extracts. Env Sci Technol. 2006;40:4880–4886. doi: 10.1021/es0515957. [DOI] [PubMed] [Google Scholar]
- Connell DP, Winter SE, Conrad VB, Kim M, Crist KC. The Steubenville Comprehensive Air Monitoring Program (SCAMP): Concentrations and solubilities of PM2.5 trace elements and their implications for source apportionment and health research, J. Air Waste Manage. Assoc. 2006;56:1750–1766. doi: 10.1080/10473289.2006.10464580. [DOI] [PubMed] [Google Scholar]
- Damodaran S. Estimation of disulfide bonds using 2-Nitro-5-thiosulfobenzoic acid – limitations. Anal Biochem. 1985;145:200–204. doi: 10.1016/0003-2697(85)90348-3. [DOI] [PubMed] [Google Scholar]
- Delhomme O, Millet M, Herckes P. Determination of oxygenated polycyclic aromatic hydrocarbons in atmospheric aerosol samples by liquid chromatography-tandem mass spectrometry. Talanta. 2008;74:703–710. doi: 10.1016/j.talanta.2007.06.037. [DOI] [PubMed] [Google Scholar]
- DiStefano E, Eiguren-Fernandez A, Delfino RJ, Sioutas C, Froines JR, Cho AK. Determination of metal-based hydroxyl radical generating capacity of ambient and diesel exhaust particles. Inhal Tox. 2009;21:731–738. doi: 10.1080/08958370802491433. [DOI] [PubMed] [Google Scholar]
- Eiguren-Fernandez A, Shinyashiki M, Schmitz DA, DiStefano E, Hinds W, Kumagai Y, Cho AK, Froines JR. Redox and electrophilic properties of vapor- and particle-phase components of ambient aerosols. Environ Res. 2010;110:207–212. doi: 10.1016/j.envres.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyer P, Worek F, Kiderlen D, Sinko G, Stuglin A, Simeon-Rudolf V, Reiner E. Molar absorption coefficients for the reduced Ellman reagent: Reassessment. Anal Biochem. 2003;312:224–227. doi: 10.1016/s0003-2697(02)00506-7. [DOI] [PubMed] [Google Scholar]
- Geller MD, Ntziachristos L, Mamakos A, Samaras Z, Schmitz DA, Froines JR, Sioutas C. Physicochemical and redox characteristics of particulate matter (PM) emitted from gasoline and diesel passenger cars. Atmos Environ. 2006;40:6988–7004. [Google Scholar]
- Ghio AJ, Carraway MS, Madden MC. Composition of air pollution particles and oxidative stress in cells, tissues, and living systems. J Toxicol Environ Health-Pt b-Crit Rev. 2012;15:1–21. doi: 10.1080/10937404.2012.632359. [DOI] [PubMed] [Google Scholar]
- Held KD, Biaglow JE. Role of copper in the oxygen radical-mediated toxicity of the thiol-containing radioprotector dithiothreitol in mammalian-cells. Radiat Res. 1993;134:375–382. [PubMed] [Google Scholar]
- Hu S, Polidori A, Arhami M, Shafer MM, Schauer JJ, Cho A, Sioutas C. Redox activity and chemical speciation of size fractioned PM in the communities of the Los Angeles-Long Beach harbor. Atmos Chem Phys. 2008;8:6439–6451. doi: 10.5194/acp-8-6439-2008. [DOI] [Google Scholar]
- Kachur AV, Held KD, Koch CJ, Biaglow JE. Mechanism of production of hydroxyl radicals in the copper-catalyzed oxidation of dithiothreitol. Radiat Res. 1997;147:409–415. [PubMed] [Google Scholar]
- Krezel A, Lesniak W, Jezowska-Bojczuk M, Mlynarz P, Brasun J, Kozlowski H, Bal W. Coordination of heavy metals by dithiothreitol, a commonly used thiol group protectant. J Inorg Biochem. 2001;84:77–88. doi: 10.1016/s0162-0134(00)00212-9. [DOI] [PubMed] [Google Scholar]
- Kumagai Y, Koide S, Taguchi K, Endo A, Nakai Y, Yoshikawa T, Shimojo N. Oxidation of proximal protein sulfhydryls by phenanthraquinone, a component of diesel exhaust particles. Chem Res Tox. 2002;15:483–489. doi: 10.1021/tx0100993. [DOI] [PubMed] [Google Scholar]
- Leonard SS, Harris GK, Shi XL. Metal-induced oxidative stress and signal transduction. Free Radic Biol Med. 2004;37:1921–1942. doi: 10.1016/j.freeradbiomed.2004.09.010. [DOI] [PubMed] [Google Scholar]
- Li N, Sioutas C, Cho A, Schmitz D, Misra C, Sempf J, Wang MY, Oberley T, Froines J, Nel A. Ultrafine particulate pollutants induce oxidative stress and mitochondrial damage. Environ Health Perspect. 2003;111:455–460. doi: 10.1289/ehp.6000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li QF, Wyatt A, Kamens RM. Oxidant generation and toxicity enhancement of aged-diesel exhaust. Atmos Environ. 2009a;43:1037–1042. [Google Scholar]
- Li Z, Porter EN, Sjodin A, Needham LL, Lee S, Russell AG, Mulholland JA. Characterization of PM(2.5)-bound polycyclic aromatic hydrocarbons in Atlanta-Seasonal variations at urban, suburban, and rural ambient air monitoring sites, Atmos. Environ. 2009b;43:4187–4193. [Google Scholar]
- Lin P, Yu JZ. Generation of reactive oxygen species mediated by humic-like substances in atmospheric aerosols. Env Sci Technol. 2011;45:10362–10368. doi: 10.1021/es2028229. [DOI] [PubMed] [Google Scholar]
- Majestic BJ, Schauer JJ, Shafer MM. Application of synchrotron radiation for measurement of iron red-ox speciation in atmospherically processed aerosols. Atmos Chem Phys. 2007;7:2475–2487. doi: 10.5194/acp-7-2475-2007. [DOI] [Google Scholar]
- McWhinney RD, Gao SS, Zhou SM, Abbatt JPD. Evaluation of the effects of ozone oxidation on redox-cycling activity of two-stroke engine exhaust particles. Env Sci Technol. 2011;45:2131–2136. doi: 10.1021/es102874d. [DOI] [PubMed] [Google Scholar]
- Netto LES, Stadtman ER. The iron-catalyzed oxidation of dithiothreitol is a biphasic process: Hydrogen peroxide is involved in the initiation of a free radical chain of reactions. Arc Biochem Biophys. 1996;333:233–242. doi: 10.1006/abbi.1996.0386. [DOI] [PubMed] [Google Scholar]
- Ntziachristos L, Froines JR, Cho AK, Sioutas C. Relationship between redox activity and chemical speciation of size-fractionated particulate matter. Part Fibre Toxicol. 2007;4 doi: 10.1186/1743-8977-4-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park JH, Gopishetty S, Szewczuk LM, Troxel AB, Harvey RG, Penning TM. Formation of 8-oxo-7,8-dihydro-2′-deoxyguanosine (8-oxo-dGuo) by PAH o-quinones: Involvement of reactive oxygen species and copper(II)/copper(I) redox cycling. Chem Res Tox. 2005;18:1026–1037. doi: 10.1021/tx050001a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rattanavaraha W, Rosen E, Zhang HF, Li QF, Pantong K, Kamens RM. The reactive oxidant potential of different types of aged atmospheric particles: An outdoor chamber study. Atmos Environ. 2011;45:3848–3855. [Google Scholar]
- Sauvain JJ, Deslarzes S, Riediker M. Nanoparticle reactivity toward dithiothreitol. Nanotoxicology. 2008;2:121–129. [Google Scholar]
- Shen H, Anastasio C. Formation of hydroxyl radical from San Joaquin Valley particles extracted in a cell-free surrogate lung fluid. Atmos Chem Phys. 2011;11:9671–9682. doi: 10.5194/acp-11-9671-2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen H, Anastasio C. A comparison of hydroxyl radical and hydrogen peroxide generation in ambient particle extracts and laboratory metal solutions. Atmos Environ. 2012;46:665–668. doi: 10.1016/j.atmosenv.2011.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen H, Barakat AI, Anastasio C. Generation of hydrogen peroxide from San Joaquin Valley particles in a cell-free solution. Atmos Chem Phys. 2011;11:753–765. doi: 10.5194/acp-11-753-2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shima H, Koike E, Shinohara R, Kobayashi T. Oxidative ability and toxicity of n-hexane insoluble fraction of diesel exhaust particles. Toxicol Sci. 2006;91:218–226. doi: 10.1093/toxsci/kfj119. [DOI] [PubMed] [Google Scholar]
- Shinyashiki M, Eiguren-Fernandez A, Schmitz DA, Di Stefano E, Li N, Linak WP, Cho SH, Froines JR, Cho AK. Electrophilic and redox properties of diesel exhaust particles. Environ Res. 2009;109:239–244. doi: 10.1016/j.envres.2008.12.008. [DOI] [PubMed] [Google Scholar]
- Verma V, Ning Z, Cho AK, Schauer JJ, Shafer MM, Sioutas C. Redox activity of urban quasi-ultrafine particles from primary and secondary sources. Atmos Environ. 2009a;43:6360–6368. [Google Scholar]
- Verma V, Polidori A, Schauer JJ, Shafer MM, Cassee FR, Sioutas C. Physicochemical and toxicological profiles of particulate matter in Los Angeles during the October 2007 Southern California wildfires. Environ Sci Technol. 2009b;43:954–960. doi: 10.1021/es8021667. [DOI] [PubMed] [Google Scholar]
- Verma V, Pakbin P, Cheung KL, Cho AK, Schauer JJ, Shafer MM, Kleinman MT, Sioutas C. Physicochemical and oxidative characteristics of semi-volatile components of quasi-ultrafine particles in an urban atmosphere. Atmos Environ. 2011;45:1025–1033. [Google Scholar]
- Vidrio E, Phuah CH, Dillner AM, Anastasio C. Generation of hydroxyl radicals from ambient fine particles in a surrogate lung fluid solution. Environ Sci Technol. 2009;43:922–927. doi: 10.1021/es801653u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walgraeve C, Demeestere K, Dewulf J, Zimmermann R, Van Langenhove H. Oxygenated polycyclic aromatic hydrocarbons in atmospheric particulate matter: Molecular characterization and occurrence. Atmos Environ. 2010;44:1831–1846. [Google Scholar]
- Wang Y, Arellanes C, Curtis DB, Paulson SE. Probing the source of hydrogen peroxide associated with coarse mode aerosol particles in Southern California. Env Sci Technol. 2010;44:4070–4075. doi: 10.1021/es100593k. [DOI] [PubMed] [Google Scholar]
- Ward TJ, Hamilton RF, Smith GC. The Missoula Valley semivolatile and volatile organic compound study: Seasonal average concentrations. J Air Waste Manage Assoc. 2005;55:1007–1013. doi: 10.1080/10473289.2005.10464698. [DOI] [PubMed] [Google Scholar]
- Wilson DW, Aung HH, Lame MW, Plummer L, Pinkerton KE, Ham W, Kleeman M, Norris JW, Tablin F. Exposure of mice to concentrated ambient particulate matter results in platelet and systemic cytokine activation. Inhal Toxicol. 2010;22:267–276. doi: 10.3109/08958370903278069. [DOI] [PubMed] [Google Scholar]
- Xiao ZG, Brose J, Schimo S, Ackland SM, La Fontaine S, Wedd AG. Unification of the Copper(I) binding affinities of the cetallo-chaperones Atx1, Atox1, and related proteins detection probes and affinity standards. J Biol Chem. 2011;286:11047–11055. doi: 10.1074/jbc.M110.213074. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.