A mechanistic model for bromodeoxyuridine dilution naturally explains labelling data of self-renewing T cell populations

Abstract

Bromodeoxyuridine (BrdU) is widely used in immunology to detect cell division, and several mathematical models have been proposed to estimate proliferation and death rates of lymphocytes from BrdU labelling and de-labelling curves. One problem in interpreting BrdU data is explaining the de-labelling curves. Because shortly after label withdrawal, BrdU⁺ cells are expected to divide into BrdU⁺ daughter cells, one would expect a flat down-slope. As for many cell types, the fraction of BrdU⁺ cells decreases during de-labelling, previous mathematical models had to make debatable assumptions to be able to account for the data. We develop a mechanistic model tracking the number of divisions that each cell has undergone in the presence and absence of BrdU, and allow cells to accumulate and dilute their BrdU content. From the same mechanistic model, one can naturally derive expressions for the mean BrdU content (MBC) of all cells, or the MBC of the BrdU⁺ subset, which is related to the mean fluorescence intensity of BrdU that can be measured in experiments. The model is extended to include subpopulations with different rates of division and death (i.e. kinetic heterogeneity). We fit the extended model to previously published BrdU data from memory T lymphocytes in simian immunodeficiency virus-infected and uninfected macaques, and find that the model describes the data with at least the same quality as previous models. Because the same model predicts a modest decline in the MBC of BrdU⁺ cells, which is consistent with experimental observations, BrdU dilution seems a natural explanation for the observed down-slopes in self-renewing populations.

1. Introduction

To study the population dynamics of T cells, immunologists use various labelling techniques that are based on the fact that cells duplicate their DNA during cell division. Using non-radioactively labelled molecules that are incorporated into de novo synthesized DNA strands, one can detect cell division in any particular population. The two DNA labelling techniques that are currently widely used are based on a label that can be provided in the drinking water. One is bromodeoxyuridine (BrdU), which is an analogue of thymidine (i.e. one of the four bases making up DNA). BrdU can be detected in a cell with antibodies. The other is deuterium. Deuterium labelling uses mass spectrometry to detect the deuterium atoms that have replaced some of the hydrogen atoms in newly synthesized DNA. DNA has also been labelled with radioactive thymidine (³H-thymidine), but for in vivo experiments this has mostly been replaced by BrdU and deuterium. Another important labelling technique used for tracking the division history of lymphocytes is carboxyfluorescein succinimidyl ester (CFSE). CFSE is a fluorescent dye which does not label DNA, but binds cytoplasmic proteins and equally dilutes upon cell division. Most in vivo experiments with CFSE rely on the adoptive transfer of CFSE-labelled lymphocytes [1,2]. The interpretation on CFSE data is complicated, and several dedicated mathematical models have been developed to quantify lymphocyte turnover using CFSE data [3–10].

BrdU has been used for decades in mice [11,12], and more recently in monkeys [13–15]. Because of potential problems with toxicity, it has been used infrequently in humans [16–20], and only over short-term periods. Indeed, it has been reported that BrdU is toxic for various cell types, and may trigger an injury response leading to activation and division [21,22], which would perturb the normal population dynamics. Other laboratories found little toxicity of BrdU [23,24], and BrdU data have hitherto been interpreted under the assumption that BrdU does not influence the rates of cell proliferation or death.

In the presence of BrdU, an unlabelled cell (U) that divides will give rise to two labelled daughter cells (L), and a labelled cell that divides increases the number of BrdU⁺ cells by one, i.e. 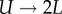and 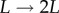. During the first part of the de-labelling phase, a BrdU⁺ cell that divides will give rise to two BrdU⁺ cells, each expressing half of the parent's BrdU content [13]. Thus, a typical BrdU experiment consists of a labelling phase during which the fraction of labelled cells increases, and a de-labelling phase during which one would expect this fraction to decrease and ultimately approach zero. We will refer to the initial slopes of these two phases as the up-slope and the down-slope, respectively.

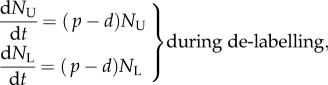
Let us consider a population such as self-renewing memory T cells that are largely maintained by random division and death [2], and let the total number of cells in the population be described by the equation dN/dt = (p − d)N. To model BrdU labelling, we let unlabelled cells disappear by proliferation and death during the labelling phase, and let labelled cells—at least initially—divide into labelled daughter cells and disappear by death during the de-labelling phase. By having no external source, the corresponding model is a simplification of the model proposed by Mohri et al. [13]:

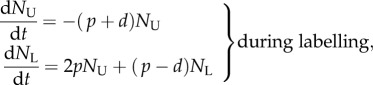and

1.1

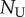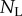where p and d are (daily) division and death rates, and and are the numbers of unlabelled and labelled cells, and 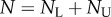. To fit this model to BrdU data, one has to define the fraction of labelled cells, i.e. 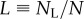, and derive the differential equation for the fraction of labelled cells from equation (1.1). Straightforward calculus reveals that dL/dt = (dN_L/dt)/N − (L/N)dN/dt. Substituting dN_L/dt and dN/dt from equation (1.1) finds that dL/dt = 2p(1 − L) during the labelling phase, and that dL/dt = 0 during the de-labelling phase. Thus, the death rate cancels and the fraction of labelled cells is expected to increase with an initial up-slope of 2p during the labelling phase. From the dL/dt = 0 result, one expects that the down-slope is—at least initially—flat during the de-labelling phase.

For most cell types, the fraction of BrdU⁺ cells indeed increases during the labelling phase, but tends to decrease during the de-labelling phase, which is at conflict with the dL/dt = 0 result. To solve this problem, different authors have proposed different solutions. Several authors [13,25–27] allowed for an external source of cells, for example coming from the thymus or from a compartment of quiescent cells, and by allowing the generation of unlabelled cells during the de-labelling phase they were able to explain the observed down-slopes. Others [28–30] argued that labelled cells have recently divided, and that recently divided cells should have a faster death rate than non-divided unlabelled cells, which also allows for a decline of the fraction of BrdU⁺ cells. Several authors in the field of immunology [23,28,31] and in the field of haematopoietic stem cells [21,24,32] have argued that the loss of BrdU⁺ cells can be explained by BrdU dilution during the de-labelling phase. Indeed, the classical paper by Tough & Sprent [11] provided evidence for a decrease in BrdU mean fluorescence intensity (MFI) of BrdU⁺ memory phenotype T cells during the de-labelling phase. However, there is ongoing discussion in immunology on the role of BrdU dilution in the loss of BrdU⁺ cells because BrdU intensity profiles sometimes do not change substantially during the de-labelling phase [13].

To track BrdU dilution during the de-labelling phase, previous authors wrote simple cascade models of the form

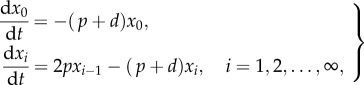1.2

where x_i is the number of cells having completed i divisions after BrdU withdrawal [21,23,24,32]. At the start of the de-labelling phase, all cells are considered to be fully labelled, and to have completed zero divisions, i.e. x₀(0) = N(0). After a critical number of divisions, the cells have diluted their BrdU content so much that they fall below a fluorescence detection limit, and will subsequently be scored as BrdU⁻. Parretta et al. [23] found their best fit of BrdU data from mouse memory CD8⁺ T cells when assuming that BrdU⁺ T cells become BrdU⁻ upon the second division. The haematopoietic stem cell studies suggest that stem cells may have to complete three [24] or five [21] divisions before they breach the detection limit. Because the critical number of divisions that is required for a BrdU⁺ cell to result in BrdU⁻ progeny should depend on the BrdU content of the cell at the end of the labelling phase and the detection limit, this difference between stem cells and T cells could be due to the number of divisions they have completed during the labelling phase.

We therefore generalize equation (1.2) into a model for BrdU accumulation and dilution during the labelling and de-labelling phases, respectively. By solving the differential equations of this random-division/death model, we find that the fraction of BrdU⁺ cells is given by the product of Poisson distributions describing the number of divisions cells are expected to have completed in each phase. These distributions also allow us to derive equations for the mean BrdU content (MBC) of the cells, which is related to the MFI of BrdU in labelled cells. Considering the MBC of the total population of cells, our results are in agreement with another simple model proposed previously for the de-labelling phase: Bonhoeffer et al. [25] argued that the total BrdU intensity is not changed by cell division, which yields two cells with approximately half the intensity each. The total fluorescence intensity, I_T, can decrease only by cell death, i.e. dI_T/dt = −dI_T. If total cell numbers obey dN/dt = (p − d)N, the average BrdU intensity, I_M = I_T/N, obeys dI_M/dt =−pI_M, suggesting that the MBC decreases exponentially at rate p during the de-labelling phase [25]. Using the Poisson distributions, we generalize this result by also considering the MBC of only labelled (BrdU⁺) cells, because in experiments one typically reports BrdU MFI of the labelled fraction. We find moderate changes in the MBC of BrdU⁺ cells in situations where the fraction of labelled cells, L, changes markedly. This reconciles the observation of a declining fraction of BrdU⁺ cells in situations where the BrdU intensity profiles are hardly changing [13].

2. Results

2.1. Homogeneous population

We start with a simple ordinary differential equation (ODE) model for cell division and death (random-division/death model [3,33]), and first consider a homogeneous cell population. At time t = 0, BrdU is administered and dividing cells start incorporating BrdU. Changes in the number of cells 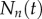, having undergone n divisions by time t, are given by the conventional system of ODEs,

2.1

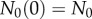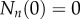where p and d are the rates of cell proliferation and death, respectively. Because we start tracing cell division at the time BrdU administration begins, the initial condition and for 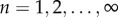. The general solution of this model is

2.2

where the total cell number is changing over time as 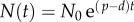, and where 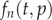is the Poisson distribution for cells dividing at rate p. For the de-labelling phase, equation (2.2) is generalized into 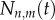for the number of cells having completed n divisions during labelling and m divisions during de-labelling,

2.3

where the 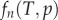term gives the Poisson distribution at the end of the labelling phase, and the latter 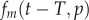term is the Poisson distribution after labelling (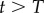), respectively. Both Poisson distributions depend on the division rate p of cells in the population.

The efficiency at which cellular DNA will become labelled during BrdU administration will probably depend on the BrdU concentration in the environment and the cell type. In the following analyses, we assume that labelling is 100 per cent efficient. Because DNA is replicated during the cell cycle, cells having completed one division, N₁, have exactly half of their DNA strands labelled (assuming 100% efficiency of labelling; figure 1). Owing to the random segregation of chromosomes, on average three-quarters of the DNA strands are labelled after two divisions,¹ and so on (figure 1). On average, the fraction of DNA strands labelled after n divisions is 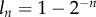. Knowing the fraction of labelled DNA strands after n divisions, and assuming that the measured fluorescence intensity increases with the fraction of chromosomes labelled, one can use equation (2.2) to define the fraction of labelled cells in the labelling phase as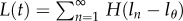 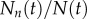, where 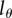is the threshold BrdU intensity below which a cell is measured as BrdU⁻. H(x) is a Heaviside function, i.e. H(x) = 0 whenever 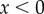and H(x) = 1 otherwise, counting cells with 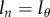and up as BrdU⁺. During the de-labelling phase, each cell on average loses half of its labelled DNA strands per division. Their fluorescence intensity is naturally defined as (figure 1), and we can use equation (2.3) to obtain the fraction of labelled cells in the de-labelling phase. For the fraction of BrdU⁺ cells, this adds up to

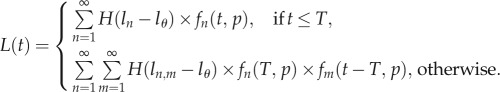2.4

Figure 1.

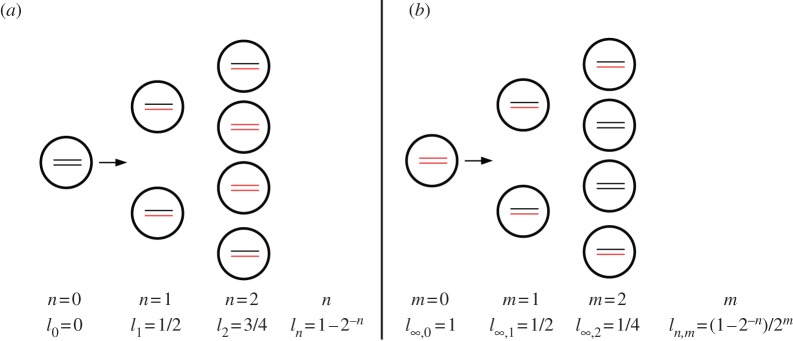
Distribution of labelled DNA strands in cells (a) during BrdU labelling and (b) during de-labelling phases. Under the assumption of 100% labelling efficacy, after one division in the labelling phase, cells will have half of their DNA strands labelled, l₁ = 1/2 (in cartoon, labelled strands are shown in red and unlabelled strands are shown in black). After two divisions, this is an average of l₂ = 3/4 strands, and so on. Let l_n,m denote the fraction of labelled strands in a cell having completed n divisions during the labelling phase, and m divisions during the de-labelling phase. During the de-labelling phase, a cell having all DNA strands labelled, for example 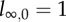, divides into daughter cells having 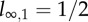labelled strands, and so on. The BrdU fluorescence of a cell is an increasing function of l and cells will be classified as BrdU⁻ when 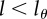. For 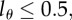the division of unlabelled cells during labelling results in two BrdU-labelled cells. If at the end of the labelling phase a cell has a BrdU content 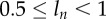, two divisions are required to make progeny of this cell to become BrdU⁻ during de-labelling for the level of detection 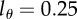. If the detection limit were set at 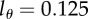, this would take three divisions.

Thus, we mechanistically derived a simple two-parameter model for self-renewing populations that—at no extra assumptions—includes the effects of BrdU dilution during the de-labelling phase, provided one knows the threshold BrdU intensity above which a cell is measured as BrdU⁺ in the experiment. Because equation (2.4) is defined as a fraction, it is independent of the death rate d, which is a property shared with the solution of equation (1.1) in §1.

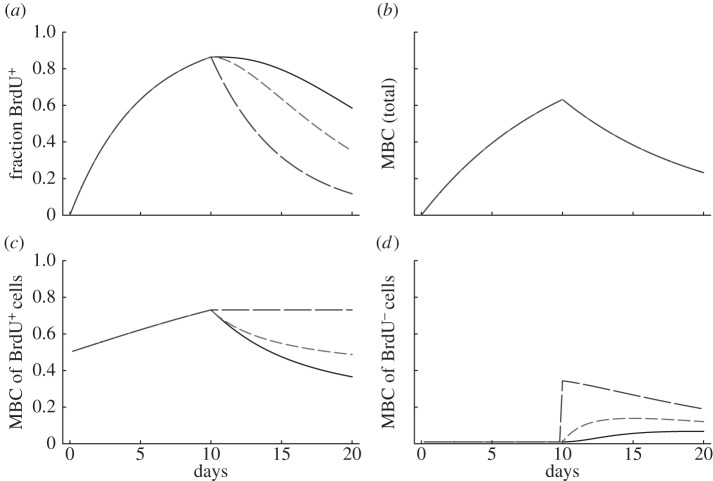
The properties of this model are illustrated in figure 2a, where we depict the fraction of BrdU⁺ cells for a population at steady state with p = d = 0.1 day⁻¹ for three reasonable values of the detection limit, i.e. 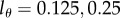and 0.5, respectively. The three labelling curves increase in the same manner because, for all three detection limits, the first division already provides two BrdU⁺ daughter cells. By equation (2.4) the initial up-slope of the curves is 2p because the mean of the Poisson distribution 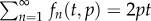and 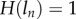for all values of 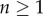. Thus, if the first division is sufficient to breach the detection limit, the up-slope equation (2.4) is identical to that of equation (1.1) in §1 (which is an expected result). The de-labelling phase starts at T = 10 days and we see that the down-slope depends on the detection limit, and hence does not reflect p, d, or p − d, as was derived in previous models [13,25–27]. Importantly, the new model allows for a decline in the fraction of BrdU⁺ cells in self-renewing populations, in the absence of additional assumptions such as a source of unlabelled cells [13,25–27] or a faster death rate of recently divided cells [28,29].

Figure 2.

Properties of the one-compartment model. Considering a population at steady state, with p = d = 0.1 day⁻¹, we depict the fraction of labelled cells (equation (2.4) in a), the mean BrdU content (MBC) of the whole population (equations (2.5) and (2.6) in b), the MBC of BrdU⁺ cells (equation (2.7) in c) and the MBC of BrdU⁻ cells (d) for three reasonable detection limits, i.e. I_θ = 0.125 (solid line), 0.25 (short dashed line) and 0.5 (long dashed line). These detection limits corresponds to 3, 2 and 1 divisions to become BrdU⁻, respectively, for a cell with high BrdU content ().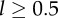

In addition to tracking the fraction of BrdU⁺ cells, the complete BrdU intensity profiles, or their MFI, have also been measured. As the fluorescence intensity is typically represented on a log scale, there is ambiguity on the meaning of the term MFI as one could take the arithmetic mean, the geometric mean, or the median. In our model, we only have a measure for the BrdU content, i.e. l_n or l_n,m, of a cell, and we therefore define the MBC as a measure for the MFI. The MFI should be an increasing function of the MBC, with an MBC of zero defining the mean autofluorescence, and an MBC of 1 corresponding to the maximum MFI. Because our model of equations (2.2) and (2.3) tracks the relative BrdU content per cell, it is natural to define the total, I_T, and the mean, I_M, BrdU content as

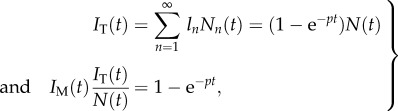2.5

which is valid because 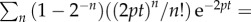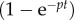. This suggests that the rate at which the MBC increases during the labelling phase reflects the division rate p. For the de-labelling phase, one obtains

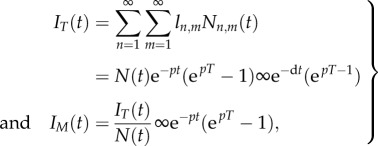2.6

which confirms the result of Bonhoeffer et al. [25] that during de-labelling the MBC decreases with the proliferation rate, whereas the total fluorescence intensity decreases with the death rate.

Because the BrdU MFI is typically estimated only for BrdU⁺ cells, and not for the total population, it is useful to also write the MBC for cells having at least a fraction 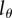of their DNA strands labelled. This is simply done by cancelling the BrdU⁻ subpopulations from the sum terms in equations (2.5) and (2.6) using the Heaviside function. For instance, for the labelling phase, this boils down to

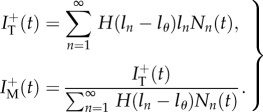2.7

Note that the latter expression is undefined for 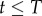if . For the de-labelling phase, one obtains the equivalent by using equation (2.3) and similarly adding Heaviside functions 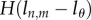. Similarly, one can calculate the MBC of BrdU⁻ cells.

This result is important in several ways. First, the BrdU dilution model can be tested by comparing predictions of the model with experimentally measured dynamics of the fraction of BrdU⁺ cells and BrdU MFI of BrdU⁺ cells. A good match between the model predictions and the data would indicate that BrdU dilution is indeed the main mechanism explaining the loss of BrdU⁺ cells during the de-labelling phase. Second, the BrdU dilution model involves an unknown parameter 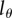(BrdU threshold level), and this parameter can be estimated by fitting the model predictions on the dynamics of MFI of BrdU⁺ or all cells in the population. Finally, as we will show next, the MBC need not decline much in circumstances where the fraction of BrdU⁺ cells is decreasing markedly.

The changes of the MBC during a typical BrdU labelling experiment are depicted in figure 2b–d. The MBC of all cells (figure 2b) does not depend on the detection limit 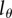and increases and decreases with slope p = d (see equations (2.5) and (2.6)). Interestingly, the MBC of the BrdU⁺ subpopulation behaves differently. The labelling phase starts at an MBC of one-half because all divided cells at 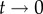will have half of their DNA strands labelled. We observe an initial linear increase in the MBC during the labelling phase because the average number of divisions increases linearly with time, and most cells have completed only one division. During the de-labelling phase, the decline of the MBC depends on the limit of detection (figure 2c). Note that the model predicts moderate changes in the MBC of BrdU⁺ cells during the de-labelling phase. For instance, when 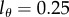, we expect a rapid loss of BrdU⁺ cells (figure 2b) in combination with a minor reduction in the MBC of BrdU⁺ cells (figure 2c). This is interesting because previous authors have argued against a role of BrdU dilution in explaining the loss of BrdU⁺ cells because they found that the BrdU MFI was hardly declining [13].

2.2. Kinetic heterogeneity

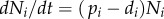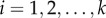Extending the work of Ganusov et al. [34], we define a kinetically heterogeneous population consisting of k-independent subpopulations, each described by , for . The total number of cells is simply 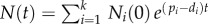. Because during a BrdU experiment the fraction of labelled cells in each of the subpopulations should obey equation (2.4), one can similarly define L_i(t) as the fraction of BrdU⁺ cells in the ith subpopulation. The fraction of labelled cells in the total population would be 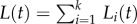. Summarizing, in theory, one can extend equation (2.4) into k populations, having k, p_i and d_i parameters, and a k-dimensional initial condition N_i(0) vector, and fit this model to BrdU data from any kinetically heterogeneous population.

This heterogeneity model becomes much simpler for populations at steady state because p_i = d_i for all i, and one can define a vector α_i for the fixed fraction of cells with turnover rate p_i = d_i [34]. Therefore, we write

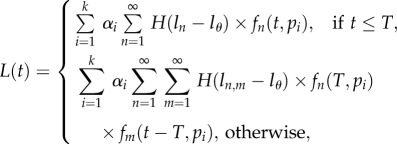2.8

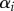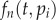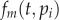where is the fraction of cells with turnover rate p_i = d_i, and and are the Poisson distributions defined earlier. Owing to kinetic heterogeneity, the labelled cells will be enriched in cell subpopulations with fast turnover rates, and the initial down-slope of labelling curves will be faster than the up-slope. Again, the decline of the BrdU⁺ cells need not be a single exponential and can account for data that appear to have an at least biphasic down-slope. A Mathematica notebook implementing this model for fitting BrdU labelling data is provided online (http://theory.bio.uu.nl/vitaly/mathematica or http://web.bio.utk.edu/ganusov).

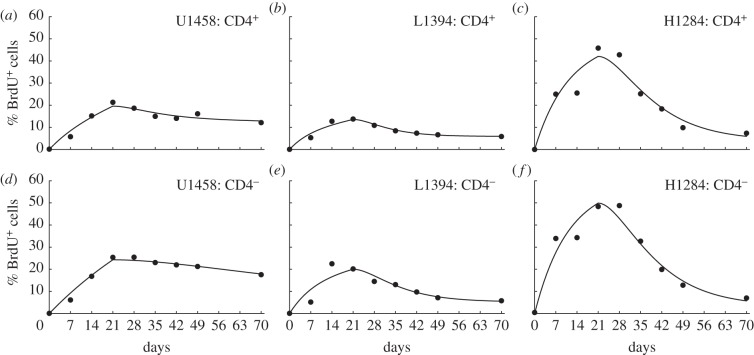
To test whether our novel model can properly describe BrdU data, we have fitted the model (equation (2.8) with k = 2) to the BrdU data of Mohri et al. [13] for which rhesus macaques were labelled with BrdU in the drinking water for a period of three weeks, and were followed during a subsequent de-labelling period of seven weeks. Total cell numbers are indeed not supposed to change during the experiment. Animals were classified into three groups: uninfected (U) and simian immunodeficiency virus (SIV)-infected monkeys with either a low (L) or high (H) viral load. Representative fits of our novel model to the data on BrdU labelling of CD3⁺CD45RA⁻CD4⁺ and CD4⁻ memory T cells in one monkey from each group are depicted in figure 3. The new model describes these data at least as well as previous models did [13,26,27]. Thanks to the kinetic heterogeneity, the model readily accounts for the biphasic down-slopes in the monkey H1284 with a high viral load. Summarizing, we can account for the decline in the fraction of BrdU⁺ cells during de-labelling without having to invoke an external source of unlabelled cells [13,26,27] or a faster death rate of recently divided cells [28,29].

Figure 3.

Fits of the novel mathematical model to experimental data on BrdU labelling of CD3⁺CD45RA⁻CD4⁺ and CD4⁻ memory T cell data in monkeys [13]. We fit the mathematical model given in equation (2.8) with k = 2 kinetic compartments and a detection limit 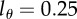. The symbols denote the data, and the lines depict the fit. Parameters for each fit can be found in tables 1 and 2. We show a representative example of an uninfected monkey (U1458), of a SIV-infected monkey with a low viral load (L1394), and an infected monkey with a high SIV load (H1284).

The MBC of this kinetically heterogeneous cell population model can be defined very similarly to above. For instance, the MBC during the labelling phase is described by

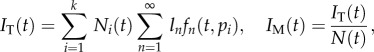2.9

where 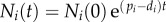, 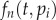is a Poisson distribution, and 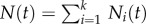. For the de-labelling phase, one similarly obtains

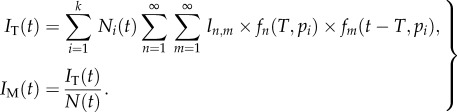2.10

To model the MBC of just the BrdU⁺ population, one can again extend the last two equations with the Heaviside functions 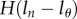and 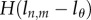, respectively. For a system at steady state, N(t) = N, p_i = d_i, 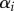is the fixed fraction of cells with turnover rate p_i, and one substitutes 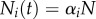into the equations.

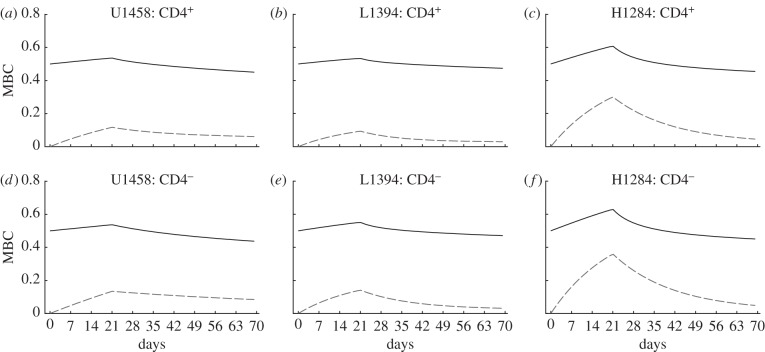
Because the model is explicit in the number of divisions that cells in the population have completed, the parameters estimated for the six monkeys in figure 3 directly allow us to predict the MBC in these monkeys. Using equations (2.9) and (2.10), and their extensions computing the MBC of BrdU⁺ cells only, we obtain the curves depicted in figure 4.

Figure 4.

Predicted changes in the mean BrdU content (MBC) of the heterogeneous model. Using the parameters estimated for three monkeys in figure 3 we compute the MBC of all cells (dashed line) and of BrdU⁺ cells (solid line). The experimentally observed BrdU MFI in these monkeys should correlate with the predicted MBC. The MBC of labelled cells hardly declines during the de-labelling phase, which is in agreement with data [13].

Interestingly, the changes in the MBC of BrdU⁺ cells remain relatively moderate, varying around a relative MBC of 0.5 within a range of 0.4–0.7. Thus, the reduction of the BrdU MFI during the de-labelling phase may be very hard to detect in BrdU experiments even though the fraction of BrdU⁺ cells is declining considerably, and our model seems consistent with the observation that the BrdU MFI hardly declines during the de-labelling phase [13].

2.3. Estimated turnover rates

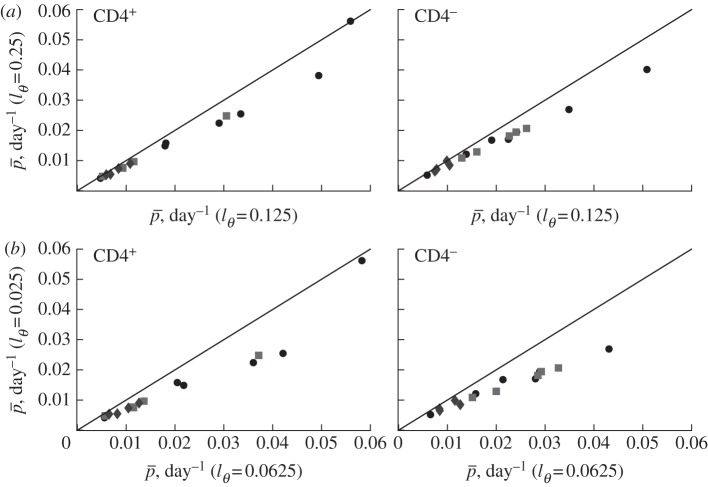
Now that we have a simple and mechanistic model for BrdU accumulation and dilution that is able to describe BrdU data at least as well as previous models, the most relevant biological question is whether the estimated turnover rates depend on the choice of the model. One complication is the choice of the detection limit, 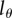, which was not determined by Mohri et al. [13]. Experiments with mice [23] and with hematopoietic stem cells [21,24] indicate that BrdU⁺ cells result in BrdU⁻ progeny after approximately two to five divisions, respectively. We have fitted all memory T cell data for several values of 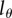, and found using the Akaike information criterion [35] that most of the data are best described when 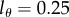. The quality of the fit is, however, very similar for data from many animals when 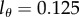or 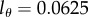(not shown). The estimated turnover rates are somewhat higher for lower detection limits because the model then requires more divisions to explain the observed loss of BrdU⁺ cells (figure 5).

Figure 5.

The effect of the detection limit 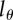on the estimate of the average turnover rate, 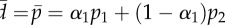, when fitting the BrdU labelling data of memory T cells in uninfected and SIV-infected rhesus macaques [13]. We consider three threshold levels, 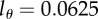, 0.125 or 0.25, corresponding to the 4, 3 or 2 divisions, respectively, that a BrdU⁺ cell must undergo to result in BrdU⁻ progeny. Diamonds denote uninfected monkeys, squares denote SIV-infected monkeys with a low viral load, and circles denote monkeys with a high viral load in the study of Mohri et al. [13]. This analysis illustrates that the estimate of the average turnover rate depends on 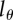but not strongly.

We therefore depict the estimated turnover rates for CD4⁺ and CD4⁻ memory T cells in figure 5 for the two reasonable values of 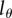, and observe that the turnover rates do not strongly depend on the choice between these detection limits.

To test whether the estimated turnover rates differ between the models, we have refitted all memory T cell data from the Mohri et al. [13], and in figure 6 we depict our best estimates together with those obtained in De Boer et al. [27].

Figure 6.

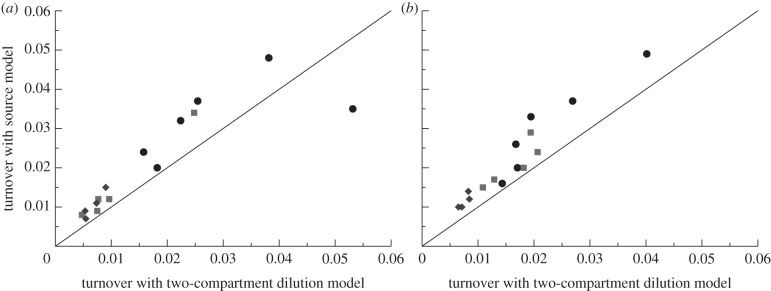
Comparing the average turnover rates as estimated by the dilution model of equation (2.8) for 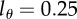with those of the source model [27]. (a) CD4⁺ memory T cells and (b) CD4⁻ memory T cells. The source model has higher estimates for the average turnover rates but the differences tend to remain fairly small. Diamonds denote uninfected monkeys (U), squares SIV-infected monkeys with a low viral load (L), and circles monkeys with a high viral load (H) in the study of Mohri et al. [13]. Monkey H1292 was not fitted by De Boer et al. [27] and is absent from this figure.

The turnover rates estimated by the source model are somewhat higher than those in the dilution model, but the estimates made by both models correlate very well. One reason for the higher average turnover rates estimated by the source model could be due to the fact that this model has a single exponential to describe the sometimes biphasic up- and down-slopes, whereas the kinetic heterogeneity in the dilution model readily accounts for biphasic curves. Fortunately, the difference between the two sets of estimates is not large, and would have been even smaller if we had fitted the data with the—slightly suboptimal—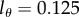 because that tends to give higher turnover rates for these data (figure 5).

The individual estimates in tables 1 and 2 show that the parameters p₁, p₂ and α have quite wide confidence intervals, and that when these get combined into an average turnover 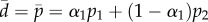, this average has much more narrow confidence limits.

Table 1.

Parameters and their 95% CIs estimated by fitting equation (2.8) to the CD4⁺ memory T cells data of Mohri et al. [13]. The detection limit was set to 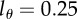. Monkey H1314 was only labelled for two weeks and was fitted with T = 14 days, all other monkeys with T = 21 days. In fits we set 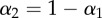. Confidence intervals were calculated by bootstrapping the residuals with 1000 simulations.

monkey	p1 (day−1)	p2 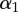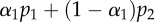(day−1)		(day−1)
H1316	0.0041 (0.0019–0.0063)	0.081 (0.063–0.105)	0.56 (0.48–0.62)	0.038 (0.032–0.046)
H1284	0.0018 (0–0.0063)	0.049 (0.035–0.087)	0.57 (0.44–0.74)	0.022 (0.018–0.031)
H1292	0.0014 (0–0.0029)	0.034 (0.002–0.441)	0.92 (0.54–0.98)	0.004 (0.002–0.031)
H1296	0.0017 (0.0013–0.002)	0.398 (0.229–0.462)	0.86 (0.85–0.88)	0.056 (0.032–0.069)
H1314	0.0023 (0–0.0049)	0.072 (0.025–0.408)	0.82 (0.63–0.91)	0.015 (0.008–0.052)
H1348	0.0016 (0–0.0031)	0.072 (0.056–0.096)	0.66 (0.6–0.72)	0.025 (0.021–0.031)
H1442	0.0018 (0–0.0048)	0.050 (0.032–0.227)	0.71 (0.59–0.85)	0.016 (0.011–0.038)
L1294	0.0013 (0–0.0025)	0.046 (0.023–0.108)	0.86 (0.75–0.93)	0.008 (0.006–0.013)
L1324	0.0025 (0–0.0033)	0.036 (0.009–0.31)	0.93 (0.58–0.98)	0.005 (0.004–0.012)
L1380	0.0020 (0.0012–0.0027)	0.069 (0.043–0.115)	0.89 (0.84–0.92)	0.010 (0.007–0.013)
L1394	0.0016 (0.001–0.0019)	0.076 (0.049–0.12)	0.92 (0.89–0.94)	0.007 (0.006–0.01)
L1436	0.0029 (0–0.0062)	0.069 (0.039–0.143)	0.67 (0.51–0.8)	0.025 (0.017–0.041)
U1372	0.0030 (0.0025–0.0032)	0.092 (0.032–0.377)	0.97 (0.94–0.98)	0.005 (0.004–0.013)
U1426	0.0006 (0–0.0035)	0.015 (0.009–0.066)	0.67 (0.5–0.95)	0.005 (0.005–0.007)
U1458	0.0037 (0–0.0044)	0.058 (0.015–0.193)	0.93 (0.6–0.97)	0.007 (0.006–0.012)
U1466	0.0016 (0–0.0036)	0.031 (0.019–0.065)	0.75 (0.59–0.88)	0.009 (0.007–0.012)

Table 2.

Parameters and their 95% CIs estimated by fitting equation (2.8) to the CD4⁻ memory T cells data of Mohri et al. [13]. The detection limit was set to 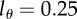. Monkey H1314 was only labelled for two weeks and was fitted with T = 14 days, all other monkeys with T = 21 days.

monkey	p1 (day−1)	p2 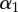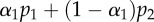(day−1)		(day−1)
H1316	0.0042 (0–0.0075)	0.076 (0.058–0.107)	0.50 (0.39–0.59)	0.040 (0.033–0.05)
H1284	0.0019 (0–0.0063)	0.049 (0.038–0.072)	0.47 (0.37–0.63)	0.027 (0.022–0.034)
H1292	0.0007 (0–0.0037)	0.023 (0.003–0.429)	0.80 (0.31–0.97)	0.005 (0.003–0.031)
H1296	0.0017 (0.0007–0.0026)	0.087 (0.057–0.134)	0.82 (0.77–0.86)	0.017 (0.013–0.023)
H1314	0.0035 (0–0.0059)	0.052 (0.019–0.22)	0.82 (0.53–0.92)	0.012 (0.008–0.028)
H1348	0.0028 (0–0.0046)	0.049 (0.037–0.065)	0.64 (0.51–0.71)	0.019 (0.017–0.023)
H1442	0.0020 (0–0.0056)	0.048 (0.029–0.183)	0.68 (0.55–0.85)	0.017 (0.01–0.037)
L1294	0.0023 (0–0.0038)	0.065 (0.03–0.15)	0.83 (0.69–0.9)	0.013 (0.009–0.021)
L1324	0.0035 (0.0027–0.0043)	0.073 (0.058–0.09)	0.75 (0.71–0.79)	0.021 (0.018–0.024)
L1380	0.0030 (0.0005–0.0041)	0.089 (0.045–0.263)	0.82 (0.71–0.88)	0.018 (0.012–0.041)
L1394	0.0016 (0–0.0029)	0.060 (0.033–0.187)	0.84 (0.74–0.91)	0.011 (0.007–0.022)
L1436	0.0025 (0–0.0057)	0.053 (0.033–0.123)	0.67 (0.52–0.81)	0.019 (0.013–0.032)
U1372	0.0028 (0–0.0038)	0.047 (0.021–0.1)	0.87 (0.67–0.92)	0.008 (0.006–0.013)
U1426	0.0024 (0–0.0032)	0.037 (0.018–0.082)	0.88 (0.69–0.94)	0.007 (0.005–0.009)
U1458	0.0037 (0–0.0064)	0.014 (0.008–0.126)	0.68 (0.24–0.98)	0.007 (0.007–0.01)
U1466	0.0010 (0–0.0028)	0.044 (0.032–0.07)	0.79 (0.72–0.88)	0.010 (0.008–0.013)

Apparently, the p₁, p₂ and α parameter estimates are not independent; for example, a high p_i can be compensated for by a small 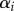. This confirms earlier conclusions that one can only robustly estimate an average turnover rate from the labelling data of heterogeneous populations [26,27,36].

2.4. Cells produced by a source

This paper is about explaining the loss of the fraction of BrdU⁺ cells during de-labelling in self-renewing populations. Still, we would like to extend our analysis for cell types that are partly, or largely, maintained by an external source. Examples would be naive T cells originating from the thymus, B cells from the bone marrow, and one could argue that even memory T cell populations are partly maintained by a source of clonally expanded naive T cells after antigenic stimulation.

Thus, we extend equation (1.1) in §1 and go back to the original model proposed by Mohri et al. [13],

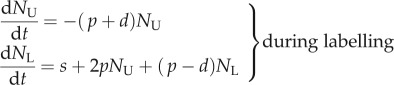and

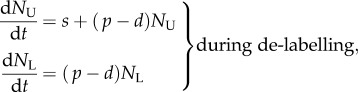2.11

where we, for simplicity, assume that the source of s cells per day consists of labelled versus unlabelled cells during the two phases of the experiment, respectively. Using the same methodology as in §1, we find that dL/dt = [2p + s/N(t)](1 − L) during the labelling phase, and that dL/dt = −[s/N(t)]L during the de-labelling phase. The s/N(t) term can be interpreted as the daily fractional replacement by the source. Indeed, we see that allowing for an unlabelled source allows for a loss of BrdU⁺ cells at a rate of turnover due to the source. If the total cell number N(t) is changing during the experiment, i.e. by dN/dt = s + (p − d)N, it is difficult to assign a simple interpretation to the up- and down-slopes, and one would have to know the total cell number, N(t), over time to fit the data. If, on the other hand, the total cell number is not changing over the experiment, one can substitute 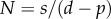to ‘rediscover’ that dL/dt = (p + d)(1 − L) during the labelling phase, and that 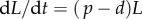during the de-labelling phase. Obviously, if s = 0 we obtain the dL/dt = 2p(1 − L) = 2d(1 − L) and the dL/dt = 0 results discussed earlier. Importantly, if one is describing a population that is solely maintained by the source, i.e. p = 0, the equations become dL/dt = d(1 − L) and dL/dt = −dL, respectively. Thus, if naive and memory T cells were to have the same expected lifespan, 1/d, i.e. the same turnover rate d, one still expects a twofold higher up-slope for self-renewing memory T cells than for the non-dividing naive T cells. In other words, if one is labelling naive and memory T cells with BrdU and observes a twofold higher up-slope in the memory T cell data, this should not be taken as evidence for a twofold faster turnover, but would rather suggest equal turnover rates. This model also predicts different down-slopes for memory and naive T cells, i.e. flat and −d, but as we argued above that at least part of the down-slope is readily explained by BrdU dilution, this has little predictive power.

2.5. Division-linked/death model

In our basic mathematical model, we assumed that division and death of cells in the population are independent processes, and that, after cell division, both daughter cells have equal chances of dying. Alternatively, cell division may be associated with an increased chance of death, or, owing to asymmetric division of cellular proteins, one of the daughter cells may experience a higher chance of death than the other cell. Such division-linked models have been discussed previously for the analysis of CFSE data [3,33]. Extending equation (1.1) with division-linked death, the dynamics of the labelled and the total number of cells during the labelling phase are then given by equations

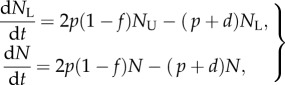2.12

where f is the probability of cell death following division. Proceeding as above, the dynamics of the fraction of BrdU⁺ cells in the population is dL/dt = 2p(1 − f)(1 − L), and is therefore increasing at the initial slope of 2p(1 − f). For the steady state of a self-renewing population in which all death is linked to division (d = 0), one obtains that f = 1/2, and that the initial up-slope is simply p, which corresponds to the average rate of cell turnover. When cell death is not linked to cell division, i.e. if f = 0, this slope is 2p (see equation (1.1)), or twice the average turnover rate at steady state. Thus, the initial slope of the fraction of labelled cells, and, as a result, the estimate of the average turnover rate, depends on the details of how death is distributed over the life cycle of the self-renewing cells. The same twofold difference in estimates of the rate of cell division complicates the quantitative interpretation of CFSE data [3,33].

3. Discussion

In this paper, the conventional birth–death model for a self-renewing population was re-formulated into a mechanistic BrdU accumulation and dilution model based upon the exact number of divisions cells have completed. The main advantage of this approach is that one can account for BrdU dilution during the de-labelling phase without having to introduce new assumptions. If the detection limit below which cells are scored as BrdU⁻ is known, this model readily accounts for the loss of BrdU⁺ cells during de-labelling where the division rate p matches the death rate d. Thanks to the simple structure of the model, it was also straightforward to extend this model with kinetic heterogeneity, and we have shown that a two-compartment model consisting of a slow and a more rapid subpopulation provides a good description of existing BrdU data.

We have seen that the de-labelling phase of this model is not reflecting the death rates, nor the difference between the division and the death rates in the population, and is influenced by the kinetic heterogeneity of the population, the detection limit and the degree of labelling that cells have achieved during the labelling phase. It is therefore not correct to use simple regression techniques to estimate the exponentials underlying observed de-labelling curves, and to interpret these exponentials as the death rates of subpopulations of the cells that were labelled [17–19].

By combining CFSE with BrdU labelling experiments, Takizawa et al. [22] showed that the BrdU intensities of cells saturate with the number of divisions these cells have completed (their figure 1b). This seems to be in a reasonable agreement with the definition 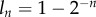(figure 1). In the data, there is a wide distribution of BrdU intensities for each value of n [22]. However, even after one division in the presence of BrdU, a large fraction of the cells remains below the detection threshold, suggesting a low efficacy of BrdU labelling in this experiment. Indeed, it is possible that the efficacy of BrdU incorporation in the DNA during the labelling phase varies with the cell type and the cell location in the body, and it probably depends on the local BrdU concentration. The incorporation of the efficacy of BrdU labelling in our mechanistic model is a challenging task. Mechanistically, one expects that a low efficacy of BrdU incorporation translates into a lower level of labelling of each newly synthesized DNA strand, and hence into a lower level of fluorescence of the whole cell. The observed distribution of BrdU intensities for each value of n [22] would then be a consequence of heterogeneity between cells in the incorporation of BrdU, as there will be a distribution of BrdU intensities of cells having a fraction 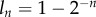of their DNA strands labelled. Because labelling efficacy can change with every division owing to cells dividing in different locations in the body, the model will have to involve a probability distribution for labelling efficacy. Extensions of the mathematical models that include probabilistic nature of BrdU incorporation in the DNA will be addressed in future work.

We have shown that the estimates of the average turnover rate obtained with BrdU labelling depend on the detection threshold 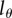, i.e. on the number of divisions required for a BrdU⁺ cell to result in BrdU⁻ progeny. Lower 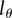in general results in higher estimates for the average turnover rates (figure 5). For obtaining precise estimates of the average turnover rate, it is therefore critical to have good estimates for the detection limit. We see at least two possible approaches for obtaining an estimate for the critical BrdU intensity, 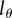, in any particular experimental set-up. First, one can harvest cells at the end of the labelling phase, label these with CFSE and trace in vitro after how many divisions these cells become BrdU⁻. Second, one could stay with the in vivo data by tracing not only the fraction of BrdU⁺ cells over time, but also the dynamics of MFI of all cells, or possibly only that of BrdU⁺ cells. Fitting these data simultaneously by the mathematical model (equations (2.8)–(2.10)) might allow one to obtain well-defined estimates for both the rate of lymphocyte turnover 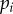and the critical BrdU intensity 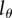. It remains to be established whether combining the data on the fraction and the BrdU MFI provides enough information to estimate these two parameters with a sufficient level of confidence.

In populations maintaining themselves with transient bursts of proliferation, one expects that a higher death rate of the recently divided, and hence BrdU⁺, cells contributes to the loss of BrdU⁺ cells during de-labelling [28–30]. This is sometimes called ‘temporal heterogeneity’ [37]. Recently, we developed simple models for temporal heterogeneity [36], and showed that if one were to perform labelling experiments with deuterium in such a system, the solutions describing the labelling curves would be very similar to those of the kinetic heterogeneity model considered here, and developed by Ganusov et al. [34]. A similar analysis has yet to be performed for BrdU labelling as it is not obvious that temporal and kinetic heterogeneity will result in similar equations for the fraction of BrdU⁺ cells.

For various reasons, it is preferable to label with deuterium rather than with BrdU, and the only good reason for using BrdU is that the fraction of BrdU⁺ cells can be determined by flow cytometry, making it cheaper and simpler than deuterium labelling. Deuterium should have no side-effects in terms of toxicity or being mitogenic, and under steady-state conditions deuterium data are much easier to interpret. During deuterium labelling, one tracks the enrichment of deuterium in the total DNA, and not in individual cells. In other words, the general equations are

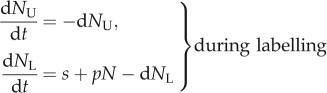and

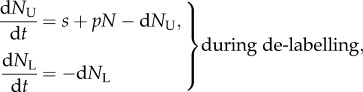3.1

where 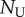and 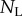are proportional to the number of labelled and un-labelled DNA strands in the population [38], and for simplicity we let the source be completely labelled or un-labelled during the two phases of the experiment, respectively. By defining 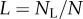as the fraction of labelled strands, one readily arrives at the 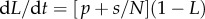and the 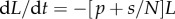during labelling and de-labelling, respectively. Thus, when the total cell number is not at a steady state, one would have to know N to be able to fit the deuterium enrichment. However, assuming steady state, these expressions become the satisfyingly simple 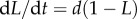and 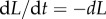, respectively. Thus, whether or not part of the cells is maintained by a source, the up- and down-slope can correctly be interpreted as the death or turnover rate of the population. This was not the case for BrdU labelling curves where we expect a twofold difference in the up-slope of cells maintained by division or a source (see equation (2.11)).

Combining BrdU and deuterium labelling may allow one to estimate the contributions of cell division and cells from a source to the overall cell turnover. Our analysis mentioned earlier suggests that during labelling the increase in the fraction of BrdU⁺ cells occurs at the initial slope of a₁ = 2p + s/N, while the deuterium enrichment during labelling will increase at an initial slope a₂ = p + s/N. The difference between the slopes, i.e. a₁ − a₂ = p, therefore provides an estimate for the rate of cell division in the population, and 2a₂ − a₁ = s/N is an estimate for the daily replacement of cells in the population from the source.

The model that we have developed seems to be a good first choice for fitting BrdU data measured in self-renewing populations because it does not require additional assumptions other than the existence of a detection limit, and because it can easily be extended with kinetic heterogeneity. Although this is a major step forward, the new model is not completely general. In order to estimate the rate of turnover of cells in a population, one needs to know how new cells in that population are produced. Production by division of cells within the population requires a different model from production by influx of cells from another cell population. Other complications include the effect of temporal heterogeneity [36], and the possibility of division-linked death whereby cell division on average leads to fewer than two daughter cells [3,33,39]. Nevertheless, the new model should improve the interpretation of BrdU data measured in self-renewing populations, and opens new venues for combining of labelling with both deuterium and BrdU.