The Relationship Between F_ST and the Frequency of the Most Frequent Allele

Abstract

F_ST is frequently used as a summary of genetic differentiation among groups. It has been suggested that F_ST depends on the allele frequencies at a locus, as it exhibits a variety of peculiar properties related to genetic diversity: higher values for biallelic single-nucleotide polymorphisms (SNPs) than for multiallelic microsatellites, low values among high-diversity populations viewed as substantially distinct, and low values for populations that differ primarily in their profiles of rare alleles. A full mathematical understanding of the dependence of F_ST on allele frequencies, however, has been elusive. Here, we examine the relationship between F_ST and the frequency of the most frequent allele, demonstrating that the range of values that F_ST can take is restricted considerably by the allele-frequency distribution. For a two-population model, we derive strict bounds on F_ST as a function of the frequency M of the allele with highest mean frequency between the pair of populations. Using these bounds, we show that for a value of M chosen uniformly between 0 and 1 at a multiallelic locus whose number of alleles is left unspecified, the mean maximum F_ST is ∼0.3585. Further, F_ST is restricted to values much less than 1 when M is low or high, and the contribution to the maximum F_ST made by the most frequent allele is on average ∼0.4485. Using bounds on homozygosity that we have previously derived as functions of M, we describe strict bounds on F_ST in terms of the homozygosity of the total population, finding that the mean maximum F_ST given this homozygosity is 1 − ln 2 ≈ 0.3069. Our results provide a conceptual basis for understanding the dependence of F_ST on allele frequencies and genetic diversity and for interpreting the roles of these quantities in computations of F_ST from population-genetic data. Further, our analysis suggests that many unusual observations of F_ST, including the relatively low F_ST values in high-diversity human populations from Africa and the relatively low estimates of F_ST for microsatellites compared to SNPs, can be understood not as biological phenomena associated with different groups of populations or classes of markers but rather as consequences of the intrinsic mathematical dependence of F_ST on the properties of allele-frequency distributions.

DIFFERENTIATION among groups is one of the fundamental subjects of the field of population genetics. Comparisons of the level of variation among subpopulations with the level of variation in the total population have been employed frequently in population-genetic theory, in statistical methods for data analysis, and in empirical studies of distributions of genetic variation. Wright’s (Wright 1951) fixation indices, and F_ST in particular, have been central to this effort.

Wright’s F_ST was originally defined as the correlation between two randomly sampled gametes from the same subpopulation when the correlation of two randomly sampled gametes from the total population is set to zero. Several definitions of F_ST or F_ST-like quantities are now available, relying on a variety of different conceptual formulations but all measuring some aspect of population differentiation (e.g., Charlesworth 1998; Holsinger and Weir 2009). Many authors have claimed that one or another formulation of F_ST is affected by levels of genetic diversity or by allele frequencies, either because the range of F_ST is restricted by these quantities or because these quantities affect the degree to which F_ST reflects population differentiation (e.g., Charlesworth 1998; Nagylaki 1998; Hedrick 1999, 2005; Long and Kittles 2003; Jost 2008; Ryman and Leimar 2008; Long 2009; Meirmans and Hedrick 2011). For example, Nagylaki (1998) and Hedrick (1999) argued that measures of F_ST may be poor measures of genetic differentiation when the level of diversity is high. Charlesworth (1998) suggested that F_ST can be inflated when diversity is low, arguing that F_ST might not be appropriate for comparing loci with substantially different levels of variation. In a provocative recent article, Jost (2008) used the diversity dependence of forms of F_ST to question their utility as differentiation measures at all.

One definition that is convenient for mathematical assessment of the relationship of an F_ST-like quantity and allele frequencies is the quantity labeled G_ST by Nei (1973), which for a given locus measures the difference between the heterozygosity of the total (pooled) population, h_T, and the mean heterozygosity across subpopulations, h_S, divided by the heterozygosity of the total population:

$$G_{\text{ST}}=\frac{h_{\text{T}}-h_{\text{S}}}{h_{\text{T}}}.$$ (1)

In terms of the homozygosity of the total population, H_T = 1 − h_T, and the mean homozygosity across subpopulations, H_S = 1 − h_S, we can write

$$G_{\text{ST}}=\frac{H_{\text{S}}-H_{\text{T}}}{1-H_{\text{T}}}.$$ (2)

The Wahlund (1928) principle guarantees that H_S ≥ H_T and, therefore, because H_S ≤ 1 and for a polymorphic locus with finitely many alleles, 0 < H_T < 1, G_ST lies in the interval [0,1].

Using G_ST for their definition of F_ST, Hedrick (1999, 2005) and Long and Kittles (2003) pointed out that because h_T < 1, F_ST cannot exceed the mean homozygosity across subpopulations, H_S:

$$F_{\text{ST}}=1-h_{\text{S}}/h_{\text{T}}<1-h_{\text{S}}=H_{\text{S}}.$$ (3)

Hedrick (2005) obtained this result by considering a set of K equal-sized subpopulations, in which each allele is private to a single subpopulation. In the limit as K → ∞, a stronger upper bound on F_ST as a function of H_S and K reduces to Equation 3 (see also Jin and Chakraborty 1995 and Long and Kittles 2003).

While Hedrick (1999, 2005) and Long and Kittles (2003) have clarified the relationship between F_ST and the mean homozygosity H_S across subpopulations, their approaches do not easily illuminate the connection between F_ST and allele frequencies themselves. A formal understanding of the relationship between F_ST and allele frequencies would make it possible to more fully understand the behavior of F_ST in situations where markers of interest differ substantially in allele frequencies or levels of genetic diversity. Our recent work on the relationship between homozygosity and the frequency of the most frequent allele (Rosenberg and Jakobsson 2008; Reddy and Rosenberg 2012) provides a mathematical approach for formal investigation of bounds on population-genetic statistics in terms of allele frequencies. In this article, we therefore seek to thoroughly examine the dependence of F_ST on allele frequencies by investigating the upper bound on F_ST in terms of the frequency M of the most frequent allele across a pair of populations. We derive bounds on F_ST given the frequency of the most frequent allele and bounds on the frequency of the most frequent allele given F_ST. We consider loci with arbitrarily many alleles in a pair of subpopulations. Using theory for the bounds on homozygosity given the frequency of the most frequent allele, we obtain strict bounds on F_ST given the homozygosity of the total population. Our analysis clarifies the relationships among F_ST, allele frequencies, and homozygosity, providing explanations for peculiar observations of F_ST that can be attributed to allele-frequency dependence.

Model

We examine a polymorphic locus with at least two alleles in a setting with K subpopulations that contribute equally to a total population. Denote the number of distinct alleles by I, the frequency of allele i in population k by p_ki, and the mean frequency of allele i across populations by ${\stackrel{-}{p}}_i=\frac{1}{K}{\displaystyle {\sum }_{k=1}^K{p}_{ki}}.$ We primarily report our results in terms of homozygosities, which can be easily transformed into heterozygosities.

We consider F_ST formulated as a property of nonnegative numbers between 0 and 1 such that within populations, the allele frequencies sum to 1 (${\displaystyle {\sum }_{i=1}^I{p}_{ki}}=1$ for each k). This formulation is the same as the formulation of Nei’s G_ST, which we hereafter denote by F. We have (Nei 1973)

$$F=\frac{h_{\text{T}}-h_{\text{S}}}{h_{\text{T}}}=\frac{H_{\text{S}}-H_{\text{T}}}{1-H_{\text{T}}},$$

where

$$H_{\text{T}}={\displaystyle \sum _{i=1}^I{\stackrel{-}{p}}_i^2}={\displaystyle \sum _{i=1}^I{\left(\frac{1}{K}{\displaystyle \sum _{k=1}^K{p}_{ki}}\right)}^2}$$

and

$$H_{\text{S}}=\frac{1}{K}{\displaystyle \sum _{k=1}^K\left({\displaystyle \sum _{i=1}^I{p}_{ki}^2}\right)}=\frac{1}{K}{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=1}^I{p}_{ki}^2}}.$$

The assumption that the locus is polymorphic guarantees that H_T < 1. The assumption that I, the number of distinct alleles at the locus, is finite guarantees that H_T > 0 (and hence, H_S > 0 because H_S ≥ H_T). Thus, 0 < H_T < 1 and 0 < H_S ≤ 1.

We assume that all allele frequencies are the parametric allele frequencies of the population under consideration. Thus, the frequency of an allele is the probability of drawing the allele from the parametric frequency distribution; homozygosity is then the probability that two independent random draws carry the same allelic type, and heterozygosity is the probability that two independent random draws carry different allelic types. We emphasize that in our formulation, F, H_T, and H_S are functions of the parametric allele frequencies, and our interest is in the properties of these functions and their relationships with the allele frequencies; we do not investigate their estimation from data, nor do we consider how evolutionary models affect the underlying allele frequencies involved in their computation.

We focus on the case of two subpopulations (K = 2). In this case, the allele frequencies are denoted p_1i for population 1 and p_2i for population 2. For each i from 1 to I, let σ_i = p_1i + p_2i be the sum across populations of the frequency of allele i. Each σ_i lies in (0, 2), and the number of alleles I counts only those alleles with σ_i > 0. We denote ${\stackrel{-}{p}}_i={\sigma }_i/2$. Without loss of generality, we place the alleles in decreasing order, such that σ₁ ≥ σ₂ ≥ … ≥ σ_I. We denote the frequency of the most frequent allele in the total pooled population by M = σ₁/2, and we find it convenient to express some results in terms of σ₁ and others in terms of M. Because ${\displaystyle {\sum }_{i=1}^I{\sigma }_i}=2$ and each σ_i is positive, we have 1/I ≤ M < 1.

Let δ_i = |p_1i − p_2i| be the absolute difference between p_1i and p_2i. We can write the homozygosity of the total population as

$$H_{\text{T}}={\displaystyle \sum _{i=1}^I{\stackrel{-}{p}}_i^2}=\frac{1}{4}{\displaystyle \sum _{i=1}^I{\sigma }_i^2},$$

and the mean homozygosity across subpopulations as

$$H_{\text{S}}=\frac{1}{2}{\displaystyle \sum _{k=1}^2{\displaystyle \sum _{i=1}^I{p}_{ki}^2}}=\frac{1}{2}{\displaystyle \sum _{i=1}^I\left(p_{1i}^2+p_{2i}^2\right)}.$$

We then have (Boca and Rosenberg 2011)

$$F=\frac{{\displaystyle {\sum }_{i=1}^I{\delta }_i^2}}{4-{\displaystyle {\sum }_{i=1}^I{\sigma }_i^2}}.$$ (4)

In other words, F can be computed solely using the allele-frequency sums and differences between the two populations.

Bounds on F

Our goal is to study the relationship between F and M in the general case of I alleles in two populations. For convenience, we write F as a function of σ₁, keeping in mind that σ₁/2 = M, and we begin by considering the special case in which I = 2.

Bounds on F for two alleles

This case has two alleles, with frequencies p₁₁ and p₁₂ in population 1, and p₂₁ and p₂₂ in population 2 (Table 1). The frequency of the second allele is p₁₂ = 1 − p₁₁ in population 1 and p₂₂ = 1 − p₂₁ in population 2. Using Equation 4, we have a simple expression for F (Weir 1996; Rosenberg et al. 2003):

$$F=\frac{{\delta }_1^2+{\left[\left(1-p_{11}\right)-\left(1-p_{21}\right)\right]}^2}{4-{\sigma }_1^2-{\left[\left(1-p_{11}\right)+\left(1-p_{21}\right)\right]}^2}=\frac{{\delta }_1^2}{{\sigma }_1\left(2-{\sigma }_1\right)}.$$ (5)

We determine the upper and lower bounds of F in terms of the frequency of the most frequent allele M = σ₁/2. Because the alleles are arranged to satisfy σ₁ ≥ σ₂ and because σ₁ + σ₂ = 2, σ₁ must lie in [1, 2). For the lower bound on F as a function of σ₁, we note that if allele 1 has the same frequency in both populations, then p₁₁ = p₂₁ = σ₁/2. The frequency of allele 2 will also be the same in the two populations, p₁₂ = p₂₂ = 1 − σ₁/2, and δ₁ and δ₂ will both equal zero. For these allele frequencies, we see that H_S = H_T, and it is clear from Equation 5 that F(σ₁) ≥ 0 for all values of σ₁ in [1, 2), with equality if and only if p₁₁ = p₂₁ = σ₁/2.

Table 1 . Notation for two alleles in two populations.

	Allele
Population	1	2	Sum
1	p11	p12	1
2	p21	p22	1
Sum	σ1	σ2	2
Absolute difference	δ1	δ2	—

For the upper bound, we first note that because δ₁ = 2p₁₁ − σ₁ when p₁₁ ≥ p₂₁ and δ₁ = 2p₂₁ − σ₁ when p₂₁ ≥ p₁₁,

$${\delta }_1^2\le {\left(2-{\sigma }_1\right)}^2,$$ (6)

with equality if and only if p₁₁ = 1 or p₂₁ = 1. Using Equations 5 and 6, we have

$$F\left({\sigma }_1\right)\le \frac{{\left(2-{\sigma }_1\right)}^2}{{\sigma }_1\left(2-{\sigma }_1\right)}=\frac{2-{\sigma }_1}{{\sigma }_1}.$$

Thus, the upper bound on F as a function of σ₁ is achieved when the allele frequencies of the two populations differ as much as possible, that is, when (p₁₁, p₂₁) = (1, σ₁ − 1) or (p₁₁, p₂₁) = (σ₁ − 1, 1). The bounds on F are

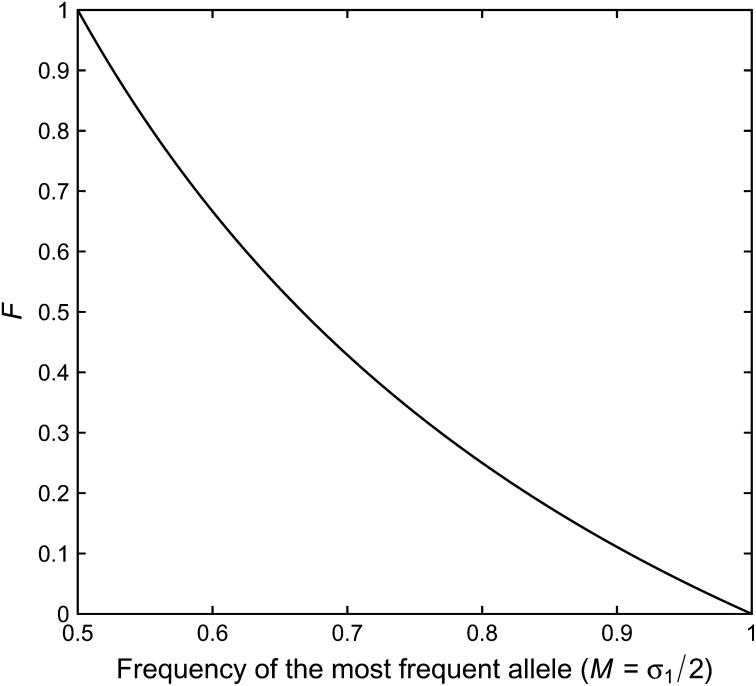
$$F\epsilon \left[0,\frac{2-{\sigma }_1}{{\sigma }_1}\right].$$ (7)

Figure 1 shows the upper bound as a function of the most frequent allele, illustrating a monotonic decline from q(1/2) = 1 to q(1) = 0.

Figure 1 .

The upper bound on F as a function of the frequency M of the most frequent allele, for the two-allele case. The upper bound is computed from Equation 7. The lower bound on F is 0 for all values of M.

Lower bound on F for an unspecified number of alleles

For any number of alleles I and any set of σ_i, by noting that the denominator of F in Equation 4 is positive and that the numerator is ${\displaystyle {\sum }_{i=1}^I{\delta }_i^2}\ge 0$, we see that Equation 4 takes the value of zero if and only if for each i, p_1i = p_2i = σ_i/2. Thus, the lower bound on F as a function of σ₁ is achieved when the allele frequencies are the same in both populations for all I alleles. Thus, F = 0 is attainable for any value of σ₁ in (0, 2).

Upper bound on F for an unspecified number of alleles

The upper bound on F as a function of σ₁ has different properties for σ₁ ε (0, 1) and for σ₁ ε [1, 2). We begin with σ₁ ε (0, 1).

Using Equation 4, we can rearrange F(σ₁) to obtain

$$F\left({\sigma }_1\right)=-1+2\frac{2-2{\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}}{\left(4-{\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}-{\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}\right)-2{\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}}.$$ (8)

As we assume that the locus of interest is polymorphic, both the numerator and denominator in the fraction in Equation 8 are positive. Fix ${\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}$ and ${\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}$. Because the same quantity $2{\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}$ is subtracted in the numerator and denominator from quantities that must exceed it (2 in the numerator, $4-{\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}-{\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}$ in the denominator), the fraction is maximized when ${\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}$ is minimized, that is, when ${\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}=0$. In other words, given ${\sigma }_1$, for fixed ${\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}$ and ${\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}$, F(σ₁) is maximal when each allele is found only in one of the two subpopulations.

To complete the maximization of F(σ₁) as a function of σ₁, it remains to maximize ${\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}$ and ${\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}$. These two maximizations can be performed separately, as no allele appears in both subpopulations. Further, by symmetry, ${\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}$ and ${\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}$ must have the same maximum.

Define $J=\lceil {\sigma }_1^{-1}\rceil$. The number of alleles I is unspecified; we search for an upper bound over all possible values I ≥ 2 and discover that the maximum occurs when each subpopulation has I = J distinct alleles. Because p_1i + p_2i ≤ σ₁ and because for each i, at the maximum of F(σ₁), each allele has either p_1i = 0 or p_2i = 0, it suffices to maximize ${\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}$ subject to ${\displaystyle {\sum }_{i=1}^I{p}_{1i}}=1$ and p_1i ≤ σ₁ for all i. This maximization is the same problem considered in Rosenberg and Jakobsson (2008, Lemma 3), which demonstrates that the maximum occurs if and only if the locus has J − 1 alleles of frequency σ₁ and one remaining allele of frequency 1 − (J − 1)σ₁.

Lemma 3 of Rosenberg and Jakobsson (2008) yields 1 − σ₁(J − 1)(2 − Jσ₁) for each of the two maxima, on ${\displaystyle {\sum }_{i=1}^I{p}_{1i}^2}$ and on ${\displaystyle {\sum }_{i=1}^I{p}_{2i}^2}$. We then conclude

$$F\left({\sigma }_1\right)\le \frac{1-{\sigma }_1\left(J-1\right)\left(2-J{\sigma }_1\right)}{1+{\sigma }_1\left(J-1\right)\left(2-J{\sigma }_1\right)},$$ (9)

with equality if and only if the locus has 2J alleles, J of which occur only in the first subpopulation and the other J of which occur only in the second population, and each subpopulation has J − 1 alleles of frequency σ₁ and one allele of frequency 1 − (J − 1)σ₁. Because $J=\lceil {\sigma }_1^{-1}\rceil$, we have

$$F\left({\sigma }_1\right)\le \frac{1-{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(2-\lceil {\sigma }_1^{-1}\rceil {\sigma }_1\right)}{1+{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(2-\lceil {\sigma }_1^{-1}\rceil {\sigma }_1\right)}.$$ (10)

For the case of σ₁ ε [1, 2), we separate terms in Equation 4 for the first and subsequent alleles:

$$F\left({\sigma }_1\right)=\frac{{\delta }_1^2+{\displaystyle {\sum }_{i=2}^I{\delta }_i^2}}{4-{\sigma }_1^2-{\displaystyle {\sum }_{i=2}^I{\sigma }_i^2}}.$$ (11)

The upper bound on F, given σ₁, occurs when ${\delta }_1^2$, ${\displaystyle {\sum }_{i=2}^I{\delta }_i^2}$, and ${\displaystyle {\sum }_{i=2}^I{\sigma }_i^2}$ are maximized. To maximize ${\delta }_1^2$, note that as in the two-allele case (Equation 6), for σ₁ ε [1, 2), ${\delta }_1^2\le {\left(2-{\sigma }_1\right)}^2$, with equality if and only if p₁₁ = 1 or p₂₁ = 1.

Next, for any i, δ_i ≤ σ_i, with equality if and only if p_1i = 0 or p_2i = 0. Then

$${\displaystyle \sum _{i=2}^I{\delta }_i^2}\le {\displaystyle \sum _{i=2}^I{\sigma }_i^2}\le {\left({\displaystyle {\sum }_{i=2}^I{\sigma }_i}\right)}^2={\left(2-{\sigma }_1\right)}^2,$$ (12)

where the last step follows from the fact that ${\displaystyle {\sum }_{i=1}^I{\sigma }_i}=2$. Equality in the second step requires that among the σ_i with i ≥ 2, only one can be positive, namely σ₂, by the assumption that the alleles are labeled in decreasing order of frequency. Thus, equality occurs in both inequalities if and only if σ₂ = 2 − σ₁ and either p₁₂ or p₂₂ is 0.

We have therefore found that given σ₁ ε [1, 2), ${\delta }_1^2$, ${\displaystyle {\sum }_{i=2}^I{\sigma }_i^2}$, and ${\displaystyle {\sum }_{i=2}^I{\delta }_i^2}$ are all maximized under exactly the same conditions—when (p₁₁, p₁₂, p₂₁, p₂₂) = (1, 0, σ₁ − 1, 2 − σ₁) or (σ₁ − 1, 2 − σ₁, 1, 0). Replacing the terms ${\delta }_1^2$, ${\displaystyle {\sum }_{i=2}^I{\delta }_i^2}$ and ${\displaystyle {\sum }_{i=2}^I{\sigma }_i^2}$ in Equation 11 using inequalities 6 and 12, we have

$$F\left({\sigma }_1\right)\le \frac{{\left(2-{\sigma }_1\right)}^2+{\left(2-{\sigma }_1\right)}^2}{4-{\sigma }_1^2-{\left(2-{\sigma }_1\right)}^2}=\frac{2-{\sigma }_1}{{\sigma }_1},$$ (13)

with equality if and only if p₁₁ = 1 or p₂₁ = 1 and σ₂ = 2 − σ₁. This result matches the two-allele case: when σ₁ ε [1, 2), the case of an unspecified number of alleles reduces to the case of two alleles.

Summarizing our results, the bounds of F are

$$F\epsilon \{\begin{array}{cc}\left[0,Q\left({\sigma }_1\right)\right],& 0<{\sigma }_1<1\\ \left[0,q\left({\sigma }_1\right)\right],& 1\le {\sigma }_1<2,\end{array}$$ (14)

where

$$Q\left({\sigma }_1\right)=\frac{1-{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(2-\lceil {\sigma }_1^{-1}\rceil {\sigma }_1\right)}{1+{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(2-\lceil {\sigma }_1^{-1}\rceil {\sigma }_1\right)}$$ (15)

$$q\left({\sigma }_1\right)=\frac{2-{\sigma }_1}{{\sigma }_1}.$$ (16)

Note that the upper bound on F is continuous at σ₁ = 1, as ${\text{lim}}_{{\sigma }_1\to 1}Q\left({\sigma }_1\right)=q\left(1\right)=1$.

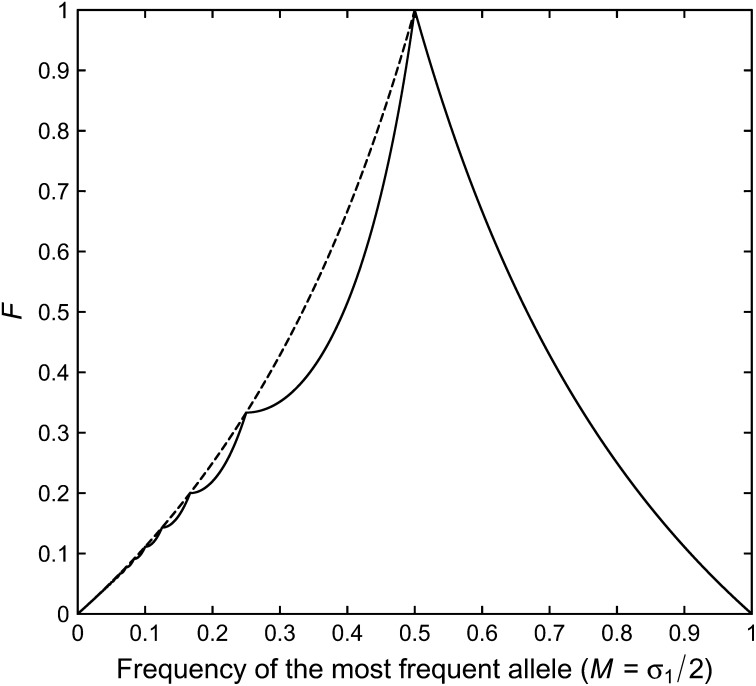
The upper bound on F is shown as the solid line in Figure 2. The plot illustrates that the upper bound on F(σ₁) has a piecewise structure on (0, 1), with changes in shape occurring when σ₁ is equal to the reciprocal of an integer. Similarly to the bounds examined by Rosenberg and Jakobsson (2008), for each J ≥ 2, Q(σ₁) is monotonically increasing on the interval [1/J, 1/(J − 1)), where $\lceil {\sigma }_1^{-1}\rceil$ has the constant value J. Further, Q(σ₁) is continuous at the boundaries 1/J between intervals, with Q(1/J) = 1/(2J − 1). On [1, 2), the upper bound has a simple monotonic decline according to q(σ₁).

Figure 2 .

The upper bound on F (solid line) as a function of the frequency M of the most frequent allele, for the general case of any number of alleles. The upper bound is computed from Equations 15 and 16. The dashed line shows Equation 21, which the upper bound touches when M = 1/(2J) for integers J ≥ 2. The lower bound on F is 0 for all values of M.

Properties of the Upper Bound on F

The region between 0 and the upper bound on F exactly circumscribes the set of possible values of F as a function of σ₁, as the upper bound is strict. We now explore a series of features of the upper bound on F as a function of σ₁.

The space between the upper and lower bounds on F

The mean maximum F across the range of possible frequencies for the most frequent allele gives a sense of the maximal F attainable on average, when M is uniformly distributed. This mean can be obtained by evaluating the area of the region between the lower and upper bounds on F.

Because the lower bound on F is zero over the entire interval σ₁ ε (0, 2), we need to determine only the area A under the upper bound on F. We integrate Q(σ₁) for σ₁ ε (0, 1) and q(σ₁) for σ₁ ε [1, 2),

$$A={\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}+{\displaystyle {\int }_1^{2}q\left({\sigma }_1\right)d{\sigma }_1}.$$ (17)

The first integral can be computed as a sum over intervals [1/J, 1/(J − 1)) for J ≥ 2. On each such interval, $\lceil {\sigma }_1^{-1}\rceil$ has a fixed value of J. We then have

$${\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}={\displaystyle \sum _{J=2}^{\mathrm{\infty }}{\displaystyle {\int }_{\frac{1}{J}}^{\frac{1}{J-1}}\frac{1-{\sigma }_1\left(J-1\right)\left(2-J{\sigma }_1\right)}{1+{\sigma }_1\left(J-1\right)\left(2-J{\sigma }_1\right)}d{\sigma }_1}}.$$

In the Appendix, we show that

$${\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}=-1+{\displaystyle \sum _{J=2}^{\mathrm{\infty }}\text{ln}\left(\frac{\sqrt{\left(J-1\right)\left(2J-1\right)}+1}{\sqrt{\left(J-1\right)\left(2J-1\right)}-1}\right)/\sqrt{\left(J-1\right)\left(2J-1\right)}}.$$ (18)

By numerically evaluating the sum in Equation 18, we obtain an approximation ${\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}\approx 0.3307808$.

The second term in Equation 17 is

$$\begin{array}{c}{\displaystyle {\int }_1^{2}q\left({\sigma }_1\right)d{\sigma }_1}={\displaystyle {\int }_1^2\frac{2-{\sigma }_1}{{\sigma }_1}d{\sigma }_1}\\ \hspace{1em}=2\hspace{0.5em}\text{ln}\hspace{0.5em}2-1,\end{array}$$ (19)

and the area under q(σ₁) for σ₁ ε [1, 2) is ∼0.3862944.

Summing the values for the two integrals, the area A under the upper bound on F is ∼0.7170751. Considering F as a function of M = σ₁/2 rather than σ₁, F is confined to a region with area ∼0.3585376. This area under the curve is the mean maximal value of F across the space of values of M, and it is substantially less than 1. Thus, on average, F is constrained within a narrow range, and across most of the space of possible values for the frequency of the most frequent allele, F cannot achieve large values. For example, only over half the range—for M between 1/4 and 3/4—is it possible for F to exceed 1/3.

Jagged points touch a simple curve

For σ₁ ε [1, 2), the upper bound on F is a smooth function q(σ₁). For σ₁ ε (0, 1), however, the upper bound is a jagged curve. At σ₁ = 1/J for any integer J ≥ 2, that is, at the “jagged points” where the upper bound is not differentiable, Q(σ₁) coincides with the reflection of q(σ₁) across the line σ₁ = 1. We have

$$Q\left({\sigma }_1=1/J\right)=\frac{1}{2J-1},$$ (20)

because $\lceil {\sigma }_1^{-1}\rceil =J$ when σ₁ = 1/J. Thus, for σ₁ = 1/J, Q(σ₁) touches the curve

$$q^{*}\left({\sigma }_1\right)=\frac{{\sigma }_1}{2-{\sigma }_1}.$$ (21)

The dashed line in Figure 2 plots q*(σ₁) on (0, 1).

Because q*(σ₁) on (0, 1) is the reflection of q(σ₁) on [1, 2) across the line σ₁ = 1, the area under q*(σ₁) on (0, 1) is the same as the area of q(σ₁) on [1, 2), or 2 ln 2 − 1. Thus, on the interval (0, 1), the space between q*(σ₁) and Q(σ₁) is

$$\left(2\hspace{0.5em}\text{ln}\hspace{0.5em}2-1\right)-{\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}\approx \mathrm{0.0555136.}$$ (22)

The contribution made by M to the upper bound on F

We denote by F₁(σ₁) the contribution of the most frequent allele to F(σ₁). By this quantity, we mean the term in F(σ₁) contributed by the difference between populations in the frequency of the most frequent allele. From Equation 4, F(σ₁) can be written

$$F\left({\sigma }_1\right)={\displaystyle \sum _{i=1}^I\frac{{\delta }_i^2}{4-{\displaystyle {\sum }_{j=1}^I{\sigma }_j^2}}}.$$ (23)

If the ith term in the summation is denoted F_i(σ₁), our interest is in the value of F₁(σ₁) obtained at the set of allele frequencies that maximizes F(σ₁).

For σ₁ in the interval (0, 1), defining $\lceil {\sigma }_1^{-1}\rceil =J$, the maximum has 2J − 2 alleles with frequency σ₁ and two alleles with frequency 1 − (J − 1)σ₁: J − 1 alleles with frequency σ₁ and one allele with frequency 1 − (J − 1)σ₁ in each subpopulation. The value of ${\delta }_1^2$ at the maximum is ${\sigma }_1^2$. Denoting the contribution F₁(σ₁) to F(σ₁) at the maximum by Q₁(σ₁), we have

$$Q_1\left({\sigma }_1\right)=\frac{{\sigma }_1^2}{2+2{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(2-\lceil {\sigma }_1^{-1}\rceil {\sigma }_1\right)}.$$ (24)

In the Appendix, we evaluate ${\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}$. The expression is unwieldy, but it provides a numerical approximation ${\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}\approx 0.1284522$.

For σ₁ ε [1, 2), at the maximum of F(σ₁), ${\delta }_1^2={\left(2-{\sigma }_1\right)}^2$, and we have

$$\begin{array}{c}{q}_1\left({\sigma }_1\right)=\frac{{\left(2-{\sigma }_1\right)}^2}{4-{\sigma }_1^2-{\left(2-{\sigma }_1\right)}^2}\\ =\frac{2-{\sigma }_1}{2{\sigma }_1}.\end{array}$$ (25)

The area under q₁(σ₁) is

$${\displaystyle {\int }_1^2{q}_1\left({\sigma }_1\right)d{\sigma }_1}=\text{ln}\hspace{0.17em}2-\frac{1}{2}\approx \mathrm{0.1931472.}$$

Summing the areas under Q₁(σ₁) and q₁(σ₁), the total area B under F₁ as σ₁ ranges from 0 to 2 is

$$B={\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}+{\displaystyle {\int }_1^2{q}_1\left({\sigma }_1\right)d{\sigma }_1}\approx \mathrm{0.3215994.}$$

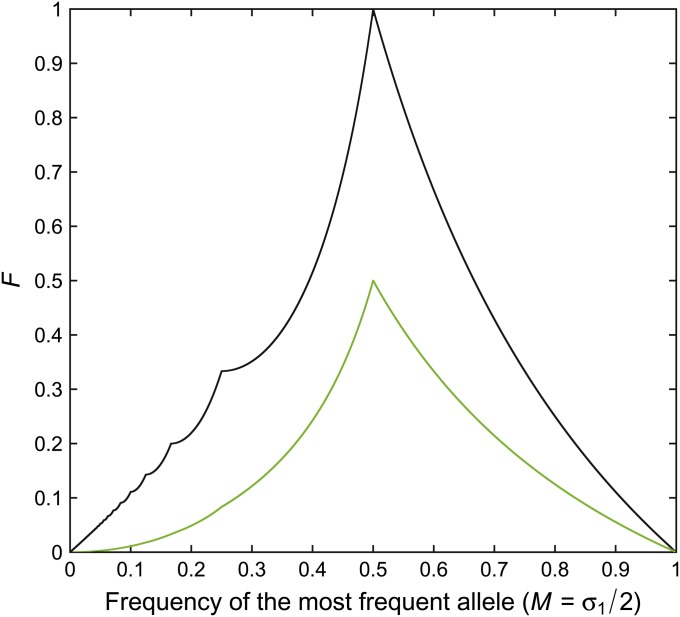
If we instead consider M = σ₁/2, we find that F₁ is confined to ∼0.1607997 of the space of possible pairs of values (M, F). The fraction of the area A under the upper bound on F contributed by the most frequent allele over the entire interval σ₁ ε (0, 2) is B/A ≈ 0.4484877. This quantity can be interpreted as the mean contribution of the most frequent allele to the maximum value of F, and it indicates a substantial role for the most frequent allele. Indeed, for σ₁ ε [1, 2), q₁(σ₁)/q(σ₁) = 1/2. The contribution made by the most frequent allele to the upper bound on F appears in Figure 3.

Figure 3 .

The contribution to F, at the upper bound, that is made by the most frequent allele (green line). The contribution by the most frequent allele is computed from Equations 24 and 25. For comparison, the upper bound on F is shown as a black line.

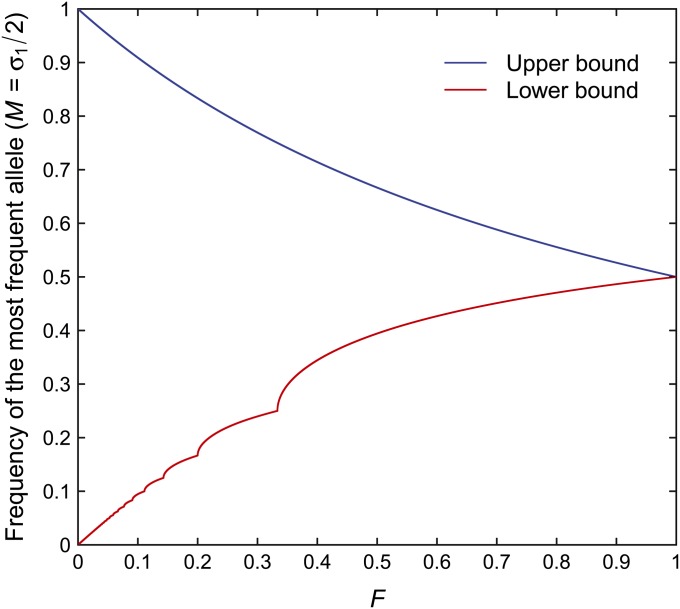
Bounds on M

Our derivation of the bounds on F as functions of the frequency M of the most frequent allele enables us to provide bounds on M as functions of F by taking the inverse of the functions q(σ₁) and Q(σ₁). For 0 < F < 1, we show that the bounds on the frequency of the most frequent allele in terms of F are

$${\sigma }_1\epsilon \left[\frac{1}{\lceil \left(1+F\right)/2F\rceil }\left(1+\sqrt{\frac{\left(2\lceil \left(1+F\right)/2F\rceil -1\right)F-1}{\left(\lceil \left(1+F\right)/2F\rceil -1\right)\left(F+1\right)}}\right),\frac{2}{1+F}\right].$$ (26)

At the trivial case of F = 1, σ₁ must equal 1, and for F = 0, σ₁ lies in the open interval (0, 2).

Bounds on σ₁ for two alleles

We first consider the two-allele case. By definition of σ₁, regardless of the value of F, σ₁ can be no smaller than 1, and when σ₁ = 1, $F\left({\sigma }_1\right)={\delta }_1^2$. For any F ε [0, 1], it is possible to choose allele frequencies p₁₁ and p₂₁ so that ${\delta }_1=\left|p_{11}-p_{21}\right|=\sqrt{F}$ and σ₁ = p₁₁ + p₂₁ = 1. We simply set $p_{11}=\left(1+\sqrt{F}\right)/2$ and $p_{21}=\left(1-\sqrt{F}\right)/2$. Thus, the lower bound of σ₁(F) = 1 can be achieved across the full domain F ε [0, 1].

For the upper bound on σ₁, recall that the upper bound on F in terms of σ₁ (Equation 7) is a continuous monotonically decreasing function on the interval σ₁ ε [1, 2). We can therefore obtain the upper bound on σ₁ as the inverse of this function. Thus, for F ε [0, 1], the bounds on σ₁ are:

$${\sigma }_1\left(F\right)\epsilon \left[1,\frac{2}{1+F}\right].$$ (27)

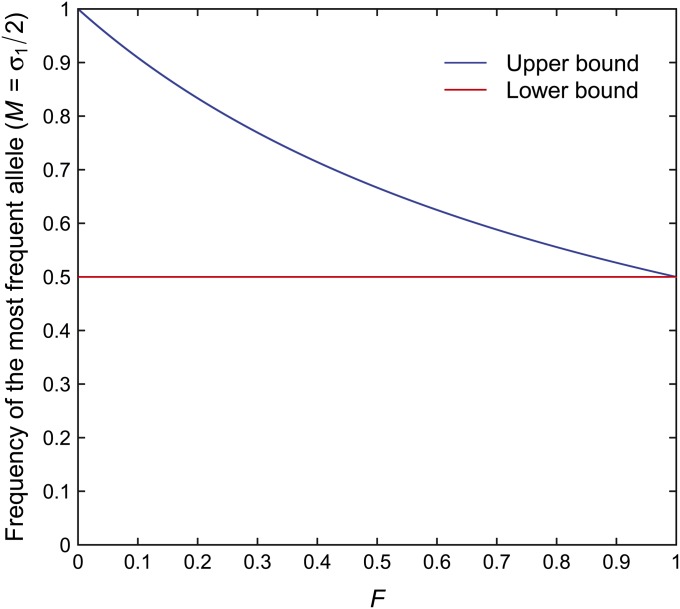
The corresponding bounds on M = σ₁/2 appear in Figure 4.

Figure 4 .

The upper and lower bounds on the frequency M of the most frequent allele as functions of F, for the two-allele case. The bounds are computed from Equation 27.

Lower bound on σ₁ for an unspecified number of alleles

For the general case, we obtain lower and upper bounds on F, considering all possible choices for the number of distinct alleles. It is useful to first recall that the function Q(σ₁) for the upper bound on F for σ₁ ε (0, 1) is monotonically increasing, while the function q(σ₁) for the upper bound on F for σ₁ ε [1, 2) is monotonically decreasing. We can therefore invert Q(σ₁) and q(σ₁), so that the lower bound on σ₁ as a function of F is obtained by solving Q(σ₁) = F for σ₁ and the upper bound by solving q(σ₁) = F for σ₁. For the lower bound, we perform the inversion piecewise. For integers J ≥ 2, if σ₁ ε [1/J, 1/(J − 1)), then Q(σ₁) ε [1/(2J − 1), 1/(2J − 3)). Therefore, for J ≥ 2, if Q ε [1/(2J − 1), 1/(2J − 3)), then the lower bound on σ₁ lies in [1/J, 1/(J − 1)). For this interval on Q, ⌈(1 + Q)/(2Q)⌉ = J, and in this region, the lower bound on σ₁, which we term r(F), also satisfies ⌈r(F)⌉ = J. We solve Equation 10 for σ₁ for Q ε[1/(2J − 1), 1/(2J − 3)), where both $\lceil {\sigma }_1^{-1}\rceil$ and ⌈(1 + Q)/(2Q)⌉ are equal to J:

$$r\left(F\right)=\frac{1}{J}\left(1+\sqrt{\frac{\left(2J-1\right)F-1}{\left(J-1\right)\left(1+F\right)}}\right),$$ (28)

A negative root is discarded because it yields values that are incompatible with the definition that σ₁ ≥ σ_i for all i > 1. The upper and lower bounds appear in Figure 5.

Figure 5 .

The upper and lower bounds on the frequency M of the most frequent allele as functions of F, for the general case of any number of alleles. The bounds are computed from Equations 29 and 28.

Upper bound on σ₁ for an unspecified number of alleles

From Equation 13 and Figure 2, we see that for any F ε [0, 1], the upper bound on σ₁ is ≥⩾1. Because Equation 13 is continuous and monotonically decreasing, we can take the inverse of this function to compute the upper bound on σ₁ as a function of F. The upper bound R(F) on σ₁ is

$$R\left(F\right)=\frac{2}{1+F},$$ (29)

the same upper bound as for the two-allele case (Equation 27).

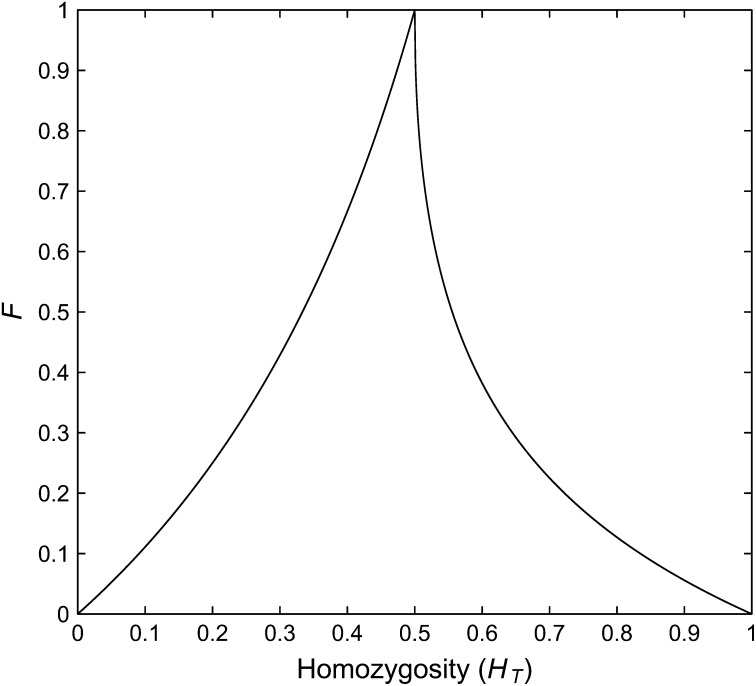
F and Homozygosity of the Total Population

The relationship between F and the frequency of the most frequent allele can be used together with the relationship between homozygosity and the frequency of the most frequent allele (Rosenberg and Jakobsson 2008; Reddy and Rosenberg 2012), to find a relationship between F and homozygosity, again in the setting of two populations. The homozygosity that we consider, H in Rosenberg and Jakobsson (2008), corresponds to the homozygosity of the total pooled population H_T. We first note that given any H_T ε (0, 1), the lower bound on F is zero. For example, for any H_T, F = 0 is obtained by using the equality condition in Theorem 1ii of Rosenberg and Jakobsson (2008) to specify a list of allele frequencies with sum of squares H_T and then assigning that same list of frequencies to both of the component subpopulations.

Upper bound on F given H_T for an unspecified number of alleles

Rosenberg and Jakobsson (2008) showed that the value of H_T constrains the frequency M of the most frequent allele to a narrow range. We have already determined the upper bound on F as a function of M. Thus, we can obtain an upper bound on F as a function of H_T by taking the maximum value of the upper bound over the range of possible values of M allowed under the results of Rosenberg and Jakobsson (2008) for a given value of H_T. This approach does not guarantee that the upper bound on F that we obtain in terms of H_T is strict; nevertheless, the approach happens to produce a strict bound for H_T ε [1/2, 1). For H_T ε (0, 1/2), it is possible to produce a strict bound by writing F in terms of H_T.

To obtain the bound for H_T ε (0, 1/2), we substitute ${\sigma }_i^2-4p_{1i}{p}_{2i}$ for ${\delta }_i^2$ in Equation 4 to write

$$F=\frac{H_{\text{T}}-{\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}}{1-H_{\text{T}}}.$$ (30)

Because ${\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}\ge 0$, we obtain the bound

$$F\le \frac{H_{\text{T}}}{1-H_{\text{T}}}.$$ (31)

Given H_T, equality is obtained in Equation 31 when ${\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}=0$. In other words, for H_T ε (0, 1/2), F is maximized when each allele occurs in only one of the two populations. To see that the upper bound is strict, note that when ${\displaystyle {\sum }_{i=1}^I{p}_{1i}{p}_{2i}}=0$, labeling the homozygosities of the two populations by H₁ and H₂, H_T = (H₁ + H₂)/4. As H_T < 1/2, 2H_T < 1, and we can choose H₁ = H₂ = 2H_T. Using the equality condition in Theorem 1ii of Rosenberg and Jakobsson (2008), we can specify a set L of exactly ⌈(2H_T)⁻¹⌉ allele frequencies whose sum of squares is H_T. We then construct a set of 2⌈(2H_T)⁻¹⌉ alleles. In population 1, the first ⌈(2H_T)⁻¹⌉ alleles in the set have exactly the allele frequencies in L and the next ⌈(2H_T)⁻¹⌉ alleles have frequency 0. In population 2, the first ⌈(2H_T)⁻¹⌉ alleles have frequency 0, and the next ⌈(2H_T)⁻¹⌉ alleles have the frequencies in L.

For H_T ε [1/2, 1), H_T/(1 − H_T) ≥ 1, so Equation 31 provides only the trivial bound of F ≤ 1, and another approach is needed. For any H_T ε [1/2, 1), using Theorem 1ii of Rosenberg and Jakobsson (2008), M ≥ 1/2. For M ≥ 1/2, the upper bound on F as a function of σ₁ is monotonically decreasing in σ₁, and consequently, the upper bound on F as a function of H_T is obtained by evaluating q(σ₁) at the smallest value of σ₁ permitted by H_T. Theorem 1ii of Rosenberg and Jakobsson (2008) indicates that this smallest allowed σ₁ satisfies

$${\sigma }_1/2=M=\frac{1}{\lceil H_T^{-1}\rceil }\left(1+\frac{\sqrt{\lceil H_T^{-1}\lceil H_T-1}}{\sqrt{\lceil H_T^{-1}\rceil -1}}\right).$$

By replacing σ₁/2 in Equation 16 with this expression, we have

$$\begin{array}{c}F\le \frac{\lceil H_T^{-1}\rceil }{1+\left(\sqrt{\lceil H_T^{-1}\rceil H_T-1}/\sqrt{\lceil H_T^{-1}\rceil -1}\right)}-1\\ =\frac{1-\sqrt{2H_T-1}}{1+\sqrt{2H_T-1}},\end{array}$$ (32)

where the last step follows from the fact that $\lceil H_T^{-1}\rceil =2$ when H_T ε [1/2, 1).

For H_T ε [1/2, 1), the set of allele frequencies that achieves the minimum M as a function of H_T and the set that achieves the maximum F as a function of M coincide. Given H_T, M is minimized by setting ${\stackrel{-}{p}}_1=\left(1+\sqrt{2H_{\text{T}}-1}\right)/2$, ${\stackrel{-}{p}}_2=\left(1-\sqrt{2H_{\text{T}}-1}\right)/2$, and ${\stackrel{-}{p}}_i=0$ for all i ≥ 2. If these mean frequencies are distributed between the two populations such that $\left(p_{11},p_{12},p_{21},p_{22}\right)=\left(1,0,\sqrt{2H_{\text{T}}-1},1-\sqrt{2H_{\text{T}}-1}\right)$ or $\left(\sqrt{2H_{\text{T}}-1},1-\sqrt{2H_{\text{T}}-1},1,0\right)$, then the upper bound on F is achieved.

Figure 6 shows our upper bound on F as a function of the total homozygosity H_T. If H_T is low, and particularly if H_T is high, then F is restricted to small values. High values of F are possible only when H_T is near 1/2. In fact, using Equations 31 and 32, F can exceed 1/2 only if H_T lies in (1/3, 5/9).

Figure 6 .

The upper bound on F as a function of H_T. The upper bound is computed from Equations 31 and 32. The lower bound on F is 0 for all values of H_T.

The space between the upper and lower bounds on F given H_T

In the same manner as in our investigation of the bounds on F as a function of M, we evaluate the area of the region between the upper and lower bounds on F to find the mean maximum F across the range of possible values of H_T.

Because the lower bound on F is zero over the entire interval H_T ε (0, 1), it suffices to evaluate the area A under the upper bound on F. This area is

$$A={\displaystyle {\int }_0^{1/2}\frac{H_{\text{T}}}{1-H_{\text{T}}}d{H}_{\text{T}}}+{\displaystyle {\int }_{1/2}^1\frac{1-\sqrt{2H_{\text{T}}-1}}{1+\sqrt{2H_{\text{T}}-1}}d{H}_{\text{T}}}.$$ (33)

The first term has indefinite integral −H_T − ln(1 − H_T) and evaluates to ln 2 − 1/2. The second term has indefinite integral $-H_{\text{T}}+2\sqrt{2H-1}-2\hspace{0.5em}\text{ln}\left(1+\sqrt{2H-1}\right)$ and evaluates to 3/2 − 2 ln 2, so that A = 1 − ln 2 ≈ 0.3068528.

Note that F is substantially more constrained when H_T ε [1/2, 1) than when H_T ε [0, 1/2). The difference between the areas under the upper bound for H_T ε [0, 1/2) and for H_T ε [1/2, 1) is 3 ln 2 − 2 ≈ 0.0794415, a sizeable fraction of the sum of the two areas. Twice the difference in areas, or 6 ln 2 − 4 ≈ 0.1588831, is the expectation of the difference between the maximum value of F for a value of H_T chosen uniformly at random from (0, 1/2) and the maximum value of F for a value of H_T chosen uniformly at random from [1/2, 1).

Application to Data

We illustrate the bounds on F, M, and H_T for a series of examples using human polymorphism data from Rosenberg et al. (2005) and Li et al. (2008). For each example, for each locus, we assume that the allele frequencies in the data sets are parametric allele frequencies. The parametric allele frequencies are obtained in each of a pair of populations, and they are then averaged to obtain parametric allele frequencies for the total population. F, M, and H_T are then computed. The data set of Rosenberg et al. (2005) considers 1048 individuals genotyped for 783 microsatellites, and the data set of Li et al. (2008) considers 938 unrelated individuals genotyped for single-nucleotide polymorphisms (SNPs); for all analyses, we restrict our attention to the 935 individuals found in both data sets. For the Li et al. (2008) data, we examine only 640,034 SNPs studied by Pemberton et al. (2012).

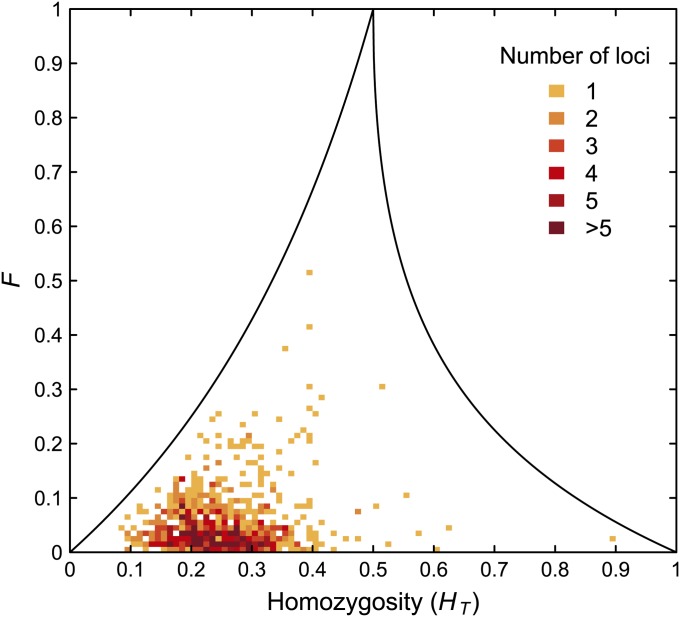
Example 1: Africans and Native Americans

Our first example considers microsatellites in 101 Africans and 63 Native Americans, and it is chosen to illustrate a relatively wide range of values of F, M, and H_T. Figure 7 shows F and M, demonstrating that for the comparison of Africans and Native Americans, F < 0.1 for most of the 783 loci. The mean value of F is 0.05 with standard deviation 0.06, and the mean value of M is 0.37 with standard deviation 0.11.

Figure 7 .

F and the frequency of the most frequent allele (M) for 101 Africans and 63 Native Americans. At each of 783 microsatellite loci, allele frequencies are computed separately for the two population groups, and the total allele frequency is the average of the two group frequencies. Each bin has size 0.01 × 0.01, and the upper bound on F as a function of M is shown for comparison.

Similarly, Figure 8 plots F and H_T for the 783 loci. The mean H_T is 0.25 with standard deviation 0.08. In both Figures 7 and 8, relatively few loci approach the upper bound on F.

Figure 8 .

F and homozygosity (H_T) for 101 Africans and 63 Native Americans. At each of 783 microsatellite loci, allele frequencies are computed separately for the two population groups, and the total allele frequency is the average of the two group frequencies. Each bin has size 0.01 × 0.01, and the upper bound on F as a function of H_T is shown for comparison.

Example 2: High-diversity and low-diversity populations

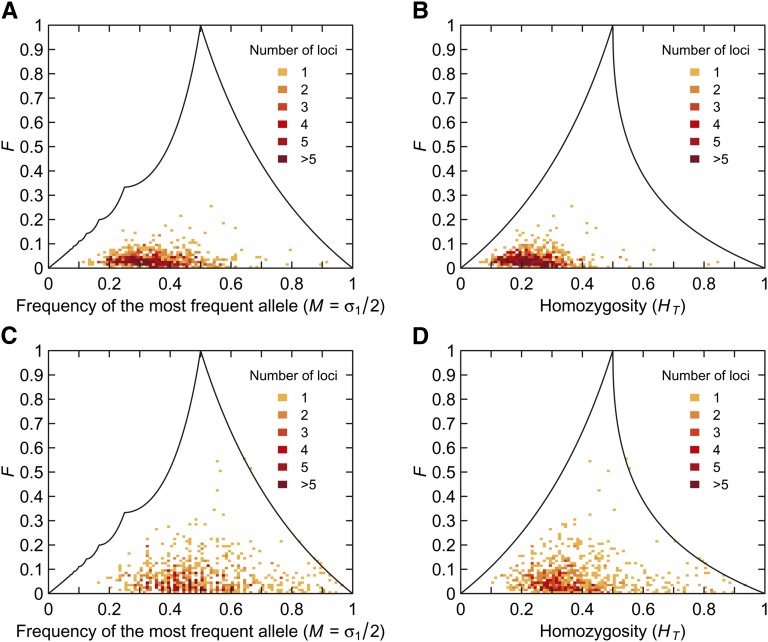
The bounds on F as a function of M and H_T indicate that genetic diversity in a pair of populations has a strong effect on the value of F between them. To illustrate this point, we compare the values of F obtained from two populations each with high within-population diversity to those obtained from two populations with lower within-population diversity.

The Yoruba and Mbuti Pygmy populations are two African populations with high genetic diversity; the Colombian and Pima populations are Native American populations with lower diversity. Figure 9A shows F and M computed from the Yoruba and Mbuti Pygmy populations, and Figure 9B shows F and H_T. The mean value of F is 0.04 with standard deviation 0.03, the mean value of M is 0.35 with standard deviation 0.11, and the mean value of H_T is 0.24 with standard deviation 0.08.

Figure 9 .

Relationships among F, M, and H_T, for pairs of African and Native American populations. (A) F and M for 21 Yoruba and 15 Mbuti Pygmy individuals. (B) F and H_T for 21 Yoruba and 15 Mbuti Pygmy individuals. (C) F and M for 7 Colombian and 14 Pima individuals. (D) F and H_T for 7 Colombian and 14 Pima individuals. In each plot, at each of 783 microsatellite loci, allele frequencies are computed separately for the two populations, and the total allele frequency is the average of the two population frequencies. Each bin has size 0.01 × 0.01, and the upper bound on F is shown for comparison.

By contrast, in corresponding plots for the less diverse Colombian and Pima populations, higher values of F, M, and H_T are apparent (Figure 9, C and D). In particular, because M and H_T tend to be nearer to 1/2, larger values of F are possible. The mean values of M and H_T are much closer to 1/2 than in the African groups; the mean M is 0.50 with standard deviation 0.15, and the mean H_T is 0.38 with standard deviation 0.15. As is suggested by the fact that F can attain its largest values when M and H_T lie near 1/2, the mean value of F for the Native American groups is nearly twice as high as in the African groups (mean 0.07, standard deviation 0.07).

Example 3: Single-nucleotide polymorphisms

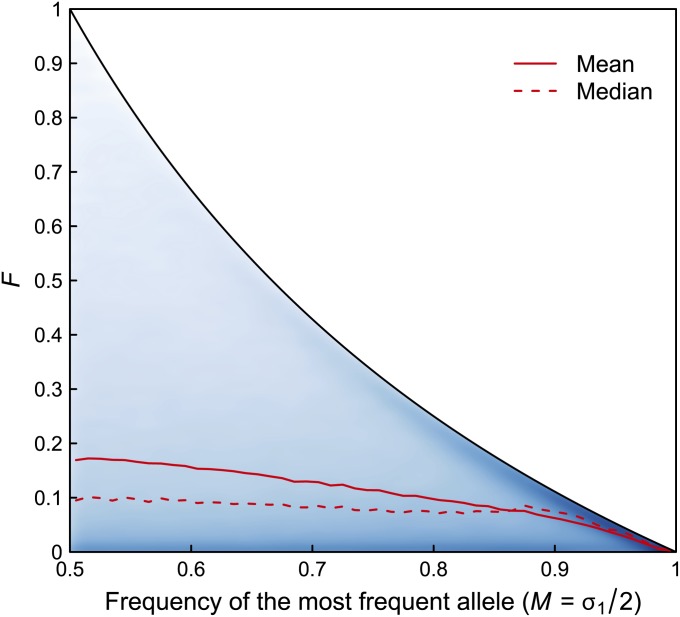
Our third example considers SNPs in the same set of Africans and Native Americans for which microsatellites were examined in Figures 7 and 8. Figure 10 shows the joint distribution of F and M as well as the mean and median of F for intervals of M ranging from 1/2 to 1 with width 0.01. Mean values of F decrease with M for M ε (1/2, 1), and this decrease is correlated with the decreasing value of the bound on F as a function of M (r = 0.94). Compared with the mean, the median value of F is less correlated with the value of the bound, although it also declines with increasing M (r = 0.77).

Figure 10 .

Smoothed scatterplot of F as a function of M for 101 Africans and 63 Native Americans, using SNP data. The shading reflects a two-dimensional kernel density estimate using a Gaussian kernel with bandwidth set to 0.007; the density was set to 0 outside the bounds on F as a function of M. For each of 640,034 SNP loci, allele frequencies are computed separately for the two population groups, and the total allele frequency is the average of the two group frequencies. The mean and median of F are computed for 50 bins of width 0.01 ranging from M = 1/2 to M = 1. The upper bound on F as a function of H_T is shown for comparison.

For biallelic markers, for M > 1/2, at least one of the two alleles must appear in both populations, and the upper bound on F occurs when one of the populations has only one allele. In Figure 10, for high values of M, more SNPs approach the upper bound on F than for low values of M. This result indicates that SNPs with high values of M are more likely to have an allele found in one but not the other of the two populations.

Discussion

The range of F depends on the level of diversity in the markers considered. In this article, we have further shown that not only does diversity constrain the range of F, the frequency of the most frequent allele has a strong influence on the values that F can take. When the frequency of the most frequent allele is small or large, F is restricted to small values far from one (Figure 2). In fact, considering all possible values of M, F is restricted on average to only ∼35.85% of the space of possibilities. This extreme reduction in range for F can be viewed as a consequence of our result that about half of the contribution to the maximal F arises from the most frequent allele (exactly half for σ₁ ε [1,2)). Using results from Rosenberg and Jakobsson (2008) on the relationship between homozygosity and the frequency of the most frequent allele, we have described a link between F and homozygosity of the total population (H_T) via separate relationships of F and homozygosity to the frequency of the most frequent allele. F is restricted by H_T even further than by M, to only ∼30.69% of the space of possibilities.

Our work extends knowledge of the connection between F and genetic diversity, providing a framework for interpreting a variety of features of values of F measured in population-genetic data. We have presented empirical computations that illuminate recently observed phenomena in human population genetics. In particular, even without a formal understanding of the ways in which evolutionary processes and the population-genetic models that encode them give rise to values of M, H_T, and F, the mathematical constraints linking these quantities can aid in interpreting the patterns found in the data.

Low F_ST values in human populations from Africa

Estimates of F_ST in human populations have been low in Africa compared with other geographic regions, such as among Native Americans (Rosenberg et al. 2002; Tishkoff et al. 2009). This pattern appears to belie the extensive genetic differentiation known to exist among African populations. For example, using microsatellite loci, Tishkoff et al. (2009) identified a number of genetically distinctive subgroups of African populations despite confirming that F_ST in Africa has an unexpectedly small value. The apparent discrepancy between the extensive genetic differentiation among populations in Africa and counterintuitively low values of F_ST can be explained using our results. Because Africa has high within-population genetic diversity—including microsatellite homozygosities well below 1/2 in many populations (Tishkoff et al. 2009, Figure S2B)—the maximum F_ST for comparisons of African populations at microsatellite loci is relatively constrained compared with the maximum F_ST for comparisons of groups that have less within-population diversity and mean homozygosities nearer 1/2. Figure 9 shows that F_ST values comparing African populations are more constrained by M and H_T than are those comparing Native American populations. Thus, the observation for microsatellites of low F_ST in African populations can be attributed to high within-population genetic diversities.

That F_ST is more tightly constrained for high-diversity populations than for populations where H_T ≈ 1/2 has an additional consequence. When considering two pairs of populations with the same F_ST value and H_T < 1/2, it is likely that a pair of populations with higher within-group diversity is more differentiated than is a pair of populations with relatively low within-group diversity. In other words, the higher the level of genetic diversity within a population, the greater the extent to which raw values of F_ST underpredict the intuitive level of differentiation among subpopulations; the result of Tishkoff et al. (2009) exactly follows this pattern.

Lower F_ST values for microsatellites than for SNPs

Computations of F_ST in human populations have generally found that F_ST estimates based on multiallelic loci such as microsatellites are lower than those obtained from biallelic loci such as SNPs (e.g., Rosenberg et al. 2002; Li et al. 2008). This observation is apparent in the difference between F_ST-like computations from nearly the same sets of individuals for microsatellites and for SNPs. When separating human populations into seven geographic regions and computing the within-population component of genetic variation, a quantity analogous to 1 − F_ST, Rosenberg et al. (2002) obtained an estimate of 0.941 with microsatellites, whereas Li et al. (2008) obtained 0.889 with SNPs. Our results provide a simple explanation for this difference. The SNPs of Li et al. (2008) each have only two alleles, so for each locus, the frequency of the most frequent allele is at least 1/2; further, the minor alleles tend to be common, such that many of the loci have M near 1/2. By contrast, the microsatellites in the study of Rosenberg et al. (2002) have ∼12 alleles on average, so M is typically smaller than 1/2 and often much smaller (Rosenberg and Jakobsson 2008). Thus, for microsatellites, because of lower frequencies of the most frequent allele and higher levels of genetic diversity, the maximum value of F is substantially more constrained than the corresponding maximum of F for SNPs (Figure 2). We can explain the difference in the magnitudes of the Rosenberg et al. (2002) and Li et al. (2008) F_ST values via this phenomenon.

Recently, attention has increasingly focused on biallelic sites for which the rarer allele has low frequency (Keinan and Clark 2012; Nelson et al. 2012; Tennessen et al. 2012). In our terms, these are sites for which the frequency of the most frequent allele, M, is high. Because F is tightly constrained for high values of M, we might expect that when F_ST is calculated using sites with rare minor alleles, small F_ST values will be produced. Indeed, Figure 10 shows that when F is used to compare Africans with Native Americans at SNP loci, mean values of F decrease as M increases from 1/2 to 1.

Conclusions

Measures of F_ST have often been used for making inferences about such phenomena as population structure, migration patterns, and range expansions. However, we have found that without a proper understanding of the dependence of F_ST on diversity and allele frequencies, F_ST can potentially produce puzzling or misleading results. We have described mathematical relationships between F_ST, the frequency of the most frequent allele, and homozygosity that are useful for interpreting the properties of differentiation measures when features of allele frequencies and diversity statistics vary across loci or populations—as they inevitably do in typical scenarios.

Beginning with Charlesworth (1998), Nagylaki (1998), and Hedrick (1999), recent studies have noted that F_ST is constrained by diversity, and the issue was described as early as in the work of Sewall Wright (Wright 1978, p. 82). Jost (2008) generated new interest in the dependence of F_ST on diversity, illustrating that the dependence can produce substantial discord between intuitions about and measurements of differentiation levels. Jost (2008) also used a multiplicative definition of diversity to propose a pair of new differentiation indices that have the feature of reaching their maximum value if and only if each allele is private to a single subpopulation. In our view, the key to choosing and applying measures of differentiation lies not in “fixation on an index” (Long 2009), be it F_ST, the measures of Jost (2008), or other indices that have recently been proposed (Meirmans and Hedrick 2011), but in developing an understanding of the ways in which possible statistics relate both to intuitive aspects of differentiation and to mathematical features of allele frequencies and genetic diversity. In this context, F_ST remains of particular interest on the basis of its long history of use in population genetics and its connection to features of biological models (Whitlock 2011). Our examples provide only a few among many ways in which the mathematical properties we have obtained for F_ST can be used to interpret its behavior in the analysis of empirical data.

Appendix

The appendix provides the derivations of two integrals described in the main text.

Integral ${\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}$ (Equation 18)

To obtain ${\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}$, we first note that for any integer k ≥ 1, $\lceil {\sigma }_1^{-1}\rceil =k+1$ if 1/(k + 1) ≤ σ₁ < 1/k. We have

$$\begin{array}{c}{\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}={\displaystyle {\int }_0^1\frac{1+{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(\lceil {\sigma }_1^{-1}\rceil {\sigma }_1-2\right)}{1-{\sigma }_1\left(\lceil {\sigma }_1^{-1}\rceil -1\right)\left(\lceil {\sigma }_1^{-1}\rceil {\sigma }_1-2\right)}d{\sigma }_1}\\ \hspace{1em}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\displaystyle {\int }_{1/\left(k+1\right)}^{1/k}\frac{1+k{\sigma }_1\left(\left(k+1\right){\sigma }_1-2\right)}{1-k{\sigma }_1\left(\left(k+1\right){\sigma }_1-2\right)}d{\sigma }_1}}\\ \hspace{1em}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\displaystyle {\int }_{1/\left(k+1\right)}^{1/k}\left[-1-\frac{2}{-1+k\left(k+1\right){\sigma }_1^2-2k{\sigma }_1}\right]d{\sigma }_1}}.\end{array}$$

Defining $D=\sqrt{k+2k^2}$, we then have

$$\begin{array}{c}{\displaystyle {\int }_0^{1}Q\left({\sigma }_1\right)d{\sigma }_1}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\displaystyle {\int }_{1/\left(k+1\right)}^{1/k}\left[-1+\frac{D^{-1}}{{\sigma }_1+{\left(k+D\right)}^{-1}}-\frac{D^{-1}}{{\sigma }_1-{\left(-k+D\right)}^{-1}}\right]d{\sigma }_1}}\\ \hspace{1em}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\left[-{\sigma }_1+D^{-1}\left[\text{ln}\left(1+k{\sigma }_1+D{\sigma }_1\right)-\text{ln}\left(-1-k{\sigma }_1+D{\sigma }_1\right)\right]\right]}_{1/\left(k+1\right)}^{1/k}}\\ \hspace{1em}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}\left(-\frac{1}{k}+\frac{1}{k+1}\right)}+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}{D}^{-1}\hspace{0.5em}\text{ln}\left[\frac{\left(1+k\frac{1}{k}+\frac{D}{k}\right)\left(-1-k\frac{1}{k+1}+\frac{D}{k+1}\right)}{\left(-1-k\frac{1}{k}+\frac{D}{k}\right)\left(1+k\frac{1}{k+1}+\frac{D}{k+1}\right)}\right]}\\ \hspace{1em}=-1+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}{D}^{-1}\hspace{0.5em}\text{ln}\left(\frac{D+1}{D-1}\right)}.\end{array}$$ (A1)

Integral ${\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}$ (with Q₁ as in Equation 24)

To obtain ${\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}$, we first note that for any integer k ≥ 1, $\lceil {\sigma }_1^{-1}\rceil =k+1$ when ${\sigma }_1\epsilon \left[1/\left(k+1\right),1/k\right)$. We have

$$\begin{array}{c}{\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\displaystyle {\int }_{1/\left(k+1\right)}^{1/k}\frac{{\sigma }_1^2}{-2k\left(1+k\right){\sigma }_1^2+4k{\sigma }_1+2}d{\sigma }_1}}\\ ={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\displaystyle {\int }_{1/\left(k+1\right)}^{1/k}\left[-\frac{1}{2k\left(1+k\right)}-\frac{2k{\sigma }_1+1}{2k\left(1+k\right)\left(k\left(1+k\right){\sigma }_1^2-2k{\sigma }_1-1\right)}\right]d{\sigma }_1}}.\end{array}$$

The second term can be decomposed, defining

$$A=\frac{1+\left(3k+1\right)/\left(2k\sqrt{2+1/k}\right)}{2k{\left(1+k\right)}^2}\hspace{1em}\text{and}\hspace{1em}B=\frac{1-\left(3k+1\right)/(2k\sqrt{2+1/k})}{2k{\left(1+k\right)}^2}.$$

We have

$$\begin{array}{c}{\displaystyle {\int }_0^1{Q}_1\left({\sigma }_1\right)d{\sigma }_1}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}{\displaystyle {\int }_{1/\left(k+1\right)}^{1/k}\left[-\frac{1}{2k\left(1+k\right)}-\frac{A}{{\sigma }_1-\left(1+\sqrt{2+1/k}\right)/\left(1+k\right)}-\frac{B}{{\sigma }_1-\left(1-\sqrt{2+1/k}\right)/\left(1+k\right)}\right]d{\sigma }_1}}\\ \hspace{1em}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}[-\frac{{\sigma }_1}{2k\left(1+k\right)}+\frac{1}{2k{\left(1+k\right)}^2}\left[-\text{ln}\left(-1-\sqrt{2+1/k}+{\sigma }_1+n{\sigma }_1\right)-\text{ln}\left(-1+\sqrt{2+1/k}+{\sigma }_1+n{\sigma }_1\right)\right]}\\ \hspace{0.5em}{+\frac{1}{2k{\left(1+k\right)}^2}\frac{3k+1}{2k\sqrt{2+1/k}}\left[-\text{ln}\left(-1-\sqrt{2+1/k}+{\sigma }_1+n{\sigma }_1\right)+\text{ln}\left(-1+\sqrt{2+1/k}+{\sigma }_1+n{\sigma }_1\right)\right]]}_{1/\left(k+1\right)}^{1/k}\\ \hspace{1em}={\displaystyle \sum _{k=1}^{\mathrm{\infty }}\left(-\frac{1}{2k^2\left(1+k\right)}+\frac{1}{2k{\left(1+k\right)}^2}\right)}\\ \hspace{0.5em}+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}\frac{1}{2k{\left(1+k\right)}^2}\hspace{0.5em}\text{ln}\left[\frac{\left(-1-\sqrt{2+1/k}+1/\left(1+k\right)+k/\left(1+k\right)\right)\left(-1+\sqrt{2+1/k}+1/\left(1+k\right)+k/\left(1+k\right)\right)}{\left(-1-\sqrt{2+1/k}+\left(1/k\right)+\left(k/k\right)\right)\left(-1+\sqrt{2+1/k}+\left(1/k\right)+\left(k/k\right)\right)}\right]}\\ \hspace{0.5em}+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}\frac{3k+1}{4k^2{\left(1+k\right)}^2\sqrt{2+1/k}}\text{ln}\left[\frac{\left(-1-\sqrt{2+1/k}+1/\left(1+k\right)+k/\left(1+k\right)\right)\left(-1+\sqrt{2+1/k}+\left(1/k\right)+\left(k/k\right)\right)}{\left(-1-\sqrt{2+1/k}+\left(1/k\right)+\left(k/k\right)\right)\left(-1+\sqrt{2+1/k}+1/\left(1+k\right)+k/\left(1+k\right)\right)}\right]}\\ \hspace{1em}=\frac{9-{\pi }^2}{6}+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}\frac{1}{2k{\left(1+k\right)}^2}\hspace{0.5em}\text{ln}\left[1+\frac{1}{2k^2+k-1}\right]}+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}\frac{3k+1}{4k^2{\left(1+k\right)}^2\sqrt{2+1/k}}\hspace{0.5em}\text{ln}\left[1+\frac{2}{k\sqrt{2+1/k}-1}\right]}.\end{array}$$ (A2)