Abstract
The effective population size (Ne) quantifies the effectiveness of genetic drift in finite populations. When generations overlap, theoretical expectations for Ne typically assume that the sampling of offspring genotypes from a given individual is independent among successive breeding events, even though this is not true in many species, including humans. To explore the effects on Ne of nonindependent mate pairing across breeding events, we simulated the genetic drift of mitochondrial DNA, autosomal DNA, and sex chromosome DNA under three mating systems. Nonindependent mate pairing across breeding seasons has no effect when all adults mate pair for life, a small or moderate effect when females reuse stored sperm, and a large effect when there is intense male–male competition for reproduction in a harem social system. If adult females reproduce at a constant rate irrespective of the type of mate pairing, the general effect of nonindependent mate pairing is to decrease Ne for paternally inherited components of the genome. These findings have significant implications for the relative Ne values of different genomic regions, and hence for the expected levels of DNA sequence diversity in these regions.
THE effective population size (Ne) is a fundamental parameter of population genetics, which quantifies the effect of genetic drift, the stochastic change in allele frequencies over time in a population of finite size (Wright 1931). The magnitude of Ne affects both the level of genetic variability within a population and the efficiency with which populations retain mildly beneficial mutations and purge mildly deleterious ones. This influences a myriad of genetic phenomena, such as the level of DNA sequence polymorphism, the rate of substitution of nonsynonymous and functional noncoding nucleotide positions, the abundance of transposable elements, levels of variation, and the rate of evolution of gene expression, the persistence of duplicate genes, and genome size and organization (Lynch 2007; Charlesworth 2009). There are a variety of definitions of Ne; here we use the definition in terms of the mean coalescence time of a pair of neutral alleles, which is given by 2Ne (Charlesworth 2009). This definition has the useful feature that the expected pairwise nucleotide site diversity under the widely used infinite sites model is equal to 4Neμ, where μ is the neutral mutation rate (Kimura 1971).
As a result of differences in their ploidy level and mode of inheritance, autosomal DNA (aDNA), the X chromosome (xDNA), the Y chromosome (yDNA), and maternally transmitted organelle DNA such as mitochondrial DNA (mtDNA) generally have a different Ne values. Under certain conditions, such as constant population size, discrete generations, a Poisson distribution of reproductive success, and a sex ratio equal to one, the relative Ne values of these genomic regions (Ne-a, Ne-x, Ne-mt, and Ne-y) are expected to be 4:3:1:1 (Charlesworth 2009). This is because aDNA is biparentally inherited and diploid; xDNA is biparentally inherited, diploid in females, and haploid in males (with female heterogamety, the reverse applies to the Z chromosome), and yDNA (the W chromosome, with female heterogamety) and mtDNA are both effectively uniparentally inherited and haploid in most species.
However, several characteristics of natural populations, such as unequal numbers of males and females and nonrandom variation in reproductive success, can affect the value of Ne, even for populations with discrete generations (reviewed in Caballero 1994; Hedrick 2007; Charlesworth 2009). In addition, natural selection at sites linked to neutral markers also has the potential to increase Ne (under balancing selection) (Charlesworth 2006) or to decrease Ne (with background selection or selective sweeps) (Hudson and Kaplan 1988; Charlesworth et al. 1993). Because the nature of natural selection varies in different genomic regions, especially in relation to the rate of recombination, Ne may also vary among unlinked regions with the same ploidy and mode of inheritance, for example, different portions of an autosomal chromosome (Gossmann et al. 2011). In natural populations, these factors can skew the relative Ne values away from the 4:3:1:1 expectation. Even when the effects of natural selection and “nonideal” demography are ignored, the 4:3:1:1 relation still has a large variance when applied to individual loci (Hudson and Turelli 2003).
When generations overlap, an additional source of possible deviations from these idealized relations arises from variation among individuals in survival and reproductive success among breeding seasons (Felsenstein 1971; Hill 1972, 1979; Johnson 1977) and from sex differences in demographic parameters and stochastic changes in population size (Engen et al. 2007). In contrast, the effect of a high variance in reproductive success caused by male–male competition is lessened when generations overlap for many breeding seasons (Nunney 1993; Charlesworth 2001). Conversely, overlapping generations with nonindependent mate pairing across breeding seasons could increase the variance in reproductive success. For example, in humans, paternity is correlated with paternal confidence in paternity (Anderson 2006), and married individuals tend to repeatedly produce offspring with each other more frequently than expected by chance. Nonindependent mate pairing among breeding seasons occurs in many other species as well—for example, long-term pair bonding in prairie voles (DeVries et al. 1995), harems in gorillas (Gatti et al. 2004), and sperm storage in fruit flies (Neubaum and Wolfner 1999).
Current theoretical models that allow calculation of the effective population size with overlapping generations and age structure make several simplifying assumptions, notably constant sizes of each age class, sufficiently large numbers of individuals in each age class that second-order terms in their reciprocals can be neglected, and independent sampling of offspring genotypes from the same individual reproducing at different times (Hill 1972; Nunney 1991, 1993; Caballero 1994; Charlesworth 1994, 2001). The latter assumption in particular makes it difficult to provide accurate expressions for species such as humans and Drosophila, which reproduce nonindependently because of long-term pair bonds and sperm storage, respectively (Charlesworth 2001).
The goal of this study is therefore to explore the consequences of nonindependence of reproductive events across time in different social systems and with different age structures, using simulations of genetic drift in two types of age-structured populations, under different scenarios of independent and nonindependent mate pairing among breeding events. We have explored how these scenarios affect the relative values of Ne-a, Ne-x, Ne-mt, and Ne-y using the infinite alleles model of mutation (Kimura and Crow 1964), with particular emphasis on comparisons of similar mating systems that differ in the extent of nonindependence among breeding events.
Theory and Methods
Age structure
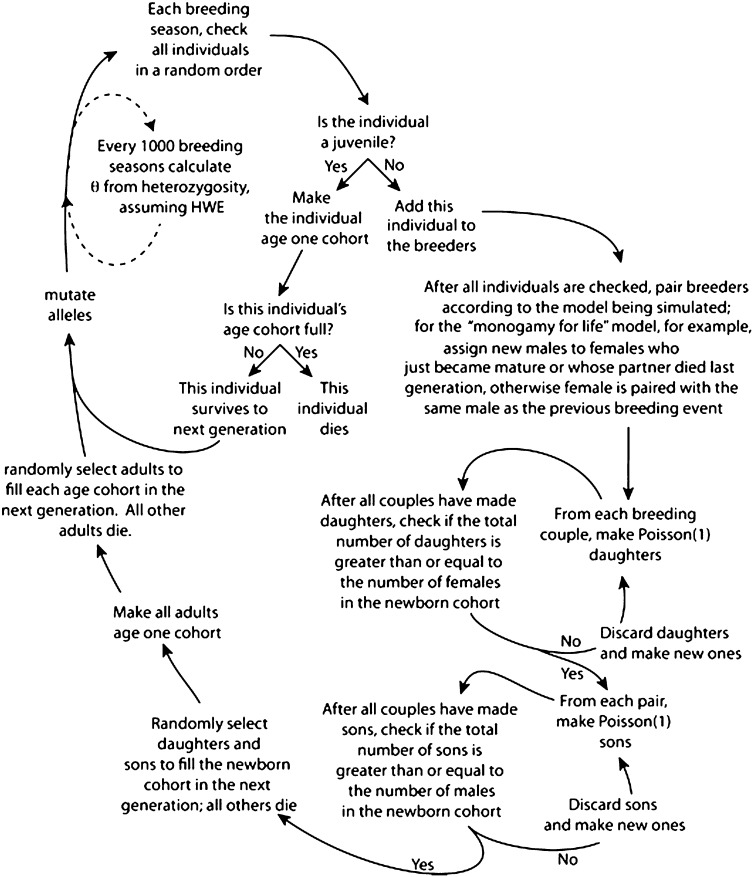
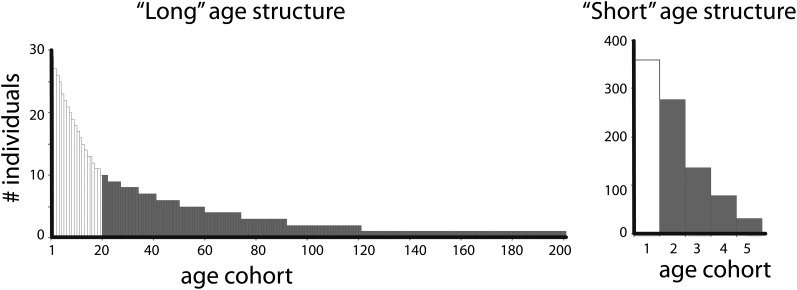
A flowchart illustrating the steps involved in these simulations is shown in Figure 1, with further details of each model provided below. We performed simulations of the two types of age-structured populations depicted in Figure 2. The first “long” age structure model had a large number of age-classes (n = 200), intended to approximate the life history of organisms such as Drosophila or primates that reproduce quasi-continuously. The second “short” age structure model had only five age classes and applies to organisms that have only a few opportunities to reproduce within an individual’s lifespan. The following assumptions are made: a constant population size, an equal number of males and females, reproduction and death over discrete time intervals, a demographic model that includes nonreproductive juveniles, age-independent adult mortality and fecundity, and no sex differences in age-specific survival probabilities (and hence age distributions) or mutation rate. A fixed age distribution was assigned to the population consistent with regulation by density-dependent fecundity or mortality (Charlesworth 1994, Chap. 1). Mating was at random with respect to genotype and age of parent. For details, see Supporting Information, File S1, File S2, and File S3.
Figure 1 .
Flowchart illustrating details of simulations. The boxed steps describe the pairing of adult breeding individuals and reproductive outcomes in a given cycle. This description refers to the “seasonal monogamy” and “monogamy for life” models. For the “harem” and “storage” models, the boxed step differs in that females are instead paired with males or stored sperm as described in the text.
Figure 2 .
Age distribution for each sex used in simulations. (Left) In the long age structure, males and females each have a nonreproductive juvenile phase consisting of 20 breeding seasons and an adult phase consisting of 180 breeding seasons. (Right) In the short age structure, males and females each have a nonreproductive juvenile phase consisting of 1 breeding season and an adult phase consisting of 4 breeding seasons.
Mating systems
The mating systems explored here are divided into those in which females pair with males that are chosen randomly with replacement from the set of adult males and those in which females pair randomly with males chosen randomly without replacement. When mate pairing occurs without replacement, each male reproduces with a maximum of one female per breeding season for monogamy models (or with one harem of females per breeding season for harem models, provided that the male holds a harem). When mate pairing occurs with replacement, all males have an equal probability of mating with each female (provided she is not using stored sperm) but the same male may by chance mate with multiple females in a given breeding season.
For mate pairing without replacement, we explored a system with either mate pairing between male–female pairs (“monogamy” models) or with males and groups of females (“harem” models). We considered two versions of the monogamy and harem models. In the first version, following Nunney (1991, 1993), mate pairing occurs independently in each breeding season. We call these models the “seasonal monogamy” and “seasonal harem” models. In the second version, mate pairing occurs for life and is thus nonindependent among breeding seasons. We call these models the “monogamy for life” and “harem for life” models. Details are given in File S1, File S2, and File S3.
In the seasonal harem and the harem for life models, we first focused on a system in which all adult females are mate paired in harems composed of nine females and one male. Because the number of males and females are equal, eight out of every nine adult males cannot reproduce in each breeding season in both cases. In the seasonal harem model, each adult male gets a chance to be in a harem every breeding season, because the male that occupies each harem is chosen randomly each breeding season. In the long age structure simulations, most males do not successfully reproduce each breeding season, so that the effect of harems on Ne is modest in the seasonal harem model. However, this effect is more pronounced in the short age structure. These effects are quantified below in the Theoretical expectations section. In the harem for life model, the same males occupy harems for multiple breeding seasons. Half siblings can be produced each breeding season if offspring from multiple females within the same harem survive. Nonreproductive adult males get the chance to reproduce in subsequent breeding seasons only if they are randomly chosen for joining a harem where the male died after the previous breeding season. In this way, in the harem for life model harems are expected to have a more pronounced effect on the variance in reproductive success among males in both age structures as compared to the seasonal harem model. As discussed below, we also modeled other harem sizes for the seasonal harem and the harem for life models.
For mate pairing with replacement, we performed simulations that are similar to the “lottery polygyny” mating system explored by Nunney (1993), which we refer to as the “storage” models. In lottery polygyny, all females mate each breeding season with a male drawn randomly with replacement. Drawing males with replacement generates an additional variance in male reproductive success beyond the Poisson expectation; this effect is quantified below in the Theoretical expectations section. In the storage models, Poisson distributions of numbers of offspring of each sex are produced by a female with a randomly selected male; the progeny are thus full siblings. Half siblings can be produced each generation if the same male is by chance paired with two or more females. A subset of the resulting offspring from these pairings is chosen for survival, based on the number of newborns in the youngest age cohort dictated by density-dependent equilibrium (as in the monogamy and harem models).
To examine nonindependent mate pairing across breeding seasons in the models with replacement (the storage models), we simulated sperm storage (Neubaum and Wolfner 1999). Virgin females initially mate with a male chosen randomly with replacement; in subsequent breeding seasons there is a fixed probability of reproduction with sperm stored from this mating, with the decision to use or not use the stored sperm made by drawing a random number. In the event that stored sperm is not used, females are paired again with a male selected randomly with replacement. We assumed that females store sperm for their entire life and that stored sperm is exclusively derived from the most recent copulation.
Simulations were performed with a 0% probability of using stored sperm (the “no-storage” model, analogous to lottery polygyny), a 50% probability of using stored sperm (the “half-storage” model), and a 100% probability of using stored sperm (the “all-storage” model). The all-storage model is therefore identical to the monogamy for life model with the exceptions that (1) the initial pairing of males with each female is performed with replacement and (2) in the monogamy for life model, a female receives a new partner if her male dies, whereas in the storage models, a female continues to use stored sperm after her male dies. The all-storage model (and also the other storage models—no storage and half storage) therefore have an additional variance in male reproductive success compared to the monogamy models, which stems from mate pairing with replacement. In the all-storage model, and to some degree the half-storage model, this additional variance is partially offset by a lower variance in partner number per female, because in the monogamy for life model some females outsurvive their partners and pair again with another male. We expect the magnitude of this offset to be small, because only half of the females outlive their partners, and because in these cases the disparity in life spans is generally small.
Of course, many assumptions of these models are not met by species in nature. For example, the assumption of a constant population size, including a male to female sex ratio of 1:1 in each age cohort, is unrealistic. Overall, our focus was to evaluate the effect of nonindependent mate pairing on the relative Ne values for different parts of the genome. In doing so, however, we were unable to emulate various details of the breeding systems of real species, and we also violate to some degree various key theoretical assumptions that are commonly made in deriving formulae for Ne.
Estimating Ne from simulations of genetic systems
We estimated Ne-a, Ne-x, Ne-mt, and Ne-y by conducting individual-based Monte Carlo simulations that incorporated the above demographic assumptions into single-locus genetic models of each of these modes of transmission. Effective population sizes were estimated from genetic diversity under the infinite alleles model of neutral mutation (Kimura and Crow 1964), under which each new mutation at a locus represents a new allele. Forward simulations were performed in which mutations occurred at a rate μ per time interval, such that μ is the probability that a gamete produced by a parent at time t contains an allele that was not present in the zygote that formed the parent in question (Charlesworth 2001, Equation A1). Plots of H/(1 − H), where H is the heterozygosity (the probability that two random alleles are different is state) vs. time were used to assess when the simulations had progressed for a sufficient number of breeding seasons for the system to reach mutation–drift equilibrium (at which point the heterozygosity reaches an equilibrium (Heq). Under the infinite-alleles model, Heq is determined by the scaled mutation rate parameter θ = 4Neμ, giving the (nonlinear) relation θ = Heq/(1 – Heq) (Kimura and Crow 1964). Heq was estimated from the mean heterozygosity across all simulations; this mean was then used to calculate θ. Simulations were performed on the sharcnet computer cluster (http://www.sharcnet.ca) and scripts that perform these simulations are available by request.
Theoretical expectations
Theoretical expectations for Ne for aDNA, xDNA, mtDNA, and yDNA under the assumption of independent mate pairing among breeding seasons are given by Equations 4, 8, 11, 12, and 13 of Charlesworth (2001). Equations 4, 8, and 11 provide expressions for Ne that take age structure into account, assuming Poisson distributions of per capita offspring number for individuals breeding at a given time. Equations 12 and 13 include parameters for adult males (ΔVm) and adult females (ΔVf) that represent additional variances in offspring number over Poisson expectations, standardized by the squared mean offspring number per breeding season per adult of each sex (note that this differs from the usage in Vicoso and Charlesworth (2009), where unstandardized variances were discussed). For all models considered here, ΔVf is equal to zero because adult females always have an equal opportunity of reproducing. For the monogamy models, ΔVm is also equal to zero, because all adult males also have an opportunity to reproduce that is equivalent to each other and to the adult females.
For the no-storage model with lottery polygyny, based on random sampling of males each breeding season, the argument of Vicoso and Charlesworth (2009, Appendix, Equation A5) can be used, generalizing it to assume a mean number of offspring per individual of x instead of 2. This gives the result that ΔVm is approximately equal to the binomial variance in offspring number, divided by the squared mean offspring number per adult male per breeding season, i.e.,
| (1) |
where x is the mean number of offspring per male adult per breeding season and p is the probability that a female selects a given adult male for a mating event (with a large number of breeding males, p ≪ 1). This formula for ΔVm accommodates the additional variance in male reproductive success due to mate pairing with replacement (cf. Nunney 1993; Vicoso and Charlesworth 2009).
For the seasonal harem model, since a male that is not in a harem has no offspring, ΔVm is given by
| (2) |
where p1 is the probability that an adult male is in a harem, x1 is the expected number of offspring per harem male, and the mean number of offspring per male is x = p1x1. Numerical values for ΔVm from these equations for the models analyzed here are given in File S1, File S2, and File S3.
Comparing simulations with the theoretical expectation and with each other
Ninety-five percent confidence intervals for Ne estimated from the simulations were generated by adding or subtracting 1.96 times the standard error from the mean Heq and then converting these values to Ne according to the relation Ne = Heq/[4μ(1− Heq)]. These 95% confidence intervals were essentially the same as those calculated with an alternative approach in which we recalculated the mean from resampling subsets of the data (jackknifing) 1000 times, including each simulation in each iteration with 50% probability (data not shown). The theoretical variance of Heq for a Wright–Fisher population, which is equal to 2θ/((2+θ)(3+θ)(1+θ)2 (Nei 1987, p. 369) was also compared to the simulated variance of Heq. Ninety-five percent confidence intervals for the ratios Ne-x:Ne-a, Ne-mt:Ne-a, and Ne-y:Ne-a for each model were also estimated from the resampled data subsets.
We compared the theoretical θ to the simulated θ using two tailed z-tests (test 1). The null hypothesis for test 1 is that the mean of the simulated θ is not different from the theoretical θ, calculated as described above. An approximation for the variance of θ was obtained from the theoretical variance of Heq (as defined above) using the Delta method—i.e., by multiplying the variance of Heq by the square of the derivative of H/(1 − H), which is (1 − Heq)−4. This approximation for the variance of θ was then used to calculate the standard error of θ for the z-test. We also performed the z-test using the standard error of θ estimated from the simulated variance of Heq instead of the theoretical variance of Heq, with similar results.
We compared the relative sizes of Ne-a, Ne-x, Ne-mt, and Ne-y from each of the simulations to the theoretical expectations under the null hypothesis that the relative sizes of Ne-a, Ne-x, Ne-mt, and Ne-y are not different from the theoretical expectations discussed above (test 2). A two-sided normal deviate test was used to test whether the difference between the θ value for xDNA, multiplied by the theoretical value of the ratio Ne-a/Ne-x, and the θ value for aDNA, was significantly different from zero. For example, for the monogamy models, 1.333 times the simulated θ value for xDNA was compared to 1 times the simulated θ value for aDNA. A significant departure of this difference from zero was inferred if the difference of the means was >1.96 standard errors, using the following expression for the variance of this difference
| (3) |
where Rxa is the theoretical value of the ratio Ne-a/Ne-x, and Var(θx) and Var(θa) refer to the variances in θ of xDNA and θ of aDNA, respectively, which are approximated from the variance of Heq as described above. Test 2 was also used to compare simulated scaled θ values for mtDNA to simulated θ values for aDNA and to compare simulated scaled θ values for yDNA to simulated θ values for aDNA.
We also compared the simulations with nonindependent mate pairing across breeding seasons (the monogamy for life, harems for life, and the half-storage or all-storage models) to the corresponding simulations with independent mate pairing across breeding seasons (the seasonal monogamy, seasonal harem, and the no-storage models, respectively) for each type of locus (aDNA, xDNA, mtDNA, and yDNA; test 3). The null hypothesis of test 3 is that, for a given locus type, the mean θ from the simulations with independent mate pairing across breeding seasons is not different from the mean θ from the simulations without independent mate pairing. The statistical approach was similar to test 2 in that we used a two-sided normal deviate test to test whether the difference between the θ value from the model with independent mate pairing among breeding seasons and the θ value from the model with nonindependent mate pairing among breeding seasons was significantly different from zero.
A premise of tests 1, 2, and 3 is that the statistics being compared have an approximately Gaussian distribution. While this is not precisely the case, this assumption is approximately met because of the large number of replicate simulations used to generate the mean θ values (4000). This assumption is justified in File S3.
Results
Theoretical expectations
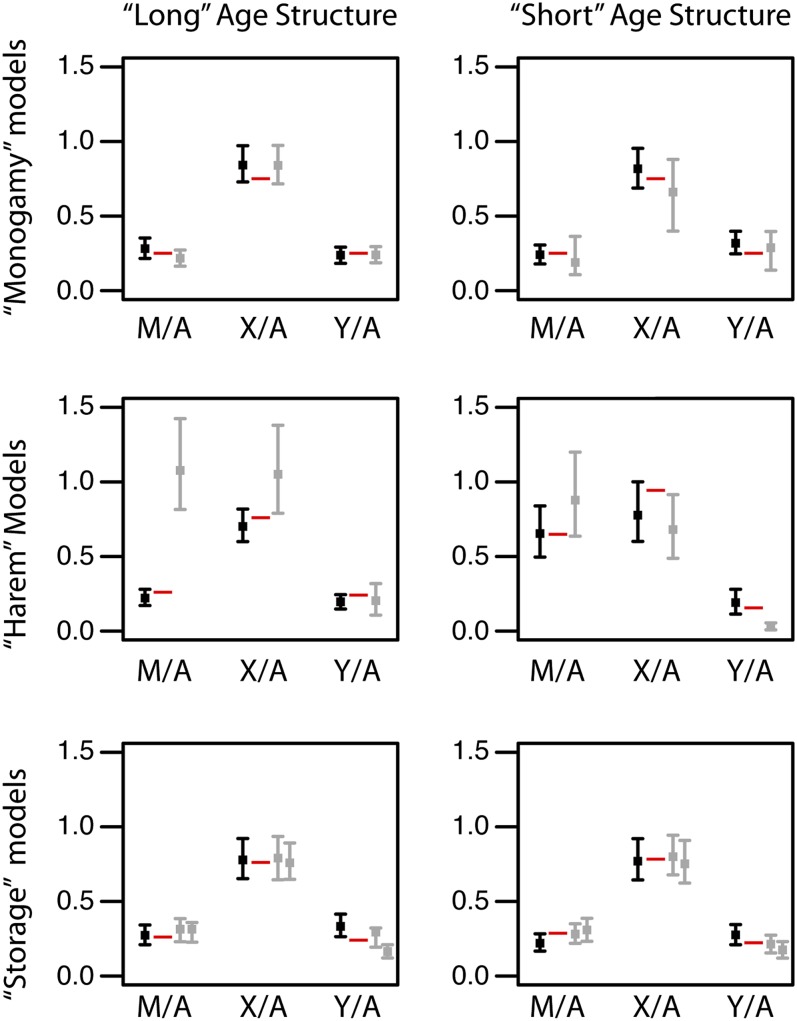
Table 1 and Table 2 show theoretical expectations for the Ne values for the case of independent mate pairing across breeding events, based on Equations 1 and 2 and the relevant formulas in Charlesworth (2001), and using the numerical values for demographic parameters provided in File S1 and File S2. The theoretical values of Ne-m/Ne-a, Ne-x/Ne-a, and Ne-y/Ne-a are also presented in Table 1 and Table 2 and summarized in Figure 3. The theoretical value for Ne-mt for each of the age structures is the same for all models, because the variance in female reproductive success is the same in all models, although the expectations differ substantially for each of the age structures. In general, overlapping generations reduce Ne relative to the census size for adults (Nc) (Nunney 1991, 1993; Charlesworth 2001) and as a result, the theoretical expectations for Ne are substantially lower for the long age structure (Table 1) than for the short age structure (Table 2) for each of the models. In our simulations, Nc for the long and short age structures is equal to 1044 individuals and 1062 adults, respectively.
Table 1 . Theoretical expectations and simulation results for each model with the long age structure.
| Monogamy model | Ne-mt | Ne-x | Ne-a | Ne-y | Ne-mt/Ne-a | Ne-x/Ne-a | Ne-y/Ne-a |
|---|---|---|---|---|---|---|---|
| Theoretical expectation | 182.0 | 545.9 | 727.9 | 182.0 | 0.250 | 0.750 | 0.250 |
| Seasonal monogamy | 194.9 (155.5 – 234.4) | 580.6 (515.4 – 646.2) | 689.9 (618.2 – 762.1) | 164.3 (130.0 – 198.7) | 0.282 (0.216 – 0.353) | 0.842 (0.729 – 0.972) | 0.238 (0.183 – 0.292) |
| Monogamy for life | 154.2 (121.3 – 187.2) | 596.1 (527.7 – 664.8) | 710.0 (636.1 – 784.3) | 170.1 (134.6 – 205.7) | 0.217 (0.164 – 0.272) | 0.840 (0.716 – 0.974) | 0.240 (0.187 – 0.295) |
| Harem model | |||||||
| Theoretical expectation | 182.0 | 532.3 | 700.9 | 169.0 | 0.260 | 0.759 | 0.241 |
| Seasonal harem | 157.1 (119.7 – 194.63) | 498.8 (426.2 – 571.8) | 710.9 (627.2 – 795.2) | 139.1 (104.8 – 173.5) | 0.221 (0.171 – 0.280) | 0.702 (0.600 – 0.818) | 0.196 (0.148 – 0.244) |
| Harem for life | 207.3 (163.9 – 250.8) | 202.2 (159.0 – 245.5)1,3 | 192.4 (150.0 – 234.9)1,3 | 39.3 (18.0 – 60.6)1,3 | 1.077 (0.815 – 1.424)2 | 1.051 (0.790 – 1.380)2 | 0.204 (0.107 – 0.318) |
| Storage models | |||||||
| Theoretical expectation | 182.0 | 530.7 | 697.8 | 167.5 | 0.261 | 0.761 | 0.240 |
| No storage | 173.5 (137.7 – 209.5) | 494.3 (432.9 – 556.0) | 634.9 (566.7 – 703.6) | 211.2 (170.9 – 251.6)1 | 0.273 (0.210 – 0.342) | 0.7786 (0.653 – 0.922) | 0.333 (0.264 – 0.415)2 |
| Half storage | 212.2 (170.0 – 261.9) | 533.9 (472.0 – 618.4) | 675.1 (625.4 – 797.7) | 198.5 (139.7 – 223.6) | 0.314 (0.230 – 0.385) | 0.791 (0.645 – 0.936) | 0.294 (0.193 – 0.322) |
| All storage | 197.1 (152.9 – 241.4) | 516.2 (442.2 – 590.7) | 679.9 (592.7 – 767.7) | 111.5 (81.2 – 141.9)1,3 | 0.290 (0.227 – 0.359) | 0.759 (0.648 – 0.892) | 0.164 (0.121 – 0.210)2 |
Ne-mt, Ne-x, Ne-a, and Ne-y refer to Ne of mitochondrial DNA, X chromosome DNA, autosomal DNA, and Y chromosome DNA, respectively. Superscripted numbers reflect significance of tests 1, 2, and 3 (see text) respectively. Confidence intervals (95%) for Ne and ratios are indicated in parentheses. Theoretical expectations are available only for the models with independent mate pairing among breeding seasons (the seasonal monogamy, seasonal harem, and no-storage models).
Table 2 . Theoretical expectations and simulation results for each model with the short age structure.
| Monogamy model | Ne-mt | Ne-x | Ne-a | Ne-y | Ne-mt/Ne-a | Ne-x/Ne-a | Ne-y/Ne-a |
|---|---|---|---|---|---|---|---|
| Theoretical expectation | 291.2 | 873.5 | 1164.6 | 291.2 | 0.250 | 0.750 | 0.250 |
| Seasonal monogamy | 278.1 (214.5 – 341.8) | 944.1 (827.8 – 1061.1) | 1156.1 (1027.4 – 1285.5) | 367.8 (292.5 – 443.4)1 | 0.241 (0.179 – 0.306) | 0.817 (0.688 – 0.954) | 0.318 (0.247 – 0.398) |
| Monogamy for life | 253.9 (193.3 – 314.7) | 887.5 (776.0 – 1000.0) | 1209 (1076.7 – 1343.6) | 347.9 (278.7 – 417.2) | 0.189 (0.107 – 0.364) | 0.661 (0.399 – 0.880) | 0.288 (0.137 – 0.397) |
| Harem model | |||||||
| Theoretical expectation | 291.2 | 423.9 | 449.5 | 69.6 | 0.648 | 0.943 | 0.155 |
| Seasonal harem | 308.3 (245.2 – 371.5) | 366.2 (296.5 – 436.2) | 471.1 (389.2 – 553.3) | 90.0 (53.2 – 126.0) | 0.654 (0.496 – 0.839) | 0.777 (0.601 – 1.001) | 0.191 (0.114 – 0.280) |
| Harem for life | 278.3 (216.0 – 340.7) | 215.8 (162.7 – 269.1)1,3 | 317.1 (248.2 – 386.2)1,3 | 9.4 (1.7 – 17.1)1,3 | 0.878 (0.636 – 1.200) | 0.681 (0.488 – 0.915) | 0.030 (0.008 – 0.055)2 |
| Storage models | |||||||
| Theoretical expectation | 291.2 | 796.2 | 1016.6 | 225.5 | 0.286 | 0.783 | 0.222 |
| No storage | 251.5 (194.6 – 308.5) | 881.8 (769.9 – 994.3) | 1145.0 (1017.8 – 1272.9)1 | 316.3 (247.9 – 385.0)1 | 0.220 (0.167 – 0.283)2 | 0.770 (0.644 – 0.921) | 0.276 (0.210 –0.345) |
| Half storage | 301.3 (235.2 – 367.5) | 858.7 (748.8 – 969.1) | 1073.4 (950.3 – 1197.3) | 229.5 (173.5 – 285.7) | 0.281 (0.219 – 0.350) | 0.800 (0.678 – 0.944) | 0.214 (0.155 – 0.274) |
| All storage | 285.2 (222.9 – 347.7) | 694.0 (593.8 – 794.6)1,3,a | 922.4 (809.8 – 1035.7)3 | 161.0 (114.0 – 208.1)1,3 | 0.309 (0.233 – 0.387) | 0.752 (0.623 – 0.909) | 0.175 (0.120 – 0.231) |
Ne-mt, Ne-x, Ne-a, and Ne-y refer to Ne of mitochondrial DNA, X chromosome DNA, autosomal DNA, and Y chromosome DNA respectively. Superscripted numbers reflect significance of tests 1, 2, and 3 (see text), respectively. Confidence intervals (95%) for Ne and ratios are indicated in parentheses. Theoretical expectations are available only for the models with independent mate pairing among breeding seasons (the seasonal monogamy, seasonal harem, and no-storage models).
Test 1 was significant when the observed standard error was used but not when the theoretical standard error was used.
Figure 3 .
Summary of Ne-m/Ne-a (M/A), Ne-x/Ne-a (X/A), and Ne-y/Ne-a (Y/A) ratios expected in theory (red dashes), and from simulations with or without independent mate pairing among breeding seasons (black and gray points respectively reflect mean values) with bars indicating 95% confidence intervals. For the storage models with nonindependent mate pairing (in gray), results of the half-storage simulations are plotted to the right of the results of the all-storage simulations.
Simulations with independent mate pairing across breeding seasons
Simulations of mitochondrial DNA can be considered as “controls” for comparison across simulations within each age structure. In no case did these Ne-mt simulations deviate significantly from the theoretical value; as expected, the simulated Ne-mt values for each age structure were similar, irrespective of the model (Table 1 and Table 2). Ne estimates from the simulations with independent mate pairing among breeding seasons were never individually significantly lower than the theoretical expectations (test 1, Table 1 and Table 2). Unexpectedly, on three occasions simulations with independent mate pairing across breeding seasons were individually significantly higher than the theoretical expectation (test1; Table 1 and Table 2). These included Ne-y values from the no-storage model in the long and short age structure simulations and also Ne-a values from the no-storage model in the short age structure simulations. However, none of these was significant after Bonferroni correction for four locus types tested per simulation (Rice 1989), and it is clear from inspection of plots of θ vs. time that these values are atypically high at the generation we choose to study (400,00 for the long age structure and 200,000 for the short age structure; see black arrows in Figure S1).
The variance in heterozygosity among replicate simulations was generally similar to the theoretical variance: for all three models with independent mate pairing, the variance in heterozygosity of the simulations was <30% higher or lower than the theoretical variance for each locus type. Exceptions to this were yDNA in the no-storage and in the seasonal monogamy models in the short age structure simulations, which had simulated variances that were >35% higher than the theoretical expectations. Overall, it appears that the simulations with independent reproduction across time intervals agreed well with the theoretical predictions of the behavior of populations with overlapping generations.
In the seasonal monogamy model, males have the same distribution of reproductive success as females, so that the difference between Nc and the theoretical value of Ne reflects the presence of juveniles and mortality between successive age classes, which together cause a departure from the discrete-generation equivalent N. In the seasonal monogamy model, the theoretical expectation for Ne-a/2Nc for autosomes is 0.349 and 0.548, respectively, for the long and short age structures (Table 1 and Table 2). The theoretical values of the relative Ne of different parts of the genome are the same as for the discrete generation equivalent (that is, 4: 3: 1: 1 for Ne-a: Ne-x: Ne-mt: Ne-y), as found previously (Charlesworth 2001).
In the seasonal harem models, males have unequal access to reproduction depending on whether or not they are in a harem. This is expected to decrease the Ne of paternally inherited portions of the genome. However, in the long age structure this difference is small with a harem size of nine females, with independent mate pairing among breeding seasons (Table 1). This is because male membership in harems is reassigned each breeding season and because relatively few offspring are produced each breeding season in our model. Thus, because most males do not reproduce in each breeding season in the long age structure, the harem system did not substantially increase the variance in male reproductive success within a given breeding season, as long as males are reassigned to harems each breeding season. The theoretical value of Ne-a/2Nc for the seasonal harem model is equal to 0.336 and 0.212, respectively, for the long and short age structures.
Differences in Ne/Nc between the seasonal monogamy and the seasonal harem models illustrate a more prominent role of the harem social system in a population where on average most adults breed during their lifetime (the short age structure), as compared to a population where on average most adults do not breed during their lifetime (the long age structure). Because of the different paternal contributions, the theoretical expectations for Ne-mt /Ne-a and Ne-x/Ne-a in the seasonal harem model are higher than 1/4 and 3/4, respectively, but lower than 1/4 for Ne-y/Ne-a (Table 1 and Table 2). In the storage model, mate pairing occurs with replacement, and an additional variance in male reproductive success is generated by resampling males each breeding season. Compared to the monogamy models, the expectation for Ne for the no-storage model is again lower for paternally inherited portions of the genome, but not substantially so for either age structure (Table 1 and Table 2). For the no-storage model, Ne-a/2Nc is equal to 0.334 and 0.479, respectively, for the long and short age structures.
Simulations with nonindependent mate pairing across breeding events
The theoretical expectations discussed above assume independent mate pairing across successive breeding events involving the same individual. We anticipated that nonindependent mate pairing among breeding seasons in our models would increase the variance in male reproductive success. We therefore expected a reduction in Ne for wholly or partially paternally inherited portions of the genome (xDNA, aDNA, and yDNA) in simulations with nonindependent mate pairing across breeding seasons compared to these theoretical expectations and compared to the simulations with independent mate pairing across breeding seasons. Theoretical expressions for Ne when mate pairing is not independent across breeding seasons are not available in these cases; for this reason, we relied on simulations to quantify the effect of this nonindependence.
The seasonal monogamy and monogamy for life models differ in that the first model has independent mate pairing among breeding seasons. However, these models are identical in terms of the variances in female and male reproductive success in a given breeding season, which are close to the Poisson values. As expected, there was no significant difference for any locus type between the theoretical Ne values for the seasonal monogamy model and the simulated values for the monogamy for life model (P > 0.05, test 1, Table 1 and Table 2). The relative Ne values from the monogamy for life simulations were also not significantly different from the theoretical expectations for the seasonal monogamy model (P > 0.05, test 2; Table 1 and Table 2); the same applies to the difference between the simulated Ne values from the monogamy for life model and the seasonal monogamy models (P > 0.05, test 3; Table 1 and Table 2). Thus, nonindependent mate pairing among breeding seasons does not greatly affect Ne in the monogamy model, provided that all adults are paired for reproduction in each breeding season. This model requires an equal number of males and females to make possible the 1:1 matching of adults of each sex in every breeding season—a condition rarely met in natural populations.
To explore a more realistic scenario where males have a higher variance in reproductive success than females, we performed simulations where one male reproduces with a harem of nine females. Because there is an equal number of males and females, eight out of every nine males do not reproduce each breeding season. In both age structures, the harem for life model has significantly lower Ne values than the theoretical expectation under independence across seasons and the results from simulations with independent mate pairing across breeding seasons in all portions of the genome with paternal inheritance (Ne-x, Ne-a, and Ne-y, P < 0.05, tests 1 and 3; Table 1 and Table 2). As expected, simulated values of Ne-mt from the harem for life model were not significantly different from the theoretical expectation or simulations with independent mate pairing across breeding seasons (P > 0.05, tests 1 and 3, Table 1 and Table 2). In the harem for life model, the effect of nonindependent mate pairing on Ne of paternally inherited portions of the genome is more severe for parts of the genome with a higher proportion of paternal inheritance. Nonindependent mate pairing in the harem for life model thus decreases Ne-a compared to Ne-mt and Ne-x, so that Ne-mt/Ne-a and Ne-x/Ne-a are higher, but decreases Ne-y compared to Ne-a, so that Ne-y/Ne-a is lower (Figure 3).
As expected, Ne-x/Ne-a was significantly higher than the theoretical expectation with independent mate pairing across breeding seasons for the long age structure. There was no significant difference between these ratios for the short age structure and, contrary to expectations, Ne-x/Ne-a from the harem for life simulations for the short age structure was almost significantly lower (Figure 3). However, this unexpected result was caused by an atypically high Ne-a and atypically low Ne-x that were sampled at the 200,000th simulated breeding season in these simulations (see red arrows in Figure S1). Consistent with expectations, Ne-mt/Ne-a from the long age structure was higher and Ne-y/Ne-a from the short age structure was lower than the theoretical expectation with independent mate pairing across breeding seasons (test 2; Table 1 and Table 2), although the significance of these disparities differed between the age structures.
A significant effect of nonindependent mate pairing among breeding seasons was also recovered from simulations involving sperm storage, although the effect was much smaller than that caused by nonindependent mate pairing among breeding seasons in the harem for life model. We considered three scenarios for sperm storage: the no-storage model where females do not store sperm, the half-storage model where females use stored sperm half of the time, and the all-storage model where females always use stored sperm derived from their first reproduction. As expected, the effect of sperm storage on Ne was most pronounced for Ne-y. When the half-storage model was compared to the no-storage model, Ne was not significantly different for any locus type for either age structure (P > 0.05, test 3; Table 1 and Table 2). But when the all-storage model was compared to the no-storage model, Ne-y was significantly lower for the long age structure model and Ne-x, Ne-a, and Ne-y were significantly lower with the short age structure (P < 0.05, tests 1 and 3; Table 1 and Table 2). The relative Ne of the different loci in the half-storage model was not significantly different from the theoretical expectations for either age structure (P > 0.05, test 2; Table 1 and Table 2). The relative Ne values of the different loci in the all-storage model were also not significantly different from the theoretical expectations (P > 0.05, test 2; Table 1), except for Ne-y/Ne-a, which was significantly lower than the theoretical expectation with the long age structure (P < 0.05, test 2; Table 1).
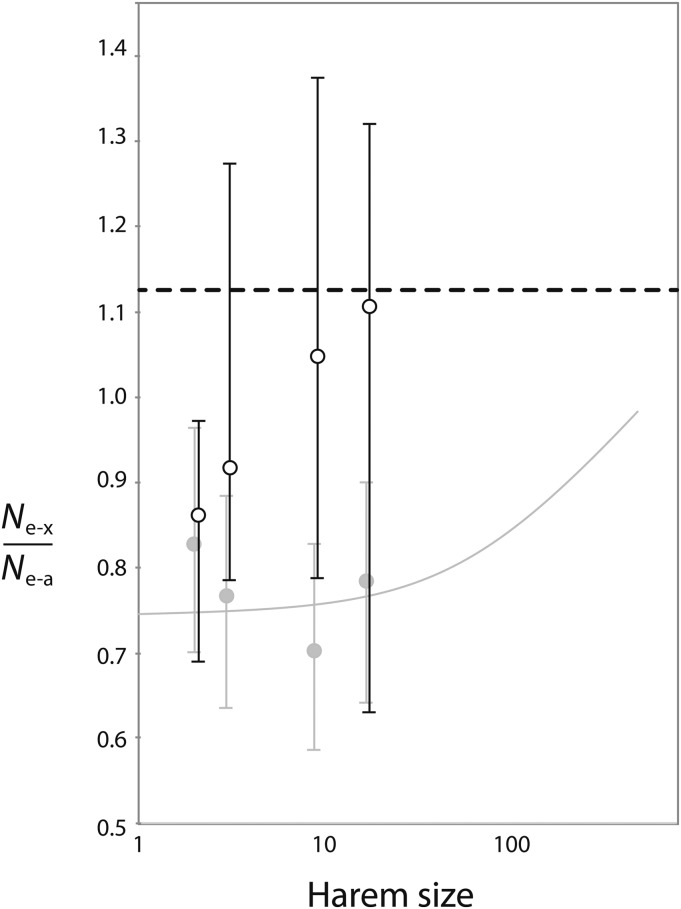
Using the long age structure model, we also performed simulations with harem sizes equal to 2, 3, or 18 females, with or without independent mate pairing among breeding seasons. As expected, Ne for paternally inherited portions of the genome decreases with increasing harem size. For all of these harem sizes, Ne for paternally inherited portions of the genome was significantly smaller for the harem for life model than the theoretical expectation with independent mate pairing among breeding seasons (test 1, P < 0.05; Table S1) and than the seasonal harem (test 3, P < 0.05; Table S1). As expected, for harem sizes of 2, 3, or 18 there was no significant difference between the simulated Ne-mt and the theoretical expectation (test 1, P > 0.05) or between the Ne-mt simulated in the seasonal harem and harem for life models (test 3, P > 0.05). When the Ne-x/Ne-a, Ne-mt/Ne-a, and Ne-y/Ne-a ratios from the seasonal harem model and the harem for life models were compared with harem sizes of 2, 3, or 18, the only ratio that was significantly different from the theoretical expectation was Ne-mt/Ne-a for harem sizes of 3 or 18 (test 2, P < 0.05; Table S1). Nonetheless, it is clear that nonindependent mate pairing across breeding seasons increases Ne-x/Ne-a when the simulations from multiple harem sizes are considered collectively (Figure 4). Based on simulations with harem sizes of 2, 3, 9, and 18 and the long age structure, a permutation test (File S3) indicates that the fit of the jackknifed harem for life Ne-x/Ne-a ratios to the theoretical expectation is significantly worse than the fit of the jackknifed seasonal harem Ne-x/Ne-a ratios (P < 0.0001).
Figure 4 .
Nonindependent mate pairing in the harem for life model using the long age structure has a large effect on the relative Ne of xDNA vs. aDNA compared to the independent mate pairing in the seasonal harem model. Open circles indicate ratios for simulations of the harem for life model, with harem sizes of 2, 3, 9, and 18 for a population with 522 adult males and 522 adult females, plotted on a log scale. Bars indicate 95% confidence intervals. Gray circles are ratios for the seasonal harem model with the same harem sizes. All of these ratios are based on 4000 simulations. The thick dashed line indicates the theoretical maximum of 1.125 for the relative Ne of xDNA vs. aDNA, and the thin gray line is the theoretical expectation for the seasonal harem model. The fit of the harem for life simulations to the theoretical expectation for the seasonal harem model is significantly worse than the fit of the seasonal harem simulations to this expectation (see Results).
Discussion
The standard models of genetic drift in age-structured populations (Felsenstein 1971; Hill 1972, 1979; Johnson 1977; Charlesworth 2001; Engen et al. 2007) assume that reproductive events involving the same individual in different breeding seasons occur independently. This assumption is violated by many species in nature. To explore the effect of nonindependent mate pairing among breeding seasons, we simulated genetic drift under three different mating systems: (1) couples pair randomly without replacement—the monogamy models, (2) multi-female groups pair with one male sampled without replacement—the harem models, and (3) females pair with males chosen with replacement, and potentially store sperm (the storage models, also known as lottery polygyny), in two types of population age structures that differed greatly in their numbers of age classes.
Although we generally did not find significant differences between theoretical and simulated Ne values in the models with independent mate pairing among breeding seasons (see Table 1 and Table 2), there are in fact reasons to expect modest differences that we did not have the statistical power to detect. In particular, the models use approximations that ignore terms of the order of the squares of the reciprocals of the sizes of the reproductive age classes, relative to first-order terms (Felsenstein 1971; Johnson 1977; Emigh and Pollak 1979; Charlesworth 2001). The small populations used in these simulations could thus deviate noticeably from the theoretical predictions for this reason alone. It appears from Table 1 and Table 2, however, that this and other sources of departure from the assumptions used to obtain the theoretical results have only minor effects, given the generally fairly good agreement between the theoretical expectations and the simulation results. However, the theoretically expected high level of stochastic variability for heterozygosity (Nei 1987, p. 369) means that only quite large deviations could be detected, as can be seen from the confidence intervals shown in Table 1, Table 2, Table S1, and in Figure 3 and Figure 4. Greatly increasing the number of replicates would increase our ability to detect deviations from the prediction, but simulations with large numbers of age classes are inherently time consuming.
In contrast, comparisons between the simulation results with independence and those with nonindependent mate pairing among breeding seasons demonstrated a significant effect of nonindependent mate pairing on genetic drift, except in the monogamy model; here, all adults are continuously mate paired for life irrespective of whether mate pairing was independent across breeding seasons. The effect of nonindependent mate pairing among breeding seasons in the harem and storage models was to decrease the Ne of portions of the genome that are at least in part transmitted paternally. In the harem for life model, this effect was significant for Ne-x, Ne-a, and Ne-y. The relative magnitude was generally largest for Ne-y, intermediate for Ne-a, and the smallest for Ne-x, but the ratios of these values did not always differ significantly from the expectations with independent mate pairing among breeding seasons. The effect of nonindependent mate pairing among breeding seasons was similar, but of smaller magnitude, in the all-storage model, with Ne-x, Ne-a, and Ne-y substantially affected in the all-storage simulations with the short age structure.
In the long age structure, we suspect that the nonsignificant effect of nonindependent mate pairing for xDNA and aDNA in the all-storage model is due to the relatively small magnitude of this effect and that a significant effect could be detected if statistical power were increased with more simulations. The same is probably true for xDNA, aDNA, and yDNA in the half-storage model for both age structures. This raises the question of how many more replicates would be needed to reduce the standard error enough to detect a significant difference between the simulations with nonindependent mate pairing among breeding seasons and the theoretical expectation that assumes independent mate pairing among breeding seasons. Using the theoretical expectations for the variance of θ from the approximations discussed above, we explored this question with respect to test 2 with the long age structure, which tests whether the ratio of θ for xDNA to aDNA differs from the null expectation of 0.759 in the harem and storage models. In general, as expected, for a given number of replicates (or independent nucleotide sites in a real data set), the statistical power to detect departure from expectation increases with θ and with the magnitude of the departure from the null expectation. When θ for aDNA is 0.03, 4000 independent replicates provide a >95% probability (at the P = 5% level) of rejecting the null hypothesis that the ratio of θ of xDNA to θ of aDNA is 0.759, when it is actually 0.85 or higher. However, when θ of aDNA is 0.001 (which is closer to the situation in humans), ∼54,000 replicates are needed to achieve a >95% probability of rejecting the null hypothesis that the ratio of θ of xDNA to θ of aDNA is 0.759, when it is actually 0.95 or higher. This shows that data on a large number of SNPs are needed to test for biologically plausible differences in variability among different components of the genome.
The effect of nonindependent mate pairing on Ne-x/Ne-a
Natural selection, mutation, and demographic effects vary between the sex chromosomes, mtDNA, and aDNA, and this influences their Ne and level of polymorphism. The relative Ne of different parts of the genome can offer insight into intricacies of species social systems and natural selection (Ellegren 2009; Charlesworth 2012). After controlling for variation in mutation rate, a paucity of polymorphism on xDNA relative to aDNA could, for example, suggest natural selection on slightly deleterious hemizygous X-linked mutations in males, whereas an excess of polymorphism on xDNA is consistent with a female biased sex adult ratio or an excess variance in male reproductive success (e.g., Charlesworth 2001; Evans et al. 2010). Population size changes can also skew relative Ne values of different components of the genome; for example, Ne-x/Ne-a may become ephemerally higher after population expansion, but lower after population contraction (Pool and Nielsen 2007).
The harem models studied here provide a useful tool with which to explore the effect of another variable that can influence Ne-x /Ne-a—namely, variance in male reproductive success that stems from nonindependent mate pairing across breeding seasons. This could arise, for example, in species with intense male–male competition, where the same males tend to repeatedly win reproductive access over multiple breeding seasons. With the harem models, Ne-x/Ne-a reaches a maximum of 9/8 when only one male reproduces with all females, and a minimum of 9/16 when only one female reproduces with all males (Figure 4; Caballero 1995; Charlesworth 2001), the same as in the discrete generation case (Wright 1931; Caballero 1995). To characterize the effect of nonindependent mate pairing across generations on Ne-x/Ne-a, we performed simulations with various harem sizes (either 2, 3, 9, or 18 females per harem) using the seasonal harem model and the harem for life models. These simulations indicate that a relatively modest amount of nonindependent mate pairing across breeding seasons could potentially account for estimates of Ne-x/Ne-a that are significantly >0.759 (Figure 4). In humans, for example, there appears to be a significant excess of polymorphism for xDNA compared to aDNA in regions far from genes (Hammer et al. 2010). Of note, however, is the high variance of this ratio, even when averaged over 4000 independent sites (see above).
Conclusions
This study demonstrates that, in some circumstances, nonindependent mate pairing across breeding seasons can significant decrease the Ne of wholly or partially paternally inherited portions of the genome, including yDNA, aDNA, and xDNA. In our simulations, the magnitude of this effect is a function of the degree of paternal inheritance and is generally, therefore, largest for yDNA, intermediate for aDNA, and smallest for xDNA. Because this differential effect depends on the mode of inheritance, nonindependent mate pairing across breeding seasons increases Ne-x/Ne-a when all females have purely random variation in reproductive success. Population age structure and lifetime fecundity influenced the effect of nonindependent mate pairing. For example, a statistical signature of nonindependent mate pairing among breeding seasons was more readily detected in the short age structure, in which individuals had a higher lifetime fecundity, than with the long age structure. The simulations performed here were biologically unrealistic in the sense that multiple haploid genomes (mtDNA and yDNA), each with independent genealogical histories, were generated. In reality of course, these genomes have only one genealogy for a given population, and yDNA and mtDNA each offer only one realization of a highly variable coalescent process (Hudson and Turelli 2003). Additionally, because of linkage, yDNA and mtDNA are subject to background and hitchhiking effects, which tend to lower their Ne below neutral expectations. Furthermore, our simulations were performed under the assumption of neutrality—an assumption that may frequently be violated in data sets from real genomes. For these reasons, it is potentially challenging to use molecular polymorphism data from natural populations to distinguish nonindependent mate pairing across breeding seasons from alternative demographic scenarios that also increase Ne-x/Ne-a but that have different expected affects on Ne-y and Ne-mt, such as a skewed adult sex ratio, or recent population growth.
Supplementary Material
Acknowledgments
We thank the Institute for Evolutionary Biology at the University of Edinburgh for hosting B.J.E. during his sabbatical and Jonathan Dushoff and Bill Hill for helpful discussion. We also thank Lindi Wahl and two anonymous reviewers for helpful suggestions.
Footnotes
Communicating editor: L. M. Wahl
Literature Cited
- Anderson K. G., 2006. How well does paternity confidence match actual paternity?: evidence from worldwide nonpaternity rates. Curr. Anthropol. 47: 513–520 [Google Scholar]
- Caballero A., 1994. Developments in the prediction of effective population size. Heredity 73: 657–679 [DOI] [PubMed] [Google Scholar]
- Caballero A., 1995. On the effective size of populations with separate sexes, with particular reference to sex-linked genes. Genetics 139: 1007–1011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B., 1994. Evolution in Age-Structured Populations, 2nd Ed. Cambridge University Press, Cambridge [Google Scholar]
- Charlesworth B., 2001. The effect of life-history and mode of inheritance on neutral genetic variability. Genet. Res. 77: 153–166 [DOI] [PubMed] [Google Scholar]
- Charlesworth B., 2009. Effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 10: 195–205 [DOI] [PubMed] [Google Scholar]
- Charlesworth B., 2012. The role of background selection in shaping patterns of molecular evolution and variation: evidence from variability on the Drosophila X chromosome. Genetics 191: 233–246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B., Morgan M. T., Charlesworth D., 1993. The effect of deleterious mutations on neutral molecular variation. Genetics 134: 1289–1303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth D., 2006. Balancing selection and its effects on sequences in nearby genome regions. PLoS Genet. 2: e64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeVries A. C., DeVries M. B., Taymans S., Carter C. S., 1995. Modulation of pair bonding in female prairie voles (Microtus ochrogaster) by corticosterone. Proc. Natl. Acad. Sci. USA 92: 7744–7748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellegren H., 2009. The different levels of genetic diversity in sex chromosomes and autosomes. Trends Genet. 25: 278–284 [DOI] [PubMed] [Google Scholar]
- Emigh T. H., Pollak E., 1979. Fixation probabilities and effective population numbers in diploid populations with overlapping generations. Theor. Popul. Biol. 15: 86–107 [Google Scholar]
- Engen S., Ringsby T. H., Saether B., Lande R., Jensen H., et al. , 2007. Effective size of fluctuating populations with two sexes and overlapping generations. Evolution 61: 1873–1885 [DOI] [PubMed] [Google Scholar]
- Evans B. J., Pin L., Melnick D. J., Wright S. I., 2010. Sex–linked inheritance in macaque monkeys: implications for effective population size and dispersal to Sulawesi. Genetics 185: 923–937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J., 1971. Inbreeding and variance effective numbers in populations with overlapping generations. Genetics 68: 581–197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatti S., Levréro F., Ménard N., Gautier-Hion A., 2004. Population and group structure of Western Lowland gorillas (Gorilla gorilla gorilla) at Lokoué, Republic of Congo. Am. J. Primatol. 63: 111–123 [DOI] [PubMed] [Google Scholar]
- Gossmann T. I., Woolfit M., Eyre-Walker A., 2011. Quantifying the variation in the effective population size within a genome. Genetics 189: 1389–1402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer M. F., Woerner A. E., Mendez F. L., Watkins J. C., Cox M. P., et al. , 2010. The ratio of human X chromosome to autosome diversity is positively correlated with genetic distance from genes. Nat. Genet. 42: 803–831 [DOI] [PubMed] [Google Scholar]
- Hedrick P. W., 2007. Sex: Differences in mutation, recombination, selection, gene flow, and genetic drift. Evolution 61: 2750–2771 [DOI] [PubMed] [Google Scholar]
- Hill W. G., 1972. Effective size of populations with overlapping generations. Theor. Popul. Biol. 3: 278–289 [DOI] [PubMed] [Google Scholar]
- Hill W. G., 1979. A note on effective population size with overlapping generations. Genetics 92: 317–322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. R., Kaplan N. L., 1988. The coalescent process in models with selection and recombination. Genetics 120: 831–840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. R., Turelli M., 2003. Stochasticity overrules the “three-times rule”: genetic drift, and coalescence times for nuclear vs. mitochondrial loci. Evolution 57: 182–190 [DOI] [PubMed] [Google Scholar]
- Johnson D. L., 1977. Inbreeding in populations with overlapping generations. Genetics 87: 581–591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., 1971. Theoretical foundations of population genetics at the molecular level. Theor. Popul. Biol. 2: 174–208 [DOI] [PubMed] [Google Scholar]
- Kimura M., Crow J. F., 1964. The number of alleles that can be maintained in a finite population. Genetics 49: 725–738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., 2007. The Origins of Genome Architecture. Sinauer, Sunderland [Google Scholar]
- Nei M., 1987. Molecular Evolutionary Genetics. Columbia University Press, New York [Google Scholar]
- Neubaum D. M., Wolfner M. F., 1999. Wise, winsome or weird: mechanisms of sperm storage in female animals. Curr. Top. Dev. Biol. 41: 67–97 [DOI] [PubMed] [Google Scholar]
- Nunney L., 1991. The influence of age structure and fecundity on effective population size. Proc. Biol. Sci. 246: 71–76 [DOI] [PubMed] [Google Scholar]
- Nunney L., 1993. The influence of mating systems and overlapping generations on effective population size. Evolution 47: 1329–1341 [DOI] [PubMed] [Google Scholar]
- Pool J. E., Nielsen R., 2007. Population size changes reshape genomic patterns of diversity. Evolution 61: 3001–3006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice W. R., 1989. Analyzing tables of statistical tests. Evolution 43: 223–225 [DOI] [PubMed] [Google Scholar]
- Vicoso B., Charlesworth B., 2009. Effective population size and the faster-X effect: an extended model. Evolution 63: 2413–2426 [DOI] [PubMed] [Google Scholar]
- Wright S., 1931. Evolution in Mendelian populations. Genetics 16: 97–159 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.