Synchronization in complex oscillator networks and smart grids

Abstract

The emergence of synchronization in a network of coupled oscillators is a fascinating topic in various scientific disciplines. A widely adopted model of a coupled oscillator network is characterized by a population of heterogeneous phase oscillators, a graph describing the interaction among them, and diffusive and sinusoidal coupling. It is known that a strongly coupled and sufficiently homogeneous network synchronizes, but the exact threshold from incoherence to synchrony is unknown. Here, we present a unique, concise, and closed-form condition for synchronization of the fully nonlinear, nonequilibrium, and dynamic network. Our synchronization condition can be stated elegantly in terms of the network topology and parameters or equivalently in terms of an intuitive, linear, and static auxiliary system. Our results significantly improve upon the existing conditions advocated thus far, they are provably exact for various interesting network topologies and parameters; they are statistically correct for almost all networks; and they can be applied equally to synchronization phenomena arising in physics and biology as well as in engineered oscillator networks, such as electrical power networks. We illustrate the validity, the accuracy, and the practical applicability of our results in complex network scenarios and in smart grid applications.

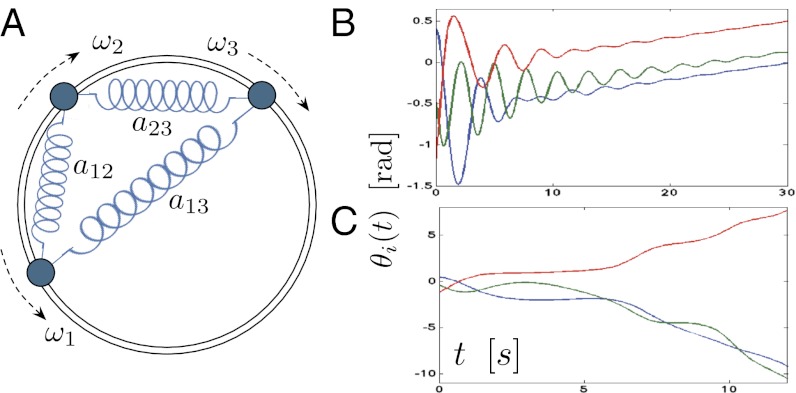
The scientific interest in the synchronization of coupled oscillators can be traced back to Christiaan Huygens’ seminal work on “an odd kind sympathy” between coupled pendulum clocks (1), and it continues to fascinate the scientific community to date (2, 3). A mechanical analog of a coupled oscillator network is shown in Fig. 1A and consists of a group of particles constrained to rotate around a circle and assumed to move without colliding. Each particle is characterized by a phase angle θ_i and has a preferred natural rotation frequency ω_i. Pairs of interacting particles i and j are coupled through an elastic spring with stiffness a_ij. Intuitively, a weakly coupled oscillator network with strongly heterogeneous natural frequencies ω_i does not display any coherent behavior, whereas a strongly coupled network with sufficiently homogeneous natural frequencies is amenable to synchronization. These two qualitatively distinct regimes are illustrated in Fig. 1 B and C.

Fig. 1.

Mechanical analog of a coupled oscillator network (A) and its dynamics in a strongly coupled network (B) and a weakly coupled network (C). With the exception of the coupling weights a_ij, all parameters in simulations B and C are identical.

Formally, the interaction among n such phase oscillators is modeled by a connected graph G(, ℰ, A) with nodes = {1, …, n}, edges ℰ ⊂ × , and positive weights a_ij > 0 for each undirected edge {i, k} ∈ ℰ. For pairs of noninteracting oscillators i and j, the coupling weight a_ij is 0. We assume that the node set is partitioned as 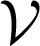= ₁ ∪ 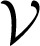₂, and we consider the following general coupled oscillator model:

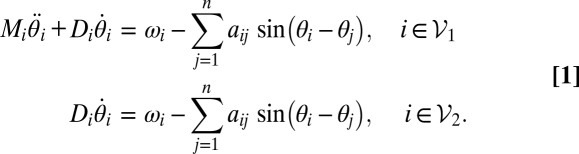The coupled oscillator model [1] consists of the second-order oscillators 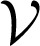₁ with Newtonian dynamics, inertia coefficients M_i, and viscous damping D_i. The remaining oscillators ₂ feature first-order dynamics with time constants D_i. A perfect electrical analog of the coupled oscillator model [1] is given by the classic structure-preserving power network model (4), our enabling application of interest. Here, the first- and second-order dynamics correspond to loads and generators, respectively, and the right-hand sides depict the power injections ω_i and the power flows a_ij sin(θ_i − θ_j) along transmission lines.

The rich dynamic behavior of the coupled oscillator model [1] arises from a competition between each oscillator’s tendency to align with its natural frequency ω_i and the synchronization-enforcing coupling a_ij sin(θ_i − θ_j) with its neighbors. If all natural frequencies ω_i are identical, the coupled oscillator dynamics [1] collapse to a trivial phase-synchronized equilibrium, where all angles θ_i are aligned. The dissimilar natural frequencies ω_i, on the other hand, drive the oscillator network away from this all-aligned equilibrium. Moreover, even if the coupled oscillator model [1] synchronizes, the motion of its center of mass still carries the flux of angular rotation, respectively, the flux of electrical power from generators to loads in a power grid. Despite all these complications, the main result of this article is that, for a broad range of network topologies and parameters, an elegant and easily verified criterion characterizes synchronization of the nonlinear and nonequilibrium dynamic oscillator network [1].

Review of Synchronization in Oscillator Networks

The coupled oscillator model [1] unifies various models in the literature, including dynamic models of electrical power networks. Modeling of electrical power networks is discussed in SI Text in detail. For 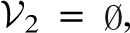the coupled oscillator model [1] appears in synchronization phenomena in animal flocking behavior (5), populations of flashing fireflies (6), and crowd synchrony on London’s Millennium bridge (7), as well as in Huygen’s pendulum clocks (8). For the coupled oscillator model (1) reduces to the celebrated Kuramoto model (9), which appears in coupled Josephson junctions (10), particle coordination (11), spin glass models (12, 13), neuroscience (14), deep brain stimulation (15), chemical oscillations (16), biological locomotion (17), rhythmic applause (18), and countless other synchronization phenomena (19–21). Finally, coupled oscillator models of the form shown in [1] are canonical models of coupled limit cycle oscillators (22) and serve as prototypical examples in complex networks studies (23–25).

The coupled oscillator dynamics [1] feature the synchronizing effect of the coupling described by the graph G(, ℰ, A) and the desynchronizing effect of the dissimilar natural frequencies ω_i. The complex network community asks questions of the form “What are the conditions on the coupling and the dissimilarity such that a synchronizing behavior emerges?” Similar questions also appear in all the aforementioned applications, for instance, in large-scale electrical power systems. Because synchronization is pervasive in the operation of an interconnected power grid, a central question is “Under which conditions on the network parameters and topology, the current load profile, and power generation does there exist a synchronous operating point (26, 27), when is it optimal (28), when is it stable (29, 30), and how robust is it (31–34)?” A local loss of synchrony can trigger cascading failures and possibly result in widespread blackouts. In the face of the complexity of future smart grids and the integration challenges posed by renewable energy sources, a deeper understanding of synchronization is increasingly important.

Despite the vast scientific interest, the search for sharp, concise, and closed-form synchronization conditions for coupled oscillator models of the form shown in [1] has been in vain so far. Loosely speaking, synchronization occurs when the coupling dominates the dissimilarity. Various conditions have been proposed to quantify this tradeoff (21, 23–25, 30, 35–36). The coupling is typically quantified by the nodal degree or the algebraic connectivity of the graph G, and the dissimilarity is quantified by the magnitude or the spread of the natural frequencies ω_i. Sometimes, these conditions can be evaluated only numerically because they depend on the network state (33, 34) or arise from a nontrivial linearization process, such as the Master stability function formalism (23, 24). To date, exact synchronization conditions are known only for simple coupling topologies (17, 21, 37, 38). For arbitrary topologies, only sufficient conditions are known (25, 30, 33–35), as well as numerical investigations for random networks (39–41). Simulation studies indicate that the known sufficient conditions are very conservative estimates on the threshold from incoherence to synchrony. Literally, every review article on synchronization concludes emphasizing the quest for exact synchronization conditions for arbitrary network topologies and parameters (19–21, 23–25). In this article, we present a concise and sharp synchronization condition that features elegant graph-theoretical and physical interpretations.

Synchronization Condition

For the coupled oscillator model [1] and its applications, the following notions of synchronization are appropriate. First, a solution has synchronized frequencies if all frequencies 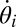are identical to a common constant value ω_sync. If a synchronized solution exists, it is known that the synchronization frequency is 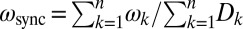and that by working in a rotating reference frame, one may assume ω_sync = 0. Second, a solution has cohesive phases if every pair of connected oscillators has a phase distance smaller than some angle γ ∈ [0, π/2[, that is, |θ_i − θ_j| ≤ γ for every edge {i, j} ∈ ℰ.

Based on a previously unexplored analysis approach to the synchronization problem, we propose the following synchronization condition for the coupled oscillator model [1].

Synchronization Condition.

The coupled oscillator model [1] has a unique and stable solution θ* with synchronized frequencies and cohesive phases 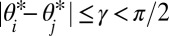for every connected pair of connected oscillators {i, j} ∈ ℰ if

Here, L^† is the pseudoinverse of the network Laplacian matrix L and 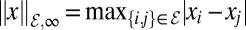is the worst-case dissimilarity for x = (x₁, …, x_n) over the edges ℰ.

We establish the broad applicability of the proposed condition [2] to various classes of networks via analytical and statistical methods in the next section. Before that, we provide some equivalent formulations for the proposed condition [2] to develop deeper intuition and obtain insightful conclusions.

Complex Network Interpretation.

Surprisingly, topological or spectral connectivity measures, such as nodal degree or algebraic connectivity, are not key to synchronization. In fact, these often advocated connectivity measures (23–25, 30, 33–35) turn out to be conservative estimates of the synchronization condition [2]. This statement can be seen by introducing the matrix U of orthonormal eigenvectors of the network Laplacian matrix L with corresponding eigenvalues 0 = λ₁ < λ₂ ≤ … ≤ λ_n. From this spectral viewpoint, condition [2] can be equivalently written as

In words, the natural frequencies ω are projected on the network modes U, weighted by the inverse Laplacian eigenvalues, and evaluates the worst-case dissimilarity of this weighted projection. A sufficient condition for the inequality [3] to be true is the algebraic connectivity condition . Likewise, a necessary condition for inequality [3] is 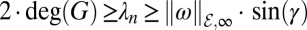, where deg(G) is the maximum nodal degree in the graph G(, ℰ, A). Clearly, compared with [3], this sufficient condition and this necessary condition feature only one of n − 1 nonzero Laplacian eigenvalues and are overly conservative.

Kuramoto Oscillator Perspective.

Notice that in the limit γ → π/2, condition [2] suggests that there exists a stable synchronized solution if

For classic Kuramoto oscillators coupled in a complete graph with uniform weights a_ij = K/n, the synchronization condition [4] reduces to the condition 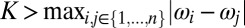, known for the classic Kuramoto model (21).

Power Network Perspective.

In power systems engineering, the equilibrium equations of the coupled oscillator model [1], given by 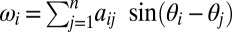, are referred to as the AC power flow equations, and they are often approximated by their linearization (31–34), known as the DC power flow equations. In vector notation, the DC power flow equations read as ω = Lθ and their solution satisfies . According to condition [2], the worst phase distance 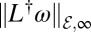obtained by the DC power flow equations needs to be less than or equal to sin(γ) such that the solution to the AC power flow equations satisfies . Hence, our condition extends the common DC power flow approximation from infinitesimally small angles γ ≪ 1 to large angles γ ∈ [0, π/2[.

Auxiliary Linear Perspective.

As detailed in the previous section, the key term L^†ω in condition [2] equals the phase differences obtained by the linear Laplacian equation ω = Lθ. This linear interpretation is not only insightful but practical, because condition [2] can be quickly evaluated by numerically solving the linear system ω = Lθ. This linear system is possibly of high dimension, but it inherits the sparsity of the graph G(, ℰ, A). Thus, condition [2] can be verified efficiently even for large-scale sparse networks. Despite this linear interpretation, we emphasize that our derivation of condition [2] is not based on any linearization arguments.

Energy Landscape Perspective.

Condition [2] can also be understood in terms of an appealing energy landscape interpretation. The coupled oscillator model [1] is a system of particles that aim to minimize the energy function

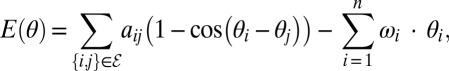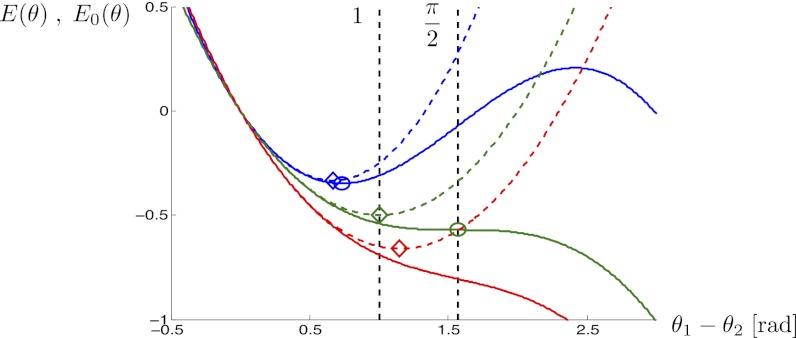
where the first term is a pairwise nonlinear attraction among the particles and the second term represents the external force driving the particles away from the “all-aligned” state. Because the energy function E(θ) is difficult to study, it is natural to look for a minimum of its second-order approximation 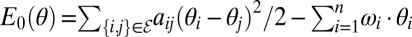, where the first term corresponds to a Hookean potential. Condition [2] is then restated as follows: E(θ) features a phase-cohesive minimum with interacting particles no further than γ apart if E₀(θ) features a minimum with interacting particles no further from each other than sin(γ), as illustrated in Fig. 2.

Fig. 2.

Energy function E(θ) and its quadratic approximation E₀(θ) for a two-particle system are shown as solid and dashed curves, respectively, for the stable (blue), marginal (green), and unstable (red) cases. The circles and diamonds represent stable critical points of E(θ) and E₀(θ).

Analytical and Statistical Results

Our analysis approach to the synchronization problem is based on algebraic graph theory. We propose an equivalent reformulation of the synchronization problem that reveals the crucial role of cycles and cut-sets in the graph, and ultimately leads to the synchronization condition [2]. In particular, we analytically establish the synchronization condition [2] for the following interesting cases.

Analytical Result.

The synchronization condition [2] is necessary and sufficient for (i) the sparsest (acyclic) and (ii) the densest (complete and uniformly weighted) network topologies G(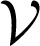, ℰ, A), (iii) the best (phase synchronizing) and (iv) the worst (cut-set inducing) natural frequencies, (v) cyclic topologies of length strictly less than five, (vi) arbitrary cycles with symmetrical parameters, and (vii) combinations of networks each satisfying one of the conditions (i)–(vi), which are connected to another and share no common cycles.

A detailed and rigorous mathematical derivation and statement of the above analytical result can be found in SI Text.

In many applications, the natural frequencies ω_i and coupling weights a_ij are known only with a certain degree of accuracy, or they may be variable within certain ranges. For instance, in power networks, these variations arise from uncertain demand or unmodeled voltage dynamics. To address these uncertainties, condition [2] can be extended to a robust synchronization condition for variable parameters 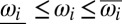and . In this case, it is necessary and sufficient to verify condition [2] at the vertices of the parameter space and 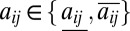to guarantee condition [2] for all possible parameter variations. The detailed results are reported in SI Text.

After having analytically established condition [2] for a variety of particular network topologies and parameters, we establish its correctness and predictive power for a broad range of networks. Extensive simulation studies lead to the conclusion that the proposed synchronization condition [2] is statistically correct. To verify this hypothesis, we conducted Monte Carlo simulation studies over a wide range of natural frequencies ω_i, network sizes n, coupling weights a_ij, and different random graph models of varying degrees of sparsity and randomness. We select a set of nominal network models with topologies constructed from Erdös–Rényi graphs, random geometric graphs, and Watts–Strogatz small world networks, and the natural frequencies and coupling weights are sampled from uniform distributions. In total, we constructed 1.2⋅10⁶ samples of such nominal networks, each with a connected graph G(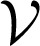, ℰ, A) and natural frequencies ω satisfying for some γ < π/2. The detailed construction and precise results can be found in SI Text and allow us to establish the following probabilistic result with a confidence level of at least 99% and accuracy of at least 99%.

Statistical Result for Nominal Networks.

With a 99.97% probability for a nominal network, condition [2] guarantees the existence of a unique and stable solution θ* with synchronized frequencies and cohesive phases for every connected pair {i, j} ∈ ℰ.

From this statistical result, we deduce that the proposed synchronization condition [2] holds true for almost all topologies and parameters of the considered nominal network models. Indeed, we also show the existence of possibly thin sets of network topologies and parameters for which our condition [2] is not sufficiently tight. We refer to SI Text for an explicit family of carefully engineered and “degenerate” counterexamples. Overall, our analytical and statistical results validate the correctness of the proposed condition [2].

After having established the statistical correctness of condition [2], we now investigate its predictive power for arbitrary networks. Because we analytically establish that condition [2] is exact for sufficiently small pairwise phase cohesiveness |θ_i − θ_j| ≪ 1, we now investigate the other extreme, . To test the corresponding condition [4] in a low-dimensional parameter space, we consider a complex network of Kuramoto oscillators

where all coupling weights a_ij are either 0 or 1 and the coupling gain K > 0 serves as a control parameter. If L is the corresponding unweighted Laplacian matrix, condition [4] reads as 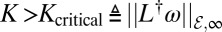. Of course, the condition K > K_critical is only sufficient, and the critical coupling may be smaller than K_critical. To test the accuracy of the condition K > K_critical, we numerically found the smallest value of K leading to synchrony with phase cohesiveness π/2.

Fig. 3 reports our findings for various network sizes, connected random graph models, and sample distributions of the natural frequencies. We refer to SI Text for the detailed simulation setup. First, note from Fig. 3 A, B, D, and E that condition [4] is extremely accurate for a sparse graph, that is, for small p and n, as expected from our analytical results. Second, for a dense graph with p ≈ 1, Fig. 3 A, B, D, and E confirms the results known for classic Kuramoto oscillators (21): For a bipolar distribution, condition [4] is exact, and for a uniform distribution, a small critical coupling is obtained. Third, Fig. 3 C and F shows that condition [4] is scale-free for a Watts–Strogatz small world network, that is, it has almost constant accuracy for various values of n and p. Fourth and finally, observe that condition [4] is always within a constant factor of the exact critical coupling, whereas other proposed conditions (23–25, 30, 33–35) on the nodal degree or on the algebraic connectivity scale poorly with respect to network size n.

Fig. 3.

Numerical evaluation of the exact critical coupling K in a complex Kuramoto oscillator network. The subfigures show K normalized by for an Erdös–Rényi graph with probability p of connecting two nodes, for a random geometric graph with connectivity radius p, and for a Watts–Strogatz small world network with rewiring probability p. Each data point is the mean over 100 samples of the respective random graph model for values of ω_i sampled from a bipolar or a uniform distribution supported on [−1, 1] and for the network sizes n ∈ {10, 20, 40, 80, 160}.

Applications in Power Networks

We envision that condition [2] can be applied to assess synchronization and robustness quickly in power networks under volatile operating conditions. Because real-world power networks are carefully engineered systems with particular network topologies and parameters, we do not extrapolate the statistical results from the previous section to power grids. Rather, we consider 10 widely established Institute of Electrical and Electronics Engineers (IEEE) power network test cases provided by Zimmerman et al. (42) and Grigg et al. (43).

Under nominal operating conditions, the power generation is optimized to meet the forecast demand while obeying the AC power flow laws and respecting the thermal limits of each transmission line. Thermal limit constraints are precisely equivalent to phase cohesiveness requirements. To test the synchronization condition [2] in a volatile smart grid scenario, we make the following changes to the nominal network: (i) We assume fluctuating demand and randomize 50% of all loads to deviate from the forecasted loads; (ii) we assume that the grid is penetrated by renewables with severely fluctuating power outputs, for example, wind or solar farms, and we randomize 33% of all generating units to deviate from the nominally scheduled generation; and (iii) following the paradigm of smart operation of smart grids (44), the fluctuations can be mitigated by fast-ramping generation, such as fast-response energy storage, including batteries and flywheels, and controllable loads, such as large-scale server farms or fleets of plug-in hybrid electrical vehicles. Here, we assume that the grid is equipped with 10% fast-ramping generation and 10% controllable loads, and that the power imbalance (caused by fluctuating demand and generation) is uniformly dispatched among these adjustable power sources. For each of the 10 IEEE test cases, we construct 1,000 random realizations of scenarios (i)–(iii) described above, we numerically check for the existence of a synchronous solution, and we compare the numerical solution with the results predicted by our condition [2]. Our findings are reported in Table 1, and a detailed description of the simulation setup can be found in SI Text.

Table 1.

Evaluation of condition [2] for 10 IEEE test cases under volatile operating conditions

Randomized test case (1,000 instances)	Correctness*	Accuracy†, rad	Cohesive‡, rad
Chow 9 bus system	Always true	4.1218⋅10−5	0.12889
IEEE 14 bus system	Always true	2.7995⋅10−4	0.16622
IEEE RTS 24	Always true	1.7089⋅10−3	0.22309
IEEE 30 bus system	Always true	2.6140⋅10−4	0.16430
New England 39	Always true	6.6355⋅10−5	0.16821
IEEE 57 bus system	Always true	2.0630⋅10−2	0.20295
IEEE RTS 96	Always true	2.6076⋅10−3	0.24593
IEEE 118 bus system	Always true	5.9959⋅10−4	0.23524
IEEE 300 bus system	Always true	5.2618⋅10−4	0.43204
Polish 2383 bus system (winter 1999)	Always true	4.2183⋅10−3	0.25144

Accuracy and phase cohesiveness results are averaged over 1,000 instances of randomized load and generation.

*Correctness: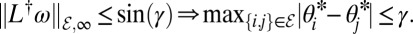

^†Accuracy: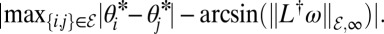

^‡Phase cohesiveness:

It can be observed that condition [2] predicts the correct phase cohesiveness |θ_i − θ_j| along all transmission lines {i, j} ∈ ℰ with extremely high accuracy, even for large-scale networks featuring 2,383 nodes. These conclusions can also be extended to power network models with variable parameters, which account for uncertainty in demand or unmodeled voltage dynamics. Further details are provided in SI Text.

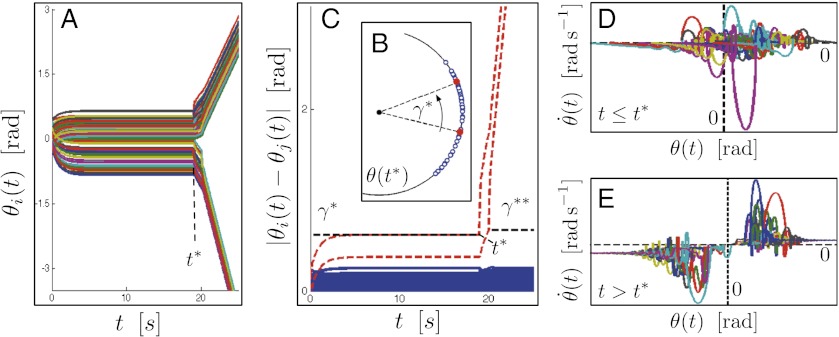
As a final test, we validate the synchronization condition [2] in a stressed power grid case study. We consider the IEEE Reliability Test System 96 (RTS 96) (43) illustrated in Fig. 4. We assume that the following two contingencies have taken place, and we characterize the remaining safety margin. First, we assume generator 323 is disconnected, possibly due to maintenance or failure events. Second, we consider the following imbalanced power dispatch situation: The power demand at each load in the southeastern area deviates from the nominally forecasted demand by a uniform and positive amount, and the resulting power deficiency is compensated for by uniformly increasing the generation in the northwestern area. This imbalance can arise, for example, due to a shortfall in predicted load and renewable energy generation. Correspondingly, power is exported from the northwestern to the southeastern area via the transmission lines {121, 325} and {223, 318}. At a nominal operating condition, the RTS 96 power network is sufficiently robust to tolerate each single one of these two contingencies, but the safety margin is now minimal. When both contingencies are combined, our synchronization condition [2] predicts that the thermal limit of the transmission line {121, 325} is reached at an additional loading of 22.20%. Indeed, the dynamic simulation scenario shown in Fig. 5 validates the accuracy of this prediction. It can be observed that synchronization is lost for an additional loading of 22.33% and that the areas separate via the transmission line {121, 325}. This separation triggers a cascade of events, such as an outage of the transmission line {223, 318}, and the power network is en route to a blackout. We remark that, if generator 323 is not disconnected and there are no thermal limit constraints, by increasing the loading, we observe the classic loss of synchrony through a saddle-node bifurcation. This bifurcation can also be predicted accurately by our results (a detailed description is provided in SI Text).

Fig. 4.

Illustration of contingencies in the RTS 96 power network. Here, square nodes are generators and round nodes are loads, large amounts of power are exported from the northwestern area to the southeastern area, and generator 323 is tripped.

Fig. 5.

RTS 96 dynamics for a continuous load increase from 22.19% to 22.24%. (A) Angles θ(t) that lose synchrony at t* = 18.94 s, when the thermal limit γ* = 0.1977 rad of the transmission line {121, 325} is reached. (B) Angles θ(t) at t = t*. (C) Angular distances and the thermal limits γ* and γ**, where the lines {121, 325} and {223, 318} are plotted as dashed curves. (D and E) Generator phase space before and after t*, where the loss of a common synchronization frequency can be observed.

In summary, the results in this section confirm the validity, the applicability, and the accuracy of the synchronization condition [2] in complex power network scenarios.

Discussion and Conclusions

In this article, we studied the synchronization phenomenon for broad class of coupled oscillator models proposed in the scientific literature. We proposed a surprisingly simple condition that accurately predicts synchronization as a function of the parameters and the topology of the underlying network. Our result, with its physical and graph theoretical interpretations, significantly improves upon the existing tests in the literature on synchronization. The correctness of our synchronization condition is established analytically for various interesting network topologies and via Monte Carlo simulations for a broad range of generic networks. We validated our theoretical results for complex Kuramoto oscillator networks as well as for smart grid applications.

Our results pose as many questions as they answer. Among the important theoretical problems to be addressed is a characterization of the set of all network topologies and parameters for which our proposed synchronization condition 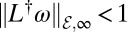is not sufficiently tight. We conjecture that this set is “thin” in an appropriate parameter space. Our results suggest that an exact condition for synchronization of any arbitrary network is of the form , and we conjecture that the constant c is always strictly positive, upper-bounded, and close to 1. However, another important question not addressed in the present article concerns the region of attraction of a synchronized solution. We conjecture that the latter depends on the gap in the presented condition.

On the application side, the results contained in this paper need to be extended to more detailed power network models, including voltage dynamics, reactive power flows, and higher order generator dynamics. We envision that our synchronization conditions enable emerging smart grid applications, such as power flow optimization subject to stability constraints, distance to failure metric, and the design of control strategies to avoid cascading failures.