Restraints on backbone conformations in solid state NMR studies of uniformly labeled proteins from quantitative amide ¹⁵N–¹⁵N and carbonyl ¹³C–¹³C dipolar recoupling data

Abstract

Recent structural studies of uniformly ¹⁵N, ¹³C-labeled proteins by solid state nuclear magnetic resonance (NMR) rely principally on two sources of structural restraints: (i) restraints on backbone conformation from isotropic ¹⁵N and ¹³C chemical shifts, based on empirical correlations between chemical shifts and backbone torsion angles; (ii) restraints on inter-residue proximities from qualitative measurements of internuclear dipole–dipole couplings, detected as the presence or absence of inter-residue crosspeaks in multidimensional spectra. We show that site-specific dipole–dipole couplings among ¹⁵N-labeled backbone amide sites and among ¹³C-labeled backbone carbonyl sites can be measured quantitatively in uniformly-labeled proteins, using dipolar recoupling techniques that we call ¹⁵N-BARE and ¹³C-BARE (BAckbone REcoupling), and that the resulting data represent a new source of restraints on backbone conformation. ¹⁵N-BARE and ¹³C-BARE data can be incorporated into structural modeling calculations as potential energy surfaces, which are derived from comparisons between experimental ¹⁵N and ¹³C signal decay curves, extracted from crosspeak intensities in series of two-dimensional spectra, with numerical simulations of the ¹⁵N-BARE and ¹³C-BARE measurements. We demonstrate this approach through experiments on microcrystalline, uniformly ¹⁵N, ¹³C-labeled protein GB1. Results for GB1 show that ¹⁵N-BARE and ¹³C-BARE restraints are complementary to restraints from chemical shifts and inter-residue crosspeaks, improving both the precision and the accuracy of calculated structures.

1. Introduction

Much progress has been made recently in the development and application of solid state nuclear magnetic resonance (NMR) methods for the determination of complete protein structures, based on multidimensional spectroscopy of uniformly or extensively ¹⁵N, ¹³C-labeled samples. In the case of unoriented samples, which are nearly always studied under magic-angle spinning (MAS), structures are determined primarily from two types of restraints. First, isotropic ¹⁵N and ¹³C chemical shifts serve as restraints on backbone conformations, based on well-established empirical correlations between chemical shifts and backbone conformation [1-3]. Second, inter-residue crosspeaks in various types of multidimensional spectra serve as restraints on inter-residue proximities [4-10]. Solid state NMR methods that can provide precise, quantitative information about specific internuclear distances [11-16] or torsion angles [17-20] have not been extensively utilized. Recent exceptions include studies in which paramagnetic relaxation effects [21-23], tensor correlation techniques [24], or quantitative heteronuclear dipolar recoupling techniques [25,26] have been employed. Because existing methods do not provide sufficient restraints to answer important structural questions in all cases, development of new methods that provide complementary structural restraints remains an active area of research.

In this paper, we demonstrate a set of techniques that provide quantitative restraints on protein backbone conformations in solid state NMR studies of uniformly ¹⁵N, ¹³C-labeled samples, through measurements of magnetic dipole–dipole couplings among ¹⁵N-labeled backbone amide nitrogens and among ¹³C-labeled backbone carbonyl carbons. As is well known, dipole–dipole couplings are proportional to the inverse cubes of internuclear distances. As shown in Fig. 1, in a uniformly labeled protein, the strongest ¹⁵N–¹⁵N couplings involving the amide nitrogen of residue k are couplings to the amide nitrogens of residues k − 1 and k + 1, at distances $R_{k,k-1}^{\mathit{NN}}$ and $R_{k,k+1}^{\mathit{NN}}$. Assuming that chemical bond lengths and angles are fixed, these distances depend on the backbone torsion angles ψ_k−1 and ψ_k. Additionally assuming planar peptide bonds, the angle between the two internuclear vectors (which also affects the data as discussed below) depends on the backbone torsion angle ϕ_k. Similarly, the strongest ¹³CO–¹³CO couplings involving the carbonyl carbon of residue k depend on distances $R_{k-1}^{\mathit{CC}}$ and $R_{k+1}^{\mathit{CC}}$ to carbonyl carbons of residues k − 1 and k + 1, which depend on ϕ_k and ϕ_k+1. The angle between the two internuclear vectors depends on ψ_k. Therefore, if one could record signal decay curves under ¹⁵N–¹⁵N couplings for all backbone amide nitrogen sites and signal decay curves under ¹³CO–¹³CO couplings for all backbone carbonyl sites, using appropriate homonuclear dipolar recoupling techniques [16,27-29], the resulting large data set would be expected to place strong restraints on the torsion angles that define the protein backbone conformation.

Fig. 1.

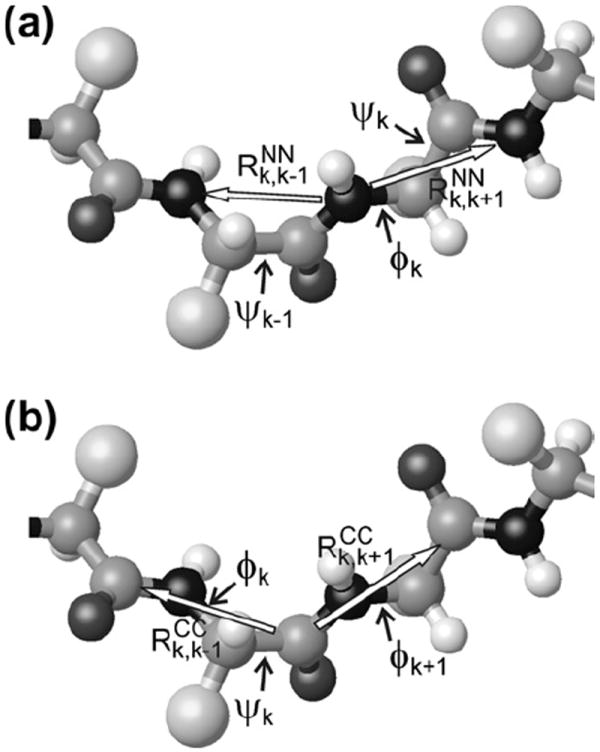
(a) Segment of a polypeptide backbone, showing the two amide nitrogen–nitrogen distances and three backbone torsion angles that affect ¹⁵N-BARE data for residue k. Darkest and lightest spheres represent nitrogen and hydrogen atoms, respectively. Largest spheres represent amino acid sidechains. (b) Segment of a polypeptide backbone, showing the two carbonyl carbon–carbon distances and three backbone torsion angles that affect ¹³C-BARE data for residue k.

As described below, we have developed and implemented radio-frequency (rf) pulse sequence techniques that allow data sets of the type described above to be obtained. For ¹⁵N–¹⁵N measurements, we use a homonuclear dipolar recoupling technique called PITHIRDS-CT (constant-time recoupling with π pulses lasting one-third of the MAS rotation period) to create nonzero ¹⁵N–¹⁵N couplings under MAS in a non-selective manner. As previously shown, the PITHIRDS-CT technique produces signal decay curves that can be compared quantitatively with numerical simulations to determine internuclear distances, without adjustable parameters [27,30]. Non-selective recoupling of ¹⁵N–¹⁵N interactions is sufficient because only the backbone amide nitrogens of residues k − 1 and k + 1 are sufficiently close to the backbone amide nitrogen of residue k to influence its dipolar decay curve. For ¹³CO–¹³CO measurements, frequency-selective dipolar recoupling is required because the carbonyl carbon of residue k is closer to the α- and β-carbons of residues k and k + 1 than to the carbonyl carbons of residues k − 1 and k + 1. We therefore use a frequency-selective variant of the PITHIRDS-CT technique called ZQ-SEASHORE (Zero-Quantum Shift-Evolution-Assisted HOmonuclear REcoupling), which allows the homonuclear couplings among neighboring carbonyl carbons to be measured without being obscured by couplings to other carbon sites, whose isotropic chemical shifts are quite different [16]. In order to measure signal decays from many sites simultaneously, we incorporate the PITHIRDS-CT and ZQ-SEASHORE techniques into two-dimensional (2D) spectroscopic techniques that allow signals from many individual residues to be detected as resolved crosspeaks. Signal decay curves are measured as the volumes of crosspeaks in a series of 2D spectra, recorded with incremented values of the effective evolution period under ¹⁵N–¹⁵N or ¹³CO–¹³CO couplings. In what follows, we refer to these techniques by the acronyms ¹⁵N-BARE (BAckbone REcoupling) and ¹³C-BARE.

Experiments described below were performed on the B1 domain of streptococcal protein G (GB1), a 56-residue model protein with both α-helical and β-sheet secondary structure [31] that has been used in previous demonstrations of solid state NMR methods [21,23-26,32-34]. In microcrystalline form, 2D spectra of uniformly-labeled GB1 are well resolved, allowing complete site-specific assignment of the ¹⁵N and ¹³C chemical shifts [33]. We obtain 52 ¹⁵N-BARE curves and 48 ¹³C-BARE curves for GB1, limited by overlap of certain crosspeaks. We then calculate χ² deviations between experimental curves and numerical simulations, performed over grids of values of ψ_k−1, ϕ_k, and ψ_k (for ¹⁵N-BARE) or ϕ_k, ψ_k, and ϕ_k+1 (for ¹³C-BARE), yielding a total of 96 tables of ${\chi }_{N,k}^2({\psi }_{k-1},{\varphi }_k,{\psi }_k)$ and ${\chi }_{C,k}^2({\varphi }_k,{\psi }_k,{\varphi }_{k+1})$ (not including data for N- and C-terminal residues). The χ² tables are then treated as three-dimensional (3D) torsion angle potential energy surfaces in the structure determination program Xplor-NIH [35]. Examination of structures generated by Xplor-NIH with and without the ¹⁵N-BARE and ¹³C-BARE restraints, and in combination with more traditional restraints from isotropic chemical shifts and inter-residue crosspeaks, allows us to assess the accuracy and information content of the ¹⁵N-BARE and ¹³C-BARE data. Results presented below indicate that ¹⁵N-BARE and ¹³C-BARE restraints are complementary to restraints from isotropic chemical shifts and inter-residue crosspeaks, resulting in improved precision and accuracy of the final structures when the new restraints are included.

We emphasize that ¹⁵N-BARE and ¹³C-BARE restraints are not intended to replace torsion angle restraints derived from isotropic chemical shifts. ¹⁵N-BARE and ¹³C-BARE restraints will be most valuable when the chemical shifts do not lead to unambiguous or sufficiently precise torsion angle predictions. We also emphasize that ¹⁵N-BARE and ¹³C-BARE restraints are not intended to replace structural restraints from medium- and long-range distance measurements, and that ¹⁵N-BARE and ¹³C-BARE restraints provide no information about sidechain conformations or non-sequential inter-residue contacts.

2. Experimental and numerical methods

2.1. Preparation of microcrystalline GB1

Transformed E. coli BL21 cells containing the GB1 pET-11a plasmid were obtained from Dr. John Louis at the National Institutes of Health. The GB1 gene contained the T2Q mutation to prevent particle cleavage of the N-terminal methionine residue during expression. Cells were grown on Luria–Bertani (LB) plates with 100 μM ampicillin overnight. A single colony was picked and cultured in 50 mL of LB/ampicillin at 37 °C for 14 h in an incubator shaker (New Brunswick Scientific model I2500, 230 rpm). Ten ml was used to inoculate 1 l of M9 medium (containing 11.3 g Na₂HPO₄·7H₂O, 3.0 g KH₂PO₄, 0.5 g NaCl, 1.0 g ¹⁵NH₄Cl, 4.0 g ¹³C-d-glucose, 2 mM MgSO₄, 0.1 mM CaCl₂, and 10 mg vitamin B1). The culture was incubated at 37 °C for 5 h. GB1 expression was then induced by adding isopropyl thiogalactoside (IPTG) to 1 mM. Expression was allowed to continue for 4 h at 37 °C. Cells were harvested by centrifugation at 11,300g for 20 min at 4 °C.

The cell pellet was resuspended in 50 ml of phosphate buffered saline (PBS, containing 50 mM sodium phosphate and 200 mM sodium chloride, pH 7.4). The mixture was heated to 80 °C for 10 min in a water bath, then centrifuged at 25,000g for 20 min at 4 °C. The pellet was discarded and the supernatant was subjected to fast protein liquid chromatography with a gel filtration column (GE Superdex Peptide 75/300 GL). Protein was eluted with PBS containing 50 mM sodium phosphate and 100 mM sodium phosphate at pH 6.9. The protein peak was collected and subjected to high performance liquid chromatography with a preparative C18 reverse-phase column (Grace Vydac 218TP1022). Final yield of purified GB1 was ~50 mg/l. Purity was verified using matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. The measured molecular mass was 6560.2 Da while the expected mass for the [M + H]⁺ peak was 6560.0 Da. The protein was lyophilized and stored at −80 °C.

For crystallization, the protein powder was dissolved in deionized water to a concentration of ~10 mg/ml. The solution was dialyzed against a 1000-fold volume of 50 mM phosphate buffer (pH 5.5) using a 2000 Da molecular weight cutoff cassette (Thermo Scientific Slide-A-Lyzer, 3–12 ml volume). To ensure the complete removal of salt, the dialysis buffer was refreshed twice after 2 h periods at room temperature. The third and final dialysis proceeded overnight at 4 °C. After dialysis, the protein solution was mixed with a threefold volume of precipitant, containing 2-methyl-2,4-pentanediol (MPD) and isopropyl alcohol (IPA) in 2:1 volume ratio. The precipitant was added in three equal aliquots, with vortex mixing after each aliquot. The mixture was then incubated at room temperature 48 h to allow the formation of microcrystals. The final microcrystalline GB1 typically contained over 85% of the initial protein as determined by ultraviolet absorption of the supernatant. Microcrystalline GB1 was pelleted at 2000g for 10 min, and the bulk supernatant was removed. The pellet was transferred into a 1.8 mm diameter MAS rotor (11 μl volume) by centrifugation. Final sample mass was 8 mg.

Solid state NMR measurements were performed at 14.1 T (150.7 MHz ¹³C NMR frequency, 60.7 MHz ¹⁵N NMR frequency) and 17.6 T (187.9 MHz ¹³C NMR frequency, 75.7 MHz ¹⁵N NMR frequency) using Varian InfinityPlus and Infinity spectrometers and three-channel MAS NMR probes with 1.8 mm diameter rotors produced by the group of Dr. Ago Samoson (Tallinn University of Technology). Sample temperature was maintained near 20 °C during NMR measurements by cooled nitrogen gas from an FTS Systems AirJet unit.

2.2. Assignment of ¹⁵N and ¹³C chemical shifts

GB1 can crystallize into several lattice types with different chemical shifts, depending on subtle variations in crystallization conditions [32]. Therefore, we determined the site-specific ¹⁵N and ¹³C chemical shifts for our sample from the 2D NCACX, NCOCX, and ¹³C–¹³C correlation spectra shown in Fig. S1. These spectra were recorded at 17.6 T, with MAS at 17.00 kHz. 2D NCACX and NCOCX spectra used 1.5 ms ¹H–¹⁵N cross-polarization periods, followed by t₁ evolution periods with two-pulse phase-modulated (TPPM) ¹H decoupling [36] (104 kHz rf field) and a 19.1 ms maximum t₁ value, 4.0 ms frequency-selective ¹⁵N–¹³C cross-polarization periods (40 kHz and 23 kHz rf fields on ¹⁵N and ¹³C, respectively), a 20 ms (NCACX) or 40 ms (NCOCX) rf-assisted diffusion (RAD) period for ¹³C–¹³C polarization exchange [5,9], and 20.5 ms t₂ periods with TPPM decoupling. The 2D ¹³C–¹³C spectrum used a maximum t₁ value of 14.7 ms, a 50 ms RAD exchange period, and a 20.5 ms t₂ period. 2D data were processed with NMR-Pipe [37] and analyzed with Sparky (available at http://www.cgl.ucsf.edu/home/sparky/). Contour levels in all 2D spectra increase by successive factors of 1.6. Signal lists with partial residue-type assignments were prepared from the 2D NCACX and NCOCX spectra, using the 2D ¹³C–¹³C spectrum to assist the residue-type assignments. The signal lists were used as input for the MCASSIGN2 program as previously described [38,39]. Fifty independent MCASSIGN2 runs yielded a single set of chemical shift assignments, shown in Table S1.

2.3. Ancillary structural restraints

Assigned chemical shifts for backbone ¹⁵N, ¹³CO, ¹³C_α, and ¹³C_β sites were used as input to TALOS+ [1], producing the ϕ, ψ predictions shown in Table S1, which were used as angular restraints. Restraints on inter-residue proximities were obtained from 2D CHHC [6-8], NHHC [7,8], and RAD [5,9] spectra shown in Fig. S2. These spectra were recorded at 17.6 T, with MAS at 17.00 kHz. Between the t₁ and t₂ periods, the 2D CHHC spectrum used 150 μs periods for ¹³C–¹H and ¹H–¹³C cross-polarization, separated by a 200 μs ¹H–¹H spin diffusion period. The 2D NHHC spectrum used a 200 μs ¹⁵N–¹H cross-polarization period, a 250 μs ¹H–¹H spin diffusion period, and a 200 μs ¹H–¹³C cross-polarization period. The 2D RAD spectrum used a 350 ms exchange period. A set of 42 inter-residue crosspeaks were identified in these spectra and used as the intra-molecular distance restraints shown in Table S2. Assignment of some of these crosspeaks was assisted by the known structure of GB1. It is worth noting that the GB1 structure contains a four-stranded β-sheet in which the two central strands (β1 and β4, comprised of residues 1–8 and 51–55, respectively) have a parallel alignment, while the outer strands (β2 and β3, comprised of residues 13–20 and 42–46, respectively) are antiparallel to the central strands. As expected, interstrand ¹³C_α–¹³C_α crosspeaks connecting strands β1 and β2 were observed in the 2D CHHC spectrum, due to the unusually short (~2.2 Å) interstrand ¹H_α–¹H_α distances that occur exclusively in antiparallel β-sheets [4,6]. Interstrand ¹³C_α–¹³C_α crosspeaks connecting strands β3 and β4 were not observable because of unfortunate degeneracy of the ¹³C_α chemical shifts of the relevant pairs of residues, but interstrand ¹³C_β–¹³C_β crosspeaks were observed. Due to the relatively short (~2.7 Å) interstrand ¹H_N–¹H_α distances in a parallel β-sheet, interstrand ¹⁵N–¹³C_α crosspeaks connecting strands β1 and β4 were observed in the 2D NHHC spectrum. Crosspeaks connecting the α-helical segment (residues 23–36) to the β-sheet were observed in the 2D CHHC and RAD spectra.

¹³C_α–¹³C_α crosspeaks connecting residues 14 and 44 and residues 12 and 46 were also observed in the 2D CHHC spectrum. These crosspeaks are inconsistent with the known structure of the GB1 monomer but are consistent with intermolecular backbone hydrogen bonding between β2 and β3 in PDB file 2GI9, an orthorhombic GB1 crystal structure determined by Franks et al. for the T2Q mutant [40]. Crosspeaks connecting C_α of G38 to C_β and C_γ of M1 and to C_β of Q2 were also observed in the 2D CHHC spectrum, consistent with intermolecular M1-G38 and Q2-G38 proximity in PDB 2GI9. In contrast, the trigonal crystal structure in PDB file 2QMT [32] has similar intermolecular hydrogen bonding, but does not have close intermolecular M1-G38 and Q2-G38 contacts. We therefore believe that our sample corresponds to the 2GI9 structure. (If the monomer structure was not already known, intermolecular crosspeaks could be identified by additional measurements on an isotopically diluted sample.)

2.4. Pulse sequences for ¹⁵N-BARE and ¹³C-BARE

Fig. 2a shows the rf pulse sequence used in ¹⁵N-BARE measurements. Longitudinal ¹⁵N spin polarization is created by ¹H–¹⁵N cross-polarization, followed by a π/2 “flip-back” pulse on the ¹⁵N channel. A second ¹⁵N π/2 pulse initiates the ¹⁵N PITHIRDS-CT evolution period, during which the finite-pulse radio-frequency-driven recoupling (fpRFDR) [41,42] blocks in Fig. 2b are applied. Blocks A, B, and C differ in the location of the π pulses within the MAS rotation period τ_R, with the pulses beginning at 0, τ_R/3, or 2τ_R/3, respectively. Isotropic and anisotropic chemical shifts are averaged to zero by fpRFDR [41]; symmetry considerations guarantee that the average homonuclear dipole–dipole coupling is also zero when A, B, and C blocks of equal length are concatenated [27]. Therefore, the effective ¹⁵N–¹⁵N evolution period in Fig. 2a is nMτ_R, the length of the final B period, where n is the number of rotor periods in a single A, B, or C block. In the ¹⁵N-BARE measurements described below, which were performed at 14.1 T, n = 16, τ_R = 73.53 (13.60 kHz MAS), and ¹⁵N π pulses were 24.51 μs. Constant-time dipolar decay curves were recorded with N = 8, 6, 4, 2, 0 and M = 0, 6, 12, 18, 24, corresponding to a total fpRFDR period of 28.235 ms.

Fig. 2.

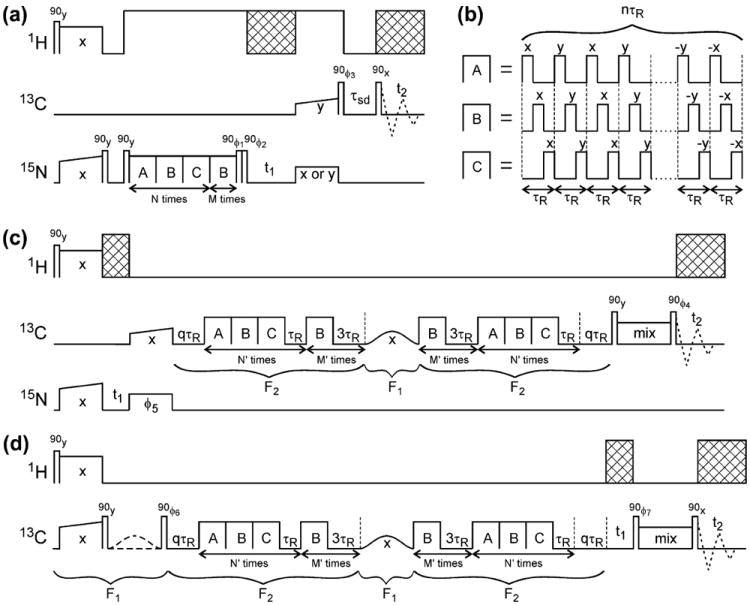
(a) Rf pulse sequence for ¹⁵N-BARE measurements in which the signal decay curves are extracted from crosspeaks in a series of 2D ¹⁵N–¹³C correlation spectra. Cross-hatched areas represent phase-modulated ¹H decoupling. Rf phase cycling includes ϕ₁ = 90°, 270°, 90°, 270°, 90°, 270°, 90°, 270°; ϕ₂ = 270°, 270°, 90°, 90°, 270°, 270°, 90°, 90°; ϕ₃ = 0°, 0°, 0°, 0°, 180°, 180°, 180°, 180°. Signals detected in t₂ are co-added with phases 0°, 180°, 180°, 0°, 180°, 0°, 0°, 180°. Real or imaginary signals in t₁ are acquired with the final ¹⁵N pulse phase set to x or y as indicated. (b) fpRFDR blocks used for ¹⁵N–¹⁵N and ¹³C–¹³C dipolar recoupling, differing in the positions of π pulses within the MAS rotation period τ_R. (c) Rf pulse sequence for ¹³C-BARE measurements in which the signal decay curves are extracted from crosspeaks in a series of 2D ¹⁵N–¹³C correlation spectra. Rf phase cycling includes ϕ₄ = 0°, 0°, 90°, 90°, 180°, 180°, 270°, 270°; ϕ₅ = 0°, 180°, 0°, 180°, 0°, 180°, 0°, 180° or 90°, 270°, 90°, 270°, 90°, 270°, 90°, 270° for real or imaginary signals in t₁. Signals detected in t₂ are co-added with phases 0°, 180°, 90°, 270°, 180°, 0°, 270°, 90°. (d) Rf pulse sequence for ¹³C-BARE measurements in which the signal decay curves are extracted from crosspeaks in a series of 2D ¹³C–¹³C correlation spectra. Rf phase cycling includes ϕ₆ = 90°, 270°, 90°, 270°, 90°, 270°, 90°, 270°; ϕ₇ = 90°, 90°, 270°, 270°, 90°, 90°, 270°, 270° or 0°, 0°, 180°, 180°, 0°, 0°, 180°, 180° for real or imaginary signals in t₁. The first Gaussian-shaped frequency-selective π pulse is present in the first four scans and absent in the second four scans. Signals detected in t₂ are co-added with phases 0°, 180°, 180°, 0°, 180°, 0°, 0°, 180°.

A pair of ¹⁵N pulses after the fpRFDR period in Fig. 2a selects the x-component of transverse ¹⁵N polarization, which evolves under isotropic ¹⁵N chemical shifts in t₁. Either the x-component or the y-component is transferred to directly-bonded ¹³C_α nuclei by frequency-selective cross-polarization and stored as longitudinal ¹³C polarization by a ¹³C flip-back pulse. A ¹³C–¹³C spin diffusion period, with τ_sd = 13 ms in the measurements described below, precedes the t₂ period, which is initiated by a final ¹³C π/2 pulse. In this way, the ¹⁵N-BARE data were obtained as a series of NCACX-type 2D spectra, with increasing ¹⁵N–¹⁵N evolution periods.

Pulse sequences for ¹³C-BARE are shown in Fig. 2c and d. Both sequences use modified PITHIRDS-CT (i.e., ZQ-SEASHORE) periods, in which each concatenated ABC block is followed by a τ_R period of spin precession under isotropic chemical shifts and each separate B block is followed by a 3τ_R period. Precession in the τ_R periods has the effect of attenuating residual nonzero ¹³C–¹³C couplings due to imperfect averaging in the ABC blocks. Precession in the 3τ_R periods has the effect of truncating ¹³C–¹³C couplings created by the B blocks to the “weak coupling” form d_ijS_ziS_zj, where d_ij is the effective coupling between spins i and j, with z-components of angular momentum S_zi and S_zj. A frequency-selective π pulse at the carbonyl ¹³C NMR frequency in the middle of the recoupling period then refocuses the couplings of carbonyl ¹³C spins to all other ¹³C-labeled sites, ideally leaving only the ¹³CO–¹³CO couplings [16].

Experiments were performed at 14.1 T, with τ_R = 25.0 μs (40.00 kHz MAS) and n = 8. The 3τ_R precession periods after B blocks were chosen to produce efficient truncation of both the ¹³CO–¹³C_α couplings (roughly 18 kHz chemical shift difference, corresponding to 1.35 precession cycles in 3τ_R) and most of the ¹³C_α–¹³C_β couplings (1.5–4.5 kHz chemical shift differences, corresponding to 0.11–0.34 precession cycles in 3τ_R). ¹³C π pulses were 7.0 μs (less than τ_R/3 in length, but still starting at 0, τ_R/3, and 2τ_R/3, as described above). The ¹³C carrier frequency was set to F2 = 99 ppm during the ZQ-SEASHORE recoupling periods and to F1 = 174 ppm for the frequency-selective π pulse, which had a duration of 250 μs (100 μs full-width at half maximum). Constant-time dipolar decay curves were recorded with N′ = 5, 4, 3, 2, 1, 0 and M′ = 0, 3, 6, 9, 12, 15. A constant total time of 6.25 ms (not including the selective π pulse) was maintained by the additional qτ_R precession periods, with q = 0, 2, 4, 6, 8, 10.

¹³C-BARE data were acquired as a series of 2D ¹⁵N–¹³C_α correlation spectra with the pulse sequence in Fig. 2c. In this sequence, the ZQ-SEASHORE period is preceded by ¹H–¹⁵N cross-polarization, a t₁ period of ¹⁵N chemical shift evolution period, and frequency-selective ¹⁵N–¹³CO cross-polarization. The ZQ-SEASHORE period is followed by a mixing period for ¹³CO–¹³C_α polarization transfer before t₂, which consisted of a 3.1 ms DREAM [43] period in the experiments described below. ¹³C-BARE data were also acquired as a series of 2D ¹³CO–¹³C_α correlation spectra with the pulse sequence in Fig. 2d. In this sequence, the ZQ-SEASHORE period is preceded by ¹H–¹³C cross-polarization, a flip-back pulse to create longitudinal ¹³C polarization, and a frequency-selective π pulse on half of the scans to select carbonyl polarization. The ZQ-SEASHORE period is followed by a t₁ period of ¹³CO shift evolution, a mixing period for ¹³CO–¹³C_α polarization transfer, and the t₂ period. Experiments described below used a 2.40 ms fpRFDR period for ¹³CO–¹³C_α transfer. Although the PITHIRDS-CT and ZQ-SEASHORE techniques have been described previously, application to uniformly labeled proteins using the 2D pulse sequences in Fig. 2 has not been demonstrated previously. Inclusion of the resulting data sets in structure calculations, as described below, has also not been reported.

In ¹⁵N-BARE measurements, ¹H decoupling at 104 kHz was applied during the PITHIRDS-CT, t₁, ¹⁵N–¹³C cross-polarization, and t₂ periods, with TPPM in t₁ and t₂. In ¹³C-BARE measurements, XiX decoupling [44] at 4 kHz was applied only during t₁ and t₂. All measurements used active synchronization of the rf pulses with the MAS tachometer signal, as previously described [27]. ¹⁵N-BARE data were acquired with 3.0 s recycle delays, maximum t₁ and t₂ periods of 21.0 ms and 15.3 ms, and a total measurement time of 22 h per value of M. ¹³C-BARE data were acquired with 1.5 s recycle delays, maximum t₁ and t₂ periods of 15.1 ms and 30.7 ms, and a total of 7 h (Fig. 2c) or 15 h (Fig. 2d) per value of M′.

Crosspeak volumes were extracted from rectangular areas within the 2D spectra using the seriesTab program of NMRPipe (see http://spin.niddk.nih.gov/NMRPipe/ref/prog/). Root-mean-squared (rms) noise in the crosspeak volume measurements was evaluated from the volumes in multiple rectangular areas within areas of the 2D spectra that were devoid of crosspeaks.

2.5. Simulations of ¹⁵N-BARE and ¹³C-BARE measurements

Simulations were performed with Fortran programs NPI-THIRDS2.F and ZQSEASH2.F, respectively (available upon request from robertty@mail.nih.gov). These programs calculate the evolution of the coupled-spin density matrix under the time-dependent nuclear spin Hamiltonian in the PITHIRDS-CT or ZQ-SEASHORE periods of the pulse sequences in Fig. 2, including homonuclear dipole–dipole couplings, isotropic and anisotropic chemical shifts, and all rf pulses (including the frequency-selective π pulses in ¹³C-BARE measurements). The initial density matrix was assumed to be S_x. The S_x component was evaluated at the end of the recoupling period and taken to represent the measured signal. Results were averaged over 512 orientations in ¹⁵N-BARE simulations and 125 orientations in ¹³C-BARE simulations, determined to be sufficient for convergence in test simulations.

¹⁵N-BARE simulations included three ¹⁵N spins, representing the backbone amide nitrogens of residues k − 1, k, and k + 1, with identical isotropic shifts and chemical shift anisotropy (CSA) principal values (110 ppm, −55 ppm, and −55 ppm relative to the isotropic shift). In simulations of ¹⁵N-BARE data for N-terminal or C-terminal residues, the amide nitrogen of residue k − 1 or k + 1 was omitted. The unique axis of the ¹⁵N CSA tensor was assumed to make an angle of 22° with the amide N–H bond in each residue, as indicated by experiments [45,46]. Rf pulses were applied at the isotropic shift. Standard chemical bond lengths and bond angles and planar peptide bonds were assumed. Simulation of one ¹⁵N-BARE curve (five data points) required 1.4 s on a 2.20 GHz Intel Core 2 Duo T7500 processor.

¹³C-BARE simulations included five ¹³C spins, representing the backbone carbonyl carbons of residues k − 1, k, and k + 1 and the α- and β-carbons of residue k. Carbonyl carbons were assumed to have isotropic shifts of 176 ppm, 174 ppm, and 172 ppm, and identical CSA principal values (−70 ppm, −10 ppm, and 80 ppm relative to the isotropic shift). Isotropic, but not anisotropic, chemical shifts of α- and β-carbons were included, and were set to the experimentally-determined values (within 2 ppm) for each residue. In simulations of ¹³C-BARE data for N-terminal or C-terminal residues, the carbonyl carbon of residue k − 1 or k + 1 was omitted. In simulations of glycine data, the β-carbon was omitted. The δ₂₂ carbonyl CSA tensor axis was assumed to make a 130° angle to the CO–N bond and the δ₃₃ axis was assumed to be perpendicular to the peptide plane, as indicated by experiments [47,48]. The rf carrier frequency was set to 99 ppm during the ZQ-SEASHORE sequence, and to 174 ppm during the selective π pulse, as in experiments. Simulation of one ¹³C-BARE curve (six data points) required 23 s on a 2.20 GHz Intel Core 2 Duo T7500 processor.

The α- and β-carbons were included in ¹³C-BARE simulations with their experimentally determined isotropic shifts because these carbons have an effect on the simulated carbonyl decay curves that is non-negligible when the simulated curves are compared with experimental data with high signal-to-noise ratios, as in the GB1 experiments discussed below. In particular, when the difference between ¹³C_α and ¹³C_β chemical shifts is small (less than 10 ppm under our experimental conditions), the ¹³C_α–¹³C_β coupling is not fully truncated by the 3_τR precession periods discussed above. Non-commutativity of the partially untruncated ¹³C_α–¹³C_β coupling and the truncated ¹³CO–¹³C_α coupling then prevents the ¹³CO–¹³C_α coupling from being fully refocused by the selective π pulse in the middle of the ZQ-SEASHORE period. This effect produces a larger signal decay in the ¹³C-BARE data, typically by up to 5%.

Rf inhomogeneity also has a non-negligible effect on the simulated ¹⁵N-BARE and ¹³C-BARE decay curves. Therefore, four sets of simulations were performed, with all rf fields scaled by factors of 1.00, 0.95, 0.90, and 0.80. Experimental rf field distributions were estimated from ¹³C and ¹⁵N nutation measurements, performed on the GB1 sample itself. Based on the experimental measurements of rf inhomogeneity, the four simulations were averaged with respective weighting factors equal to 0.45, 0.25, 0.20, and 0.10 for ¹⁵N-BARE data, and 0.45, 0.25, 0.25, and 0.05 for ¹³C-BARE data. Use of the standard ¹⁵N and ¹³C CSA parameters given above is adequate, as the ¹⁵N-BARE and ¹³C-BARE decay curves do not depend sensitively on these parameters.

Simulations of ¹⁵N-BARE measurements were performed over a grid of ψ_k−1, ϕ_k, and ψ_k values, with 10° increments. Values of ψ_k−1 and ψ_k ranged from −180° to +180°; values of ϕ_k ranged from −180° to 0°. Positive values of ϕ_k were not simulated because the simulations are symmetric under a simultaneous change in sign of all three angles. Dependence on ϕ_k was weak (<3%), except when both |ψ_k−1| and |ψ_k| were small. Simulations of ¹³C-BARE measurements were performed over a grid of ϕ_k, ψ_k, and ϕ_k+1 values, also with 10° increments. Values of ϕ_k and ψ_k ranged from −180° to +180° values of ϕ_k+1 ranged from −180° to 0°. Dependence on ψ_k was also weak.

2.6. Xplor-NIH calculations

Structural models were generated by molecular dynamics/simulated annealing in Xplor-NIH. To include ¹⁵N-BARE and ¹³C-BARE data as restraints, 3D χ² surfaces were constructed from the simulations described above, according to the formulae

$${\chi }_{N,k}^2\left({\psi }_{k-1},{\varphi }_k,{\psi }_k\right)=\frac{1}{{\sigma }_{N,\mathit{rms}}^2}\sum _{j=1}^{M_N}{[E_{N,k}(j)-{\lambda }_{N,k}({\psi }_{k-1},{\varphi }_k,{\psi }_k)S_N({\psi }_{k-1},{\varphi }_k,{\psi }_k;j)]}^2$$ (1a)

$${\chi }_{C,k}^2({\varphi }_k,{\psi }_k,{\varphi }_{k+1})=\frac{1}{{\sigma }_{C,\mathit{rms}}^2}\sum _{j=1}^{M_C}{[E_{C,k}(j)-{\lambda }_{C,k}({\varphi }_{k,}{\psi }_k,{\varphi }_{k+1})S_{C,k}({\varphi }_k,{\psi }_k,{\varphi }_{k+1};j)]}^2$$ (1b)

where M_N and M_C are the number of data points in ¹⁵N-BARE and ¹³C-BARE curves, respectively, E_N,k(i) and E_{C, k}(i) are experimental crosspeak volumes in the experimental 2D spectra for residue k, σ_N,rms and σ_C,rms are rms noise in the crosspeak volumes, λ_N,k and λ_C,k are scaling factors calculated to minimize χ² for each choice of the three torsion angles, and S_N and S_C,k are simulated data points. When ¹³C-BARE curves for a given residue could be extracted from 2D spectra obtained with pulse sequences in both Fig. 2c and d, the curve with the higher signal-to-noise ratio was used. Note that the choice of simulated ¹³C-BARE data depends on the residue number, since the simulations depend on ¹³C_α and ¹³C_β chemical shifts. A single set of simulations was used for ¹⁵N-BARE experiments, except for C-terminal and N-terminal residues. χ² surfaces were first created as tables in which each row contained the three angles and the corresponding χ² value. These tables were converted to a format appropriate for Xplor-NIH by the Python script gen_energyfiles.py (available upon request). Xplor-NIH calculations were performed with Python scripts, where each χ² surface was directly implemented as a 3D torsion angle spline potential. Specifically, tricubic interpolation in three dimensions [49] was performed between the grid points of each χ² surface, resulting in a differentiable function, i.e., a potential surface, whose gradient was evaluated during molecular dynamics and energy minimization.

¹⁵N-BARE and ¹³C-BARE data for the N- and C-terminal residues were interpreted directly as restraints on ¹⁵N–¹⁵N and ¹³CO–¹³CO distances between residues 1 and 2 and between residues 55 and 56, as shown in Table S2. Data for other residues cannot be represented as simple distance restraints because each ¹⁵N-BARE or ¹³C-BARE curve depends on two ¹⁵N–¹⁵N or ¹³CO–¹³CO distances, as well as the angle between the two distance vectors.

In addition to the ¹⁵N-BARE and ¹³C-BARE restraints, backbone torsion angle restraints from TALOS+ predictions and inter-residue distance restraints were included in the Xplor-NIH calculations, as shown in Tables S1 and S2, using the standard CDIH and NOE potential terms. Torsion angle ranges were set to twice the uncertainties listed in Table S1. Standard bond length, bond angle, improper angle, and repulsive van der Waals potentials were also included. Except as noted below, simulated annealing was performed in torsion angle space and in two stages, starting from a randomly generated, extended structure. In the first stage (simulation temperatures from 3000 K to 500 K), TALOS+ torsion angle restraints were applied at full strength (force constant 50 kcal/mol rad²) and inter-residue distance restraints were applied with increasing strength (force constant 1–5 kcal/mol Ų). In the second stage (500–10 K), ¹⁵N-BARE and ¹³C-BARE restraints were added with increasing strength (force constant 0–0.01 kcal/mol) and distance restraints were strengthened further (force constant 5–50 kcal/mol Ų). Annealing was followed by energy minimization, first in torsion angle space and finally in Cartesian coordinate space. Xplor-NIH scripts are available upon request. Torsion angles were extracted from PDB coordinate files with the Torsions program from the group of Dr. A.C.R. Martin at University College London (see http://www.bioinf.org.uk/software/). Structures were displayed and analyzed with MOLMOL [50].

3. Results and discussion

3.1. Properties of ¹⁵N-BARE and ¹³C-BARE data

Fig. 3a shows the 2D spectrum of microcrystalline, uniformly ¹⁵N, ¹³C-labeled GB1 that was obtained with the ¹⁵N-BARE pulse sequence in Fig. 2a, with M = 0. Assignments of crosspeaks that are sufficiently well resolved that their volumes can be measured are indicated in Fig. 3a. Fig. 3b shows examples of the dependence of crosspeak volumes on the effective evolution time (i.e., nMτ_R) under ¹⁵N–¹⁵N dipole–dipole couplings. Signals from different residues clearly have different decay curves, reflecting local conformational differences. The ratios of crosspeak volumes at M = 24 (i.e., the maximum evolution time) to those at M = 0 are plotted in Fig. 3c. There is a clear correlation between the ¹⁵N-BARE data and GB1 secondary structure, with signals from residues in the β-strands decaying more slowly than those in the central α-helical segment and in the loops that connect secondary structure elements. This behavior is expected, as sequential ¹⁵N–¹⁵N distances are longer in β-strands (~3.5 Å) than in α-helices (~2.8 Å), corresponding to a factor of ~2.0 difference in coupling strengths.

Fig. 3.

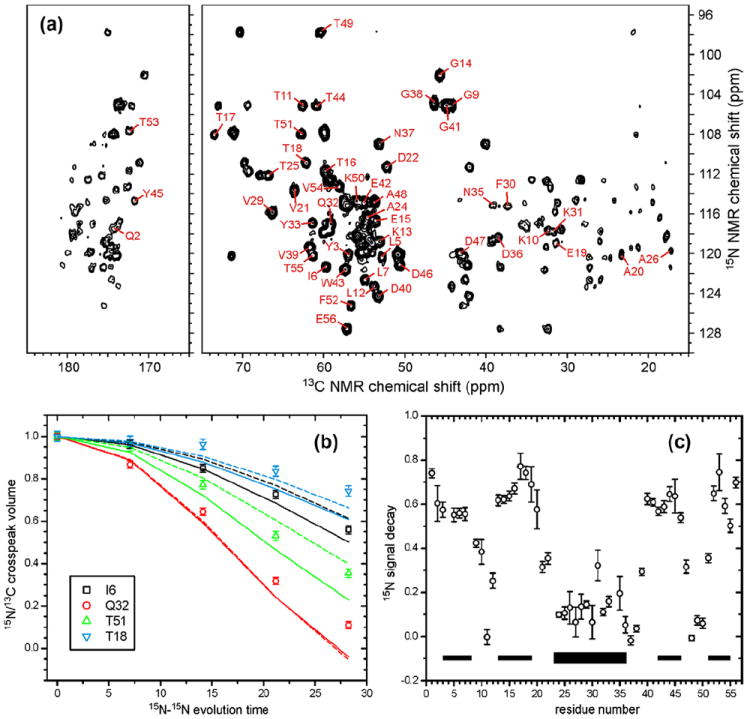
(a) 2D ¹⁵N–¹³C correlation spectrum of microcrystalline, uniformly ¹⁵N, ¹³C-labeled GB1, obtained at 14.1 T using the pulse sequence in Fig. 2a, with M = 0, N = 8, n = 16, and τ_R = 73.53 μs. Crosspeaks from which ¹⁵N-BARE decay curves were extracted are indicated with their residue-specific assignments. (b) Representative ¹⁵N-BARE decay curves. Solid and dashed curves are simulations using backbone torsion angles from PDB 2GI9, before (solid) and after (dashed) refinement against the ¹⁵N-BARE and ¹³C-BARE data as described in the text. Experimental data and simulations are normalized to 1.00 at zero evolution time. (c) Signal decay at the maximum evolution time for all residues with measureable ¹⁵N-BARE curves. Thin and thick bars indicate β-strand and α-helix segments in GB1, respectively.

Fig. 4a and b shows 2D spectra obtained with the ¹³C-BARE pulse sequences in Fig. 2d and d, respectively, with M′ = 0. Fig. 4c shows representative signal decay curves, and Fig. 4d shows the ratios of crosspeak volumes at M′ = 15 (i.e., the maximum effective ¹³C–¹³C evolution time) to those at M′ = 0. Again, the ¹³C-BARE data correlate with GB1 secondary structure as expected. Sequential carbonyl ¹³C–¹³C distances are ~3.5 Å in β-strands and ~3.0 in α-helices, corresponding to a factor of ~1.6 difference in coupling strengths. Thus, the range of decay curves in ¹³C-BARE data may be expected to be somewhat narrower than in ¹⁵N-BARE data, as is apparent in Figs. 3 and 4. The underlying spin dynamics that produce the signal decays in the two measurements are also different, with ¹⁵N-BARE measurements using the full second-rank, zero-quantum homonuclear coupling created by fpRFDR [41] and ¹³C-BARE measurements using the truncated coupling [16]. Differences in spin dynamics affect the shapes of the signal decay curves. In particular, ¹⁵N-BARE curves have an intrinsically stronger oscillatory modulation (which would be apparent at longer evolution times), arising from polarization transfers among the coupled spins that do no occur when the coupling is truncated, which also contributes to the greater range of decay curves in ¹⁵N-BARE measurements. It should also be noted that, as discussed above, ¹³C-BARE data are somewhat sensitive to ¹³C_α and ¹³C_β chemical shift differences in addition to ¹³CO–¹³CO distances, so that the simple correlation of the raw data with secondary structure is weakened.

Fig. 4.

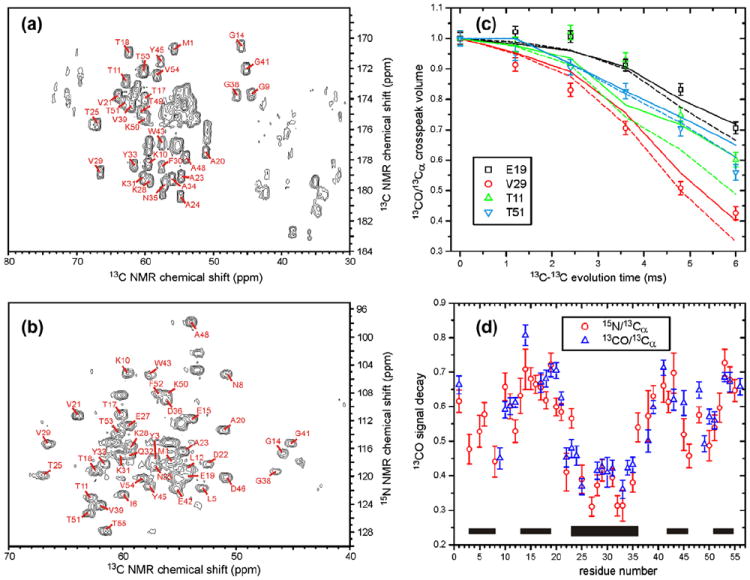
(a and b) 2D ¹³C–¹³C and ¹⁵N–¹³C correlation spectra of GB1, obtained at 14.1 T using the pulse sequences in Fig. 2d and c, respectively, with M′ = 0, N′ = 5, n = 8, and τ_R = 25.00 μs. Crosspeaks from which ¹³C-BARE decay curves were extracted are indicated with their residue-specific assignments. (c) Representative ¹³C-BARE decay curves, using the pulse sequence in Fig. 2d. Solid and dashed curves are simulations using backbone torsion angles from PDB 2GI9, before (solid) and after (dashed) refinement against the ¹⁵N-BARE and ¹³C-BARE data as described in the text. Experimental data and simulations are normalized to 1.00 at zero evolution time. The evolution time on the abscissa does not include the chemical shift precession periods. (d) Signal decay at the maximum evolution time for all residues with measureable ¹³C-BARE curves using pulse sequences in Fig. 2c (circles) or Fig. 2d (triangles). Thin and thick bars indicate β-strand and α-helix segments in GB1, respectively.

Solid lines in Figs. 3b and 4c are simulated ¹⁵N-BARE and ¹³C-BARE curves, in which backbone ϕ and ψ torsion angles were taken from the 2GI9 crystal structure, rounded to the nearest 10° increment to correspond to entries in our simulation tables. Agreement between simulations and experiments is good, but not perfect. One possible source of discrepancy is imprecision in the crystal structure. Comparison of ϕ and ψ values from the 2GI9 and 2QMT structures [32,40] reveals differences up to 22° in ϕ and ψ values (at T11), with the angular rmsd being 8°. The positional rmsd between the two sets of backbone atom coordinates is 0.45 Å. Differences in sequential backbone N–N distances are less than 0.1 Å (except 0.15 Å at T18); differences in sequential backbone CO–CO distances are also less than 0.1 Å (except 0.15 Å at T18, 0.12 Å at G38, 0.13 Å at D46, and 0.12 Å at A48). Comparison of ϕ and ψ values from the 2GI9 with values from the solution NMR structure in PDB file 2PLP [51] reveals differences greater than 20° at G9, K10, L12, G38, D40, and G41, and an angular rmsd of 11°. Peptide bonds are assumed to be perfectly planar in 2PLP, but not in 2GI9 or 2QMT. Overall, it appears that imprecision in the crystal structure is not a dominant source of discrepancy between simulations and experiments in Figs. 3b and 4c, except possibly at isolated residues in loop segments.

Molecular motions may also contribute to the discrepancies between simulations (which assume perfect rigidity) and experiments. Solution NMR studies indicate the presence of motions that reduce the apparent strengths of residual dipolar couplings by site-specific factors between 0.6 and 1.0 [51,52]. Although we have not yet investigated effects of motions on ¹⁵N-BARE and ¹³C-BARE data in any detail, it is reasonable to expect that motions would systematically reduce the experimental decay rates relative to simulations, as observed in Fig. 3b. Other factors that may be important include orientation dependences of the initial ¹⁵N or ¹³C spin polarization created by cross-polarization from protons, orientation dependences of subsequent polarization transfers, and anisotropy of transverse relaxation processes.

3.2. Incorporation of ¹⁵N-BARE and ¹³C-BARE data into structure calculations

Panels a–e of Figs. 5 and 6 show backbone structures of GB1 obtained from Xplor-NIH calculations with various sets of restraints. In each case, 24 independent Xplor-NIH runs were performed. The 12 lowest-energy structures are displayed after adjusting their positions and orientations to minimize the rmsd from the average backbone coordinates calculated in MOLMOL [50]. Results are summarized in Table 1. When ¹⁵N-BARE and ¹³C-BARE restraints are added to distance restraints, or to a combination of distance and TALOS+ torsion angle restraints, the precision to which the backbone structure is defined improves, as indicated by a reduction in the rmsd of the 12 lowest-energy structures from their average backbone coordinates. Although the correct overall “topology” of the GB1 backbone structure is discernible when only distance restraints are included (Figs. 5a and 6a), the full details of the secondary structure, including an ordered α-helix, are clear only when all restraints are included. Thus, the ¹⁵N-BARE and ¹³C-BARE restraints contain structural information that complements and is not redundant with information in the distance restraints and TALOS+ torsion angle restraints.

Fig. 5.

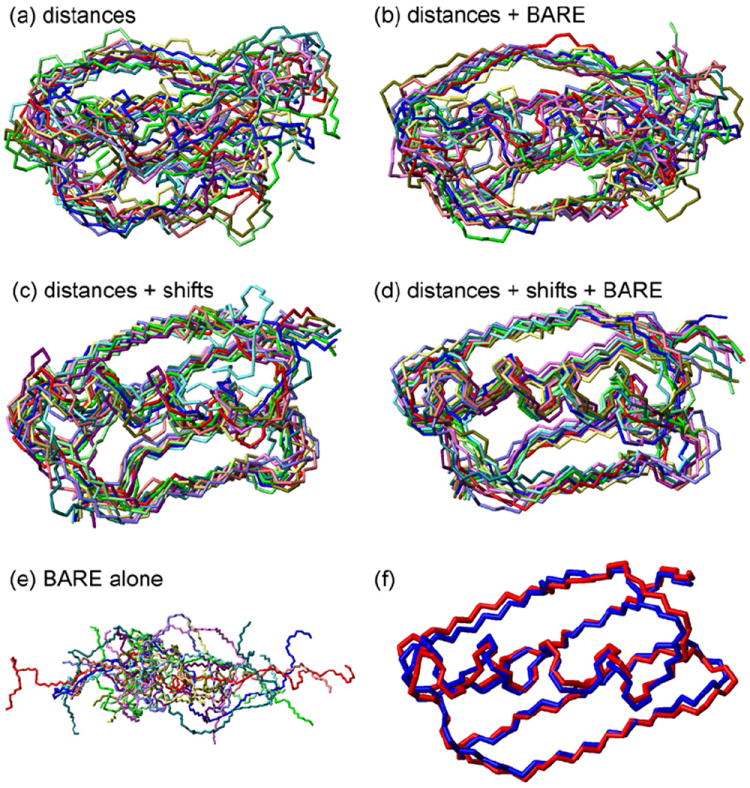
(a–e) Bundles of the 12 lowest-energy backbone structures for GB1 from 24 independent Xplor-NIH calculations using the combinations of distance restraints listed in Table 1. Individual structures are rotated and translated to minimize the total rmsd from the average coordinates of all structures. Panel d uses the full set of restraints, including distance restraints from inter-residue crosspeaks in 2D CHHC, NHHC, and RAD spectra, restraints from torsion angle predictions generated from ¹⁵N and ¹³C chemical shifts by the TALOS+ algorithm, and restraints from ¹⁵N-BARE and ¹³C-BARE measurements. (f) Superposition of backbone structures from PDB 2GI9, both before (blue) and after (red) refinement against the ¹⁵N-BARE and ¹³C-BARE data as described in the text. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

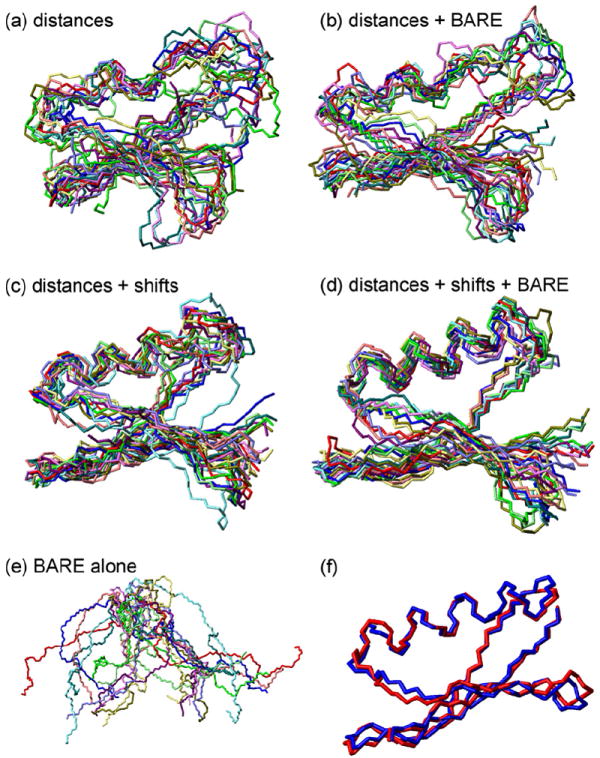
Same as Fig. 5, but with all structures rotated by 90° about a horizontal axis.

Table 1.

Summary of Xplor-NIH calculations.

Panel in Figs. 5–7	Experimental restraints	Backbone rmsd values (Å) between:			χ2 for lowest-energy structurec
		Bundlea and average structure	Bundlea and 2GI9 structure	Regularized average structureb and 2GI9
a	Distancesd	2.77 ± 0.62	4.87 ± 0.81	4.10	3541
b	Distances, 15N, 13C-BARE	2.29 ± 0.56	3.83 ± 0.41	3.84	318
c	Distances, TALOS+e	1.61 ± 0.60	2.67 ± 0.49	2.55	3113
d	Distances, TALOS+, 15N, 13C-BARE	1.33 ± 0.22	2.68 ± 0.26	2.28	302
e	15N, 13C-BARE	12.06 ± 1.96	20.96 ± 4.19	17.92	196

^aTwelve lowest-energy structures from 24 independent Xplor-NIH calculations, after translations and rotations to minimize the rmsd values for N, C_α, and backbone carbonyl atoms.

^bRegularized average of 12 lowest-energy structures, calculated within Xplor-NIH.

^cTotal χ² deviation between experimental and simulated ¹⁵N-BARE and ¹³C-BARE data for all residues. Simulations used ϕ and ψ torsion angles from the lowest-energy structure.

^dDistance restraints from 2D CHHC, NHHC, and RAD spectra (see Table S2), plus N- and C-terminal backbone distance restraints from ¹⁵N-BARE and ¹³C-BARE data.

^eBackbone torsion angle restraints from TALOS+ analysis of chemical shifts (see Table S1). Only restraints for β-strand and α-helical segments were used. TALOS+ predictions that disagree with torsion angles in 2GI9 by more than 25° were also discarded.

Inclusion of ¹⁵N-BARE and ¹³C-BARE restraints also improves the accuracy of the final structures slightly, as indicated by reductions in the backbone positional rmsd values between regularized average structures and the 2GI9 structure. Regularized average structures were calculated within Xplor-NIH, by energy-minimizing the average coordinates of the 12 lowest-energy structures (including restraint energies). Large improvements in absolute accuracy, as measured by rmsd values between atomic coordinates, do not occur because the accuracy is primarily limited by the number and precision of the internuclear distance restraints. Without a larger set of distance restraints, torsion angle restraints alone cannot produce small positional rmsd values between the atomic coordinates of the calculated structures and those of the 2GI9 crystal structure.

The average ϕ and ψ angles from these Xplor-NIH calculations, and their standard deviations, are compared with values from 2GI9 in Fig. 7. To avoid issues arising from the equivalence of −180° and +180° torsion angles, average values were calculated according to

$${\theta }_{\mathit{ave}}\equiv \{\begin{array}{lll}{\tan }^{-1}\frac{{(\sin \theta )}_{\mathit{ave}}}{{(\cos \theta )}_{\mathit{ave}}},& \mathrm{if}{(\cos \theta )}_{\mathit{ave}}>0& \\ {\tan }^{-1}\frac{{(\sin \theta )}_{\mathit{ave}}}{{(\cos \theta )}_{\mathit{ave}}}-\pi ,& \mathrm{if}{(\cos \theta )}_{\mathit{ave}}<0& \mathrm{and}{(\sin \theta )}_{\mathit{ave}}<0\\ {\tan }^{-1}\frac{{(\sin \theta )}_{\mathit{ave}}}{{(\cos \theta )}_{\mathit{ave}}}+\pi ,& \mathrm{if}{(\cos \theta )}_{\mathit{ave}}<0& \mathrm{and}{(\sin \theta )}_{\mathit{ave}}>0\end{array}$$ (2)

where θ = ϕ, ψ and “ave” indicates average values. In Fig. 7a, it is clear that distance restraints alone do not greatly restrict most backbone torsion angles, while inclusion of ¹⁵N-BARE and ¹³C-BARE restraints leads to average values that correspond more closely to the 2GI9 values. The agreement is quite good when all restraints are included (Fig. 7d). Angular rmsd values between residuespecific ϕ_ave and ψ_ave values and the corresponding torsion angles in the 2GI9 structure are 53° and 84° in Fig. 7a, 43° and 56° in Fig. 7b, 40° and 42° in Fig. 7c, and 31° and 31° in Fig. 7d. Thus, restraints from ¹⁵N-BARE and ¹³C-BARE data result in improvements in the accuracy of backbone torsion angles that are comparable to improvements from TALOS+ restraints, although TALOS+ restraints are especially important for the α-helical segment. When only ¹⁵N-BARE and ¹³C-BARE restraints are used (Fig. 7e) angular rmsd values are 48° and 64°, respectively, somewhat lower than the angular rmsd values obtained when only distance restraints are used.

Fig. 7.

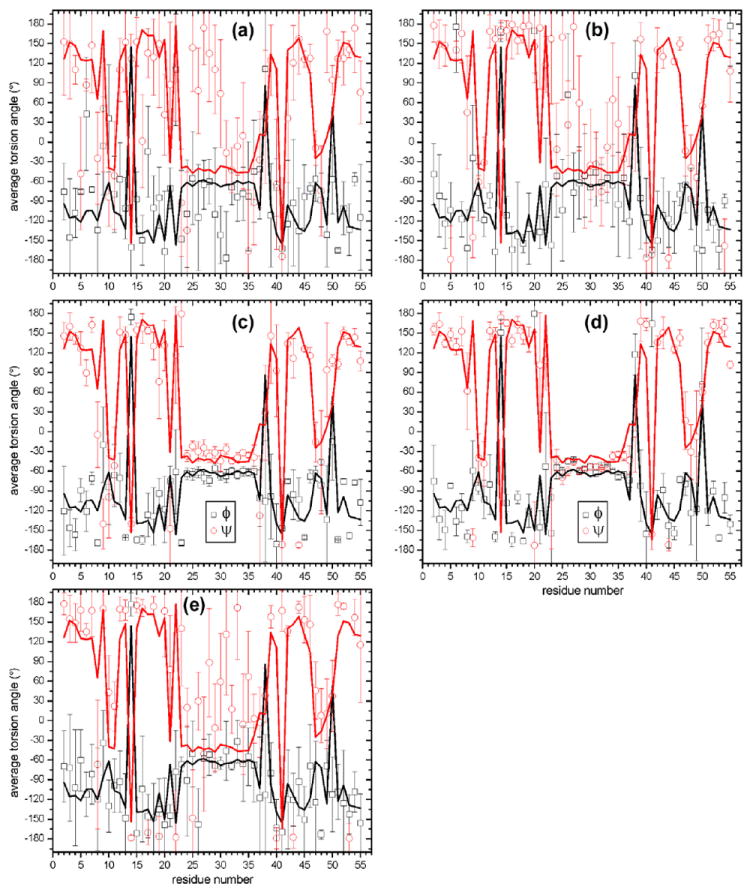
(a–e) Distributions of backbone torsion angles in the structural bundles in panels a–e of Figs. 5 and 6. Circles and squares are average ϕ and ψ values, respectively. Error bars are angular rmsd values. Solid lines are torsion angles in PDB 2GI9.

As shown in Figs. 5e and 6e, ¹⁵N-BARE and ¹³C-BARE restraints alone are not sufficient to produce the correct GB1 structure (or any other unique structure). This result is not surprising, for several reasons: (i) ¹⁵N-BARE and ¹³C-BARE data are local structural restraints. Without long-range restraints, it is impossible to determine a protein structure unless the local structural restraints are extremely precise; (ii) Torsion angle potentials derived from ¹⁵N-BARE and ¹³C-BARE data have multiple minima, for example because a rapidly decaying curve can result from either a short k − 1 ↔ k distance or a short k ↔ k + 1 distance (or both); (iii) Due to incomplete resolution in the 2D spectra, ¹⁵N-BARE data are missing for residues 4, 8, 23, and 34; ¹³C-BARE data are missing for residues 2, 4, 7, 26, 37, 40, 44, and 47.

As a measure of the degree to which the ¹⁵N-BARE and ¹³C-BARE restraints are satisfied in structures obtained from Xplor-NIH calculations, Table 1 includes the total χ² deviation between experimental and simulated ¹⁵N-BARE and ¹³C-BARE data, using ϕ and ψ values from the lowest-energy structure in each set of calculations (rounded to the nearest 10° increment). The lowest-energy structure obtained with only ¹⁵N-BARE and ¹³C-BARE restraints has total χ² = 195.9. We take this value to represent a lower bound, corresponding to the best possible agreement with the experimental data. For comparison, when random values of ϕ and ψ are assigned to each residue in GB1, total χ² values typically exceed 15,000. Xplor-NIH calculations that include distance and TALOS+ restraints, but not ¹⁵N-BARE and ¹³C-BARE restraints, have intermediate χ² values. Xplor-NIH calculations that combine ¹⁵N-BARE and ¹³C-BARE restraints with other restraints result in total χ² values that are less than twice the lower bound, indicating that the various restraints do not conflict with one another strongly.

When ϕ and ψ values are taken from 2GI9, the total χ² value is 1551. In order to refine the 2GI9 structure against our torsion angle restraints, we performed an Xplor-NIH calculation in which 2GI9 was used as the initial structure. TALOS+, ¹⁵N-BARE, and ¹³C-BARE restraints were applied, with annealing from 200 K to 10 K followed by energy minimization. Artificial distance restraints were also included, representing all carbon–carbon, nitrogen–nitrogen, and carbon–nitrogen distances under 4.5 Å in 2GI9, with ±0.5 Å distance ranges (total of 455 artificial distance restraints). With this approach, the 2GI9 structure can change slightly to improve the fit to the solid state NMR data, without expanding or distorting greatly. Initial and final backbone structures are superimposed in Figs. 5f and 6f. The backbone rmsd between initial and final structures is 0.81 Å. Only 3 out of the 455 distance restraints are violated by more than 0.5 Å in the final structure, with the largest violation being 0.67 Å. Values of ϕ and ψ change by rms values of 28° and 24°, respectively. Average changes are 0.3° and 1.4°, respectively, indicating the absence of an overall systematic shift of the backbone conformation. In the α-helical segment, the average value of ϕ increases from −63° to −54°; the average value of ψ decreases from −42° to −51°. In β-strand segments, the average value of ϕ increases from −115° to −108°; the average value of ψ increases from 142° to 146°. Dashed lines in Figs. 3b and 4c are simulations using the final ϕ and ψ values. Although the quality of fit to experimental data does not improve dramatically for the residues that are shown as examples in Figs. 3b and 4c, the total χ² deviation for all residues decreases to 416.

Only torsion angle predictions from TALOS+ for β-strand and α-helical segments were included as restraints in the Xplor-NIH calculations discussed above. We took this approach to mimic more closely the situation that would arise in studies of a larger or less compact protein, where chemical shift assignments might be less complete, and torsion angle predictions might also be less complete and less reliable. Predictions that differed from torsion angles in 2GI9 by more than 25° were also omitted to prevent Xplor-NIH from converging towards less accurate structures.

The work of Rienstra and coworkers demonstrates that very extensive sets of structural restraints can be obtained in solid state NMR studies of microcrystalline GB1 [24,25,32-34,40]. We have deliberately used only a minimal set of distance restraints and TALOS+ restraints to ensure that the structural information content of the ¹⁵N-BARE and ¹³C-BARE data can be assessed. Our Xplor-NIH calculations consequently result in structural ensembles with relatively low precision and accuracy compared with the work of Rienstra and coworkers, in which backbone coordinate rmsd values from GB1 crystal structures as low as 0.5 Å [34] were obtained by combining many hundreds of distance restraints [25], TALOS-based restraints [33], dipolar tensor correlation (or vector angle) restraints [24], and chemical shift tensor restraints [34]. Our work resembles that of Wylie et al. [34] and Franks et al. [24] in that we convert ¹⁵N-BARE and ¹³C-BARE data to potential surfaces for incorporation into Xplor-NIH, and these potential surfaces serve to refine backbone conformations that are already defined to lower precision by more conventional restraints. Future studies may reveal which combinations of these advanced solid state NMR methods have the broadest applicability in studies of non-crystalline proteins. Important considerations include the spectral resolution requirements and the sensitivity to transverse relaxation rates of the various methods (see below), as well as their potential information content.

3.3. Additional remarks

Only backbone nitrogen sites and backbone carbonyl sites are included in the simulations described above. For residues with sidechain nitrogens or sidechain carbonyl/carboxyl groups, couplings to these sidechain sites might conceivably affect the ¹⁵N-BARE or ¹³C-BARE data. In fact, in the 2GI9 structure, distances from backbone ¹⁵N or ¹³CO sites to sidechain ¹⁵N or ¹³CO sites in all Glu and Gln residues are 4.2 Å or more, i.e., significantly greater than the sequential backbone ¹⁵N–¹⁵N or ¹³CO–¹³CO distances. The same is true of Lys and Trp residues. GB1 does not contain His or Arg residues. The only potentially problematic residues are N8 (3.0 Å CO–Cγ distance), D22 (3.1 Å CO–Cγ distance), N35 (3.6 Å CO–Cγ distance, 3.3 Å N–N_δ distance), D40 (3.0 Å CO–Cγ distance), D46 (3.0 Å CO–Cγ distance), and D47 (2.9 Å CO–Cγ distance). Distances to sidechain sites are less than sequential backbone distances in only four cases, namely the CO–Cγ distances of N8, D40, D46, and D47. ¹³C-BARE data are available for only two of these residues, namely N8 and D46. Results in Fig. 7d and e do not show anomalous backbone conformations at these residues, nor is the agreement between experimental and simulated ¹³C-BARE data anomalously poor for these residues. Thus, couplings to sidechain ¹⁵N or ¹³CO sites do not affect our results for GB1 significantly. Nonetheless, it may be important to consider such couplings in studies of other proteins.

In our simulations of ¹⁵N-BARE and ¹³C-BARE data, we have been careful to include the relatively minor effects of several parameters, both because the signal-to-noise ratio of the experimental data for GB1 is high and because it is important to examine the influence of these effects in initial tests of the ¹⁵N-BARE and ¹³C-BARE techniques. As discussed above, these parameters include rf inhomogeneity, ¹³C_α and ¹³C_β chemical shifts, and the third torsion angle (ϕ_k for ¹⁵N-BARE, ψ_k for ¹³C-BARE). Unless rf homogeneity is very poor or ¹³C_α–¹³C_β shift differences are very small, these parameters produce variations in simulated signal decays that are less than 5% of the initial signals. When the experimental signal-to-noise ratios are not high, it may be safe to ignore these parameters. In particular, ignoring the dependence on ψ_k in ¹³C-BARE simulations would reduce the time required to generate a full table of simulations from many days to less than half of a day. Ignoring the dependence on ¹³C_α–¹³C_β shift differences would eliminate the need to generate multiple simulation tables. The structural information content of the ¹⁵N-BARE and ¹³C-BARE data is obviously reduced when signal-to-noise is low. Plots in Figs. 3b and 4c indicate that signal-to-noise ratios as low as 5 for ¹⁵N-BARE and 10 for ¹³C-BARE data still provide useful structural information, roughly speaking.

An important strength of ¹⁵N-BARE and ¹³C-BARE measurements is that they are applicable to any system with resolved 2D ¹⁵N–¹³C or ¹³C–¹³C spectra. If the spectral resolution in 2D is inadequate, extensions to 3D spectroscopy are straightforward. ¹⁵N-BARE and ¹³C-BARE decay curves are created from the same intra-residue or sequential crosspeaks that are used to make chemical shift assignments. In contrast, inter-residue distance restraints are generally obtained from weaker crosspeaks in 2D spectra, which are often obscured by the intra-residue and sequential crosspeaks and which often have ambiguous assignments even in favorable cases [53,54]. From the standpoint of sensitivity, useful ¹⁵N-BARE and ¹³C-BARE data can be acquired from 2D spectra as long as the signal-to-noise ratio for one- or two-bond crosspeaks in a standard 2D NCA, 2D NCOCA, or 2D ¹³C–¹³C spectrum is roughly 10–20, taking into account an approximate 50% loss of signal due to transverse relaxation during the constant-time dipolar evolution periods in Fig. 2. Of course, sensitivity considerations depend on the quantity of spectrometer time that can be allotted to the ¹⁵N-BARE and ¹³C-BARE measurements.

In conclusion, we have shown that the ¹⁵N-BARE and ¹³C-BARE techniques allow quantitative measurements of backbone ¹⁵N–¹⁵N and ¹³CO–¹³CO dipole–dipole couplings in solid state NMR studies of uniformly ¹⁵N, ¹³C-labeled proteins. These measurements can serve as quantitative restraints on protein backbone conformation. Although the ¹⁵N-BARE and ¹³C-BARE measurements alone are not sufficient to determine a unique backbone structure, they provide information that is complementary to the commonly used restraints from isotropic chemical shifts and inter-residue crosspeaks. The precision and accuracy of solid state NMR structures can therefore be improved by including ¹⁵N-BARE and ¹³C-BARE restraints. These restraints are particularly valuable for protein segments where torsion angle predictions based on isotropic chemical shifts are incomplete, insufficiently precise, or potentially unreliable. In the case of microcrystalline GB1, the precision (defined by the rmsd among backbone coordinates of low-energy structures) is improved by about 0.3 Å when ¹⁵N-BARE and ¹³C-BARE restraints are added to distance and TALOS+ restraints. The accuracy of backbone torsion angles (defined by the rmsd between average angles in NMR-derived structures and angles in the crystal structure) is improved by about 10°. In solid state NMR studies of other protein systems, improvements in precision and accuracy are likely to depend on the quality and completeness of the various restraint sets.