Abstract
How neurons in the primary motor cortex control arm movements is not yet understood. Here we show that the equations of motion governing reaching simplify when expressed in spatial coordinates. In this fixed reference frame, joint torques are the sums of vector cross products between the spatial positions of limb segments and their spatial accelerations and velocities. The consequences that follow from this model explain many properties of neurons in the motor cortex, including directional broad, cosinelike tuning, nonuniformly distributed preferred directions dependent on the workspace, and the rotation of the population vector during arm movements. Remarkably, the torques can be directly computed as a linearly weighted sum of responses from cortical motoneurons, and the muscle tensions can be obtained as rectified linear sums of the joint torques. This allows the required muscle tensions to be computed rapidly from a trajectory in space with a feedforward network model.
Keywords: motor control, computational model, visually guided reaching, cosine tuning, population vector, spatial representation, joint-angle representation, reference frame
the motor cortex is the final cortical pathway to motor circuits in the spinal cord. The response properties of neurons in the motor cortex have been correlated with a wide variety of behavioral and cognitive variables, including extrinsic, spatial variables of hand movements such as endpoint position (Georgopoulos et al. 1984), endpoint velocity (Georgopoulos et al. 1982; Moran and Schwartz 1999), endpoint acceleration (Flament and Hore 1988), and endpoint movement fragments (Hatsopoulos et al. 2007), as well as intrinsic variables such as joint angles (Thach 1978), joint velocities (Reina et al. 2001), endpoint force (Georgopoulos et al. 1992; Taira et al. 1996), and muscle tensions (Evarts 1968; Fetz and Cheney 1980). Several studies have reported neural activities in the motor cortex consistent with an internal model of muscle forces for both reaching and isometric force tasks (Sergio and Kalaska 1998; Sergio et al. 2005). This has led to an impasse in deciding whether the internal representation in the motor cortex is based on extrinsic spatial variables or an intrinsic reference frame.
Many neurons in the motor cortex and other motor-related areas exhibit broad, cosinelike extrinsic tuning with respect to movement direction. Hand movement direction can be reconstructed with a population vector algorithm either from neurons that encode extrinsic endpoint velocity (Georgopoulos 1996; Lukashin et al. 1996; Sanger 1996) or from neurons that encode intrinsic joint angular velocity (Mussa-Ivaldi 1988). The preferred directions (PDs) of motor cortical neurons exhibited a shoulder-centered reference frame when a few parts of the workspace were examined (Caminiti et al. 1990). In a more recent study that systematically investigated the entire workspace, coexisting multiple reference frames were reported, including joint-angle and shoulder-based coordinates as well as extrinsic coordinates (Wu and Hatsopoulos 2006). Other studies have reported that neuronal activities correlated with motor-related cognitive variables such as movement preparation (Churchland et al. 2006), mental rotation (Georgopoulos et al. 1989; Lurito et al. 1991), or movement sequences (Carpenter et al. 1999). Given the observed complexity and heterogeneity of neuronal responses, Churchland and Shenoy (2007) have suggested that it may be necessary to discard the notion that the motor cortex represents movement parameters.
The movements of the arm are governed by muscle forces that exert torques around joints. Models of arm movements typically use joint-angle coordinates, which require the solution of nonlinear inverse kinematics (the computation of joint angles) and inverse dynamics (the computation of joint torques) in motor planning and execution (Flash and Sejnowski 2001). This raises many questions: 1) How are trajectories in Cartesian space converted by neurons in the motor cortex into joint torques and muscle tensions (Kalaska 2009)? 2) Are there multiple reference frames in the motor cortex? 3) How are the desired joint angles computed from the planned arm trajectory? 4) How are the desired torques computed from the joint angles? 5) What further transformations are needed to convert the desired joint torques into muscle tensions (Kawato et al. 1988; Todorov and Jordan 2002)?
For single-joint wrist movements starting from distinct postures there are neurons in the motor cortex that encode wrist movement directions in the extrinsic space or muscle activations, but no neurons have been reported that encode intrinsic movements in terms of joint angles (Kakei et al. 1999). For multijoint reaching movements, there are reports of an extrinsic coordinate system in the motor cortex (Georgopoulos et al. 1982), an intrinsic joint-based coordinate system (Scott and Kalaska 1997), an intrinsic muscle-based coordinate system (Morrow and Miller 2003), a shoulder-centered coordinate system (Caminiti et al. 1990), and evidence against a single-coordinate system representation (Wu and Hatsopoulos 2006). From a computational perspective, the explicit use of a joint-angle representation requires computation of the joint angles from the geometry of the arm and the joint torques from the equations of motion (EOMs) (Bullock et al. 1993; Soechting and Flanders 1989). There are obstacles along this route, first because the computation of joint angles is ill-posed and may not have unique solutions (Atkeson 1989) and second because for moving reference frames based on joint angles the EOMs have many terms (Fig. 1A).
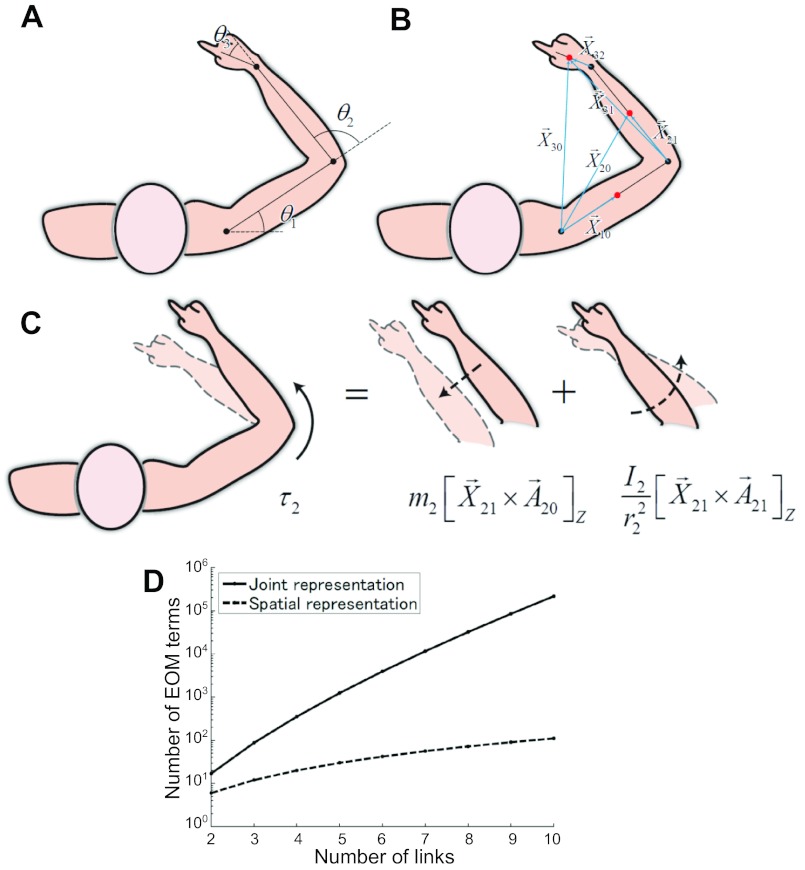
Fig. 1.
Motor control in joint-angle and spatial coordinates. A and B: a link model represented in joint-angle space (A) and in Cartesian space (B). For a 2-link model joint angles (θ1, θ2) or Cartesian vectors (X⃗10, X⃗20, X⃗21) were used, and for a 3-link model joint angles (θ1, θ2, θ3) or Cartesian vectors (X⃗10, X⃗20, X⃗30, X⃗21, X⃗31, X⃗32) were used. C: the equation of motion (EOM) includes translational (proportional to mass) and rotational (proportional to inertia moment) terms. D: number of terms required in EOMs of n-link system for joint-angle (solid line) and spatial (dashed line) representations.
An alternative to the dynamics-based approach is the equilibrium-point hypothesis in a fixed spatial reference frame that exploits viscoelastic properties of the musculoskeletal system and solves motor control problems without computing the joint angles and joint torques explicitly (Feldman 1966; Feldman and Levin 1995). This approach has been extended to the virtual trajectory control, in which temporally moving equilibrium points guide the endpoint movements (Bizzi et al. 1984; Hogan 1984), and to the passive motion paradigm, in which the goal of action is expressed by means of an attractive force field (Mohan and Morasso 2011; Morasso et al. 2010; Mussa Ivaldi et al. 1988). The equilibrium-point control and its extensions emphasize the control of stiffness for the purpose of stabilization, whereas the dynamics-based approaches emphasize the computation of muscle tensions and explicit dynamical equations. There is no reason why both of these approaches could be used by the motor system depending on conditions.
This study addresses the representation problem in the motor cortex for visually guided reaching movements. Several invariant characteristics of reaching movements are expressed in spatial variables such as straight paths and bell-shaped velocity profiles (Abend et al. 1982; Morasso 1981), so it is conceivable that the motor cortex employs spatial trajectory information directly. We show here that the EOMs for reaching based on the spatial positions of limbs in Cartesian coordinates (Fig. 1B) are considerably more concise than for joint-based reference frames and have physically intuitive interpretations (Hinton 1984). The dynamics of linked rigid bodies using spatial vectors, known as the Newton-Euler method (reviewed in appendix a), has been well studied, especially in robotics, but it has not been used for understanding the functions of motor cortex. The problems in computing the joint angles arise in the joint-angle representation because only the endpoint position is given, which our model resolves by introducing redundant Cartesian vectors that are closely related to the joint-angle representation. In robotics and computational modeling of motor control, the joint-angle representation is popular because it provides a concise description for movement without redundancy, but the EOMs expressed in joint angles are substantially more complex and scale exponentially with the degrees of freedom. Spatial vectors, on the other hand, yield considerably more concise and structured expressions for the EOM, but consistency among the spatial vector must be maintained.
The terms in the EOMs in a fixed spatial reference frame are vector cross products between spatial positions and velocities or accelerations of the limbs and have many of the properties of neurons in the motor cortex. The geometric nature of vector cross-product terms could explain why broad, cosinelike tuning curves are so ubiquitous in motor-related areas (Georgopoulos et al. 1982; Johnson et al. 1999; Kalaska et al. 1983), although a recent study reported directional tuning considerably narrower than cosine tuning and even bimodal directional tuning (Amirikian and Georgopoulos 2000). Moreover, the visual system provides input to the motor system in spatial coordinates, and vector cross products can be computed from the spatial representation in the parietal cortex in a feedforward neural network with a single layer of connections (Pouget and Sejnowski 1997).
A model for smooth reaching motions of a three-joint arm in a two-dimensional plane was simulated with a Cartesian spatial representation, and the terms in the model were compared with recordings from neurons in the motor cortex during similar movements. There was a close correspondence in the distribution of PDs, dependence on the workspace, and the rotation of the population vector. Finally, we show how vector cross products allow the muscle tensions for agonist and antagonist muscles in an arm to be computed based on a minimum squared tension criterion. In this scheme, instead of the explicit computation of joint angles, we introduce a set of redundant spatial vectors for the computation of reaching dynamics. Although this study focused mainly on point-to-point reaching movements in the horizontal plane, the computational scheme also applies to general movements in three dimensions.
MATERIALS AND METHODS
Equations of motion for a two-link system.
The EOMs can be derived in different coordinate systems. We first derive the equations in the traditional way, using joint angles as the coordinate system, and then compare the complexity of the equations with those derived with fixed spatial coordinates. To simplify the derivation, we consider degrees of freedom only in the horizontal plane without gravity. The derivation here for a two-link system (Fig. 1, A and B) can be straightforwardly extended to general n-link systems. Another derivation based on the Newton-Euler method, which is directly related to spatial coordinates without using joint angles, is given in appendix a.
With the Euler-Lagrange method, the Lagrangian for a two-link system is given by
| (1) |
where mi and Ii are the ith segment's mass and inertial moment around the z-axis, respectively. The first and second terms in the Lagrangian are, respectively, the translational and rotational kinetic energies of the system. The Cartesian coordinates of center-of-mass position of the ith segment, Xi and Yi, are explicitly determined by the joint angles as
| (2) |
| (3) |
where li is the ith segment's total length and ri is the distance from the (i − 1)th segment endpoint to the ith segment center of mass (Fig. 1A).
The EOMs can be derived with the Euler-Lagrange equation:
| (4) |
where τi (i = 1,2) are joint torques on the shoulder and elbow, respectively.
With the Lagrangian in Eq. 1, the EOMs for a two-link model in the horizontal plane in the joint-angle representation are
| (5) |
| (6) |
These EOMs, which are the joint-angle representation, contain Coriolis and centrifugal terms because the reference frame defined with respect to the links changes as the arm moves. The intrinsic joint-angle representation in Eqs. 5 and 6 provides no physical intuition about how limb segments move in the extrinsic coordinates. Furthermore, physical parameters such as mass (m) and moment of inertia (I) appear in a wide range of combinations. A more physically intuitive representation can be obtained by deriving the EOMs in spatial coordinates where the physical parameters are more transparent.
If the terms are reorganized with respect to masses and moments of inertia, we obtain
| (7) |
| (8) |
Each of these terms can be rewritten as mass or inertia moment times a vector cross product:
| (9) |
where X⃗ji(j > i; j = 1, 2; i = 1) and X⃗j0(j = 1, 2) are the center-of-mass positions of the jth link measured from the ith link endpoint and from the origin (defined at the shoulder position, 0), respectively (see Fig. 1B). The velocities (V⃗ji, V⃗j0) and accelerations (A⃗ji, A⃗j0) are the first and second temporal derivatives of the positions (X⃗ji, X⃗j0), respectively. The operator [X⃗]Z extracts a z-component from vector X⃗ and restricts motion to the X–Y plane. These spatial vectors specify the center-of-mass positions and can be computed by appropriately rescaling spatial vectors connecting the joints (shoulder, elbow, or wrist) and the endpoint. Substituting Eq. 9 into Eqs. 7 and 8 yields much simpler and more structured EOMs expressed in an extrinsic spatial representation:
| (10) |
| (11) |
Note that all the terms in Eqs. 10 and 11 consist of vector cross products of position vectors and their derivatives. The physics of the two-link model can be read from the equations: Each term proportional to a mass represents the translational movement of the center of mass of a limb segment, and each term proportional to a moment of inertia represents the rotational movement around the center of mass of a limb segment. For example, see Fig. 1C for a graphical explanation of the action of τ2 (Eq. 11).
Equations of motion for a general n-link system.
The EOMs in a Cartesian spatial representation for a general n-link system are
| (12) |
and are derived with the Newton-Euler method in appendix a. We list below some of their properties in comparison with the joint-angle representation.
1) The EOMs in a spatial representation are shorter and more concise than in an intrinsic representation: As n increases the number of terms required in the joint-angle representation grows exponentially, whereas the number of equations for the spatial representation only increases quadratically (Fig. 1D).
2) Torques that operate on a joint influence the translational and rotational movements of segments that are more distal. For example, the equation containing τ2 has two terms representing the changes to the translational and rotational motions of segment 2 (Fig. 1C), and this generalizes for τ1. This intuitive physical interpretation is apparent in the spatial representation.
3) When some dynamical inertial parameters such as mass or inertia are modified, the coefficients in multiple terms in the joint representation must be fine-tuned simultaneously. If, for example, the mass of the second link m2 is modified, 11 terms in Eqs. 5 and 6 must accordingly be adjusted. In contrast, EOMs in the spatial representation (Eqs. 10 and 11) contain only two terms that need adjustment.
4) In a spatial representation the EOMs can be easily generalized to three dimensions (appendix a):
| (13) |
where Ij is a 3 × 3 inertia matrix of the jth segment. The terms quadratic in V⃗ take nonzero values when the angular velocity and the angular momentum are not parallel to each other, and disappear when the movement is restricted to the horizontal plane, reducing to Eq. 12.
5) One disadvantage in using a spatial representation is that it explicitly requires the n(n + 1)/2 center-of-mass positions measured from the origin (shoulder) or from the edge of more proximal segments. In contrast, the joint-angle representation requires only n independent angular variables and all values of the joint angles within the limits set by mechanical constraints yield a valid hand position. The more concise description of state in the joint-angle representation makes it attractive for robotics and models of motor control.
6) The redundant set of spatial vectors in our model must be constrained to provide a valid configuration of limb. In contrast, in the joint representation, joint angles can provide a concise description of limb without any constraints.
In summary, although mathematically these two representations are equivalent, they differ in what aspects of computation are emphasized. The joint-angle representation gives a concise, nonredundant basis for describing body movements, but the EOMs become complicated and unstructured. In contrast, the spatial representation has a much shorter and structured description for EOMs, with the computational price of maintaining consistency between all the spatial vectors.
Contribution of muscle viscosity to the EOMs.
The activities of motoneurons mainly reflect temporal changes of muscle lengths, which can be approximated by joint-angle velocities, θ̇i. Therefore, in order for motor cortex to control the arm motion, viscosity terms (Biθ̇i) must be included on the right-hand sides of the EOMs. Note that these viscous terms do not represent a mechanical property of limbs but rather the change of muscle lengths.
The explicit use of the joint-angle velocities might seem to imply the indispensability of an explicit representation of joint angles given that they depend on the inverse Jacobian matrix J of the coordinate transformation:
| (14) |
Fortunately, the joint-angle velocity has a much simpler spatial representation composed of vector cross products of position (X⃗) and velocity (V⃗):
| (15) |
and
| (16) |
The resulting viscous terms
| (17) |
and
| (18) |
are included in the EOMs. These cross-product representations are an efficient method for computing the joint angular velocities bypassing the Jacobian matrix and its inverse.
For an n-link system, the ith torque equation in a fixed spatial reference frame is
| (19) |
| (20) |
where X⃗j,i and X⃗j,0 are location vectors in the Cartesian coordinates of the jth segment measured with respect to the ith segment endpoint and to the shoulder and V⃗ and A⃗ are their velocity and acceleration, respectively. Equations 19 and 20 directly relate the kinematic variables (spatial positions and derivatives on the right-hand side) to dynamic variables (joint torques on the left-hand side), thereby directly transforming the visual trajectories of limb segments into the joint torques without computing joint angles. The first acceleration-dependent term on the right-hand side represents the mechanical properties of the limb, and the second velocity-dependent term represents the viscous properties of the muscle.
Vector cross products as neuronal firing rates.
All of the terms in these EOMs are vector cross products in a fixed spatial reference frame, which greatly simplifies the computation of joint torques. This suggests that, instead of explicitly computing the joint angles, the joint torques can be computed directly from vector cross products. We thus postulate that the terms in the vector cross products would be identified with the firing rates of neurons in motor cortex:
| (21) |
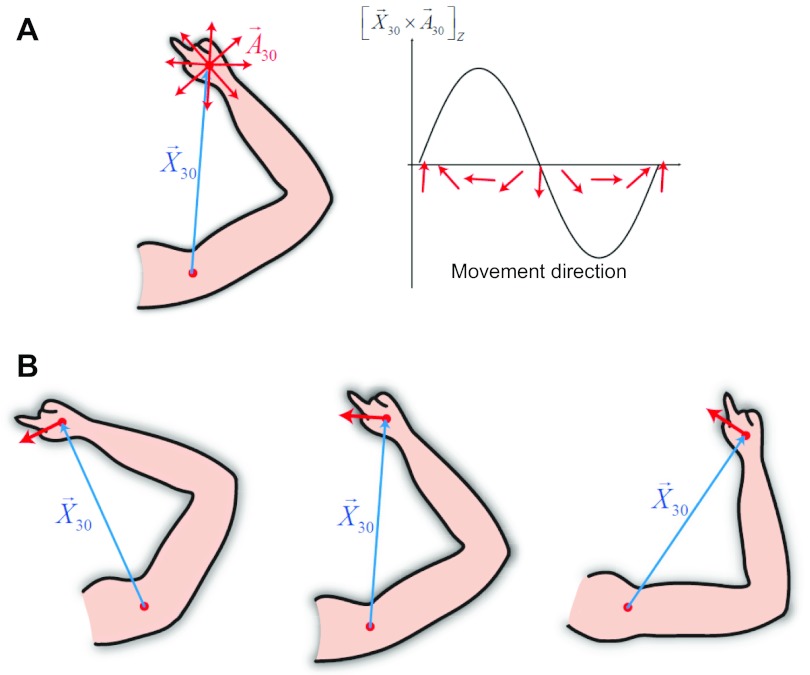
Thus each term is the multiplicative response of the spatial position of a limb and a velocity or acceleration, variables that are represented by neurons in motor cortex that have been characterized as either “acceleration cells” (RA) or “velocity cells” (RV). Because firing rates of cortical neurons are constrained to a narrow range, the terms in Eq. 21 should not be identified with single neurons but rather with neural populations having similar preferences. The magnitudes of the cross products could be implemented similarly as the number of motor cortex neurons encoding the same cross product. The vector cross products yield cosine tuning curves (Fig. 2A) and explain a workspace-dependent change of PD of a cell (Fig. 2B). The geometry of limb configurations determines the distribution of PDs of model neurons. The assumption that each cross-product term corresponds to activity in a single neuronal population is consistent with a recent study showing that single movement parameters dominated individual neuronal activities (Stark et al. 2007).
Fig. 2.
Cosine tuning with respect to movement direction and its workspace dependence. A: cosine tuning due to the geometric property of vector cross product (left) and the resulting tuning curve (right). B: rotation of preferred direction as the hand moves from the left to the right workspace.
Network computation of vector cross products.
We show here that a simple neural network model can compute vector inner and cross products. Let a group of neurons have activities that are multiplicatively modulated by a limb position vector, X⃗, and a limb velocity vector, V⃗. Without loss of generality, assume that these vectors lie in the horizontal plane. Then the firing rate should be given by
| (22) |
where θ and φ are hand position and velocity direction, respectively, and θi and φj are the preferred hand position direction and hand velocity direction of this neuron. A single-layer neural network with a sum of multiplicatively formed basis functions of the input variables allows general, nonlinear sensorimotor transformations to be computed (Pouget and Sejnowski 1997). Such multiplicative responses can be realized in a recurrently connected network (Salinas and Abbott 1996).
Assume cosine tuning for hand position and velocity direction and a linear dependence on vector magnitude:
| (23) |
where (‖X⃗‖,θ) and (‖V⃗‖,φ) are polar coordinate representations of the hand position and velocity vectors. Sinusoidal activity modulation for static limb positions has been reported in the motor cortex and area 5 of the parietal cortex (Georgopoulos et al. 1984; Wang et al. 2007), as well as for velocity in the motor cortex (Moran and Schwartz 1999; Wang et al. 2007).
A weighted sum over these multiplicative response activities is given by
| (24) |
where the sum is approximated by an integral over preferred hand directions and velocity directions, θi and φj are replaced with continuous variables θ′ and φ′, and the weight coefficients wij become a continuous weight function w(θ′, φ′). If the weight function is a cosine function, w(θ′, φ′) = cos(θ′ − φ′), or a delta function for velocity, w(θ′, φ′) = δ(θ′ − φ′), then Eq. 24 becomes
| (25) |
which is the inner product between X⃗ and V⃗. If instead the weight function is a sine function, w(θ′,φ′) = sin(θ′ − φ′), then
| (26) |
is the z component of the cross product. Other components of the cross product can be computed similarly. Therefore, with the known properties of cortical motoneurons, a neural network can perform the vector inner and cross products required for motor control.
Thus the computation of torques is reduced to a weighed sum of multiplicative responses. Furthermore, the linear coefficients can be easily learned with Widrow-Hoff regression (Schwartz et al. 2006).
Modeling neural activity for reaching movements with a three-link model.
Reaching movements will be simulated for a three-link model corresponding to the shoulder, elbow, and wrist joints (Fig. 1B). The corresponding EOMs for the torques are
| (27) |
| (28) |
| (29) |
For comparison of complexity, an explicit expression of the same EOMs Eqs. 27, 28, and 29 expressed in the joint-angle representation is provided in appendix b. In these equations, there are 12 independent vector cross-product terms corresponding to a model with 12 populations of neurons in the motor cortex:
| (30) |
To model reaching, we first computed a point-to-point trajectory of the center of mass of the third segment according to the minimum jerk criterion (Flash and Hogan 1985):
| (31) |
where an initial position X⃗initial and a final position X⃗final were assumed to lie in the horizontal plane. Although we used minimum jerk to generate arm trajectories, the following results are valid even when the trajectory is computed from sensory feedback signals. For the simulations of directional tuning, PDs, and muscle tensions (Figs. 3, 4, 7 and 8), the movement duration tf was fixed at 200 ms and the amplitude was 3 cm. For the simulations of population vectors (Figs. 5 and 6), the movement duration was fixed at 500 ms and the amplitude was 5 cm. For a cloverleaf drawing simulation (Fig. 8E), the movement duration was 1,000 ms, an initial and final position was fixed at (x, y)=(0 cm, 15 cm), and four via-points (and velocity there) were taken for four leaves, respectively: (10 cm, 25 cm) and (−40 cm/s, +40 cm/s) for top right, (−10 cm, 25 cm) and (−40 cm/s, −40 cm/s) for top left, (−10 cm, 5 cm) and (+40 cm/s, −40 cm/s) for bottom left, and (10 cm, 5 cm) and (+40 cm/s, +40 cm/s) for bottom right. The wrist angle (θ3) was assumed to be fixed to zero, as in most experiments, so that the shoulder and elbow angles (θ1 and θ2) were uniquely determined. The segment-position vectors X⃗10, X⃗20, X⃗21, X⃗31, and X⃗32 were computed from X⃗30. Therefore, the six vectors always give a valid posture. We assumed that the consistency between the spatial vectors is maintained and concentrated on the problem of finding the joint torques or muscle tensions needed to obtain a desired endpoint trajectory, which is a difficult inverse dynamics problem.
Fig. 3.
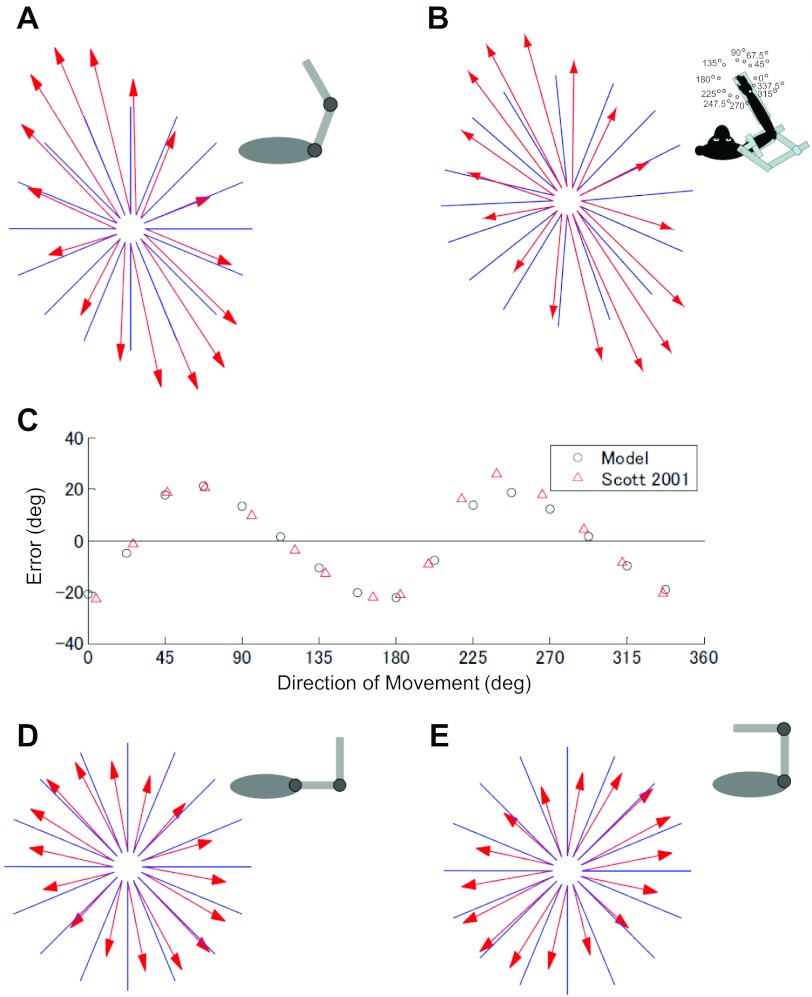
Cosine tuning and distribution of preferred directions. A: tuning curves for 12 model neurons and preferred directions (PDs) indicated by arrows for 6 of them. Inset shows the starting posture and 16 movement directions. B: distribution of PDs predicted by the model in a polar plot with radius scaled by activity amplitude (max activity − min activity) with separate vectors for the positive and negative peaks. Muscles can pull but cannot push, so separate neurons whose PDs were oppositely directed to PDs of model neurons in Eq. 21 were also included. C: distribution of PDs reported for motor cortex neurons (from Naselaris et al. 2006; Scott 2005; Scott et al. 2001). D: directions of the 6 PDs shown in A rotated clockwise over the 3 corresponding workspaces in C.
Fig. 4.
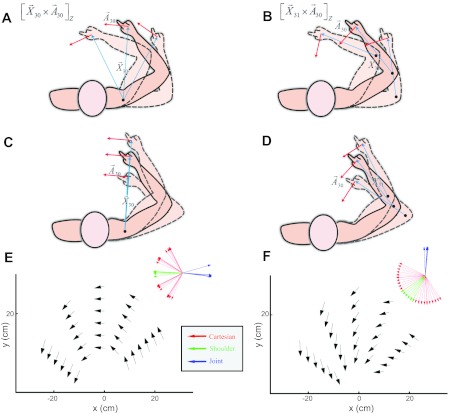
Multiple coordinate systems in model neurons. The PD of model neurons [X⃗30 × A⃗30]Z (A) and [X⃗31 × A⃗30]Z (B) changes when the shoulder is rotated with a fixed elbow. The PD of model neurons [X⃗30 × A⃗30]Z (C) and [X⃗31 × A⃗30]Z (D) changes when the elbow angle is rotated with a fixed shoulder-to-hand direction. The PD changes over the workspace locations according to shoulder-centered ([X⃗30×A⃗30]Z) (E) and joint-based ([X⃗31 × A⃗30]Z) (F) reference frames. Arrows indicate PDs of the neurons at various locations in the workspace. Insets show PDs represented in the Cartesian (red), joint-based (blue), and shoulder-based (green) frames.
Fig. 7.
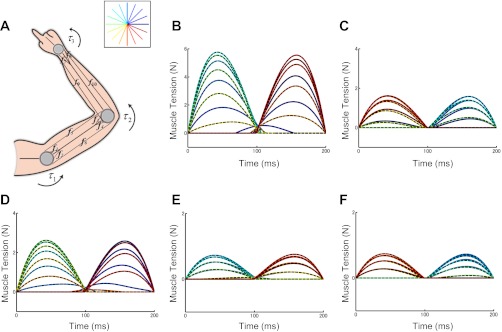
Muscle tensions derived from spatial representation. A: a 3-link model with 10 muscles [shoulder extensor (f1) and flexor (f2), elbow flexor (f3) and extensor (f4), biarticular flexor (f5) and extensor (f6) for shoulder and elbow, wrist flexor (f7) and extensor (f8), biarticular flexor (f9) and extensor (f10) for elbow and wrist]. Sixteen movement directions of the hand are color coded in inset. B–F: muscle tensions obtained with a quadratic cost function [fi(i = 1, …, 10), solid color lines] and corresponding approximations [f̂i(i = 1, …, 10), black dashed lines] for shoulder flexor (f1, B), elbow flexor (f3, C), shoulder-elbow biarticular flexor (f5, D), wrist flexor (f7, E), and elbow-wrist biarticular flexor (f9, F). Best fits for flexor muscles are shown here; similarly good fits were obtained for extensor muscles. The starting posture is shown in A, and the same colors for movement directions are used in B–F.
Fig. 8.
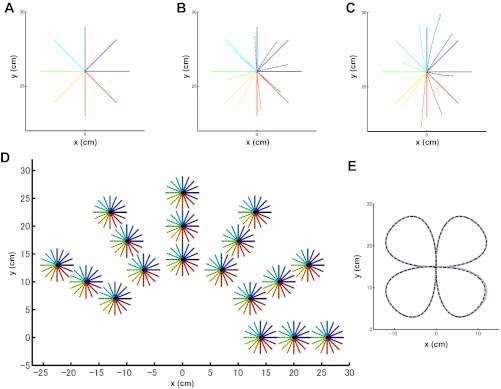
Hand trajectories computed from approximate muscle tensions. A–C: computed trajectories using the rectified sum approximation from vector cross products (A), extrinsic cells (B), and intrinsic cells (C). Solid color lines indicate desired movement paths (based on the minimum-jerk criterion) of 8 directions starting from (x, y) = (0 cm, 26 cm) in the workspace compared with dashed color lines for the trajectories computed from approximate muscle tensions (f̂i). In A, the solid and dashed lines overlap almost completely. D: desired and approximated trajectories using the cross-product approximation. E: cloverleaf drawing. Gray solid lines and black dashed lines are desired minimum-jerk trajectories and approximate trajectories computed from approximate muscle tensions, respectively.
Fig. 5.
Spatial properties of population vectors constructed from the model neurons. Deviations are shown between the hand movement directions (blue lines) and population vectors (red arrows) predicted by the model (A) and found in motor cortex neurons (B) (Scott et al. 2001). In A, the shoulder and elbow angles at the starting posture are 70° and 50°, respectively. C: difference between the direction of population vector and the direction of hand movement predicted by the model (black circles) and reported in the experiment (red triangles). D and E: the model further predicts that the deviations are posture dependent in different workspaces (D: shoulder 0°, elbow 90°; E: shoulder 90°, elbow 90°). Insets represent the postures on initiating movements used for the simulations and the experiment. In these simulations population vectors over 500 ms (time step 5 ms) were calculated for minimum-jerk trajectories (average population vectors in the initial 50 ms are shown).
Fig. 6.
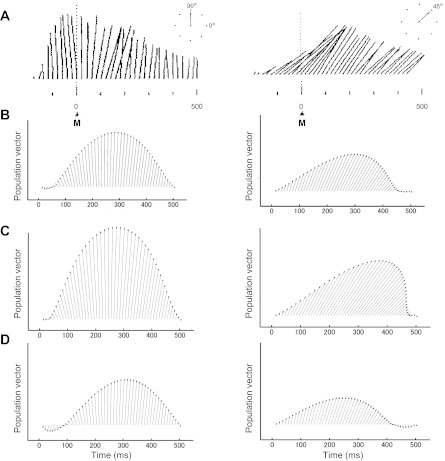
Temporal properties of population vectors constructed from the model neurons. A and B: temporal changes of population vectors computed from motor cortex neuron activities (A) (Georgopoulos 1988) and the model's population vectors for 90° and 45° directions (B). The horizontal axes are aligned to movement onset (indicated by “M” in A). Minimum-jerk trajectories were used to compute the model neural activities, and corresponding population vectors were computed every 5 ms over 500 ms. C and D: the model's population vectors when the viscous coefficients were doubled (C) or halved (D).
The 15 biomechanical parameters in the EOMs (mi, Ii, li, and ri) were based on data from monkeys (Macaca mulatta) (Cheng and Scott 2000), summarized in Table 1. Viscous coefficients (Bi) were included not because of mechanical properties of the limbs but because muscle shortening dominates activities of the motoneurons, and their values were adjusted so that the activity levels of the velocity cells were about the same as those of the acceleration cells. The choice for the values of viscous coefficients was critical in simulations reconstructing temporal changes of population vectors, which implies that the effects of muscle shortening in motoneuron activities dominate the inertial properties of limbs. We have also simulated the two-link model (appendix c) and confirmed that essentially the same results were obtained.
Table 1.
Model parameters for three-link model
| Mass (mi), kg | Inertial Moment (Ii), kg·m2 | Viscous Coefficient (Bi), kg·s | Total Length (li), m | COM Length (ri), m | |
|---|---|---|---|---|---|
| Segment 1 | 0.25 | 4 × 10−4 | 0.080 | 0.15 | 0.075 |
| Segment 2 | 0.18 | 4 × 10−4 | 0.080 | 0.15 | 0.060 |
| Segment 3 | 0.030 | 4 × 10−5 | 0.050 | 0.05 | 0.020 |
COM, center of mass.
Computing muscle tensions directly from vector cross-product terms.
Limb movements are produced by activating muscles, which can pull but not push. Therefore, the motor cortex needs eventually to compute not joint torques but muscle tensions. We next asked whether the computation of muscle tensions simplifies in a spatial representation. To model muscle tensions, six monoarticular (model muscles 1, 2, 3, 4, 7, and 8) and four biarticular (model muscles 5, 6, 9, and 10) muscles were introduced (see Fig. 7A). The joint torques are composed of inertial terms (proportional to the mass and the inertial momentum) and the viscous terms (proportional to the viscous coefficients):
| (32) |
The computation of muscle tensions may, accordingly, be decomposed into inertial and viscous terms:
| (33) |
Viscous terms of muscle tensions are rectified temporal changes of muscle lengths (Winter 2009; Zajac 1989), i.e., muscles are resistant to lengthening their lengths but not to shortening,
| (34) |
where denotes rectification, in which negative values are set to zero. The muscle tensions have length-dependent, elastic terms, but for simplicity we do not include them. These viscous terms can be readily expressed by vector cross products between limb position and velocity (or velocity cells), namely,
| (35) |
However, the computation of inertial terms is nontrivial. Joint torques can be computed as weighted sums of muscle tensions of monoarticular and biarticular muscles (fi):
| (36) |
where the ais are coefficients derived from the moment arms of corresponding muscle insertions and the tensions fis are nonnegative (fi ≥ 0) because the muscles can pull but not push. For the following simulations of muscle tensions (see Figs. 7 and 8), the values of the moment arms were assumed to be constant, as summarized in Table 2. Computing the muscle tensions required to produce given joint torques is an ill-posed problem because the muscle tensions have more degrees of freedom than the joint torques, and a solution is usually found by imposing an optimization criterion such as minimization of a squared sum of muscle tensions.
Table 2.
Moment arms
| a1, m | a2, m | a3, m | a4, m | a5, m | a6, m | a7, m |
|---|---|---|---|---|---|---|
| 0.02 | 0.0125 | 0.014 | 0.0175 | 0.01 | 0.012 | 0.012 |
Here, an alternative, computationally efficient method for obtaining muscle tensions with vector cross products is proposed. We assume that muscle tensions can be represented by rectified sums of vector cross products:
| (37) |
where RAs are acceleration neurons
| (38) |
and cijs are coefficients to be adjusted shortly. Eight acceleration neurons instead of nine acceleration neurons in Eq. 30 were used because the coefficients multiplying the cross products were irrelevant and thus [m1X⃗10 × A⃗10]Z and were equivalent.
Equation 37 can be considered a feedforward neural network with one layer of weights. A similar neural network that transforms directionally tuned neurons into endpoint force was proposed previously (Georgopoulos 1996). We further assumed that agonist and antagonist muscles receive reciprocal innervations from the motor cortex:
| (39) |
There were 5 pairs of agonist and antagonist model muscles, and accordingly 40 coefficients to be optimized. Temporal profiles of joint torques were computed with Eqs. 27–29 for a given point-to-point trajectory based on minimum jerk (Eq. 31). Temporal profiles of muscle tensions (fi) were obtained for 16 movement directions starting from 18 starting postures by optimizing a quadratic cost function () subject to the nonnegative constraint (fi ≥ 0) and Eq. 36. The choice of the minimum squared muscle tension is a computational convenience, and many other optimization criteria produce qualitatively similar results for approximating the dynamics of the lower limb (Prilutsky and Zatsiorsky 2002). The 40 coefficients were then chosen to minimize the cost function, defined as the temporal integral of the squared difference between muscle tensions (fi) and corresponding approximations (f̂i) averaged over all muscles, initial postures, and movements:
| (40) |
The goal is to find the coefficients (cij) in f̂is to approximate the fis. The initial hand positions in the polar coordinates were 14, 20, or 26 cm for the distance between hand and shoulder and 0°, 30°, 60°, 90°, 120°, or 150° for the angle of hand position relative to the horizontal axis, giving 18 distinct starting postures. The approximate muscle tensions were then substituted into the EOMs to see how well this linear-sum approximation worked. Also, using the same optimized values of coefficients, we tested a cloverleaf trajectory with a larger amplitude and high curvature (Viviani and Flash 1996).
Modeling neural activity for reaching movements in extrinsic and intrinsic coordinates.
For a comparison with conventional views of the motor cortex, we considered kinematic and dynamic neural representations. According to the kinematics viewpoint, the activities in motor cortex M1 reflect the endpoint kinematics in the external coordinates. These velocity- and acceleration-tuned cells are modeled as
| (41) |
where (‖V⃗‖,φv) and (‖A⃗‖,φa) are polar coordinate representations of the hand velocity and acceleration vectors. We used 10 acceleration- and 10 velocity-tuned model neurons whose PDs were uniformly distributed, ranging from 0° to 360°, thereby a total of 20 model neurons.
Alternatively, in an intrinsic, joint-angle reference frame the motor cortical activity may represent movements and is modeled as angular velocity and angular acceleration tuning as
| (42) |
where and and and are polar coordinate representations of the angular velocity and angular acceleration vectors.
Georgopoulos (1996) generated endpoint forces by using a linear sum of these model neurons. Similarly, using either the extrinsic or the intrinsic reference frame, we approximated muscle tensions as rectified sums of motor cortical activities as
| (43) |
There were 20 coefficients for an agonist-antagonist muscle pair, yielding 100 coefficients for the 5 muscle pairs. These coefficients were optimized globally by minimizing the cost function in Eq. 40.
RESULTS
Broad, cosinelike tuning and preferred directions of model neurons.
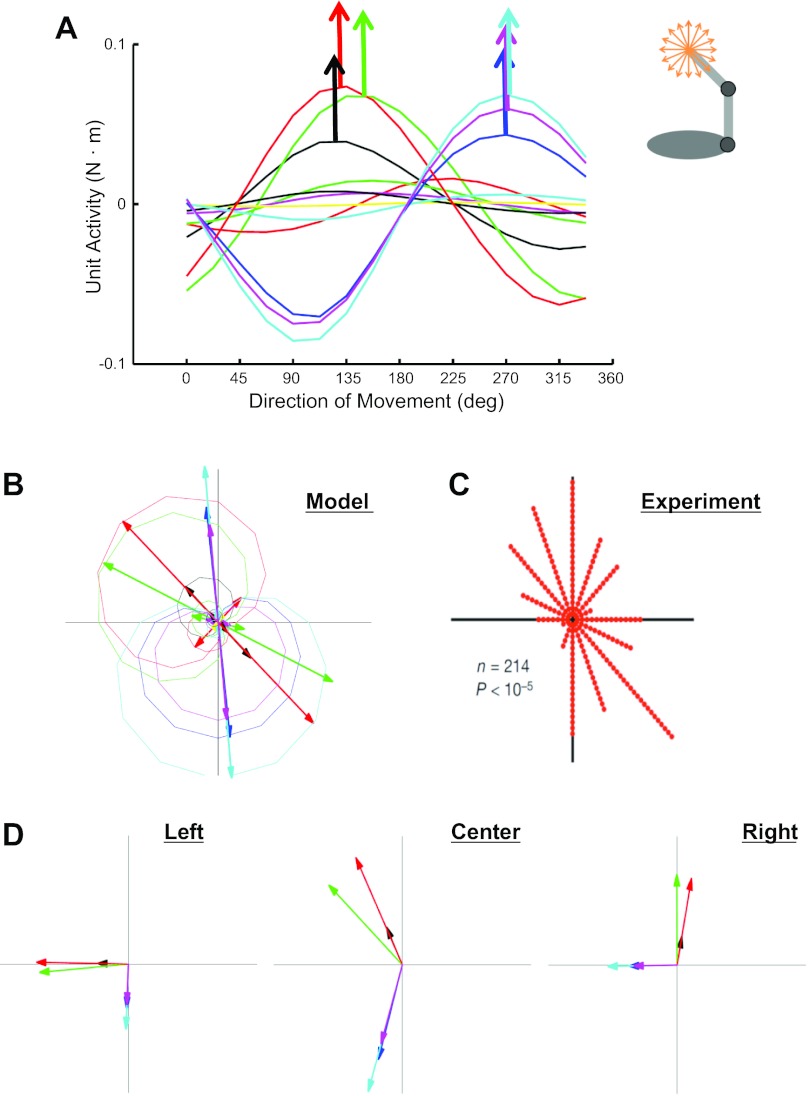
Using the trajectory in Eq. 31, we derived the time courses of neuronal activities for straight trajectories in 16 uniformly distributed directions (d⃗k, k = 1, …, 16) and then averaged the activity of the i-th neuron (R̄ik) in Eq. 30 over the initial 100 ms for each trajectory. The tuning curve (Fig. 3A) was obtained by plotting R̄ik as a function of movement directions. The firing rates of the model neurons as a function of movement direction were sinusoidally modulated with respect to each limb's center-of-mass position due to vector cross product (Fig. 2A), consistent with recordings from neurons in motor cortex (Georgopoulos et al. 1982).
The highest firing rate of a neuron occurs in its preferred direction (PD) (arrows in Fig. 3A), obtained by taking a normalized weighted sum,
| (44) |
The PDs in the model were nonuniformly distributed (Fig. 3B), in agreement with the experimental distribution in motor cortex (Fig. 3C), which was concentrated in the second and fourth quadrants (Naselaris et al. 2006; Scott et al. 2001; Scott 2005). The skewness of the distribution is a consequence of constraints on possible geometric configurations of the limb.
The model also predicted that the PDs should rotate when the workspace is displaced because the cross products depend on the starting location of the hand (Fig. 2B). In experimental recordings, the PDs of most motor cortex neurons consistently rotated clockwise along the vertical axis when the workspace shifted from the left side, to the middle, and to the right side of the body (Caminiti et al. 1990). The model neurons exhibited PDs that rotated similarly (Fig. 3D). We further predicted that when the workspace is vertically displaced the PDs should rotate along the horizontal axis. These posture-dependent changes of the PDs cannot be explained by the extrinsic coding hypothesis, which posits that the cells represent endpoint velocity, acceleration, or the sum of velocity and acceleration.
The dependence of the PD of a neuron on position in the workspace reveals its reference frame (Ajemian et al. 2000, 2001; Wu and Hatsopoulos 2006). Figure 4 depicts the PDs of two representative neurons at various locations in the workspace. A neuron whose activity varies with [m3X⃗30 × A⃗30]Z, for example, contains activity modulated by hand position (X⃗30) and acceleration (A⃗30) relative to the shoulder. The PD of this neuron becomes rotated by the amount of shoulder rotation (Fig. 4A) and remains invariant if the elbow angle is altered with the shoulder-to-hand direction kept constant (Fig. 4C), thereby exhibiting a shoulder-centered preference. PDs in the shoulder-centered frame stay invariant over the workspace position, whereas PDs in the joint-angle or Cartesian frames vary considerably (Fig. 4E).
Another model neuron representing [m3X⃗31 × A⃗30]Z has hand position dependence relative to the elbow (X⃗31) and hand acceleration dependence relative to the shoulder (A⃗30). The PD of this neuron gets rotated by the amount of both shoulder rotation (Fig. 4B) and elbow rotation (Fig. 4D), thereby exhibiting a joint-based reference frame. PDs in the joint-angle frame change over the workspace less than those in other frames (Fig. 4F). Other neurons have intermediate reference frames between the shoulder-centered and joint-based frames. The neurons in the model exhibited the same range of preferred reference frames as those reported experimentally in motor cortex (Kakei et al. 1999; Wu and Hatsopoulos 2006).
Spatiotemporal properties of population vectors.
The population vector of movement direction has been used to estimate the direction of hand motion from a weighted average of PDs from cortical neurons (Georgopoulos et al. 1988):
| (45) |
The population vector for the model neurons had systematic deviations, following an oblique ellipse (Fig. 5A) that closely matched experimental results for the same workspace position (Fig. 5B) (Scott et al. 2001). The directional errors predicted by the model were almost the same with those reported in the experiment (Fig. 5C). These deviations stem from the nonuniform distribution of PDs that depends on posture (Fig. 3, B and C), consistent with a previous analysis (Sanger 1996). The model predicts a workspace dependence of the deviations with much less skew in the right workspace (Fig. 5D) and skewed toward the opposite direction in the left workspace (Fig. 5E). Differences in the bias of population vectors (Georgopoulos 2002; Scott 2005) may therefore arise from postural differences.
The directions of population vectors change during reaching (Fig. 6A) (Georgopoulos 1988), and qualitatively similar shifts have been observed in the model (Fig. 6B). For the population vectors to track the limb velocity, the values of viscous coefficients in the model needed to be chosen so that the activity levels of acceleration cells and velocity cells were comparable, consistent with a dominant contribution of muscle length change to motor cortex activity. There was uncertainty in the choice of viscous coefficients (B1, B2, and B3 in Table 1) used for the simulations. To evaluate how sensitive our results were, we repeated the same simulations with the values that were halved or doubled from the standard values. Most results were not highly sensitive to the parameter values, except for the temporal profiles of population vectors. When the value of the viscosity was doubled, the population vectors more accurately reflected the endpoint velocity (Fig. 6C). When the viscosity was halved, reversals in the directions of population vectors reversed at the beginning or end of movement (Fig. 6D). These simulations suggest that, for the population vector algorithm to be able to accurately reconstruct a movement trajectory, motor cortex needs to have neurons whose firing rates reflect the temporal changes in muscle lengths.
Computing muscle tensions from spatial representations.
The motoneurons in the final common pathway of the motor system create the muscle tensions that together produce the joint torques needed for reaching. The vector cross products represented in the motor cortex should therefore form a basis for computing muscle tensions. We explored this transformation in a three-link model with 10 muscles (shoulder flexor and extensor, elbow flexor and extensor, wrist flexor and extensor, and biarticular flexors and extensors) (Fig. 7A). Because the number of muscles exceeds the number of joint torques, inverting Eq. 36 is underdetermined and an additional constraint must be imposed such as energy minimization (Fagg et al. 2002; Prilutsky and Zatsiorsky 2002) or reciprocal activation of agonist and antagonist muscles (Thoroughman and Shadmehr 1999). None of these constraints is biologically plausible because they require iteration between the estimates of the torques and muscle tensions to ensure they are satisfied. We show here that the vector cross products form a computationally efficient basis for approximating muscle tensions.
The resulting approximation in Eq. 39 was excellent for all 10 muscles, not only for the monoarticular muscles (Fig. 7, B, C, and E) but also for the biarticular muscles (Fig. 7, D and F). The resulting movement trajectories computed from these approximate muscle tensions almost perfectly matched the corresponding minimum-jerk trajectories over the workspace [exemplar trajectories for 8 directions starting from (0 cm, 26 cm) are shown in Fig. 8A]; the direction and the amplitude errors measured at the endpoint averaged over the entire workspace were −0.8 × 10−5° (SD 0.053°) and 8.8 × 10−4 cm (SD 1.6 × 10−3 cm), as shown in Fig. 8D.
In contrast, if extrinsic (Eq. 41) or intrinsic (Eq. 42) movement neurons were used instead of the cross products, the optimized linear approximation was a poor approximation: the direction and the amplitude errors were −2.87° (SD 51.9°) and 0.72 cm (SD 0.17 cm) for extrinsic movement neurons (exemplar trajectories in Fig. 8B) and 0.42° (SD 15.6°) and 0.12 cm (SD 0.66 cm) for intrinsic movement neurons (exemplar trajectories in Fig. 8C). Therefore, a simple feedforward network that transforms directional motor commands to muscle activation (Georgopoulos 1996) does not work if the coefficients are optimized globally.
Using the same globally optimized values of the coefficients, the linear approximation of muscle tensions using vector cross products smoothly traced a cloverleaf pattern that involved movement with large amplitudes and high curvatures (Viviani and Flash 1995) (Fig. 8E). Note that the coefficients in Eq. 39 were optimized globally over the workspace but nonetheless produced good local approximations. Thus, with our simplified muscle model and the optimality criterion of minimizing squared muscle tensions, muscle tensions can be computed rapidly and without iteration by a rectified linear sum of neural activities from motor cortex neurons that represent vector cross products.
DISCUSSION
The disparate properties of neural activities in motor cortex can be explained parsimoniously by the spatial representation hypothesis. Joint torques can be computed without explicitly computing the joint angles, and muscle tensions simplify compared with traditional approaches that require iterative optimization. Because the muscle tensions required to make a reaching movement can be accurately approximated by a linearly weighted sum of motoneuron activities, the muscle tensions could be computed directly from the cross products represented by neurons in the motor cortex with our simplified muscle model. This could explain how the neurons in primate motor cortex that project directly to lower motoneurons in the spinal cord can effectively control muscle tension activities. Most electrophysiological studies have correlated the firing rates in the motor cortex with endpoint kinematics. However, in the proposed framework, the spatial vectors of all limb segments are required for the computation of cross products. Therefore, to test our model, a simultaneous recording of trajectories of all limb segments and neuronal activities is necessary.
The essential feature of the spatial coordinate frame is that it is fixed with respect to the world to avoid the centrifugal and Coriolis terms that proliferate in a moving coordinate system, such as joint-based coordinates. Motor structures based on spatial coordinates evolved early, such as the optic tectum, a sensorimotor structure in lower vertebrates used for orienting the body in space. Since sensory information is represented in spatial coordinates, and the body is oriented in space, interacting with the world simplifies in a common spatial reference frame. In mammals the superior colliculus controls eye movements in a spatial reference frame, and the motor cortex may have evolved to elaborate on this strategy.
Related models.
A previously proposed optimal control approach to motor control using a biomechanical skeletomuscular model that minimized the sum of squared control signals for a reaching task and an isometric task reproduced experimental findings such as broad directional tuning, nonuniform distribution of PDs, skewed movement directions in population vectors, and some temporal changes of firing rates (Guigon et al. 2007; Trainin et al. 2007). These biomechanically detailed models, however, did not consider how spatial information in Cartesian coordinates could be transformed into the joint-angle space. For an isometric force task, they attributed shifts of PDs and changes of neuronal gains for endpoint force to the Jacobian transformation from the force to the joint-torque space (Ajemian et al. 2008). The crucial feature of these models is the geometric configuration of segmented limb, which determines the stiffness ellipse of the limb and the Jacobian matrix. Although the equations and interpretations of the results are quite different, these models share with our model the importance of the biomechanical properties of the upper limb in understanding the neuronal activities in the motor cortex.
Equally important for the motor cortex is how dynamics is stabilized by controlling the impedance of the limbs, which has been emphasized in equilibrium-point control models and their extensions (Feldman 1966; Feldman and Levin 1995). The motor system could have two separate yet interacting mechanisms for computing dynamics and stiffness, respectively. Indeed, recent studies of human neuroimaging suggest that reciprocal activation (net joint torque) and coactivation (stiffness) of wrist muscles can be reconstructed from blood oxygen level-dependent signals (Ganesh et al. 2008) and that the activity in the dorsal premotor cortex was correlated with reciprocal activation of muscles whereas the activity in the ventral premotor cortex was correlated with the level of cocontraction (Haruno et al. 2012). Our proposed model of dynamics and the equilibrium-point approaches are therefore not mutually exclusive but rather are complementary.
Reconciling kinematic and dynamic perspectives.
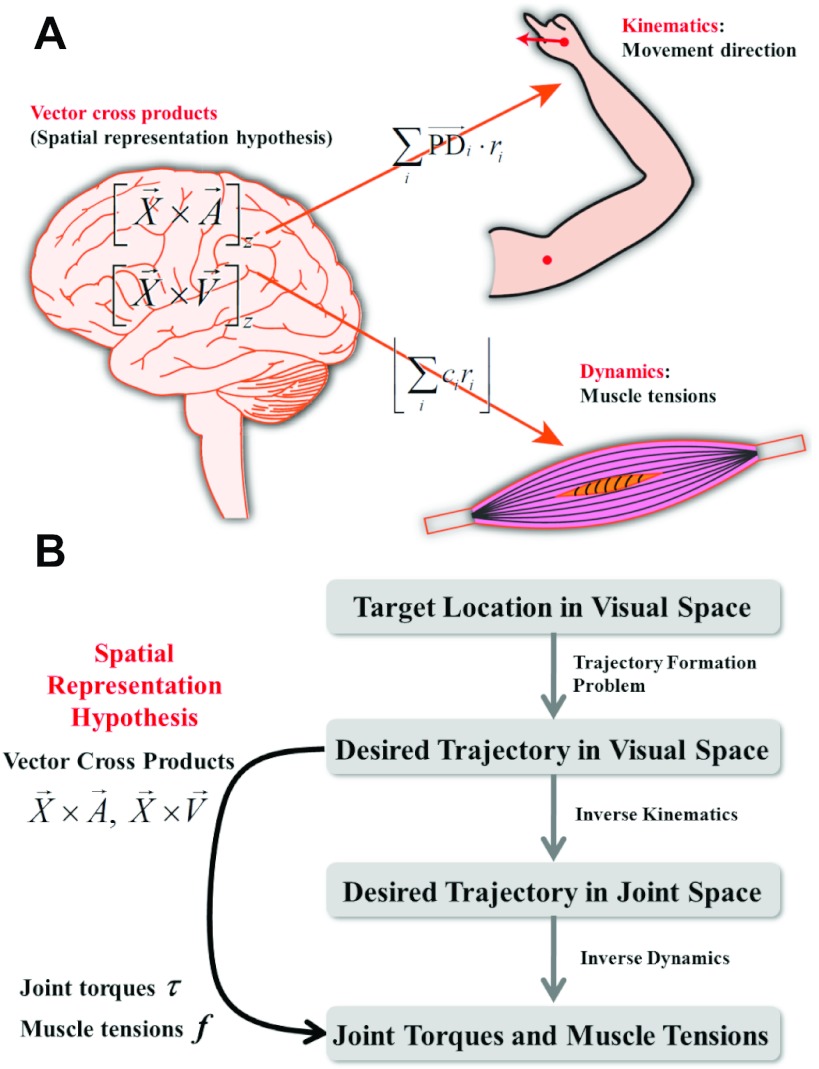
The spatial representation model analyzed here reconciles an apparent disagreement about the contribution of neurons in the motor cortex to arm movements. From a dynamics perspective, neurons have been found in motor cortex that compute joint torques and muscle tensions (Evarts 1968; Fetz and Cheney 1980), but other neurons in the motor cortex carry kinematic spatial information that encodes hand movement direction and velocity (Georgopoulos et al. 1982, 1986). Even in the kinematic perspective, whether the motor cortex represents an intrinsic joint-angle coordinate or an extrinsic Cartesian coordinate is an open issue (Kalaska 2009). We have shown in a spatial representation that movement trajectories and muscle tensions can be reconstructed at the same time from model neuronal activities identified with vector cross products (Fig. 9A). This is consistent with evidence for both kinematic and dynamic signals in the motor cortex.
Fig. 9.
Proposed representation and computation in motor cortex. A: achematic of how both kinematic (hand trajectory) and dynamic (muscle tension) variables can be reconstructed from the cross-product representation. B: steps in planning and executing body movements. The computation of joint angles is required to compute the control signals in the conventional scheme but is unnecessary in the new scheme because the control signals can be computed directly from the spatial representation of the trajectory.
We have shown that muscle tensions can be reconstructed from a rectified sum of weighted cross-product responses for our simplified muscle model, but this is not possible from model neurons tuned either to extrinsic (endpoint movement) or intrinsic (joint angles) movements with constant coefficients over the global workspace. In particular, a linearly weighted sum of model neuron activities directionally tuned to endpoint movements cannot generate the muscle tensions needed to perform accurate reaching, as previously proposed (Georgopoulos 1996). This does not rule out the use of extrinsic or intrinsic neurons for computing muscle tensions, since the spinal cord could well perform a more complex transformation of these activities. However, we can conclude that vector cross products could be a more computationally efficient basis than either extrinsically or intrinsically tuned neurons.
A previous model reproduced some properties of motor cortex activities by assuming that motor cortex encodes the dynamics of linear movement and suggested that direction tuning in the motor cortex might be an epiphenomenon (Todorov 2000). However, the linear dynamics approximation used in that study was limited to a small portion of the workspace and did not represent the actual structure of a multijointed limb. Directional tuning with respect to movement direction appeared in the model simply because the model assumed directional tuning with respect to endpoint force in the linear dynamics. The spatial hypothesis provides a more general framework in which the representation of spatial movements is an indispensable intermediate step in computing the torques from dynamical equations and therefore integrates both the dynamical and spatial views.
Whether activities of the motor cortical neurons represent single movement variables or weighted sums of movement variables is an open question. One possibility is that single neurons compute a linear sum of these cross-product terms, consistent with a previous study reporting multiparameter responses in individual neuronal activities (Ashe and Georgopoulos 1994). However, it is difficult to dissociate multiple movement parameters in a center-out reaching task as used in this and other studies because the movement parameters are often temporally correlated. A recent study resolved this issue by designing continuous movement tasks and considering temporal correlations among kinematic parameters and reported that most neurons correlated with single dominant parameters (Stark et al. 2007). Among the kinematic parameters, velocity was the most dominant (80%) compared with position (9%) or acceleration (11%).
In our model, the cross-product terms were computed from kinematic variables with a feedforward neural network and muscle tensions were computed as rectified linear sums of cross-product terms. This suggests a hierarchical organization. The primary motor cortex of primates is divided into rostral and caudal subareas defined by cytoarchitectural zones (Geyer et al. 1996), descending pathways (Rathelot and Strick 2009), and functional representations (Sergio et al. 2005). Of particular relevance to our study is the proposal based on data from various recording studies that neuronal activity in the rostral M1 correlates with overall directions and kinematics of endpoint motion, whereas activity in the caudal M1 correlates with the temporal pattern of force production and motor output (Sergio et al. 2005). From the perspective of our model, it is tempting to identify the rostral M1 with the cross-product representation (Eq. 21) and the caudal M1 with the linear-sum representation of muscle tensions (Eq. 37). This leads to the prediction that there should be functional connections from the kinematic representation in the rostral part to the force representation in the caudal part.
Motor cortex neuronal activities explained by geometric properties of cross products.
The ubiquity of broad, cosinelike tuning curves in motor cortex and the position dependence of the PDs follow naturally from vector cross products and the geometry of space. How motor cortex neuron activities vary in different workspaces is not completely understood, but similar response modulation by eye or head positions has been described in parietal visual neurons by the so-called gain fields (Andersen et al. 1985). We have proposed a feedforward neural network that computes vector cross products from limb position and velocity or acceleration, similar to a previous model for wrist movements with distinct postures in which multiplicative responses between posture and extrinsic movement reproduced the response of musclelike neurons in the motor cortex (Kakei et al. 2003). Together with our simulation results that linear summation of purely movement-related model neurons failed to approximate muscle tensions, our model predicts that posture and movement variables for multijointed movements in the motor cortex should be represented multiplicatively, in the same way that eye position is represented as a gain field for visual receptive fields in the parietal cortex (Andersen et al. 1985). The workspace dependence may reflect a general solution for population coding of spatial transformations involving large body movements.
In endpoint force generation, broad, cosinelike tuning could also arise as a result of minimizing the detrimental effects of signal-dependent multiplicative noise (Todorov 2002). However, in that study the broad tuning curves were derived with respect to the force direction and not to movement direction. For a linear model that approximates full nonlinear multisegmented limb dynamics in a small part of the workspace, a force direction may approximate the movement direction, but, in general, a force direction would differ from a movement direction with full multisegmented limb dynamics. Another computational study reproduced the posture dependence of PDs at the single-neuron level in an isometric force task by postulating that the motor cortical neurons are tuned to preferred torque directions, but cosine tuning to torque directions was assumed rather than derived from a computational principle (Ajemian et al. 2008). Neurons have been reported in the motor cortex for which tuning to isometric force generation and tuning to reaching movement direction are not the same, as expected from the arguments made here (Sergio et al. 2005).
The model makes the strong prediction that neural activities in motor cortex should reflect not only hand endpoint movement in the workspace coordinates but also the center of mass movements of other limb segments. Moreover, we predict that some neurons should have not only shoulder- but also elbow- or wrist-based reference frames. Some neurons in the dorsal premotor cortex have visual receptive fields anchored to the hand irrespective of gaze direction (Graziano et al. 2000), consistent with this prediction. It should be possible to reanalyze existing experimental data to confirm these model predictions.
Cross products as motor primitives in motor adaptation.
The three-link model can be expanded to include more joints and muscles, which requires more cosine-tuned neurons. Also, as the body grows, and as the masses of the limbs change over time, the dynamics must be continually recalibrated; this can be accomplished by reweighting the terms in Eq. 37. The constraints between the various terms in this equation could be similarly learned through experience, since not all combinations of joint angles and limb positions are feasible. An initially uniform distribution of PDs could be pruned by learning to form the nonuniform distribution in Fig. 3B, reflecting the geometric constraints. Experiments could be designed to test this hypothesis by artificially lengthening limbs and seeing how the tuning curves of neurons in motor cortex adapt to the changes.
Studies of how motor adaptation at one workspace or direction generalizes to other untrained workspaces or directions provide a window as to what basis functions of movements, or motor primitives, are adopted in the motor cortex. Human psychophysical experiments reported that generalization of adaptation to viscous force field at one workspace occurs in the shoulder-based reference frame (Shadmehr and Mussa-Ivaldi 1994). This pattern of generalization can be naturally explained by the position dependence of cross products: Model neural activities identified with cross products remain invariant if movement direction is rotated by the same angle at which the shoulder is rotated (Fig. 4). We modeled the force-field adaptation experiment by adjusting the coefficients of velocity-dependent cross products and reproduced the patterns of generalization in a shoulder-based reference frame.
In contrast, generalization of visuomotor adaptation between spatially displaced workspaces occurs in an extrinsic reference frame (Krakauer et al. 2000; Wang and Sainburg 2005). These psychophysical studies could also be reproduced with the model under the assumption that the coefficients of inertia-related cross-product terms underwent adaptive changes under these conditions. These adaptation results provide strong support that not only reaching dynamics but also motor adaptation uses vector cross products as computational basis functions. Motor adaptation in a spatial representation is the focus of a forthcoming paper (Tanaka and Sejnowski, manuscript in preparation).
Computing joint torques and muscle tensions without an explicit joint-angle representation.
It is interesting to note that Kakei et al. (1999) reported neurons encoding wrist movement directions in the extrinsic space regardless of posture (“extrinsic-like” cells) and neurons encoding posture-dependent muscle activities (“musclelike” cells) but no neurons that exhibited a joint-angle reference frame (“jointlike” cells). This implies that the motor cortex represents both spatial movements and muscle activities but not joint angles for wrist movements, although some studies have reported neural activity in intrinsic joint-angle reference frame for arm reaching movements (Reina et al. 2001; Scott and Kalaska 1997; Thach 1978). In a spatial representation the computation of joint torques and muscle tensions simplifies if movements are expressed with cross products of spatial vectors but not with joint angle, so the motor cortex may have exploited the computational efficiency of computing limb dynamics with spatial vectors. Also, the absence of an explicit joint-angle representation (Kakei et al. 1999) is inconsistent with a conventional serial scheme of movement planning and execution that requires an explicit computation of joint angles (Fig. 9B) (Buneo and Andersen 2006; Flash and Sejnowski 2001; Hollerbach 1982; Kalaska and Crammond 1992; Kawato et al. 1987).
Our model postulates a computational scheme that is an alternative to schemes with an explicit joint-angle representation. The direct transformation from limb trajectory to muscle tensions is consistent with vectorial movement planning (Gordon et al. 1994). Although the final computation of muscle tensions in Eq. 37 as a linear sum of neural activities implies that an explicit representation of joint torques may be unnecessary, neural activities will still be correlated with them. Despite the diverse properties of neurons that have been found in M1, there may be a simple geometric principle underlying the complex properties of neurons in motor cortex based on vector cross products of postural and kinematic variables. The identification of vector cross-product terms in the torque equations with single neurons is a minimal representation, which in the motor cortex could be expanded to provide more diversity and redundancy in computing the final muscle tensions.
Sensory feedback.
One limitation of the present model is that there is no direct force control in Eq. 21, which would preclude control of stiffness when interacting with an unstable environment. Recent human psychophysical studies have shown that the control of reaching dynamics involves feedback in the presence of dynamical and sensory noise (Chen-Harris et al. 2008; Liu and Todorov 2007; Nagengast et al. 2009; Todorov and Jordan 2002). In contrast to feedforward control, in which the desired trajectory is preplanned before being transformed into joint torques or muscle tensions, in an optimal feedback model deviations of sensory feedback signals from their estimates are used to modify the control signal during the movement and thus there is no need for a preplanned trajectory. Although feedforward and feedback control differ in this respect, they both need to map sensory signals onto control signals. Vector cross products could provide a convenient framework for optimal feedback control since they span a computationally efficient basis for converting sensory signals into control signals. Furthermore, cross products can be computed from either visual or proprioceptive signals, so both can be represented in the same bases without the need for the computation of joint angles.
The model avoided the explicit computation of joint angles at the cost of introducing a redundant representation of spatial vectors. How the brain maintains consistency among all the spatial vectors is a nontrivial problem. Because the proprioceptive feedback always provides a valid configuration of posture, comparing the feedback from proprioceptive inputs can maintain the consistency in the spatial representation. In this view, motor planning and sensory feedback are no longer separable but inherently integrated. The problem of maintaining the consistency among spatial vectors is closely related to the concept of the body schema, a representation of body parts in space used for controlling body movements, which may be found in the parietal cortex (Haggard and Wolpert 2005). Therefore, our model of the motor cortex might be extended to the parieto-frontal motor areas.
Conclusion.
This study focused on arm reaching movements in the horizontal plane. For three-dimensional movements there are additional terms (Eq. 13), but they are all vector cross products. Thus similar conclusions will hold for more general movements, which can be tested. Knowing how a population of neurons in the motor cortex represents an action is only a first step toward understanding how actions are planned and carried out with sensory feedback. The next step is to generalize the model to include both feedback control and proprioceptive feedback. Work in progress will resolve these limitations.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: H.T. and T.J.S. conception and design of research; H.T. performed experiments; H.T. analyzed data; H.T. and T.J.S. interpreted results of experiments; H.T. prepared figures; H.T. drafted manuscript; H.T. and T.J.S. edited and revised manuscript; H.T. and T.J.S. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Dr. Shinichi Furuya for inspiring discussions on initiating this work, Dr. Hiroshi Imamizu for suggestions on the cortical joint representations, Dr. Geoffrey Hinton for discussion on learning mechanisms of spatial representations, Dr. Stephen H. Scott for discussion on control of reaching, and three anonymous reviewers for insightful comments.
APPENDIX A
Derivation of Spatial Representation with the Newton-Euler Method
The physics of a linked rigid body under constraints has been studied for centuries in physics and more recently in robotics. Our derivation of the EOMs is based on standard methods of rigid body dynamics. The spatial representation for EOMs in Eq. 12 was derived by explicitly using joint angles with the Euler-Lagrange method. There is another, recursive method in robotics for deriving EOMs for a segmented system, known as the Newton-Euler method (Luh et al. 1980). Although the two methods are mathematically equivalent, the Newton-Euler method is far more intuitive because it uses spatial vectors rather than joint angles and more systematic because the computation is recursive backward from the distal segments to more proximal segments. Moreover, the computation of three-dimensional motion with the Newton-Euler method is no more complicated than that of two-dimensional motion, whereas in the Euler-Lagrange method a two-dimensional movement computation does not straightforwardly generalize to three dimensions. Although the spatial representation has been known for a long time in physics and robotics, it has not been used for the purpose of understanding the functions of motor cortex.
The recursive equations for translational forces and rotational torques, which are solved backward from distal to proximal segments, are
| (A1) |
where X⃗j,j−1e is a vector connecting the (j − 1)th joint to the jth joint, Ii is the 3 × 3 inertial matrix, and ω⃗i and α⃗i are angular velocity and acceleration, respectively. F⃗i and τ⃗i are force and torque vectors exerted on the ith joint, respectively. No external force F⃗n+1 or torque τ⃗n+1 at the endpoint is imposed, for simplicity. To illustrate how to derive EOMs, we first consider a two-link (n = 2) segmental model. First we begin with equations of the second segment as
| (A2) |
where we used F⃗3 = 0 and τ⃗3 = 0. Recursively, the equations of the first segment are
| (A3) |
By noting using F⃗2 = m2A⃗20 and X⃗20 = X⃗10e + X⃗21, the torque at the shoulder joint in Eq. A3 now reads
| (A4) |
The angular velocities and angular accelerations have the following spatial representations:
| (A5) |
so the EOMs Eqs. A2 and A4 in the spatial representation become
| (A6) |
| (A7) |
If the movement is restricted in the horizontal plane, the terms quadratic in ω⃗ vanish because ω⃗ and Iω⃗ are parallel to each other, and only the z-components of joint torques take nonzero values. For this special case,
| (A8) |
| (A9) |
Here, the τis are z-components of the torque vector, τ⃗i, and Iis are the inertial momentum of the ith segment around the z-axis. These are the EOMs we derived by using the Euler-Lagrange method in Eqs. 10 and 11 of the main text. The recursive nature of the Newton-Euler method allows us to derive a general formula for an n-link system in three dimensions:
| (A10) |
This is Eq. 13 in the main text. Again, by restricting the movement in the horizontal plane, we finally arrive at the special case:
| (A11) |
which is Eq. 12 in the main text.
As already shown for the two-dimensional movements, the computation of torque for three-dimensional movements greatly simplifies for spatial vector cross products compared with the expressions when joint angles are used, in both the number and the complexity of the terms. Therefore, our computational framework that postulates the use of spatial representation is not restricted to two-dimensional movements in the horizontal plane but generalizes to three-dimensional movements.
APPENDIX B
EOMs in Intrinsic Coordinates for a Three-Link Articulated Model
EOMs for the three-link system in the joint-angle representation are shown for comparison with those in a spatial representation. These equations are equivalent to Eqs. 27, 28, and 29 in the main text.
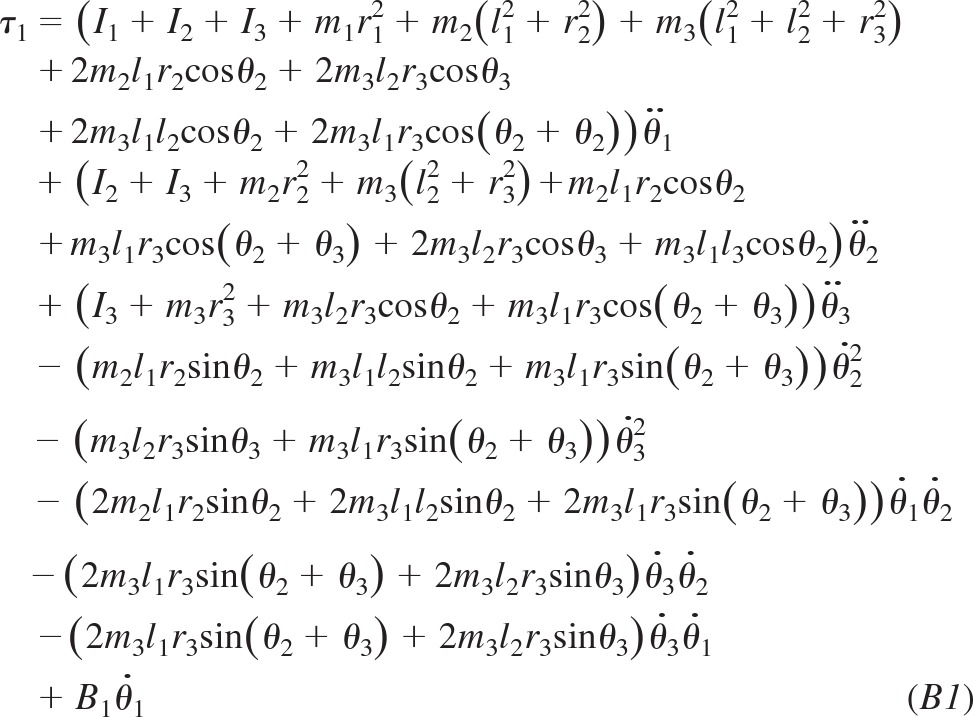 |
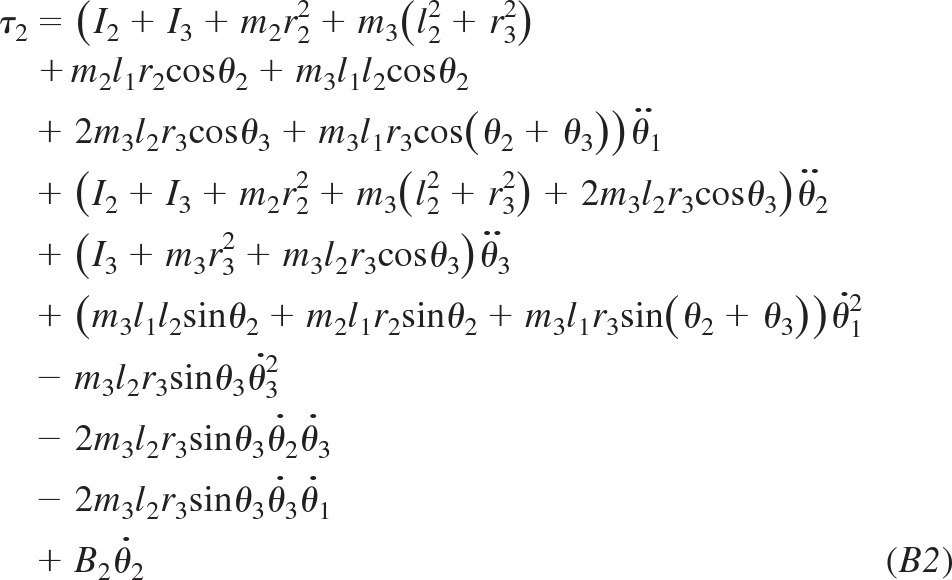 |
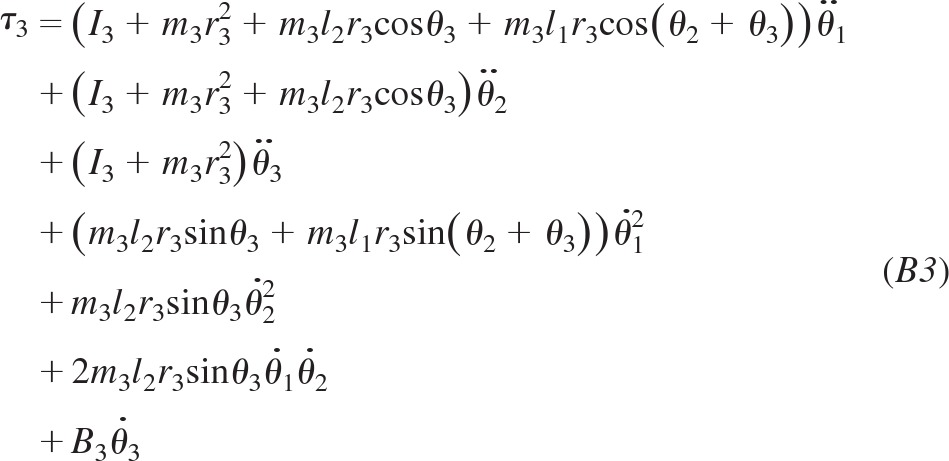 |
APPENDIX C
Two-Link Articulated Model
Reaching movements and neural activities are modeled with the three-link model in the main text, and qualitatively similar results were obtained when a two-link model was used. For an articulated arm model with two connected links, the spatial representation of the EOMs including the viscosity terms is
| (C1) |
| (C2) |
There are five acceleration terms and two velocity terms, so a total of seven model neurons are introduced.
| (C3) |
With these expressions and a minimum-jerk trajectory (Eq. 31), temporal profiles of model neurons are computed. Essentially the same results were obtained for cosine tuning (Fig. 3A), nonuniform distribution of preferred directions (Fig. 3B), multiple coordinate systems (Fig. 4, E and F), population vectors (Figs. 5 and 6), and muscle computation (Figs. 7 and 8).
REFERENCES
- Abend W, Bizzi E, Morasso P. Human arm trajectory formation. Brain 105: 331–348, 1982 [DOI] [PubMed] [Google Scholar]
- Ajemian R, Bullock D, Grossberg S. Kinematic coordinates in which motor cortical cells encode movement direction. J Neurophysiol 84: 2191–2203, 2000 [DOI] [PubMed] [Google Scholar]
- Ajemian R, Bullock D, Grossberg S. A model of movement coordinates in the motor cortex: posture-dependent changes in the gain and direction of single cell tuning curves. Cereb Cortex 11: 1124–1135, 2001 [DOI] [PubMed] [Google Scholar]
- Ajemian R, Green A, Bullock D, Sergio L, Kalaska J, Grossberg S. Assessing the function of motor cortex: single-neuron models of how neural response is modulated by limb biomechanics. Neuron 58: 414–428, 2008 [DOI] [PubMed] [Google Scholar]
- Amirikian B, Georgopoulos AP. Directional tuning profiles of motor cortical cells. Neurosci Res 36: 73–79, 2000 [DOI] [PubMed] [Google Scholar]
- Andersen RA, Essick GK, Siegel RM. Encoding of spatial location by posterior parietal neurons. Science 230: 456–458, 1985 [DOI] [PubMed] [Google Scholar]
- Ashe J, Georgopoulos AP. Movement parameters and neural activity in motor cortex and area 5. Cereb Cortex 4: 590–600, 1994 [DOI] [PubMed] [Google Scholar]
- Atkeson CG. Learning arm kinematics and dynamics. Annu Rev Neurosci 12: 157–183, 1989 [DOI] [PubMed] [Google Scholar]
- Bizzi E, Accornero N, Chapple W, Hogan N. Posture control and trajectory formation during arm movement. J Neurosci 4: 2738–2744, 1984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullock D, Grossberg S, Guenther FH. A self-organizing neural model of motor equivalent reaching and tool use by a multijoint arm. J Cogn Neurosci 5: 408–435, 1993 [DOI] [PubMed] [Google Scholar]
- Buneo CA, Andersen RA. The posterior parietal cortex: sensorimotor interface for the planning and online control of visually guided movements. Neuropsychologia 44: 2594–2606, 2006 [DOI] [PubMed] [Google Scholar]
- Caminiti R, Johnson PB, Urbano A. Making arm movements within different parts of space: dynamic aspects in the primate motor cortex. J Neurosci 10: 2039–2058, 1990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter AF, Georgopoulos AP, Pellizzer G. Motor cortical encoding of serial order in a context-recall task. Science 283: 1752–1757, 1999 [DOI] [PubMed] [Google Scholar]
- Chen-Harris H, Joiner WM, Ethier V, Zee DS, Shadmehr R. Adaptive control of saccades via internal feedback. J Neurosci 28: 2804–2813, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng EJ, Scott SH. Morphometry of Macaca mulatta forelimb. I. Shoulder and elbow muscles and segment inertial parameters. J Morphol 245: 206–224, 2000 [DOI] [PubMed] [Google Scholar]
- Churchland MM, Shenoy KV. Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. J Neurophysiol 97: 4235–4257, 2007 [DOI] [PubMed] [Google Scholar]
- Churchland MM, Santhanam G, Shenoy KV. Preparatory activity in premotor and motor cortex reflects the speed of the upcoming reach. J Neurophysiol 96: 3130–3146, 2006 [DOI] [PubMed] [Google Scholar]
- Evarts EV. Relation of pyramidal tract activity of force exerted during voluntary movement. J Neurophysiol 31: 14–27, 1968 [DOI] [PubMed] [Google Scholar]
- Fagg AH, Shah A, Barto AG. A computational model of muscle recruitment for wrist movements. J Neurophysiol 88: 3348–3358, 2002 [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics 11: 565–578, 1966 [Google Scholar]
- Feldman AG, Levin MF. The origin and use of positional frames of reference in motor control. Behav Brain Sci 18: 723–744, 1995 [Google Scholar]
- Fetz EE, Cheney PD. Postspike facilitation of forelimb muscle activity by primate corticomotoneuronal cells. J Neurophysiol 44: 751–772, 1980 [DOI] [PubMed] [Google Scholar]
- Flament D, Hore J. Relations of motor cortex neural discharge to kinematics of passive and active elbow movements in the monkey. J Neurophysiol 60: 1268–1284, 1988 [DOI] [PubMed] [Google Scholar]
- Flash T, Hogan N. The coordination of arm movements: an experimentally confirmed mathematical model. J Neurosci 5: 1688–1703, 1985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flash T, Sejnowski TJ. Computational approaches to motor control. Curr Opin Neurobiol 11: 655–662, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganesh G, Burdet E, Haruno M, Kawato M. Sparse linear regression for reconstructing muscle activity from human cortical fMRI. Neuroimage 42: 1463–1472, 2008 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP. Spatial coding of visually guided arm movements in primate motor cortex. Can J Physiol Pharmacol 66: 518–526, 1988 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP. On the translation of directional motor cortical commands to activation of muscles via spinal interneuronal systems. Brain Res Cogn Brain Res 3: 151–155, 1996 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP. Cognitive motor control: spatial and temporal aspects. Curr Opin Neurobiol 12: 678–683, 2002 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Caminiti R, Kalaska JF. Static spatial effects in motor cortex and area 5: quantitative relations in a two-dimensional space. Exp Brain Res 54: 446–454, 1984 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science 233: 1416–1419, 1986 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Kettner RE, Schwartz AB. Primate motor cortex and free arm movements to visual targets in three-dimensional space. II. Coding of the direction of movement by a neuronal population. J Neurosci 8: 2928–2937, 1988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci 2: 1527–1537, 1982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Ashe J, Smyrnis N, Taira M. The motor cortex and the coding of force. Science 256: 1692–1695, 1992 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Lurito JT, Petrides M, Schwartz AB, Massey JT. Mental rotation of the neuronal population vector. Science 243: 234–236, 1989 [DOI] [PubMed] [Google Scholar]
- Geyer S, Ledberg A, Schleicher A, Kinomura S, Schormann T, Burgel U, Klingberg T, Larsson J, Zilles K, Roland PE. Two different areas within the primary motor cortex of man. Nature 382: 805–807, 1996 [DOI] [PubMed] [Google Scholar]
- Gordon J, Ghilardi MF, Ghez C. Accuracy of planar reaching movements. I. Independence of direction and extent variability. Exp Brain Res 99: 97–111, 1994 [DOI] [PubMed] [Google Scholar]
- Graziano MS, Cooke DF, Taylor CS. Coding the location of the arm by sight. Science 290: 1782–1786, 2000 [DOI] [PubMed] [Google Scholar]
- Guigon E, Baraduc P, Desmurget M. Coding of movement- and force-related information in primate primary motor cortex: a computational approach. Eur J Neurosci 26: 250–260, 2007 [DOI] [PubMed] [Google Scholar]
- Haggard P, Wolpert DM. Disorders of body schema. In: Higher-Order Motor Disorders: From Neuroanatomy and Neurobiology to Clinical Neurology. Oxford, UK: Oxford Univ. Press, 2005, p. 261–271 [Google Scholar]
- Haruno M, Ganesh G, Burdet E, Kawato M. Differential neural correlates of reciprocal activation and cocontraction control in dorsal and ventral premotor cortices. J Neurophysiol 107: 126–133, 2012 [DOI] [PubMed] [Google Scholar]
- Hatsopoulos NG, Xu QQ, Amit Y. Encoding of movement fragments in the motor cortex. J Neurosci 27: 5105–5114, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinton G. Parallel computations for controlling an arm. J Mot Behav 16: 171–194, 1984 [DOI] [PubMed] [Google Scholar]
- Hogan N. An organizing principle for a class of voluntary movements. J Neurosci 4: 2745–2754, 1984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollerbach JM. Computers, brains and the control of movement. Trends Neurosci 5: 189–192, 1982 [Google Scholar]
- Johnson MT, Coltz JD, Hagen MC, Ebner TJ. Visuomotor processing as reflected in the directional discharge of premotor and primary motor cortex neurons. J Neurophysiol 81: 875–894, 1999 [DOI] [PubMed] [Google Scholar]
- Kakei S, Hoffman DS, Strick PL. Muscle and movement representations in the primary motor cortex. Science 285: 2136–2139, 1999 [DOI] [PubMed] [Google Scholar]
- Kakei S, Hoffman DS, Strick PL. Sensorimotor transformations in cortical motor areas. Neurosci Res 46: 1–10, 2003 [DOI] [PubMed] [Google Scholar]
- Kalaska JF. From intention to action: motor cortex and the control of reaching movements. Adv Exp Med Biol 629: 139–178, 2009 [DOI] [PubMed] [Google Scholar]
- Kalaska JF, Crammond DJ. Cerebral cortical mechanisms of reaching movements. Science 255: 1517–1523, 1992 [DOI] [PubMed] [Google Scholar]
- Kalaska JF, Caminiti R, Georgopoulos AP. Cortical mechanisms related to the direction of two-dimensional arm movements: relations in parietal area 5 and comparison with motor cortex. Exp Brain Res 51: 247–260, 1983 [DOI] [PubMed] [Google Scholar]
- Kawato M, Furukawa K, Suzuki R. A hierarchical neural-network model for control and learning of voluntary movement. Biol Cybern 57: 169–185, 1987 [DOI] [PubMed] [Google Scholar]
- Kawato M, Isobe M, Maeda Y, Suzuki R. Coordinates transformation and learning control for visually-guided voluntary movement with iteration: a Newton-like method in a function space. Biol Cybern 59: 161–177, 1988 [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Pine ZM, Ghilardi MF, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci 20: 8916–8924, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D, Todorov E. Evidence for the flexible sensorimotor strategies predicted by optimal feedback control. J Neurosci 27: 9354–9368, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luh JY, Walker MW, Paul RP. On-line computational scheme for mechanical manipulators. J Dyn Syst Measurement Cont 102: 69, 1980 [Google Scholar]
- Lukashin AV, Amirikian BR, Georgopoulos AP. Neural computations underlying the exertion of force: a model. Biol Cybern 74: 469–478, 1996 [DOI] [PubMed] [Google Scholar]
- Lurito JT, Georgakopoulos T, Georgopoulos AP. Cognitive spatial-motor processes. 7. The making of movements at an angle from a stimulus direction: studies of motor cortical activity at the single cell and population levels. Exp Brain Res 87: 562–580, 1991 [DOI] [PubMed] [Google Scholar]
- Mohan V, Morasso P. Passive motion paradigm: an alternative to optimal control. Front Neurorobot 5: 4, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran DW, Schwartz AB. Motor cortical representation of speed and direction during reaching. J Neurophysiol 82: 2676–2692, 1999 [DOI] [PubMed] [Google Scholar]
- Morasso P. Spatial control of arm movements. Exp Brain Res 42: 223–227, 1981 [DOI] [PubMed] [Google Scholar]
- Morasso P, Casadio M, Mohan V, Zenzeri J. A neural mechanism of synergy formation for whole body reaching. Biol Cybern 102: 45–55, 2010 [DOI] [PubMed] [Google Scholar]
- Morrow MM, Miller LE. Prediction of muscle activity by populations of sequentially recorded primary motor cortex neurons. J Neurophysiol 89: 2279–2288, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA. Do neurons in the motor cortex encode movement direction? An alternative hypothesis. Neurosci Lett 91: 106–111, 1988 [DOI] [PubMed] [Google Scholar]
- Mussa Ivaldi FA, Morasso P, Zaccaria R. Kinematic networks. A distributed model for representing and regularizing motor redundancy. Biol Cybern 60: 1–16, 1988 [DOI] [PubMed] [Google Scholar]
- Nagengast AJ, Braun DA, Wolpert DM. Optimal control predicts human performance on objects with internal degrees of freedom. PLoS Comput Biol 5: e1000419, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naselaris T, Merchant H, Amirikian B, Georgopoulos AP. Large-scale organization of preferred directions in the motor cortex. I. Motor cortical hyperacuity for forward reaching. J Neurophysiol 96: 3231–3236, 2006 [DOI] [PubMed] [Google Scholar]
- Pouget A, Sejnowski TJ. Spatial transformations in the parietal cortex using basis functions. J Cogn Neurosci 9: 222–237, 1997 [DOI] [PubMed] [Google Scholar]
- Prilutsky BI, Zatsiorsky VM. Optimization-based models of muscle coordination. Exerc Sport Sci Rev 30: 32–38, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rathelot JA, Strick PL. Subdivisions of primary motor cortex based on cortico-motoneuronal cells. Proc Natl Acad Sci USA 106: 918–923, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reina GA, Moran DW, Schwartz AB. On the relationship between joint angular velocity and motor cortical discharge during reaching. J Neurophysiol 85: 2576–2589, 2001 [DOI] [PubMed] [Google Scholar]
- Salinas E, Abbott LF. A model of multiplicative neural responses in parietal cortex. Proc Natl Acad Sci USA 93: 11956–11961, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanger TD. Probability density estimation for the interpretation of neural population codes. J Neurophysiol 76: 2790–2793, 1996 [DOI] [PubMed] [Google Scholar]
- Schwartz AB, Cui XT, Weber DJ, Moran DW. Brain-controlled interfaces: movement restoration with neural prosthetics. Neuron 52: 205–220, 2006 [DOI] [PubMed] [Google Scholar]
- Scott SH. Conceptual frameworks for interpreting motor cortical function: new insights from a planar multiple-joint paradigm. In: Motor Cortex in Voluntary Movements , London: CRC, 2005, p. 157–180 [Google Scholar]
- Scott SH, Kalaska JF. Reaching movements with similar hand paths but different arm orientations. I. Activity of individual cells in motor cortex. J Neurophysiol 77: 826–852, 1997 [DOI] [PubMed] [Google Scholar]
- Scott SH, Gribble PL, Graham KM, Cabel DW. Dissociation between hand motion and population vectors from neural activity in motor cortex. Nature 413: 161–165, 2001 [DOI] [PubMed] [Google Scholar]
- Sergio LE, Kalaska JF. Changes in the temporal pattern of primary motor cortex activity in a directional isometric force versus limb movement task. J Neurophysiol 80: 1577–1583, 1998 [DOI] [PubMed] [Google Scholar]
- Sergio LE, Hamel-Paquet C, Kalaska JF. Motor cortex neural correlates of output kinematics and kinetics during isometric-force and arm-reaching tasks. J Neurophysiol 94: 2353–2378, 2005 [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soechting JF, Flanders M. Sensorimotor representations for pointing to targets in three-dimensional space. J Neurophysiol 62: 582–594, 1989 [DOI] [PubMed] [Google Scholar]
- Stark E, Drori R, Asher I, Ben-Shaul Y, Abeles M. Distinct movement parameters are represented by different neurons in the motor cortex. Eur J Neurosci 26: 1055–1066, 2007 [DOI] [PubMed] [Google Scholar]
- Taira M, Boline J, Smyrnis N, Georgopoulos AP, Ashe J. On the relations between single cell activity in the motor cortex and the direction and magnitude of three-dimensional static isometric force. Exp Brain Res 109: 367–376, 1996 [DOI] [PubMed] [Google Scholar]
- Thach WT. Correlation of neural discharge with pattern and force of muscular activity, joint position, and direction of intended next movement in motor cortex and cerebellum. J Neurophysiol 41: 654–676, 1978 [DOI] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Electromyographic correlates of learning an internal model of reaching movements. J Neurosci 19: 8573–8588, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat Neurosci 3: 391–398, 2000 [DOI] [PubMed] [Google Scholar]
- Todorov E. Cosine tuning minimizes motor errors. Neural Comput 14: 1233–1260, 2002 [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci 5: 1226–1235, 2002 [DOI] [PubMed] [Google Scholar]
- Trainin E, Meir R, Karniel A. Explaining patterns of neural activity in the primary motor cortex using spinal cord and limb biomechanics models. J Neurophysiol 97: 3736–3750, 2007 [DOI] [PubMed] [Google Scholar]
- Viviani P, Flash T. Minimum-jerk, 2/3-power law, and isochrony—converging approaches to movement planning. J Exp Psychol Hum Percept Perform 21: 32–53, 1995 [DOI] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. Adaptation to visuomotor rotations remaps movement vectors, not final positions. J Neurosci 25: 4024–4030, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Chan SS, Heldman DA, Moran DW. Motor cortical representation of position and velocity during reaching. J Neurophysiol 97: 4258–4270, 2007 [DOI] [PubMed] [Google Scholar]
- Winter DA. Biomechanics and Motor Control of Human Movement. Hoboken, NJ: Wiley, 2009 [Google Scholar]
- Wu W, Hatsopoulos N. Evidence against a single coordinate system representation in the motor cortex. Exp Brain Res 175: 197–210, 2006 [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng 17: 359–411, 1989 [PubMed] [Google Scholar]