Calcium Alternans in Cardiac Myocytes: Order From Disorder

Abstract

Calcium alternans is associated with T-wave alternans and pulsus alternans, harbingers of increased mortality in the setting of heart disease. Recent experimental, computational, and theoretical studies have led to new insights into the mechanisms of Ca alternans, specifically how disordered behaviors dominated by stochastic processes at the subcellular level become organized into ordered periodic behaviors. In this article, we summarize the recent progress in this area, outlining a holistic theoretical framework in which the complex effects of Ca cycling proteins on Ca alternans are linked to three key properties of the cardiac Ca cycling network: randomness, refractoriness, and recruitment. We also illustrate how this ‘3R theory’ can reconcile many seemingly contradictory experimental observations.

1. Introduction

Intracellular calcium (Ca) alternans has been documented to occur under either current clamp or voltage clamp conditions [1-21], the latter unequivocally demonstrating that the Ca cycling system in cardiac myocytes is capable of producing dynamical instabilities that generate alternans, independent of electrical alternans. Indeed, the available evidence indicates that electromechanical alternans, a known risk factor conferring increased mortality in the setting of heart disease [22-25], is more often initiated by instabilities in the Ca cycling system than by restitution-related electrical properties [9, 26].

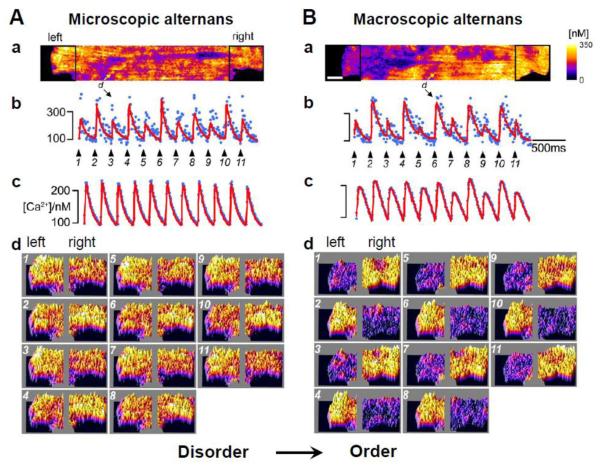
Cardiac myocytes contain a network of ~20,000 Ca release units (CRUs or couplons) [27-29], each consisting of a cluster of L-type Ca channels (LCCs) in the sarcolemmal membrane apposed to a larger cluster of ryanodine receptors (RyRs) in the junctional sarcoplasmic reticulum (SR) membrane. By the process of Ca-induced Ca release (CICR), Ca entry through the LCCs triggers Ca release from a CRU, which is called a Ca spark [30, 31]. Ca sparks are considered the elementary events in Ca signaling, not only in cardiac myocytes but also in many other cell types. Spontaneous Ca sparks (i.e. sparks not triggered by LCCs) may also occur. Since the openings of LCCs and RyRs are stochastic events, the timing of onset and other properties of Ca sparks exhibit randomness, even when elicited by action potentials [32, 33]. It is not difficult to understand how the disorder inherent to the randomness of individual Ca sparks nevertheless produces the same whole-cell Ca transient from beat to beat, as the whole-cell Ca transient is the summation of all Ca sparks whether they arise from the same or different CRUs. That is, even though the macroscopic Ca transient is regular from beat to beat, the system is in a microscopically disordered state, similar to a typical thermodynamic system (e.g., a gas at constant temperature, volume and pressure). When Ca alternans occurs, the whole-cell Ca transient remains a large-small-large-small alternating pattern, which represents a new temporal order of the system. At the microscopic level, however, pure randomness cannot explain why a larger number of CRUs consistently release Ca on one beat (e.g. the even beat) rather than on the next beat (e.g. the odd beat). To give rise to the whole-cell (macroscopic) alternans, an order must be self-organized at the microscopic (spark) level. Therefore, the transition from no alternans to alternans represents a transition from disorder to order, a fundamental topic of nonequilibrium statistical physics and self-organization pattern formation in natural systems [34-38]. Such a transition has been demonstrated in recent experiments by Tian et al [39] who showed that as the heart rate increased, alternans first occurred at the microscopic scale (coupling site or CRU alternans) without macroscopic (whole-cell) alternans (Fig.1A). Because alternans in different CRUs occurred in a disordered manner, the whole-cell Ca transient remained constant from beat to beat. As the heart rate was increased further, however, the microscopic CRU alternans developed an ordered pattern resulting in macroscopic alternans (Fig.1B). The question is then: how does the distribution of CRUs become preferentially biased towards releasing Ca on one type of beat, rather than remaining equally distributed between odd and even beats? Put differently, how do randomly occurring Ca sparks self-organize to generate the beat to beat alternating pattern at the whole-cell level?

Figure 1. Transition from microscopic to macroscopic alternans (or from disorder to order).

A. At a slower heart rate, microscopic alternans occurs (panel b) but no macroscopic alternans is present (panel c) due to random distribution between even:odd and odd:even phases of alternans among CRUs. B. At a faster heart rate, macroscopic alternans occurs as the phase of alternans among CRUs synchronizes. Panel a: Snapshot of the spark amplitude distribution in the myocyte. Panel b: Local alternans for a site as marked in panel a. Panel c: Whole-cell Ca transient. Panel d: Snapshots of spark amplitudes from the left and right ends of the myocyte. This figure was modified from Tian et al [39].

Answering these questions not only is necessary for understanding the mechanisms of Ca alternans in general but can also provide essential precursors for understanding how the properties of specific Ca cycling proteins affect the genesis of Ca alternans. The difficulty in understanding the effects of a specific Ca cycling protein on Ca alternans is that alteration of its properties may cause a cascade of complex interactions [40]. For example, experimental studies showed that Ca alternans could be either suppressed or enhanced by mutations causing catecholaminergic polymorphic ventricular tachycardia (CPVT) [21, 41, 42] or by blocking LCCs [8, 16, 43, 44]. Therefore, in order to develop effective therapies that prevent alternans and its deleterious consequences, a unified understanding of the underlying mechanisms is required, both on a general level to reconcile inconsistencies between experimental observations, and on a physiologically specific level to provide a framework for linking alterations of key Ca cycling proteins to suppression of alternans in a therapeutic context.

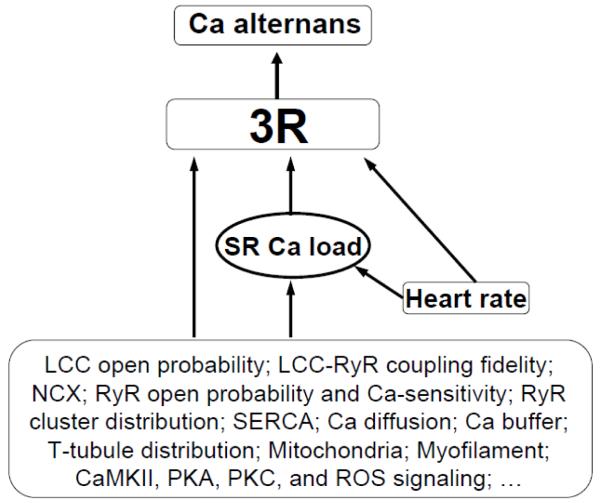
Insights into the mechanisms of Ca alternans have been gained from many experimental, computational, and theoretical studies. In this article, we first review the experimental observations, mechanistic insights, and apparent inconsistencies between experiments. We then discuss recent computer simulations using spatially-distributed stochastic models of Ca cycling. Lastly, we describe a theory of Ca alternans that mechanistically links random sparks to alternans through the 3R’s: randomness, recruitment, and refractoriness. We illustrate how the 3R theory can be used as a unifying theoretical framework to understand the complex effects of Ca cycling proteins on Ca alternans, which serves to reconcile some of the seemingly contradictory experimental observations.

2. The experimental observations

The voltage clamp experiments by Chudin et al [4], in which isolated cardiac myocytes were paced at physiological heart rates with an action potential waveform, directly demonstrated that the Ca cycling system alone is capable of instabilities that cause alternans, independent of electrical alternans. Subsequently, many experimental studies have been carried out to explore the underlying mechanisms of Ca alternans and understand how specific Ca cycling proteins affect Ca alternans.

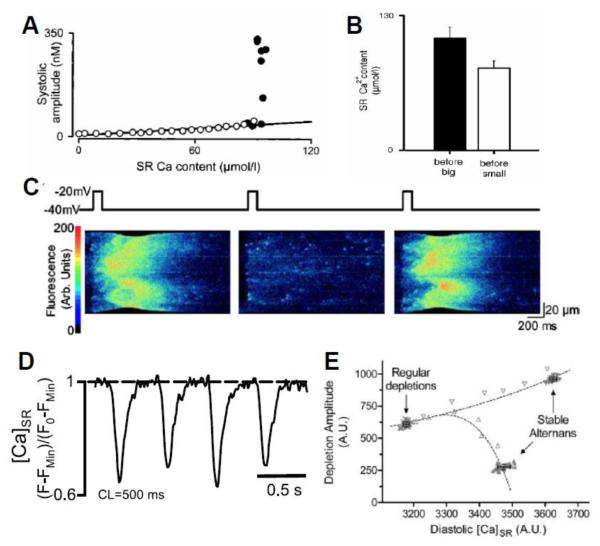
In a series of studies [6, 8, 16, 45], Diaz and colleagues made the following observations: 1) when Ca alternans occurs, the amount of Ca released increases steeply with the diastolic SR Ca load immediately preceding the release (Fig.2A), consistent with the steep fractional release-load relationship measured by Bassani and Shannon et al [46, 47]; 2) The diastolic SR Ca load alternates concomitantly with SR Ca release (Fig.2B); 3) Asynchronous Ca releases or mini-waves are required for alternans (Fig.2C); 4) Alternans can be induced by reducing the LCC or RyR open probability. The first two observations form the basis for the theory, first proposed by Eisner et al [45], that a steep fractional release curve is responsible for alternans. This theory was more rigorously established later in theoretical studies by other authors [25, 48, 49] and supported by computer simulations [50-52].

Figure 2. Experimental observations on Ca alternans.

A. Systolic Ca amplitude vs SR Ca content from an experiment by Diaz et al [8], illustrating a steep release-load relationship. B. SR Ca content before the large and small Ca releases during alternans, from an experiment by Diaz et al [8]. C. A line scan of cytosolic Ca during alternans from an experiment by Diaz et al [8]. Chevrons indicate miniwaves during the large Ca releases (1^st and 3^rd panels). D. SR Ca during alternans measured by Shryl et al [20], illustrating that maximal diastolic SR Ca is constant despite alternating large and small releases. E. SR Ca depletion vs SR Ca content obtained using a ramp pacing protocol from an experiment by Picht et al [11]. Note that the SR content during regular (non-alternating) beats is lower than during stable alternans, even though the Ca release is less during the small release beat during alternans.

However, experiments from other groups have shown that Ca alternans can occur without diastolic SR Ca load alternans (Fig.2D) [5, 11, 20]. In addition, the Ca released from the small beat during alternans is less than that released from non-alternating beats, even though the SR load is higher in the former case (Fig.2E), indicating that Ca release is not totally determined by the SR Ca load. These observations do not agree with the theory by Eisner et al and other authors, suggesting that other factors must be considered. Refractoriness of SR Ca release was proposed as a primary mechanism underlying Ca alternans [11], and supported in recent studies [20, 21].

Ca alternans in different regions of a myocyte may be spatially in phase, but, as observed in many experiments [6, 12, 14, 18, 39, 53, 54], can also be out of phase, called spatially discordant alternans. Shiferaw and Karma [55] proposed a Turing instability mechanism for discordant alternans in which a negative Ca-to-voltage coupling is required and voltage plays the role of long range inhibition. This theory was later experimentally demonstrated by Gaeta et al [54]. However, spatially discordant alternans has also been observed under voltage clamp conditions [6, 14], which cannot be explained by the proposed theory, indicating that other mechanisms for spatially discordant alternans exist. For example, it has been shown that a local Ca wave can reset the phase of alternating Ca release to cause spatially discordant alternans [14].

In addition to the above studies focusing on general mechanisms of Ca alternans, there have also been many experimental studies exploring how the properties of specific Ca cycling proteins affect the propensity for Ca alternans. It has been shown that SERCA2a overexpression suppresses Ca alternans [13, 15], whereas reducing SERCA2a enhances Ca alternans [10]. Caffeine and ryanodine, which increase RyR open probability, suppress alternans [1, 13, 56, 57], while tetracaine, which reduces RyR open probability, promotes alternans [6]. In mouse models of CPVT, alternans is promoted by RyR mutations which cause RyRs to become leaky [41, 42, 58], agreeing with U-wave alternans shown in clinical CPVT [59]. This also agrees with the observation that stabilization of RyRs by the drug FK506 suppresses alternans [13]. On the other hand, in mouse model of CPVT due to calsequestrin knockout [21], Ca alternans is suppressed. Agreeing with this observation, calsequestrin overexpression promotes pulsus alternans [60]. Ca alternans has been induced by partially blocking LCCs in some experiments [8, 16, 43], but suppressed in other experiments [44]. Saitoh et al [61] also showed that either LCC agonist, BayK8644, or LCC blocker, nisodipine, suppress mechanical alternans in ventricular myocytes. However, BayK8644 has also been shown to promote Ca alternans [13, 14].

In summary, despite the important insights obtained from the experimental studies, the lack of consistent agreement and seemingly contradictory findings indicate that our understanding of the mechanisms underlying Ca alternans is incomplete.

3. Ca alternans in spatially-distributed Ca cycling models

Spatially-distributed models of Ca cycling have been developed to study the mechanisms of Ca alternans. Early models [50, 52, 54, 55, 62] generally assumed deterministic and continuous Ca release, without accounting for the discrete nature and stochastic behavior of Ca sparks. Recently, however, spatially-distributed Ca cycling models with stochastic ion channels that simulate discrete and random Ca sparks have subsequently been developed to investigate the relationship between Ca sparks and Ca alternans [40, 63-67]. These studies have recapitulated many of the experimental observations and provided additional insights into the mechanisms of Ca alternans.

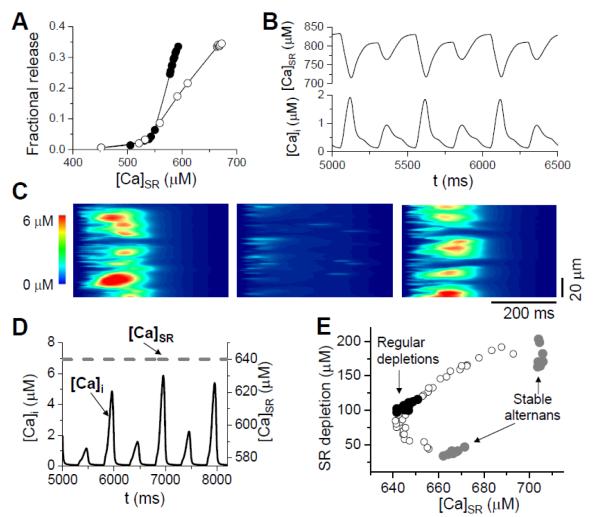
In our simulations [40, 66, 68], we have made the following observations: 1) A steep fractional release relation arises from the nonlinear properties of CICR and is enhanced by the coupling between CRUs (Fig.3A); 2) Diastolic SR Ca load alternans occurs concomitantly with cytosolic Ca alternans (Fig.3B); 3) Asynchronous Ca release and mini-waves occur during alternans (Fig.3C); 4) Alternans occurs with reduced LCC open probability. These features agree well with the experimental observations by Diaz and colleagues [6, 8, 16, 45]. However, if SR Ca content is clamped at a certain value in the model, Ca alternans still occurs (Fig.3D), indicating that diastolic SR Ca load alternans is not required for SR depletion or cytosolic Ca alternans, which agrees with the observations by Picht et al [11] and others [5, 20]. This also indicates that the steep fractional release relation is a consequence of the nonlinear response of the RyR clusters to Ca and the coupling between CRUs [66, 68], which does not necessarily have a causal relation to Ca alternans. Using a ramp pacing protocol as in Picht et al [11], a similar Ca release dependence on SR Ca load was observed (Fig.3E). Although diastolic SR Ca load alternans is not required for cytosolic Ca altenans, SR Ca load still plays an important role in the genesis of Ca alternans, as shown in our recent modeling study [40]. In addition, these models have revealed the relationship between random Ca sparks and whole-cell alternans [65, 66] and that alternans is promoted by stronger Ca diffusion [63, 64] and closer CRU spacing [66].

Figure 3. Computer simulations from coupled CRU networks.

A. Steep fractional release–load relationship when the CRUs are uncoupled (open circles) and coupled (solid circles). B. Whole-cell SR Ca (upper trace) and cytoplasmic Ca (lower trace) during alternans. C. A line scan plot of cytoplasmic Ca during alternans, illustrating miniwaves during the large release beats. D. Ca alternans can persist when the SR Ca load is clamped (dashed line). E. SR Ca depletion vs SR Ca content obtained using a similar ramp pacing protocol as Picht et al [11], reproducing the finding that the SR content during regular (non-alternating) beats is lower than during stable alternans, even though the Ca release is less during the small release beat during alternans.

Thus, the computer simulations using detailed Ca cycling models have been very useful in explaining experimental findings and producing new observations. However, they are still too complex to reveal a general mechanistic understanding.

4. The 3R theory

In our recent studies [65, 66], we proposed a theory which links the generic properties of Ca sparks to whole-cell Ca alternans. In this ‘3R theory’, alternans arises via an instability caused by the interactions between three critical properties: Randomness of Ca sparks; Recruitment of a Ca spark by neighboring CRUs; and Refractoriness of a CRU. These are all well-established properties of Ca sparks. In the following discussion, we illustrate how the 3R theory provides a rigorous framework for describing how the above three properties interact to cause alternans. Most importantly, we show how this allows the effects of molecular interventions to be interpreted, based on how they affect the 3R’s.

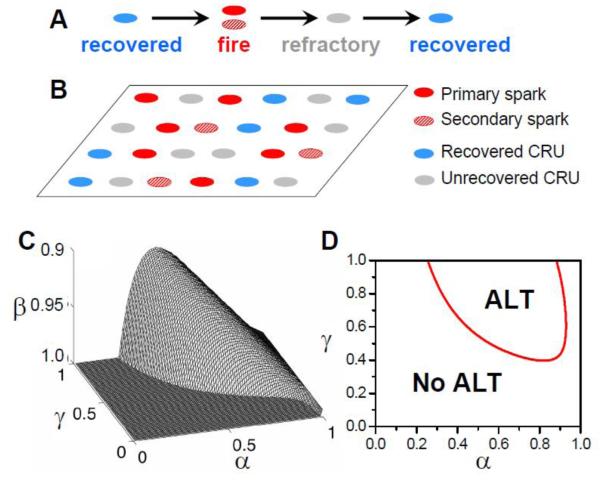
At any time, a CRU is in one of the three states (as illustrated in Fig.4A): recovered, firing (i.e. releasing Ca during a spark), or refractory. A recovered CRU may fire spontaneously due to high SR Ca load or be activated directly by the opening of the LCCs. We call these types of sparks primary sparks (Fig.4B). Ca released from a primary spark may diffuse to its neighboring CRUs, potentially causing recovered CRUs to fire [69]. We call this type of spark a secondary spark. After the firing, a CRU remains refractory for a finite period of time. Due to the random opening properties of LCCs and RyRs, sparks are probabilistic events, thus, we assume the probability of a primary spark to be α and that of a secondary spark to be γ. The recovery of the RyRs and SR refilling in a CRU may give rise to spark amplitude restitution [70, 71] and also random refractory periods [72, 73]. Here we assume that the probability of a CRU not recovering after its previous release is β. If there are a total of N₀ CRUs in the system, and at the k^th beat, N_k sparks occur, then at the following (k+1)^th beat, there are βN_k unrecovered CRUs and (N₀-βN_k) recovered CRUs. The number of primary sparks in this beat is then α(N₀-βN_k), and thus (1-α)(N₀-βN_k) recovered CRUs are available for recruitment. If a fraction f of these CRUs are recruited to fire, then the total number of sparks at (k+1)^th beat is:

$$N_{\mathrm{k}+1}=\alpha (N_0-\beta N_{\mathrm{k}})+(1-\alpha )(N_0-\beta N_{\mathrm{k}})f,$$ (1)

As illustrated in Fig.4B, unless a recovered CRU is adjacent to a CRU that has just fired, it cannot be recruited. Therefore, the fraction f of recruitment is not simply the recruitment probability γ, but a complex function that is determined by the distribution of CRUs in different states. In principle, an exact formulation of f cannot be obtained due to the complex spatial coupling between CRUs. However, using a mean-field approach in which we assume that the system is well mixed so that the firing probability of a CRU is uniform in space, we were able to derive a formulism for f as a function of α, β, γ, and N_k as [65, 66]:

$$f(\alpha ,\beta ,\gamma ,N_{\mathrm{k}})=1-{[1-\alpha \gamma (1-\beta N_{\mathrm{k}}∕N_0)]}^M,$$ (2)

where M is the number of nearest neighbors of a CRU, which is 4 in a two-dimensional array (Fig.4B) and 6 in a three-dimensional array. Note that in a real myocyte, a CRU may be capable of recruiting not only its nearest neighbors, but also non-neighboring CRU’s due to Ca diffusion, such that M can be larger than 6. Eq.1 is an iterative map and can be used to study the beat-to-beat spark dynamics, and thus predict the occurrence of Ca alternans.

Figure 4. 3R theory of alternans.

A. The transition between three CRUs states. B. Schematic plot of spatial distribution of CRUs in different states. C. Alternans region (underneath the surface) in the α-β-γ parameter space. D. Alternans in a two-dimensional slice from the three-dimensional space with β=0.98. Red line demarcates the boundary between alternating (ALT) and non-alternating behavior (No ALT).

Based on Eqs.1 and 2, no alternans can occur in the following three cases: 1) If there is no recruitment (γ=0), then f=0, such that Eq.1 becomes a linear equation with the equilibrium state being N_eq=αN₀/(1+αβ). 2) If α=1, all sparks are primary, and no recruitment can occur (even if γ>0), such that Eq.1 also becomes a linear equation with the equilibrium state of N_eq=N₀/(1+β). 3) If the CRUs fully recover from their previous firings (β=0), then the right side of Eq.1 becomes a constant and N_eq=N₀-(1-α)N₀(1-αγ)^M. Therefore, for alternans to occur in Eq.1, refractoriness, recruitment, and a certain degree of randomness are required. Through performing a linear stability analysis or numerical simulation of Eq. 1, one can predict that alternans occurs at large β (>0.9), large γ, and intermediate α (Figs.4C and D).

Several implications arise from predictions of the 3R theory. Intermediate α means that there must be enough CRUs available for recruitment such that neighboring CRUs all fire in one beat and remain refractory in the next beat, which also requires strong coupling (large γ). If α=1, all recovered CRUs fire as primary sparks, and no recruitment can occur. This explains why asynchronous Ca release and mini-waves were required for alternans to occur in experiments by Diaz et al [6, 8, 16]. Large β means that the majority of CRUs are refractory after firing during the previous beat, which indicates that these CRUs will fire on every other beat due to refractoriness, causing alternans at the individual CRU scale. However, if there is no spark recruitment (no coupling between CRUs), then due to randomness, the individual CRU alternans are randomly out of phase, resulting in microscopic alternans without whole-cell Ca alternans. Large γ allows for spark recruitment to synchronize alternating CRUs more or less together in the same phase so that there are more Ca sparks in one beat than the next beat, resulting in macroscopic alternans. This agrees with simulations in detailed models showing that alternans is promoted by stronger Ca diffusion [63] or closer CRU spacing [66]. This may also explain the transition from microscopic alternans to macroscopic alternans seen by Tian et al [39] in their recent experimental study (shown in Fig.1). Specifically, at the slower pacing rate, alternans occur at individual coupling sites or CRUs due to refractoriness, but the refractoriness β and the coupling strength γ are not large enough to result in macroscopic alternans. At the faster pacing rate, more sites become refractory (larger β) and the overall Ca accumulation at faster rates enhances CRU coupling, causing macroscopic alternans to occur. Finally, unlike α, β, and γ, SR Ca content is not an explicit parameter in the 3R theory, which means that SR Ca load alternans is not a requirement for Ca alternans, in line with the observation that Ca alternans can occur without diastolic SR Ca load alternans [5, 11, 20] and under SR Ca clamp conditions [40, 66].

5. Linking Ca cycling protein properties to alternans via the 3R theory

Due to its complex interactions, the effect of a Ca cycling protein (e.g., RyR) on Ca alternans is typically not straightforward, and, as described in Section 2, can lead to seemingly contradictory outcomes. The 3R theory, when combined with computer simulations, can be used as a unifying framework to understand how Ca cycling protein properties affect alternans and often resolve these contradictions. Based on our recent simulation studies [40, 66], we conclude that the effects of Ca cycling proteins on Ca alternans are mediated both by their direct effects on the 3R’s and by their effects on SR Ca load, which then indirectly affect the 3R’s (see section 5.1 below), as illustrated in Fig.5. To establish the key links, one can estimate the functional values of α, β, and γ from a simple CRU system (Fig.6). Although one cannot quantitatively match results between the simple and the whole system due to several limitations [40], this approach can still provide valuable insights into how Ca cycling proteins and other parameters influence Ca alternans, potentially reconciling the inconsistencies between experiments, as described below.

Figure 5.

Schematic diagram shows how Ca cycling proteins and other regulatory parameters affect Ca alternans via the common pathway of the 3R’s.

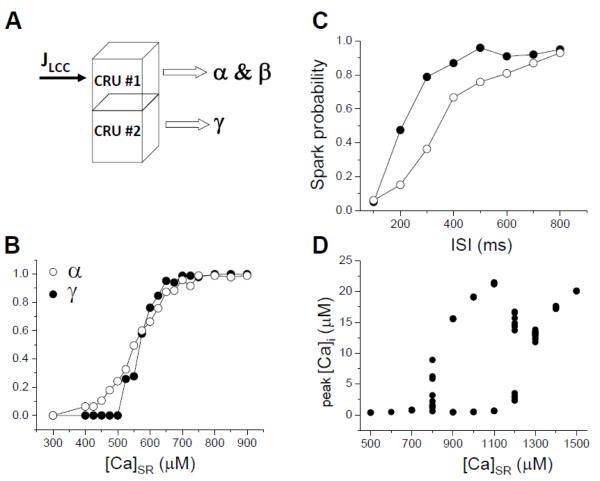
Figure 6.

A. A simple two-CRU system for functionally estimating α, β, and γ. B. α and γ vs SR load calculated from the two-CRU system with SR clamped. C. Spark probability vs the time interval after the first spark for two different RyR recovery time constants in the RyR model when [Ca]_SR was clamped at 800 μM, as an estimate of spark refractoriness (β). D. Ca alternans (double-valued region) vs clamped SR Ca load.

5.1. SR Ca load

Although both experiments and simulations show that diastolic SR Ca load alternans is not required for Ca alternans, this does not mean that SR Ca load is unimportant. To the contrary, SR Ca load plays a very important role in Ca alternans. As shown in simulations [40, 66], alternans can only occur over a limited range of SR Ca load when SR Ca is clamped, and is otherwise suppressed at lower and higher SR Ca loads (Fig.6D). This can be understood as follows. Since Ca flux through an open RyR is proportional to SR Ca content, higher SR Ca load results in a larger Ca flux, facilitating CICR. This makes it easier for LCCs to trigger Ca sparks, and thus increases the primary spark probability α and the secondary spark probability γ (Fig.6B). At low SR Ca, both α and γ are small and thus no alternans occurs. At high SR Ca load, both α and γ are large, with α too large for alternans to occur (see Fig.4D). Only in the intermediate range, when γ is large enough and α is in the proper range, does alternans develop. In addition to this direct effect, many experimental studies [74-77] have shown that the RyR open probability is also affected by luminal Ca, i.e., for a higher SR Ca load, the RyR open probability is higher. This will further enhance the effects of SR Ca load on α and γ.

SR Ca load also affects the refractoriness (β) of Ca release. First, SR Ca load may directly affect on refractoriness. Specifically, when the SR Ca load is higher, it takes less time to refill the junctional SR to a level permissive for sparks. Under conditions in which the recovery time of RyRs is shorter than the SR refilling time, the refractoriness of Ca release is then determined by the SR refilling time. Second, SR Ca load has indirect effects on refractoriness via luminal Ca regulation of RyR excitability. Two mechanisms have been proposed. In the first, RyR sensitivity is co-regulated by a Ca-binding site in the RyR C terminus [76], which senses SR luminal free Ca, such that RyR recovery is affected by luminal Ca refilling and the site’s Ca rebinding kinetics. In the second, Ca and calsequestion binding to the RyR complex are proposed to regulate refractoriness [74, 75] such that recovery is affected by luminal Ca refilling and Ca-calsequestrin binding kinetics. Therefore, a higher SR Ca load will result in a shorter refractory period. It is important to note, however, that the qualitative behaviors predicted by the 3R theory depend only on a general mechanism of refractoriness, whether mediated by luminal Ca regulation or intrinsic RyR properties.

5.2. Heart rate

In most studies, Ca alternans occurs as heart rate increases. The most direct effect of heart rate is on the refractory parameter β, since shortening cycle length increases the probability (β) of a CRU still being in the refractory state after firing during the previous beat. As indicated by the 3R theory, cycle length needs to be short enough so that the majority of the CRUs remain refractory from the previous cycle. Another effect of increased heart rate is that the LCC open probability is reduced due to the incomplete recovery from inactivation of the LCCs. This reduces α which also affects Ca alternans. Heart rate can also affect Ca alternans by altering SR Ca load [78]. A possible scenario occurring in the transition from microscopic alternans to macroscopic alternans observed by Tian et al [39] is the following. For cycle lengths at which microscopic alternans occurs, the refractory period of the CRUs is longer than the cycle length, causing the CRUs to fire on every other beat. However, the coupling between CRUs is yet not strong enough to synchronize the microscopic alternans into macroscopic alternans. As the cycle length becomes shorter, the Ca load increases, which increases the coupling between the CRUs causing the phase of microscopic alternans to synchronize and result in macroscopic alternans.

5.3. Ca cycling proteins

5.3.1. LCC

I_NCX and I_Ca,L are the two sarcolemmal ionic currents that affect Ca cycling most directly. Other currents also affect Ca cycling through their effects on voltage, but are diminished under voltage clamp conditions. The effect of LCCs on Ca alternans is complex. First, increasing (or decreasing) the LCC open probability or conductance directly increases (or decreases) the primary spark probability α. Second, increasing (or decreasing) the LCC open probability or conductance increases (or decreases) the Ca load of the cell, which increases (or decreases) both α and γ. Therefore, if the CRU coupling is strong (large γ), both high and low LCC open probability or conductance will suppress alternans due to α being too large or too small. This could be the scenario observed by Saitoh et al [61] that either LCC agonist, BayK8644, or LCC blocker, nisodipine, suppressed mechanical alternans in ventricular myocytes. However, if γ is small due to low Ca or weak CRU coupling, then increasing the LCC open probability or conductance may promote alternans. This could be what occurs in the experiments in which BayK8644 promotes Ca alternans [13, 14]. Thus, the 3R theory can explain in principle the contradictory experimental observations using LCC agonists or antagonists to affect Ca alternans [8, 13, 14, 16, 43, 44, 61]. In practice, the exact interpretation depends on the experimental conditions. For example, in the experiments by Diaz et al [8, 16], the LCC open probability was reduced by clamping voltage to a less depolarized level to lower α, but a higher extracellular [Ca] was needed to maintain the Ca load so that γ remained strong enough to allow recruitment (as indicated by mini-waves) to occur. These two changes bring α and γ in the alternans regime as predicted by the 3R theory.

In addition, the sarcolemmal distribution of LCC and LCC-RyR coupling fidelity also affect the genesis of Ca alternans by affecting α. For example, in heart failure the RyR sensitivity is increased, which increases both α and γ, suppressing alternans based on simulations and the 3R theory [40]. However, many studies have shown that T-tubules are disrupted or disorganized in heart failure [79-81], which causes the LCC distribution to change, leading to orphaned RyR clusters, which reduce α. Therefore, the combined effects of increased RyR sensitivity and T-tubule disorganization may be responsible for Ca alternans in heart failure.

5.3.2. NCX

The effect of I_NCX on Ca alternans can be understood as follows. NCX operates in two modes during the cardiac cycle. At depolarized voltages, NCX favors the reverse mode, bringing Ca into the cells, while repolarized voltages favor the forward mode, removing Ca from the cell. Therefore, the reverse mode of NCX may help to induce Ca sparks, although this effect is small since the Ca brought in by NCX is less than that brought in by LCCs, and NCX does not necessarily co-localize with the RyR clusters. Since the net effect of NCX is to remove Ca from the cell, increasing NCX reduces the Ca load of the cell, which suppresses alternans if the myocyte is already in the alternans regime, as shown in our simulations [40].

5.3.3. RyR

RyRs are the SR Ca release channels, and thus their properties directly affect the Ca spark rate, the refractoriness of Ca release, and the coupling between CRUs. Increasing RyR open probability or sensitivity increases both α and γ if the SR Ca is fixed. However, an increase in RyR sensitivity causes the SR to be more leaky due to more frequent random RyR channel openings as well as more spontaneous Ca sparks. This causes a decrease in SR Ca load, which in turn causes a decrease in α and γ. Therefore, altering RyR open probability or sensitivity has competing effects on α and γ. Depending on which effect is dominant, it can either promote or suppress alternans. In our recent computer simulations [40], we showed that increasing RyR sensitivity suppressed alternans due to lowered SR Ca. Lowering SR Ca may be the primary cause for alternans suppression by caffeine and ryanodine [1, 13, 56, 57]. However, many experiments show that increasing RyR sensitivity increases the susceptibility to alternans, such as in redox modification of RyR sensitivity [17] or in RyR mutations causing CPVT [41, 42, 58], while stabilizing RyR by FK506 suppressed alternans [13]. In these experiments, the effect of RyR sensitivity on γ may be the dominant factor promoting alternans.

The roles of RyRs on the refractoriness of Ca release are still under debate [73]. Computer simulations show that increasing the sensitivity of RyRs to myoplasmic Ca appears to speed the recovery of Ca sparks [72]. Calsequestrin has been shown to regulate RyR refractoriness in experimental studies [21, 82]. Changes in refractoriness may be the dominant factor suppressing alternans in the mouse model of CPVT by calsequestrin knockout [21], and promoting alternans in calsequestrin overexpressing mice [60].

RyR cluster distribution [83, 84] may also play a role in alternans. It is not clear how heterogeneity may directly influence alternans, but the RyR cluster size and the distance between clusters indirectly affects the coupling strength between CRUs, and thus the spark recruitment. RyR cluster spacing has been shown to be reduced in failing myocytes [85] and has been shown to promote Ca alternans [66] and Ca waves [86] in computer simulation studies due to enhanced spark recruitment [87].

5.3.4. SERCA

SERCA pump affects coupling between CRUs, but also determines the SR Ca load. Increasing the strength of SERCA results in a faster removal of Ca from the cytosol, and thus less Ca is available to diffuse to neighboring CRUs, decreasing the recruitment rate γ if the SR Ca load remains the same. However, increased SERCA also causes a higher SR Ca load, which then increases both α and γ. In our simulations [40], we observed that increasing SERCA activity above the control value in our model suppressed alternans, even though SR Ca load became higher, agreeing with experimental observation that overexpressing SERCA2a suppresses Ca alternans [13, 15] and reducing SERCA2a enhances Ca alternans [10]. Our simulations also showed that severely attenuating the SERCA pump abolished Ca alternans due to reduced SR Ca load. SERCA may also alter refractoriness by altering the refilling rate of the SR, as shown experimentally at both the cellular [88] and the spark [72] levels.

5.4. Cytosolic Ca buffer

Cytosolic Ca buffers affect the coupling between CRUs and the SR Ca load. Increasing Ca buffering in the cytosol reduces Ca available to diffuse to neighboring CRUs, and thus decreases the coupling strength. However, increased Ca buffering may also increase SR Ca load due to reduced spontaneous Ca release. In addition, myoplasmic Ca buffers may slow refilling of SR Ca, and thereby slow recovery from refractoriness [89]. Our simulations showed that a decrease in the buffering concentration increased γ and promoted alternans [40], even though the average SR Ca load was lower, indicating that the direct effect of buffering on CRU coupling dominates. This agrees with the experimental results that enhancing cytosolic Ca buffering suppressed Ca alternans [90].

6. Conclusions

As reviewed above, experimental, computational and theoretical studies have generated considerable insights into the mechanisms of Ca cycling dynamics in cardiac myocytes. The local control theory developed by Stern [91], validated by the experimental observation of Ca sparks by Cheng et al [31], has provided a fundamental theory of excitation-contraction coupling under normal conditions. This theory integrates CICR and randomness to explain the graded response of Ca release, such that during normal excitation-contraction coupling, Ca sparks caused by CICR occur as probabilistic events proportional to the Ca entry from the LCCs. Due to the random nature of Ca sparks, the cell is a microscopically disordered system. For physiological excitation-contraction coupling, the whole-cell Ca transient remains regular from beat to beat as long as the total number CRUs firing remains constant from beat to beat (by a simple application of the law of averages). When whole-cell alternans occurs, however, a new non-trivial temporal order emerges in which the phase of alternating Ca release (even:odd versus odd:even) has become synchronized between the majority of CRUs. The key to understanding the mechanisms of Ca alternans is to explain the self-organization of random Ca sparks into macroscopic patterns, or more generally the transition from disorder to order, a fundamental topic in nonequilibrium statistical physics and pattern formation in nature [34-38].

The 3R theory [65, 66] has been successful in providing a unifying holistic theory to explain this transition and integrate the complex effects of Ca cycling proteins and other sub-cellular and cellular parameters on Ca alternans that have been observed in experiments and computer simulations. An important corollary is that because alternans is an emergent property arising from the complex sub-cellular interactions between the 3R’s, individual Ca cycling proteins have complex effects on Ca alternans (Fig.5), which cannot be understood by studying the properties of the protein alone. Future refinements of the 3R theory will require accounting for the effects of physiologically relevant heterogeneities, such as the heterogeneous distribution of the RyR clusters [83], spark amplitude restitution [70], and incorporating networks of mitochondria and myofilaments. The 3R theory is not likely to be the only theory capable of explaining Ca alternans, and other theoretical frameworks may exist. However, whatever the underlying mechanisms, a key requirement for any successful theory must be to reveal how order arises from disorder, as random Ca sparks synchronize to give rise to macroscopic alternans. In addition, to fully understand electromechanical alternans in cardiac myocytes, the coupled dynamics of Ca and voltage systems, both independently capable of generating alternans, must be integrated. As shown in previous studies [49, 54, 55, 92, 93], this coupling not only modulates Ca and electrical alternans, but also results in novel excitation-contraction coupling dynamics. Moreover, to understand the roles of Ca alternans in T-wave alternans and arrhythmogenesis at the tissue and organ levels [68, 94, 95], one needs also to understand how these cellular properties, which represent the integrated behavior of Ca sparks, interact at the multi-cellular level to manifest as cardiac arrhythmias.

Highlights.

• Calcium alternans is a self-organized pattern from random sparks.

• Alternans arises due to interaction of randomness, recruitment, and refractoriness.

• The 3R theory is a unifying theoretical framework for calcium alternans.

• The 3R theory can reconcile inconsistence between experiments.

• The 3R theory can be used to link calcium cycling protein properties to alternans.