Real-time single airborne nanoparticle detection with nanomechanical resonant filter-fiber

Abstract

Nanomechanical resonators have an unprecedented mass sensitivity sufficient to detect single molecules, viruses or nanoparticles. The challenge with nanomechanical mass sensors is the direction of nano-sized samples onto the resonator. In this work we present an efficient inertial sampling technique and gravimetric detection of airborne nanoparticles with a nanomechanical resonant filter-fiber. By increasing the nanoparticle momentum the dominant collection mechanism changes from diffusion to more efficient inertial impaction. In doing so we reach a single filter-fiber collection efficiency of 65 ± 31% for 28 nm silica nanoparticles. Finally, we show the detection of single 100 nm silver nanoparticles. The presented method is suitable for environmental or security applications where low-cost and portable monitors are demanded. It also constitutes a unique technique for the fundamental study of single filter-fiber behavior. We present the direct measurement of diffusive nanoparticle collection on a single filter-fiber qualitatively confirming Langmuir's model from 1942.

The industrial use of engineered nanoparticles has increased dramatically in recent years, raising the risk of human exposure to nanomaterials. The uptake of airborne nanoparticles by inhalation is a major exposure scenario¹,². Engineered airborne nanoparticles can cause severe harm such as pulmonary inflammation, asthma, chronic obstructive pulmonary disease, and lung cancer when inhaled³,⁴. From the respiratory tract they can translocate to secondary organs such as the lymphatic or blood circulation⁵. Low-cost, portable personal airborne nanoparticle monitors have been demanded for years by authorities and the nanoparticle producing industry⁶.

Nanomechanical resonators have been used to detect single biomolecules⁷, viruses⁸,⁹, and nanoparticles¹⁰,¹¹,¹². The mass sensitivity of a mechanical resonator is a function of its resonance frequency and inverse of its mass. This has led to the realization of nanomechanical resonators with a mass resolution down to the yoctogram (10⁻²⁴ g) range¹³. The superiority of nanomechanical mass sensors is restricted to point mass measurements compared to distributed mass sensing where the added mass is homogeneously covering an entire surface¹⁴. Thus, the main application-field of nanomechanical mass sensors lies in the detection of single sample entities, e.g. in nanomechanical mass spectrometry⁷. In order to achieve the high mass resolution, nanomechanical resonators are often kept in ultrahigh vacuum and/or cryogenic temperatures⁷,¹⁰,¹³,¹⁵,¹⁶. This is impractical in case a small and portable sensor is required. It has been shown that nanomechanical resonators driven at room temperature and ambient pressure have a mass resolution in the attogram (10⁻¹⁸ g) range¹⁷. This is sufficient to detect single airborne viruses or nanoparticles.

The challenge with all nanomechanical mass sensors is the small probability that a sample entity will spontaneously hit the small resonator surface. In high vacuum, absorption events in minute cycles have been recorded⁷. In air, the generally poor sampling efficiency has been improved by dielectrophoretic attraction¹¹ or by partial vacuum¹². Nevertheless, sampling times of several minutes to hours are typically required in order to collect a small number of particles.

Here, we show that it is possible to efficiently collect and detect single airborne nanoparticles on a nanomechanical resonator in real-time. Nanomechanical resonators have shown the required sensitivity to detect the mass of single nanoparticles in air. But a suitable method to collect airborne nano-samples on a nanomechanical resonator with a high collection efficiency has been missing. In our sampling approach we utilize a method well known from air filtration in which the nanomechanical resonator acts as a single filter-fiber. The aerosol containing the nanoparticles is streaming through the sensor chip passing the doubly-clamped resonator, see Fig. 1a. We show that the sampling efficiency can be enhanced by 3 orders of magnitude by increasing the nanoparticle momentum.

Figure 1.

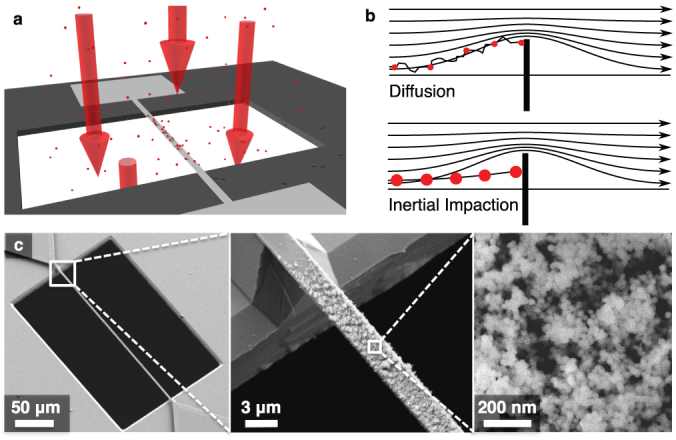
(a) Schematic drawing of a nanomechanical resonant filter-fiber exposed to an aerosol stream.The aerosol containing the nanoparticles is flowing through an orifice in the chip thereby passing the resonant filter-fiber. (b) The airborne nanoparticles are collected on the filter-fiber either by Brownian diffusion or inertial impaction, depending on their momentum. Particles with a small momentum (small size or low velocity) are most efficiently collected by diffusion. The thermal wiggling of the particles increases the probability of adsorption on the fiber when passing by on an intercepting streamline. Particles with a large momentum (large size or high velocity) are collected most efficiently by inertial impaction. If the momentum is big enough the particle trajectory leaves the streamline and it impinges on the fiber. (c) Scanning electron microscope image of a used filter-fiber covered with 28 nm silica nanoparticles. It can be seen that the nanoparticles are exclusively captured on the fiber and not on the achor area.

Using fibrous filters is a very common and well established method to clean air from micron and submicron sized particles. The airborne particles are streaming through the filter and are captured by individual filter-fibers. The main mechanisms considered in this work by which nanoparticles are captured are inertial impaction and diffusion¹⁸, as schematically depicted in Fig. 1b. In inertial impaction the particle mass can, due to its mass, not follow the air streamline which bends abruptly around the fiber. The particle trajectory leaves the streamline and the particle impinges on the fiber. Collection due to diffusion is based on the Brownian motion of small particles. The thermal wiggling of the particles increases the probability of adsorption on the fiber when passing by on an intercepting streamline. Inertial impaction is generally most effective for filtering micro-sized particles. The mechanism is often used as low pass particle filters in so called “impactors”. Diffusion is most effective filtering nano-sized particles. Other deposition mechanisms such as interception and electrostatic precipitation are neglected in our work because the particles are a lot smaller than the filter fiber and they are uncharged.

The single filter-fiber collection efficiency is defined as the fraction of particles deposited on the filter-fiber to the total number of particles that would have passed through the fiber if they had moved on straight lines. We define the total collection efficiency E_c as the sum of the collection efficiencies due to Brownian diffusion E_D and inertial impaction E_I¹⁸,¹⁹,²⁰,²¹

where d_f is the fiber diameter and u the air velocity. a₁ and a₂ are constant depending on the particle and the fluid in which they are suspended (see supplementary information). A multitude of analytical and often empirical expressions for the collection efficiency have been developed over the years. Equation (1) represents the common denominator of the majority of models. Even though the models for collection efficiency are based on cylindrical filter-fibers, equation (1) is also true for rectangular fibers²². It can be seen that the collection efficiency is maximum for narrow fibers, which is supporting the use of nanomechanical filter-fibers. The number of particles collected per time is given by

with the particle number concentration C_p, and the fiber length L. It can be seen that there are two sampling regimes. At low velocities diffusion is dominant with (u^1/3) and at higher velocities most particles are collected by inertial impaction with (u²). Thus the number of collected particles can be maximized by increasing the velocity of the nanoparticles until the momentum becomes large enough such that the nanoparticles escape the air streamline and collect on the fiber by inertial impaction. In order to increase the aerosol velocity the chips feature a small orifice through which the air is accelerated. The nanomechanical resonant filter-fiber is spanned over the orifice and the aerosol passes the fiber perpendicularly. Fig. 1c shows a typical device used in this work after an experiment. It is fully covered with nanoparticles.

Assuming that the fiber surface is homogeneously covered with nanoparticles it can be modelled as a lumped element linear resonator with a resonance frequency f_r. For low damping and small mass changes, the mass sensitivity can be written as

where m₀ is the mass of the fiber. For monodisperse nanoparticles with an individual mass Δm, the change in mass is equal to

Based on (3), (4), and (2), and assuming that the particle collection is dominated by inertial impaction, the gravimetric frequency change per time then becomes a linear function of the particle concentration C_p(t)

Results

From diffusive to inertial sampling

To study the collection mechanisms predicted by (2), a single resonant filter-fiber was exposed to silica aerosol with varying velocities. Fig. 2a shows the resonance frequency change as a function of aerosol velocity through the orifice. At low velocities the measured frequency slopes follow a u^1/3 curve representing the diffusive particle collection. At higher aerosol flows, the slope steepens and follows a quadratic curve expected for inertial impaction. At the maximum aerosol velocity of 52.5 m/s the resonance frequency decreases with −1950 Hz/s which corresponds to 42100 ± 14400 particles/s. The resulting single filter-fiber collection efficiency, calculated from (5), is E_I = 65 ± 31%. In Fig. 2b the resonance frequency trend for the lowest and highest measured air velocities is shown.

Figure 2. The response of a resonant filter-fiber (3 μm wide, 138 μm long, and 220 nm thick silicon nitride fiber coated with a layer of 50 nm Al) to 28.0 ± 3.2 nm silica nanoparticles with a concentration of 3 × 10⁶ ± 1 × 10⁶ particles/cm³.

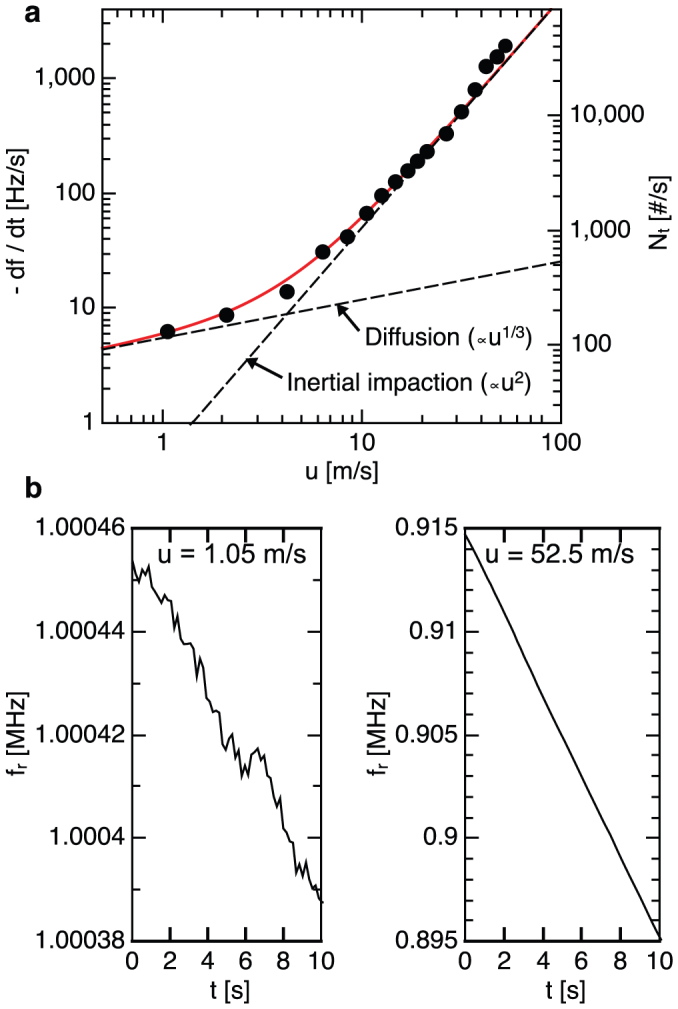
(a) Frequency slope of the fiber resonance for different aerosol velocities from 1.05 to 52.5 m/s. The red line represent the fit with equation (2). (b) Frequency trend for the lowest and highest air velocity.

Detection of particle concentrations

According to (5), the frequency shift is a linear function of the nanoparticle concentration. In Fig. 3a the resonance frequency as a function of nanoparticle concentration is shown and in Fig. 3b the frequency derivation is compared to the corresponding particle concentration. It can be seen that the frequency derivative is accurately following the nanoparticle concentration. At the highest particle concentration of C_p = 5.4 × 10⁵ particles/cm³ a slope of −390 Hz/s was measured which corresponds to 19500 ± 4000 particles/s. With a fiber Reynolds number of Re_f = 20 the flow around the resonator is laminar. The collection efficiency can be further enhanced by increasing the velocity without leaving the laminar regime. The damping of the resonator is a linear function of the air velocity (see supplementary information) and thus the frequency resolution drops with increasing aerosol velocity. At some point the damping is too high for the electronic feedback to maintain a stable oscillation.

Figure 3.

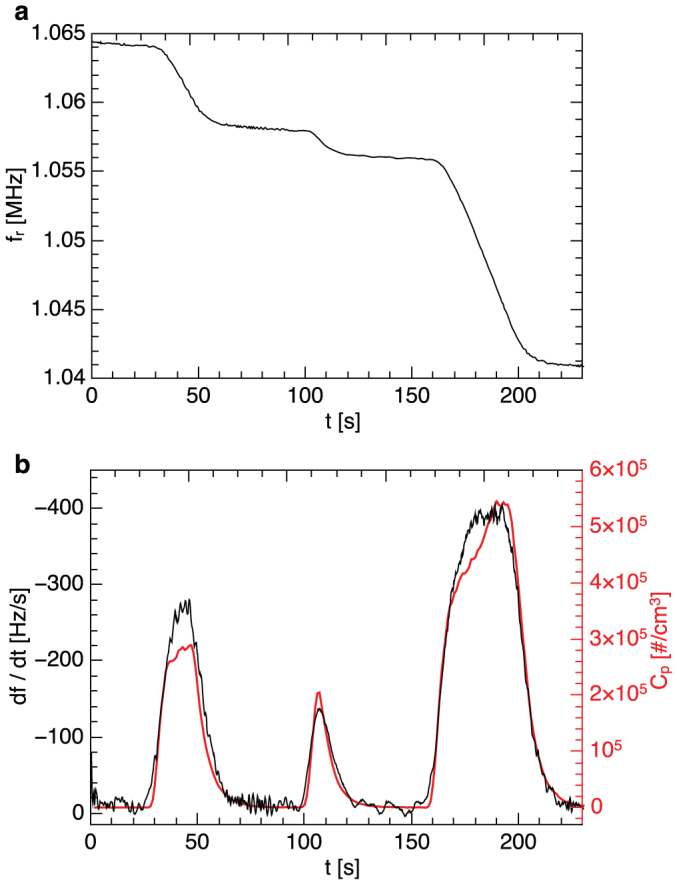
(a) Frequency response of a resonant filter-fiber (w = 3 μm, h = 220 nm, L = 138 μm long silicon nitride string coated with layer of 50 nm Al) to bursts of 24.6 ± 7.4 nm sucrose nanoparticles with different concentrations.The aerosol velocity was 105 m/s. (b) Comparison of the frequency derivative to the nanoparticle concentration. The frequency derivative is a linear function of the particle concentration, as predicted by the model (2). For taking the derivative the frequency curve was smoothed with a moving window average of 50 points.

Detection of single particles

Measuring the mass increase induced by a homogeneous nanoparticle deposition on a resonant filter-fiber requires the knowledge of particle concentration of a monodisperse aerosol in order to resolve the mass of individual particles. It is therefore advantageous to detect the adsorption event of every individual nanoparticle. In Fig. 4a the frequency jumps of a nanomechanical filter-fiber due to collection events of single nanoparticles is shown. The maximum frequency shift of a resonant string due to a single mass is given by Δf = −f_rΔm/m₀²³, which results in Δf = 1117 ± 403 Hz for 100 ± 8 nm Ag particles. In Fig. 4b this theoretical value is compared to the measured frequency jumps. The histrogram of adsorption events versus frequency shifts shows that the largest measured frequency jumps coincide with the expected values. The high event numbers for small frequency jumps are due to frequency noise with a value of 150 Hz which results in a calculated mass resolution of 740 ag.

Figure 4.

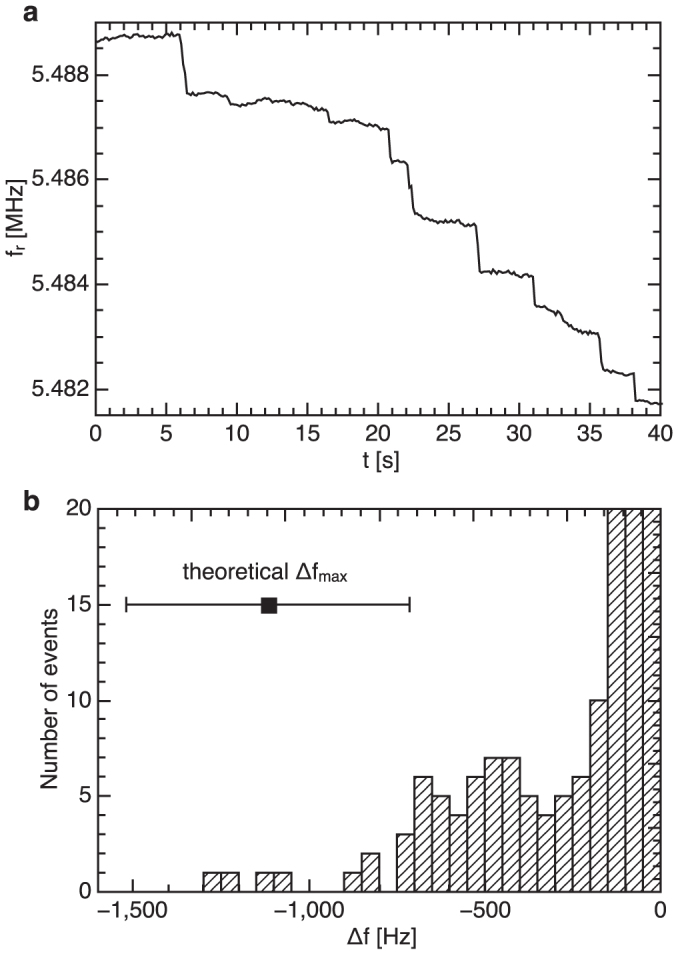
(a) Resonance frequency response of a nanomechanical filter-fiber (1240 nm wide, 50 μm long, 100 nm thick silicon nitride coated with a layer of 50 nm Al) to 100 ± 8 nm silver nanoparticles with a mass of 5.5 ± 1.3 fg at an aerosol velocity of 133 m/s.The impaction of single nanoparticles is causing specific jumps in the resonance frequency of the nanomechanical resonant filter-fiber. The magnitude of the individual frequency jumps is a function of particle mass and landing position along the length of the fiber. The frequency is drift corrected. (b) Histogram of frequency shifts of all measurements recorded with the same filter-fiber. The error bars of the theoretical value of the maximal frequency shift is coming from geometrical uncertainties of the nanoparticles and filter-fiber.

Discussion

The presented experiments were all performed with different nanoparticles. This shows that presented method is applicable for arbitrary nanoparticles. Nanoparticles stick firmly to the resonant filter-fiber by Van-der-Waals forces at room temperature compared to molecules which require cooling of the sensor in order to facilitate physisorption⁷,¹⁰. The silica and silver aerosol was generated from an aqueous nanoparticle suspension. Nanoparticles can form agglomerates in solution which would results in airborne nanoparticle clusters. The used silica particles are known for their high dispersion stability and have shown to produce an aerosol with single particles with only a small number of agglomerates²⁴. The sucrose aerosol is generated by forming droplets of sucrose solution. The droplets dry and single sucrose nanoparticles remain. All the calculations were done under the assumption of zero agglomerations.

The analytical models for the collection efficiency of air filters are based on fluid mechanics of a single filter-fiber. The theory on nanoparticle deposition on single filter-fibers due to Brownian diffusion goes back to Langmuir who made the first approximate calculations in 1942¹⁹,²¹,²⁵,²⁶. Until now, the filter efficiency due to diffusion has only been measured with dense air filters consisting of a multitude of single fibers. The measurement in Fig. 2 presents to our knowledge the first direct measurement of diffusion based nanoparticle precipitation on a single filter-fiber. The measured slope of df/dt = −6.4 ± 0.1 Hz/s is of the same order of magnitude as the calculated value from the theoretical model for a cylindrical fiber (see supplementary information) of df/dt = −2.1 ± 0.7 Hz/s for a fiber Reynolds number of Re_f = 0.2.

Captured nanoparticles adhere to the resonant filter-fiber and do not fall off spontaneously. The coverage of the resonator with particles has not caused any observable degradation of the sensitivity. From experience, a deterioration of the sensor performance was observable once the total particle mass approached the mass of the resonant filter-fiber. During the experiments saturation of the sensor with particles was reached only after extensive exposure to high particle concentrations for hours. Once the resonator is saturated it has to be replaced with a clean one. The used sensor chips feature 3 single resonant filter-fibers each having an individual orifice. In future applications, single sensor strings can be adressed individually by guiding the aerosol through a single orifice, without the need to replace an entire sensor chip.

In conclusion we have shown that airborne nanoparticles can be efficiently collected on a nanomechanical resonant filter-fiber. The collection is most efficient at high aerosol velocities when nanoparticles gain sufficient momentum to leave the streamline and impinge on the resonator. It is possible to collect 28 nm silica nanoparticles with a single filter-fiber collection efficiency of up to 65 ± 31%. The additional mass due to the collected particles from a monodisperse aerosol results in a linear frequency change as a function of particle concentration. Also, frequency jumps due to the collection of individual nanoparticles have been detected.

For a future application in order to obtain a nanoparticle mass spectrum, the mass of individual particles can be determined in real-time by applying a dual-mode operation of the resonator. Therefore the frequency shift of the first and the second bending mode is measured for every particle collection event. The information obtained from the two modes allows the calculation of both, the position of a particle along the length of the fiber and the particle mass. The mass spectrum can then be derived from the real-time mass calculation for every individual particle when it lands on the resonator⁷,²³. By downscaling the resonator it is possible to detect smaller single nanoparticles.

The presented sensor presents a feasible concept for low-cost portable monitors for detection of airborne nanoparticles. The presented inertial collection constitutes a generic technique for efficient sampling of airborne nano-sized samples on nano-sized sensors. It also provides a tool for the fundamental study of single filter-fiber nanoparticle collection. It is our hope that this efficient and simple sampling technique can facilitate the spread and usability of nano-scale sensors.

Methods

Fabrication of nanomechanical resonators

The nanomechanical resonators were fabricated by standard cleanroom micro processing, similar to the process described in²⁷. 100 nm or 220 nm silicon nitride (SiN) was grown on double sided polished silicon wafers by low pressure chemical vapor deposition (LPCVD). The silicon nitride layers were patterned by UV contact and deep-UV projection lithography and structured with a deep reactive ion etcher. The front side with the resonator pattern was covered with a 500 nm thick layer of plasma enhanced chemical vapor deposited (PECVD) silicon nitride. The orifice was then etched through the wafer from the backside with an anisotropic KOH etch. The front side PECVD was removed in buffered HF, releasing the resonators. Finally, a 50 nm thick Al layer was evaporated on the front-side.

Measurement setup

The sensor chip was mounted in an aluminium packaging providing electrical connection, a window for optical readout and connections allowing the aerosol flow through the chip's orifice. The mechanical resonators were driven magnetically by placing them perpendicularly to a static magnetic field and passing an alternating current. The magnetic field was created by neodymium magnets. The vibration of the nanomechanical resonator was read-out by a laser Doppler vibrometer (MSA-500 from Polytec GmbH). The resonator was driven as an oscillator with a phase-locked loop (PLL) with a digital lock-in amplifier (HF2LI from Zurich Instruments with PLL option). The resonance frequency was detected with a frequency counter (53131A from Agilent Technologies) and recorded with a Labview program. The aerosol was produced with an electrospray aerosol generator (EAG 3480 from TSI), neutralizing the aerosol with a radioactive ionizer (Polonium source). The air for the aerosol was filtered with a filtered air supply (3074B from TSI). The aerosol was generated from 28.0 ± 3.2 nm²⁴ silica particles (LUDOX TM-50 colloidal silica from Sigma-Aldrich), sucrose solution resulting in particles of 24.6 ± 7.4 nm, and 100 ± 8 nm Ag particles (nanoComposix NanoXact Silver Citrate). The nanoparticles and sucrose was mixed in 20 mM ammonium acetate buffer with pH 8 for the use with the electrospray. The nanoparticle concentration was varied by dilution of the aerosol with clean air. The aerosol concentration was measured with a diffusion size classifier (DiSCmini from Matter Aerosol) with an accuracy of ±30%, a maximal number concentration of 1 × 10⁶ particles/cm³, and a time resolution of 1 s. The flow rate through the chip was measured with a mass flow meter (4140 from TSI) with an accuracy of ±0.005 L/min. Schematic drawings of the experimental setup are depicted in the supplementary information.

Author Contributions

S. S. designed and conducted the experiments, designed and developed the measurement setup, and designed and planned the fabrication of the nanomechanical resonators. M. K. fabricated the nanomechanical resonators and designed and developed part of the measurement setup. J. Q. A. fabricated the nanomechanical resonators, A. B. supervised the work.

Supplementary Material

Supplementary Information

Supplementary Information