Radiation force of an arbitrary acoustic beam on an elastic sphere in a fluid

Abstract

A theoretical approach is developed to calculate the radiation force of an arbitrary acoustic beam on an elastic sphere in a liquid or gas medium. First, the incident beam is described as a sum of plane waves by employing conventional angular spectrum decomposition. Then, the classical solution for the scattering of a plane wave from an elastic sphere is applied for each plane-wave component of the incident field. The net scattered field is expressed as a superposition of the scattered fields from all angular spectrum components of the incident beam. With this formulation, the incident and scattered waves are superposed in the far field to derive expressions for components of the radiation stress tensor. These expressions are then integrated over a spherical surface to analytically describe the radiation force on an elastic sphere. Limiting cases for particular types of incident beams are presented and are shown to agree with known results. Finally, the analytical expressions are used to calculate radiation forces associated with two specific focusing transducers.

INTRODUCTION

The acoustic radiation force on a spherical scatterer has been investigated for many decades. The first series of papers was devoted to the case of plane1, 2, 3, 4 or spherical5, 6, 7, 8 incident waves. In practice, the incident acoustic field frequently has the form of a beam that cannot be considered as a plane or spherical wave. If the size of the spherical scatterer is much smaller than the beam width, plane-wave theory can still be used if a beam-pattern correction is included. However, for high-frequency focused transducers, the incident field is not necessarily uniform on the scale of the scatterer diameter, which makes such a quasi-plane wave approach incorrect. The case of narrow beams is more difficult to analyze theoretically, which may explain why most later publications were limited to analyzing the radiation force on a sphere positioned on the axis of axisymmetric beams.9, 10, 11 The latest series of publications on this subject has dealt with radiation force on the axis of Bessel beams that are either axisymmetric (zero-order beam)12 or angularly dependent (high-order beams).13, 14

In one important special situation, the radiation force on a sphere can be analytically expressed for an acoustic field of an arbitrary structure. This is the case of a sphere with a diameter much smaller than the wavelength. For such a small scatterer, it is sufficient to consider only the monopole and dipole terms in the diffracted field. Under this approximation, the radiation force F on a small sphere can be expressed as $\mathbf{F}=-\nabla \hspace{0.17em}U$, where the potential U is a known function of mean square fluctuations of the acoustic pressure and particle velocity at the point where the scatterer is located.15

For many applications, it is desirable to have a formulation for the radiation force produced by arbitrary incident waves, regardless of the acoustic beam structure or the size and position of the scatterer. When an incident wave acts on a scatterer, radiation force appears as a result of both the incident and scattered waves. Therefore, the force calculation is based on the solution of the scattering problem. There are several approaches for calculating the scattered field. The most direct way is to numerically compute the acoustic field using a straightforward technique such as finite differences. The calculated acoustic field can then be used to calculate the radiation force on a given scatterer.16, 17 Such an approach is very powerful because it can be implemented for any acoustic field and a scatterer of any shape or size. However, at present this approach remains computationally challenging and is practical only for axisymmetric or two-dimensional (2D) geometries. Accordingly, analytical calculations are still of interest because they can help to provide fast, precise, and easy-to-implement algorithms for calculating radiation forces. In particular, analytic methods are especially effective for cases of spherical objects in fluids, for which scattering theory is well-developed. For instance, a multipole expansion can be used to represent the acoustic field,18, 19 which makes it possible to express the radiation force for an arbitrary beam. In Ref. 20 such an approach was used to calculate the radiation force on a rigid sphere from a plane wave propagating in an arbitrary direction.

The current paper describes an approach that allows derivation of analytical expressions for the radiation force components due to the incidence of an arbitrary acoustic beam on any spherical scatterer. First, the incident wave is decomposed into a sum of plane waves by the conventional angular spectrum formulation. Then, the known expression for scattering of a plane wave from an elastic sphere (i.e., the spherical harmonics series) is applied for each plane-wave component of the incident field. The net scattered field is expressed as a superposition of the scattered fields from all angular spectrum components of the incident beam. Next, the full acoustic field described by the superposition of incident and scattered waves is considered at an infinitely large distance from the scatterer (in the far field), where corresponding expressions are derived for the components of the radiation stress tensor. Finally, these expressions are integrated over a far field spherical surface to provide analytic formulas for the radiation force components on the sphere. Various limiting cases for several types of incident waves are presented and are shown to agree with results known from the literature. In addition, the obtained expressions are used to calculate radiation forces for ultrasound beams of two specific focusing transducers.

BASIC EQUATIONS

On the radiation force calculation

If the acoustic field is known, the radiation force can be calculated for a given scatterer. In calculating acoustic fields and radiation force in this paper, we assume that the medium is an ideal fluid where the effects of viscosity and thermal conductivity are neglected. Within the second-order approximation, radiation force is known to be expressed in terms of quantities of first order only21

$$\mathbf{F}=\underset{\mathrm{\Sigma }}{∯}\frac{d\mathbf{F}}{d\mathrm{\Sigma }}d\mathrm{\Sigma },$$ (1)

$$\frac{d\mathbf{F}}{d\mathrm{\Sigma }}=\langle \left(\frac{\rho {\tilde{\mathbf{v}}}^2}{2}-\frac{{\tilde{p}}^2}{2\rho c^2}\right)\hspace{0.17em}\mathbf{n}-\rho \tilde{\mathbf{v}}\hspace{0.17em}\left(\tilde{\mathbf{v}}\cdot \mathbf{n}\right)\rangle ,$$ (2)

where Σ is any fixed surface enclosing the scatterer, ρ and c are the fluid density and sound velocity, $\tilde{p}$ and $\tilde{\mathbf{v}}$ are the acoustic pressure and particle velocity, ${\tilde{\mathbf{v}}}^2=\tilde{\mathbf{v}}\cdot \tilde{\mathbf{v}}$, and n is the external unit normal vector for the surface element $d\hspace{0.17em}\mathrm{\Sigma }$. The angular brackets $\langle ·\rangle$ denote averaging over the sound wave period. The expressions for radiation force F in Eqs. 1, 2 come from linear acoustic theory and considerably facilitate radiation force calculations. If the incident beam is known, the problem is reduced to modeling the linear scattering.

Throughout this paper the acoustic field is considered to be a harmonic wave

$$\tilde{p}=\frac{p}{2}{e}^{-i\omega t}+\frac{p^{*}}{2}{e}^{i\omega t},\hspace{1em}\tilde{\mathbf{v}}=\frac{\mathbf{v}}{2}{e}^{-i\omega t}+\frac{{\mathbf{v}}^{*}}{2}{e}^{i\omega t},$$ (3)

where p and v are the pressure and velocity complex amplitudes, the asterisks denote complex conjugates, and $\omega /\left(2\pi \right)$ is the frequency. Substituting expressions 3 into Eq. 2, it follows that

$$\frac{d\mathbf{F}}{d\mathrm{\Sigma }}=\left(\frac{\rho {\left|\mathbf{v} \right|}^2}{4}-\frac{{\left|p\right|}^2}{4\rho c^2}\right)\hspace{0.17em}\mathbf{n}-\frac{\rho }{2}\mathrm{Re}\left[{\mathbf{v}}^{*}\left(\mathbf{v}\cdot \mathbf{n}\right)\right].$$ (4)

Here $\mathrm{Re} \left[ \cdot \right]$ indicates the real part of the term in brackets, ${\left|\mathbf{v} \right|}^2=\mathbf{v}\cdot {\mathbf{v}}^{\ast }$, and ${\left|p \right|}^2=p p^{\ast }$. Note also that the linearized momentum equation $\rho \hspace{0.17em}\partial \tilde{\mathbf{v}}/\partial \hspace{0.17em}t=-\nabla \tilde{p}$ can be used to express the velocity amplitude as

$$\mathbf{v}=\nabla p/\left(i\rho \omega \right),$$ (5)

which implies that the spatial dependence of the pressure amplitude $p=p\left(\mathbf{r}\right)$ contains all necessary information about the acoustic field.

Radiation force is a result of a change in wave momentum due to scattering at an obstacle. The rate of momentum change, averaged over the wave period, equals the radiation force. Because wave momentum is conserved while the wave propagates in an inviscid fluid, the surface Σ in Eq. 1 can be arbitrary.15 In several papers on radiation force, the integration surface used was the surface of the scatterer (e.g., see Refs. 1, 2). Another convenient possibility is to place the integration surface in the far field, where the expressions for $\tilde{p}$ and $\tilde{\mathbf{v}}$ are simplified.15, 11, 12 In the current paper, the latter approach is employed: As in the mentioned publications, the surface Σ is taken to be a spherical surface of infinitely large radius. The vector quantity $d \mathbf{F}/d \mathrm{\Sigma }$, which is used in Eq. 1 for calculating radiation force, is defined from the acoustic field parameters as expressed in Eq. 2. The challenge is therefore determining the scattered field. Next, we describe the calculation of the scattered field and conversion of that field to radiation force.

Scattering and radiation force due to an axisymmetric field—case of a plane wave

The theoretical solution for the scattering of a plane wave from an elastic sphere is a foundation for the approach considered in the current paper. However, the description here will be brief as it summarizes derivations presented elsewhere.11, 22, 23, 24

In the scattering problem, the pressure outside the scatterer can be considered as a superposition of incident and scattered waves

$$p=p_i+p_s.$$ (6)

If the problem is axisymmetric, it is convenient to represent the incident wave as a series of spherical harmonics:

$$p_i={\displaystyle \sum _{n=0}^{\infty }{Q}_n{P}_n\left(\cos \theta \right)j_n\left(\mathit{k}\mathit{r}\right)},$$ (7)

where $P_n(\cdot )$ and $j_n(\cdot )$ are Legendre polynomials and spherical Bessel functions, respectively, $k=\omega /c$ is the wavenumber, r and θ are spherical coordinates, and the coefficients $Q_n$ depend on the specific structure of the incident wave. Consider, for instance, plane-wave scattering. A plane wave is axially symmetric relative to the axis oriented along the propagation direction. In this case, the incident pressure field can be expressed as

$$p_i^{\left(\text{plane}\hspace{0.17em}\text{wave}\right)}=p_0{e}^{\mathit{i}\mathit{k}\mathit{z}}=p_0{e}^{ikr\hspace{0.17em}\cos \theta }.$$ (8)

Here $p_0$ is the wave amplitude and z is the distance along the propagation direction ($z=r\cos \theta$). The theory of a plane wave scattering from a sphere is presented in many publications—e.g., see Refs. 22, 23. The series coefficients $Q_n$ can be defined as follows:

$$Q_n^{\left(\text{plane}\hspace{0.17em}\text{wave}\right)}=p_0{i}^n\left(2n+1\right).$$ (9)

A plane wave is a particular case of an axisymmetric wave. For other cases of axially symmetric fields, Eq. 7 remains valid but the coefficients $Q_n$ are defined differently. For instance, if the incident wave is a spherical wave, $p_i=A{e}^{\mathit{i}\mathit{k}\mathit{R}}/R$, originating from a point source located on the z axis at $z=-r_0$, then

$$Q_n^{\left(\text{spherical}\hspace{0.17em}\text{wave}\right)}=A\cdot ik{\left(-1\right)}^n\left(2n+1\right)h_n^{\left(1\right)}\left(k{r}_0\right),$$ (10)

where $h_n^{\left(1\right)}(\cdot )$ are spherical Hankel functions of the first kind.

For the incident wave described by Eq. 7, the scattered wave can be expressed as a superposition of outgoing waves described by the following series:

$$p_s={\displaystyle \sum _{n=0}^{\infty }{Q}_n{c}_n{h}_n^{\left(1\right)}\left(\mathit{k}\mathit{r}\right)P_n\left(\cos \hspace{0.17em}\theta \right)}.$$ (11)

Here the coefficients $c_n$ depend on the boundary conditions on the sphere's surface at $r=a$. These conditions are a continuity of normal velocity and normal stress, and the absence of tangential stress (because the fluid is assumed to be inviscid). For an isotropic elastic sphere22, 23

$$c_n=-\frac{{\mathrm{\Gamma }}_n{j}_n\left(\mathit{k}\mathit{a}\right)-ka\hspace{0.17em}{j}_n\prime \left(\mathit{k}\mathit{a}\right)}{{\mathrm{\Gamma }}_n{h}_n^{\left(1\right)}\left(\mathit{k}\mathit{a}\right)-ka\hspace{0.17em}{h}_n^{\left(1\right)}\prime \left(\mathit{k}\mathit{a}\right)},$$ (12)

where ${\mathrm{\Gamma }}_n$ are real numbers that depend on the sphere's material properties and the primes indicate differentiation with respect to the argument. The ${\mathrm{\Gamma }}_n$'s are defined as

$${\mathrm{\Gamma }}_n=\frac{\rho \hspace{0.17em}{k_t}^2{a}^2}{2{\rho }_{*}}\frac{{\alpha }_n{\delta }_n+{\beta }_n{\chi }_n}{{\alpha }_n{\eta }_n+{\beta }_n{\epsilon }_n},$$ (13)

where the following notations are used: ${\alpha }_n=j_n\left(k_{l}a\right)-k_{l}a\hspace{0.17em}{j}_n\prime \left(k_{l}a\right)$, ${\beta }_n=\left(n^2+n-2\right)\cdot j_n\left(k_{t}a\right)+{k_t}^2{a}^2{j}_n″\left(k_{t}a\right)$, ${\chi }_n=k_{l}a\hspace{0.17em}{j}_n\prime \left(k_{l}a\right)$, ${\delta }_n=2n\left(n+1\right)j_n\left(k_{t}a\right)$, ${\epsilon }_n=k_l^2{a}^2\left[j_n\left(k_{l}a\right)\hspace{0.17em}\sigma /\left(1-2\sigma \right)-j_n″\left(k_{l}a\right)\right]$, ${\eta }_n=2n\left(n+1\right)\left[j_n\left(k_{t}a\right)-k_{t}a\hspace{0.17em}{j}_n\prime \left(k_{t}a\right)\right]$. Also, a is the radius of the sphere, ${\rho }_{*}$ is its density, $\sigma =\left(c_l^2/2-c_t^2\right)/\left(c_l^2-c_t^2\right)$ is Poisson's ratio, $c_l$ and $c_t$ are longitudinal and shear wave velocities of the sphere material, and $k_l=\omega /c_l$ and $k_t=\omega /c_t$ are the corresponding wavenumbers.

Note that in the absence of absorption and for each index n, the complex coefficient $c_n$ from Eq. 12 can be expressed through a coefficient $s_n=1+2c_n$, which is unimodular: $\left|s_n\right|=1$. The property $\left|s_n\right|=1$ directly follows from Eq. 12, which gives for real wavenumbers k the following representation: $s_n={\Omega }_n^{\ast }/{\Omega }_n$, where ${\Omega }_n={\mathrm{\Gamma }}_n{h}_n^{\left(1\right)}\left(\mathit{k}\mathit{a}\right)-ka\hspace{0.17em}{h}_n^{\left(1\right)}\prime \left(\mathit{k}\mathit{a}\right)$. In fact, the coefficient $s_n$ is a reflection coefficient for the incoming wave $\sim h_n^{\left(2\right)}\left(\mathit{k}\mathit{r}\right)P_n\left(\cos \theta \right)$ described by the nth spherical harmonic of the full solution described by Eqs. 6, 7, and 11. The corresponding outgoing wave $\sim h_n^{\left(1\right)}\left(\mathit{k}\mathit{r}\right)P_n\left(\cos \hspace{0.17em}\theta \right)$ (i.e., the wave reflected from the sphere) in the absence of dissipation has to have the same energy, which sets the condition $\left|s_n\right|=1$. Therefore, the complex coefficient $c_n$ is expressed through a single real coefficient ${\gamma }_n$, which is the phase of the unimodular scattering function $s_n=e^{i{\gamma }_n}$.

In the axisymmetric case, the radiation force in aligned Cartesian coordinates has only an axial component: $\mathbf{F}=\left(0,\hspace{0.17em}0,\hspace{0.17em}{F}_z\right)$. It is convenient to calculate the radiation force by integrating along a sphere of radius r and letting $r\to \infty$. Then Eqs. 1, 4 yield

$$F_z=-\frac{\pi }{2\rho c^2}{\displaystyle {\int }_0^{\pi }{\left({\left|\mathit{r}\mathit{p}\right|}^2+\frac{1}{k^2}{\left|r\frac{\partial p}{\partial r}\right|}^2\right)|}_{r\to \infty }\sin \hspace{0.17em}\theta \hspace{0.17em}\cos \hspace{0.17em}\theta \hspace{0.17em}d\theta }.$$ (14)

Using Eqs. 6, 7, and 11, and the asymptotes of Bessel and Hankel function as $kr\to \infty$, Eq. 14 becomes

$$\begin{array}{c}{F}_z=-\frac{\pi }{4\rho c^2{k}^2}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }{Q}_n{Q}_m^{*}\left\{i^{m-n}\left(1+2c_n\right)\left(1+2c_m^{*}\right)+i^{-\left(m-n\right)}\right\}}}{\displaystyle {\int }_0^{\pi }{P}_n\left(\cos \theta \right)P_m\left(\cos \theta \right)\sin \theta \cos \theta \hspace{0.17em}d\theta }\hspace{0.17em}\hspace{0.17em}.\end{array}$$ (15)

After using recurrence properties and the orthogonality of Legendre polynomials, the following expression can be derived:

$$F_z=\frac{2\pi }{\rho c^2{k}^2}{\displaystyle \sum _{n=0}^{\infty }\frac{\left(n+1\right)}{\left(2n+1\right)\left(2n+3\right)}\mathrm{Im}\hspace{0.17em}\left\{Q_n{Q}_{n+1}^{*}\left(c_n+c_{n+1}^{*}+2c_n{c}_{n+1}^{*}\right)\right\}}.$$ (16)

Here $\mathrm{Im}\left\{\hspace{0.17em}\cdot \hspace{0.17em}\right\}$ means the imaginary part of the quantity in brackets. This result is in accord with Eqs. (24)–(26) of Ref. 11. As a specific example of an axisymmetric field, consider a plane wave propagating along the axis. Then $Q_n$ is defined by Eq. 9, and

$$F_z^{\left(\text{plane}\hspace{0.17em}\text{wave}\right)}=-\frac{2\pi \hspace{0.17em}{p}_0^2}{\rho c^2{k}^2}{\displaystyle \sum _{n=0}^{\infty }\left(n+1\right)\mathrm{Re}\left(c_n+c_{n+1}^{*}+2c_n{c}_{n+1}^{*}\right)}.$$ (17)

Scattering of an arbitrary beam

In this paper, the goal is to determine the scattered field and the resulting radiation force for an arbitrary beam incident on an elastic sphere. Similar to the specific cases already done in Sec. 2B, in this section first we calculate the scattered field for the arbitrary case. The arbitrary beam is treated as a sum of plane waves.

Consider an acoustic source radiating a beam along the z axis. The source is assumed to be time-harmonic in that the radiated wave is described by Eq. 3. The acoustic field can be characterized by a 2D pressure distribution at some $x\hspace{0.17em}y$ plane in front of the source. Let us choose the origin of the coordinate system at the center of the spherical scatterer. The incident acoustic field is then presumed to be known at $z=0$ so that the complex pressure amplitude is a known function

$${p_i|}_{z=0}=p_i\left(x,y,\hspace{0.17em}0\right).$$ (18)

Note that this function can be calculated from the source vibration pattern using a method such as the Rayleigh integral.25, 26

The scattering problem in the case of an arbitrary incident field does not have a straightforward solution and generally requires several steps to implement.27 The linearity of the problem provides a way around this difficulty as the incident beam can be represented by a superposition of elementary waves for which the solution to the scattering problem is known. There are several alternative descriptions of these waves. For instance, the incident wave can be represented as a series of spherical harmonics;18, 19 the advantage in such an approach is that each spherical harmonic of the incident wave gives rise to the same spherical harmonic of the scattered wave [e.g., compare Eqs. 7, 11]. Another possibility is a superposition of elementary spherical waves in the form of the Rayleigh integral, which is a mathematical formulation of the classical Huygens–Fresnel principle. The problem of the scattering of a spherical wave from an elastic sphere has a known solution given by Eqs. 7, 10, and 11, and thus can be used to calculate the scattered field for any incident beam. The third alternative is to represent the incident beam in the form of the superposition of plane waves of different propagation directions. The corresponding representation is possible because of the Fourier theorem and is known as the angular spectrum method. Again, each elementary wave scatters at the elastic sphere in a known fashion [see Eqs. 7, 9, and 11] and a superposition of such scattered fields provides the solution for any incident wave. Among the three approaches described above, the last one benefits computationally from the fact that all elementary waves are identical (plane waves) and differ only in their direction. Accordingly, the angular spectrum approach is adopted in the current paper.

The superposition of plane waves composing the incident field has the following form:

$$p_i\left(x,y,z\right)=\frac{1}{4{\pi }^2}{\displaystyle {\iint }_{k_x^2+k_y^2\le k^2}d{k}_{x}d{k}_y}S\left(k_x,k_y\right)\hspace{0.17em}{e}^{i{k}_{x}x+i{k}_{y}y+i\sqrt{k^2-k_x^2-k_y^2}\hspace{0.17em}z}.$$ (19)

Here, the integration region $k_x^2+k_y^2\le k^2$ is chosen to neglect the evanescent waves that are exponentially decaying away from the source. The angular spectrum $S\left(k_x,k_y\right)$ characterizes the plane waves' amplitudes. It is expressed from the initial pressure distribution Eq. 18

$$S\left(k_x,k_y\right)={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle {\int }_{-\infty }^{+\infty }dxdy\hspace{0.17em}{p}_i\left(x,y,0\right)\hspace{0.17em}{e}^{-i{k}_{x}x-i{k}_{y}y}}}.$$ (20)

Now consider an elementary plane wave $p_i^{\left(\mathbf{k}\right)}\left(x,y,z\right)=S\left(k_x,k_y\right)\hspace{0.17em}{e}^{i{k}_{x}x+i{k}_{y}y+i\sqrt{k^2-k_x^2-k_y^2}\hspace{0.17em}z}=S\left(k_x,k_y\right)\hspace{0.17em}{e}^{i\mathbf{k}\cdot \mathbf{r}}$ from Eq. 19. It has the wave vector $\mathbf{k}=\left(k_{x\hspace{0.17em}},k_{y\hspace{0.17em}},k_z\right)$ with

$$k_z=\sqrt{k^2-k_x^2-k_y^2}.$$

Note that $\left| \mathbf{k} \right|=k=\omega /c$. The vector k components can be characterized by the spherical angle ${\theta }_k$ and polar angle ${\phi }_k$:

$$\begin{array}{c}{k}_x=k\hspace{0.17em}\sin \hspace{0.17em}{\theta }_k\hspace{0.17em}\cos \hspace{0.17em}{\phi }_k,\\ k_y=k\hspace{0.17em}\sin \hspace{0.17em}{\theta }_k\hspace{0.17em}\sin \hspace{0.17em}{\phi }_k,\\ k_z=k\hspace{0.17em}\cos \hspace{0.17em}{\theta }_k.\end{array}$$ (21)

With consideration of the beam propagation direction, the following expressions follow from Eq. 21: $\cos \hspace{0.17em}{\theta }_k=\sqrt{1-\left(k_x^2+k_y^2\right)/k^2}$, $\sin \hspace{0.17em}{\theta }_k=\sqrt{1-{\cos }^2{\theta }_k}$, and ${\phi }_k=\arctan \left(k_y/k_x\right)$. Similarly, the observation point $\mathbf{r}=\left(x,y,z\right)$ can be described using spherical coordinates

$$\begin{array}{c}x=r\hspace{0.17em}\sin \hspace{0.17em}\theta \hspace{0.17em}\cos \hspace{0.17em}\phi ,\\ y=r\hspace{0.17em}\sin \hspace{0.17em}\theta \hspace{0.17em}\sin \hspace{0.17em}\phi ,\\ z=r\hspace{0.17em}\cos \hspace{0.17em}\theta .\end{array}$$ (22)

From here, $\cos \hspace{0.17em}\theta =z/r$, $\sin \theta =\sqrt{1-{\cos }^2\theta }$, and $\phi =\arctan \left(y/x\right)$. If we define γ to be the angle between the vectors r and k, then $\mathbf{k}\cdot \mathbf{r}=k\hspace{0.17em}r\cos \gamma$. From here and Eqs. 21, 22

$$\cos \gamma =\cos {\theta }_k\cos \theta +\sin \hspace{0.17em}{\theta }_k\hspace{0.17em}\sin \hspace{0.17em}\theta \hspace{0.17em}\cos \hspace{0.17em}\left({\phi }_k-\phi \right).$$ (23)

With use of the angle γ, each elementary plane wave $p_i^{\left(\mathbf{k}\right)}\left(x,y,z\right)=S\left(k_x,k_y\right)\hspace{0.17em}{e}^{i kr\cos \gamma }$ has a form suitable for solving the scattering problem. According to Eqs. 7, 9, the incident plane wave $p_i^{\left(\mathbf{k}\right)}$ has the following representation:

$$p_i^{\left(\mathbf{k}\right)}\left(x,y,z\right)=S\left(k_x,k_y\right){\displaystyle \sum _{n=0}^{\infty }{i}^n\left(2n+1\right)P_n\left(\cos \hspace{0.17em}\gamma \right)j_n\left(\mathit{k}\mathit{r}\right)}.$$ (24)

From Eq. 11, the corresponding scattered wave is

$$p_s^{\left(\mathbf{k}\right)}\left(x,y,z\right)=S\left(k_x,k_y\right){\displaystyle \sum _{n=0}^{\infty }{i}^n\left(2n+1\right)c_n{P}_n\left(\cos \hspace{0.17em}\gamma \right)h_n^{\left(1\right)}\left(\mathit{k}\mathit{r}\right)},$$ (25)

where the scattering coefficients $c_n$ are expressed by Eqs. 12, 13. Note that the superscript $\left(\mathbf{k}\right)$ in the notation of $p_s^{\left(\mathbf{k}\right)}$ indicates the wave vector of the corresponding incident plane wave $p_i^{\left(\mathbf{k}\right)}$ (the scattered wave itself is not a plane wave).

It is desirable to write Eqs. 24, 25 not through the auxiliary angle γ but directly through the angles θ and φ. This can be accomplished with the Legendre addition theorem.28 The theorem states that for $\cos \hspace{0.17em}\gamma$ of Eq. 23 the following equality is valid:

$$P_n\left(\cos \hspace{0.17em}\gamma \right)=\frac{4\pi }{2n+1}{\displaystyle \sum _{m=-n}^n{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)}.$$ (26)

Here, the spherical harmonics $Y_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)$ are expressed in terms of associated Legendre polynomials $P_n^m\left(\cos \hspace{0.17em}\theta \right)$ as

$$Y_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)=\sqrt{\frac{\left(2n+1\right)}{4\pi }\frac{\left(n-m\right)\hspace{0.17em}!}{\left(n+m\right)\hspace{0.17em}!}}\hspace{0.17em}{P}_n^m\left(\cos \hspace{0.17em}\theta \right)\hspace{0.17em}{e}^{im\phi },$$ (27)

where

$$P_n^m\left(x\right)={\left(-1\right)}^m{\left(1-x^2\right)}^{m/2}\frac{d^m{P}_n\left(x\right)}{d x^m}.$$ (28)

In Eq. 27 it is supposed that $m\ge 0$. For the negative indices $m<0$, the following relation should be used:

$$Y_{n,-m}\left(\theta ,\phi \right)={\left(-1\right)}^m{Y}_{n\hspace{0.17em}m}^{\ast }\left(\theta ,\phi \right).$$ (29)

With Eq. 26, the formulas in Eqs. 24, 25 become

$$p_i^{\left(\mathbf{k}\right)}\left(x,y,z\right)=4\pi \hspace{0.17em}S\left(k_x,k_y\right){\displaystyle \sum _{n=0}^{\infty }{i}^n{j}_n\left(\mathit{k}\mathit{r}\right){\displaystyle \sum _{m=-n}^n{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)}},$$ (30)

$$p_s^{\left(\mathbf{k}\right)}\left(x,y,z\right)=4\pi \hspace{0.17em}\hspace{0.17em}S\left(k_x,k_y\right){\displaystyle \sum _{n=0}^{\infty }{i}^n{c}_n{h}_n^{\left(1\right)}\left(\mathit{k}\mathit{r}\right){\displaystyle \sum _{m=-n}^n{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)}}.$$ (31)

In accordance with Eq. 19, the full incident and scattered pressure fields are obtained from Eqs. 30, 31 by multiplying $p_i^{\left(\mathbf{k}\right)}$ and $p_s^{\left(\mathbf{k}\right)}$ by the factor $d{k}_{x}d{k}_y/\left(4{\pi }^2\right)$ and integrating over the region $k_x^2+k_y^2\le k^2$. This gives

$$p_i=\frac{1}{\pi }{\displaystyle \sum _{n=0}^{\infty }{i}^n{j}_n\left(\mathit{k}\mathit{r}\right){\displaystyle \sum _{m=-n}^n{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right){\displaystyle {\iint }_{k_x^2+k_y^2\le k^2}d{k}_{x}d{k}_{y}S\left(k_x,k_y\right)Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)}}},$$ (32)

$$p_s=\frac{1}{\pi }{\displaystyle \sum _{n=0}^{\infty }{i}^n{c}_n{h}_n^{\left(1\right)}\left(\mathit{k}\mathit{r}\right){\displaystyle \sum _{m=-n}^n{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right){\displaystyle {\iint }_{k_x^2+k_y^2\le k^2}d{k}_{x}d{k}_{y}S\left(k_x,k_y\right)Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)}}}.$$ (33)

We now introduce the following notation:

$$H_{\mathit{n}\mathit{m}}={\displaystyle {\iint }_{k_x^2+k_y^2\le k^2}d{k}_{x}d{k}_{y}S\left(k_x,k_y\right)Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)}.$$ (34)

Note that here $\left| m \right|\le n$, i.e., it is supposed that $H_{\mathit{n}\mathit{m}}=$ 0 for $\left|m \right|>n$. The array of constants $H_{\mathit{n}\mathit{m}}$ fully defines the incident acoustic beam and does not depend on the scattering sphere's radius or material properties. The resulting complex amplitude of the total pressure $p=p_i+p_s$ is therefore

$$p=\frac{1}{\pi }{\displaystyle \sum _{n=0}^{\infty }{i}^n\left\{\hspace{0.17em}{j}_n\left(\mathit{k}\mathit{r}\right)+c_n{h}_n^{\left(1\right)}\left(\mathit{k}\mathit{r}\right)\hspace{0.17em}\right\}{\displaystyle \sum _{m=-n}^n{H}_{\mathit{n}\mathit{m}}{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)}}.$$ (35)

The corresponding expressions for particle velocity components can then be derived using Eq. 5. In spherical coordinates having basis vectors ${\mathbf{e}}_r$, ${\mathbf{e}}_{\phi }$, and ${\mathbf{e}}_{\theta }$, Eq. 5 becomes

$$\mathbf{v}=v_r{\mathbf{e}}_r+v_{\phi }{\mathbf{e}}_{\phi }+v_{\theta }{\mathbf{e}}_{\theta }=\frac{1}{i\rho ck}\left({\mathbf{e}}_r\frac{\partial p}{\partial r}+{\mathbf{e}}_{\phi }\frac{1}{r\sin \theta }\frac{\partial p}{\partial \phi }+{\mathbf{e}}_{\theta }\frac{1}{r}\frac{\partial p}{\partial \theta }\right).$$ (36)

Equation 35 then implies that

$$v_r=\frac{1}{i\rho c\pi }{\displaystyle \sum _{n=0}^{\infty }{i}^n\left[j_n\prime \left(\mathit{k}\mathit{r}\right)+c_n{h}_n^{\left(1\right)}\prime \left(\mathit{k}\mathit{r}\right)\right]{\displaystyle \sum _{m=-n}^n{H}_{\mathit{n}\mathit{m}}{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)}}.$$ (37)

Expressions for $v_{\phi }$ and $v_{\theta }$ are similar but more cumbersome. They will not be used in the calculation of radiation force and are not presented here.

Equations 35, 37 are known representations of the solution of the Helmholtz equation in spherical coordinates. The new result here is that the weights of the corresponding spherical harmonics $H_{\mathit{n}\mathit{m}}$ are expressed by Eq. 34 through the angular spectrum of the incident beam. Note that the values $H_{\mathit{n}\mathit{m}}$ are independent of the scatterer. The mechanical properties and diameter of the spherical scatterer enter into the solution through the coefficients $c_n$, which are defined in the theory of plane-wave scattering by Eq. 12.

Radiation force of an arbitrary beam

Now the newly obtained expressions for the scattered field for an arbitrary beam can be used to obtain the corresponding radiation force on a sphere. The radiation force calculation is based on Eqs. 1, 4. Consider a spherical surface Σ having radius r. The unit vector outwardly normal to such a sphere is $\mathbf{n}={\mathbf{e}}_r$. The force components acting on a surface element $d\hspace{0.17em}\mathrm{\Sigma }$ then become

$$\begin{array}{c}\frac{d{F}_x}{d\mathrm{\Sigma }}=D\hspace{0.17em}\sin \hspace{0.17em}\theta \hspace{0.17em}\cos \hspace{0.17em}\phi +\frac{\rho }{2}\hspace{0.17em}\mathrm{Re}\left(v_r{v}_{\phi }^{\ast }\right)\hspace{0.17em}\sin \hspace{0.17em}\phi -\frac{\rho }{2}\hspace{0.17em}\mathrm{Re}\left(v_r{v}_{\theta }^{\ast }\right)\cos \hspace{0.17em}\theta \hspace{0.17em}\cos \hspace{0.17em}\phi ,\\ \frac{d{F}_y}{d\mathrm{\Sigma }}=D\hspace{0.17em}\sin \hspace{0.17em}\theta \hspace{0.17em}\sin \hspace{0.17em}\phi -\frac{\rho }{2}\hspace{0.17em}\mathrm{Re}\left(v_r{v}_{\phi }^{\ast }\right)\cos \hspace{0.17em}\phi -\frac{\rho }{2}\hspace{0.17em}\mathrm{Re}\left(v_r{v}_{\theta }^{\ast }\right)\cos \hspace{0.17em}\theta \hspace{0.17em}\sin \hspace{0.17em}\phi ,\\ \frac{d{F}_z}{d\mathrm{\Sigma }}=D\hspace{0.17em}\cos \hspace{0.17em}\theta +\frac{\rho }{2}\hspace{0.17em}\mathrm{Re}\left(v_r{v}_{\theta }^{\ast }\right)\sin \hspace{0.17em}\theta ,\end{array}$$ (38)

where

$$D=\frac{\rho \hspace{0.17em}}{4}\left(\hspace{0.17em}{\left|\hspace{0.17em}{v}_{\phi }\right|}^2+{\left|\hspace{0.17em}{v}_{\theta }\right|}^2-{\left|\hspace{0.17em}{v}_r\right|}^2\right)-\frac{{\left|p\right|}^2}{4\rho c^2}.$$ (39)

When the radius of the integration surface goes to infinity in the far field, these expressions can be simplified. The corresponding behavior of pressure and velocity follows from the asymptotes ${h_n^{\left(1\right)}\left(\varsigma \right)|}_{\varsigma \to \infty }\to {\left(-i\right)}^{n+1}{e}^{i\varsigma }/\varsigma$ and ${j_n\left(\varsigma \right)|}_{\varsigma \to \infty }\to \left[{\left(-i\right)}^{n+1}{e}^{i\varsigma }+i^{n+1}{e}^{-i\varsigma }\right]/\left(2\varsigma \right)$. From Eqs. 35, 37, it follows that

$${p|}_{r\to \infty }\to -i\frac{1}{2\pi kr}{\displaystyle \sum _{n=0}^{\infty }\left[\left(1+2c_n\right)e^{\mathit{i}\mathit{k}\mathit{r}}-{\left(-1\right)}^n{e}^{-ikr}\right]{\displaystyle \sum _{m=-n}^n{H}_{\mathit{n}\mathit{m}}{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)}},$$ (40)

$${v_r|}_{r\to \infty }\to \frac{1}{i2\pi \rho \hspace{0.17em}ckr}{\displaystyle \sum _{n=0}^{\infty }\left[\left(1+2c_n\right)e^{\mathit{i}\mathit{k}\mathit{r}}+{\left(-1\right)}^n{e}^{-ikr}\right]{\displaystyle \sum _{m=-n}^n{H}_{\mathit{n}\mathit{m}}{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)}}.$$ (41)

It is seen that $p=O\left(r^{-1}\right)$ and $v_r=O\left(r^{-1}\right)$, where $O\hspace{0.17em}\left( \cdot \right)$ means “on the order of.” Without derivation of the angular component of the particle velocity, it is seen from Eq. 36 that $v_{\phi }=O\left(r^{-2}\right)$ and $v_{\theta }=O\left(r^{-2}\right)$. The surface element $d\hspace{0.17em}\mathrm{\Sigma }=r^2\sin \theta \hspace{0.17em}d\phi \hspace{0.17em}d\theta \sim r^2$, and therefore as $r\to \hspace{0.17em}\hspace{0.17em}\infty$ only the term proportional to $(\hspace{0.17em}{\left| p \right|}^2/\left(\rho c^2\right)+\rho \hspace{0.17em}{\left|\hspace{0.17em}{v}_r\right|}^2)\hspace{0.17em}d\mathrm{\Sigma }$ does not vanish in the expression for $d\mathbf{F}=(d\mathbf{F}/d\mathrm{\Sigma })d\mathrm{\Sigma }$. As a result, in the far field the force components reduce to the following:

$$\begin{array}{c}{\frac{d{F}_x}{d\mathrm{\Sigma }}|}_{r\to \infty }=-E\sin \theta \cos \phi \hspace{0.17em},\\ {\frac{d{F}_y}{d\mathrm{\Sigma }}|}_{r\to \infty }=-E\sin \theta \sin \phi \hspace{0.17em},\\ {\frac{d{F}_z}{d\mathrm{\Sigma }}|}_{r\to \infty }=-E\cos \theta \hspace{0.17em},\end{array}$$ (42)

where E is acoustic energy density

$$E=\frac{{\left|p\right|}^2}{4\rho c^2}+\frac{\rho \hspace{0.17em}{\left|v_r\right|}^2}{4}.$$ (43)

From Eqs. 40, 41 it follows that

$$\begin{array}{c}E=\frac{1}{8{\pi }^2\rho c^2{k}^2{r}^2}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{n\prime =0}^{\infty }\left[\left(1+2c_n\right)\left(1+2c_{n\prime }^{*}\right)+{\left(-1\right)}^{n+n\prime }\right]}}\\ \times {\displaystyle \sum _{m=-n}^n\hspace{0.17em}{\displaystyle \sum _{m\prime =-n\prime }^{n\prime }{H}_{\mathit{n}\mathit{m}}{H}_{n\prime m\prime }^{*}{Y}_{\mathit{n}\mathit{m}}\left(\theta ,\phi \right)Y_{n\prime m\prime }^{*}\left(\theta ,\phi \right)}}.\end{array}$$ (44)

Finally, Eq. 1 for the radiation force gives

$$\mathbf{F}=r^2{\displaystyle {\int }_0^{\pi }\sin \theta \hspace{0.17em}d\theta }{\displaystyle {\int }_0^{2\pi }d\phi \hspace{0.17em}{\frac{d\mathbf{F}}{d\mathrm{\Sigma }}|}_{r\to \infty }},$$ (45)

where ${d \mathbf{F}/d \mathrm{\Sigma }\hspace{0.17em}|}_{r\to \infty }$ is expressed by Eqs. 42. Thus, the derivation of the force is reduced to the integration of the spherical functions. This can be accomplished based on the orthogonality and recurrence equalities that exist for the associated Legendre polynomials.28 The corresponding algebra is omitted here. Integration of Eq. 45 results in the following expressions for the components of radiation force:

$$F_x=\frac{1}{8{\pi }^2\rho c^2{k}^2}\mathrm{Re}\left\{{\displaystyle \sum _{n=0}^{\infty }{\Psi }_n{\displaystyle \sum _{m=-n}^n\hspace{0.17em}{A}_{\mathit{n}\mathit{m}}\left(H_{\mathit{n}\mathit{m}}{H}_{n+1,m+1}^{*}-H_{n,-m}{H}_{n+1,-m-1}^{*}\right)}}\right\},$$ (46)

$$F_y=\frac{1}{8{\pi }^2\rho c^2{k}^2}\mathrm{Im}\left\{{\displaystyle \sum _{n=0}^{\infty }{\Psi }_n{\displaystyle \sum _{m=-n}^n\hspace{0.17em}{A}_{\mathit{n}\mathit{m}}\left(H_{\mathit{n}\mathit{m}}{H}_{n+1,m+1}^{*}+H_{n,-m}{H}_{n+1,-m-1}^{*}\right)}}\right\},$$ (47)

$$F_z=-\frac{1}{4{\pi }^2\rho c^2{k}^2}\mathrm{Re}\left\{{\displaystyle \sum _{n=0}^{\infty }{\Psi }_n}{\displaystyle \sum _{m=-n}^n\hspace{0.17em}{B}_{\mathit{n}\mathit{m}}\hspace{0.17em}{H}_{\mathit{n}\mathit{m}}{H}_{n+1,m}^{*}}\right\}.$$ (48)

Here the following notations are introduced:

$${\Psi }_n=\left(1+2c_n\right)\left(1+2c_{n+1}^{*}\right)-1,$$ (49)

$$A_{\mathit{n}\mathit{m}}=\sqrt{\frac{\left(n+m+1\right)\left(n+m+2\right)}{\left(2n+1\right)\left(2n+3\right)}},$$ (50)

$$B_{\mathit{n}\mathit{m}}=\sqrt{\frac{\left(n+m+1\right)\left(n-m+1\right)}{\left(2n+1\right)\left(2n+3\right)}}.$$ (51)

Earlier, it was mentioned that for the scattering coefficients $c_n$ in the case of a nonabsorbent scatterer (which is supposed in this paper) the following expression is valid: $1+2c_n=s_n=e^{i{\gamma }_n}$, where ${\gamma }_n$ is some real number. Therefore, $1+{\Psi }_n=e^{i\left({\gamma }_n-{\gamma }_{n+1}\right)}$ has a similar expression in the form of a phase factor. Note that ${\Psi }_n=2\left(c_n+c_{n+1}^{*}+2c_n{c}_{n+1}^{*}\right)$ as defined in Eq. 48 is in accord with Eq. 17, which was derived earlier for axisymmetric beams. Note also that the presented equations for the force components should be equivalent to Eqs. (11)–(13) in Ref. 20 but the exact veracity has not yet been checked.

SPECIFIC CASES

Equations 46, 47, 48, 49, 50, 51 are the main result of the current paper. In this section it will be shown that in simplified situations, these equations can be reduced to known expressions from the literature.

Radiation force of a plane wave

Consider first the simplest case of a plane wave propagating along the z-axis: $p_i\left(x,y,0\right)=p_0$. Then Eq. 20 provides $S\left(k_x,k_y\right)=p_0{\left(2\pi \right)}^2\delta \left(k_x\right)\delta \left(k_y\right)$. Therefore, the integration in Eq. 34 becomes trivial: $H_{\mathit{n}\mathit{m}}=p_0\sqrt{\left(2n+1\right)}\hspace{0.17em}\hspace{0.17em}2{\pi }^{3/2}{\delta }_{0m}$. Here the relation $P_n^m\left(1\right)={\delta }_{0m}$, where ${\delta }_{\mathit{n}\mathit{m}}$ is the Kronecker delta, was used. The resulting coefficients $H_{\mathit{n}\mathit{m}}$ lead to $F_z=-\pi p_0^2/(\rho c^2{k}^2)\mathrm{Re}\left\{{\sum }_{n=0}^{\infty }\left(n+1\right)\left[\left(1+2c_n\right)\left(1+2c_{n+1}^{*}\right)-1\right]\right\}$, which coincides with Eq. 17 as well as results from Refs. 11, 22, 23.

Consider next a plane wave having the following wave vector: $\mathbf{k}=k\left(\sin {\theta }_0\cos {\phi }_{0\hspace{0.17em}},\sin {\theta }_0\sin {\phi }_{0\hspace{0.17em}},\hspace{0.17em}\cos {\theta }_0\right)$. In such a situation, Eq. 20 gives $S\left(k_x,k_y\right)=p_0{\left(2\pi \right)}^2\delta \left(k_x-k\sin {\theta }_0\cos {\phi }_0\right)\delta \left(k_y-k\sin {\theta }_0\sin {\phi }_0\right)$, which is an inclined plane wave. Then Eq. 34 yields $H_{\mathit{n}\mathit{m}}=p_0{\left(2\pi \right)}^2{Y}_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_0,{\phi }_0\right)$ and Eqs. 46, 47, 48 become

$$\begin{array}{c}{F}_x=\frac{2p_0^2{\pi }^2}{\rho c^2{k}^2}\mathrm{Re}\hspace{0.17em}\{{\displaystyle \sum _{n=0}^{\infty }{\Psi }_n{\displaystyle \sum _{m=-n}^n\hspace{0.17em}{A}_{\mathit{n}\mathit{m}}[\hspace{0.17em}{Y}_{n+1,m+1}\left({\theta }_0,{\phi }_0\right)Y_{\mathit{n}\mathit{m}}^{*}\left({\theta }_0,{\phi }_0\right)+}}\\ Y_{\mathit{n}\mathit{m}}\left({\theta }_0,{\phi }_0\right)Y_{n+1,m+1}^{\ast }\left({\theta }_0,{\phi }_0\right)\hspace{0.17em}]\},\end{array}$$ (52)

$$F_y=\frac{2p_0^2{\pi }^2}{\rho c^2{k}^2}\mathrm{Im}\hspace{0.17em}\{{\displaystyle \sum _{n=0}^{\infty }{\Psi }_n{\displaystyle \sum _{m=-n}^n\hspace{0.17em}{A}_{\mathit{n}\mathit{m}}[\hspace{0.17em}{Y}_{n+1,m+1}\left({\theta }_0,{\phi }_0\right)Y_{\mathit{n}\mathit{m}}^{*}\left({\theta }_0,{\phi }_0\right)-}}{Y}_{\mathit{n}\mathit{m}}\left({\theta }_0,{\phi }_0\right)Y_{n+1,m+1}^{\ast }\left({\theta }_0,{\phi }_0\right)\hspace{0.17em}]\},$$ (53)

$$F_z=\frac{2p_0^2{\pi }^2}{\rho c^2{k}^2}\mathrm{Re}\hspace{0.17em}\left\{{\displaystyle \sum _{n=0}^{\infty }{\Psi }_n}{\displaystyle \sum _{m=-n}^n\hspace{0.17em}{B}_{\mathit{n}\mathit{m}}\hspace{0.17em}{Y}_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_0,{\phi }_0\right)Y_{n+1,m}\left({\theta }_0,{\phi }_0\right)\hspace{0.17em}}\right\}.$$ (54)

Using Eq. 27, these expressions can be rewritten in terms of the associated Legendre polynomials

$$F_x=\cos {\phi }_0\frac{p_0^2\pi }{\rho c^2{k}^2}{\displaystyle \sum _{n=0}^{\infty }\mathrm{Re}\left[\left(1+2c_n^{*}\right)\left(1+2c_{n+1}\right)-1\right]\times G_n\left(\cos {\theta }_0\right)\hspace{0.17em}},$$ (55)

$$F_y=\sin {\phi }_0\frac{p_0^2\pi }{\rho c^2{k}^2}{\displaystyle \sum _{n=0}^{\infty }\mathrm{Re}\left[\left(1+2c_n^{*}\right)\left(1+2c_{n+1}\right)-1\right]\hspace{0.17em}\times G_n\left(\cos {\theta }_0\right)},$$ (56)

$$F_z=-\frac{p_0^2\pi }{\rho c^2{k}^2}{\displaystyle \sum _{n=0}^{\infty }\left(n+1\right)\mathrm{Re}\left[\left(1+2c_n^{*}\right)\left(1+2c_{n+1}\right)-1\right]\times R_n\left(\cos {\theta }_0\right)},$$ (57)

where the following notations have been introduced:

$$G_n\left(x\right)=P_n^0\left(x\right)\hspace{0.17em}{P}_{n+1}^1\left(x\right)+{\displaystyle \sum _{m=1}^n\hspace{0.17em}\frac{\left(n-m\right)\hspace{0.17em}!}{\left(n+m\right)\hspace{0.17em}!}{P}_n^m\left(x\right)\hspace{0.17em}\left[\hspace{0.17em}{P}_{n+1}^{m+1}\left(x\right)-\left(n-m+1\right)\left(n-m+2\right)P_{n+1}^{m-1}\left(x\right)\hspace{0.17em}\right]},$$ (58)

$$R_n\left(x\right)=P_n^0\left(x\right)\hspace{0.17em}{P}_{n+1}^0\left(x\right)+2{\displaystyle \sum _{m=1}^n\hspace{0.17em}\frac{\left(n-m+1\right)}{\left(n+1\right)}\frac{\left(n-m\right)\hspace{0.17em}!}{\left(n+m\right)\hspace{0.17em}!}{P}_n^m\left(x\right)\hspace{0.17em}{P}_{n+1}^m\left(x\right)}.$$ (59)

The recurrence relations for the associated Legendre polynomials28 allow Eqs. 58, 59 to be reduced to the following simple expressions: $G_n\left(x\right)=-\left(n+1\right)\sqrt{1-x^2}$ and $R_n\left(x\right)=x$. Then Eqs. 55, 56, 57 give the expected result

$$\mathbf{F}=-\frac{\pi p_0^2}{\rho c^2{k}^2}\mathrm{Re}\left\{{\displaystyle \sum _{n=0}^{\infty }\left(n+1\right)\left[\left(1+2c_n\right)\left(1+2c_{n+1}^{*}\right)-1\right]}\right\}\times \frac{\mathbf{k}}{k},$$ (60)

in which the force is directed along the wave vector. Moreover, the absolute value of the force is the same for all propagation directions and coincides with the coaxial plane-wave result [see Eq. 17 and Refs. 11, 22, 23].

Radiation force due to Bessel beams

Bessel beams represent a family of “non-diffracting” solutions of the Helmholtz equation

$$p_i\left(x,y,z\right)=p_0{e}^{ikz\cos \beta }{J}_M\left(k{r}_{\perp }\sin \beta \right)\hspace{0.17em}{e}^{iM\phi },$$ (61)

where $r_{\perp }=\sqrt{x^2+y^2}$, $\phi =\arctan \left(y/x\right)$, β is a characteristic angle, and M is the order of the Bessel beam. Equation 20 gives the following formula for the angular spectrum of the beam described by Eq. 61:

$$S\left(k_x,k_y\right)=2\pi p_0\frac{\delta \left(k_{\perp }-k\sin \beta \hspace{0.17em}\right)}{k_{\perp }}{i}^{-M} e^{iM{\phi }_k}.$$ (62)

Here $k_{\perp }=\sqrt{k_x^2+k_y^2}$ and ${\phi }_k=\arccos \hspace{0.17em}\left(k_x/k_{\perp }\right)$. The delta-function in Eq. 62 simplifies the integration in Eq. 34

$$H_{\mathit{n}\mathit{m}}=i^{-M}{\delta }_{\mathit{M}\mathit{m}}\sqrt{\frac{\left(n-M\right)\hspace{0.17em}!}{\left(n+M\right)\hspace{0.17em}!}}\cdot \sqrt{2n+1}\cdot 2{\pi }^{3/2}{p}_0{P}_n^m\left(\cos \beta \right).$$

As earlier, ${\delta }_{\mathit{n}\mathit{m}}$ is the Kronecker delta here. Therefore, $H_{\mathit{n}\mathit{m}}{H}_{n+1,m+1}^{*}-H_{n,-m}{H}_{n+1,-\left(m+1\right)}^{*}=0$ and $H_{\mathit{n}\mathit{m}}{H}_{n+1,m+1}^{*}+H_{n,-m}{H}_{n+1,-\left(m+1\right)}^{*}=0$, implying that the lateral force components vanish $\left(F_x=F_y=0\right)\hspace{0.17em}.$ To evaluate $F_z$, it can be written that

$$\begin{array}{c}{H}_{\mathit{n}\mathit{m}}{H}_{n+1,m}^{*}={\delta }_{\mathit{M}\mathit{m}}\cdot 4{\pi }^3{p}_0^2\sqrt{\left(2n+1\right)\left(2n+3\right)}\hspace{0.17em}\frac{\left(n-M\right)\hspace{0.17em}!}{\left(n+M\right)\hspace{0.17em}!}\\ \sqrt{\frac{\left(n+1-M\right)}{\left(n+1+M\right)}}{P}_n^M\left(\cos \beta \right)\cdot P_{n+1}^M\left(\cos \beta \right).\end{array}$$

Note that $H_{\mathit{n}\mathit{M}}=0$ for $M>n$ so that the summation in Eq. 48 should start from $n=M$. This gives

$$\begin{array}{c}{F}_z=-\frac{\pi p_0^2}{\rho c^2{k}^2}{\displaystyle \sum _{n=M}^{\infty }\hspace{0.17em}\frac{\left(n-M+1\right)\hspace{0.17em}!}{\left(n+M\right)\hspace{0.17em}!}}{P}_n^M\left(\cos \beta \right)P_{n+1}^M\left(\cos \beta \right)\mathrm{Re}\left[\hspace{0.17em}\left(1+2c_n\right)\left(1+2c_{n+1}^{*}\right)-1\hspace{0.17em}\right].\end{array}$$ (63)

This expression coincides with that obtained in Ref. 12 for the zeroth-order Bessel beam, as well as with the general expression derived in Ref. 14 for any high-order Bessel beam.

Radiation force of an arbitrary beam on a small spherical scatterer ($ka\ll 1$)

To calculate the radiation force for a small scatterer with $ka\ll 1$, it is necessary to first approximate the scattering coefficients $c_n$ given by Eqs. 12, 13. Let us consider the leading terms in the approximation for the auxiliary coefficients ${\mathrm{\Gamma }}_n$. According to Eq. 13, in the limit $k_{t}a\ll 1$ and $k_{l}a\ll 1$ the coefficients ${\mathrm{\Gamma }}_n$ can be approximated as follows: ${\mathrm{\Gamma }}_0\approx -\rho /{\rho }_{*}\hspace{0.17em}{\left(k_{l}a\right)}^2/3-4c_t^2/c_l^2$, ${\mathrm{\Gamma }}_1\approx \rho /{\rho }_{*}$, ${\mathrm{\Gamma }}_{n>1}\approx \text{const}\cdot \rho /{\rho }_{*}{\left(k_{t}a\right)}^2$. The case of a fluid sphere should be considered separately because then $k_{t}a\to \infty$. When $k_{l}a\ll 1$, for the fluid scatterer, Eq. 13 gives ${\mathrm{\Gamma }}_0\approx -\rho /{\rho }_{*}\hspace{0.17em}{\left(k_{l}a\right)}^2/3$ and ${\mathrm{\Gamma }}_{n>0}\approx n(\rho /{\rho }_{*})$ so that ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ have the same approximations for both solid and fluid spheres. In contrast, ${\mathrm{\Gamma }}_{n>1}$ is sensitive to the solid or fluid nature of the sphere.

Consider now approximations for $c_n$. From the aforementioned approximations for ${\mathrm{\Gamma }}_n$, the following leading terms for the real and imaginary parts of $c_n$ can be derived from Eq. 12:

$$c_0\approx -\frac{{\left(\mathit{k}\mathit{a}\right)}^6}{9}{f}_1^2-i\frac{{\left(\mathit{k}\mathit{a}\right)}^3}{3}{f}_1,$$ (64)

$$c_1\approx -\frac{{\left(\mathit{k}\mathit{a}\right)}^6}{36}{f}_2^2+i\frac{{\left(\mathit{k}\mathit{a}\right)}^3}{6}{f}_2,$$ (65)

$$c_{n>1}=O\hspace{0.17em}\left\{{\left(\mathit{k}\mathit{a}\right)}^{4n+2}\right\}+i\hspace{0.17em}O\hspace{0.17em}\left\{{\left(\mathit{k}\mathit{a}\right)}^{2n+1}\right\}.$$ (66)

Here the following constants $f_1$ and $f_2$ have been introduced to characterize the relative compressibility and density of the sphere material as compared to those of the surrounding fluid (following Ref. 15):

$$f_1=1-\frac{\rho \hspace{0.17em}{c}^2\hspace{0.17em}}{{\rho }_{*}{c}_l^2}\frac{\hspace{0.17em}1}{1-\frac{4c_t^2}{3c_l^2}},$$ (67)

$$f_2=2\frac{{\rho }_{*}-\rho }{2{\rho }_{*}+\rho }.$$ (68)

Note that the approximations [Eqs. 64, 65, 66] are valid for both solid and fluid sphere materials. With the definition of ${\Psi }_n$ from Eq. 49, Eqs. 64, 65, 66 imply the following:

$${\Psi }_0\approx -\frac{2{\left(\mathit{k}\mathit{a}\right)}^6}{9}\left(f_1^2+\frac{1}{4}{f}_2^2+f_1{f}_2\right)-i\frac{{\left(\mathit{k}\mathit{a}\right)}^3}{3}\left(2f_1+f_2\right),$$ (69)

$${\Psi }_1\approx -\frac{{\left(\mathit{k}\mathit{a}\right)}^6}{18}{f}_2^2+i\frac{{\left(\mathit{k}\mathit{a}\right)}^3}{3}{f}_2,$$ (70)

$${\Psi }_{n>1}=O\hspace{0.17em}\left\{{\left(\mathit{k}\mathit{a}\right)}^{4n+2}\right\}+i\hspace{0.17em}O\hspace{0.17em}\left\{\hspace{0.17em}{\left(\mathit{k}\mathit{a}\right)}^{2n+1}\right\}.$$ (71)

It follows that only ${\Psi }_0$ and ${\Psi }_1$ contribute to the leading terms in the approximation for radiation force.

It is seen that $\mathrm{Re}\left({\Psi }_{0,\hspace{0.17em}1}\right)=O\left(k^6{a}^6\right)$ is much smaller than $\mathrm{Im}\left({\Psi }_{0,\hspace{0.17em}1}\right)=O\left(k^3{a}^3\right)$ so that $\mathrm{Re}\left({\Psi }_{0,\hspace{0.17em}1}\right)$ can be omitted at first glance. This is indeed true for most situations. However, there is an important exception when the incident wave is a traveling plane wave. If the traveling plane wave propagates along the z axis, then, as shown earlier, $H_{\mathit{n}\mathit{m}}=p_0\sqrt{\left(2n+1\right)}\hspace{0.17em}\hspace{0.17em}2{\pi }^{3/2}{\delta }_{0m}$. Equations 46, 47 give $F_x=F_y=0$, and Eq. 48 provides $F_z=-\pi \hspace{0.17em}{p}_0^2/(\rho \hspace{0.17em}{c}^2{k}^2)\mathrm{Re}\left({\Psi }_0+2{\Psi }_1\right)$. As such, only the real parts of ${\Psi }_0$ and ${\Psi }_1$ contribute to the radiation force and thus even small $\mathrm{Re}\left({\Psi }_{0,1}\right)$ cannot be omitted. From Eqs. 69, 70

$${F_z^{\left(\text{plane}\hspace{0.17em}\text{wave}\right)}|}_{ka\ll \hspace{0.17em}1}\approx \frac{\pi a^2{\left|p_0\right|}^2}{\rho c^2}\frac{2}{9}\left(f_1^2+f_1{f}_2+\frac{3}{4}{f}_2^2\right)\hspace{0.17em}{\left(\mathit{k}\mathit{a}\right)}^4.$$ (72)

This formula coincides with that obtained by Gor'kov15 for the radiation force on a small compressible sphere due to a traveling plane wave.

Consider now an acoustic beam of arbitrary structure. Then Eqs. 46, 47, 48 along with Eqs. 69, 70, 71 give

$$F_x\approx \frac{1}{8{\pi }^2\rho c^2{k}^2}\mathrm{Re}\hspace{0.17em}\{\sqrt{\frac{2}{3}}\hspace{0.17em}{\Psi }_0\hspace{0.17em}{H}_{0,0}\left(H_{1,1}^{*}-H_{1,-1}^{*}\right)+\sqrt{\frac{2}{15}}\hspace{0.17em}{\Psi }_1\hspace{0.17em}[\hspace{0.17em}\left(H_{1,-1}-H_{1,1}\right)H_{2,0}^{*}+\sqrt{3}\hspace{0.17em}{H}_{1,0}\left(H_{2,1}^{*}-H_{2,-1}^{*}\right)+\sqrt{6}(H_{1,1}{H}_{2,2}^{*}-H_{1,-1}{H}_{2,-2}^{*})\hspace{0.17em}]\},$$ (73)

$$\begin{array}{c}{F}_y\approx \frac{1}{8{\pi }^2\rho c^2{k}^2}\mathrm{Im}\hspace{0.17em}\{\sqrt{\frac{2}{3}}\hspace{0.17em}{\Psi }_0{H}_{0,0}\left(H_{1,1}^{*}+H_{1,-1}^{*}\right)\\ +\sqrt{\frac{2}{15}}\hspace{0.17em}{\Psi }_1\hspace{0.17em}[\hspace{0.17em}\left(H_{1,-1}+H_{1,1}\right)H_{2,0}^{*}\\ +\sqrt{3}\hspace{0.17em}{H}_{1,0}\left(H_{2,1}^{*}+H_{2,-1}^{*}\right)\\ +\sqrt{6}\left(H_{1,1}{H}_{2,2}^{*}+H_{1,-1}{H}_{2,-2}^{*}\right)\hspace{0.17em}\left]\right\},\end{array}$$ (74)

$$\begin{array}{c}{F}_z\approx -\hspace{0.17em}\frac{1}{4{\pi }^2\rho c^2{k}^2}\mathrm{Re}\hspace{0.17em}\{\frac{{\Psi }_0}{\sqrt{3}}{H}_{0,0}{H}_{1,0}^{*}+\frac{{\Psi }_1}{\sqrt{15}}(\sqrt{3}\hspace{0.17em}{H}_{1,-1}{H}_{2,-1}^{*}+\\ 2\hspace{0.17em}{H}_{1,0}{H}_{2,0}^{*}+\sqrt{3}\hspace{0.17em}{H}_{1,1}{H}_{2,1}^{*})\}\hspace{0.17em}.\end{array}$$ (75)

These expressions include all terms to $O\left(k^6{a}^6\right)$. The reader is reminded that the coefficients $H_{\mathit{n}\mathit{m}}$ are defined by Eq. 34 using spherical harmonics $Y_{\mathit{n}\mathit{m}}^{\ast }\left({\theta }_k,{\phi }_k\right)$, where ${\theta }_k$ and ${\phi }_k$ are expressed through the wave vector components $k_{x\hspace{0.17em}}$, $k_{y\hspace{0.17em}}$, and $k_{z\hspace{0.17em}}$ in accordance with Eq. 21. This gives the following representation for the spherical harmonics that are used to define $H_{\mathit{n}\mathit{m}}$ in Eqs. 73, 74, 75:

$$Y_{00}\left({\theta }_k,{\phi }_k\right)=1/\sqrt{4\pi }\hspace{0.17em},$$

$$Y_{10}\left({\theta }_k,{\phi }_k\right)=\sqrt{3/\left(4\pi \right)}\hspace{0.17em}{k}_z/k,$$

$$Y_{11}\left({\theta }_k,{\phi }_k\right)=-\sqrt{3/\left(8\pi \right)}\hspace{0.17em}\left(k_x+i{k}_y\right)/k\hspace{0.17em},$$

$$Y_{1,-1}\left({\theta }_k,{\phi }_k\right)=\sqrt{3/\left(8\pi \right)}\hspace{0.17em}\left(k_x-i{k}_y\right)/k,$$

$$Y_{20}\left({\theta }_k,{\phi }_k\right)\hspace{0.17em}=\sqrt{5/\left(16\pi \right)}\hspace{0.17em}\left(2k_z^2-k_x^2-k_y^2\right)/k^2,$$

$$Y_{21}\left({\theta }_k,{\phi }_k\right)=-\sqrt{15/\left(8\pi \right)}\hspace{0.17em}\left(k_x+i{k}_y\right)k_z/k^2,$$

$$Y_{22}\left({\theta }_k,{\phi }_k\right)=\sqrt{15/\left(32\pi \right)}\hspace{0.17em}{\left(k_x+i{k}_y\right)}^2/k^2.$$

The incident wave $p_i\left(x,y,z\right)$ is defined by Eq. 19. For brevity, let us temporarily (in this section only) omit the subscript i in the incident wave notation, i.e., use p for $p_i$ and v for ${\mathbf{v}}_i$. Note that because of Eq. 19 the following expressions are valid: $\int \int d{k}_{x}d{k}_{y}S\left(k_x,k_y\right)=4{\pi }^2{p|}_{\left(0,0,0\right)}\hspace{0.17em},$$\int \int d{k}_{x}d{k}_{y}S\left(k_x,k_y\right)\left(i{k}_x\right)=4{\pi }^2{\partial p/\partial x|}_{\left(0,0,0\right)}$, and so on. As a result, Eqs. 73, 74, 75 can be transformed as follows:

$$\begin{array}{c}{F}_x\approx -\hspace{0.17em}\frac{\pi }{\rho c^2{k}^5}\mathrm{Re}\hspace{0.17em}\{\hspace{0.17em}{k}^{2}i\hspace{0.17em}{\Psi }_{0}p\frac{\partial p^{\ast }}{\partial x}+k^{2}i\hspace{0.17em}{\Psi }_1{p}^{\ast }\frac{\partial p}{\partial x}\\ +3i\hspace{0.17em}{\Psi }_1\left(\frac{\partial p}{\partial x}\frac{{\partial }^2{p}^{\ast }}{\partial x^2}+\frac{\partial p}{\partial y}\frac{{\partial }^2{p}^{\ast }}{\partial x\partial y}+\frac{\partial p}{\partial z}\frac{{\partial }^2{p}^{\ast }}{\partial x\partial z}\right)\},\end{array}$$

$$\begin{array}{c}{F}_y\approx -\hspace{0.17em}\frac{\pi }{\rho c^2{k}^5}\mathrm{Re}\hspace{0.17em}\{\hspace{0.17em}{k}^{2}i\hspace{0.17em}{\Psi }_{0}p\frac{\partial p^{\ast }}{\partial y}+k^{2}i\hspace{0.17em}{\Psi }_1\hspace{0.17em}{p}^{\ast }\frac{\partial p}{\partial y}\\ +3i\hspace{0.17em}{\Psi }_1\left(\frac{\partial p}{\partial x}\frac{{\partial }^2{p}^{\ast }}{\partial x\partial y}+\frac{\partial p}{\partial y}\frac{{\partial }^2{p}^{\ast }}{\partial y^2}+\frac{\partial p}{\partial z}\frac{{\partial }^2{p}^{\ast }}{\partial y\partial z}\right)\},\end{array}$$

$$\begin{array}{c}{F}_z\approx -\frac{\pi }{\rho c^2{k}^5}\mathrm{Re}\hspace{0.17em}\{\hspace{0.17em}{k}^{2}i\hspace{0.17em}{\Psi }_{0}p\frac{\partial p^{\ast }}{\partial z}+k^{2}i\hspace{0.17em}{\Psi }_1\hspace{0.17em}{p}^{\ast }\frac{\partial p}{\partial z}\\ +3i\hspace{0.17em}{\Psi }_1\left(\frac{\partial p}{\partial x}\frac{{\partial }^2{p}^{\ast }}{\partial x\partial z}+\frac{\partial p}{\partial y}\frac{{\partial }^2{p}^{\ast }}{\partial y\partial z}+\frac{\partial p}{\partial z}\frac{{\partial }^2{p}^{\ast }}{\partial z^2}\right)\}.\end{array}$$

Here the incident wave pressure p and its derivatives are taken in the center of the scatterer $\left(0,0,0\right)$. According to Eq. 5, $\nabla p=i\rho ck \mathbf{v}$, where $\mathbf{v}=\left(v_{x\hspace{0.17em}},\hspace{0.17em}{v}_{y\hspace{0.17em}},\hspace{0.17em}{v}_z\right)$ is the particle velocity of the incident wave. Therefore, each force component $F_{\xi }$, where $\xi =x$, y, or z, has the following expression:

$$\begin{array}{c}{F}_{\xi }\approx -\hspace{0.17em}\frac{\pi }{\rho c^2{k}^3}\mathrm{Re}\hspace{0.17em}[i\hspace{0.17em}{\Psi }_{0}p\frac{\partial p^{\ast }}{\partial \xi }+i\hspace{0.17em}{\Psi }_1\hspace{0.17em}{p}^{\ast }\frac{\partial p}{\partial \xi }+\\ 3i\hspace{0.17em}{\Psi }_1\hspace{0.17em}{\rho }^2{c}^2\left(v_x\frac{\partial v_x^{\ast }}{\partial \xi }+v_y\frac{\partial v_y^{\ast }}{\partial \xi }+v_z\frac{\partial v_z^{\ast }}{\partial \xi }\hspace{0.17em}\right)].\end{array}$$ (76)

From Eqs. 69, 70, and 76, it follows that

$$\begin{array}{c}{F}_{\xi }\approx -\hspace{0.17em}\frac{\pi \hspace{0.17em}{a}^3}{3}\frac{\partial }{\partial \xi }\left(f_1\hspace{0.17em}\frac{{\left|p\hspace{0.17em}\right|}^2}{\rho c^2}-\frac{3}{2}\hspace{0.17em}{f}_2\rho {\left| \mathbf{v}\right|}^2\right)-\frac{2}{9}\frac{\pi {\left(\mathit{k}\mathit{a}\right)}^6}{\rho c^2{k}^3}\mathrm{Im}\hspace{0.17em}[\left(f_1^2+f_1{f}_2\right)p\frac{\partial p^{\ast }}{\partial \xi }\hspace{0.17em}+\\ \frac{3}{4}{f}_2^2{\rho }^2{c}^2\left(v_x\frac{\partial v_x^{\ast }}{\partial \xi }+v_y\frac{\partial v_y^{\ast }}{\partial \xi }+v_z\frac{\partial v_z^{\ast }}{\partial \xi }\hspace{0.17em}\right)]\hspace{0.17em}\hspace{0.17em}.\end{array}$$ (77)

The second term ∼${\left(\mathit{k}\mathit{a}\right)}^6$ can be neglected compared to the first term ∼${\left(\mathit{k}\mathit{a}\right)}^3$ in most of the cases, except when the factor $\partial (\cdot )/\partial \xi$ in the first term vanishes (e.g., when ${\left|p \right|}^2$ and ${\left| \mathbf{v}\right|}^2$ are uniform in space). Therefore, with accuracy ∼${\left(\mathit{k}\mathit{a}\right)}^3$, the radiation force can be written as a gradient from some function (a potential) taken at the point of the scatterer center

$$\mathbf{F}=-{\nabla U\hspace{0.17em}|}_{\left(0,0,0\right)}.$$ (78)

According to Eq. 77, the potential U has the following representation:

$$U=\frac{\pi a^3}{3}\left\{f_1\frac{{\left|p\right|}^2}{\rho c^2}-\frac{3}{2}\hspace{0.17em}{f}_2\rho {\left|\mathbf{v}\right|}^2\right\}.$$ (79)

This formula is identical to that obtained by Gor'kov.15 Consider now a plane wave $p=p_0{e}^{i \mathbf{k}\cdot \mathbf{r}}$. Then $\mathbf{v}=(\mathbf{k}/k)(p_0/\rho c)e^{i \mathbf{k}\cdot \mathbf{r}}$ so that both ${\left|p \right|}^2$ and ${\left|\mathbf{v}\right|}^2$ are uniform in space. Then the first term in Eq. 77 disappears and the second term ∼${\left(\mathit{k}\mathit{a}\right)}^6$ is non-negligible. The radiation force in this case is expressed as

$$\mathbf{F}=\frac{\mathbf{k}}{k}\frac{\pi \hspace{0.17em}{a}^2{\left|p_0\right|}^2}{\rho c^2}\frac{2}{9}\left(f_1^2+f_1{f}_2+\frac{3}{4}{f}_2^2\right){\left(\mathit{k}\mathit{a}\right)}^4,$$ (80)

which coincides with Eq. 72.

RADIATION FORCE CREATED BY FOCUSED BEAMS OF TYPICAL ULTRASOUND SOURCES

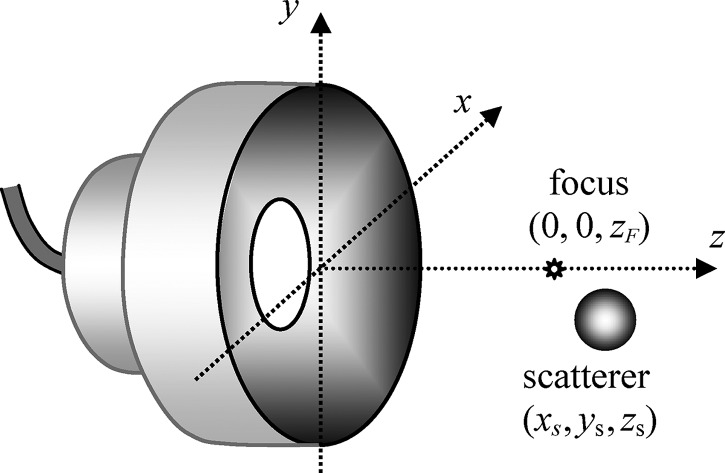
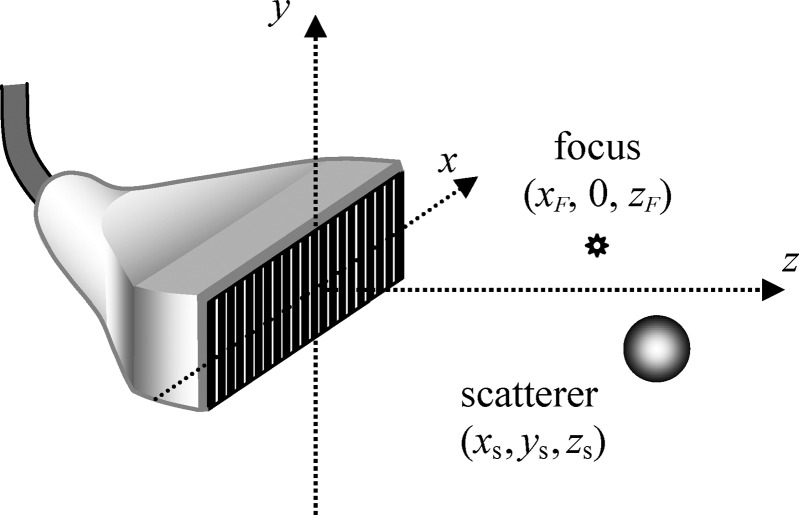
In this section, the proposed approach is used to calculate the radiation force exerted on a spherical scatterer by representative focused ultrasound beams. Beam focusing is usually realized by means of either a curved transducer, a planar transducer coupled to a lens, or a multi-element array with an appropriate phasing of the elements. To illustrate the approach for these types of focused sources, we will consider two transducers: An axisymmetric concave spherical transducer with a hole in the center (Fig. 1) and a rectangular multi-element linear array (Fig. 5).

Figure 1.

Geometry of the problem when the acoustic source has the form of a spherical cap with a circular central opening.

Figure 5.

Geometry of the problem in the case of a linear array source. The focal point can be steered within the imaging plane y = 0.

In Secs. 1, 2, 3, the origin of the coordinate system was placed at the center of the spherical scatterer. However, the choice of coordinate system should not influence the predicted radiation force. To calculate radiation forces for different scatterer positions relative to a focused source, it is convenient to adopt a coordinate system with the origin tied to the source. In this section we define the origin as the central point of the aperture region (see Figs. 15).

The change of location of the origin modifies only the coefficients $H_{\mathit{n}\mathit{m}}$ in Eqs. 46, 47, 48 through the angular spectrum $S\left(k_x,k_y\right)$ in Eq. 34. Let the scatterer's coordinates be $\left( x_s,\hspace{0.17em}{y}_s,\hspace{0.17em}{z}_s\right)$. If ${\widehat{p}}_i\left(x,y,z\right)$ is the pressure amplitude of the incident wave written as a function of the new coordinates, then $p_i\left(x,y,z\right)={\widehat{p}}_i\left(x+x_s,y+y_s,z+z_s\right)$. From Eqs. 19, 20 it follows that the new angular spectrum

$$\widehat{S}\left(k_x,k_y\right)={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle {\int }_{-\infty }^{+\infty }\hspace{0.17em}dxdy\hspace{0.17em}{\widehat{p}}_i\left(x,y,0\right)\hspace{0.17em}{e}^{-i{k}_{x}x-i{k}_{y}y}}},$$ (81)

is related to the original angular spectrum $S\left(k_x,k_y\right)$ simply through a phase factor

$$S\left(k_x,k_y\right)=\widehat{S}\left(k_x,k_y\right)\hspace{0.17em}{e}^{i{k}_x{x}_s+i{k}_y{y}_s+i\sqrt{k^2-k_x^2-k_y^2}\hspace{0.17em}{z}_s}.$$ (82)

The radiation force is a second-order quantity and thus is proportional to the square of the wave amplitude. Consequently, in the case of a plane wave, the radiation force is usually normalized by the wave intensity. More precisely, the force is represented in the form $F=Y_p\hspace{0.17em}\pi a^{2}I/c$, where the radiation force factor $Y_p$ (with the subscript “p” indicating the plane character of the incident wave) depends only on the scatterer material properties and not on the wave intensity.4 In the case of a large target, the force is proportional to the total power of the beam, W, and therefore it is more reasonable to normalize the force by $W/c$ by considering another dimensionless factor $Y_b$, so that $F=Y_{b}W/c$. For instance, $Y_b=1$ when a quasi-plane wave is incident on a perfectly absorbing target.29 Note that if the angular spectrum is known, the total power W that is needed for the force normalization can be calculated as follows:

$$W=\frac{1}{8{\pi }^2\rho c}{\displaystyle {\iint }_{k_x^2+k_y^2\le k^2}\sqrt{1-\frac{k_x^2+k_y^2}{k^2}}{\left|S\left(k_x,k_y\right)\right|}^2}d{k}_{x}d{k}_y.$$ (83)

Focused transducer in the form of a spherical cap with a circular central opening

Consider first an axisymmetric source. The radiation force then has only two components: Axial and lateral. The geometry of the problem is shown in Fig. 1. The transducer creates a focused beam because of its concave spherical shape. Such a source represents a typical piezoelectric transducer used in therapeutic applications of ultrasound.30

The angular spectrum of a curved source can be calculated based on the Rayleigh integral representation of the source field. Two possible approaches are described in Appendix A. Once $\widehat{S}\left(k_x,k_y\right)$ is calculated, it can be used to find $S\left(k_x,k_y\right)$ from Eq. 82, and finally calculate the coefficients $H_{\mathit{n}\mathit{m}}$ that are necessary to find the radiation force.

We will suppose that the transducer surface vibrates uniformly with the normal velocity amplitude $V_0$. In such a case, the accuracy of the incident field representation by the calculated angular spectrum can be checked by comparison to an analytical solution. It is known that on the z-axis the Rayleigh integral provides31

$$P_{\text{axis}}={\widehat{p}}_i \left(0,0,z\right)=p_{\text{source}}\frac{R}{z_F-z}\left({\mathrm{e}}^{ik{D}_{\max }}-{\mathrm{e}}^{ik{D}_{\min }}\right)\hspace{0.17em}.$$ (84)

Here $p_{\text{source}}=\rho c\hspace{0.17em}{V}_0$ is a characteristic pressure amplitude at the radiating surface and $\hspace{0.17em}{D}_{\max }$, $\hspace{0.17em}{D}_{\min }\hspace{0.17em}$ are distances from a given point on the axis to the transducer outer and inner edges, respectively: $\hspace{0.17em}{D}_{\max }=\sqrt{z^2+r_{\max }^2}\hspace{0.17em}$, $\hspace{0.17em}{D}_{\min }=\sqrt{{\left(z-z_F\right)}^2+R^2+2\left(z-z_F\right)\sqrt{R^2-r_{\min }^2}}\hspace{0.17em}$. Equation 84 can be used as a benchmark solution to check the accuracy of the numerical implementation of angular spectrum approach of Eqs. A6, A7.

To be specific, the results below are presented for a source used in experiments.30, 32, 33 The transducer operates at frequency $\omega /\left(2\pi \right)=$ 2 MHz in water ($c=$1500 m/s, $\rho =$1000 kg/m³). The source aperture diameter is $2r_{\max }=$ 63 mm, the central opening diameter is $2r_{\min }=$ 10 mm, and the focal length is $R=$ 62 mm. The spherical scatterer mimics a kidney stone with the following parameters: $a=$ 1 mm, ${\rho }_{*}=$ 2040 kg/m³, $c_l=$  4540 m/s, and $c_t=$2130 m/s, which corresponds to COM stones.34 Figure 2 shows the distribution of acoustic pressure amplitude for the incident focused beam and corresponding components of radiation pressure normalized by $W/c$. For these plots, the stone is presumed to be positioned within the xz plane that intersects the focal point; then the lateral component of the force equals $F_x$ and $F_y=0$. It is seen that the axial component $F_z$ is positive and exceeds the value of the lateral component $F_x$ almost everywhere (i.e., the radiation force is mostly directed along the wave propagation direction). From Fig. 2 it is also clear that the distribution of the lateral component $F_x$ is less uniform than the axial one. As expected, $F_x$ disappears on the beam axis. Close to the axis $F_x$ is directed away from the axis but at larger distances off-axis there is a region where it changes direction and pushes the sphere toward the axis. This effect is additionally illustrated in Fig. 3, where the full acoustic pressure $\tilde{p}$ distribution at $t=0$, given by $\mathrm{Re}\hspace{0.17em}\left(p\right)$, and the direction and value of the radiation force are shown by an arrow for different positions of the scatterer in the focal plane. When the stone is on the axis, the force is maximal and oriented co-axially. Displacement of the stone by $x=$ 0.4 mm results in some decrease of the force amplitude and a significant change (approximately by 30°) of the force direction: The stone is pushed further off-axis. Positioning the stone further from the axis ($x=$ 0.8 mm) makes the force co-axial again but with much smaller amplitude than when the stone is on axis. When $x=$ 1.2 mm, the force is about the same amplitude as at $x=$ 0.8 mm but its direction is almost perpendicular to the axis. With further increases in x, the force remains directed toward the axis but decreases in magnitude.

Figure 2.

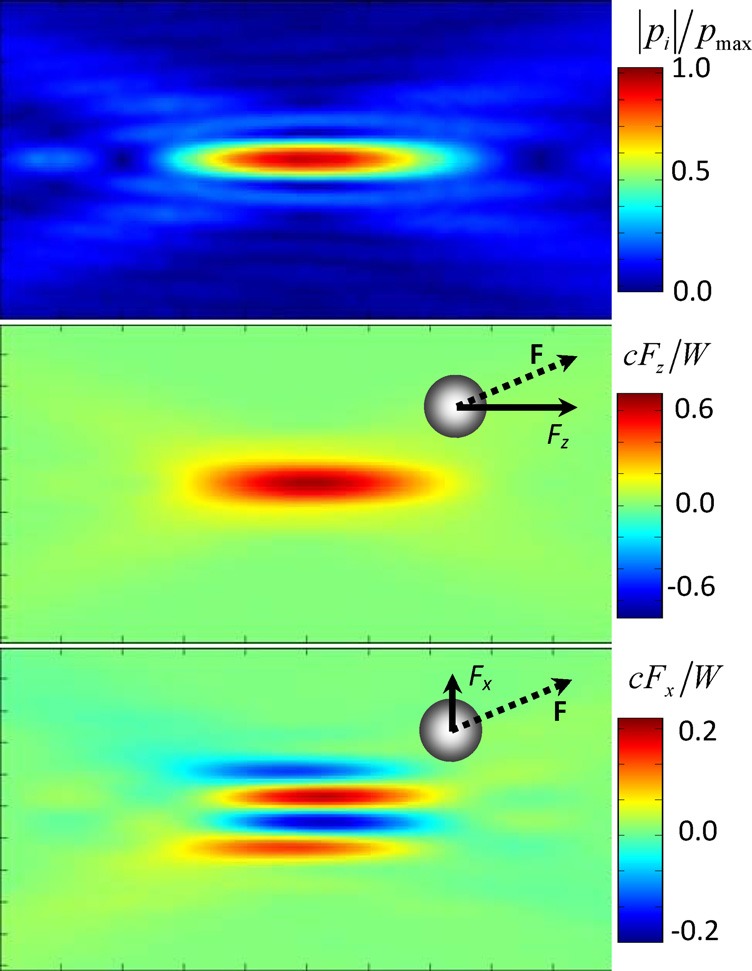
(Color online) Spatial distributions in the $x z$ plane of the amplitude of the incident pressure wave (top), the radiation force axial component $F_z$ (middle), and the lateral component $F_x$ (bottom) when the sphere is positioned on the x axis for the source shown in Fig. 1. The image box size is 20 × 10 mm. Note the sphere is included for scale and is not in fact fixed in only the shown position.

Figure 3.

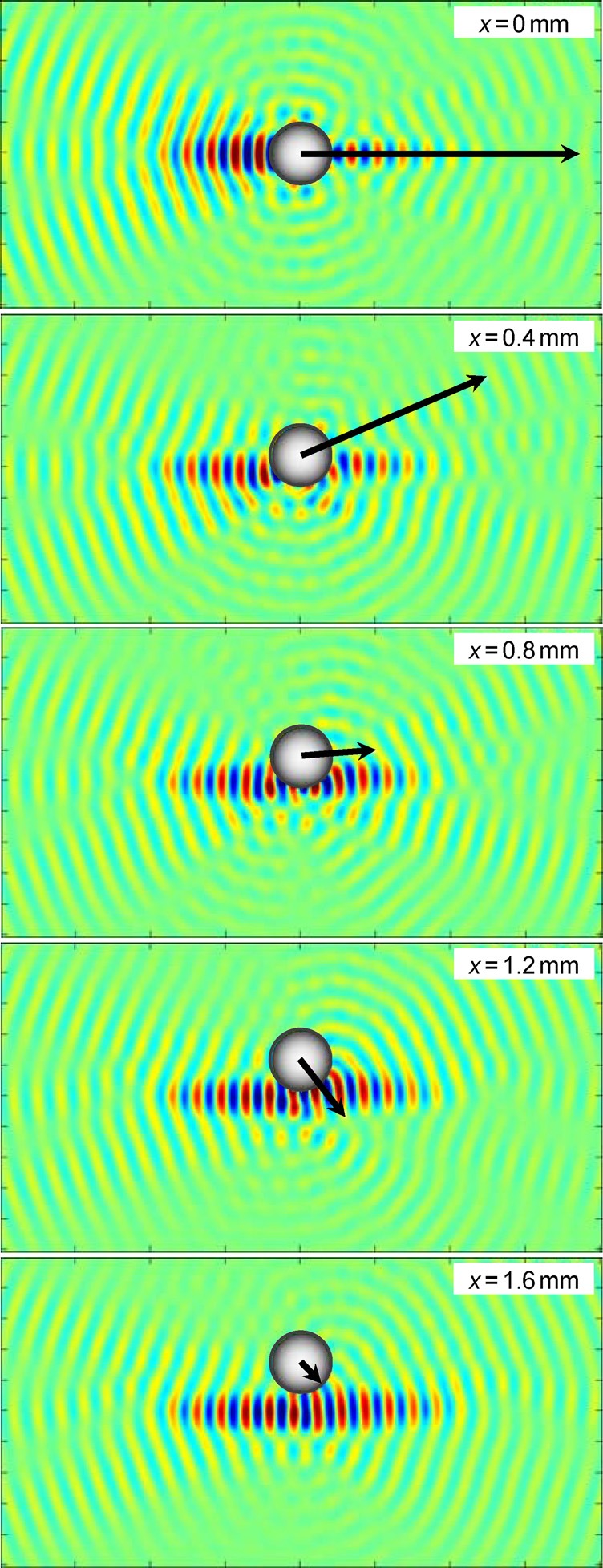
(Color online) Spatial distributions in the $x z$ plane of the full acoustic pressure at time $t=0$ for different positions of the 2-mm spherical stone. The lateral coordinate x of the stone center is marked in the left-upper corner of each image, and the colors denote pressure magnitudes. An arrow shows the radiation force direction and relative magnitude. The image box size is 20 × 10 mm. The incident beam axis is directed to the right.

It may be also useful to analyze the radiation force for a small scatterer ($ka\ll 1\hspace{0.17em}$) on the acoustic beam axis, where the lateral component of the force disappears due to symmetry. According to Eqs. 78, 79, 80, the axial component of the force on the axis can be approximated as follows:

$$\begin{array}{c}{F}_z\approx -\hspace{0.17em}\frac{\pi a^3}{3\rho c^2}\frac{d}{\mathit{d}\mathit{z}}\left(\hspace{0.17em}{f}_1{\left|P_{\text{axis}}\right|}^2-\frac{3f_2}{2k^2}{\left|\frac{d{P}_{\text{axis}}}{\mathit{d}\mathit{z}}\right|}^2\hspace{0.17em}\right)\\ +\frac{\pi a^2{\left|P_{\text{axis}}\right|}^2}{\rho c^2}\frac{2}{9}\left(f_1^2+f_1{f}_2+\frac{3}{4}{f}_2^2\right){\left(\mathit{k}\mathit{a}\right)}^4\hspace{0.17em}\hspace{0.17em}.\end{array}$$ (85)

Here the relation $\nabla p=i\rho ck \mathbf{v}$ was used. Along with Eq. 84, this expression represents the force analytically. The second term is of higher order (in terms of the small parameter $\mathit{k}\mathit{a}$) relative to the first term but it may become important in regions where spatial variations of velocity and pressure amplitudes are small. For calculations, the derivatives in Eq. 85 have to be evaluated. The expression for $F_z$ becomes unwieldy and is omitted here for brevity.

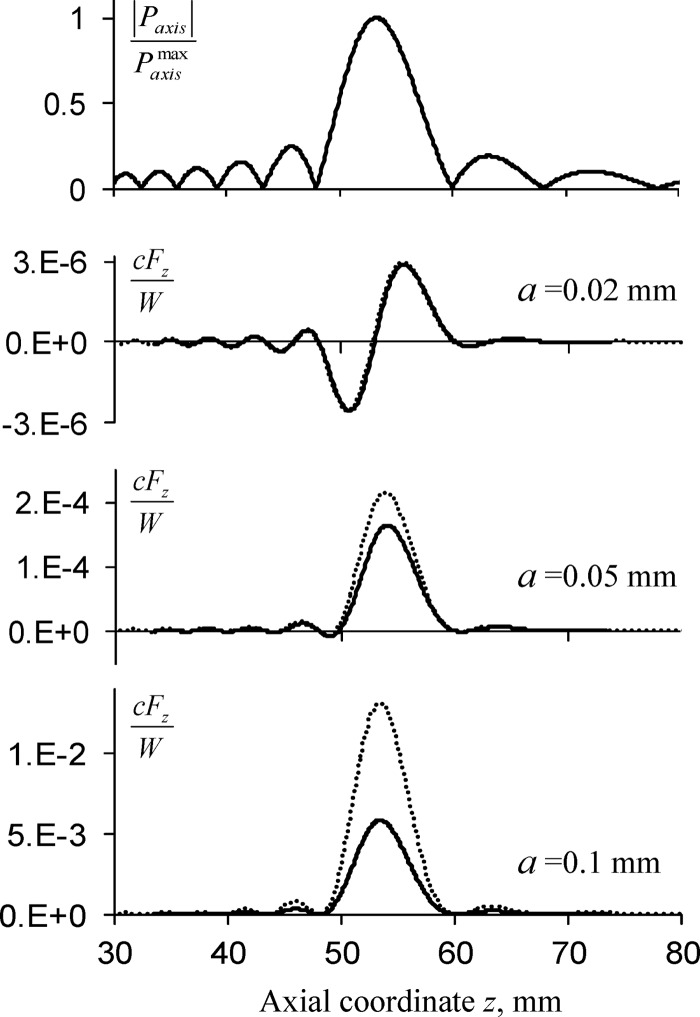
Figure 4 compares the axial distribution of the radiation force $F_z$ for different stone radii a = 0.02, 0.05, and 0.1 mm, calculated using either Eq. 48 (with no limitation to the value of $\mathit{k}\mathit{a}$) or the asymptotic result of Eq. 85. Note that the wavelength that corresponds to 2 MHz in water is λ = 0.75 mm so that $\lambda \gg a$ in all calculated cases. For reference, the axial distribution of pressure amplitude is shown at the top. For the smallest scatterer a = 0.02 ($ka\approx$ 0.17), the asymptote Eq. 85 agrees well with the result obtained from the full model. It is worth noting that the force is negative in the prefocal region and in some other locations. This result is in accordance with the first term of Gor'kov's asymptote Eq. 85, which is expressed as a derivative of an oscillating potential function. The appearance of negative radiation force is not uncommon for acoustic beams.12, 14 As is seen from Eq. 85, any beam with an oscillating spatial structure of the near field will create a negative force if the scatterer is sufficiently small. With the increase of $\mathit{k}\mathit{a}$, the second term in Eq. 85 starts to dominate the first one, and the negative force regions become smaller or disappear. Then, the radiation force behavior resembles that of the square of the pressure amplitude ${\left|P_{\text{axis}}\right|}^2$. Also, the asymptote Eq. 85 overestimates the true force [e.g., by 30% for a = 0.05 mm ($ka\approx$ 0.42) and 120% for a = 0.1 mm ($ka\approx$ 0.84)—see Fig. 4]. Modeling results indicate that for the considered cases, Eq. 85 is only valid when $ka\le$0.2.

Figure 4.

Axial distribution of pressure amplitude $\left|P_{\text{axis}}\right|/P_{\text{axis}}^{\max }$ (top) and normalized radiation force $c{F}_z/W$ for different radii a of the scatterer. Solid lines represent calculations based on the full model, while dotted lines correspond to the low-frequency approximation, Eq. 85.

Multi-element linear array

Consider next a linear array (Fig. 5), which represents a typical transducer used either for medical ultrasound imaging or nondestructive testing. Although imaging utilizes short pulses, such transducers also can be excited continuously.35 Focusing is created differently in the $\mathit{x}\mathit{z}$ and $\mathit{y}\mathit{z}$ planes. In the $\mathit{y}\mathit{z}$ plane (elevation plane), focusing is achieved by a cylindrical lens attached to the transducer face. In the $\mathit{x}\mathit{z}$ plane (imaging plane), focusing is obtained by introducing appropriate time delays to the signals emitted by the array elements.

The array consists of M identical rectangular elements. Let h and w be the elements' height and width, and g be the gap between the neighboring elements. All the elements are excited at frequency $\omega /\left(2\pi \right)$. The angular spectrum of the array is a superposition of angular spectra of the individual elements. It is convenient to consider first one of the elements, say the mth, which is a rectangular source of dimensions $w\times h$ with its center being at $\left(x_m,\hspace{0.17em}0,\hspace{0.17em}0\right)$, where

$$x_m=\left(m-\frac{M+1}{2}\right)\left(w+g\right),$$ (86)

and $m=1,\hspace{0.17em}2,\hspace{0.17em}\mathrm{...}\hspace{0.17em},M$. The source occupies the region $x_m-w/2\le x\le x_m+w/2$, $-h/2\le y\le h/2$. As mentioned earlier, the array focuses in the $\mathit{y}\mathit{z}$ plane because of the presence of a cylindrical lens. To account for this feature, let us introduce the following phase distribution for the normal velocity on the mth element surface: $v_m\left(y\right)=V_0\hspace{0.17em}{e}^{i {\Phi }_n}\hspace{0.17em}{e}^{-i\hspace{0.17em}(k\hspace{0.17em}{y}^2/2R)}$, where R is the wavefront curvature radius after the wave passes the cylindrical lens, $V_0$ is the velocity amplitude, and ${\Phi }_m$ is a phase shift added to the mth element signal to provide beamforming in the $\mathit{x}\mathit{z}$ plane. Focusing at a point $(x_F,\hspace{0.17em}0,\hspace{0.17em}{z}_F)$ can be achieved by choosing ${\Phi }_m=k(z_F-\sqrt{{\left(x_F-x_m\right)}^2+z_F^2})$. The angular spectrum of the acoustic pressure of the mth element can then be written as follows [see Eqs. 5, 19, 20]:

$${\widehat{S}}_m\left(k_x,k_y\right)=\frac{p_{\text{source}}\hspace{0.17em}{e}^{ik\left(z_F-\sqrt{{\left(x_F-x_m\right)}^2+z_F^2}\right)}}{\sqrt{1-\left(k_x^2+k_y^2\right)/k^2}}{\displaystyle {\int }_{x_m-w/2}^{x_m+w/2}dx\hspace{0.17em}{e}^{-i{k}_{x}x}}{\displaystyle {\int }_{- h/2}^{h/2}dy\hspace{0.17em}\hspace{0.17em}{e}^{-i\left(k_{y}y+\hspace{0.17em}(k{y}^2/2R)\right)}}.$$ (87)

Here $p_{\text{source}}=\rho c{V}_0$ is the characteristic pressure amplitude at the element surfaces. The integrals in Eq. 87 can be calculated analytically; the resulting expressions are presented in Appendix B. Equation B5 gives the angular spectrum $\widehat{S}\left(k_x,k_y\right)$ for the particular case $x_F=0$, $z_F=R$ that will be considered below. According to the algorithm discussed earlier, from $\widehat{S}\left(k_x,k_y\right)$ we find $S\left(k_x,k_y\right)$ with the use of Eq. 82, then calculate the coefficients $H_{\mathit{n}\mathit{m}}$, and finally compute the radiation force components.

Consider an array with the following parameters: M = 128, h = 15 mm, w = 0.25 mm, $g=$0.05 mm, R = 40 mm, and $\omega /\left(2\pi \right)$ = 5 MHz. Such an array has parameters similar to those of the Philips/ATL HDI L7-4 ultrasound probe. The spherical scatterer is the same as in the case of Sec. 4A: A 2-mm diameter sphere with the elastic parameters similar to those of a COM kidney stone. Modeling results are shown in Fig. 6 for the particular case $x_F=0$, $z_F=R$. Because the problem in such a case is not axisymmetric, the results are presented for the xz and yz planes that include the focal point. The incident acoustic pressure amplitude distribution is shown at the top of Fig. 6. It is seen that the focal region is narrower in the xz plane than in the yz plane, which is a consequence of the larger source aperture in the x direction (38 mm) relative to the y direction (15 mm). Note that because of the small wavelength (0.3 mm), the focal width in each direction is much smaller than the target diameter. As a result, the radiation force distribution appears to be almost identical in the x and y directions. Similar to the force behavior shown in Fig. 2, when the stone is positioned a little off the axis, the force is directed away from the axis.

Figure 6.

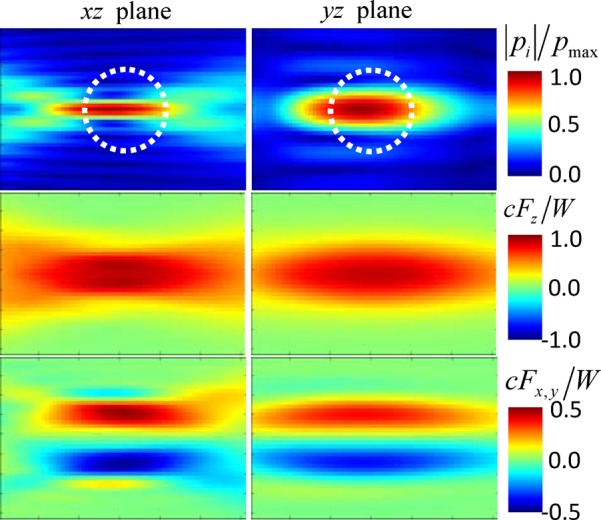
(Color online) Spatial distributions in the $x z$ plane (left column) and $y z$ plane (right column) of the amplitude of the incident pressure wave (upper), the radiation force axial component $F_z$ (center), and lateral component $F_x$ (lower left) and $F_y$ (lower right) for the 5-MHz source shown in Fig. 5. The target diameter 2a = 2 mm is shown by the dotted white circles in the top plots. The image box size is 6 × 4 mm.

DISCUSSION AND CONCLUSIONS

In this paper we propose a systematic approach for calculation of the radiation force produced by an arbitrary acoustic beam on an elastic sphere in a fluid. The method is based on an important fact that for the calculation of radiation force, which is a second order quantity in terms of acoustic perturbations, it is necessary to know the acoustic field only to the first-order linear approximation. Accordingly, determining the scattering field of any arbitrary incident beam can be reduced to the simpler problem of the scattering of a plane wave because any propagating beam can be represented as a superposition of plane waves through an angular spectrum decomposition. Instead of using such plane-wave decomposition, one could represent the acoustic beam as a sum of elementary fields of other types—e.g., point-source fields or spherical harmonics. However, the angular spectrum approach is more attractive computationally. The form of the scattering solution based on plane-wave decomposition looks natural and even trivial. However, a direct technical realization of such an approach is greatly aided by analytical simplifications. In the current paper it has been shown that the Legendre addition theorem, Eq. 26, makes it possible to express the incident beam as an expansion of spherical harmonics with a fairly simple expression for the series coefficients—see Eq. 35. The auxiliary coefficients $H_{m n}$, defined by Eq. 34, allow one to go from the angular spectrum to the amplitudes of the spherical harmonics in a series representing the corresponding solution of the Helmholtz equation. Note that radiation force is a second order quantity and thus a nonlinear function of acoustic pressure and particle velocity. Therefore, the principle of superposition is not applicable to force calculations, which means that calculation of radiation force requires all angular spectrum components to be used together, as a complete acoustic field. The problem can be simplified by considering the acoustic wave at infinitely large distances from the scatterer. Using such an approach, we have obtained fairly compact expressions for the Cartesian components of radiation force—see Eqs. 46, 47, 48, 49, 50, 51. These equations make it possible to numerically calculate radiation force easily and quickly, with the need of only a personal computer.

In practical computations, it is important to know the angular spectrum of the incident beam. For known sources, the spectrum can be found analytically from the geometrical characteristics of the source. Two examples of such an approach have been presented in Sec. 4. However, the source geometry and behavior are not always known accurately. In practice, a more reliable and attractive approach can be realized using the method of acoustic holography.36, 37, 38 In this method, acoustic pressures are measured along some plane surface in front of the source by scanning a hydrophone over the plane. Then the amplitude and phase of the wave (or the entire waveform, in the transient regime) are recorded for a 2D rectangular grid in the plane. These measurements can be used to calculate the angular spectrum and thus obtain the coefficients $H_{m n}$ that are present in the radiation force expressions, Eqs. 46, 47, 48. If the hydrophone sensitivity is not known, such a scanning technique would provide the angular spectrum with an indeterminate source power. Then, direct measurements of radiation force on a spherical target of known size and elastic properties could be used to calibrate the source power along with the hydrophone sensitivity. The idea of using the radiation force acting on a spherical scatterer as a calibration method was proposed previously by others;11 however, their approach had limited applicability because it was only strictly valid for plane waves or similarly idealized beam structures. In using radiation force measurements to determine beam power, it is worth noting that the scatterer can be dragged by acoustic streaming in addition to being pushed directly by the scattered beam. This additional force is difficult to predict because it depends not only on the acoustic attenuation and viscosity but also on the geometry of the tank containing the liquid. An acoustically thin membrane may be placed in front of the scatterer to eliminate streaming effects on power measurements, similar to what is done in an absorptive radiation force balance.39

Contrary to the plane-wave scattering case, when the incident wave has the form of a beam with a beam width smaller than or of similar size to the diameter of the scatterer, the radiation force direction can significantly differ from that of the beam axis. This peculiarity is shown in Fig. 3, and an additional illustration is provided in Fig. 7. In Fig. 7, white arrows indicate the direction of the force that would be created on a scatterer at different locations within the field while colors denote magnitudes of the radiation force $F=\sqrt{F_x^2+F_y^2+F_z^2}$. This plot corresponds to the force distribution in the $x z$ plane presented at the left-hand side of Fig. 6. It is seen that near the beam axis there is a trend of pushing the scatterer off-axis. On the other hand, in some regions not as close to the axis, the force is directed toward the axis. Such an irregular distribution of the force direction can be important to know in practical applications. Note also that if the scatterer is sufficiently small, the radiation force can be directed even opposite to the beam propagation direction (i.e., the axial force can be negative—see Fig. 4).

Figure 7.

(Color online) Spatial distribution in the $x z$ plane of the radiation force F for the same parameters used in Fig. 6. The force magnitude $F=\left| \mathbf{F} \right|$ is plotted by color. The force direction is shown by the white arrows.

Acoustic radiation force by real sources has many applications. In medical ultrasound, radiation force on solid targets has the potential for developing new imaging modalities.40 Another promising application is the ability to non-invasively expel stones from the kidney.30, 32 The theory presented here for determining acoustic radiation forces of arbitrary beams on elastic spheres may be used as a basis for these and possibly other applications.

APPENDIX A: ANGULAR SPECTRUM CALCULATION FOR A CURVED SOURCE

The complex amplitude ${\widehat{p}}_i$ of the incident pressure wave for commonly shaped ultrasound sources can be accurately calculated using the Rayleigh integral25, 26, 41

$$\hspace{0.17em}{\widehat{p}}_i\left(\mathbf{r}\right)\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}-\hspace{0.17em}i\rho \hspace{0.17em}c\frac{k}{2\pi }{\displaystyle {\int }_{\mathrm{\Sigma }}\frac{u\left(\mathbf{r}\prime \right)\hspace{0.17em}\hspace{0.17em}{\mathrm{e}}^{ik\left|\mathbf{r}\mathit{-}\mathbf{r}\prime \right|}}{\hspace{0.17em}\left|\hspace{0.17em}\mathbf{r}\mathit{-}\mathbf{r}\prime \right|}d\mathrm{\Sigma }\prime }\hspace{0.17em}.$$ (A1)

Here the integration is taken over the source surface Σ. The surface element $d\mathrm{\Sigma }\prime$ has coordinates $\mathbf{r}\prime$, and $u\left(\mathbf{r}\prime \right)$ is the corresponding complex amplitude of the normal surface velocity. The Rayleigh integral represents the acoustic field in the form of the superposition of monopole sources distributed over the surface Σ. A point source positioned at $\mathbf{r}\prime =\left(x\prime ,y\prime ,z\prime \right)$, in turn, can be represented as the following angular spectrum superposition at half space $z\ge z\prime$:42

$$\frac{{\mathrm{e}}^{ik\left|\mathbf{r}\mathit{-}\mathbf{r}\prime \right|}}{\left|\hspace{0.17em}\mathbf{r}\mathit{-}\mathbf{r}\prime \right|}=\frac{i}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }d{k}_{x}d{k}_y\frac{e^{i\hspace{0.17em}\left[k_x\left(x-x\prime \right)+k_y\left(y-y\prime \right)+\sqrt{k^2-k_x^2-k_y^2}\left(z-z\prime \right)\right]}}{\sqrt{k^2-k_x^2-k_y^2}}}}.$$ (A2)

With the use of Eq. A2, the Rayleigh integral [Eq. A1] transforms to the angular spectrum representation for the pressure amplitude

$$\hspace{0.17em}{\widehat{p}}_i\left(\mathbf{r}\right)=\frac{1}{4{\pi }^2}{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }d{k}_{x}d{k}_y\widehat{S}\left(k_x,k_y\right)\hspace{0.17em}{e}^{i\hspace{0.17em}\left[k_{x}x+k_{y}y+\sqrt{k^2-k_x^2-k_y^2}z\right]}}},$$ (A3)

with the following expression for the angular spectrum:43

$$\widehat{S}\left(k_x,k_y\right)=\frac{\rho \hspace{0.17em}c}{\sqrt{1-\frac{k_x^2+k_y^2}{k^2}}}{\displaystyle {\int }_{\mathrm{\Sigma }}u\left(\mathbf{r}\prime \right)\hspace{0.17em}{e}^{-i\hspace{0.17em}\left[k_{x}x\prime +k_{y}y\prime +\sqrt{k^2-k_x^2-k_y^2}z\prime \right]}d\mathrm{\Sigma }\prime }.$$ (A4)

The angular spectrum can therefore be calculated by integration along the radiator surface Σ. In practice it is convenient to perform the integration over a lateral plane $\left(x\prime ,y\prime \right)$. Then the elementary surface $d\mathrm{\Sigma }\prime$ can be expressed as $d\mathrm{\Sigma }\prime =dx\prime dy\prime /n_z$, where $n_z$ is the z-component of the unit normal vector to $d\mathrm{\Sigma }\prime$. If the surface Σ is represented by a function $z\prime =Z\left(x\prime ,y\prime \right)$, then the z-component of the normal vector has the following expression: $n_z=1/\sqrt{1+{\left(\partial Z/\partial x\prime \right)}^2+{\left(\partial Z/\partial y\prime \right)}^2}$. Consider a transducer in the form of a spherical cap with a circular central opening (Fig. 1). Let $r_{\max }$ be the radius of the source aperture, $r_{\min }$ be the radius of the central opening, and R be the radius of curvature of the radiating surface. Then the focal point coordinate is $z_F=\sqrt{R^2-r_{\max }^2}$. The surface Σ of the transducer under consideration is a spherical one

$$Z\left(x\prime ,y\prime \right)=z_F-\sqrt{R^2-x^{\prime 2}-y^{\prime 2}}.$$ (A5)

Equation A4 becomes

$$\begin{array}{c}\widehat{S}\left(k_x,k_y\right)=\frac{\rho \hspace{0.17em}c}{\sqrt{1-\frac{k_x^2+k_y^2}{k^2}}}{\displaystyle \int {\displaystyle \int \frac{u\left(x\prime ,y\prime \right)}{\sqrt{1-\frac{x^{\prime 2}+y^{\prime 2}}{R^2}}}\hspace{0.17em}{e}^{-i\hspace{0.17em}\left[k_{x}x\prime +k_{y}y\prime +\sqrt{k^2-k_x^2-k_y^2} Z\left(x\prime ,y\prime \right)\right]}dx\prime dy\prime }}.\end{array}$$ (A6)

The integration here is made on the $\left(x\prime ,y\prime \right)$-plane over the ring $r_{\min }^2\le x^{\prime 2}+y^{\prime 2}\le r_{\max }^2$.

Another possible approach for calculating the angular spectrum $\widehat{S}\left(k_x,k_y\right)$ is first to use the Rayleigh integral to compute the incident pressure distribution $\hspace{0.17em}{\widehat{p}}_i \left(x,y,z_0\right)$ at some plane $\hspace{0.17em}z=z_0>0$ in front of the transducer. The plane coordinate $z_0$ can be arbitrary. It is natural to place the plane at the source aperture ($z_0\to 0$) but as in the case in Eq. A1, $\left|\hspace{0.17em}\mathbf{r}\mathit{-}\mathbf{r}\prime \right|\to 0$ at the source edge, which would create numerical difficulties. To avoid this problem, finite $z_0$ can be used, say $z_0=10\lambda$, where λ is the wavelength. Once $\hspace{0.17em}{\widehat{p}}_i \left(x,y,z_0\right)$ is calculated, the corresponding angular spectrum $\widehat{S}\left(k_x,k_y\right)$ can be computed using the following expression that results from Eq. 81:

$$\widehat{S}\left(k_x,k_y\right)=e^{-i{z}_0\sqrt{k^2-k_x^2-k_y^2}}{\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle {\int }_{-\infty }^{+\infty }\hspace{0.17em}dxdy\hspace{0.17em}{\widehat{p}}_i\left(x,y,z_0\right)\hspace{0.17em}{e}^{-i{k}_{x}x-i{k}_{y}y}}}.$$ (A7)

Both mentioned approaches for calculating the angular spectrum $\widehat{S}\left(k_x,k_y\right)$ are approximate. Also, they describe the radiated field somewhat differently. Equation A2 represents radiation of a transducer surface element having a coordinate $\mathbf{r}\prime$ under the assumption that the corresponding wave is a uniform hemi-spherical wave that freely propagates into the medium. In reality, part of this wave is reflected by the curved transducer surface and thus contributes to the radiated acoustic beam different in a way from that of a hemi-spherical wave. When employing the Rayleigh integral Eq. 84 directly, this self-shadowing by the curved radiator is partly taken into account because the zone where the secondary diffraction waves are directed is usually far from the region of interest (e.g., the focal zone).44, 45 Therefore, calculation of the angular spectrum using Eq. A7 is more precise than that using Eq. A6. However, the difference between the acoustic fields calculated by these two approaches should not be significantly far from the source, and so either of the two approaches can be used. For the results presented in this paper, the angular spectrum was calculated from Eq. A6. Calculations presented in this paper show no difference between the two approaches.

APPENDIX B: ANGULAR SPECTRUM CALCULATION FOR A MULTI-ELEMENT LINEAR ARRAY

Consider the multi-element array shown in Fig. 5. The angular spectrum ${\widehat{S}}_m\left(k_x,k_y\right)$ for such a source is expressed by Eq. 87. After integrating we obtain

$$\begin{array}{c}{\widehat{S}}_m\left(k_x,k_y\right)=\frac{p_{\text{source}}\hspace{0.17em}{e}^{ik\left(z_F-\sqrt{{\left(x_F-x_m\right)}^2+z_F^2}\right)}\sqrt{\pi w^{2}R/k}}{\sqrt{1-\left(k_x^2+k_y^2\right)/k^2}}\\ \times \frac{\sin \left(k_{x}w/2\right)}{\left(k_{x}w/2\right)}\hspace{0.17em}\exp \left(-i{k}_x{x}_m+i\frac{k_y^{2}R}{2k}\right)\left[E\left({\eta }_{+}\right)-E\left({\eta }_{-}\right)\hspace{0.17em}\right],\end{array}$$ (B1)

where the function $E\left(\eta \right)$ is expressed through Fresnel integrals $C\left(\eta \right)$ and $S\left(\eta \right),$

$$E\left(\eta \right)={\displaystyle {\int }_0^{\eta }\exp \hspace{0.17em}\left(-i\frac{\pi }{2}{\xi }^2\right)}d\xi =C\left(\eta \right)-iS\left(\eta \right),$$ (B2)

and has the following arguments:

$${\eta }_{\pm }=\sqrt{\frac{k}{\pi R}}\left(\frac{k_{y}R}{k}\pm \frac{h}{2}\right).$$ (B3)

The angular spectrum of the entire linear array is a superposition of the elements' spectra

$$\begin{array}{c}\widehat{S}\left(k_x,k_y\right)=p_{\text{source}}\sqrt{\frac{\pi w^{2}R}{k}}\frac{\sin \left(k_{x}w/2\right)}{\left(k_{x}w/2\right)}\frac{E\left({\eta }_{+}\right)-E\left({\eta }_{-}\right)}{\sqrt{1-\left(k_x^2+k_y^2\right)/k^2}}\\ \times \exp \left[i\left(k{z}_F+\frac{k_y^{2}R}{2k}\right)\right]\hspace{0.17em}{\displaystyle \sum _{m=1}^M\exp \left[-i\left(k\sqrt{{\left(x_F-x_m\right)}^2+z_F^2}+k_x{x}_m\right)\right]}.\end{array}$$ (B4)

Here $x_m$ and ${\eta }_{\pm }$ are defined by Eqs. 86 and B3, respectively. Let us consider a particular case when the electronic focus coincides with the cylindrical lens focus—i.e., when $x_F=0$, $z_F=R$. Then Eq. B4 takes the following form:

$$\begin{array}{c}\widehat{S}\left(k_x,k_y\right)=p_{\text{source}}\sqrt{\frac{\pi w^{2}R}{k}}\frac{\sin \left(k_{x}w/2\right)}{\left(k_{x}w/2\right)}\frac{E\left({\eta }_{+}\right)-E\left({\eta }_{-}\right)}{\sqrt{1-\left(k_x^2+k_y^2\right)/k^2}}\\ \times \exp \left[ikR\hspace{0.17em}\left(1+\frac{k_y^2}{2k^2}\right)\right]\hspace{0.17em}{\displaystyle \sum _{m=1}^M\exp \left[-i\left(\hspace{0.17em}k\sqrt{x_m^2+R^2}+k_x{x}_m\right)\hspace{0.17em}\right]}.\end{array}$$ (B5)