Integrative modelling of animal movement: incorporating in situ habitat and behavioural information for a migratory marine predator

Abstract

A fundamental goal in animal ecology is to quantify how environmental (and other) factors influence individual movement, as this is key to understanding responsiveness of populations to future change. However, quantitative interpretation of individual-based telemetry data is hampered by the complexity of, and error within, these multi-dimensional data. Here, we present an integrative hierarchical Bayesian state-space modelling approach where, for the first time, the mechanistic process model for the movement state of animals directly incorporates both environmental and other behavioural information, and observation and process model parameters are estimated within a single model. When applied to a migratory marine predator, the southern elephant seal (Mirounga leonina), we find the switch from directed to resident movement state was associated with colder water temperatures, relatively short dive bottom time and rapid descent rates. The approach presented here can have widespread utility for quantifying movement–behaviour (diving or other)–environment relationships across species and systems.

1. Introduction

Animal movement fundamentally influences the distribution and abundance of organisms as well as many ecological processes operating at the population, community and ecosystem levels. These include habitat selection and conservation [1], territorial and home-range dynamics [2], predator–prey dynamics [3], disease spread and invasions [4], and the biological production, transfer and transport of energy [5]. Within this critical area of research, technological advances in telemetry [6] are increasingly leading researchers to focus on the movement of individuals as the spatio-temporal bridge between the individual and the population [7]. Of prime (but often elusive) interest is the exploration of how individual movement behaviour is influenced by environmental (and other) factors [1] as this is key to understanding animal responsiveness to environmental change.

Inference on complex animal–environment interactions is driving the development of increasingly sophisticated methods for analysing movement data [8,9]. Individual-based telemetry data are associated with a number of well-documented issues, producing large volumes of high-resolution auto-correlated observations that are often incomplete and/or containing significant error, with the high cost resulting in small sample sizes [10]. To develop population-level inference necessitates a modelling framework that appropriately treats both the data (observation process) and the movement process, with each source of error [11,12], providing a realistic representation of movement behaviour [13,14] and allowing meta-analysis across individuals [15]. How to appropriately characterize the environment can represent a significant additional challenge [16,17], particularly in the marine context, where wide-ranging migratory species may spend the majority of their time deep diving in a remote and inaccessible three-dimensional habitat.

A recent innovation in marine telemetry is the data logger, which relays via satellite high-accuracy vertical profiles of two key physical oceanographic variables, temperature and salinity [18,19]. This provides local-scale in situ oceanographic habitat information obtained within the animal's immediate perceptual range. Summarized information on vertical diving behaviour is also recorded. Global tagging efforts of southern elephant seals (Mirounga leonina) have collected such data across vast spatial and temporal scales throughout annual winter foraging migrations in the Southern Ocean, a significant proportion within the remote Antarctic sea ice zone [18,19]. This presents an unprecedented opportunity for a highly migratory marine species to quantify individual movement and foraging responses to environmental influences, and to infer how individual behaviour can shape population ecology, a fundamental first step towards predicting responses in a zone highly sensitive to climate change [20,21].

Here we focus on the East Antarctic continental shelf, a highly productive coastal region influenced by seasonal changes in sea ice [22] and sensitive to climate change [21]. This area has previously identified as a highly favourable foraging zone for southern elephant seals [18], in particular, for benthically foraging male animals [23]. While apparently less frequented by females, recent evidence indicates that this habitat is more profitable, in terms of energy gain, than alternative sea ice or oceanic habitats [24].

In this study, we aimed to identify and quantify relationships between horizontal movements, diving behaviour and the physical ocean environment within an integrated modelling framework. State-space models (SSMs) are an ideal method for analysing tag data to discriminate behavioural state—for example, ‘resident’ and ‘directed’ movement (putatively ‘foraging’ and ‘travelling’ states)—but these commonly incorporate only information from horizontal movements [11–13]. Here, we extend for the first time a hierarchical Bayesian state-space modelling framework [15] so the vertical (diving) component of movement and/or the environmental cues can both influence the probability of switching between states. Simulation studies are used to evaluate the sensitivity of the SSM to estimating parameters for known environmental relationships. We then focus on the southern elephant seals migrating from Kerguelen Islands (KI) and Macquarie Island (MI) that targeted the sea ice zone over the Antarctic shelf. Our approach achieves a quantitatively rigorous understanding of animal–environment interaction, incorporating the vertical component of this multi-dimensional process.

2. Material and methods

(a). Instrumentation and data

Conductivity–temperature–depth (CTD) satellite relay data loggers were built by the Sea Mammal Research Unit (University of St Andrews, UK). Details of the tags, deployment and data relay procedures have been described elsewhere [18,19]. Briefly, CTD and dive depth data are collected every 4 s during a dive ascent and compressed onboard [25] for limited bandwidth transmission via the Argos satellite system. Temperature and salinity profiles are based on the deepest dive made in each 6 h period. The accuracy of corrected pressure, temperature and salinity data is better than 2–5 dbar, 0.02–0.03°C and 0.02–0.05 psu, respectively [18,19,26], and has been continuously improved since 2005.

The tags were deployed on juvenile male southern elephant seals (length = 3.09 ± 0.45 m) from KI (69°30 E, 49°30 S) during 2009 and adult females (length = 2.39 ± 0.03 m) from MI (158°54 E, 54°36 S) during 2010. Tags were deployed in the late austral summer to cover winter foraging trips. Here we focused on those animals that travelled to the East Antarctic shelf and slope environment (KI: n = 5 seals, 7607 Argos locations; MI: n = 3 seals, 4992 Argos locations). To increase the MI sample size an additional 2005 deployment (length = 2.55 ± 0.06 m) was also included (n = 4 seals, 3655 Argos locations).

To examine the movement of seals in relation to oceanographic conditions, two environmental variables were derived from the CTD profiles (KI: n = 1498, MI: n = 1082/1533 during 2005/2010), mean ocean temperature (Temp, °C) at the bottom of a dive, and thermocline strength (Tcline, kg m⁻³). Both provide potentially important information on the vertical structure of the water column in which the animals forage [27]. For example, strong thermoclines may concentrate phytoplankton and thereby attract higher trophic levels [28]. Ocean temperature influences species distribution and physiology (e.g. low temperatures may lower metabolism, hence speed, of potential prey [23]). The dive bottom was considered to include more than 80 per cent of the maximum recorded depth. The CTD data were first linearly interpolated onto 1 m vertical levels for the surface 10 m, and 10 m levels thereafter. Thermocline strength was determined based on potential density (σ), calculated relative to the surface from temperature, salinity and pressure using standard seawater equations. For each profile, the bottom of the surface mixed layer depth was determined where the density difference to the surface Δσ > 0.125 kg m⁻³ [29], and the base of the thermocline where the vertical density gradient Δσ/Δz ≤ 0.0001 kg m⁻¹. Thermocline strength was calculated as the absolute difference between the densities at these two depths.

To examine the movement of seals in relation to their diving behaviour, two variables were developed from the raw dive data (KI: n = 21739, MI: n = 9287/11894 during 2005/2010), the proportion of time spent at the bottom of an individual dive (pTime), and the absolute descent rate (Des, m s⁻¹). When actively foraging, we may expect seals to both increase their descent rates and maximize their time at the dive bottom [27,30], particularly when targeting benthic prey at relatively consistent depths. As pTime varied strongly across individuals it was necessary to centre this variable such that pTime_k,t = pTime_k,t – mean(pTime_k)/sd(pTime_k), where k is the individual and t is the timestamp.

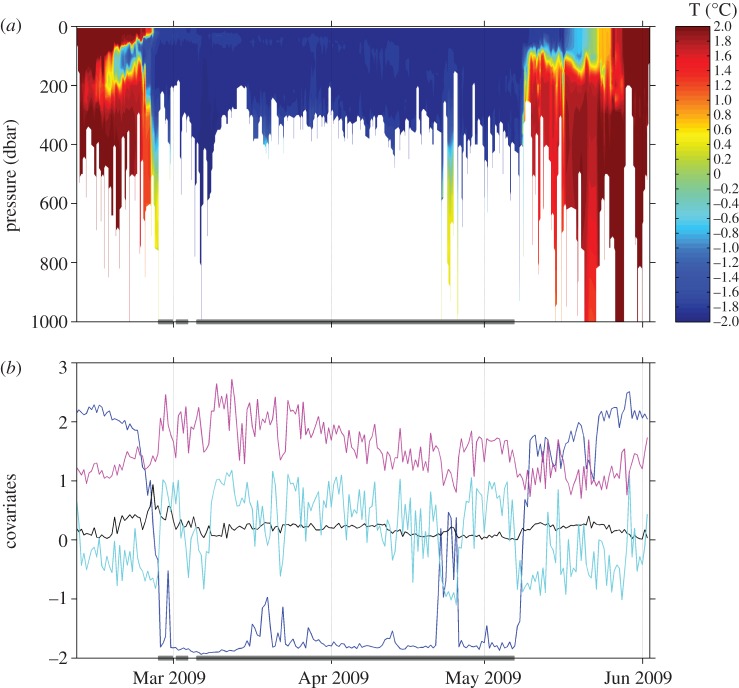
Only data beyond 10 km of the island release sites were examined. Prior to analysis, all covariate time series were regularized to match the regular 12 h time steps of the correlated random walk being fit in the SSM [11]. Missing environmental or diving information was filled by loess fitting with a span α = 28/n (i.e. a 14 day neighbourhood). While this generally represented less than or equal to 10 per cent of the data (KI Temp: 8.0%, Tcline: 10.2%, pTime: 1.3%, Des: 1.3%), it was higher for the environmental covariates obtained from the 2005 deployment (MI Temp: 40.3/3.4%, Tcline: 46.0/8.7%, pTime: 9.9/2.1%, Des: 9.9/2.1% for 2005/2010 respectively). An alternative approach in future would be to set priors for missing covariates; however, it is likely this will substantially increase the computational time. An example CTD time-series and the derived environmental and dive variables are shown in figure 1.

Figure 1.

Example environmental and diving time-series data from a KI juvenile male (3.62 m length) southern elephant seal (ct36-F-09). (a) Vertical temperature-at-depth (°C) profiles recorded 10 February to 3 June 2009. (b) Covariates derived from tag data (see §2). Two environmental covariates—temperature at the bottom of a dive (°C, blue) and thermocline strength (kg m⁻³, black)—and two diving covariates—proportion of time spent at the bottom of a dive (centred, cyan; see §2) and descent rate (m s⁻¹, pink). Grey bars show where the best-ranked model estimates the resident movement state to occur.

(b). State-space model

The SSM provides an appropriate framework for modelling movement and simultaneously dealing with inherent telemetry location error [11,12]. Using Bayesian methods all locations in a track can be probabilistically assigned to one of two (unobservable) behavioural states, nominally labelled as ‘resident’ (R) and ‘directed’ (D). In a hierarchical formulation parameters may be estimated across multiple individuals [15]. To enable environment–behaviour and dive–behaviour relationships to be directly quantified within a single model, we extend this SSM framework so the transition (switch) between states varies explicitly as a function of (environment and/or dive) covariates.

Suppose there are two behavioural states with the state variable b_t representing the state at time t. The transition matrix determines the switching probabilities (ϕ),

2.1

whose elements are constrained so that 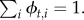We modelled these as dependent on both the previous state b_t−1 and n covariates X_t via a logistic function:

2.2

Here β and m are the intercept and coefficient parameters, j is the covariate index and 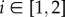is the behavioural state index, where 1 = ‘directed’ and 2 = ‘resident’. Hereby at any time t the switch probability Pr[R|D] = 1 − ϕ₁ and the reverse switch Pr[D|R] = ϕ₂. Which of these transitions occurs at any time step is determined by the previous behavioural state,

2.3

where η represents the probability of being in either state. This is modelled using a categorical distribution such that b_t ∼ Cat(η_t). We used vague priors throughout [11,12,15], and set both β and m ∼ N(0, 10). The model code is available in the electronic supplementary material, appendix S1.

(i). Simulations

To assess the performance of the covariate SSM, we set up a series of experiments with simulated data and known environment–behaviour relationships, and compared the parameter estimates to the true values. To emulate a realistic ocean temperature field, we simulated a random Gaussian field with spatial correlation (using the R ‘fields’ package [31]), overlaid on a north–south gradient (from 10 to −2). We set a 1600 × 400 grid covering the observed spatial range of KI southern elephant seals (see the electronic supplementary material, figure S1). Six tracks of 290 time steps were simulated in each experiment and environmental data were sampled along the track. Each location had Argos errors added from randomly drawn location classes using the real class proportions as the probability vector (p = 0.01, 0.12, 0.14, 0.10, 0.19, 0.44 for the classes 3, 2, 1, 0, A, B/Z respectively). All tracks were generated using identical parameter values, differing only in the environment–behaviour coefficients used in each simulation (see the electronic supplementary material, table S1). Ten combinations of coefficients (m₁, m₂) over the range 0.25–2 were investigated, where positive coefficients indicate a higher (lower) probability of switching into (out of) ‘resident’ behaviour in cold water.

(ii). The influence of behaviour and environment on movement

Two hierarchical models [15] were then fitted separately to the KI and MI seals using a half-day time step (selected since only 2 Argos uplinks per day is common in ice environments). For each, the model parameters were estimated across the group of animal tracks. The SSM is run using the software packages WinBUGS and R [32], freely available online (http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/contents.shtml and http://www.R-project.org). To fit the model two Markov chain Monte Carlo (MCMC) chains of 20 000 iterations were run with a burn-in of 10 000. Each chain was thinned so one in every 10 samples was retained, for a final MCMC sample size of 2000.

It is logical that animals should be more likely to switch from a directed to resident movement state where they can obtain forage, but it is also plausible that the reverse switch (from resident to directed) may be related more strongly to the internal state of the animal (e.g. satiation) or some other factor (e.g. the need to return to breeding grounds) [13]. Hence we explored two scenarios, where covariates are not included in the determination of the reverse switch probabilities (a one-way switch influence) and are included (two-way). To assess how well a particular model fitted the data, we used the Bayesian deviance information criterion (DIC) [33]. DIC was not used as a strict basis for model choice, but rather as a means for producing a candidate set of model formulations [13].

Developing diagnostics for Bayesian SSMs remains a field of active research. Particularly for the relatively complex SSMs used here, with the observation (treating Argos data) and process (treating the behavioural state switching) models simultaneously being fitted, (i) discriminating poor fit and (ii) determining the source and any consequence of poor fit is not simple. For evidence of fundamental problems, we investigated four avenues. To assess for convergence, we used two approaches: (i) visual inspection and autocorrelation functions were applied to the MCMC sample chains for estimated movement and covariate parameters, and (ii) the Brooks–Gelman–Rubin potential scale reduction factor (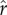) [34] was examined for all estimated parameters, using 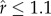as a threshold for convergence. (iii) To check for parameter identifiability issues (i.e. whether sufficient contrast existed within the data to estimate the intercept and covariate coefficient parameters well), we checked whether the posterior samples for the parameters were correlated, in particular between the two switches. (iv) Finally, we examined to what extent the behavioural state estimations were ultimately influenced by the various model formulations.

3. Results

(a). Simulation study

The covariate SSM produced good estimates of the known environment–behaviour parameters (see the electronic supplementary material, table S2 and figure S1b). In all of the simulation experiments, the true values of the slope parameters (m₁, m₂) fell within the 95% credible limits (CL) of the posterior distributions for these parameters. However, estimates for the weakest slope value tested (0.25) tended to straddle zero, indicating low confidence. In a few simulations, one intercept (β₁) fell on (n = 1 experiment) or just outside (n = 2 experiments) the relatively narrow 95% CL. However, the effect of these errors on the estimation of behavioural state as ‘resident’ or ‘directed’ appeared minor, with greater than or equal to 88 per cent correct allocation achieved in all simulations.

(b). Case study: shelf ice migrants from Kerguelen Islands and Macquarie Island

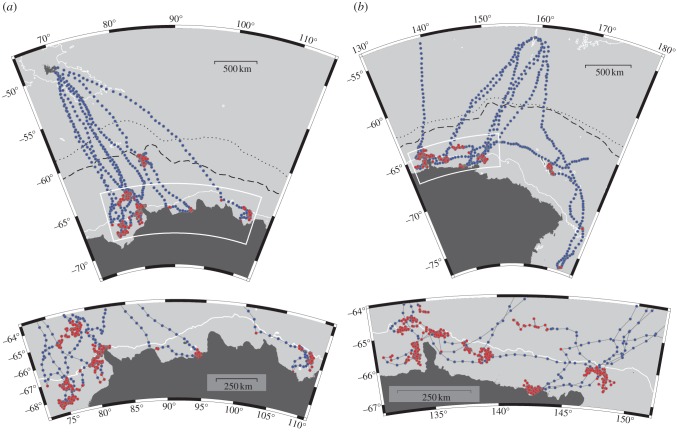
Having evaluated the model performance using simulated data, we applied it to data from southern elephant seals tagged on KI and MI. The four diagnostic avenues investigated showed no evidence of any fundamental problems (see the electronic supplementary material, appendix S2). The tracks generated by the SSM using the 12 h time step comprised 1146 and 1083 locations for KI and MI seals, respectively. Individual tracks ranged from 116 to 287 and 123 to 219 locations, respectively, spanning approximately 2 to 6 months (figure 2). In general, seals showed rapid travel south to the East Antarctic continental shelf. Seals from both islands spent approximately half their trip over the shelf, on average 50 and 46 days for KI males and MI females, respectively (table 1). During this time, animals displayed between one and four periods of ‘resident’ movement, averaging 14 days and 25 days for KI males and MI females, respectively (see table 1 and electronic supplementary material, figure S2). Above three-quarters of the shelf time was characterized as putative foraging (‘resident’), with the majority of dives (76 and 81%) identified as benthic (table 1). Following their shelf visit seals moved north and engaged in one or more additional resident periods within the sea ice zone or returned to their breeding island (figure 2; electronic supplementary material, figure S2). Horizontal swim speeds tended to be much lower during resident periods, but this was not always the case (see the electronic supplementary material, figure S3).

Figure 2.

Map showing estimated positions and movement state (directed, blue; resident, red) from the best-ranked models for (a) Kerguelen Islands (KI, n = 5) and (b) Macquarie Island (MI, n = 7) seals. Lower panels show detail of inset area over the East Antarctic shelf indicated by white box in upper panels. Bathymetric 1000 m contour (white line), climatological mean maximum ice extent during 1978–2008 (black dotted line) and during May–June 2005–2008 (black dashed line) are also shown for reference (sea ice data from http://data.aad.gov.au/aadc/metadata/metadata_redirect.cfm?md=AMD/AU/sea_ice_extent_winter).

Table 1.

Summary movement, foraging and diving information for 2009 KI (n = 5) and 2005/2010 MI (n = 7) seals which migrated to the East Antarctic shelf region. The term forage denotes periods defined (using the covariate SSM) as ‘resident’ movement. Values represent mean ± s.d. (range) across individual animals.

	KI males (n = 5)	MI females (n = 7)
percentage trip on shelf	49 ± 15 (30–65)	56 ± 20 (20–79)
daysa on shelf	101 ± 31 (65–132)	92 ± 40 (36–159)
percentage shelf time forage	82 ± 13 (64–95)	76 ± 30 (11–97)
no. forage events	4 ± 1 (3–5)	2.3 ± 1.1 (1–4)
no. shelf forage events	3.2 ± 0.8 (2–4)	1.6 ± 0.8 (1–3)
forage run lengths (daysa)	32 ± 14 (12–46)	47 ± 27 (17–103)
shelf forage run lengths (daysa)	29 ± 15 (12–46)	51 ± 30 (4–103)
percentage shelf dives benthicb	75 ± 22 (43–95)	78 ± 20 (42–97)
percentage shelf forage dives benthic	76 ± 25 (40–100)	81 ± 22 (44–100)

^aNote that ‘days’ actually represents model days, which are 12 h time steps. Behavioural switches of less than 2 time steps were discounted.

^bBenthic diving was ascertained where the maximum dive per time step was within 50 m of the bathymetry for an estimated location, based on the fine-scale (2 min) ETOPO2 v. 2 grid from the National Oceanic and Atmospheric Administration National Geophysical Data Center (http://www.ngdc.noaa.gov/mgg/global/relief/ETOPO2/ETOPO2v2-2006/ETOPO2v2c/).

The majority of covariate SSMs showed a substantially improved fit to the KI data, when compared with the no-covariate base SSM, on the basis of DIC values (see the electronic supplementary material, table S3). Best results were obtained for the multi-covariate models, where the two-way influence on switch rates generally performed better than the one-way switch models. The best-ranked model was the most complex model tested, which included all four covariates with a two-way influence. Given only a small DIC difference with the corresponding one-way switch model, it is arguable that the latter could be selected on the basis of parsimony. However, all models yielded very similar posterior estimates of the covariate coefficients (see the electronic supplementary material, figures S4 and S5), which engenders confidence in the suite of results. Hence, we present the full-covariate two-way model results here for completeness. For MI, the best-performing models generally contained dive bottom temperature, thermocline strength and/or dive bottom time (see the electronic supplementary material, table S3). Performance of the one- or two-way switch varied between different model formulations.

The influence of the covariates on switching rates is not straightforward to interpret. For the KI seals, the positive ϕ₁ coefficient for temperature and the negative coefficient for thermocline strength (see table 2 and electronic supplementary material, figure S4) indicate that the probability of switching from a directed to a resident state was more likely to occur in colder waters and where the thermocline was relatively strong (figure 3a). Interestingly, switching from directed to resident movement was actually associated with a decrease in the proportion of time spent at the bottom of the dive, and with increased dive descent rates. Examination of individual time series (figure 1b) appears to support this finding: for example, the initial switch into a resident movement state (near the end of February in this case) occurred in correspondence with distinct disjuncture in all covariates. Somewhat unexpectedly, perhaps, the coefficients for the reverse switch (governing ϕ₂, from resident to directed movement) all had the opposite signs (table 2; electronic supplementary material, figure S5). This indicates that the reverse switch was also most likely under all the same circumstances, although the effect in most cases tended to be weaker (figure 3a).

Table 2.

Parameter estimates from the best-ranked model for KI (n = 5) seals. Estimated values are given as the posterior mean, s.d. and median, along with the 2.5% and 97.5% credible limits (CL). Also shown is the proportion of posterior samples falling below (above) zero for positive (negative) median parameter estimates. Note for KI the best-ranked model is the full-covariate model.

parameter	effect	mean	s.d.	2.5% CL	median	97.5% CL	% < 0 <
Temp	ϕ1	1.01	0.21	0.62	1.01	1.46	0
	ϕ2	−0.54	0.29	−1.15	−0.52	−0.03	0.02
Tcline	ϕ1	−1.68	1.16	−3.90	−1.71	0.59	0.08
	ϕ2	3.83	1.64	0.65	3.77	7.15	0.01
pTime	ϕ1	1.00	0.62	−0.18	1.00	2.20	0.06
	ϕ2	−0.68	0.65	−1.92	−0.69	0.64	0.15
Des	ϕ1	−1.30	0.79	−2.84	−1.32	0.23	0.05
	ϕ2	0.36	0.86	−1.47	0.39	1.87	0.33

Figure 3.

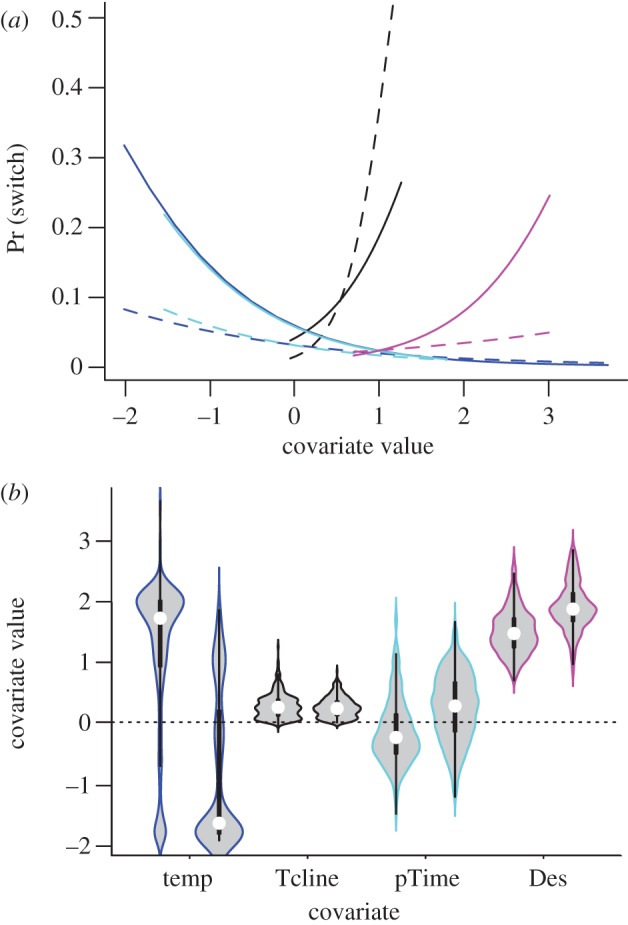
(a) Estimated relationships between environmental and diving covariates and switching probabilities, from directed to resident (solid lines), and resident to directed (dashed lines) movement. Shown are predictions from the best-ranked KI model based on the median coefficients (m₁, m₂) drawn from the posterior samples. The covariates are ocean temperature at the dive bottom (Temp, °C, dark blue), thermocline strength (Tcline, kg m⁻³, black), the proportion of time spent at the dive bottom (pTime, light blue) and the absolute dive descent rate (Des, m s⁻¹, pink). To illustrate the effect of each covariate, each of the other covariates is held constant at its median value. (b) Covariate distribution within the two predicted movement states. For each covariate, the distributions within the directed and resident movement states are presented on the left-hand side and right-hand side, respectively. Presented as a traditional boxplot combined with a kernel density plot (R software package vioplot v. 0.2 [35]). Data are resampled to ensure equal representation across animals.

The temperature and bottom time patterns in the best-ranked MI model were similar to KI, although the effect of temperature was weaker (see the electronic supplementary material, table S4). However, in the full-covariate model the opposite effect of the thermocline occurred (i.e. switching from directed to resident movement was more likely where the thermocline was relatively weak). The final column of table 2 is helpful in interpreting the strength of the estimated covariates: estimates that strongly overlap zero (greater than 10%) can be seen to be poorly defined. In the case of the KI seals (table 2), this includes the reverse switch effects of both biological covariates and, for MI (see the electronic supplementary material, table S4), both descent rate coefficients and all the reverse switch coefficients.

In our model, the covariates only influence switch rates directly. How environment and/or dive parameters alter between the different behavioural states is a subtly but importantly different question. In the KI example (figure 3b), dive bottom temperatures tended to be lower, and dive descent rates higher, during resident movement periods (compared with directed movement periods), which is consistent with the observed switch rate patterns. However, while the switch into resident state is associated with spikes in thermocline strength, the resident periods are then characterized by generally weaker thermoclines, compared with directed movement periods. Another disjuncture is evident: while the switch into resident movement is associated with lower proportional dive bottom time, the actual resident periods themselves are actually characterized by higher dive bottom times in comparison with periods of directed movement. The same patterns are observed for MI (data not shown); however, the dive parameter patterns are more variable between individuals, and hence somewhat less differentiated overall.

4. Discussion

Modern telemetry methods provide a wealth of information on the movement and behaviour of individual animals. However, quantitative ecological interpretation, particularly the drawing of inference across individuals, is hampered by both the inherent complexity of, and the error contained within, these data. SSMs represent state-of-the-art methods appropriate for these analyses. Here, we present an SSM approach where the movement state directly incorporates environmental and diving information, such that the predicted state is influenced by these variables in a biologically realistic way. Our application demonstrates biologically interpretable results for a migratory marine predator commuting to a known ‘hotspot’ foraging region [18,23,24]. This represents the most integrated application to telemetry data to date, where observation and process model parameters, including movement–habitat relationships, are estimated within a single framework. This approach can have widespread utility for quantifying movement–diving (or other behaviour)–environment relationships across species and systems. Importantly, it represents a significant step towards the goal of developing predictions for future scenarios, which properly account for multiple sources of uncertainty.

In the movement context, there is a suite of common ecological questions, which span species and systems (both terrestrial and aquatic). For example, how does animal movement relate to environmental variability, specifically the spatio-temporal distribution of heterogeneous resources? In this study, we derived environmental covariates (temperature at the dive bottom and thermocline strength) that contained information on the vertical structure of the water column, to investigate the three-dimensional habitat used by these marine predators. The covariate SSM generally estimated strong relationships between both of these covariates and the probability of switching between movement states. Specifically, for seals from KI the probability of switching into resident state tended to increase strongly at ocean temperatures around −1.8°C (i.e. in the sea ice zone) and where the thermocline strengthened temporarily (figures 1b and 3a). This is consistent with the broad-scale oceanographic changes that occur as seals cross the Antarctic Slope Front (ASF) and enter the very cold Antarctic shelf and surface waters [36].

For seals from MI, the models containing ocean temperatures and thermocline strength were also supported; however, the temperature relationship was weaker and the probability of switching into resident state increased at low not high thermocline strengths (see the electronic supplementary material, table S4 and figure S4). This probably reflects the different position the islands occupy with respect to the major fronts of the Antarctic Circumpolar Current [19]. Migrating south, MI seals must cross multiple bands of both the Subantarctic and Polar Fronts, hence their approach to the Antarctic continent is usually marked by a weakening thermocline strength, and the temporary spike associated with the ASF can be small relative to that of the more northerly fronts. Resident periods for the shelf migrants from both islands primarily occurred within very cold Antarctic shelf and surface waters [36], which were generally well mixed during the austral autumn months.

A second major question, particularly relevant to aquatic animals, presents itself: how do changes in horizontal movements correspond with changes in vertical movements? In our study, the most unusual result related to this enquiry. It is widely expected that actively foraging diving mammals will spend more time at the dive bottom in areas of higher prey [27,30]. This essentially extends the prediction of increasing time spent in a profitable patch [37] to the vertical dimension. However, there are contradictory theoretical models [38], so this remains a topic of debate. Our results showed KI seals had a high probability of switching into the resident state associated with both high dive descent rates and a low proportion of time spent at the dive bottom. This appears consistent with the idea that at this point animals are actively scanning their local environment and locating their prey field. Subsequently, during the resident periods dive descent rates and relative bottom time were both high. This in turn may indicate active foraging particularly as most shelf dives appeared to target benthic prey (table 1). These distinctions are quite subtle and not easily discriminated from voluminous telemetry data. Patterns for MI animals were similar but weaker. The diving parameters were generally more variable than the environmental variables, which may partially explain why these tended to be weaker predictors. However, this may also reflect the higher frequency with which dive data are recorded compared with horizontal movements, making this component of foraging appear more dynamic. Whether this is a false appearance, or highlights the weakness of the lower-resolution horizontal position data, is an open question. Alternative telemetry methods such as accelerometers [39,40], which give a truer picture of foraging as a three-dimensional continuous space–time process, may provide a resolution.

Changes in diving behaviour associated with foraging have been widely observed across species and systems, including turtles, seabirds, mammals and fish [30,41]. These patterns can often be qualitatively apparent, or even obvious. However, quantifying these changes from tracking data, and making inferences, remains challenging, so a variety of approaches have proliferated. As scientists are increasingly called on to provide robust management advice, and complex environmental influences are ever more in focus, the growing trend in ecology is a shift towards quantitative methods, such as SSMs [42]. We hope the advances presented here will provide a useful contribution to the toolbox available to modern ecologists.

Modelling the reverse switch, from resident to directed movements, can present a complicated problem. Overall, our reverse predictions mimicked the results described above. At the simplest level, this suggests that it is within the primary foraging grounds of the Antarctic shelf that seals are most likely to switch back and forth between behaviours. Given classic central place foraging trips, little else but transit occurs farther north. The results might be very different for models of animals targeting sea ice, ice edge or frontal regions [23,43], which may show less directed movements. However, we also found differences between the two islands, which may have real biological implications. For KI seals, the environmental factors generally appeared predictive of switching out of resident state (see the electronic supplementary material, tables S2 and S3). For MI seals, support for reverse coefficients was weaker and variable. This may reflect real biological imperatives: the KI animals were all juvenile males, whereas the MI animals were all adult females needing to return to their breeding island.

This highlights the influence of external versus internal drivers for migrating animals [44], and the potential importance of incorporating the role of internal state in models. For example, it may be useful to include a process model for gestational state, or even a simple biological clock to monitor when the ‘time's up’ for foraging animals to return for the breeding cycle. Alternatively, for non-breeding animals a process model for body condition may be feasible for this species on the basis of buoyancy information [18], which gives a relative index of fat content. Linking such process models into a realistic movement framework is not a simple task, and requires ecologists and statisticians to work ever more closely together.

While there are specific difficulties associated with predicting onset of directed travel, as described above, the incorporation of relevant covariates is a valid concern for the general problem of modelling animal movements. For many species, resources such as prey distribution are not directly observable at the scales over which movement occurs. Hence the measurable variables (e.g. on the physical environment) are often expected to influence movement only indirectly, and which will be important predictors is often unclear. Here, extensive preliminary investigations using mixed-effect models were conducted to inform covariate choice (S. Bestley 2010, unpublished data). However, although the model might be lacking a central (e.g. internal) driver, the covariates may continue to correlate with such a missing driver. It is here that the role of model diagnostics is fundamental for identifying problems in model structure. Developing robust diagnostic and model selection methods, particularly within the Bayesian framework, is currently an active statistical research field [33,45], and it may be timely for ecologists to vocalize the growing need in this area.

State-space models are the most likely approach to deliver the analytical basis for a synthesis in movement ecology, and ecologists will increasingly be called to contribute knowledge to strengthen their biological foundation [8]. Here, we discriminated largely the same series of behavioural states using covariate and non-covariate SSM formulations. This indicates that the horizontal movement information dominated, but that the covariates added value by (i) modifying probabilities often in shorter runs of states (see the electronic supplementary material, figure S6), and (ii) directly quantifying relationships between horizontal movement, diving and environment. This result may change in a different system where there tend to be shorter and more variable forage events (e.g. in a dynamic pelagic frontal or sea ice edge zone). However, given the process model structure we imposed, a substantially different result is unlikely. Alternative structures may be considered. For example, here we quantified fairly broad-scale changes, and a model with three behavioural states [13] may be warranted to hone in on finer scale inter-patch processes occurring over the Antarctic shelf. It may also be appropriate to have covariates directly influence behaviour (e.g. speed) rather than switching probabilities [12]. Alternatively, using a non-switching structure, where all parameters continuously vary [40], may elicit a much more varied influence of covariates on animal behaviour. Given that any result is likely to be massively dependent on the process model structure, this choice should be carefully considered at the outset in the light of the ecological question of interest, and to ensure that the model output makes sense with the empirical observations.

The overarching strength of the SSM approach is that having an underpinning mechanistic movement process enables predictions (e.g. for new individuals, novel environments or future climate scenarios). Importantly, the uncertainty in both the process and observations can be carried through in forecasting. This will be fundamentally important for climate simulations that will bring their own sources of uncertainty to the problem. Predicting for current and future scenarios is a non-trivial task since linking tracking data to remotely sensed ocean data, or four-dimensional global ocean–climate model output, requires methods accounting for the uncertainty in the animal's position—a significant algorithmic challenge. However, it is a challenge that needs to be embraced as our community is increasingly called on to provide conservation and management advice in a rapidly changing global context.