When an ecological regime shift is really just stochastic noise

Populations of marine species wax and wane over time and space, reflecting environmental forcing, biological dynamics, and in some cases human perturbations, such as fishing, habitat destruction, and climate change (1). The growing availability of multidecadal observational records opens new windows on how ocean ecosystems function, but the analysis and interpretation of such long time-series also requires new mathematical tools and conceptual models (2). Population time-series often show strong variations at decadal time-scales, and a central question is whether this arises from nonlinear biological processes or simply tracking of external physical variability (3). Borrowing from climate research, Di Lorenzo and Ohman (4) develop a new approach for deciphering links between physical forcing and biological response, using as a test case time-series of marine zooplankton abundances off the coast of California.

Upwelling favorable winds bring cold, nutrient-rich water to the surface near the coast, supporting the highly productive California Current System. The California Cooperative Oceanic Fisheries Investigations (www.calcofi.org) and California Current Ecosystem Long-Term Ecological Research site (cce.lternet.edu) have sampled a grid of coastal and open-ocean stations since 1950, one of the longest comprehensive marine ecological datasets. Di Lorenzo and Ohman (4) examine two krill species, Nyctiphanes simplex and Euphausia pacifica, large planktonic crustaceans that feed on smaller phytoplankton and microzooplankton, export sinking fecal pellets to depth, and are preyed upon by higher trophic level organisms, fish, marine mammals, and seabirds (Fig. 1). E. pacifica is a resident species in the California Current that exhibits substantial interannual variability tied to rates of coastal upwelling. In contrast, N. simplex is a subtropical species largely found south of the California Current System; multiyear variations in its abundance off California appear to reflect regional-scale poleward transport (5).

Fig. 1.

(Left) A photo of the dominant species of Southern Ocean krill, Euphausia superba, similar to the crustacean zooplankton analyzed by Di Lorenzo and Ohman (4) (Photo courtesy of A. McDonnell, University of Alaska, Fairbanks, AK). (Right) Spectral analysis of results from a linear stochastic model (Eq. 1), where low-frequency responses in ocean physics and biology can be generated by integrating high-frequency atmospheric forcing over time (see text for more details).

Ecological metrics often are correlated with one or more large-scale climate indices, such as El Niño-Southern Oscillation or the Pacific Decadal Oscillation (PDO) (6). Standard techniques can be used to test the statistical significance of such cross-correlations (7), but this approach implicitly assumes a linear relationship between the physical forcing and biological response. In fact, populations of organisms have an inherent time-scale, roughly a generation or so, and biological responses to environmental variability should reflect the cumulative effects over this time-scale (8). Unlike many short-lived planktonic species, krill can live for months to several years, setting up the possibility for interesting dynamics with sub- to interannual climate forcing.

Similar temporal inertia is common to many geophysical systems, where low-frequency signals can emerge naturally from stochastic or random forcing. Expressed mathematically, the response of a slowly-evolving variable y(t) depends on the time-integral of a forcing variable f(t):

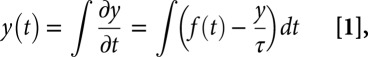where τ is the time-scale of y, and y and f are anomalies from some mean state. The damping term y/τ modulates the effective integration window for the forcing and keeps the system stable. The integral transforms high-frequency variability in the forcing f(t) into a time-lagged, smoothly varying response in y(t). Consider a simple illustration in Fig. 1, Right. Monthly atmospheric weather variations are assumed to be purely random, white noise (black line with approximately constant power at all frequencies); the resulting ocean physical response is red-shifted (blue line with reduced power at high frequencies and elevated power at low frequencies) (9). The stochastic forcing-response model generates broad-band, physical red noise spanning from days to decades. If the model in Eq. 1 holds, then the response variable should be better correlated with the integral of forcing rather than raw-forcing time-series.

Using just such a test, Di Lorenzo and Ohman (4) argue that they detect the influence of physical and biological inertia, as well as remote forcing, in the subtropical N. simplex zooplankton time-series. The strength of the Aleutian Low atmospheric pressure index reflects North Pacific wind patterns, which in turn affect basin-scale sea surface temperatures and ocean circulation encapsulated in the PDO index. Thus, a double integration is required: first from the Aleutian Low index to a model estimate of the PDO; the second from the PDO to an estimate of zooplankton trends. Similar to the model results in Fig. 1, Right, each integration step shifts more of the variance to lower frequencies when the biological timescale τ_bio is longer than the ocean physical timescale τ_ocean. In Di Lorenzo and Ohman (4) the resulting modeled zooplankton time-series is well correlated with the actual N. simplex data, better than any correlation with direct or time-filtered physical climate variables.

This finding brings us back to the vigorous debate in the literature on whether low-frequency biological variability reflects external forcing or internal ecological dynamics (or likely some combination). In a seminal paper, Hare and Mantua (10) argue that North Pacific climate and ecological metrics undergo relatively abrupt transitions from one state to another on decadal time-scales, referred to as regime shifts. Subsequent analysis suggests a simpler explanation for physical variations like the PDO; patterns arise by chance because of the integration of random weather events (3, 11). To show the presence of more complicated nonlinear regime shifts, one must first reject the null hypothesis of stochastic red-noise, as in the blue ocean physics line in Fig. 1, Right.

Di Lorenzo and Ohman (4) go one step further, showing that smoothly varying decadal patterns in a coastal zooplankton population can be explained by a “double-integration” stochastic process model; white-noise atmospheric weather produces red-noise in ocean physics that in turn produces even redder (lower frequency) biological trends. The further shift to lower frequencies in the biological time series arises because of the relatively long lifespan for krill (months to years) and would not hold for all zooplankton, such as the tiny microzooplankton that may only live for a few days. Not all biological time-series arise so simply (or randomly), and many do indeed exhibit more interesting nonlinear behavior (3). Linear tracking of environmental variability, such as shown for N. simplex, may be a special case occurring when organism lifespans approximately match physical forcing time scales (8). Nevertheless the double-integration model presented in Di Lorenzo and Ohman (4) offers a straightforward and linear baseline for unraveling the growing number of long ecological data records (2).

Understanding the role of random versus nonlinear deterministic processes has important implications for marine resource management (12). Statistical indicators can be designed for some nonlinear systems to forecast imminent abrupt transitions (13), perhaps forewarnings of dramatic climate change or anthropogenic damage. In contrast, purely random processes have limited inherent predictability (14).

The stochastic integration model (Eq. 1) predicts a temporal lag between climate forcing and population trends that would hinder detection of ecological transitions; faster responding metrics—recruitment, physiology, reproduction—should be examined where possible. Climate-driven fluctuations in individual zooplankton populations also shift wholescale planktonic food-web structure and dynamics (15). Finally, climate variations alter spatial patterns as well as temporal trends: for example, large-scale reorganizations of zooplankton in the North Atlantic (16) and poleward displacements of marine species along the West Antarctic Peninsula (17). Thus, time-series need to be augmented by spatial surveying of large-scale population distributions (18) and exploiting new capabilities with autonomous robotic instruments and remote sensing (17). Together, enhanced observations and improved theory and modeling may help disentangle the potential wide range of abrupt and continuous ecosystem responses to subannual to decadal, stochastic ocean physical variability (19).