A Comparison of Coarse-Grained and Continuum Models for Membrane Bending in Lipid Bilayer Fusion Pores

Abstract

To establish the validity of continuum mechanics models quantitatively for the analysis of membrane remodeling processes, we compare the shape and energies of the membrane fusion pore predicted by coarse-grained (MARTINI) and continuum mechanics models. The results at these distinct levels of resolution give surprisingly consistent descriptions for the shape of the fusion pore, and the deviation between the continuum and coarse-grained models becomes notable only when the radius of curvature approaches the thickness of a monolayer. Although slow relaxation beyond microseconds is observed in different perturbative simulations, the key structural features (e.g., dimension and shape of the fusion pore near the pore center) are consistent among independent simulations. These observations provide solid support for the use of coarse-grained and continuum models in the analysis of membrane remodeling. The combined coarse-grained and continuum analysis confirms the recent prediction of continuum models that the fusion pore is a metastable structure and that its optimal shape is neither toroidal nor catenoidal. Moreover, our results help reveal a new, to our knowledge, bowing feature in which the bilayers close to the pore axis separate more from one another than those at greater distances from the pore axis; bowing helps reduce the curvature and therefore stabilizes the fusion pore structure. The spread of the bilayer deformations over distances of hundreds of nanometers and the substantial reduction in energy of fusion pore formation provided by this spread indicate that membrane fusion can be enhanced by allowing a larger area of membrane to participate and be deformed.

Introduction

Bending of lipid bilayer membranes occurs during many biological processes such as changes in cell shape, viral fusion, and intracellular membrane trafficking (1–4). During membrane trafficking, membranes combine and separate, and these fusion and fission processes create intermediate structures with especially high membrane curvature. The energy cost of these deformations plays a major role in shaping the energetic landscape of these structural transformations (2,4). To gain a better understanding of the impact of bending energetics on the function of biological membranes, theoretical studies have approached this problem from a broad range of perspectives. Continuum elastic models have built on the classical model in which the energy of bending is expressed as a function of mean and Gaussian curvatures (5). This model has been used heavily in the field of membrane fusion to provide estimates of the energies of hypothesized intermediates (6–10). The structures analyzed in these studies generally have highly curved surfaces, and there is some concern about the validity of linear elasticity with such extreme deformations. It has been proposed that energies estimated from the continuum model become less reliable for radii of curvature less than several times the thickness of a lipid bilayer (11), but it is not clear how large the deformations have to be before the continuum models start to fail.

In contrast to continuum models, curvature in itself does not pose a challenge to the validity of detailed models based on molecular dynamics (MD) simulations of all-atom (AA) (12–14) and coarse-grained (CG) (15,16) lipid membranes. These approaches have been used by a number of groups to examine the kinetics of membrane fusion. While these more detailed models are very powerful in capturing molecular details and identifying intermediate structures with very high curvature, the MD models can only treat systems of limited size; the issues of force-field accuracy (17) and degree of sampling also lend uncertainty to the MD results. Between the continuum and MD approaches, we are left without a method for studying highly curved membranes in large systems. This could be remedied by the use of hybrid models (18,19) which treat the highly deformed regions (and possibly proteins involved) in detail and leave the rest as a continuum. The propagation of scales can also be done in a serial fashion (20), in which information at the atomic level gets fed into the mesoscopic level, which is more appropriate for describing large-scale deformations of membranes (21,22). However, to develop model reliability guidelines and determine how to best partition a hybrid model, improved testing of the classical continuum model under large deformations is required.

To address this need we sought a way to compare the continuum and MD models. We chose the fusion pore as a suitable test structure. This hourglass-shaped formation connects two bilayers immediately after they have fused. The fusion pore is a critical intermediate in membrane trafficking and has been especially well studied experimentally in membrane fusion during exocytosis (23,24). Experimental work on the fusion of lipid vesicles (25) and viruses (26) with planar lipid bilayers have indicated that lipidic fusion pores are metastable on timescales of 10 ms to a few seconds, and theoretical work indicates fusion pores can occupy a local energy minimum (10,27). The diameter of a fusion pore and the separation between the two fusing bilayers is generally only a few nanometers so this structure has highly curved membranes. Fusion pores are small enough for MD simulations and curved enough to test the continuum model. We have constructed CG models of fusion pores and compared the shapes with the corresponding prediction from continuum models; the CG model has also been reverse-mapped to atomistic scale and evaluated following ∼100 ns of relaxation (see the Supporting Material).

We find here that minimizing the continuum elastic energy of fusion pores generated by CG simulations produces very small and insignificant changes in shape and reductions in energy in many cases. These results indicate that the continuum models and CG models are in excellent agreement even with radii of curvature on the order of the bilayer thickness. Furthermore, both the CG and continuum models reveal a seemingly new feature of fusion pores that we refer to as “bowing”, in which the bilayers close to the pore axis separate from one another more than at greater distances from the pore axis. We see only very slight bowing in systems small enough for MD simulations, and the continuum model replicates this feature. Extending the size of the system with the continuum model generates structures with quite dramatic bowing. Furthermore, this bowing can lead to a substantial reduction in the energy of membrane fusion.

Computational Methods

Preparation of the fusion pore using a coarse-grained model

Fig. 1 illustrates how we build a fusion pore system (CG-DOPC in Table 1) using the MARTINI coarse-grained model (28) (see Other Simulation Details). The initial structure is built by combining two preequilibrated flat Dioleoylphosphatidyl-Choline (DOPC) bilayers (∼45 nm × 45 nm) and a DOPC tubule of ∼10-nm in diameter and ∼10-nm in height. The two parallel bilayers are separated by a ∼10-nm water layer, and the tubule is placed in the center of the double bilayer system. Tubule axis is aligned to the membrane-normal direction. Then, bilayer lipid molecules that overlap with the tubule are deleted. This initial structure is equilibrated for ∼100 ns using the simulation scheme described below after a short energy minimization. Note that all the simulations in this study are subject to a periodic boundary condition. A Dipalmitoylphosphatidyl-Choline (DPPC) fusion pore is prepared by shortening the tail length of the DOPC fusion pore. Overall, such prepared fusion pores resemble the structures reported by Yang and Huang (29).

Figure 1.

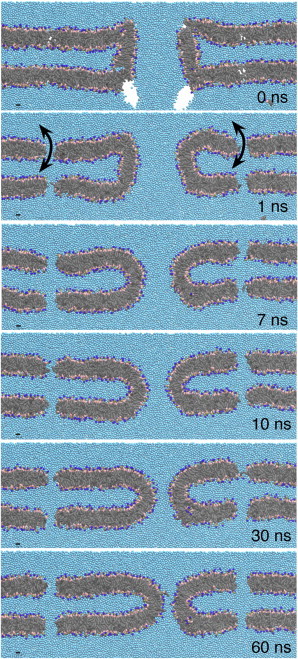
Coarse-grained model of a fusion pore structure is constructed by combining a DOPC tubule of ∼10 nm diameter and ∼10 nm height with two flat DOPC bilayers (0 ns). The tubule and the bilayer are separately equilibrated before the assembly. After the beginning of the simulation, the pore region becomes smooth (10 ns). The pore size decreases monotonically and converges to the metastable size within 100 ns. Note that two compartments are connected by four holes at the corners far from the fusion pore region so that water and lipid molecules can move toward a local equilibrium (see Computational Methods). (Coarse-grained beads are colored by their types: hydrocarbon, gray; glycerol, pink; phosphate, tan; choline, blue; water, cyan.)

Table 1.

Summary of the simulation setups

System	Composition		Box dimension (nm3)	Simulation time (ns)	Exchange holesa	Planar restraintsb
	Lipid	Water
CG-DOPC	10,083	125,223	41 × 41 × 19	1700	Yes	No
CG-DOPC-PERT1	28,261	430,456	60 × 60 × 20	560	Yes	No
CG-DOPC-PERT2	10,455	203,899	41 × 41 × 23	830	Yes	No
CG-DOPC-PERT3	10,083	125,223	41 × 41 × 20	2800	Yes	No
CG-DOPC-Rbc	10,455	203,899	41 × 41 × 23	300e	Yes	Yes
CG-DPPC-Rbd	10,455	203,899	41 × 41 × 23	300e	Yes	Yes

^aExchange holes are created with a soft harmonic potential (Eq. 1) to allow water and lipids to exchange (see Fig. 1 and Computational Methods) as they are essential to allow the fusion pore to adjust to the low free energy structure in a simulation with constant number of particles.

^bThe planar restraints (see the Supporting Material) are used to maintain a specific value of R_b.

^cFive simulations are performed at R_b = 4.85, 5.45, 6.35, 6.85, and 7.85 nm.

^dFive simulations are performed at R_b = 3.7, 4.7, 5.7, 6.7, and 7.7 nm.

^eSimulation time for each R_b is specified.

A fusion pore consists of two curved monolayers that exchange lipid molecules with the surrounding lipid reservoir. This fusion pore divides the space into two separate compartments, each of which is connected to a large water reservoir at a pressure of 1 bar. Thus, in principle, the fusion pore is an open system. However, for the purpose of simulation, the fusion pore is a closed system; the numbers of lipid molecules in each monolayer and of water molecules in each compartment are constant. Therefore, failure to assign an optimal number of lipid molecules in each monolayer can cause artificial surface-tension/stress over the fusion pore structure (30). To circumvent these limitations arising primarily from the finite size of the simulation model, we connect the two water compartments by holes at the corners of the membranes far from the fusion pore region so that water and lipid molecules can exchange, as schematically indicated by the arrow in Fig. 1. The exchange holes are implemented using a soft harmonic potential that is applied only to lipid beads,

$$V^{\text{hole}}\left(r\right)=0.5k\Theta \left(r_c-r\right){\left(r-r_c\right)}^2,$$ (1)

where r is the distance from an axis parallel to the membrane-normal, r_c = 15 Å, and k is a force constant of 100 kJ/(mol·nm²). The value Θ is the Heaviside function: Θ(r) = 1 for r > 0 and 0 otherwise. We have implemented the hole potential into the MDRUN program in GROMACS Ver. 4.5.1 (31), which is used for all the simulations in this study. In the simulations, four holes are created at (x,y) = (−17, −17), (−17, 17), (17, −17), and (17, 17), in nanometers. The fusion pore is located near the origin. Fig. 1 shows some of the holes in the membrane during the simulation. Because the holes are hydrated, a toroidal pore is formed; in other words, lipids in the vicinity of the holes are reoriented so that their headgroups move toward the center of the bilayer. This lipid reorientation allows lipids to adjust their local number density not only in the plane of the monolayer but also across the bilayer. As demonstrated in the Supporting Material, simulations of several test systems that include lipid vesicles consisting of lipid mixtures indicate that the hole protocol is effective at equilibrating lipid/water distributions at the hundreds-of-nanoseconds scale.

As discussed in Results, the bowing feature observed in the CG simulations might be related to the slow relaxation of the lipids in regions far from the fusion pore. To explore this possibility, we have carried out several additional sets of simulations in which we either perturb the fusion pore structure or apply planar restraints to asymptotic regions of the CG system (summarized in Table 1). As described in more detail in the Supporting Material, these simulations indicate that a complete relaxation of the fusion pore likely takes substantially longer than the current simulation time of ∼1–2 μs; nevertheless, the most essential structural features of the fusion pore appear to have converged after 200–300 ns of CG simulations.

Other simulation details

We use the MARTINI coarse-grained model (28) to describe all lipids and water. Although we have developed an extension of the MARTINI model based on a careful consideration of electrostatics (32), we expect that the original MARTINI model is appropriate here because it describes the mechanical properties of lipids well. All CG simulations are carried out under constant temperature (300 K) and zero surface tension using the Berendsen scheme (33), with an integration time step of 40 fs. Simulation time reported in this study has not been scaled by any factor although a factor of 4 has been suggested by Marrink et al. (28). A semiisotropic pressure coupling simulation with a periodic boundary condition is used to decouple the box size in the lateral and normal directions. The semiisotropic setup in combination with the artificial holes that allow water and lipid exchange enables the fusion pore structure to adjust its height and radius naturally.

The algorithms used to compute the phosphate surfaces from the CG simulations are summarized in the Supporting Material. Fig. 2 illustrates a representative phosphate density map in the x-z plane, and displays the average phosphate surfaces computed using the density map.

Figure 2.

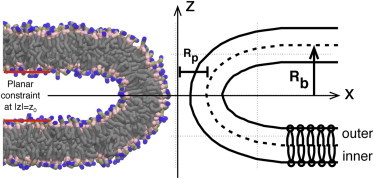
A representative fusion pore configuration from the CG-DOPC simulation at 1700 ns, and the average phosphate surfaces of monolayers are shown (black solid lines in the right panel). The bilayer midplane is shown (black dashed line). R_p is the pore radius from the central axis to the bilayer midplane. R_b is half the distance between the parallel midplanes at large x. In some simulations (summarized in Table 1), lipids far away from the fusion pore (schematically indicated in red) are subject to a planar restraint (see the Supporting Material).

To qualitatively evaluate the key structural features of the CG fusion pore, we have also constructed an all-atom (AA) model based on the CG model. Due to the high computational cost, the AA model is substantially smaller in size and the simulation substantially shorter (∼100 ns). For additional details and discussions, see the Supporting Material.

Continuum modeling

Continuum models offer a sharply contrasting approach to the study of lipid membrane deformations compared to the CG model just described. The continuum model for membrane bending generally assumes that deformations produce a linear response, so that the relevant bending energy, E_b, can be expressed as an integral of the square of the curvature over the surface (5,34) (note that, although the Helfrich model describes the free energy of bending, we follow the convention of elasticity and refer to it as “bending energy”). The curvature has two components—the mean curvature and Gaussian curvature—but the integral of the Gaussian curvature is shape invariant, so for the purposes of this article, we focus on the mean curvature,

$$E_b=\frac{B}{2}\underset{S}{\int }{\left(\frac{1}{R_1}+\frac{1}{R_2}-C_0\right)}^{2}dS,$$ (2)

where R₁ and R₂ denote the principal radii of curvature of a neutral surface, C₀ denotes the spontaneous curvature of a lipid monolayer, and B denotes the flexural rigidity of the membrane; the value of C₀ is taken to be −0.11 nm⁻¹ for DOPC and −0.035 nm⁻¹ for DPPC (28) unless otherwise stated (0 and +0.11 nm⁻¹), and B is taken to be 10 k_BT (35). Because a bilayer is composed of two monolayers, we take the sum of two expressions of the form of Eq. 2 for each of the two surfaces (8,10). Note that this representation does not address other forms of elastic deformation such as compression and tilting (5,34); evidence that compression can play a role will be presented in Results.

At local equilibrium, a fusion pore will assume a shape that minimizes Eq. 2 for a particular set of constraints such as system size and pore dimensions (i.e., R_b and R_p; see Fig. 2). Thus, we will compare the CG and continuum models by using Eq. 2 to calculate the bending energy of a neutral surface derived from a CG simulation. We will then minimize this energy while fixing the size and dimensions to see how much the system changes. This procedure allows for a direct comparison of the shape and energy of bending predicted by the CG and continuum models.

Applying Eq. 2 to a CG fusion pore requires a calculation of the principal radii of curvature of the monolayer neutral surfaces from the simulation. However, CG particle positions include thermal fluctuations, making direct application of Eq. 2 difficult. To circumvent this problem we find a smooth function that can be fitted very closely to the phosphate positions of a CG simulation along a contour in the x-z plane. We assume that the neutral surface occupies a position of minimum lateral pressure (36,37). The lateral pressure minimum in our CG simulations fell 0.45 nm below the peak in the position of the phosphates. Our fitting procedure focuses initially on the outer monolayer (farthest from the z axis, closest to the x-y plane). We initially determine the neutral surface of the outer layer as a parallel surface 0.45 nm from the phosphates, and then determine the neutral surface of the inner monolayer as a parallel surface separated by a distance h. The value h is determined from the CG pressure profiles as the distance between the two pressure minima; it is 3.30 nm for DPPC and 3.56 nm for DOPC.

We develop the smooth function for the phosphate positions implicitly, starting with the natural equation for a plane curve R(s) (38). We take R(s) to represent the meridian radius of curvature of the fusion pore as a function of s, the displacement along the contour. The neutral surface of the entire outer monolayer is then the surface of revolution of this plane curve around the x = 0 axis. The inner monolayer is then represented as the parallel curve R(s) + h. Once an explicit form for R(s) has been found, one then has R₁, which appears in Eq. 2. To find R₂, one derives the angle of R(s) relative to the x-y plane (θ(s)) and x(s) by straightforward geometric calculations; R₂(s) is then cos(θ(s))/x(s). These expressions enable the evaluation of Eq. 2 by numerical integration (10). Expressing x(s) and z(s) of the phosphates as integrals containing R(s), a polynomial for R(s) can then be selected to fit to the phosphate positions generated by a CG simulation. We find that a polynomial of the form R(s) = a + bs + cs² + ···, used previously in (10), cannot reproduce the bowing feature apparent in the CG simulations because with this choice for R(s), the contours rise smoothly from $z=0$ to R_b without curving down. To replicate the bowing, we instead used the function

$$R\left(s\right)=a\frac{1+bs+c{s}^2+d{s}^3}{1+es}.$$ (3)

With this expression we obtain fits to the phosphate data for all the CG simulations with deviations of ∼0.2 Å/point.

Neutral surface contours for the inner and outer monolayers obtained from the fits of Eq. 3 to the CG model (Fig. 3; see Continuum Analysis for additional discussions) are then used to calculate E_b from Eq. 2. The integration in Eq. 2 is taken from s = 0 to a limit s = s_L, with s_L varied as a free parameter in the minimization. The value θ(s_L) is fixed at π/2 and z(s_L) is fixed at the value at the outermost part of the pore derived from the CG simulation result; z(s_L) is generally within 0.1 Å of R_b – h/2. A small horizontal annulus of planar bilayer is added around the outer margin of the fusion pore, and the outer diameter of this annulus is treated as a free parameter. Fixing the total area of the system to the initial value of the CG simulation plus the annulus and allowing the outer margin to vary replicate the zero tension/conserved mass condition of the CG simulations. The value E_b is minimized subject to these constraints by varying a, b, c, d, and e in Eq. 3, together with s_L and the size of the outer annulus. The minimization is carried out with the computer program MATHCAD Ver. 14. In several trials, varying the minimization algorithm and tolerance does not alter the outcomes. Moreover, as shown in the Supporting Material, multiple independent initial guesses are used to thoroughly explore the parameter space during minimization. Although we cannot prove that the obtained solution represents the global minimum, the consistent trends observed in an extensive exploration of parameter space suggest that the chance of missing a significantly different and more stable solution is very low.

Figure 3.

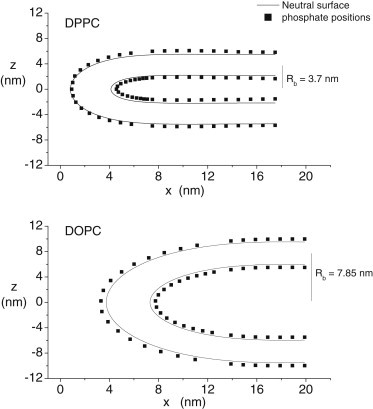
Phosphate positions of CG-DPPC-R_b (top panel) and CG-DOPC-R_b (bottom panel) simulations are used to generate smooth contours for use in the continuum model. The contours are neutral surfaces calculated from Eq. 3 that generate phosphate positions within ∼0.2 Å of the CG values. The offset between the contour and phosphate positions at large x reflects the 0.45-nm distance between the phosphate position and the lateral pressure minimum of the CG simulations. The intersection between the phosphate positions and continuum neutral surface for small x with DPPC reflects a slight thinning of the bilayer at the center of the fusion pore for this CG simulation.

When the total area (the sum of the inner and outer monolayer areas) is constrained, the area of one monolayer can increase at the expense of the other. This corresponds to lipid flip-flop between the two monolayers. It should be noted that the area constraint was not incorporated into the minimization in previous work using this strategy (10). The area constraint is irrelevant when C₀ = 0 because the energy of the flat annulus is zero, but for the nonzero C₀ values used here the amount of bilayer in the flat annulus makes a contribution to the energy, and this constraint becomes important.

Results

The fusion pore structure from CG simulations

Fig. 4 shows the phosphate density map of the CG-DOPC system after a 1.7-μs simulation. This phosphate density averaged over azimuthal angle in a cylindrical coordinate system (see Fig. 2 for definitions) is homogenous and exhibits well-defined narrow bands (width of 1–2 nm). The fusion pore structure is also symmetric about the z axis and x-y plane. The homogeneity in phosphate density and structural symmetry indicate that DOPC lipids are successfully redistributed through the exchange holes and the final structure is close to being metastable.

Figure 4.

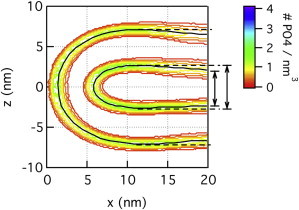
Phosphate density map of the fusion pore from CG-DOPC simulation. (Dashed horizontal line) Maximum distance between the monolayers on each side. (Vertical arrows, right) Reduction in this distance due to bowing. For a comparison with results from other perturbative simulations and a short (∼100 ns) atomistic simulation, see the Supporting Material.

In Fig. 4, a subtle but clearly visible feature of the fusion pore structure is a bowing shape (i.e., R_b decreases at r > 10 nm) not observed in prior continuum theories (10). The term “bowing” is used here to represent a greater separation of the fusing bilayers along the z axis for small x, close to the pore axis. This feature is highlighted in Fig. 4 with dashed horizontal lines drawn through the phosphates at their point of greatest separation (x = ∼11 nm) and extended to the right z axis. The larger separation of the inner contour is highlighted with a vertical arrow; the shorter arrow indicates the separation of the phosphates at x = 20 nm. The small system illustrated in this figure exhibits rather modest bowing, but larger systems analyzed below with the continuum model show that bowing can be quite dramatic.

Additional CG simulations for the structural features of the fusion pore

To explore the robustness of the bowing feature, we perform three additional coarse-grained simulations (CG-DOPC-PERT1-3 in Table 1), in which we start a simulation with a structural perturbation from the final snapshot of CG–DOPC (see the Supporting Material for details). As shown in Fig. S4 in the Supporting Material, all three perturbed systems quickly change their configurations toward one that is similar to the result of CG-DOPC, but the final structures are indeed slightly different from each other. This suggests that the bowing shape likely reflects a realistic feature of the fusion pore (also see Continuum Analysis below), although the structure reached at the end of the CG-DOPC simulation has not reached the true free energy minimum even after ∼2 μs. Because water molecules can move between two compartments (as indicated by the black arrow in Fig. 2), the slow relaxation process must reflect a mechanical property of the lipid bilayer.

Another trend we note from the perturbation simulations is that the R_p value by the end of the simulation is related to R_b (see Fig. 2 for labels); the larger the R_b value, the larger the R_p value as well (see Fig. S5). Motivated by these observations, we ran a series of simulations (CG-DOPC-R_b and CG-DPPC-R_b in Table 1) with R_b restrained to specific values to search the configuration space more efficiently. In these simulations, we assume that bilayers are flat at r > 13 nm; this is enforced by restraining the z positions of ∼20% phosphate groups in the outer monolayer at r > 13 nm to a specific value (see the Supporting Material). Fig. S5 shows that R_p indeed monotonically increases as R_b increases. As R_b is varied between ∼4 and 8 nm, R_p varies from 13 to 21 Å. Moreover, for large R_b values, the bowing feature in the fusion pore disappears (also see below for results from a continuum analysis).

Overall, these additional CG simulations clearly indicate that the complete equilibration of the fusion pore takes substantially longer than the typical simulation time of ∼1–2 μs. Nevertheless, the key structural features of the fusion pore, such as the dimension and shape near the pore center, appear to have converged during the CG simulations (see Fig. S4), as demonstrated by the consistent trends that have emerged after diverse perturbations of the model.

Continuum analysis

The best-fitting neutral surface contours (following Eq. 3) are plotted together with phosphate positions from CG-DPPC-R_b and CG-DOPC-R_b simulations in Fig. 3. For one case, DOPC with R_b = 7.85 nm, the neutral surface contour falls 0.45 nm from the phosphate positions throughout the pore in both the inner and outer monolayers. However, for the other case shown, DPPC with R_b = 3.7 nm, only the outer contour falls 0.45 nm from the phosphate positions. For the inner monolayer, the curve approaches and contacts the phosphate positions at the pore center. Because the outer monolayer is used for the fit and the neutral surface of the inner monolayer is calculated simply as R(s) + h, the contact between these two curves for the inner monolayer simply means that the CG simulation yields a pore in which the membrane is thinner at the center. In fact, we see some bilayer thinning at the pore center in all CG simulations (see Fig. S1 for an illustration), and this thinning is much greater with small R_b.

The interphosphate distance between the two monolayers at the outer margins of the fusion pore is generally 4.2 nm for DPPC and 4.46 nm for DOPC. At the center of DOPC pores, this distance ranges from 4.44 nm for R_b = 7.85 to 4.39 nm for R_b = 4.85 nm; at the center of the DPPC pore, this distance ranges from 4.04 nm for R_b = 7.7 to 3.64 nm for R_b = 3.7 nm. These results suggest that at the center of a CG pore, stresses compress the bilayer to reduce the very high curvature; this is reminiscent of observations from bilayer edge simulations, which also feature highly curved regions (39,40). This stress is greater for small values of R_b, for which pores have greater curvature. The continuum elastic model implemented here does not treat compression, so the thinning of the bilayer at the pore center in the CG simulations can be taken as an indication of a shortcoming in the continuum model. However, it is not clear that this shortcoming reflects the lack of molecular detail in the continuum model. It is quite possible that introducing a continuum expression for bilayer compression energy (5,34) will eliminate this disparity between the CG and continuum models.

Fig. 5 displays initial CG neutral surface contours plotted along with minimum energy neutral surface contours for small, intermediate, and large R_b. Deviations between the CG and continuum contours are small but clearly visible for DPPC with small and large R_b and for DOPC with small R_b. For the other cases, the minimized contours are indistinguishable from the initial CG contours. Thus, the CG simulations yield fusion pores that are very similar in structure to the minimum energy fusion pores of the continuum model.

Figure 5.

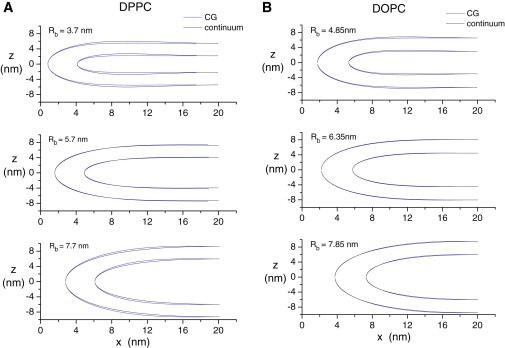
Neutral surfaces obtained from fits to CG simulation results (see Fig. 3) are then adjusted to minimize E_b in Eq. 2 by varying parameters including those of Eq. 3. (A) DPPC; (B) DOPC. The energy minimized continuum models (solid) and CG models are indistinguishable for intermediate R_b and very close for small and larger R_b values.

The continuum model exhibits greater bowing than the CG model and this is clear for the smallest R_b values for both DPPC and DOPC (Fig. 5). This indicates that bowing is a realistic feature of energy minimized fusion pores, and the qualitative bowing feature seen with the CG simulations is unlikely to be an artifact of insufficient sampling, despite the slow relaxation discussed above. The bowing would be eliminated during the minimization of the continuum model by allowing parameter e in Eq. 3 to go to zero, so bowing represents an energy-reducing change in the shape of the continuum fusion pore. As discussed in the Supporting Material, we have explored extensively the initial condition for the continuum minimization, and the solution with the bowing feature consistently emerges as the lowest in energy.

To compare the CG and continuum models more critically, the energy differences are plotted versus R_b (Fig. 6 for DOPC and see Fig. S9 for DPPC). These energy differences are generally small, as low as 1–2 k_BT for intermediate values of R_b. The largest is slightly less than 30 k_BT for DPPC at the lowest R_b of 3.7 nm. In general, the deviations are greater for low R_b than for high R_b and greater for DPPC than for DOPC. The comparison of the energies thus confirms the impression from inspecting the actual contours. In general, the comparison between the two models does not reveal major disparities, and suggests that both approaches can capture important features and properties of fusion pores.

Figure 6.

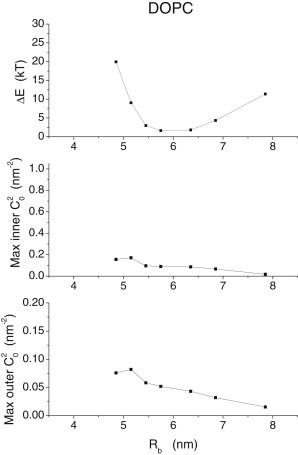
(Top row) The energy reduction achieved by minimization of E_b is plotted versus R_b for DOPC (see Fig. S9 in the Supporting Material for DPPC). These plots show very low reductions in energy for intermediate values of R_b and somewhat larger reductions for larger and smaller values of R_b. The maximum square mean curvatures of the inner (middle row) and outer (bottom row) monolayers show sharp increases at low R_b and become very small for large R_b.

Fig. 6 and Fig. S9 also plot the maximum values of the mean curvature squared for the inner and outer monolayer contours. We expect the continuum model to be less accurate for larger curvatures due to nonlinearity in the response to bending. Curvatures are greater for small R_b and this may account for the larger energy differences between the shapes predicted by the CG and continuum models at small R_b values. But this clearly cannot account for the significant differences also seen at larger R_b values. The underlying causes for the various trends in differences between the CG and continuum models will be addressed more fully in Discussions.

Continuum analysis: larger systems and the bowing feature

The continuum model produces results that are indistinguishable from the CG model for intermediate values of R_b, so we also explore the structure of these fusion pores in larger systems with R_b = 5.7 nm for DPPC and R_b = 5.75 nm for DOPC. The size is increased by enlarging the annulus of planar bilayer surrounding the fusion pore. This increases the total area of the system and provides a way for the fusion pore curvature to spread over greater distances if energy can be reduced.

Minimized neutral surface contours for DOPC (Fig. 7) and DPPC (see Fig. S10) show dramatically increased bowing as the size of the system is increased. The bowing is especially clear in these plots because the x axis is expanded 10-fold over the z axis. The upper and lower bilayer midplanes extend to a separation of ∼10.5 nm for DPPC before returning to the constrained value of R_b = 5.7 nm at large x. For DOPC, the bilayer midplane separation extends to ∼12.5 nm before returning to R_b = 5.75 nm. The bowing indicates that fusion pores with larger R_b have lower bending energy, and this is confirmed by running minimizations with R_b = 12.5 nm for DOPC. Contours with these larger R_b values yield curved regions that extend only 40–50 nm, and are flat beyond these points (Fig. 7 B).

Figure 7.

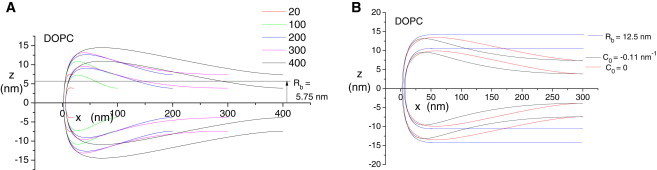
Continuum model fusion pores of systems of various sizes. (A) For both DOPC and DPPC (see Fig. S10 in the Supporting Material), increasing the size allows for profound bowing during energy minimization. For the largest systems, the maximal distance between the two fusing bilayers is roughly twice the limiting distance at large x. (B) Continuum model fusion pores reveal the effect of changing the spontaneous curvature (C₀) to zero and increasing R_b to about that seen at the height of bowing. Zero C₀ shifts the bowing to large x. Larger R_b values eliminate bowing.

To evaluate the consequences of bowing for the energy of fusion pore formation we plot the difference in E_b between a minimized continuum fusion pore and two fully planar bilayers (Fig. 8). This gives the change in bending energy contributed by mean curvature to the fusion transition. Note that fusion pore formation also entails a change in energy contributed by Gaussian curvature. This contribution is not known, but according to some estimates it adds 200 k_BT to the energy cost of creating a fusion pore (41). Whatever this value is it will be the same for all fusion pores because it does not depend on shape or size. So the energy due to the change in Gaussian curvature will shift the plot up uniformly for all sizes by an unknown amount based solely on the choice for the energy modulus of Gaussian curvature.

Figure 8.

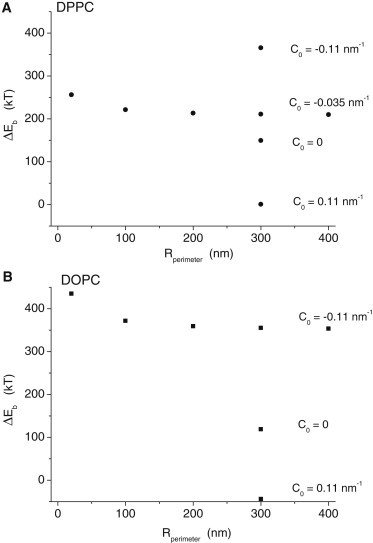
Energy of fusion pore formation from flat bilayers. For both DPPC (A) and DOPC (B), increasing the size of the system reduces the energy of fusion pore formation to limiting values of ∼200 k_BT and ∼340 k_BT for DPPC and DOPC, respectively. Increasing the spontaneous curvature (C₀) to zero and 0.11 nm⁻¹ (for systems with radii of 300 nm) greatly reduces the energy of fusion pore formation.

Fig. 8 indicates that bowing of fusion pores can aid in the process of membrane fusion and increasing the size of the region that can be deformed in this way allows for more of the membrane to bow and reduces the energy barrier to fusion pore formation. Minimization of the system with C₀ = 0 reduces the energy of fusion pore formation, and changing the sign of the value used here (0.11 nm⁻¹) makes the energy about zero for DPPC (Fig. 8 A) and ∼−45 k_BT for DOPC (Fig. 8 B). This result confirms the widely recognized observation that positive values of C₀ promote fusion pore formation (2,42).

Discussions

The primary goal of this study is to compare descriptions of lipid fusion pores that model membrane deformations at different levels of detail. This serves at least two purposes:

First, we are able to evaluate the validity of the continuum model and gain a more detailed understanding of its limitations.

Second, we hope to identify physical parameters and properties that govern the energy landscape of membrane remodeling.

Of particular interest is our finding that coarse-grained (MARTINI) simulations yield fusion pores with metastable structures, and that these structures resemble those generated by the continuum model. With no a priori assumptions of parameters the simulations in the present study give structures with similar dimensions; it’s worth noting that we see clear evidence of slow relaxation of the fusion pore beyond the microsecond simulation time, although the main structures of the fusion pore, such as the dimension and shape near the pore center, are consistent among independent simulations (see Fig. S4). The validity of the MARTINI model in this context is not entirely surprising because it has been parameterized to give reliable mechanical properties of common lipid bilayers (28), but the near quantitative agreement between MARTINI and a relatively simple continuum model (Fig. 5) was not anticipated considering the high degree of curvature in a fusion pore.

The CG and continuum fusion pores have slightly different shapes (Fig. 5), and these differences are noticeable for the largest and smallest values of R_b. Notable energy differences accompany these disparities in shape (Fig. 6 and see Fig. S9, see discussions below). The similar shapes and small energy differences for intermediate R_b values are quite striking and suggest that for fusion pores with these dimensions the two models can be substituted for one another and that hybrid models can be constructed essentially seamlessly.

The disparities at large and small R_b values merit some attention in the hope of gaining some insight into lipid bilayers with very high curvature. The greatest disparities in both energy and shape occur with small R_b, and the disparities are greater for DPPC than for DOPC. The most plausible explanation for these disparities is higher order contributions to the dependence of energy on curvature, which will manifest at the highest curvatures. The mean curvatures are especially high at the centers of fusion pores with small R_b. Most of this high curvature arises because of the very small radius (R_p) of the fusion pore yielded by the CG simulation. The DPPC simulation for R_b = 3.7 nm yields an especially narrow pore.

Examination of Fig. 5 indicates that the minimization of the continuum model energy for these small R_b simulations actually reduces the amount of curvature at the pore center, to spread the bilayers out and increase the amount of bowing. This indicates that the CG model has an effective energy versus curvature with a negative higher order term, which reduces the energy of high curvature relative to the continuum model. A CG bilayer can accommodate high curvature more easily than a continuum elastic bilayer. It is likely that bilayer thinning at the pore center (Fig. 3, DPPC) contributes to this difference. With the small value of R_p seen with DPPC at R_b = 3.7 nm, the parallel curvature of the inner monolayer at the pore center is somewhat greater than 1 nm⁻¹. This can be taken as the point at which linear continuum elasticity starts to break down for lipid bilayers. It is a surprising result that this break down point is so high.

Disparities between the continuum and CG models also appear for the largest R_b values that we tested (7.7 and 7.75 nm for DPPC and DOPC, respectively). The disparities are generally smaller than for smallest R_b values, and it is interesting that with regard to shape, they are in the opposite direction. That is, the CG fusion pore has less curvature at the pore center and produces a greater separation of the upper and lower bilayers. Given that for intermediate R_b values the continuum and CG fusion pores are almost identical, the origin of this discrepancy is difficult to explain. All components of curvature, parallel and meridian of both the inner and outer monolayers, are smaller for larger R_b values than for small R_b values (Fig. 6 and Fig. S4). Given the trends at small R_b it is unlikely that this disparity reflects a higher order contribution to the dependence of energy on curvature.

One possibility is that the CG models predict different spontaneous curvature (C₀) values from those used in the continuum model and therefore prefer slightly different optimal shapes. The MARTINI force field gives a value between −0.02 and −0.05 nm⁻¹ for DPPC and between −0.07 and −0.15 nm⁻¹ for DOPC; the continuum analyses mostly use the midpoint values of −0.035 nm⁻¹ for DPPC and −0.11 nm⁻¹ for DOPC. Test calculations using different values of C₀ lead to different bending energies and have a significant impact on the optimal shape (Fig. 7). The other possibility is that the CG model needs more time to reach its energy minimum for large R_b values. Perhaps a deeper analysis of the two models will reveal more subtle contributions to the energy that can account for these disparities and provide models for more quantitative studies.

Regarding the magnitude of the bending energy disparity between the CG and continuum contours, it is as high as 20–30 k_BT (Fig. 6 and Fig. S9). For a membrane system with a lateral length scale of 40 nm (Fig. 5), there is a large number of lipid molecules. However, the relevant degrees of freedom here are the bending undulations, which occur at very large length scales, as characterized by the long persistence length of membrane bending (34). For a system of 40 nm, the number of thermally active undulation modes is minimal, suggesting that the difference of 20–30 k_BT is significant and not thermally partitioned among many modes.

The combined CG and continuum analysis confirms the results of recent continuum analysis (10) that the fusion pore is a metastable structure and that its optimal shape is neither toroidal (6,43,44) nor curvature-free (8). Moreover, we find a seemingly novel bowing feature of fusion pores that stabilizes their energies, especially at relatively small R_b values; by allowing bowing, curvature for regions near the fusion pore is reduced and therefore the bending energy of the system is substantially lowered. It is worth emphasizing that the analysis of bowing nicely demonstrates the complementary nature of CG and continuum analysis. The bowing feature was first observed in the CG simulations (Fig. 4), which motivated us to revise the functional form of the neutral surface representation in the continuum model (Eq. 3) to allow bowing to occur. On the other hand, the CG results are complicated by the slow relaxation of lipids (see the Supporting Material), thus the physical significance of bowing is established only by a careful analysis using the continuum model (Fig. 7), for which sampling is not an issue. We anticipate that this combined CG and continuum strategy will be valuable to the analysis of many membrane remodeling processes.

The spread of the bilayer deformations over distances of hundreds of nm (Fig. 7) and the substantial reduction in energy of fusion pore formation provided by this spread indicate that membrane fusion can be enhanced by allowing a larger area of membrane to participate and be deformed. This provides fusion proteins with greater areas to work on in generating membrane deformation. Furthermore, the large size of these fusion pores is relevant to efforts to use lipid phase behavior to investigate membrane fusion (45). Although lipids can form periodic phases with unit cells that resemble fusion pores (29), the structures formed when lipid bilayers fuse will have different shapes afforded by incorporating larger areas of membrane.

Conclusions

Although continuum mechanics models have been used extensively in many analyses of membrane remodeling processes, their validity in the presence of considerable membrane curvature has not been thoroughly studied. We fill in this important void by comparing the shape and energies of the membrane fusion pore predicted by coarse-grained (MARTINI) and continuum mechanics models. We find that the CG and continuum models give surprisingly consistent descriptions for the shape of the fusion pore, the deviation between the continuum and coarse-grained models becomes notable only when the radius of curvature approaches the thickness of a monolayer. These observations provide solid support to the use of coarse-grained and continuum models for the analysis of membrane remodeling and the properties of membrane fusion intermediates.

The combined coarse-grained and continuum analysis confirms the results of recent continuum analysis (10) that the fusion pore is a metastable structure and that its optimal shape is neither toroidal nor catenoidal. Moreover, our results help reveal a new, to our knowledge, bowing feature that reduces the curvature and therefore stabilizes the fusion pore structure. In particular, spread of the bowing deformation over a large area (with length scale of hundreds of nm) substantially reduces the energy of the fusion pore, suggesting that membrane fusion can be enhanced by allowing a larger area of membrane to participate.

It is worth noting that we see clear evidence from CG simulations that the fusion pore undergoes slow relaxation at a timescale beyond microseconds. Fortunately, the key structural features, such as dimension and shape near the pore center, are consistent among independent simulations, thus the comparison between CG and continuum models is still meaningful. Nevertheless, we caution that in CG simulation studies of lipid systems with complex shapes, a careful examination of convergence as we have done here with the perturbative simulations is essential. In fact, this highlights the value of combining CG and continuum analysis because the former has a smaller number of assumptions while the latter suffers less from convergence issues. The identification of the bowing structure from CG simulations and subsequent confirmation of the feature with the continuum model is a good example.

As future work, we will extend the comparison of CG and continuum models to multicomponent membranes, which are more closely related to biological membranes. The challenge to a quantitative comparison of these systems is a better understanding of their mechanical properties (e.g., various mechanical moduli and pressure profiles (37)) and optimal ways of representing the neutral surface in a continuum model. Efficient numerical algorithms (46,47) for simultaneously optimizing the shape and composition distribution of multicomponent membranes are also needed to make the analysis applicable to a broad range of systems.

Finally, including protein components in the analysis of membrane fusion and other membrane remodeling process represents an exciting research topic, for which a hybrid model (48) that represents the protein and nearby lipids at the CG level while treating the rest of the membrane at a continuum level is likely most appropriate. Along this line, this article supports the use of continuum models for even substantially curved membrane regions, and the key challenge lies in the treatment of the boundary between CG and continuum regions (49); adapting more sophisticated continuum models of membranes (50,51) is also likely beneficial.