Deriving benefit of early detection from biomarker-based prognostic models

Abstract

Many prognostic models for cancer use biomarkers that have utility in early detection. For example, in prostate cancer, models predicting disease-specific survival use serum prostate-specific antigen levels. These models typically show that higher marker levels are associated with poorer prognosis. Consequently, they are often interpreted as indicating that detecting disease at a lower threshold of the biomarker is likely to generate a survival benefit. However, lowering the threshold of the biomarker is tantamount to early detection. For survival benefit to not be simply an artifact of starting the survival clock earlier, we must account for the lead time of early detection. It is not known whether the existing prognostic models imply a survival benefit under early detection once lead time has been accounted for. In this article, we investigate survival benefit implied by prognostic models where the predictor(s) of disease-specific survival are age and/or biomarker level at disease detection. We show that the benefit depends on the rate of biomarker change, the lead time, and the biomarker level at the original date of diagnosis as well as on the parameters of the prognostic model. Even if the prognostic model indicates that lowering the threshold of the biomarker is associated with longer disease-specific survival, this does not necessarily imply that early detection will confer an extension of life expectancy.

1. Introduction

Many models for cancer prognosis include as predictors biomarkers that may have utility in early detection (Shariat and others, 2008). For example, the prostate-specific antigen (PSA) is used as a key predictor in models for prostate cancer survival (Kattan and others, 2008) and CA-125 has been explored for its utility in predicting ovarian cancer survival (Gupta and Lis, 2009).

In these models, higher biomarker values are typically associated with poorer prognosis in terms of disease-specific survival from diagnosis. While the models themselves do not sanction a causal interpretation of the association between marker values and survival, this interpretation is often made in practice since markers typically increase as disease progresses and since a disseminated tumor is typically much less curable than a localized one.

Because these models include early detection biomarker as a predictor of prognosis, they models are often interpreted as making a statement about the improvement in survival that would arise from detecting disease at a lower threshold of the biomarker. However, to lower the threshold of the biomarker requires advancing diagnosis. The interval by which diagnosis is advanced is called the lead time, and this must be taken into account when projecting survival benefit consequences of lowering the threshold of the biomarker value. For example, assume that median survival is 8 years when PSA is 10 ng/mL at diagnosis and 12 years when PSA is 2.5 ng/mL at diagnosis. If it takes only 2 years for PSA to rise from 2.5 to 10 ng/mL, the prognostic model would imply a survival benefit of 2 years. However, if it takes 4 years for PSA to rise from 2.5 to 10 ng/mL, there is no real increase in life expectancy and no true survival benefit. In this case, the apparent improvement in disease-specific survival is entirely accounted for by the lead time (see Figure 1). Thus, whether the prognostic model implies a true survival benefit, and the magnitude of any such benefit, depends on the lead time. The lead time, in turn, is determined by the difference in marker values (in the above example, 2.5 and 10 ng/mL) and the rate of change of the biomarker.

Figure 1.

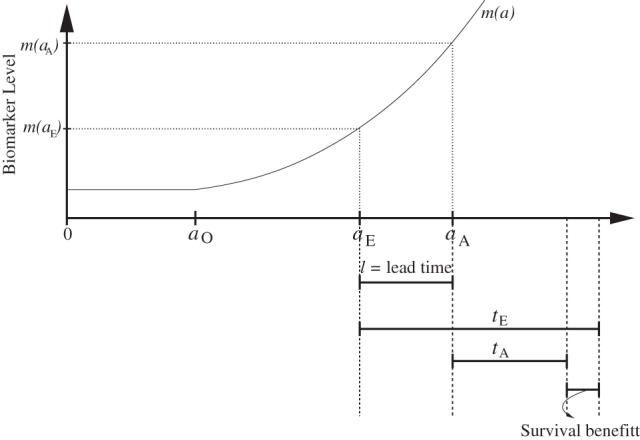
Timeline of disease history events for an individual. Disease onset occurs at age a_O. In the absence of early detection, actual diagnosis occurs at age a_A when the biomarker level is m(a_A). With early detection, diagnosis occurs at age a_E when the biomarker threshold is m(a_E). The difference ℓ=a_A−a_E is called the lead time. Observed disease-specific survival from actual diagnosis is t_A and from early diagnosis is t_E. Early diagnosis confers benefit only if t_E−t_A>ℓ. We refer to this as a true survival benefit due to early detection.

In this article, we aim to quantify the consequences of models for cancer prognosis that include an early detection biomarker. The central question that we address is: “Based on a prognostic model, if the threshold for the marker value at diagnosis could be lowered by a specific amount, what would be the corresponding change in the distribution of the patient’s life expectancy?” In our development we focus on net disease-specific survival, or disease-specific survival in the absence of other-cause mortality. We consider two different measures that capture the change in life expectancy when lowering the threshold of the marker. The first is the difference in median disease-specific survival from diagnosis at a lower versus a higher threshold for the marker. We derive conditions under which this difference exceeds the corresponding lead time. The second is the ratio of the hazard of disease-specific mortality under the lower versus the higher threshold for the marker value. We determine parameter settings for both the prognostic and biomarker models that produce a lower value of this ratio and, correspondingly, a greater benefit due to early detection. We then build on these results in an investigation of the relative benefits associated with different marker thresholds for early detection. In both the median survival and hazard ratio settings, we provide results assuming that disease-specific survival has an exponential distribution. We also explore extensions of our findings to the Weibull distribution and, in the case of the HR, to more general survival distributions.

2. Methods

2.1. Background and notation

Many cancer survival models are proportional hazards models (Iasonos and others, 2008; Kattan and others, 2008) where the hazard function for disease-specific death, h(⋅), is of the form 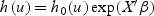with h₀(⋅) denoting the baseline hazard function, X the vector of covariates, β the vector of corresponding regression coefficients, and u the time from disease detection.

Figure 1 illustrates the mean biomarker trajectory and key disease events before and after the detection for a hypothetical subject with disease onset at age a_O. This individual has disease that is diagnosed at age a_A. At that age, the biomarker level is equal to m(a_A). We write actual diagnosis to refer to the time and marker level at diagnosis in the prognostic dataset. With early detection, the disease can be detected earlier at age a_E, where a_O<a_E<a_A, when the biomarker threshold level is equal to m(a_E). We write early diagnosis to refer to the hypothetical earlier timepoint and corresponding marker threshold value. We define the lead time as the difference ℓ=a_A−a_E. Note that this definition of lead time is consistent with that used in the screening literature when a_A represents age at diagnosis in the absence of screening and a_E represents age at screen detection.

We assume that the underlying biomarker mean level m(t) is a function {m(t);t>0} and 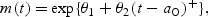where t relates to subject’s age, , and θ₂>0. To make the intercept interpretable, t=0 refers to a known reference age, say 20 years old (correspondingly, ages at disease events depicted in Figure 1 would be in the same scale). The above implies that before disease onset the biomarker mean level is 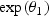and after disease onset the annual change in the biomarker mean level is 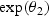. For simplicity, we refer to θ₂ as the biomarker change rate. Given this model, biomarker thresholds greater than 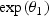allow for disease detection. In Appendix A1 (see supplementary material available at Biostatistics online), we derive results using an alternative change-point mean function that has been previously utilized to fit PSA data (Slate and Turnbull, 2000; Pauler and Finkelstein, 2002; Inoue and others, 2004, 2008). The qualitative results are, however, similar to those discussed in this manuscript. Using the above expression, we can re-write lead time in terms of the biomarker change rate and the biomarker levels at a_A and a_E as .

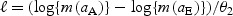Let T_A and T_E denote random variables representing disease-specific survival from a_A and a_E, respectively. Let the lowercase t_A and t_E denote the corresponding observed values of the above random variables. The covariate process is {X(t);t>0}, where t as seen earlier, relates to subject’s age. For simplicity of notation we refer to X_A=X(a_A) and X_E=X(a_E).

2.2. Derivation of conditions implying survival benefit due to early detection

Early diagnosis implies a survival benefit if the disease-specific survival from early detection exceeds the lead time, that is, if t_E−t_A>ℓ. However, neither survival time is known at the time of diagnosis, so we derive conditions such that:

(2.1)

where the lead time is known given X_A and X_E and the biomarker rate of change, and the medians are over the disease-specific survival distributions.

Under the assumption of exponential disease-specific survival, we elucidate the role of the biomarker rate of change in determining whether there is likely to be a survival benefit associated with lowering the biomarker threshold for diagnosis. In Appendix A2 (see supplementary material available at Biostatistics online), we generalize this assumption to a Weibull model. We assume that the biomarker change rate (θ₂) and the regression coefficients (β) in a prognostic model of disease-specific survival are positive and that (X_E−X_A)^′β<0. We do not explicitly model treatment; the treatment distribution is assumed to be as in the prognostic dataset and our projections of survival benefit assume that the same treatment will be used in the case of early detection.

Under the exponential model, denote the baseline hazard function by h₀(u)=γ for all u>0. Then, the difference in median survival is

One can show that condition (2.1) simplifies to

(2.2)

Under our assumptions, 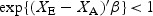. Thus, given X_E and X_A, the condition is more likely to be met when γ is small (i.e. under a favorable baseline survival) or when ℓ is small (i.e. under a short lead time). If X_A and X_E are biomarker values at actual and early detection, respectively, a larger value for the biomarker rate of change (θ₂) implies a shorter lead time. Thus, condition (2.2) implies that early detection is more likely to be beneficial if the biomarker has a high rate of change and/or if disease, once diagnosed, is not rapidly fatal.

2.3. Investigating the magnitude of the implied benefit

In this section, we investigate the extent to which survival is improved by early detection and how the improvement depends on the parameters of the biomarker and prognostic models. The HR is the most commonly used metric for quantifying survival benefit when proportional hazards models are used. Therefore, we consider this measure here. Specifically, we summarize survival improvement using the ratio of the hazard following early detection to the corresponding hazard following actual diagnosis. Let h(⋅|X_A) and h(⋅|X_E) denote the hazard functions describing the risk of disease-specific death from diagnosis at a_A and a_E conditional on predictors X_A and X_E, respectively. We assume the baseline hazard is the same in each case so that any differences between these are fully accounted for by the observed covariates. Since h(⋅|X_E) is not defined before a_A, we compute the post-lead-time HR:

(2.3)

where v>0 denotes time from diagnosis at a_A. See Appendix A3 (see supplementary material available at Biostatistics online) for the derivation of this HR. Note that the HR depends on time from actual diagnosis unless the baseline hazard is constant. A lower HR indicates a greater improvement in life expectancy with lowering the biomarker threshold for early diagnosis.

Next we derive results concerning survival improvement under three hazard models: (1) sole predictor is age at disease detection, denoted by a (in years), (2) sole predictor is the biomarker level at disease detection, denoted by m(a) (in ng/mL), or (3) both age and biomarker level at detection are predictors. The corresponding hazard functions for disease-specific death in the prognostic model are given by

1. 

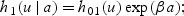
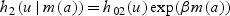2. ; or

3. .

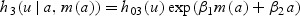In the remainder of this section we investigate the implied early detection benefit under each of these hazard functions assuming a constant baseline hazard, i.e. under exponential disease-specific survival.

2.3.1. Hazard functionh₁

Using the hazard function h₁, the HR for survival benefit is

Thus, as might be expected, the survival benefit depends only on lead time. For each 1 year increase in lead time, the hazard of disease-specific death is decreased by .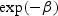

2.3.2. Hazard functionh₂

Observing that we can write the biomarker level at early detection as

the hazard function h₂ implies that the HR for survival benefit takes the form

This expression shows that the HR for disease-specific death depends not only on the lead time but also on the biomarker level at the actual detection (m(a_A)), the biomarker rate of change (θ₂), and the biomarker effect on the risk of disease-specific death (β).

For a given lead time (ℓ), faster biomarker rate of change (θ₂) is associated with greater benefit from advancing diagnosis. Similarly, for a given biomarker rate of change, a longer lead time is associated with greater benefit. Both of these settings will lead to a greater difference between m(a_E) and m(a_A) and, consequently, to a lower HR₂. Also, since θ₂>0 and ℓ>0, we have 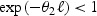. Therefore, as expected, a higher prognostic biomarker effect (β) or a higher biomarker level at actual diagnosis (m(a_A)) is associated with greater benefit. For example, if two individuals have the same lead time and the same biomarker rate of change, the one with the higher biomarker level at actual diagnosis will benefit more from being detected early.

2.3.3. Hazard functionh₃

The hazard function h₃ combines features from h₁ and h₂ so that the HR for survival benefit takes the form

The dependence of HR₃ on the prognostic and biomarker models is similar to that of HR₂. For a given biomarker rate of change (θ₂), a longer lead time (ℓ) yields greater benefit from early detection. Likewise, for a given lead time, a higher biomarker rate of change is associated with greater benefit. In this model, both a higher prognostic biomarker effect (β₁) and a higher prognostic age effect (β₂) are associated with greater benefit. Once again, a higher biomarker level at actual detection (m(a_A)) is associated with greater benefit.

2.4. More general survival distributions

In the case of exponential survival, the ratio h₀(ℓ+v)/h₀(v) cancels out in equation (2.3). For more general survival distributions, however, this ratio will be a component of the post-lead-time HR. Under hazard functions h₁ to h₃, an increase in lead time is associated with a lower HR under the exponential distribution, and this will be true in general if the hazard is not increasing. In this case we will always have h₀(ℓ+v)/h₀(v)<1, and it will also be decreasing with the lead time. However, if the hazard is increasing, then we may have h₀(ℓ+v)/h₀(v)>1, and if it is large enough, it may cause (2.3) to exceed one, which would imply that early detection induces poorer disease-specific survival. In the case of a Weibull survival distribution, for example, we have

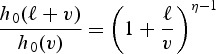for a shape parameter η. Note that this ratio is larger than 1 at small values of v but approaches 1 for larger values of v. Thus, the survival benefit of early detection, as measured by the HR, changes over the course of follow-up. Early detection confers benefit when 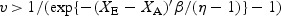. Thus, given X_A and X_E, the longer the lead time, the longer the delay until the early detection benefit manifests in terms of the hazard of disease-specific death. In our application, we found that under the Weibull survival model, the baseline hazard is increasing, and there is no survival benefit within a reasonable life span.

2.5. Comparing biomarker thresholds for early detection

When using a continuous biomarker for early detection, one of the key decisions concerns the biomarker threshold that will be used to declare a test result positive and to refer a patient to biopsy. In the case of PSA, the standard threshold is 4.0 ng/mL, but there have been calls to lower this to 2.5 ng/mL given the observation that latent disease can be prevalent at non-trivial frequencies even at low PSA levels. We can use the HR formulations above to examine the improvement in disease-specific survival over a range of early detection thresholds for a biomarker.

Define the relative hazard ratio RHR(m₀,m₁) as the ratio of the post-lead-time hazard ratios for PSA thresholds m₁ and m₀. In what follows, we assume that m₁<m₀. The lower the RHR, the greater the incremental improvement in post-lead-time survival for cutoff m₁ compared with m₀.

We consider hazard functions h₂ and h₃. Recall that h₂ depends only on PSA. It can be shown that under h₂,

Recall that hazard function h₃ depends on both PSA and age. Using the PSA model, we can re-express age at early detection as 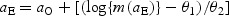. Thus, when considering PSA cutoffs m₁ and m₀ with corresponding ages at early detection a_S1 and a_S0 (obtained using the above expression), the ratio of the post-lead-time HRs under h₃ is

When using a prognostic model based only on the biomarker, lowering the threshold is always associated with an improvement in survival benefit (i.e. RHR₂<1). RHR₂ does not depend on the biomarker rate of change but only on the effect of the biomarker in the prognostic model. Under a prognostic model based on both the biomarker and age at detection, the improvement in survival benefit grows (i.e. RHR₃ shrinks) as the age interval a_S1−a_S0 expands. For fixed m₀ and m₁, this interval depends on the biomarker rate of change and will be longer for slower rates. Therefore, the slower the biomarker rate of change, the more preferable the lower threshold will be. Conversely, if the biomarker changes quickly, this interval will shorten and there will be less of a difference between the HRs at the different thresholds.

2.6. Application

We illustrate our methods using prostate cancer survival data from a study that enrolled 11 521 patients with localized prostate cancer. These patients were treated with radical prostatectomy at four institutions (Memorial Sloan-Kettering Cancer Center, Cleveland Clinic, University of Michigan, and Baylor College of Medicine) from 1987 to 2005. The overall prostate cancer mortality was 7%. The cohort is described in detail in Eggener and others (2011). We fit parametric exponential and Weibull models which either included only PSA at disease diagnosis or included both PSA and age at disease diagnosis as predictors of prostate cancer-specific survival.

We based our ranges for PSA coefficients on Etzioni and others (2005) and Inoue and others (2004) who analyzed longitudinal PSA levels from subjects in the Prostate Cancer Prevention Trial (Thompson and others, 2003) and the Baltimore Longitudinal Study of Aging (Carter and others, 1992). Specifically, for the biomarker model, we use θ₁=0.30 and θ₂=0.10 or 0.20; that is, before disease onset the biomarker level remains fixed at 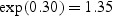 ng/mL, and after disease onset the biomarker grows at a rate of 10% or 20% per year.

In the next section, we present overall results and results stratified by grade of disease (Gleason <7 versus ≥7). In our sample, 10 890 patients were classified with low-grade disease and 631 patients were classified with high-grade disease. We expect the baseline disease-specific hazard to be considerably higher for the high-grade cases.

3. Results

Table 1 presents the results of the prognostic model fits and our projections of the post-lead-time HR when moving from a higher to a lower PSA level at diagnosis under the exponential survival model. The prognostic model results indicate that, although PSA at diagnosis is predictive of disease-specific survival, its effect is rather modest. For a 1 ng/mL increase in PSA at diagnosis, the disease-specific hazard increases by 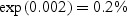. The effect of a 1 year increase in age is an order of magnitude greater estimated at 3% for the overall sample. Based on our analytical results, we therefore anticipate than even if we lower PSA by several points, this will not greatly impact life expectancy; the impact of detecting disease at a younger age is likely to be considerably greater. However, in the case of high-grade cases, detecting disease at a younger age is likely to adversely impact prognosis.

Table 1.

Lead times (ℓ) and HRs when actual diagnosis occurs at a PSA of m(a_A)=10.0 ng/mL and early diagnosis occurs at a PSA threshold of m(a_E)=2.5 or 4.0 ng/mL under hazard functions h₂ (using PSA only) and h₃ (using PSA and age). Results assume an exponential survival model

Hazard function	θ2		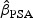	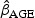m(aE)	ℓ	HR	SE	95% CI
Overall
h2	0.10	0.002		2.50	13.86	0.99	0.00	0.98, 0.99
	0.10	0.002		4.00	9.16	0.99	0.00	0.98, 1.00
	0.20	0.002		2.50	6.93	0.99	0.00	0.98, 0.99
	0.20	0.002		4.00	4.58	0.99	0.00	0.98, 1.00
h3	0.10	0.002	0.03	2.50	13.86	0.68	0.10	0.50, 0.90
	0.10	0.002	0.03	4.00	9.16	0.77	0.08	0.63, 0.93
	0.20	0.002	0.03	2.50	6.93	0.82	0.06	0.70, 0.94
	0.20	0.002	0.03	4.00	4.58	0.87	0.04	0.79, 0.96
Low grade
h2	0.10	0.002		2.50	13.86	0.99	0.01	0.97, 1.00
	0.10	0.002		4.00	9.16	0.99	0.01	0.98, 1.00
	0.20	0.002		2.50	6.93	0.99	0.01	0.97, 1.00
	0.20	0.002		4.00	4.58	0.99	0.01	0.98, 1.00
h3	0.10	0.002	0.04	2.50	13.86	0.59	0.15	0.36, 0.93
	0.10	0.002	0.04	4.00	9.16	0.70	0.11	0.51, 0.95
	0.20	0.002	0.04	2.50	6.93	0.76	0.09	0.59, 0.96
	0.20	0.002	0.04	4.00	4.58	0.83	0.07	0.71, 0.97
High grade
h2	0.10	0.015		2.50	13.86	0.89	0.05	0.80, 0.99
	0.10	0.015		4.00	9.16	0.91	0.04	0.84, 0.99
	0.20	0.015		2.50	6.93	0.89	0.05	0.80, 0.99
	0.20	0.015		4.00	4.58	0.91	0.04	0.84, 0.99
h3	0.10	0.014	−0.02	2.50	13.86	1.25	0.32	0.74, 2.00
	0.10	0.014	−0.02	4.00	9.16	1.14	0.19	0.80, 1.56
	0.20	0.014	−0.02	2.50	6.93	1.05	0.14	0.80, 1.36
	0.20	0.014	−0.02	4.00	4.58	1.02	0.09	0.85, 1.21

Regression coefficients for the prognostic model under the Weibull survival model are similar, but the baseline hazard is increasing. For example, in the model that includes only PSA and all grades, the estimate of the shape parameter is η=2.33 with 95% confidence interval (CI)=[2.11,2.58]. Thus, based on our analytical results, under the Weibull model there is no implied benefit from early detection.

3.1. Projecting the impact of early detection for a specified shift in PSA levels

Consider the example from Section 1. Suppose an individual is diagnosed when PSA is m(a_A)=10.0 ng/mL. What would the projected survival benefit be if he is detected when PSA threshold is m(a_E)=4.0 ng/mL? How does it compare with the survival benefit if he is detected when PSA threshold is m(a_E)=2.5 ng/mL?

Table 1 answers these questions using hazard functions h₂ and h₃. For each hazard function, we consider different fixed values for the PSA rate of change. The estimated standard errors (SEs) and 95% CIs for the HRs were derived under asymptotic normality of the maximum likelihood estimators of the regression coefficients of the exponential survival model for disease-specific death.

Examining the overall results, when moving from a PSA of 10.0 to a PSA of 4.0 ng/mL, the PSA model implies a lead time of 9.2 years when θ₂=0.10 and of 4.6 years when θ₂=0.20. In both cases, however, when including only PSA, the HR of disease-specific death for an early diagnosis relative to his actual diagnosis is 0.99 (95% CI=[0.98,1.00]). In other words, the model does not rule out no benefit from earlier detection. The results are similar if instead disease is detected when PSA first exceeds 2.5 ng/mL. In contrast, the model that includes both PSA and age at diagnosis implies a survival benefit in this context. With early detection at a PSA threshold of 4.0 ng/mL when θ₂=0.10, the hazard of disease-specific death for a subject detected early is 0.77 times that for his actual diagnosis [95% CI=(0.63,0.93)]. The HR is 0.87 (95% CI=[0.79,0.96]) when θ₂=0.20. Moreover, the HR is lower if early detection occurs at a PSA threshold of 2.5 ng/mL.

Similar conclusions apply to low-grade disease. For high-grade disease, the model that uses only PSA as a predictor of disease-specific survival implies some survival benefit. However, the model that includes both PSA and age does not rule out harm from early detection. This is because the regression coefficient for age is negative. Thus, for example, when θ₂=0.10, when moving from a PSA of 10.0 to a PSA of 4.0 ng/mL, the hazard of disease-specific death for an early diagnosis is 1.25 times higher than his actual diagnosis [95% CI=(0.74,2.00)].

3.2. Illustrating the relative survival benefit when comparing biomarker thresholds for test positivity

Figure 2 presents the relative HRs corresponding to h₂ and h₃ to illustrate the added benefit, if any, of lowering the threshold for PSA positivity from 4.0 to 2.5 ng/mL. For example, considering overall results, RHR₂(2.5,4.0)=1.00 and so lowering the threshold from 4.0 to 2.5 ng/mL is associated with no improvement in survival benefit under a hazard for prognosis that depends only on PSA. This does not vary with the biomarker rate of change. In contrast, RHR₃ depends on the biomarker rate of change. In this case, if the biomarker changes at a rate of 10% per year, we find that RHR₃(2.5,4.0)=0.88 [95% CI=(0.79,0.97)], indicating that the 2.5 ng/mL threshold is associated with a 12% improvement in survival benefit relative to the 4.0 ng/mL threshold. As the biomarker rate of change increases, the lead time decreases, and the corresponding RHR is higher. Thus, men with a faster PSA change rate do not gain as much from a lower PSA threshold as do men with a slower PSA change rate.

Figure 2.

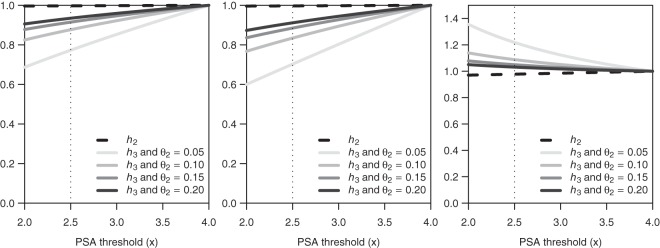
Relative hazard ratios (RHRs) for selected early detection rules under exponential survival overall grade (left panel), or stratified by low grade (middle panel) and high grade (right panel). The RHRs compare HRs derived under hazard functions h₂ and h₃ when the PSA threshold for early detection is in the range of 2.0–4.0 ng/mL relative to the rule that uses PSA threshold of 4.0 ng/mL.

Finally, lowering the threshold for PSA positivity for low-grade disease is associated with added benefit. However, we cannot rule out harm from lowering the threshold for high-grade disease since, for example, RHR₃(2.5,4.0)=1.09 [95% CI=(0.92,1.28)].

4. Conclusion

Quantifying the likely benefit of early detection is notoriously difficult. Even in randomized trials of early detection, inferences about benefit are limited by trial protocols and short follow-up or contaminated by non-compliance. Prognostic models that include early detection biomarkers as covariates make implicit statements about the expected benefit of early detection. Our work on this topic has focused on quantifying the benefit and determining whether and how it goes beyond a lead time effect. Under exponential and Weibull survival models, we derived conditions on marker change rate and prognostic parameters that are associated with greater benefit due to early detection. For example, we found that cases with a faster biomarker change rate or higher biomarker levels at actual diagnosis will generally have greater benefit from advancing diagnosis by a given lead time. Conversely and as might be expected, for a given rate of biomarker change, longer lead time confers greater survival benefit.

Our results are based on several assumptions. The first is that the association between the biomarker and disease-specific survival embodied in the prognostic model is biologically based and may therefore be interpreted causally. This assumption is critical in order to interpret survival differences projected by the prognostic model for different biomarker threshold levels as the expected survival gains an individual might expect if his biomarker levels change by the same amount. The second is that post-lead-time survival times in the absence and presence of early detection have the same baseline survival hazards. Another assumption is the exponential growth of the biomarker in cancer cases. This is standard in studies modeling known cancer biomarkers such as PSA (Inoue and others, 2004; Morrell and others, 1995; Pearson and others, 1994; Slate and Turnbull, 2000) and CA-125 (Skates and others, 2001). Under this assumption, the magnitude of the survival benefit depends on the biomarker value at actual detection so that the benefit from shifting the biomarker value from m_C(a*+Δ) to m_S(a*+Δ) is greater than when shifting from m_C(a+Δ) to m_S(a+Δ) when a*>a and Δ>0. This is a consequence of the exponential growth of the biomarker and may not occur under alternative biomarker model formulations. For example, when the biomarker has linear change, the benefit for a specified lead time does not depend on the biomarker level at actual diagnosis.

Under the above assumptions, we derived conditions under which proportional hazards models of disease-specific survival, as used, for example, in prostate cancer nomograms (Kattan and others, 2008), induce a benefit in terms of median disease-specific survival. This benefit depends on lead time, but it also depends on the rate of change of the biomarker, which could be affected by other clinical and pathologic variables. For example, Inoue and others (2004) showed that PSA rates of change increased with grade of disease. Thus, the projected benefit will vary for high-versus low-grade cases as well as for men with higher versus lower PSA levels at actual detection.

We have expressed the survival benefit in two different ways: in terms of the difference in median survival and in terms of HRs. However, there may be other metrics with which to measure the implicit gains. For example, life-years saved or gains in life expectancy may be more appropriate in certain contexts. Whatever measure is used will need to account for lead time as we have done, for example, in focusing on post-lead-time HRs.

All of our results are based on models for net disease-specific mortality in the absence of competing risks mortality. We expect that estimates of survival benefit will be lower in the presence of other-cause deaths, which will reduce disease-specific deaths in both the absence and presence of early detection. In this case, the survival benefit may depend not only on the prognostic and biomarker model parameters but also on the hazard of other-cause mortality. Further work will investigate the role of the risk of other-cause death when modeling crude disease-specific survival.

We have used estimates from a prognostic model to project differences in expected post-lead-time survival among detected cases were they to be diagnosed earlier with lower PSA threshold levels. The benefits of earlier detection will only be relative to the distribution of diagnosis times in the prognostic dataset. If the prognostic dataset includes screen-detected cases, which tend to show inflated survival anyway due to lead time and overdiagnosis, then this will limit the benefit that can reasonably be expected from further lowering the PSA threshold. This is almost certainly the case in our example dataset which includes cases diagnosed through 2005. In addition, cases in this dataset were treated with radical prostatectomy and therefore were localized. Both of these factors are likely to be behind the modest benefit that we projected from lowering PSA at diagnosis.

Finally, in our application, the biomarker growth was informed from another study since PSA data were only available at diagnosis. Joint modeling of the biomarker growth and the time-to-event processes as done in Law and others (2002), Taylor and others (2005), Soto and others (2008), and Proust-Lima and Taylor (2009) is another direction for future work.

In conclusion, we have shown that models of cancer prognosis that include early detection biomarkers can be used to project the likely benefits of early detection, but only under certain assumptions and only if lead time is taken into account. The results presented here could, in principle, be used to predict long-term benefit in cancer early detection trials (Andriole and others, 2009; Schröder and others, 2009) by comparing, for example, the projected post-lead-time survival on early detection and control arms given mean ages and biomarker values at diagnosis on both arms. This will require marginalizing the expression for median benefit over the distributions of the covariates in both arms of such trials. Some adaptations to the methods will also be necessary to account for the presence of overdiagnosed cases in the early detection arm. With this information we could potentially produce long-term estimates of survival benefit due to early detection which are not currently observable in practice given the limited follow-up of these studies.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This research was supported by U01CA157224 from the National Cancer Institute and the Centers for Disease Control.

The order of authors was wrong in the original version. This has now been corrected. The authors apologize for this error.