Abstract
Motivation: Epistasis or gene–gene interaction has gained increasing attention in studies of complex diseases. Its presence as an ubiquitous component of genetic architecture of common human diseases has been contemplated. However, the detection of gene–gene interaction is difficult due to combinatorial explosion.
Results: We present a novel feature selection method incorporating variable interaction. Three gene expression datasets are analyzed to illustrate our method, although it can also be applied to other types of high-dimensional data. The quality of variables selected is evaluated in two ways: first by classification error rates, then by functional relevance assessed using biological knowledge. We show that the classification error rates can be significantly reduced by considering interactions. Secondly, a sizable portion of genes identified by our method for breast cancer metastasis overlaps with those reported in gene-to-system breast cancer (G2SBC) database as disease associated and some of them have interesting biological implication. In summary, interaction-based methods may lead to substantial gain in biological insights as well as more accurate prediction.
Contact: imichu@ust.hk; slo@stat.columnbia.edu
Supplementary information: Supplementary data are available at the Bioinformatics online.
1 INTRODUCTION
Recent high-throughput biological studies successfully identified thousands of risk factors associated with common human diseases. Most of these studies used single-variable method and each variable is analyzed individually. The risk factors so identified account for a small portion of disease heritability. Nowadays, there is a growing body of evidence suggesting gene–gene interactions as a possible reason for the missing heritability (Carlborg and Haley, 2004; Khan et al., 2011; Moore and Williams, 2009; Shao et al., 2008; Zuk et al., 2011). Recent reviews of methods for gene–gene interaction are given by (Cordell, 2009) and (Kooperberg et al., 2010).
The main difficulty in detecting gene–gene interaction is typical for many high-dimensional data analysis problems, only worse. With only tens or hundreds of observations available normally, one needs to deal with thousands or more genes. What is more challenging is that gene–gene interaction compels the consideration of variables defined by combining genes, which makes the massive number of variables even larger. Thus, feature selection is particularly crucial for effective data analysis.
An important and widely adopted approach to feature selection is to first assume that the data follow a statistical model. The effects of the explanatory variables 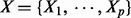 on the response variable Y are then estimated by the corresponding coefficients when fitting the data to the model. Those variables with larger estimated effects are selected. For instance, assume the data follows a linear regression model
on the response variable Y are then estimated by the corresponding coefficients when fitting the data to the model. Those variables with larger estimated effects are selected. For instance, assume the data follows a linear regression model
To improve the prediction accuracy and interpretability of ordinary least squares (OLS), LASSO of (Tibshirani, 1996) adds an 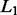 -norm penalty to OLS to continuously shrink some coefficients to zero and automatically select a subset of variables.
-norm penalty to OLS to continuously shrink some coefficients to zero and automatically select a subset of variables.
The aforesaid approach works well when the number of variables is not very large. To detect gene–gene interaction, however, it must include additional variables defined by products of original variables and thus the number of variables p is exponentially larger than n, the number of observations. That is, 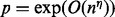 for some
for some 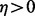 . When p is exponentially larger than n, estimating the coefficient vector
. When p is exponentially larger than n, estimating the coefficient vector 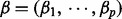 accurately is hard. This is because the noise level may be larger than some absolute coefficients
accurately is hard. This is because the noise level may be larger than some absolute coefficients 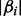 and achieving the ideal risk up to the logarithmic factor
and achieving the ideal risk up to the logarithmic factor 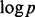 in oracle inequalities may be too large for practical purposes (Fan and Lv, 2008). These difficulties are caused by that the approach estimates the effects of all variables simultaneously. Hence (Fan and Lv, 2008) proposed a feature selection method, sure independence screening (SIS), to first screen variables separately using marginal correlation. After screening, accurate estimation for selected variables can then be done by using methods well-suited for low or moderate dimensional data. SIS improves substantially the performance of LASSO and related methods when variables only have marginal effects on Y. However, gene–gene interaction often comes with module effects (Cordell, 2009). That is, the effect of some variables can be detected only when considered jointly with other variables of the same module. When there is module effect, SIS is not expected to attain the goal of effective feature selection.
in oracle inequalities may be too large for practical purposes (Fan and Lv, 2008). These difficulties are caused by that the approach estimates the effects of all variables simultaneously. Hence (Fan and Lv, 2008) proposed a feature selection method, sure independence screening (SIS), to first screen variables separately using marginal correlation. After screening, accurate estimation for selected variables can then be done by using methods well-suited for low or moderate dimensional data. SIS improves substantially the performance of LASSO and related methods when variables only have marginal effects on Y. However, gene–gene interaction often comes with module effects (Cordell, 2009). That is, the effect of some variables can be detected only when considered jointly with other variables of the same module. When there is module effect, SIS is not expected to attain the goal of effective feature selection.
To generate useful knowledge on genetic architecture of complex diseases where interactions among genetic, biological, biochemical and environmental factors work together to produce the response, current high-dimensional statistical methods are facing a few major challenges. First, to detect the effect of a gene, it may be necessary to consider the gene jointly with others in the same functional module such as a pathway. Secondly, the genes may interact with each other in influencing the response. Thirdly, the effect of genes on the response may be highly nonlinear.
To address these challenges, the proposed method extracts different types of information from the data in several stages. In the first stage, we select variables with high potential to form influential variable modules when combining with other variables. In the second stage, we generate highly influential variable modules from variables selected in the first stage so that each variable interacts with others in the same module to produce a strong effect on the response Y. The third stage combines classifiers, each constructed from one module, to form the classification rule.
The overarching idea is that since the feature selection problem involving module, interaction and nonlinearity is too complicated to be reduced to one single optimization problem based on a model equation, we break the problem into smaller ones. As the nonlinearity, interaction and module effects can be adequately accommodated within a smaller problem, we then solve each smaller problem and put the solutions together to form the final one. Our method provides a flexible framework to analyze high-dimensional data for classification purposes. It is model-free and considers variable interaction explicitly, which aligns well with the systems-oriented biological paradigm.
LASSO related methods were developed for grouped variables (Yuan and Lin, 2006; Zou and Hastie, 2005). Comprehensive reviews of feature selection methods are available from machine learning literature (Dash and Liu, 1997; Guyon and Elisseeff, 2003; Liu and Yu, 2005) and bioinformatics (Saeys et al., 2007).
2 APPROACH: TWO BASIC TOOLS
To shed light on the effectiveness of our method, we provide preliminary illustration via a toy example. The purpose of the toy example is to demonstrate that two basic tools adopted by our method can elicit interaction information difficult for other methods.
2.1 An influence measure
For easy illustration, we assume that the response variable Y is binary (taking values 0 and 1) and all explanatory variables are discrete. Consider the partition 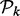 generated by a subset of k explanatory variables
generated by a subset of k explanatory variables  . If all variables in the subset are binary then there are
. If all variables in the subset are binary then there are 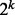 partition elements; see the first paragraph of Section 3 in (Chernoff et al., 2009). Let
partition elements; see the first paragraph of Section 3 in (Chernoff et al., 2009). Let 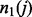 be the number of observations with Y = 1 in partition element j. Let
be the number of observations with Y = 1 in partition element j. Let 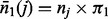 be the expected number of Y = 1 in element j under the null hypothesis that the subset of explanatory variables has no association with Y, where
be the expected number of Y = 1 in element j under the null hypothesis that the subset of explanatory variables has no association with Y, where 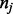 is the total number of observations in element j and
is the total number of observations in element j and 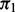 is the proportion of Y = 1 observations in the sample. The influence measure of (Lo and Zheng, 2002), henceforth LZ, is defined as
is the proportion of Y = 1 observations in the sample. The influence measure of (Lo and Zheng, 2002), henceforth LZ, is defined as
The statistic I equals the sum of squared deviations of Y-frequency from what is expected under the null hypothesis. Two properties of I make it useful. First, the measure I does not require one to specify a model for the joint effect of  on Y. It is designed to capture the discrepancy between the conditional means of Y on
on Y. It is designed to capture the discrepancy between the conditional means of Y on  and the marginal mean of Y whatever the conditional distribution may be. Secondly, under the null hypothesis that the subset has no influence on Y, the expected value of I remains non-increasing when dropping variables from the subset. The second property makes I critically different from the Pearson’s
and the marginal mean of Y whatever the conditional distribution may be. Secondly, under the null hypothesis that the subset has no influence on Y, the expected value of I remains non-increasing when dropping variables from the subset. The second property makes I critically different from the Pearson’s 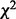 statistic whose expectation depends on the degrees of freedom and hence on the number of variables used to define the partition. To see this, we rewrite I in its general form when Y is not necessarily discrete
statistic whose expectation depends on the degrees of freedom and hence on the number of variables used to define the partition. To see this, we rewrite I in its general form when Y is not necessarily discrete
where 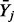 is the average of Y-observations over the jth partition element and
is the average of Y-observations over the jth partition element and 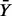 is the overall average. Under the same null, it is shown (Chernoff et al., 2009) that the normalized I,
is the overall average. Under the same null, it is shown (Chernoff et al., 2009) that the normalized I, 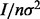 (
(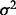 denotes the variance of Y), is asymptotically distributed as a weighted sum of independent
denotes the variance of Y), is asymptotically distributed as a weighted sum of independent 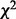 random variables of one degree of freedom each such that the total weight is less than one. This very property provides the theoretical basis for the following algorithm.
random variables of one degree of freedom each such that the total weight is less than one. This very property provides the theoretical basis for the following algorithm.
2.2 A backward dropping algorithm
The backward dropping algorithm (BDA) is a greedy algorithm to search for the variable subset that maximizes the I-score through stepwise elimination of variables from an initial subset sampled in some way from the variable space. The details are as follows.
Training set: Consider a training set
 of n observations, where
of n observations, where 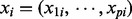 is a p-dimensional vector of explanatory variables. Typically p is very large. All explanatory variables are discrete.
is a p-dimensional vector of explanatory variables. Typically p is very large. All explanatory variables are discrete.Sampling from variable space: Select an initial subset of k explanatory variables
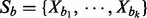 ,
, 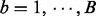 .
.Compute I-score:
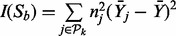
Drop variables: Tentatively drop each variable in
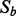 and recalculate the I-score with one variable less. Then drop the one that gives the highest I-score. Call this new subset
and recalculate the I-score with one variable less. Then drop the one that gives the highest I-score. Call this new subset 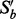 , which has one variable less than
, which has one variable less than 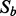 .
.Return set: Continue the next round of dropping on
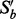 until only one variable is left. Keep the subset that yields the highest I-score in the whole dropping process. Refer to this subset as the return set
until only one variable is left. Keep the subset that yields the highest I-score in the whole dropping process. Refer to this subset as the return set
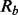 . Keep it for future use.
. Keep it for future use.
If no variable in the initial subset has influence on Y, then the values of I will not change much in the dropping process; see Figure 1b. On the other hand, when influential variables are included in the subset, then the I-score will increase (decrease) rapidly before (after) reaching the maximum; see Figure 1a.
Fig. 1.
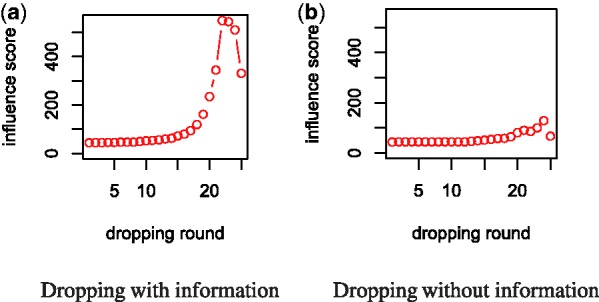
Comparison of variable subsets with/without information using BDA
2.3 A toy example
To address the three major challenges mentioned in Section 1, the toy example is designed to have the following characteristics.
Module effect: The variables relevant to the prediction of Y must be selected in modules. Missing any one variable in the module makes the whole module useless in prediction. Besides, there is more than one module of variables that affects Y.
Interaction effect: Variables in each module interact with each other so that the effect of one variable on Y depends on the values of others in the same module.
Nonlinear effect: The marginal correlation equals zero between Y and each X-variable involved in the model.
Let Y, the response variable, and 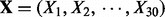 , the explanatory variables, all be binary taking the values 0 or 1. We independently generate 200 observations for each
, the explanatory variables, all be binary taking the values 0 or 1. We independently generate 200 observations for each 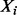 with
with 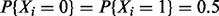 and Y is related to X via the model
and Y is related to X via the model
| (1) |
The task is to predict Y based on information in the 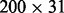 data matrix. We use 150 observations as the training set and 50 as the test set. This example has 25% as a theoretical lower bound for classification error rates because we do not know which of the two causal variable modules generates the response Y.
data matrix. We use 150 observations as the training set and 50 as the test set. This example has 25% as a theoretical lower bound for classification error rates because we do not know which of the two causal variable modules generates the response Y.
Table 1 reports classification error rates and standard errors by various methods with five replications. Methods included are linear discriminant analysis (LDA), support vector machine (SVM), random forest (Breiman, 2001), LogicFS (Schwender and Ickstadt, 2008), Logistic LASSO, LASSO (Tibshirani, 1996) and elastic net (Zou and Hastie, 2005). We did not include SIS of (Fan and Lv, 2008) because the zero correlation mentioned in (c) renders SIS ineffective for this example. The proposed method uses boosting logistic regression after feature selection.
Table 1.
Classification error rates for the toy example
| Method | LDA | SVM | Random forest | LogicFS | Logistic LASSO | LASSO | Elastic net | Proposed |
|---|---|---|---|---|---|---|---|---|
| Train error | 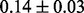 |
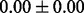 |
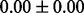 |
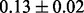 |
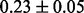 |
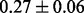 |
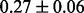 |
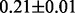 |
| Test error | 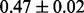 |
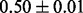 |
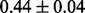 |
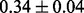 |
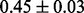 |
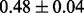 |
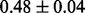 |
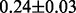 |
To assist other methods (barring LogicFS) detecting interactions, we augment the variable space by including up to 3-way interactions (4495 in total). Here the main advantage of the proposed method in dealing with interactive effects becomes apparent because there is no need to increase the dimension of the variable space. Other methods need to enlarge the variable space to include products of original variables to incorporate interaction effects.
For the proposed method, there are B = 5000 repetitions in BDA and each time applied to select a variable module out of a random subset of k = 8. The top two variable modules, identified in all five replications, were 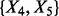 and
and 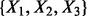 due to the strong interaction effect within them. Here the advantage of the proposed method in handling the module effect is clearly demonstrated because variables are always selected in modules. In summary, the proposed method correctly selected the two causal modules of variables and thus yields the lowest test error rate. Moreover, by comparing the train and test error rates in Table 1, we observe that all methods except for the proposed one suffer from overfitting. We also tested several other models. The general message is that LASSO and related methods work well for linear models with significant marginal effects while our method performs better for nonlinear models with module and interaction effects.
due to the strong interaction effect within them. Here the advantage of the proposed method in handling the module effect is clearly demonstrated because variables are always selected in modules. In summary, the proposed method correctly selected the two causal modules of variables and thus yields the lowest test error rate. Moreover, by comparing the train and test error rates in Table 1, we observe that all methods except for the proposed one suffer from overfitting. We also tested several other models. The general message is that LASSO and related methods work well for linear models with significant marginal effects while our method performs better for nonlinear models with module and interaction effects.
3 METHODS
The proposed method consists of three stages (Fig. 2). First, we screen variables to identify those with high potential to form influential modules when combining with other variables. Secondly, we generate highly influential variable modules from variables selected in the first stage, where variables of the same module interact with each other to produce a strong effect on Y. The third stage combines the variable modules to form the classification rule.
Fig. 2.
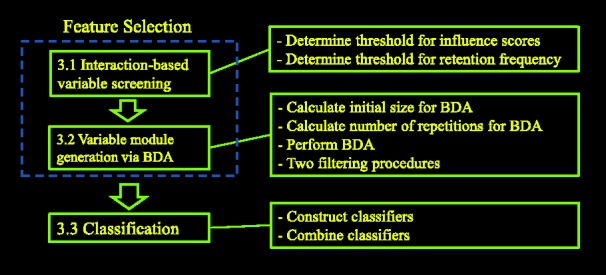
Method flowchart
We have shown in Section 2 that BDA can extract useful information from the data about module and interaction effects. However, how to determine the input to BDA and how to use the output from BDA require entirely new methods. Unless one can properly manage the input to and output from BDA, the strength of BDA as a basic tool cannot be fully realized. In this regard, the innovation of the proposed method manifests itself in three ways. First, because direct application of BDA in high-dimensional data may miss key variables, we propose a two-stage feature selection procedure: interaction-based variable screening and variable module generation via BDA. Since the quality of variables is enhanced by the interaction-based variable screening procedure in the first stage, we are able to generate variable modules of higher order interactions in the second stage. These variable modules then serve as building blocks for the final classification rule. Secondly, we introduce two filtering procedures to remove false-positive variable modules. Thirdly, we put together classifiers, each based on one variable module, to form the final classification rule. These new ideas produce significantly better results than applying BDA directly.
We believe that the analysis of high-dimensional data with module, interaction and nonlinear effects cannot be effectively resolved within one single optimization problem based on a model equation. We must extract information in several stages, each aims for a specific type of information from the data, then combining information from each to achieve the final goal. Thus dividing our method into stages, each with a specific goal, is part of the method and not just a convenient way to present the method. We use the data from van’t Veer (2002) as a running example. The background of the data is given in Section 4.
The influence measure I works best for discrete variables. If some explanatory variables are continuous, we first convert them into discrete ones for feature selection purpose (once variable modules have been generated, we use the original variables to estimate their effects). This pre-processing step induces an information tradeoff: information loss due to discretizing variables versus information gain from robust detection of interactions by discretization. By the classification error rates reported in Section 4, we demonstrate that the gain from robust detection of interactions is much more than enough to offset possible information loss due to discretization.
In this article, we use the two-mean clustering algorithm to turn the gene expression level into a variable of two categories, high and low. As an additional piece of evidence supporting the proposed pre-processing step, we have tried more than two categories; e.g. three categories of high, medium and low. The empirical results show that the more categories used the worse classification error rates. Using more categories is supposed to reduce information loss due to discretization. Hence the empirical result suggests that for the kind of problems studied in this article, robust detection of interaction in feature selection is much more important than avoiding information loss by using the original variables.
3.1 Interaction-based variable screening
When the number of variables is moderate as in the toy example, we can directly apply BDA to generate variable modules without doing variable screening first. However, when the number of variables is in the thousands or more, directly applying BDA may miss key variables and we need to do variable screening before BDA. Since we would like to screen for both module and interaction effects, the screening is not on individual variables but rather on variable combinations and thus it is interaction-based. However, the dimensionality of variable combinations grows exponentially with the size of the combinations. For example, with 5000 variables we have over 10 million pairs and over 20 billion triplets. Computational constraints arise. While screening all triplets provides information up to 3-way interactions, the computation cost is more than 1000 times that for pairs. In light of computational resource considerations, one must decide on the order of interaction to screen for.
3.1.1 Determine the threshold for influence scores
Suppose that it is decided to screen for 3-way interactions. We then obtain I-scores, one for each triplet. Now the job is to find a cut-off value for I-scores so that triplets with scores higher than the cut-off value are selected for further analysis and those with lower scores are discarded. This is a common issue for feature selection. Generally speaking, there are two approaches: controlling the size of the selected variable subset (Fan and Lv, 2008; Guyon et al., 2002;) or controlling the false discovery rate (Benjamini and Hochberg, 1995). Here, we offer a new approach based on the 2nd difference of the scores, which works as follows.
First, order the triplets from high to low according to their respective I-scores. Then go through the ordered triplets and record the I-score for, say, every one thousandth triplets. That is, record the scores for 1st, 1001st, 2001st, … triplets. Typically, the second difference (The first differences of a sequence 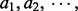 are the successive differences
are the successive differences 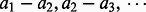 and the second differences are the successive differences of the first difference sequence.) of the aforementioned sequence of scores declines sharply in the beginning and then settles down around zero. We will choose a cut-off value corresponding to when the 2nd difference is near zero for the first time. Figure 3, obtained from the van’t Veer dataset, reveals that the second difference of I-score flattens out after 21 thousand top scored triplets, which are retained for further analysis.
and the second differences are the successive differences of the first difference sequence.) of the aforementioned sequence of scores declines sharply in the beginning and then settles down around zero. We will choose a cut-off value corresponding to when the 2nd difference is near zero for the first time. Figure 3, obtained from the van’t Veer dataset, reveals that the second difference of I-score flattens out after 21 thousand top scored triplets, which are retained for further analysis.
Fig. 3.
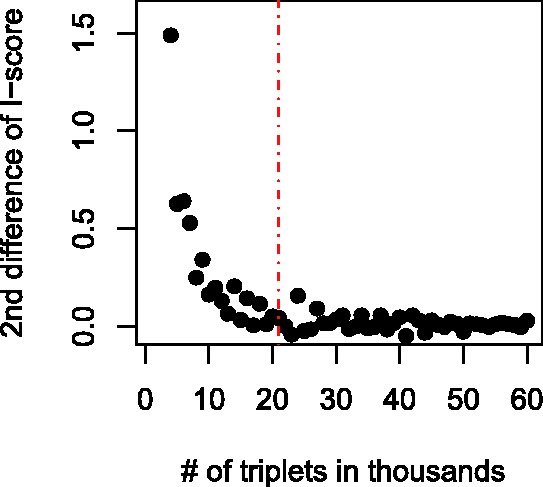
2nd difference of I-scores for every 1000 triplets
The rationale for the 2nd difference procedure is very simple: if we lower the cut-off value just a little, we will allow a lot more variables to be included and we know most of them are false positives. A calculation similar to the local false discovery rate of (Efron et al., 2001) gives almost the same result.
3.1.2 Determine the threshold for retention frequency
After determining the cut-off value for the high-scored triplets, we face a related yet different issue. Since the I-score is shared by variables in the same triplet and different triplets may overlap, we have a set of I-scores instead of one for each variable in the high-scored triplets. We use the retention frequency to select variables from the high-scored triplets.
The retention frequencies usually show big drops in the beginning and small differences after a certain point. See Figure 4, which is based on the top 21 thousand triplets obtained from Figure 3. We select the top 138 high-frequency variables because the later ones differ little as the 1st difference indicates. Moreover, retention frequency ties (1st-difference zeros) occur much more frequently after the top 138 variables.
Fig. 4.
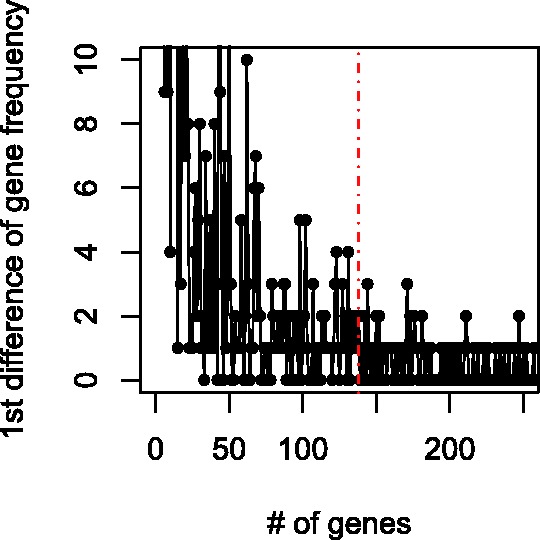
1st difference of retention frequency from top 21 000 triplets
We did sensitivity analysis on the cut-off values for both I-scores and retention frequencies. The cut-off values do not affect later analysis results if they are changed up to 10%. In Figure 3, if we use 19–23 thousands triplets, the final result is basically the same as that based on 21 thousand triplets. In Figure 4, using between 110 and 150 high-frequency variables yields the same final result.
High-frequency variables have high potential to form influential variable modules. This is because they yield high I-scores when combined with other variables and do so frequently. Usually there are only a moderate number of high-frequency variables. In the three microarray datasets that we analyzed, the variable screening procedure described above reduces the number of variables from thousands to below 150—a >95% reduction in the number of variables! This drastic reduction of variables facilitates the generation of variable modules–the next stage of the proposed method.
3.2 Variable module generation via BDA
We now apply BDA to the high potential variables obtained from the previous stage to generate variable modules. There are two quantities to be determined before applying BDA.
3.2.1 Calculate the initial size for BDA
The initial size refers to the size of initial variable subsets subjected to backward dropping. The initial size depends on the number of training cases available. If the initial size is too large, then most partition elements induced by the initial subset of variables contain no more than one training case. Hence, dropping is basically random and one can start with a smaller subset and achieve the same result with less computing time. The minimum requirement on the initial size is that at least one partition element containing two or more observations. Using Poisson approximation (Supplementary Material), we can calculate the expected number of partition elements with two or more observations. Then the minimum requirement is met if the initial size k satisfies
| (2) |
where n is the number of training cases and 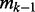 is the number of partition elements induced by a subset of k−1 variables. Thus (2) provides an upper bound for the initial size. Suppose that there are 150 training cases and all variables are binary. Since 13 variables induce a partition with
is the number of partition elements induced by a subset of k−1 variables. Thus (2) provides an upper bound for the initial size. Suppose that there are 150 training cases and all variables are binary. Since 13 variables induce a partition with 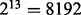 elements and
elements and 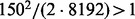 , we can choose the initial size to be 14, the largest integer satisfying (2). In Supplementary Material, another inequality gives the condition for at least one partition element containing three or more observations and it suggests an improved upper bound of 10. An argument in the next paragraph leads to a lower bound. In practice, any initial size between the upper and lower bounds can be used.
, we can choose the initial size to be 14, the largest integer satisfying (2). In Supplementary Material, another inequality gives the condition for at least one partition element containing three or more observations and it suggests an improved upper bound of 10. An argument in the next paragraph leads to a lower bound. In practice, any initial size between the upper and lower bounds can be used.
3.2.2 Calculate the number of repetitions in BDA
The number of repetitions in BDA is the number of variable subsets subjected to backward dropping, which are randomly sampled from those variables retained after the previous stage. The number of repetitions in BDA depends on the number of training cases as well. The number of training cases determines the size of variable subsets that can be supported by the training set. For example, if we have 150 training cases, then they can support a subset of size 5 assuming all explanatory variables are binary. The reason is as follows. As a rule of thumb (Agresti, 1996), the χ2 approximation is adequate if the averaged number of observations per partition element is at least 4. Since each subset of size 5 has 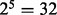 partition elements, each partition element on the average contains
partition elements, each partition element on the average contains 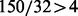 training cases. Hence, variable subsets of size 5 are adequately supported by a training set of 150 (it is also the lower bound for the initial size). In this case, we would like to make sure that the number of repetition in BDA is sufficient so that the quintuplets are covered rather completely. Here we encounter a variation of coupon-collecting problem.
training cases. Hence, variable subsets of size 5 are adequately supported by a training set of 150 (it is also the lower bound for the initial size). In this case, we would like to make sure that the number of repetition in BDA is sufficient so that the quintuplets are covered rather completely. Here we encounter a variation of coupon-collecting problem.
Let p be the number of variables and let k be the initial size. Then there are 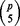 quintuplets from p variables and each repetition in BDA can cover
quintuplets from p variables and each repetition in BDA can cover 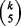 quintuplets. Consider the following coverage problem. There are a total of
quintuplets. Consider the following coverage problem. There are a total of 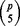 urns and each corresponds to a quintuplet. Each time
urns and each corresponds to a quintuplet. Each time 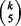 balls, the number of quintuplets contained in an initial subset of size k, are randomly placed into urns so that each ball is in a different urn. In Supplementary Material, it is shown that we are expected to have
balls, the number of quintuplets contained in an initial subset of size k, are randomly placed into urns so that each ball is in a different urn. In Supplementary Material, it is shown that we are expected to have
| (3) |
repetitions in BDA for a complete coverage of quintuplets from p variables.
The preceding result does not take into account that each time we do not place one ball but a cluster of balls into urns. It is known that clustering increases the proportion of vacant urns (Hall, 1988). Hence the expected number of repetitions to cover all quintuplets is larger than 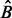 (the exact result is an open problem). We propose
(the exact result is an open problem). We propose 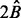 as an upper bound. In the simulated examples, this upper bound is quite sufficient and after running
as an upper bound. In the simulated examples, this upper bound is quite sufficient and after running 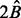 repetitions in BDA we do not miss any key variables. Applying the
repetitions in BDA we do not miss any key variables. Applying the 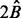 upper bound to the van’t Veer data, we use 1.5 million repetitions in BDA to cover all quadruplets of 138 selected genes using the initial size 11.
upper bound to the van’t Veer data, we use 1.5 million repetitions in BDA to cover all quadruplets of 138 selected genes using the initial size 11.
3.2.3 Two filtering procedures
The return sets generated from BDA will undergo two filtering procedures to reduce between-return-set correlation and false positives, respectively. The first procedure is to filter out return sets with overlapping variables. Since the return sets will be converted into classifiers and it is desirable to have uncorrelated classifiers, we shall keep only one of those return sets containing common variables. This can be done by sorting the return sets in decreasing order according to the I-scores and then remove those having variables in common with a higher-scored one. This procedure has another remarkable effect—it reduces the number of return sets from tens of thousands to a few dozens, which greatly simplifies the subsequent analysis. For example, in one of the cross validation (CV) experiments of van’t Veer data, the number of return sets with I-score above 300 reduced from 110 283 to 29 after this filtering procedure.
The return sets after removing overlap ones are then subjected to a forward adding algorithm to remove false positives. See Supplementary Material for details. Very often, the error rates are much improved after the filtering procedures. The return sets retained after the two filtering procedures are the variable modules that we will use to build the final classification rule.
3.3 Classification
After variable modules have been generated, we then construct classifiers, each based on one variable module. Since the number of variables in one module is quite small (2–5 typically), the traditional setting of large n small p prevails, and most existing classification methods, including those in Table 1 such as LDA related methods, SVM related kernel methods, logistic regression and different versions of LASSO etc. can be employed.
3.3.1 Construct the classifier
The classifier used in this article is logistic regression. In the logistic-regression classifier, we include all interaction terms from a variable module. Thus a module of size 4 would give rise to 16 terms including up to 4-way interaction as the full model. We can then apply Akaike information criterion (AIC) to select a submodel. A sample output of logistic regression from R programming language is shown in Supplementary Exhibit S1.
3.3.2 Combine the classifiers
The logistic regression classifiers, each based on one variable module, needs to be combined to form the final classification rule. Methods that combine classifiers are referred to as ensemble classification methods in the literature. Dietterich (2000) gave reasons for using ensemble classification methods. Two of them fit the current situation well: (i) Since the sample size is only modest, many classifiers fit the data equally well. (ii) The optimal classifier cannot be represented by any one classifier in the hypothesis space.
In this article, we employ the boosting method (Freund and Schapire, 1997) to combine classifiers. The boosting algorithm for variable modules is included in Supplementary Exhibition S2. The final classification rule is such that interactions among variables are allowed within each component classifier but not among variables in different classifiers. As the classifiers are added one by one to the classification rule via the boosting algorithm, we expect the error rates for the training set to decrease after each addition to reflect continuing improvement of fit to the training sample. However, the error rates for the test sample obtained by sequentially adding classifiers do not necessarily decrease and can be used to detect overfitting because information from the test sample is not used in constructing the classification rule via the boosting algorithm.
4 RESULTS
4.1 Classification based on van’t Veer’s data
The first dataset comes from the breast cancer study of (van’t Veer et al., 2002). The purpose of the study is to classify female breast cancer patients according to relapse and non-relapse clinical outcomes using gene expression data. Originally, it contains the expression levels of 24 187 genes for 97 patients, 46 relapse (distant metastasis  5 years) and 51 non-relapse (no distant metastasis
5 years) and 51 non-relapse (no distant metastasis  5 years). We keep 4918 genes for the classification task, which were obtained by (Tibshirani and Efron, 2002).
5 years). We keep 4918 genes for the classification task, which were obtained by (Tibshirani and Efron, 2002).
In (van’t Veer et al., 2002), 78 cases out of 97 were used as the training set (34 relapse and 44 non-relapse) and 19 (12 relapse and 7 non-relapse) as the test set. The best error rates (biased or not) on this particular test set in the literature is around 10%. Our method yields a perfect error rate on the test set of van’t Veer (Fig. 5).
Fig. 5.
Error rates of our method for the test set of van’t Veer
Since it is better to cross validate the error rates on other test sets as well, the literature offers such error rates by a wide variety of methods. The cross-validated error rates of the van’t Veer data are typically around 30%. Some papers reported error rates significantly lower than 30%. However, after careful investigation, we found all of them suffer from feature selection bias and/or turning parameter selection bias (Zhu et al., 2008). Some of them used leave-one-out cross validation (LOOCV). On top of the two kinds of biases mentioned, LOOCV has the additional problem of much larger variance than, say, 5-fold CV, because the estimates in each fold of LOOCV are highly correlated. A summary is in Table 2. The details are given in Supplementary Table S2.
Table 2.
Classification error rates by various methods on van’t Veer data
| Method | Test set | 10-fold CV |
|---|---|---|
| Literaturea | 0.316–0.632 | 0.219–0.29 |
| Proposed | 0.00 | 0.08 |
aPerformance of other methods in the literature, by the same validation procedures used in this article. A full list of literature results can be found in Supplementary Table S2.
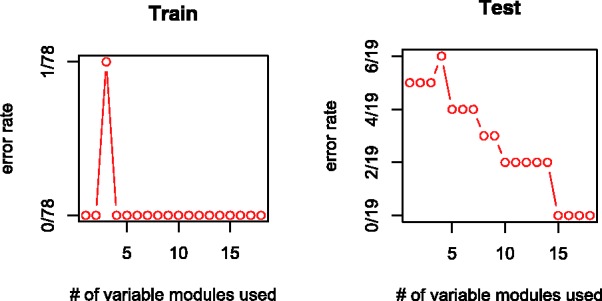
The proposed method yields an average error rate of 8% over 10 randomly selected CV test samples. To be more specific, we run the CV experiment by randomly partitioning the 97 patients into a training sample of size 87 and a test sample of 10, then repeated the experiment ten times. Since it has no tuning parameter and selects features without using any information whatsoever from the test samples, the proposed method is free from both types of biases. The error rates of the 10 training and test samples are shown in Figure 6.
Fig. 6.
10 Random CV error rates for the van’t Veer data
In all 10 CV experiments, the error rates on the test sample generally decline as more classifiers are added to the classification rule. Since the classification rule is constructed without using any information from test samples, this indicates that the proposed method does not have overfitting problems.
4.2 Biological significance of features selected
To see whether or not the identified genes are biologically meaningful, we examine the gene modules obtained from the training set of van’t Veer. There are 18 gene modules containing 64 genes yielding a perfect error rate on the 19 test cases (Fig. 5). Among the 64 genes, we found that 18 of them have been reported as breast cancer associated (genes having at least one piece of molecular evidence from the literature) by G2SBC database while others have protein folding functions. Such a result is significant, considering our method does not use any prior biological information and selects genes based on statistical analysis only.
The G2SBC database contains 2166 genes and 903 of them are among the 4918 genes we adopted from (Tibshirani and Efron, 2002). Thus the proportion of disease-associated genes in our gene pool is 903/4918 = 0.184, whereas the proportion of disease-associated genes in our classification rule is 18/64 = 0.281. This result is significant with P-value 2.3%. With a sizable proportion of replicated genes, it is not unreasonable to expect some of the remaining protein folding genes which have not been reported are new risk factors of breast cancer.
The gene modules and component genes’ biological functions can be found in Supplementary Table S3. We will elaborate on two gene modules here (Table 3). The first one has the highest I-score among all 18 modules. It consists of 5 genes, 2 of them, ICAP-1A and CCNB2, are known to be breast cancer related. The former is an integrin beta-1-binding protein 1, and the later is essential for the control of the cell cycle at the G2/M (mitosis) transition. The KRT1 (keratin 1), though not reported in breast cancer literature, binds to ICAP-1A, which is integrin cytoplasmic domain-associated protein-1 alpha and plays a critical role in beta-1-integrin-mediated cell proliferation. That is, in this top gene module, two genes with confirmed biological association are captured together. The gene KIAA1683 (19p13.1) has unknown protein function, and GNG7 (19p13.3) is gaunine nucleotide binding protein, gamma7. They are identified together probably due to closeness in their chromosome positions. The gene module suggests that GNG7, ICAP-1A, KRT1 and CCNB2 interact with each other, and KRT1 is likely to be a new breast cancer associated gene.
Table 3.
Biological implication of two gene modules identified in van’t Veer data
| Gene module | Systematic name | Gene name | Description |
|---|---|---|---|
| I | Contig45347_RC | KIAA1683 | ESTs |
| NM_005145 | GNG7 | Guanine nucleotide binding protein (G protein), gamma 7 | |
| Z34893 | ICAP-1A | Integrin cytoplasmic domain-associated protein 1 | |
| NM_006121 | KRT1 | Keratin 1 (epidermolytic hyperkeratosis) | |
| NM_004701 | CCNB2 | Cyclin B2 | |
| VI | NM_003087 | SNCG | Synuclein, gamma(breast cancer-specific protein 1) |
| D38553 | KIAA0074 | KIAA0074 protein | |
| NM_001216 | CA9 | Carbonic anhydrase IX | |
The 6th module contains 3 genes, SNCG, NCAPH and CA9. SNCG(BCSG1) is breast cancer specific protein 1, it encodes a member of the synuclein family of proteins that are believed to be involved in the pathogenesis of neurodegenerative diseases. Mutations in this gene have also been associated with breast tumor development. The NCAPH encodes a member of the barr gene family and a regulatory subunit of the condensin complex, which is required for the conversion of interphase chromatin into condensed chromosomes. The CA9, carbonic anhydrase IX, is associated with cell proliferation. It is reported (Beketic-Oreskovic et al., 2011; Pinheiro et al., 2011) that over expression of this gene results in early relapse of breast cancer. Without prior knowledge, we independently identified strong effect on breast cancer relapse status by the interaction of SNCG, NCAPH and CA9.
More interestingly, while interactions over 2-gene combinations are rarely reported in the literature, our method suggests up to 5-way interactions and some of them include 2-gene combinations reported in the literature (ICAP-1A and KRT1 by Zawistowski et al., 2002 and Zhang et al., 2001). Thus our method not only selects features important to classification, but also suggests undiscovered interactions which might lead to new signaling pathways.
4.3 Other applications
4.3.1 Breast cancer tumor subtypes
The second dataset consists of 7650 genes and 99 samples (Sotiriou et al., 2003). The task is to classify tumors according to their estrogen receptor (ER) status using gene expression information. This is different from the objective of (van’t Veer et al., 2002), where the goal is to discriminate relapse patients from non-relapse ones. We follow a similar procedure as that for the van’t Veer dataset. The average error rate over 10 CV groups is 5%. This result is slightly better than the result reported in (Zhang et al., 2006), where additional information from two other related microarray datasets (Perou et al., 2000; van’t Veer et al., 2002) were used.
4.3.2 Leukemia subtypes
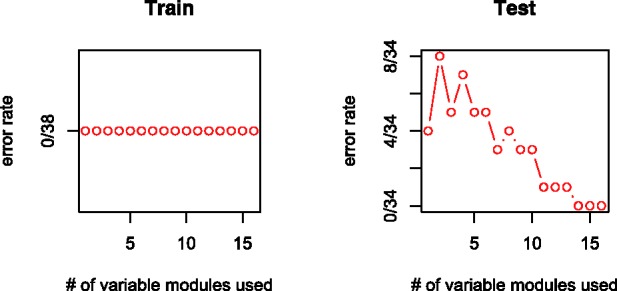
The third gene expression dataset is from (Golub et al., 1999). It contains expression levels of 7129 genes for 38 cases in the training set and 34 in the test set. The purpose is to classify acute leukemia into two subtypes: acute lymphoblastic leukemia (ALL) and acute myeloid leukemia (AML). The dataset was analyzed in the same way as that for (Sotiriou et al., 2003). Our classification rule consists of 52 genes in 16 modules and correctly classifies all test cases. That is, the error rate is zero (Fig. 7). The names and biological functions of these 52 genes are listed in Supplementary Table S4.
Fig. 7.
Error rate paths of our classification rule for Golub dataset
The dataset appears to have strong marginal effects and a few existing methods yield very low classification error rates when applied to this dataset (Fan and Lv, 2008; Zou and Hastie, 2005). One reason for including this dataset is to show that even though designed to detect interaction and module effects, the proposed method would not miss significant marginal effects either.
5 CONCLUSION
To deal with the tremendous complexity created by interactions among variables in high-dimensional data, the proposed method provides a flexible framework to extract different types of information from the data in three stages. First, variables are selected with high potential to form influential modules. The dimension of the data is drastically reduced in the first stage. Secondly, highly influential variable modules are identified from variables selected in the first stage. Since there is only a small number of variables in each variable module, the interaction and module effects can be accurately estimated by existing methods well-suited for low or moderate dimensional data. The third stage constructs classifiers and combining them into one final classification rule. The prediction errors of the proposed method outperform all other methods that ignore interactions. It also has the advantage in identifying relevant genes and their modules. In summary, our article is intended to send three messages: (i) classification rules derived from the proposed method will enjoy substantial reduction in prediction errors; (ii) influential variable modules with scientific relevance are identified in the process of deriving the classification rule and (iii) incorporating interaction information into data analysis can be very rewarding in generating fruitful scientific knowledge.
DATABASES
Gene-to-system breast cancer database: http://www.itb.cnr.it/breastcancer/php/browse.php#molecular_top
NCBI gene database: http://www.ncbi.nlm.nih.gov/gene
Breast cancer database: http://www.breastcancerdatabase.org/
Funding: Hong Kong Research Grant Council (642207 and 601312 in part to I. H.); NIH (R01 GM070789, GM070789-0551 and NSF grant DMS-0714669 in part to S-H. L. and T. Z.).
Supplementary Material
REFERENCES
- Agresti A. An Introduction to Categorical Data Analysis. New York: Wily; 1996. [Google Scholar]
- Beketic-Oreskovic L, et al. Prognostic significance of carbonic anhydrase IX (CA-IX), endoglin (CD105) and 8-hydroxy-2′-deoxyguanosine (8-OHdG) in breast cancer patients. Pathol. Oncol. Res. 2011;17:593–603. doi: 10.1007/s12253-010-9355-6. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate-a practical and powerful approach to multiple testing. JRSS B. 1995;57:289–300. [Google Scholar]
- Breiman L. Random forests. Mach. Learn. 2001;45:532. [Google Scholar]
- Carlborg O, Haley CS. Epistasis: too often neglected in complex trait studies. Nat. Rev. Genet. 2004;5:618–625. doi: 10.1038/nrg1407. [DOI] [PubMed] [Google Scholar]
- Chernoff H, et al. Discovering influential variables: a method of partitions. Ann. Appl. Stat. 2009;3:1335–1369. [Google Scholar]
- Cordell HJ. Detecting gene–gene interactions that underlies human diseases. Nat. Rev. Genet. 2009;10:392–404. doi: 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dash M, Liu H. Feature selection for classification. Intel. Data Anal. 1997;1:131–156. [Google Scholar]
- Dietterich TG. Ensemble methods in machine learning. In: Kittler J, Roli F, editors. First International Workshop on Multiple Classifier Systems, Lecture Notes in Computer Science.(.) New York: Springer; 2000. pp. 1–15. [Google Scholar]
- Efron B, et al. Empirical Bayes analysis of a microarray experiment. JASA. 2001;96:1151–1160. [Google Scholar]
- Fan J, Lv J. Sure independence screening for ultrahigh dimensional feature space (with discussion) J. R. Stat. Soc. Ser. B. 2008;70:849–911. [Google Scholar]
- Freund Y, Schapire R. A decision-theoretic generalization of online learning and an application to boosting. J. Comput. Sys. Sci. 1997;55:119–139. [Google Scholar]
- Golub TR, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- Guyon I, et al. Gene selection for cancer classification using support vector machine. Mach. Learn. 2002;46:389–422. [Google Scholar]
- Guyon I, Elisseeff A. An introduction to variable and feature selection. JMLR. 2003;3:1157–1182. [Google Scholar]
- Hall P. The Theory of Coverage Process. New York: Wily; 1988. [Google Scholar]
- Khan AI, et al. Negative epistasis between beneficial mutations in an evolving bacterial population. Science. 2011;332:1193–1196. doi: 10.1126/science.1203801. [DOI] [PubMed] [Google Scholar]
- Kooperberg C, et al. Structures and assumptions: strategies to harness gene x gene and gene x environment interactions in GWAS. Stat. Sci. 2010;24:472–488. doi: 10.1214/09-sts287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Yu L. Toward integrating feature selection algorithms for classification and clustering. IEEE Tran. Knowl Data Eng. 2005;17:491–502. [Google Scholar]
- Lo SH, Zheng T. Backward haplotype transmission association algorithm—a fast multiple-marker screening method. Hum. Her. 2002;53:197–215. doi: 10.1159/000066194. [DOI] [PubMed] [Google Scholar]
- Moore JH, Williams SM. Epistasis and its implication for personal genetics. Am. J. Hum. Gen. 2009;853:309–320. doi: 10.1016/j.ajhg.2009.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perou CM, et al. Molecular portraits of human breast tumours. Nature. 2000;406:747–752. doi: 10.1038/35021093. [DOI] [PubMed] [Google Scholar]
- Pinheiro C, et al. GLUT1 and CAIX expression profiles in breast cancer correlate with adverse prognostic factors and MCT1 overexpression. Histol. Histopathol. 2011;26:1279–1286. doi: 10.14670/HH-26.1279. [DOI] [PubMed] [Google Scholar]
- Saeys Y, et al. A review of feature selection techniques in bioinformatics. Bioinformatics. 2007;23:2507–2517. doi: 10.1093/bioinformatics/btm344. [DOI] [PubMed] [Google Scholar]
- Schwender H, Ickstadt K. Identification of SNP interactions using logic regression. Biostatistics. 2008;9:187–198. doi: 10.1093/biostatistics/kxm024. [DOI] [PubMed] [Google Scholar]
- Shao H, et al. Genetic architecture of complex traits: large phenotypic effects and pervasive epistasis. Proc. Natl Acad. Sci. USA. 2008;105:19910–19914. doi: 10.1073/pnas.0810388105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotiriou C, et al. Breast cancer classification and prognosis based on gene expression profiles from a population-based study. Proc. Natl Acad. Sci. USA. 2003;100:10393–10398. doi: 10.1073/pnas.1732912100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B. 1996;58:267–288. [Google Scholar]
- Tibshirani R, Efron B. Pre-validation and inference in microarray. Stat. Appl. Genet. Mol. Biol. 2002;1 doi: 10.2202/1544-6115.1000. Article 1. [DOI] [PubMed] [Google Scholar]
- van’t Veer LJ, et al. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B. 2006;68:49–67. [Google Scholar]
- Zawistowski JS, et al. KRIT1 association with the integrin-binding protein ICAP-1: a new direction in the elucidation of cerebral cavernous malformations (CCM1) pathogenesis. Hum. Mol. Genet. 2002;11:389–396. doi: 10.1093/hmg/11.4.389. [DOI] [PubMed] [Google Scholar]
- Zhang J, et al. Interaction between krit1 and icap1alpha infers perturbation of integrin beta1-mediated angiogenesis in the pathogenesis of cerebral cavernous malformation. Hum. Mol. Genet. 2001;10:2953–2960. doi: 10.1093/hmg/10.25.2953. [DOI] [PubMed] [Google Scholar]
- Zhang H, et al. Gene selection using support vector machine with non-convex penalty. Bioinformatics. 2006;22:88–85. doi: 10.1093/bioinformatics/bti736. [DOI] [PubMed] [Google Scholar]
- Zhu JX, et al. On selection bias with prediction rules formed from gene expression data. J. Stat. Plann. Infer. 2008;138:374–386. [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B. 2005;67:301–320. [Google Scholar]
- Zuk O, et al. The mystery of missing heritability: genetic interactions create phantom heritability. Proc. Natl Acad. Sci. USA. 2011 doi: 10.1073/pnas.1119675109. Early Edition, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


