Identifying Plausible Genetic Models Based on Association and Linkage Results: Application to Type 2 Diabetes

Abstract

When planning re-sequencing studies for complex diseases, previous association and linkage studies can constrain the range of plausible genetic models for a given locus. Here, we explore the combinations of causal risk allele frequency RAF_C and genotype relative risk GRR_C consistent with no or limited evidence for affected sibling pair (ASP) linkage and strong evidence for case-control association. We find that significant evidence for case-control association combined with no or moderate evidence for ASP linkage can define a lower bound for the plausible RAF_C. Using data from large type 2 diabetes (T2D) linkage and genome-wide association study meta-analyses, we find that under reasonable model assumptions, 23 of 36 autosomal T2D risk loci are unlikely to be due to causal variants with combined RAF_C < .005, and four of the 23 are unlikely to be due to causal variants with combined RAF_C < .05.

Introduction

Genome-wide association studies (GWAS) allow investigators to test for disease or trait (henceforward disease) association with common single nucleotide polymorphisms (SNPs) throughout the human genome. Today’s commercial GWAS platforms, when combined with genotype imputation [e.g. Marchini et al., 2007; Li et al., 2010], typically cover 80–90% of known common genetic variants (minor allele frequency (MAF) > .05). In recent years, GWAS have been conducted for many diseases [see http://www.genome.gov/gwastudies/]. The combined effects of associated variants often explain only a small proportion of the disease genetic variation [Manolio et al., 2009]. Results to date suggest that most common variants associated with complex diseases have modest effect on disease risk. Less common (.005 < MAF < .05) and rare (MAF < .005) variants have not yet been studied extensively and may (or may not) have larger effect sizes. With the recent advances in sequencing technology, it has become feasible to identify and genotype these variants. While multiple theoretical and data-driven approaches have examined genetic architecture of complex human diseases and traits [Risch and Merikangus, 2001; Reich and Lander, 2001; Pritchard and Cox, 2002; Purcell et al., 2009; Dickson et al., 2010; Anderson et al., 2011; Wray et al., 2011; Lee et al., 2011], our knowledge of their underlying architecture remains limited. Current and planned large-scale sequencing studies seek to address this issue.

Previous complex disease linkage studies generally reported limited evidence for linkage, and even in studies with strong linkage signals, most of the genome provides no evidence for linkage. These negative linkage results should limit the range of plausible effect sizes for disease risk variants and/or the cumulative frequency of risk variants. Similarly, evidence (or lack of evidence) for association in a region of interest should also limit the range of plausible models for these risk variant(s).

Existing association and/or linkage results together with simulations have been used by multiple groups to explore the likely genetic architectures underlying complex diseases. Purcell et al. [2009] showed that rare or less common causal variants are unlikely to be the sole explanation of schizophrenia genetic variation based on simulations to identify models that are consistent with GWAS results and heritability estimates. Similarly, the work of Wray et al. [2011] suggests that rare variants are unlikely to underlie a large proportion of GWAS associations as they would explain >100% of the heritability. Dickson et al. [2010] argued that many common variants identified in GWAS could reflect multiple less common (.005 < MAF_C < .02) causal variants in high linkage disequilibrium (LD); using the same models, Anderson et al. [2010] concluded that rare variants were unlikely to underlie most GWAS associated variants. Both studies provided graphical representations of the power of affected sib pair (ASP) linkage (with Anderson et al. assuming a much larger linkage sample) and SNP-disease association under limited number of models. However, they did not provide a quantitative way to define plausible models (minimum RAF_C, maximum GRR_C) for specified disease loci given the results of existing linkage and association studies.

In this paper, we seek to identify the plausible range of genetic models, in terms of genotype relative risk (GRR_C) and risk allele frequency (RAF_C), consistent with rare or less common causal variant(s) underlying a given disease association. We consider scenarios in which no or modest evidence for ASP linkage is reported, and/or significant evidence for association is reported. To do so, we calculate the power to detect ASP linkage and/or case-control association and summarize the range of genetic models that appears plausible given results from available linkage and/or association studies. Our results show that for each risk allele frequency RAF_C, the effect sizes GRR_C of causal variants are constrained byASP linkage or association results. When significant evidence for association is combined with no or modest ASP linkage evidence in the same chromosomal region, causal variants with small RAF_C can also be identified as implausible. In our calculations, we assume that a single causal variant underlies a common variant association, but our results can be extended to include multiple rare or less frequent tightly linked causal variants. Combining available T2D SNP-association[Zeggini et al., 2008; Voight et al., 2010; Dupuis et al., 2010; Qi et al., 2010] and linkage [Guan et al., 2008; unpublished results] results suggest that at least 23 of 36 autosomal T2D loci are unlikely due to single or cumulatively rare disease variants.

Methods

To understand the genetic architecture underlying a complex disease, we seek to identify a set of models that are plausible given prior results from ASP linkage and/or case-control association studies. We parameterize these models by the genotype relative risk (GRR_C) and risk allele frequency (RAF_C) of a causal variant C. We assume that the causal allele is the minor allele and is dominant, that the effects of the disease loci combine multiplicatively to determine disease risk, and that we have genotyped a sufficiently dense set of linkage markers that the identity by descent (IBD) relationship for the ASP can be observed. We assume a disease prevalence of 10%, and a standardized LD coefficient D′ = .6, .8, or 1 between the causal variant C and a nearby genotyped variant M. We discuss the impact of these assumptions in the Discussion.

Power to detect linkage in an ASP study

Let N_i be the number of ASPs sharing i = 0, 1, or 2 alleles IBD at the causal locus. Although the specified penetrance model at the causal locus is dominant, we calculate the usual additive model based maximum LOD score (MLS) [Risch, 1990]

$$\text{MLS}=\{\begin{array}{ll}({\text{N}}_1+2{\text{N}}_2){log}_{10}\left(\frac{{\text{N}}_1+2{\text{N}}_2}{\text{N}}\right)+({\text{N}}_1+2{\text{N}}_0){log}_{10}\left(\frac{{\text{N}}_1+2{\text{N}}_0}{\text{N}}\right)\hfill & \text{if}\frac{1}{2}{\text{N}}_1+{\text{N}}_2>\text{N}\hfill \\ 0\hfill & \text{if}\frac{1}{2}{\text{N}}_1+{\text{N}}_2\le \text{N}\hfill \end{array}$$

Given our assumption of a multiplicative relationship between causal loci, power to detect linkage using ASPs depends only on the locus-specific relative risks [Risch, 1990].

We calculate power to detect linkage for studies of N = 500, 1,000, and 5,000 ASPs and causalb variant RAF_C from. 001 to .05. We report results for MLS threshold values of 0 and 1, representing no or modest evidence for linkage, respectively. For a given RAF_C, we determine the value of GRR_C that results in 95% power to obtain MLS > 0 or 1, using the false position method [Press et al., 1992], an algorithm for root finding.

Power to detect association in a case-control study

We assume a GWAS with n cases and n controls. Let C be a causal variant in LD with a genotyped marker M. Let RAF_M be the risk allele frequency at M and g_C and g_M be the genotypes at C and M, coded as the number of risk alleles (0, 1, or 2). Given RAF_C, RAF_M, and D′, we calculate the conditional genotype probability P(g_C | g_M). For a specified genetic model and disease prevalence, we can then compute the penetrance of g_M:

$$\text{P}(\text{Y}\mid {\text{g}}_{\text{M}})=\sum _{{\text{g}}_{\text{C}}}\text{P}(\text{Y}\mid {\text{g}}_{\text{M}},{\text{g}}_{\text{C}})\text{P}({\text{g}}_{\text{C}}\mid {\text{g}}_{\text{M}})=\sum _{{\text{g}}_{\text{C}}}\text{P}(\text{Y}\mid {\text{g}}_{\text{C}})\text{P}({\text{g}}_{\text{C}}\mid {\text{g}}_{\text{M}})$$

which will determine the power of association test at a given locus. Under the dominant model, P(Y=1 | g_C=2) = P(Y=1 | g_C=1) = GRR_C × P(Y=1 | g_C=0). We exclude models with large GRR_C for which P(Y | g_C) > 1 for any genotype g_C. Here we assume a single causal variant C, but our results can easily be extended to multiple causal variants in the same region (see Discussion).

Although the specified penetrance model, P(Y | g_C), is dominant, we test for disease association at M using the additive-model version of the Cochran-Armitage trend test, as is typical in analysis of GWAS data. We calculate the power of the trend test by estimating the variance of the test statistic under the alternative hypothesis [Freidlin et al., 2002].

We calculate power to detect association assuming n = 1,000, 10,000, and 50,000 cases and the same number of controls and causal variant C and genotyped variant M frequencies .001 ≤ RAF_C ≤ .05 and .05 ≤ RAF_M ≤ .95. Given RAF_C and RAF_M, we calculate the GRR_C value that results in 5% power to detect disease association at M at genome-wide significance level α = 5×10⁻⁸ using the false position method.

LD in 1000 Genomes Project data

To assess the plausibility of our assumption that there exists a GWAS marker M in strong LD with the causal variant C, we evaluate the range of LD values between less common (.005 < MAF < .05) and common (MAF > .05) chromosome 1 variants identified in 283 European samples in the 1000 Genomes Project August 2010 release (http://www.1000genomes.org/). We first examine the distribution of maximum r² values for each less common variant among the less common variant-common variant pairs, and then examine the D′ values between the less common variant and common variant with the maximum r². We limit our attention to common variants within a 1000-SNP (~250kb) window of each less common variant.

Application to type 2 diabetes (T2D)

We illustrate how existing ASP linkage and case-control GWAS results provide information on plausible models for variants underlying complex diseases using results for type 2 diabetes. We carried out a joint analysis of data from 23 linkage studies as part of the International Type 2 Diabetes Linkage Analysis Consortium [Guan et al., 2008; unpublished results]. Here, we restrict our attention to an ASP linkage analysis of 6,552 individuals in 2,315 families of European ancestry, equivalent to ~4,200 ASPs, using the approximation that m affected siblings correspond approximately to m-1 independent ASPs [Hodge 1984]. In this study, the largest MLS was ~2.2, and for ~54% of the genome, MLS = 0. For T2D linkage results, we calculate power as above based on 4,200 ASPs, using the observed MLS from the linkage study at that location as the MLS threshold for power calculations [unpublished results].

Published European ancestry association studies of T2D have identified 36 autosomal T2D loci using standard case-control analysis (Table 1), most from GWAS. To place the T2D linkage and association results on the same map, we linearly interpolate positions for the 36 T2D-associated variants onto a genetic map of 2,164 microsatellite markers from our linkage analysis based on their physical positions in NCBI build 36.1. We identify the plausible genetic models at these 36 loci given the observed linkage and association results. At each locus we calculate power to detect linkage and association as above. To minimize possible overestimation of genetic effect owing to the “winner’s curse” (for example Zöllner and Pritchard, 2007), we use results from the largest available follow-up cohort when possible (28 variants), or alternatively from the largest available GWAS (8 variants where discovery samples are ~40% of the total sample). For T2D association results, we calculate power as described above, using the sum of the effective numbers of genotyped cases and controls in each study as sample size, the observed RAF_M in controls as the population allele frequency, and the observed association p-value as the significance threshold.

Table 1.

T2D susceptibility loci detected with common variants. RAF_C is a lower bound at which there is 5% power to detect association t observed p-value at marker M in a GWAS of the given effective sample size, and 95% power to detect linkage at the observed MLS value given 4,200 ASPs.

SNP	Nearby gene(s)	OR	p-value	MLS	Effective sample size	RAFM in controls	Min. RAFC	Max. GRRC	Reference*
rs1531343‡1	HMGA2	1.08	1.1×10−4	1.00	68314	0.10	<0.001	>4.1	Voight et al. (2010)
rs4607517‡2	GCK	1.07	5.0×10−8	0.88	94370	0.16	<0.001	>7.3	Dupuis et al. (2010)
rs8042680‡1	PRC1	1.06	1.6×10−6	0.82	79246	0.22	<0.001	>8.1	Voight et al. (2010)
rs10923931‡1	NOTCH2	1.11	1.9×10−3	0.00	32514	0.11	<0.001	>8.5	Zeggini et al. (2008)
rs7961581‡1	TSPAN8,LGR5	1.09	4.3×10−5	1.22	31364	0.27	<0.001	>9.8	Zeggini et al. (2008)
rs12779790‡1	CDC123, CAMK1D	1.09	1.5×10−4	0.00	31364	0.18	0.001	6.2	Zeggini et al. (2008)
rs4457053‡1	ZBED3	1.07	2.7×10−7	0.06	67214	0.26	0.002	6.0	Voight et al. (2010)
rs896854‡1	TP53INP1	1.05	2.2×10−5	0.05	67012	0.48	0.003	5.1	Voight et al. (2010)
rs11634397‡1	ZFAND6	1.05	1.2×10−5	0.69	79246	0.60	0.003	6.5	Voight et al. (2010)
rs10830963‡2	MTNR1B	1.09	8.0×10−13	0.14	94370	0.23	0.004	4.9	Dupuis et al. (2010)
rs4607103‡1	ADAMTS9	1.06	3.5×10−3	0.24	31364	0.76	0.004	5.0	Zeggini et al. (2008)
rs972283‡1	KLF14	1.06	6.4×10−6	0.35	56763	0.55	0.004	5.2	Voight et al. (2010)
rs2191349‡2	DGKB/TMEM195	1.06	1.1×10−8	0.74	94370	0.52	0.004	5.9	Dupuis et al. (2010)
rs864745‡1	JAZF1	1.10	1.3×10−7	1.09	31364	0.50	0.007	4.8	Zeggini et al. (2008)
rs7957197‡1	HNF1A	1.05	4.6×10−4	0.05	67751	0.85	0.009	3.4	Voight et al. (2010)
rs780094‡2	GCKR	1.06	1.3×10−9	0.27	94370	0.62	0.009	3.9	Dupuis et al. (2010)
rs340874‡2	PROX1	1.07	7.2×10−10	0.00	94370	0.52	0.010	3.0	Dupuis et al. (2010)
rs5215‡3	KCNJ11	1.09	1.6×10−5	0.01	22044	0.45	0.010	3.2	Voight et al. (2010)
rs243021‡1	BCL11A	1.08	6.2×10−11	0.09	64343	0.46	0.010	3.5	Voight et al. (2010)
rs1470579‡3	IGF2BP2	1.14	2.2×10−9	0.20	22044	0.30	0.010	3.6	Voight et al. (2010)
rs231362‡1	KCNQ1	1.07	3.2×10−9	0.00	73750	0.52	0.011	3.1	Voight et al. (2010)
rs9939609‡3	FTO	1.12	8.7×10−8	0.14	22044	0.38	0.011	3.4	Voight et al. (2010)
rs4430796‡1	HNF1B	1.12	1.6×10−4	0.00	13930	0.51	0.014	2.8	Voight et al. (2010)
rs7593730‡1	RBMS1	1.09	9.1×10−5	0.01	32172	0.77	0.021	2.5	Qi et al. (2010)
rs10010131‡1	WFS1	1.11	4.6×10−7	0.05	22044	0.60	0.026	2.5	Voight et al. (2010)
rs13292136‡1	CHCHD9	1.08	2.4×10−4	0.00	79246	0.93	0.029	2.3	Voight et al. (2010)
rs7578597‡1	THADA	1.12	9.2×10−5	0.18	32514	0.90	0.038	2.5	Zeggini et al. (2008)
rs7754840‡3	CDKAL1	1.18	3.1×10−15	0.00	22044	0.36	0.043	2.1	Voight et al. (2010)
rs7578326‡1	IRS1	1.10	2.2×10−15	0.00	67701	0.64	0.043	2.1	Voight et al. (2010)
rs13266634‡1	SLC30A8	1.15	1.5×10−8	0.11	20675	0.68	0.048	2.3	Voight et al. (2010)
rs1801282‡3	PPARG	1.15	8.0×10−6	0.11	22044	0.82	0.048	2.3	Voight et al. (2010)
rs1111875‡3	HHEX	1.17	9.1×10−15	0.18	22044	0.52	0.049	2.3	Voight et al. (2010)
rs7903146‡3	TCF7L2	1.40	2.2×10−51	0.08	22044	0.18	0.059	2.1	Voight et al. (2010)
rs11708067‡2	ADCY5	1.12	9.9×10−21	0.00	94370	0.78	0.090	1.8	Dupuis et al. (2010)
rs1552224‡1	CENTD2	1.14	3.2×10−18	0.09	79246	0.88	0.130	1.9	Voight et al. (2010)
rs10811661‡3	CDKN2A/B	1.19	1.4×10−10	0.00	22044	0.85	0.217	1.7	Voight et al. (2010)

^*Each locus had a single or multi-stage p-value < 5×10 . Some T2D-associated loci were reported in multiple references. We use results from the largest available follow-up cohort when possible (28 variants), or if not, from the largest available GWAS (which also contain the initial discovery samples) and list the estimated OR, p-values, and the effective sample sizes correspondingly.

^‡1Follow-up sample;

^‡2Top loci from a GWAS for fasting glucose were tested for association with T2D, equivalent to a candidate gene study;

^‡3GWAS meta-analysis including the discovery samples.

Results

Here we address the range of plausible model parameters (RAF_C and GRR_C) for rare or less common causal variants (RAF_C < .05), assuming a dominant genetic model for a genomic region given results from prior linkage and/or (common variant) association studies. To do so, we compute the power to detect linkage and/or association as a function of genetic model.

Range of plausible models given no or modest evidence for linkage

Complex disease linkage studies generally reveal no (MLS = 0) or modest (MLS ≤ 1) evidence for linkage for most of the genome. We explore the range of genetic model parameters consistent with these observations. Figure 1 displays values for GRR_C that result in 95% power to observe MLS > 0 or MLS > 1 given analysis of N = 500 to 5,000 ASPs as a function of risk allele frequency RAF_C.

Figure 1.

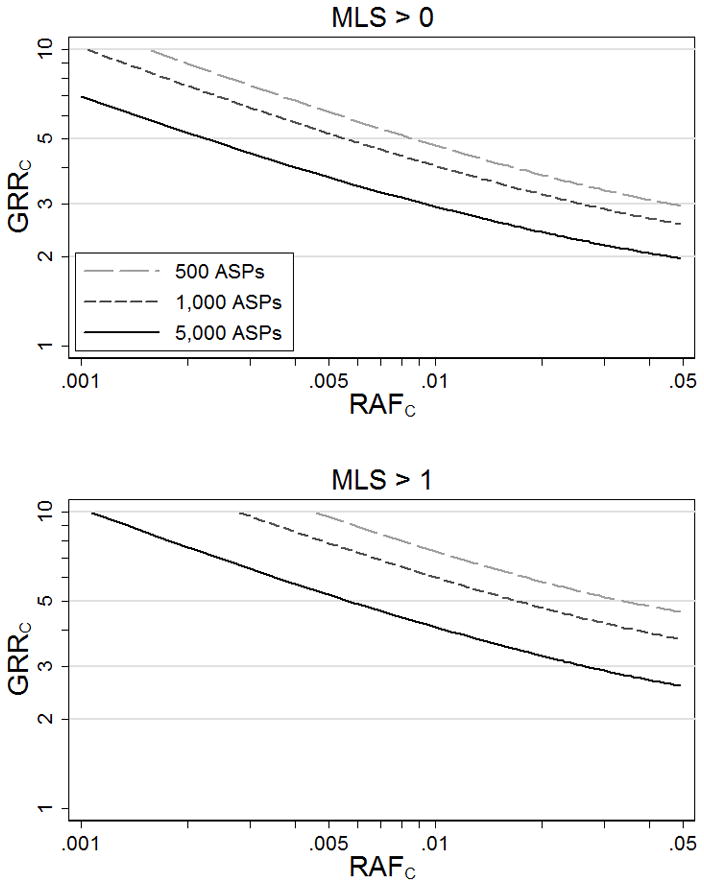
Genotype relative risks at causal variant C (GRR_C) that result in 95% power to detect some evidence for linkage at MLS > 0 and MLS > 1.

Assuming a causal variant exists, models (RAF_C, GRR_C) above the power curves in Figure 1A have ≥ 95% probability of showing at least some evidence for linkage (MLS > 0), and therefore such variants are unlikely to be present in a region with no evidence of linkage (MLS = 0). For example, given N = 5,000 ASPs, a causal variant with RAF_C = .01 and GRR_C > 2.9 or with RAF_C =.05 and GRR_C > 1.9 has ≥ 95% power to achieve MLS > 0, suggesting these models are unlikely at a locus with no evidence for linkage. Similarly, given N = 5,000 ASPs and MLS = 1, a causal variant with RAF_C = .01 is unlikely to have GRR_C > 3.9 (Figure 1B). As expected, all else being equal, the larger the linkage study sample, the more restricted the set of plausible models.

Range of plausible models given significant evidence for association

Genome-wide significant associations with common SNPs have been reported for many common diseases (http://www.genome.gov/gwastudies/). We explore the range of models (RAF_C, GRR_C) for which a disease association could be explained by a rare or less common causal variant(s). Figure 2 shows values of GRR_C that lead to 5% power to detect association (p < 5×10⁻⁸) at SNP M with RAF_M = .05–.95, assuming a study of n cases and n controls (n = 1,000 to 50,000) and D′= 1 between the genotyped variant M and causal variant C. Models below the power curves have < 5% probability of achieving such evidence for association for a genotyped variant M in high LD (D′ = 1) with the causal variant C. We have chosen 5% power so that a causal variant C with a small chance of underlying a common variant M association (based on GRR_C and RAF_C) will be considered as plausible, given the current 10s to 100s of associated loci for common diseases.

Figure 2.

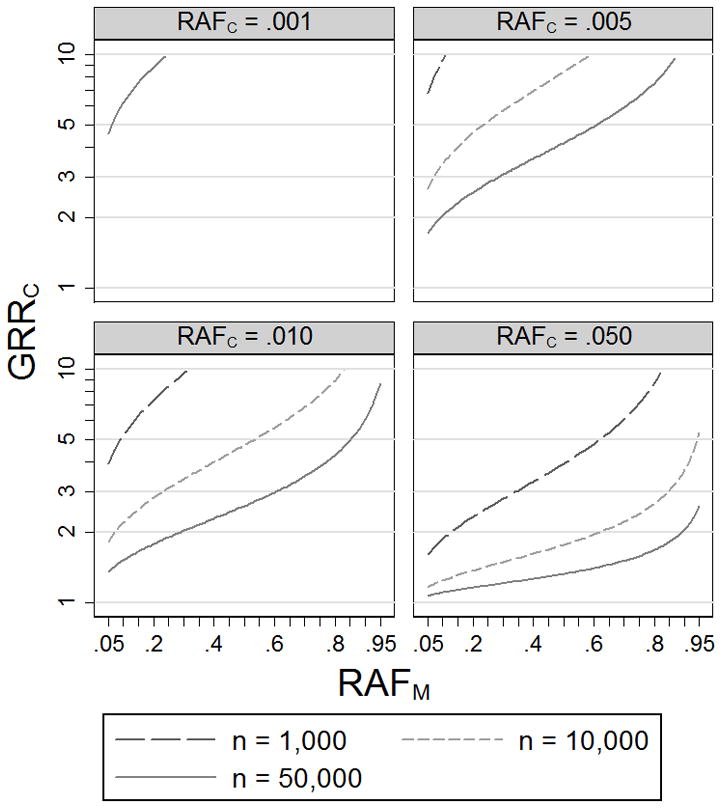
Genotype relative risks at causal variant C (GRR_C) that result in 5% power to detect association (p < 5×10⁻⁸) at genotyped variant M using n cases and n controls. We assume disease prevalence 10% and D′ = 1 between M and C.

For example, given n = 10,000 cases and 10,000 controls, a causal variant with RAF_C = .01 and GRR_C < 3.4 has < 5% power to achieve genome-wide significance (p < 5×10⁻⁸) at a genotyped variant M (D′ = 1) with RAF_M = .3, suggesting these models are unlikely to explain the corresponding association at M. Holding the significance level and sample size constant, a marker with larger GRR_M will yield a more limited set of plausible genetic models (Figure 2). We also estimate the plausible range of models assuming D′ = .8 or .6 between the causal variant C and genotyped variant M (Supplemental Figure 1). For a given significance level and RAF_C, a causal variant with D′ < 1 requires larger GRR_C to reach the same power as a causal variant with D′ = 1, resulting in a more limited set of plausible models.

Range of plausible models given results from association and linkage studies

For complex diseases for which both linkage and association scans have been carried out, we observe no evidence for linkage (MLS = 0) in most regions of the genome, and some of these regions may contain genome-wide significant association results (p < 5×10⁻⁸). Figure 3 A shows values of GRR_C that result in 5% power to detect association (p < 5×10⁻⁸) at genotyped variant M given n = 10,000 cases and n = 10,000 controls, and 95% power to detect at least some evidence for linkage (MLS > 0) given 1,000 ASPs, as a function of RAF_C, assuming D′ = 1 between the causal and common GWAS variant. The models above the 5% power curve for association but below the 95% power curve for linkage (shaded area in Figure 3) are consistent with strong evidence for association (p < 5×10⁻⁸) and no evidence for linkage (MLS = 0) at the corresponding position. Here, significant evidence for association (p = 5×10⁻⁸) and no evidence for linkage (MLS = 0) suggest RAF_C > .014.

Figure 3.

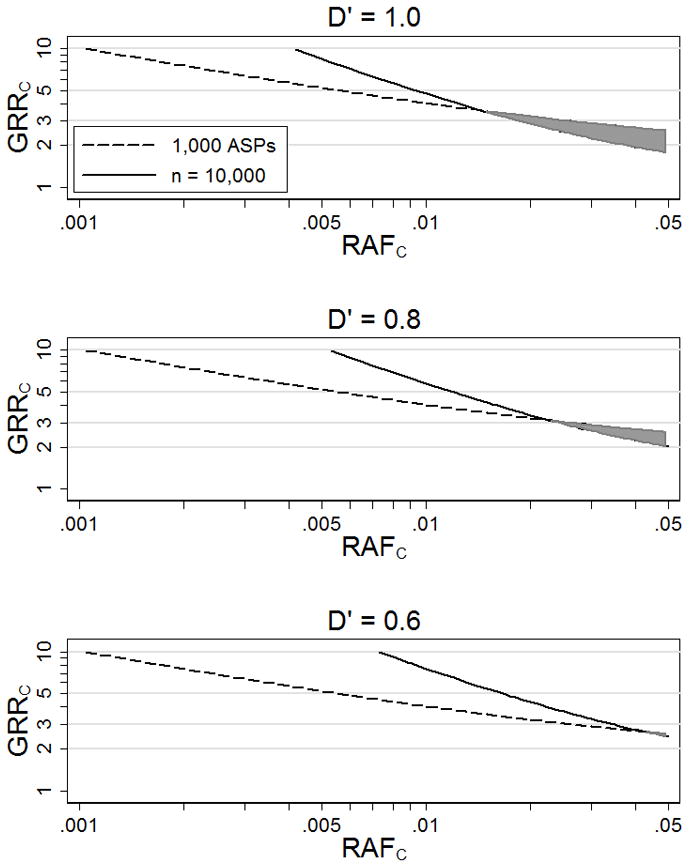
Genotype relative risks at causal variant C (GRR_C) that result in 95% power to detect some evidence for linkage (MLS > 0) using 1,000 ASPs and 5% power to detect association (p < 5×10⁻⁸) at genotyped variant M with RAF_M = .5 using n = 10,000 cases and n = 10,000 controls. The shaded area is the estimated range of plausible models. We assume disease prevalence 10% and D′ = 1, 0.8, and 0.6 between M and C.

Figure 3B and 3C shows values of GRR_C for D′ = .8 or D′ = .6 as a function of RAF_C that result in 5% power to detect association (p < 5×10⁻⁸) at genotyped variant M given n = 10,000 cases and n = 10,000 controls, and 95% power to detect some evidence for linkage (MLS > 0) given 1,000 ASPs. Again the shaded areas in the figures are consistent with strong evidence for association (p < 5×10⁻⁸) and no evidence for linkage (MLS = 0) at the corresponding position. In these scenarios, the range of plausible RAF_C values is more extensive than those for D′ = 1. For example, significant evidence for association (p = 5×10⁻⁸) and no evidence for linkage (MLS = 0) suggest RAF_{C >} .043 for D′ = .6 and RAF_C > .022 for D′ = .8 compared to RAF_{C >} .014 for D′ = 1.

Observed D′ and r² in 1000 Genomes data

In practice, the LD between an unidentified causal variant C and a common associated variant M is unknown. To explore the LD between common and less common and variants, we examine sequence data on 283 European subjects from the 1000 Genomes Project (http://www.1000genomes.org/). We calculate D′ and r² between 268,287 less common SNPs (.005 < MAF < .05) and 423,648 common SNPs (MAF > .05) on chromosome 1, limiting our attention to pairs of SNPs within ~250 kb of each other.

Given a causal variant in the region, the most strongly associated GWAS variant is expected to be the common GWAS variant in highest r² with the causal variant. For every less common 1000 Genomes Project SNP we identify the common 1000 Genomes SNP in highest r². We find that the best common pairing SNPs usually have RAF_M < .3 (Figure 4). We also find that 49% of the maximum r² SNP pairs have D′ = 1, 67% have D′ ≥ .8, and 88% have D′ ≥ .6, which suggests that an assumption of D′ = 1 between the common associated variant and the causal SNP would cause the bounds on RAF_C to be too wide about half the time.

Figure 4.

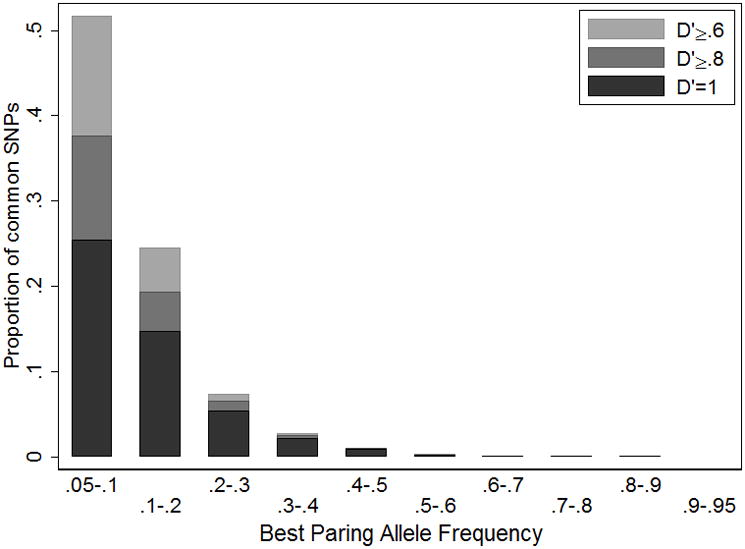
Frequency distribution of best pairing alleles for less common (.005 < MAF < .05) variants in 1000 Genome Project sequence data (August 2010 release). We define the best pairing alleles as having the highest r² but lowest minor allele frequency.

Example: type 2 diabetes (T2D)

Many linkage and association studies have been carried out for T2D. Perhaps the largest single linkage study was one based on the equivalent of 4,200 ASPs with European ancestry carried out by the International Type 2 Diabetes Linkage Analysis Consortium [Guan et al. 2008; unpublished results]. This study found no genome-wide significant evidence for linkage, and a maximum MLS genome-wide of ~2.2. In contrast, published GWAS and candidate gene association studies in European ancestry samples (through October 2011) have reported genome-wide significant association (p < 5×10⁻⁸) at 36 autosomal loci using the standard case-control test (Table 1, Figure 5). For these 36 T2D loci, we observe that higher MLS are modestly correlated with lower RAF_M (r = −.31, p= .06), suggesting that at least some of the linkage peaks may be detecting rare or less common underlying causal variants (Supplementary Figure 2). Likewise, 29 of the 36 T2D-associated SNPs are at positions with MLS > 0 (p-value = .0002 compared to an expectation of 50%, or p-value =.0009 compared to the observed proportion of 54%).

Figure 5.

T2D linkage maximum lod scores (MLS) from the International Type 2 Diabetes Linkage Analysis Consortium (families of European origin) (solid line) and significant T2D associations from various sources (Table 1) (diamonds).

Using the observed T2D linkage and association results, we estimate the range of plausible RAF_C (Table 1) assuming D′ = 1 between the causal variant and a common GWAS variant. Thirteen association signals could plausibly be explained by a very wide range of risk allele frequencies RAF_C including RAF_C < .005. Four of the five loci with the smallest plausible combined RAF_C (< .001) have modest evidence for linkage (0.82 < MLS < 1.22) and association RAF_M < .30. For the 23 other association signals, the associations are unlikely to be explained by one or more causal variants with combined RAF_C < .005, and for four of these (TCF7L2, ADCY5, CENTD2, CDKN2A/B), combined RAF_C < .05 is unlikely. In these regions, a GWAS study with a dense marker set with good coverage for variants with MAF > .01 might well result in the causal variant being genotyped or tagged by genotyped markers.

Discussion

We have sought to determine the range of disease models consistent with existing linkage and/or association results. Specifically, we have focused on determining the minimum plausible risk allele frequency RAF_C and corresponding genotype relative risk GRR_C for variants at a given locus assuming a single causal variant underlies an association signal. Our results show that a linkage study alone or an association study alone can restrict the plausible magnitude of GRR_C, while all RAF_C in the range we consider remain possible. Joint consideration of linkage and association results can further reduce the set of plausible models. In particular, at loci with significant evidence for association and no evidence for linkage, one or more causal variant(s) with a low summed risk allele frequency may be implausible.

To calculate the power for linkage and association tests, we have made several assumptions. First, we assume that only a single causal variant C exists in the region of interest in our power calculation. If multiple causal variants are present within the region, the linkage signal will reflect the combined effects of all causal variants. Using linkage results alone, our estimates of the causal allele frequency would approximately correspond to the sum of the risk allele frequencies; individual causal variants could be much rarer. In contrast, the impact of multiple variants on a given common association signal is more complex as the observed signal will only reflect the causal variants in LD with the tested common allele. Wang et al. [2010] and Dickson et al. [2010] have described scenarios where multiple rare causal variants could contribute to an apparent common variant association, a phenomenon they termed “synthetic association” (Wang et al. [2010]). If all causal alleles occur on haplotypes with the associated common allele, the synthetic causal marker will have a D′ = 1 with the common associated marker. In contrast, if the causal alleles occur on haplotypes with and without the associated allele, the synthetic causal marker will have a D′ < 1 with the common associated marker. These two scenarios described above are analogous to the ones shown in Figure 3A and B. If p-value = 5 × 10⁻⁸ is observed for a common marker and the underlying synthetic causal marker has a D′ = .8 with the common marker, analysis assuming a D′ = 1 (Figure 3A) will yield a lower estimate of the minimum plausible cumulative RAF_C than analysis under the true model of D′ = .8 (Figure 3B) (RAF_C of .014 vs .022 in this scenario). Thus, as in the case of a single causal marker, we will underestimate the lower bound of RAF_C assuming D′ = 1. Estimates of minimum plausible cumulative RAF_C for multiple causal variants under different assumptions of D′ can be used to construct more realistic simulations of multiple rare variants RAF_C and GRR_C. This will aid in the estimation of the power of burden tests (e.g. Li and Leal, 2008) for given regions.

Second, we assume a dominant model at each disease locus. Since we focus on models with uncommon or rare risk variants, risk allele homozygotes are rare, and so dominant, additive, and multiplicative models are essentially equivalent. A recessive model would result in very rare homozygotes and is not considered. Third, we assume the minor allele of variant C is causal. If instead the minor allele is protective, associations detected with high frequency RAF_M might be inconsistent with rare risk causal variants but consistent with rare protective variants. Fourth, for linkage, we assume fully informative markers. If the markers are not fully informative, our estimation results would give a smaller range of plausible models (higher RAF_C and lower GRR_C). All our assumptions, except for the assumptions of known IBD in linkage studies and no winner’s curse for the association results (see below), are conservative in the sense that they should result in less strict bounds on our model parameters: the minimum plausible RAF_C would be higher and/or the maximum plausible GRR_C would be lower if the assumptions are violated.

We explore plausible models for 36 T2D variants identified by large-scale association studies in European ancestry populations in combination with results from a T2D linkage study based on the equivalent of ~4,200 ASPs. Our results suggest that 23 of the 36 association signals are unlikely to have been caused by causal variants with combined RAF_C < .005, and four of these are unlikely to have been caused by causal variants with combined RAF_C < .05. Multiple assumptions underlie these results. We assume that D′ = 1 between the causal variant and the associated variant. This assumption will yield the widest range of plausible models, as it assumes that all of the causal alleles are on the same haplotype as the common risk allele. In the 1000 Genomes Project data, 51% of the maximum r² variant pairs have D′ < 1 so our estimates for the plausible range of models may be too wide for these loci. For example, for the CDC123/CAMK1D locus the minimum plausible MAF_C is .001 with D′ =1 and .004 for D′= .6. The majority of the significance thresholds used in our calculations are based on results from follow-up samples. However, for eight variants the discovery samples make up ~40% of the effective association sample size and our results could be impacted by the “winner’s curse”. This could cause overestimation of the strength of the association, and thus our estimate of the minimum plausible RAF_C maybe too high. This concern is balanced by our use of a fairly conservative 5% power to detect the observed association which may have caused us to underestimate the MAF_C and overestimate GRR_C for some loci. To explore the sensitivity of the minimum MAFC and maximum GRRC estimates to the set power thresholds, we repeated our analysis using 50% power for association (i.e. assuming the observed OR is the true effect size rather an overestimate of the true effect size) and 80% power for linkage (Supplementary Table 1). As expected, we found a greater number of loci that were inconsistent with the cumulatively rare causal variants. Specifically, we found that 30 (compared to 23) of the 36 association signals are unlikely to have been caused by causal variants with combined RAFC < .005, and 14 (compared to 4) of these are unlikely to have been caused by causal variants with combined RAFC < .05. For one association signal (CDKN2A/B) no plausible model could be found under this assumption, due to the large value of RAF_M and strong evidence for association but no evidence for linkage. Under either set of power assumptions, our results suggest that the causal variant(s) for many T2D loci may already have been detected by the 1000 Genomes and other sequencing projects. However, even for these loci, re-sequencing may be useful to identify other independent disease variants. For the other loci for which the summed frequency of causal variants may be < .005, sequencing studies may be particularly important for variant detection, since such uncommon variants may not have been identified in existing catalogues.

In summary, we estimate ranges of plausible genetic models based on results from association and/or linkage studies for complex diseases. Given no or modest evidence for linkage in a region of interest, we can estimate an upper bound on the GRR_C of potential rare or less common variants. Similarly, in the presence of association with a common genotyped variant, we can estimate a lower bound on the GRR for the causal variant. Taken together, significant evidence for association and no or modest evidence for linkage allow a joint estimate of a lower bound for MAF_C and upper bound for GRR_C. Our approach provides a useful starting point for modeling genetic architecture of complex diseases and has allowed us to identify T2D loci more likely to be caused by common variants. The knowledge of plausible genetic models for a given region will aid in estimating the power of burden tests(for example Li and Leal, 2008) for a given sample size and sequencing depth, and will allow more efficient design and interpretation of sequencing studies. Software to carry out this sort of analysis is available (in Stata code) at http://www.biostat.umn.edu/~wguan/software/.

Supplementary Material

Supplementary figure 1-1

Supplemental Figure 1. Genotype relative risks at causal variant C (GRR_C) that result in 5% power to detect association (p < 5×10⁻⁸) at genotyped variant M using n cases and n controls. We assume disease prevalence 10% and D′ = .6 and .8 between M and C.

Supplementary figure 2

Supplemental Figure 2. T2D linkage maximum lod scores (MLS) at the loci identified in T2D association analyses. The x-axis is the risk allele frequency (RAF_M) of T2D-associated SNPs.