A statistical modeling approach for detecting generalized synchronization

Abstract

Detecting nonlinear correlations between time series presents a hard problem for data analysis. We present a generative statistical modeling method for detecting nonlinear generalized synchronization. Truncated Volterra series are used to approximate functional interactions. The Volterra kernels are modeled as linear combinations of basis splines, whose coefficients are estimated via l1 and l2 regularized maximum likelihood regression. The regularization manages the high number of kernel coefficients and allows feature selection strategies yielding sparse models. The method's performance is evaluated on different coupled chaotic systems in various synchronization regimes and analytical results for detecting m:n phase synchrony are presented. Experimental applicability is demonstrated by detecting nonlinear interactions between neuronal local field potentials recorded in different parts of macaque visual cortex.

I. INTRODUCTION

Many natural systems generate complex collective dynamics through interactions between their component parts. A prominent example is the transient neural dynamics of the brain which presumably involve strong functional couplings between cortical regions. Determining the nature of such interactions is not easy. At the most general level, the problem is one of detecting generalized synchronization [16] between time series x(t) and y(t). That is, detecting the existence of a functional, potentially nonlinear, time delayed or other stable relationship such that y(t) = F[x](t) is predictable. Strictly speaking, generalized synchronization results from interactions between systems that create stable attractors in their total phase spaces, i.e. given x(t) the response system y has to be stable. Lag and other forms of synchronization are subsets of this problem, and systems may transition from phase, via lag, to complete synchronization as coupling strengths increase [14].

When the interactions are nonlinear, or the coupled systems themselves complex or chaotic [8, 18], standard linear methods, such as cross correlation or coherency, may not be able to detect an interaction. Nonlinear methods are therefore necessary. Existing approaches are usually based on reconstructing the phase space of the underlying system by finding an appropriate time-delay embedding [20]. Recent methodologies include the Joint Probability of Recurrence (JPR) method [10]. JPR is based on the evaluation of trajectory recurrence probabilities in small neighborhoods of the reconstructed phase space. The JPR is mathematically similar to another technique, the Synchronization Likelihood [19], which is derived from generalized mutual information concepts and popular in neuroscientific research areas. Although JPR and SL can detect nonlinear synchronization in many data sets (see e.g. [9, 13, 17]), it can be hard to determine the appropriateness of the embedding space. Further, such methods do not yield information about the functional form (nonlinearity) of the interaction.

Here we propose a different approach, directly estimating a functional which describes nonlinear interactions between two time series x(t) and y(t). In particular, we predict time series y(t) from x(t) using a Volterra series operator F on x(t). The kernels of F are expanded using a set of basis functions, the coefficients of which fit using maximum posteriori regression. After obtaining an estimated signal y_E = F[x] the degree to which y can be predicted from x is determined by computing the correlation coefficient r(y_E, y) on an independent validation data set. Modeling F using a Volterra series is a canonical choice, since Volterra series are well-known for their versatility in nonlinear system identification (see e.g. [15],[3]). They allow F to approximate arbitrary continuous functionals and flows of many non-autonomous dynamical systems, in particular systems with memory. The existence of non-zero second order or higher terms indicates nonlinear interactions. Furthermore, in agreement with the stability condition of generalized synchronization, a steady-state theorem for Volterra series (see [3]) asserts that for x(t) → x_s(t) within the radius of convergence of F, the response system is stable, i.e. F[x](t) → F[x_s(t)](t) as t → ∞.

We call F the Functional Synchrony Model (FSM) and apply our method to several coupled chaotic systems for which generalized nonlinear synchronization is known to exist. We recover the nonlinear interactions with much greater accuracy than with either linear approaches, or the JPR method. We also demonstrate the existence of nonlinear coupling between local field potentials recorded in macaque visual cortex during stimulation by natural scenes movies.

Interactions between time series $x,y\in {\mathbb{R}}^N$ are modeled using a truncated Volterra series operator of order n with a history dependence (memory) of K time steps:

$$yE\left(t\right)=F\left[x\right]\left(t\right)=\sum _{j=0}^n{Y}_{j,K}\left(t\right),$$ (1)

where Y_j is the j^th order Volterra functional

$$Y_{j,K}\left(t\right)=\sum _{k_1=0}^K\cdots \sum _{k_j=0}^K{h}_j(k_1,\dots ,k_j)x(t-k_1)\cdots x(t-k_j).$$ (2)

Restrictions of this model form, particularly for modeling m:n phase synchronization are discussed below. To flexibly capture a wide variety of interactions, we expand the Volterra kernels h_j in a set of basis functions B = {b_m(k) |m = 1, …..,M} as

$$h_j(k_1,\dots ,k_j)=\sum _{m_1=1}^M\cdots \sum _{m_j=1}^M{\tilde{a}}_j(m_1,\dots ,m_j)b_{m_1}\left(k_1\right)\cdots b_{m_j}\left(k_j\right),$$ (3)

with parameters ${\tilde{a}}_j(m_1,\dots ,m_j)\in \mathbb{R}$. Inserting eq. (3) into (2), we yield

$$Y_{j,K}=\sum _{m_1=1}^M\cdots \sum _{m_j=1}^M{\tilde{a}}_j(m_1,\dots ,m_j){\varphi }_{m_1,\dots ,m_j}.$$ (4)

Denoting ${\tilde{x}}_n=\left\{x\right(n-K),x(n-(K-1)),\dots ,x(n\left)\right\}$, the ϕ_m1,…..,mj are nonlinear basis functions in ${\tilde{x}}_n$ that constitute the covariates of our model, given by

$${\varphi }_{m_1,\dots ,m_j}=\sum _{k_1=0}^K\cdots \sum _{k_j=0}^K{b}_{m_1}\cdots b_{m_j}x(n-k_1)\cdots x(n-k_j).$$ (5)

The covariates are symmetric in {m₁, ….., m_j}, i.e. for all permutations π(m₁, ….., m_j), ϕ_{π(m1,…..,mj)} represents the same covariate and can be factored out in the model, yielding new coe cients a_j (as sums of the former ${\tilde{a}}_j$) and a corresponding reduction in summation indices

$$Y_{j,K}=\sum _{m_1=1}^M\sum _{m_2\ge m_1}^M\cdots \sum _{m_j\ge m_{j-1}}^M{a}_j(m_1,\dots ,m_j){\varphi }_{m_1},\dots ,m_j.$$ (6)

Furthermore, the covariates can be factored out into products of simple convolutions,

$$\begin{array}{cc}\hfill {\varphi }_{m_1,\dots ,m_j}\left({\tilde{x}}_n\right)& =\left(\sum _{k_1=0}^K{b}_{m_1}\left(k_1\right)x(n-k_1)\right)\hfill \\ \hfill & \cdots \left(\sum _{k_j=0}^K{b}_{m_j}\left(k_j\right)x(n-k_j)\right)\hfill \\ \hfill & ={\varphi }_{m_1,\cdots {\varphi }_{m_j}}.\hfill \end{array}$$ (7)

Consequently, all higher order covariates are simply products of 1^st order covariates ϕm_i.

In this paper we expand the kernels using cubic basis splines. This basis spans a vector space of piecewise polynomial functions with smooth nonlinearities, and is uniquely determined by a knot sequence τ_K on the memory interval [0,K]. Using the de Bohr algorithm [2] on τ_K, all basis splines are fully specified and can be constructed recursively. The first order functional is thus given by a linear combination of basis splines, corresponding to a piecewise polynomial operating on x(t) as a finite impulse response filter. Higher order kernels weight monomials of x, e.g. x(t −k₁)x(t−k₂), which intuitively represent interactions between different points t−k_j in time. Other bases, for example wavelets, could of course have been used.

Regardless of the basis chosen, the final model in eq. (6) is linear with respect to the coefficients a_j. Thus the coefficients can easily be determined by maximum likelihood based linear regression. Indexing all covariates and coefficients in eq. (6) and eq. (1) with the set [1, ….., A], we define a design matrix for time series $x,y\in {\mathbb{R}}^N$ as

$$\Phi \left(x\right)=\left(\begin{array}{cccc}\hfill {\varphi }_1\left({\tilde{x}}_1\right)\hfill & \hfill {\varphi }_2\left({\tilde{x}}_1\right)\hfill & \hfill \cdots \hfill & \hfill {\varphi }_A\left({\tilde{x}}_1\right)\hfill \\ \hfill {\varphi }_1\left({\tilde{x}}_2\right)\hfill & \hfill {\varphi }_2\left({\tilde{x}}_2\right)\hfill & \hfill \cdots \hfill & \hfill {\varphi }_A\left({\tilde{x}}_2\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\varphi }_1\left({\tilde{x}}_N\right)\hfill & \hfill {\varphi }_2\left({\tilde{x}}_N\right)\hfill & \hfill \cdots \hfill & \hfill {\varphi }_A\left({\tilde{x}}_N\right)\hfill \end{array}\right)\in {\mathbb{R}}^{N\times A}$$ (8)

and a vector of coefficients $\mathbf{a}\in {\mathbb{R}}^A$. We can now state a linear regression problem with nonlinear basis functions as Φ(xa = y.

$$\Phi \left(x\right)\mathrm{a}=y.$$

To select a sparse set of relevant coefficients and ensure the model generalizes to validation data, we use Elastic Net regularization, interpolating l₁ − l₂ norm with a hyperparameterβ [5]. Interpreted in a Bayesian maximum posteriori framework, changing the interpolation and regularization effectively changes the assumed prior distribution of model coefficients. While the l₁ norm corresponds to an isometric Laplace prior, the l₂ norm is normally distributed. As a result, the l₁ norm promotes sparse coefficient vectors, assuming few independent covariates carry most of the information, whereas the l₂ norm is known to foster clusters of correlated covariates. After fitting the model to training data, we test its generalizability by using it to predict an independent validation data set. Model accuracy is judged using the correlation coefficient between the signal and the prediction. Our statistical framework would also allow other goodness of fit measures, such as Akaike information criterion or likelihood based cross validation, to be used.

II. RÖSSLER-LORENZ SYSTEM

To study the performance of our method in a setup of two unidirectionally coupled nonidentical systems, we first consider a Rössler system driving a Lorenz system, which is a standard benchmark in the literature. We will also use this example to walk through the fitting procedure in detail. The equations of the drive system are

$$\begin{array}{cc}\hfill {\stackrel{.}{x}}_1& =2+x_1(x_2-4),\hfill \\ \hfill {\stackrel{.}{x}}_2& =-x_1-x_2,\hfill \\ \hfill {\stackrel{.}{x}}_3& =x_2+0.45x_3,\hfill \end{array}$$ (9)

while the response system is given by

$$\begin{array}{cc}\hfill {\stackrel{.}{y}}_1& =-\sigma (y_1-y_2),\hfill \\ \hfill {\stackrel{.}{y}}_2& =\mathit{ru}\left(t\right)-y_2-u\left(t\right)y_3,\hfill \\ \hfill {\stackrel{.}{y}}_3& =u\left(t\right)y_2-{\mathrm{by}}_3,\hfill \end{array}$$ (10)

where u(t) = x₁ + x₂ + x₃. With σ = 10, r = 28, $b=\frac{8}{3}$, the driven Lorenz system is asymptotically stable [8] and thus in a regime of generalized synchronization with the Rössler system.

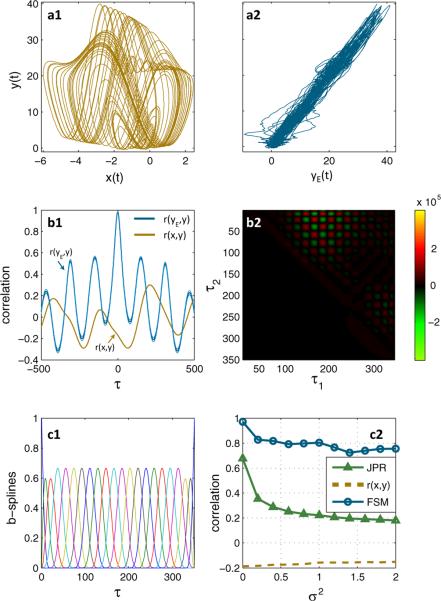
The systems' third coordinates x₃, y₃ are chosen as time series x(t), y(t) respectively, with 10000 data points sampled at Δt = 0.02. The linear correlation coe cient is r(y, x) = −0.168, corresponding to the projection of the complex generalized synchronization manifold onto (x₃, y₃), shown in figure 1a₁. We try to predict y(t) as y_E(t) = F [x](t) with a 2^nd order Volterra series model F. To fully specify the model, we merely need to choose a knot sequence τ_K over a memory interval of K time steps. By visual inspection of the time series, K = 350 is chosen to span at least a full period of both systems. Accordingly, τ_K is chosen to cover the interval [0, 350] with 22 equidistantly spaced knots, each corresponding to the onset of the nonzero compact carrier of a particular cubic basis spline. A density of 22 splines is deemed sufficient for our model to capture the variations in the signals x(t), y(t). The resulting set of basis splines is shown in figure 1c₁. We can now construct a design matrix (eq. 8) with 10000 × 276 entries, where A = 276 denotes the number of covariates, consisting of a 0 order constant, as well as 22 1^st order and 253 2^nd order covariates, as given by eq. (6). Using an isometric normally distributed prior distribution of coefficients (β = 0.01), we assume all covariates share a similar amount of information. Accordingly, using a mild regularization parameter λ = 0.001 the feature selection procedure finds 275 covariates to be constitutive for our model y_E = F[x].

FIG. 1.

(Color online) Identification of nonlinear interaction in a coupled Rössler-Lorenz system. a1): Nonlinear synchronization manifold between original sampled data x and y (the systems' 3^rd coordinates) in generalized synchronization with correlation r(x, y) = −0.168. a2: Linearized manifold between yE and y, where yE(t) = F[x](t) is the output of a 2^nd order Volterra model, yielding r(yE, y) = 0.98. b1) Delay-shifted (by τ) correlation coeffcients. b2) 2^nd order kernel corresponding to a2). c1) Set of cubic b-splines corresponding to b2), used in eq. (3). c2) Performance of the method (FSM, r(yE, y) ∈ [−1, 1]) for Rössler-Lorenz system with additive white noise over increasing variance σ², compared against correlation r(x, y), as well as the JPR ∈ [0, 1].

The model fit yields a correlation coefficient r(y, y_E) = 0.98 on an independent validation set of size 10000. Thus, generalized synchronization is detected with perfect accuracy. Moreover, the resulting model is fully predictive with respect to y(t). Figure 1a₂ shows that our method “linearized” the synchronization manifold. The lag correlation plot in figure 1b₁ shows the correlation of the two signals as a function of varying delay shift τ between the signals, where τ = 0 corresponds to r(y, y_E) = 0.98. The periodic relationship between the two chaotic oscillators is apparent. Figure 1b₂ depicts the 2^nd order Volterra kernel, i.e. the nonlinear aspects of the model that are necessary to capture the interaction. Here, the periodicity is also present, in form of alternations across the diagonal. While the regularization produced only two local clusters of covariates as main constituents of the model, the very regular weighting within the clusters reflects the assumptions encoded in the coefficient prior. Note that due to the symmetry of the kernels (see eq. (6)) only the “upper triangular” part of (τ₁, τ₂) space is populated by model covariates. Adding additional white noise to the data, our method also shows a strong noise robustness across an increasing variance σ² (fig. 1c₂).

To compare our method against the JPR, we chose embedding space parameters producing results on this data set comparable to [10]. The JPR is clearly outperformed and suffers greatly from the additive noise (fig. 1c₂). These effects may be countered by increasing the ∊-neighborhoods in which the recurrence probabilities are evaluated, however, lacking any goodness-of-fit measure for the parameter set this may also increase the number of false positives and render the results meaningless.

III. MACKEY-GLASS NODES

Our second example involves generalized synchronization between delay-coupled Mackey-Glass nodes described by the equation

$${\stackrel{.}{x}}_i\left(t\right)=\frac{2x_{i-1}(t-{\tau }_d∕n)}{1+x_{i-1}{(t-{\tau }_d∕n)}^9}-x_i\left(t\right),{\tau }_d=300$$ (11)

The data is sampled from a ring containing up to n = 16 Mackey-Glass nodes, displaying chaotic dynamics, where node i receives delay-coupled input from node i−1, with a total delay of τ_d = 300 in the whole ring. The existence of generalized synchronization for the case of x_i driving x_i−n/2 can be demonstrated using the auxiliary systems approach [1].

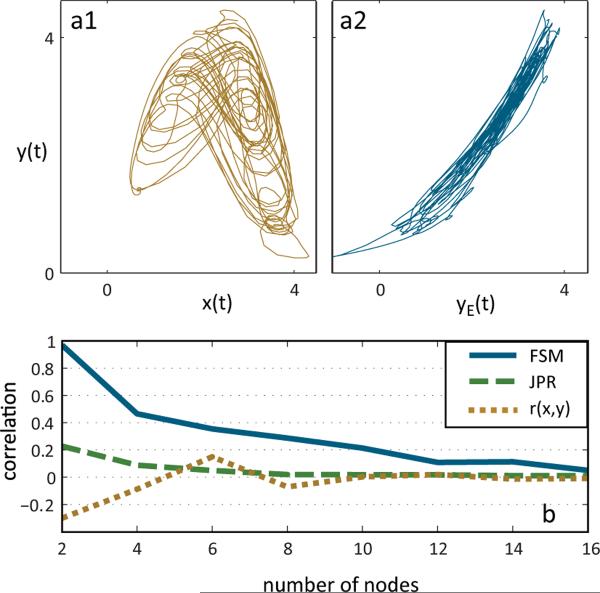
Figure 2a shows the delay-embedded chaotic attractor (nonlinear synchronization manifold, brown) of two coupled Mackey-Glass nodes, where driving time series x(t) correspondes to node x_i, and target y(t) corresponds to x_i−n/2. The blue graph shows the transformation to a linear manifold after application of our method. We use a 2^nd order model, with non-uniform knot sequence τ_K supporting local maxima in the autocorrelation function of the Mackey-Glass ring that occur due to the system's delay-feedback. In total, 28 b-splines are used to cover the interval [0, 350], encompassing the total delay-time τ_d in the ring. With β = 0.99, feature selection yields a sparse set of 158 predictive covariates that we apply to data sets of size 30000 or higher. While detection is possible with less than 10000 data points, yielding a fully predictive model on this complex data set needs more data to generalize and capture the strong nonlinear components of the interaction.

FIG. 2.

(Color online) Performance on generalized synchronized Mackey-Glass delay rings. a1): Nonlinear time-embedded GS manifold of ring with two nodes x and y. a2): Linearized synchronization manifold between y_E (2^nd order model) and y. b) Results for Mackey-Glass rings of varying size. Shown are prior correlation in data (r(x, y), dashed), JPR (light dashed) and our method (FSM, solid) using Volterra series models up to order 3.

Figure 2b summarizes the resulting correlation r(y_E, y) (blue) for functional Volterra series models of order j ≤ 3. Performance is plotted against an increasing number n of nodes in the ring. A fully predictive model is found for n = 2, while detection of significant nonlinear interaction (significance determined using bootstrapped confidence intervals) is still possible for n ≤ 16, where no linear correlation r(x, y) is measurable in the data. In comparison, the JPR (dashed green line) failed to detect the interaction in rings larger than n = 2 for all tested embedding space and recurrence parameters which we chose manually as well as automatically using mutual information and false nearest neighbours criteria. Note, however, that much less data points (up to 10000) could be used for the recurrence based method, which draws heavily on computational resources since it has to compute an N × N recurrence matrix (where N is the number of delay-embedded data points) for both time series.

IV. COUPLED RÖSSLER SYSTEMS

Our third example application is to two identical coupled Rössler systems, described by the equations

$$\begin{array}{cc}\hfill {\stackrel{.}{x}}_{1,2}& =-{\omega }_{1,2}{y}_{1,2}-z_{1,2},\hfill \\ \hfill {\stackrel{.}{y}}_{1,2}& ={\omega }_{1,2}{x}_{1,2}+0.16y_{1,2}+\mu (y_{2,1}-y_{1,2}),\hfill \\ \hfill {\stackrel{.}{z}}_{1,2}& =0.1+z_{1,2}(x_{1,2}-8.5).\hfill \end{array}$$ (12)

We use ω₁ = 0.98, ω₂ = 1.02 corresponding to a phase coherent regime of the two slightly dissimilar chaotic oscillators. These coupled three dimensional systems exhibit a wide range of synchronization dynamics as a function of the coupling strength μ [11], transitioning from an unsynchronized regime to complete synchronization via (1:1) phase synchronization as μ is increased from 0 to 0.15.

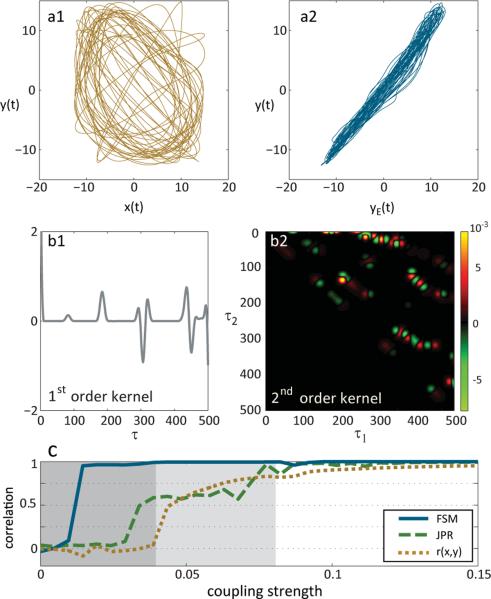
Using the first coordinates (x₁, x₂) as the driving (x) and target time series (y) respectively with 15000 data points sampled at Δt = 0.02, we can detect nonlinear interaction even for very weak coupling (μ = 0.034) with a 2^nd order model and a memory of 500 time steps, encompassing a full period of the nonlinear oscillators. Lacking further information about the interaction, we choose a dense equidistant knot sequence for 52 cubic b-splines. Consequently, many covariates will contribute only little information to the model. This is accounted for by imposing strong regularization and choosing a sparse prior for feature selection (β = 0.99), resulting in a total of 109 informative covariates for the model.

At μ = 0.034, x and y lie on a highly complex manifold (fig. 3a₁) and the correlation coefficient between x and y is zero. Our Volterra series approach ”linearizes” the synchronization manifold between the model prediction and the data (fig. 3a₂) and accurately describes the functional interaction, yielding r(y_{E, y}) = 0.97. Figure 3b shows the corresponding first and second order Volterra kernels. Both kernels are highly sparse, and strong quadratic interactions between x(t) at different times during the memory period prove necessary to predict y(t). The interaction can, in fact, be described over a broad range of coupling strengths, as demonstrated in Figure 3c. The method yielded fully predictive models for nearly all μ as indicated by correlation coefficients r(y_{E, y}) near 1 for μ ∈ [0, 0.15].

FIG. 3.

(Color online) Identification of nonlinear interaction between coupled Rössler systems. a1): Nonlinear synchronization manifold between original sampled data x and y (the systems' 1^st coordinates) at onset of phase synchronization (μ = 0.034) with correlation r(x, y) ≈ 0. a2): Linearized manifold between y_E and y, where y_E(t) = F[x](t) is the output of a 2^nd order Volterra model, yielding r(y_E, y) = 0.97. b1) 1^st order kernel corresponding to a2). b2) 2^nd order kernel corresponding to a2). c) As μ increases, the system transitions from unsynchronized, via phase (μ > 0.04) to generalized chaotic synchronization (μ > 0.08). Performance of the method (FSM, r(y_E, y) ∈ [−1, 1]) for various coupling strengths μ is compared to correlation of the raw data r(x, y), as well as the JPR ∈ [0, 1].

V. PHASE SYNCHRONY

A drawback of the current formalism is that Volterra series impose restrictions for modeling phase synchrony. By definition, two nonlinear oscillators x, y are phase synchronized if for their phases ϕ_i it holds that |nϕ_x−mϕ_y| < ∊, with n, $m\in \mathbb{Z}$, $∊\in \mathbb{R}$. The generative model may thus have to scale ϕ_x by a fraction to yield ϕ_y. In theory, Volterra series cannot achieve this, as a result of the periodic steady state theorem [3]: Periodicity present in x(t) must reoccur in the Volterra series F[x](t). The case of n:1, however, is possible by increasing the frequency of the input signal by a factor n, retaining the orginal slower periodicity in the resulting faster signal.

To illustrate the Volterra series response to a single frequency component of an oscillatory signal, consider for example the harmonic complex oscillation u(t) = α_ke^iωkt. The truncated Volterra series response breaks down into the components of the kernel functions, given by the covariates specified in eq. (7). Higher order covariates are products of 1^st order covariates ϕ_m which constitute linear time-invariant systems such that u(t) is an eigenfunction. Consequently, ϕ_m[u](t) = e^iωkt α_kH_m(iωk), where H_m(iωk) is the frequency response of ϕ_m given by the discrete Laplace transform of the corresponding 1^st order kernel basis function b_m. For an n^th order covariate Φ⁽ⁿ⁾ it follows that

$$\begin{array}{cc}\hfill {\Phi }^{\left(n\right)}\left[u\right]\left(t\right)& ={\varphi }_{m_1}\left[u\right]\left(t\right){\varphi }_{m_2}\left[u\right]\left(t\right)\cdots {\varphi }_{m_n}\left[u\right]\left(t\right)\hfill \\ \hfill & =\underset{\tilde{H}\left(\omega \right)}{\underbrace{{\alpha }_k^n{H}_{m_1}\left(i\omega k\right)\cdots H_{m_n}\left(i\omega k\right)e^{{\left(i\omega k\right)}^n}}}\hfill \\ \hfill & =\tilde{H}\left(\omega \right)e^{\mathit{in}\omega \mathit{kt}}.\hfill \end{array}$$ (13)

Hence, the phase dynamics of u(t) are scaled by a factor n, which suggests that an n^th order Volterra series operator can account for n:1 phase synchronization.

We confirmed this hypothesis using white noise jittered cosines (σ² = 0.4) with n:1 phase relationships for n ≤ 5. All models were fully predictive with r(y_{E, y}) ≈ 1. Following [4], we also applied the method to two identical Rössler systems coupled in a drive-response scenario and locked in 4:1 phase synchronization. The drive oscillator is described by

$$\begin{array}{cc}\hfill {\stackrel{.}{x}}_1& =-y_1-z_1,\hfill \\ \hfill {\stackrel{.}{y}}_1& =x_1+0.15y_1,\hfill \\ \hfill {\stackrel{.}{z}}_1& =0.2+z_1(x_1-10).\hfill \end{array}$$ (14)

The response oscillator is governed by

$$\begin{array}{cc}\hfill {\stackrel{.}{x}}_2& =-y_2-z_2+80\left(r_2\cos \right(\frac{n}{m}{\varphi }_1)-x_2),\hfill \\ \hfill {\stackrel{.}{y}}_2& =x_2+0.15y_2,+80\left(r_2\sin \right(\frac{n}{m}{\varphi }_1)-y_2)\hfill \\ \hfill {\stackrel{.}{z}}_2& =0.2+z_2(x_2-10).\hfill \end{array}$$ (15)

with phase and amplitude defined as

$$\begin{array}{cc}\hfill {\varphi }_1& =\arctan \left(\frac{y_1}{x_1}\right),\hfill \\ \hfill r_2& ={(x_2^2+y_2^2)}^{1∕2}.\hfill \end{array}$$ (16)

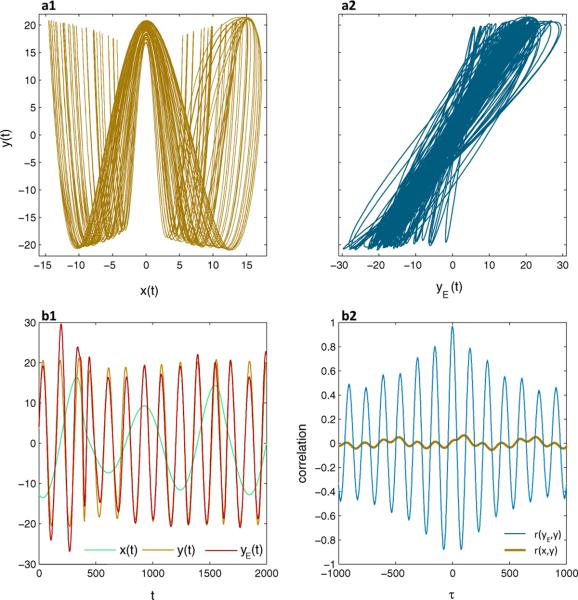
The phase synchronization was verified for m = 4, n = 1 by checking the frequency locking condition ΔΩ_4:1 = 4Ω₁ − ω₂ < 10⁻⁶, where Ω_i = 〈ϕ〉 for i = 1, 2 the mean frequency averaged over 80.000 data points sampled at Δt = 0.01.

Using the first coordinates x₁, x₂ as time series x(t), y(t) with 30000 data points each (fig. 4a₁) we fit a 4^th order model F[x](t) = y_E(t). We set β = 0.95 to enforce sparse solutions since it is expected that a few 4^th order features are most informative. An equidistant knot sequence with 14 knots in [0, 1000] is chosen to cover at least one full amplitude of each system. The feature selection process yields 117 mostly 4^th order covariates. The resulting model is fully predictive with r(y_{E, y}) = 0.97, as compared to r(x, y) = 0.02 in the original signals, and clearly captures the periodicity, as can be seen in the delay-shifted correlation coefficient plot (fig. 4b₂). Figure 4b₁ shows original time series x(t), y(t) in comparison to the prediction y_E(t) plotted against time t. We compare this result against the recurrence based phase synchronization index CPR ∈ [0, 1] [10], which essentially quantifies the coincidence of maxima in two generalized autocorrelation functions for x and y and represents a complimentary tool to the JPR. Our best result for a particular choice of parameters yields CPR = 0.5 on a corresponding data set of size 5000. The low index is explained by the fact that for phase synchronization with m, n ≠ 1, fewer coincidences of maxima in the generalized autocorrelation functions of x, y occur.

FIG. 4.

(Color online) Identification of interaction between unidirectionally coupled Rössler systems in 4:1 phase synchronization (eq. 15). a1): Nonlinear synchronization manifold projected onto first coordinates x₁, x₂ of the two systems (brown). a2): Linearized synchronization manifold after application of a 4^th order Volterra series operator (blue). b1): Time domain plots of original signals x(t) (green (light gray)) and y(t) (orange (gray)) compared to the 4^th order model prediction y_E(t) (red (dark gray)). b2): Delay-shifted (by τ) correlation plots of original signals r(x, y) (brown, thick) and model performance r(y_E, y) (blue, thin). Bootstrapped confidence intervals are shown as dashed lines in light blue.

VI. LOCAL FIELD POTENTIALS (LFPS) IN MACAQUE VISUAL CORTEX

Finally, we demonstrate the applicability of our method to noisy and unprocessed data from biological systems. To this end, we apply our method to LFP data recorded from electrodes located in macaque primary visual cortex (V1).

The monkey was watching a short (2.8 sec) natural scenes movie with 600 repetitions (for details about the experimental setup, see [7]). V1 is retinotopically organized, so the different electrodes recorded signals generated by neuronal populations receiving input from distinct parts of the visual field. However, it has been hypothesized that there are strong lateral interactions between different parts of V1 which combine information about different parts of the visual stimulus. We use our methodology to detect nonlinear interactions between electrode signals with near zero linear correlation coefficient. In particular, recordings of pairs of analyzed channels were made from the opercular region of V1 (receptive field centers 2.0° to 3.0° eccentricity) and from the superior bank of the calcarine sulcus (10.0° to 13.0°eccentricity), respectively. The distance regarding the receptive field position is therefore of the order of 7° eccentricity and thus much larger than the receptive field sizes of the projection neurons. Therefore, the populations recorded by both channels have no common bottom-up input.

No significant interactions could be detected prior to stimulus onset. Post stimlus onset we analyzed both the induced potential (IP, unaltered LFP recordings) and the evoked potential (EP, the signal average across all trials). Here, the EP signals contained 2800 data points (the length of one experimental trial) in both, validation and training set. These were obtained by randomly selecting subsets of several hundred trials for averaging. IP data sets were substantially larger as time series from individual experimental trials were chosen randomly to be concatenated and used as a single data set.

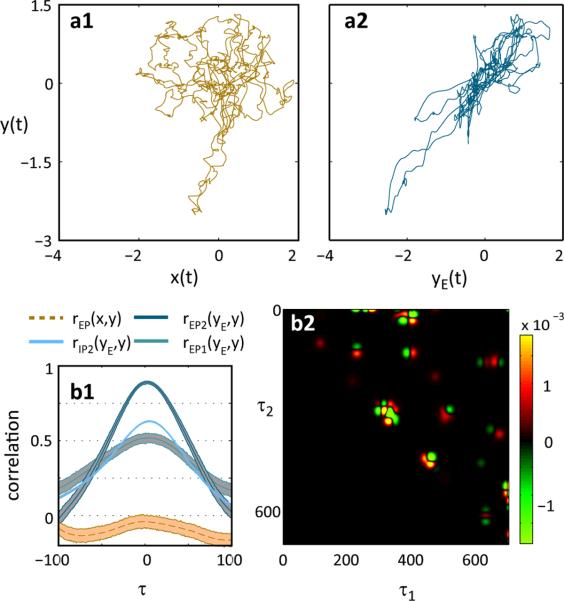
In Figure 5b₁ we use the LFP of one electrode (x), to predict the LFP of another (y) at various time lags, and show the resulting performance of our method. The data shown has close to zero linear correlation between the two LFPs (lag 0) for both EP (r_EP (x, y)) and IP (not shown). In contrast, the correlation coefficient between the model prediction and LFP is substantial, for both the IP (r_IP2(y_E, y)) and the EP (r_EP2(y_E, y)). Performance was substantially improved when second order models were used, indicating significant nonlinear interactions. This can be seen by comparing the performance of the 2^nd order model for predicting the EP (r_EP2(y_E, y) ≈ 0.89) with a first order model (r_EP1(y_E, y) ≈ 0.53). The second order interactions (Volterra kernel) are visualized in figure 5b₂. Figure 5a shows the corresponding interaction manifolds of the EP tetrode signals x and y (brown) which is clearly linearized by the method (blue). Similar results were obtained using other LFPs from both this, and a different monkey. Although it is known that the neuronal populations generating the two LFPs are directly stimulated by different parts of the visual field, our result that there are strong nonlinear interactions between the populations suggests that V1 neurons may combine information from different parts of the visual field. While the possibility of spatial correlations in the natural scene stimulus causing the synchronization (due to a common factor) is not directly discernable in this setup, we have nonetheless shown that our method could present a powerful tool to investigate these phenomena, as the result would not have been detectable by linear methods.

FIG. 5.

(Color online) Two macaque V1 LFP recordings x and y recorded from electrodes with different retinotopy. a) Interaction manifolds of the EPs. a1: Nonlinear manifold between x and y. a2: Linearized manifold corresponding to r_EP2(y_E, y) in b1). b1) Lagged correlation coefficient between EPs of x and y (r_EP (x, y)), and between a 1^st order (r_EP1(y_E, y)) and 2^nd order (r_EP2(y_E, y)) model y_E = F[x] and predicted tetrode y. For the IPs correlations are shown between a 2^nd order model y_E and y (r_IP2(y_E, y)). Lighter coloured areas show the bootstrapped confidence intervals of the respective models. b2) Shows the 2^nd order kernel.

VII. CONCLUSION

In summary, we have presented a statistical modeling framework for the detection of nonlinear interactions between time series. Interactions are modeled as Volterra series expanded in basis functions and fit using l1 and l2 regularized maximum likelihood. The method is computationally efficient and yields sparse analytic models of the interaction which generalize to new data. When compared to the Joint Probability of Recurrence method (CPR respectively) our approach showed higher detection capabilities (often close to fully predictive) for all tested data and synchronization regimes. This was despite our carefully evaluating different JPR (CPR) embedding-space parameters, both manually and algorithmically selected (false nearest neighbours, mutual information criteria) and only comparing the best results with our method. While our main goal is the detection of generalized synchronization, we showed analytically and experimentally how the method generalizes to m:n phase synchronization, the detection of which represents a hard problem in nonlinear data analysis.

One drawback of the current formalism is that it does not capture auto-structure from the target signal y(t). Perhaps more critically, the Volterra series operator cannot model m:n phase synchronization in rare cases of both m, n > 1. Both auto-structure and full m:n phase synchronization could be captured by also fitting a second Volterra functional G[y], so that F [x](t) − G[y](t) = 0. Using nonlinear synchronization as a formalization of complex interactions is intriguing with respect to information processing in the brain where oscillatory and synchronization phenomena are frequently reported [21]. Theoretical studies [12] also show the existence of generalized partial synchronization in a variety of artificial neural networks. In this context, Volterra series could be a natural model of neural transient interactions [6].