Abstract
The quantum yield of tryptophan (Trp) fluorescence was measured in 30 designed miniproteins (17 β-hairpins and 13 Trp-cage peptides), each containing a single Trp residue. Measurements were made in D2O and H2O to distinguish between fluorescence quenching mechanisms involving electron and proton transfer in the hairpin peptides, and at two temperatures to check for effects of partial unfolding of the Trp-cage peptides. The extent of folding of all the peptides also was measured by NMR. The fluorescence yields ranged from 0.01 in some of the Trp-cage peptides to 0.27 in some hairpins. Fluorescence quenching was found to occur by electron transfer from the excited indole ring of the Trp to a backbone amide group or the protonated side chain of a nearby histidine, glutamate, aspartate, tyrosine or cysteine residue. Ionized tyrosine side chains quenched strongly by resonance energy transfer or electron transfer to the excited indole ring. Hybrid classical/quantum mechanical molecular dynamics simulations were performed by a method that optimized induced electric dipoles separately for the ground and excited states in multiple π–π* and charge-transfer (CT) excitations. Twenty 0.5-ns trajectories in the tryptophan's lowest excited singlet π–π* state were run for each peptide, beginning by projections from trajectories in the ground state. Fluorescence quenching was correlated with the availability of a CT or exciton state that was strongly coupled to the π–π* state and that matched or fell below the π–π* state in energy. The fluorescence yields predicted by summing the calculated rates of charge and energy transfer are in good accord with the measured yields.
Keywords: charge-transfer transition, dipole moment, electron transfer, electrostatic interactions, fluorescence quenching, polarizable force field, protein folding, resonance energy transfer, spectroscopy
Introduction
Tryptophan fluorescence is widely used to probe changes in protein structure because of its sensitivity to interactions of the excited indole ring with the surroundings. The quantum yield of fluorescence from proteins containing a single Trp residue ranges from less than 0.01 in a mutant of the disulfide oxidoreductase DsbA to 0.31 in ribonuclease T1 and apo-azurin.1 Unraveling the factors that underlie this variation has remained a challenge because the quantum yield reflects competition of fluorescence with several different processes, each with its own complex dependence on the surroundings.
Barkley and coworkers have examined quenching of the fluorescence of 3-methylindole (3MI) by amino acid derivatives in solution.2 They found that the free amino group of glycine, the side-chain amino group of N-acetyllysine, and the phenolic side chain of N-acetyltyrosine quenched 3MI fluorescence by transfer of a proton to the excited indole ring. This process results in H-D exchange on three carbons of the indole ring, and is slowed by a factor of 2 to 4 if the solvent H2O is replaced by D2O.2a, 2c Derivatives with a thiol (N-acetylcysteine) or amide group (N-acetylglutamine and N-acetylasparagine), a peptide bond (N-acetylglycinamide) or a protonated imidazole (N-acetylhistidine at pH 5.3) or carboxylic acid group (acetic acid at pH 4.7) quench the fluorescence of 3MI by a different mechanism that involves electron transfer from the excited indole to the quencher.2a, 2c This quenching is not sensitive to deuteration of the solvent, but correlates with the electron affinity of the quencher and with the rate of reaction with hydrated electrons. Fluorescence quenching in indole derivatives by electron transfer to a peptide bond, carboxylic acid or protonated histidine also was described in early work of Cowgill,3 Shinitzky and Goldman,4 Steiner and Kirby,5 and Ricci and Nesta.6 More recently, Qiu et al.7 have observed fast fluorescence quenching in mutants of myoglobin and other proteins with a single Trp residue introduced near a Gln, Glu or Cys residue or a cystine disulfide group. Molecular-dynamics simulations suggested that the quenching in these proteins depends on structural fluctuations that bring an electron acceptor close to the benzene ring of the excited indole. Fluorescence quenching by a protonated His residue has been studied in barnase,8 and used to assay the folding of helical peptides9 and a subdomain of the protein villin.10
Callis and coworkers1c, 11 have emphasized quenching by electron transfer from the indole ring to amide groups in the protein backbone. They used hybrid quantum mechanical– molecular mechanics (QM-MM) simulations to calculate the energy and coupling matrix elements for this process in a series of 17 proteins. Low fluorescence yields were correlated with charge-transfer (CT) states close in energy to the indole's lowest excited state. One of the peptide bonds formed by the Trp residue itself usually appeared to be the most favorable electron acceptor, but electron transfer to a His or the side-chain amide of an Asn residue was calculated to be more favorable in two cases. There was no apparent correlation between the fluorescence yield and the calculated electronic coupling factor for charge transfer, indicating that this factor probably is less critical than the energetics of the reaction in most cases.11a
Although the correlation between experimental and calculated quantum yields suggests that their basic thesis is sound, Callis et al.1c, 11 found that optimizing the agreement required an ad hoc shift of the calculated CT energies relative to the energy of the excited state. The necessary shift depended on the electron acceptor. Even with this adjustment, there were multiple cases in which the predicted yield was considerably higher or lower than observed. Such discrepancies could reflect structural differences between the computational model and the protein that was studied experimentally, limited sampling of conformational space during the MD trajectories, simplifications in the treatment of quantum mechanical or dielectric effects or in relating energy differences to rates of electron transfer, or neglect of resonance energy transfer or other quenching mechanisms such as proton transfer. For example, some of the experimental data represented mutant proteins in which other Trp residues had been replaced by Phe to obtain a single fluorophore, possibly resulting in differences from the crystal structure that was used for the simulations. Capturing these structural changes during short MD simulations could be difficult. Calculations of electrostatic energies are challenging even for proteins with unambiguous structures, because of the complex dielectric effects of the surrounding protein and solvent.12
To address some of these issues, we have studied three series of designed peptides containing a single Trp whose surroundings can be changed systematically. The peptides lend themselves well both to experimental studies and to QM-MM simulations that include explicit induced dipoles and extend over the nanosecond time scale of fluorescence. The prototype of the first series is the β-hairpin peptide Ac-WVTIpGKKIWTG-NH2,13 where “p” denotes D-proline and “Ac-” and “-NH2” denote acetyl and amide caps. NMR and amide H/D-exchange experiments have shown this peptide to be 99% folded at 280 K and 96% folded at 320 K.13 Replacing one of the two Trp residues (Trp10) by Phe gave a hairpin that was almost as stable (∼88% folded at 320 K and ∼93% at 280 K), and further substitution of Ala for Lys8 also left the stability essentially unchanged.13a Figure 1A shows an NMR structure of the analog with His at position 8 (Ac-WVTIpGKHIFTG-NH2), in which the sidechains of His8 and Phe10 flank the indole ring of Trp1. Substitutions at positions 8 and 10 thus can be used to explore how the fluorescence of Trp1 depends on the presence of an acceptor or donor for electrons or protons, or on shifts in the energy of electron transfer to the backbone. It also is possible to leave Trp10 in place and substitute Phe for Trp1 instead, although the resulting peptide (Ac-FVTIpGKKIWTG-NH2) is somewhat less well folded.13a
Figure 1.
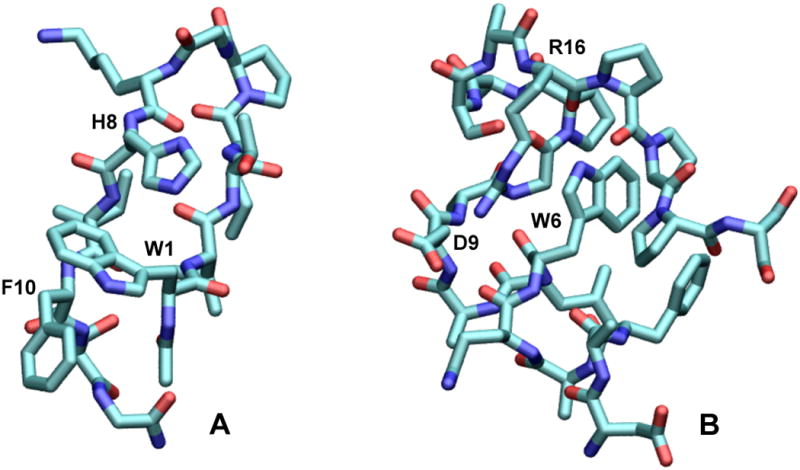
Structures of (A) the β-hairpin peptide Ac-WVTIpGKHIFTG-NH2 and (B) the Trp-cage peptide DAFAQWLADaGPASaRPPPs. The structure in A is one of an ensemble of NMR structures solved in the present work (see below and Supplementary Figure S5); the structure in B was generated by replacing Tyr3 by Phe in an NMR structure of Trp-cage 16b (DAYAQWLADaGPASaRPPPs).14
The second and third series of peptides are based on the α-helical “Trp-cage” peptides DAYAQWLADaGPASaRPPPS (Trp-cage 16b, where “a” denotes D-alanine) and DAYAQWLKDGGPASGRPPPS (the Ser13Ala variant of Trp-cage 10b).14 TrpCage 16B is almost completely folded at room temperature, having a melting temperature of 356 K. Replacing Tyr3 by Phe to simplify the fluorescence gave DAFAQWLADaGPASaRPPPS (Figure 1B) and DAFAQWLKDGGPASGRPPPS, with little effect on the stability. The ionizable residues Asp9 and Arg16 of the Trp-cage peptides can be modified in ways that might be expected to change the electric fields in the vicinity of Trp6. Lysine 8 of Trp-cage 10b also can be modified, although its side chain probably is too far from the Trp to have much effect.
Methods
Peptide Preparation and Structures
Peptides were synthesized using 9-fluorenylmethoxycarbonyl-protected amino acids on an ABI 433A peptide synthesizer, acetylated on the resin with 4.3% triethylamine and 3% acetic anhydride in dimethylformamide, released by shaking the resin with trifluoroacetic acid with 2.5% water and 2.5% triisopropylsilane, and purified by reverse-phase HPLC.13 Sequences were confirmed by NOESY connectivities, and purity by positive-ion mass spectrometry with a Bruker Esquire ion trap spectrometer. NOE, NOESY and CD (circular dichroism) spectra were obtained and analyzed as previously described.13-14
Fluorescence Measurements
Lyophilized peptides were dissolved in 10 mM potassium phosphate buffer to final concentrations of ∼3 to 20 μM. Absorption spectra were measured with a Shimadzu UV-1601 spectrophotometer and fluorescence with a Perkin-Elmer LS-50 B fluorimeter. Emission spectra were corrected for the wavelength dependence of the instrument using tyrosine, tryptophan and fluorescein standards.15 All measurements were made at 295 K except for those on the Phe10His, Phe10Leu and Phe10Trp/Trp1Phe hairpins, which were found by NMR to be less stable than the other peptides at room temperature and so were measured at 285 K. Most of the Trp-cage peptides were measured at both temperatures. Fluorescence emission spectra were recorded from 300 to 450 nm with excitation at 280 nm for all peptides except those containing tyrosine. For measurements of the fluorescence yield at neutral pH, the Tyr8 and Tyr10 hairpin peptides were excited at 295 nm, where absorption by tyrosine was negligible. For pH titrations of their fluorescence, the Tyr8 and Tyr10 peptides were excited at the isosbestic point for the tyrosine residue and its anion (281 ± 5 nm for Tyr8 and 285 ± 4 nm for Tyr10), so as to keep the fraction of the light absorbed by tryptophan (82.3% at 281 nm and 87.4% at 285 nm, based on the relative absorbances of standard Trp and Tyr solutions) essentially constant.
Absolute quantum yields were calculated as
| (1) |
where ϕ, F and A are the quantum yield, integrated emission intensity, and tryptophan absorbance at the excitation wavelength, and subscripts pep and std denote the peptide and a standard compound with a known fluorescence yield. The value reported is the mean of the yields calculated using tryptophan and tyrosine as standards (ϕstd = 0.13 and 0.14, respectively)16 and averaged over at least three samples of each peptide and three independent measurements on each sample.
Solvent isotope effects were expressed as the ratio kq(H2O)/kq(D2O), where kq(H2O) and kq(D2O) denote rate constants for fluorescence quenching in H2O and D2O, respectively. The quenching rate constant is related to the fluorescence yield by
| (2) |
where kf is the radiative rate constant and ϕ0 is the fluorescence yield in the absence of the quenching process described by kq. We assume that kf is the same for all the peptides and is independent of the solvent. The isotope effect then is
| (3) |
To evaluate isotope effects on the pH-dependent quenching by residues with ionizable side chains, we took ϕ0 to be the quantum yield in the pH region where the side chains are fully deprotonated (pH > 6.0 for Asp and Glu, pH > 9.0 for His and pH > 10.0 for Orn). For Tyr and Cys, we used ϕ0 = 0.2475, the mean ϕ0 for the eight hairpin peptides with N-acetylTrp at position 1 and non-quenching residues at positions 8 and 10 (either Ala, Asn, Gln, ε-N-acetyl-Lys, Lys, cyclohexyl-Ala, or Ser at position 8, and Phe or Leu at 10). (See below.) Absolute values of kq were obtained by setting kf = 6.11×107 s−1, which was calculated from the yield and lifetime of fluorescence from Trp in solution.16b
QM-MM simulations
Molecular-dynamics (MD) simulations were carried out with a program (ENZYQ) that used a modified version of the classical ENZYMIX force field12b, 17 and the Beeman18 algorithm to update all the coordinates, velocities and interatomic forces. Atomic charges also were treated classically, except for a portion of the system where the charges were evaluated quantum mechanically using QCFF-PI,19 a semi-empirical Hartree-Fock program for π electrons. The full system consisted of a peptide surrounded by 1060 to 1070 flexible, 3-point water molecules.20 The quantum subsystem for the hairpin peptides typically included the side chain and backbone atoms of the Trp residue, 8 to 10 backbone atoms of the adjacent residues (e.g., the N-terminal acetyl cap and the C, O, CA and HA atoms of Val2 in the case of a peptide with Trp at position 1), the side chain and backbone atoms of a potentially quenching residue (e.g., His8), the contiguous backbone atoms of the 21 residues on either side of this residue, the C and O atoms of Ile9, and the N, H, CA and HA atoms of Phe10. The quantum subsystems for the Trp-cage peptides consisted of the side chain and backbone atoms of Trp6, and the C, O and N atoms of the amide groups on the amino sides of prolines 17, 18 and 19. (Enlarging the Trp-cage quantum systems to include the H, CA and HA atoms of the amides had only minor effects on the calculated energies.)
Long-range electrostatic energies and forces were treated by using a multipole expansion of the atomic charges for groups of atoms separated by more than a specified distance.21 We used the multipole treatment for peptide groups that were more than 12 Å apart, and for interactions of water molecules separated by more than 20 Å. Trajectories were propagated in 1-fs steps, and the multipole expansion and the pair list for interactions of non-bonded atoms were updated every 40 steps. As described in more detail in the Supplementary Information, quadratic pseudopotentials were used to constrain the water molecules in the model to a sphere with the proper density, keep the center of mass of the peptide at the center of the sphere, and hold the net angular momentum of the water at zero.
Fields from the charges and induced dipoles of all the atoms were evaluated at each step of the simulation. The summed contributions of fields from non-quantum atoms to the potentials at the π atoms were sent to QCFF-PI for incorporation in the diagonal terms of the Fock matrix. QCFF-PI constructed the Fock matrix, solved the self-consistent field equations, diagonalized the configuration-interaction (CI) matrix for a specified number of configurations (typically ∼100 single excitations for a π system that included the side chains and amide groups of the Trp and a His or Tyr residue), and returned the charges of the quantum subsystem in a specified electronic state. These charges then were used in the computation of forces and induced dipoles in the next MD step. The quantum charges included both the “core” charges of nuclei and sigma electrons, which were calculated by the method of Del Re22 and held constant during the simulation, and fluctuating charges from the π electrons. QCFF-PI also computed the excitation energies, oscillator strengths and changes in permanent dipole moment for a specified set of π-π* and CT states. Although a quantum treatment using a larger basis and including doubly-excited configurations might give more accurate energies, the simplicity and speed of QCFF-PI made longer MD trajectories practicable and allowed tight coupling of the quantum and classical parts of the program. One limitation is that the program has not been parameterized for sulfur atoms or ionized carboxylate groups; however, amides and protonated carboxylic acid groups can be treated straightforwardly by using the parameters for amino, carbonyl and hydroxyl groups.
QCFF-PI uses a basis of only p-type wavefunctions and does not consider resonance integrals between atoms separated by more than two bonds, or that have orthogonal pz orientations. The CI matrix therefore lacks elements that couple local π–π* excitations to electron transfer between non-conjugated groups of π atoms, such as transfer to a backbone amide from a side-chain indole, imidazole or phenol ring, or transfer from one amide group to another. To add these matrix elements, we assigned each of the ground-state wavefunctions to a group of conjugated atoms such that
| (4) |
where cn,i is the coefficient for the pz orbital of atom n in wavefunction ψi and the sum runs over the π atoms of group a. Configuration-interaction matrix elements for mixing a singlet π–π* excitation localized mainly on group a (ψi1 → ψi2) with charge transfer from group a to group b (ψi1 → ψj2) or vice versa (ψj1 → ψi2) then were written
| (5) |
and
| (6) |
where βn,m is a semiempirical atomic resonance integral for pz electrons of atoms n and m. The resonance integrals were analyzed by resolving them into σ and π components with the forms
| (7) |
and
| (8) |
where rn,m is the interatomic distance in Å, and energies are in eV. Equations (7) and (8) are the same as eqs. (17a) and (17b) of Alden et al.23 except for the factor [1-exp(-0.6rn,m2)], which we added to truncate the integrals at short distances where the treatment would be unreliable. The terms in exp(-0.7rn,m) express the mean distance dependence of nonadiabatic electron transfer in proteins with a variety of prosthetic groups.24 They do not consider individual coupling pathways through σ- or hydrogen-bonds, and thus could miss effects of interference between parallel pathways.25
After the CI matrix had been diagonalized, the matrix elements calculated by eqs. (5) – (8) also were used to obtain overall coupling factors for charge separation. For this purpose, we considered only the wavefunctions between HOMO-2 and LUMO+2 of the electron donor and acceptor, which provide the dominant configurations in the low-energy π–π* and CT eigenstates. The coupling factor for formation of CT state j from π–π* state i was written
| (9) |
if the electron donor was excited in state i, or
| (10) |
if the acceptor was excited. Here and are the coefficients for the configurations ψi1 → ψi2 and ψj1 → ψj2 in the CI eigenvectors for states i and j, respectively, and the sums run over the reduced set of wavefunctions.
Coupling factors for resonance energy transfer were evaluated similarly from the CI matrix elements
| (11) |
where γn,m is the standard two-electron repulsion integral in QCFF-PI. Correction factors based on the difference between dipole strengths calculated with the position and gradient operators23, 26 were not applied in the present work.
Induced dipoles
Induced electric dipoles can substantial effects on electrostatic energies in proteins12b, 27 and on the excitation energy of 3-methylindole in solution.28 Following Warshel and Levitt,27a we wrote the induced dipole of atom i as
| (12) |
where αi is the polarizability of the atom and and are, respectively, the electric fields at i from the charges and induced dipoles of all the other atoms. To prevent the mutual polarization of two atoms from increasing catastrophically at short interatomic distances, we used the method introduced by Thole,29,30 in which the charge of one of the atoms is distributed around the atomic center rather than being localized at the center. In this method, a scaled distance between atoms i and j is defined as
| (13) |
where rij is the interatomic distance and a is a dimensionless parameter that is independent of the types of atoms. Swart and van Duijen30b found that using a distribution function in which the charge density of atom j falls off exponentially with distance decreases the effective electric potential at i by a factor fV, with
| (14) |
The field at i is attenuated further by
| (15) |
and the gradient of the field by
| (16) |
With these attenuation actors, the fields and are
| (17) |
| (18) |
where Qj is the charge of atom j and r⃗ij is the vector from atom j to atom i. In our implementation, the sums over j omit atoms connected to atom i by 1, 2 or 3 bonds. Bernardo et al.,31 Burnam et al.,32 Ren and Ponder33 and Elking et al.34 have used similar treatments based on other distributions of charge density.
Van Duijnen and Swart obtained a and the atomic polarizabilities of H, C, N, O and S by fitting calculated molecular polarizabilities to the measured values for 52 molecules.30a We used their value of a (2.1304) but scaled all the atomic polarizabilities by a factor of 0.50, which gave αi = 0.207, 0.644, 0.486, 0.426 and 1.237 Å3 for H, C, N, O and S, respectively. The scaling factor was optimized for consistency with the standard permanent charges of the ENZYMIX force field by maximizing the agreement between the calculated and measured dipole moments of water as described below. (The polarizabilities required such an adjustment because, unlike the vacuum charges that Van Duijnen and Swart used, the ENZYMIX charges are parameterized for molecules in solution and implicitly include some polarization.) We assumed that excitation and charge-transfer reactions did not change the atomic polarizabilities in the quantum subsystem.
Applying eq. (12) to the full set of atoms gives a matrix expression that can be solved iteratively for the induced dipoles.27a This is computationally expensive in QM-MM calculations, because the wavefunctions and charges of the quantum atoms must be recalculated along with the induced dipoles of the entire system on each iteration. The problem is compounded if one seeks the energies of multiple radiative or charge-transfer transitions, in which case the induced dipoles must be optimized separately for the initial and final state in each transition. However, if the system remains in a given electronic state, the changes in the charges and induced dipoles during a 1-fs MD step are small enough to allow the approximation
| (19) |
where the subscripts denote quantities calculated on steps n and n-1.27a We used this simplification for trajectories in the ground and first excited states, and saved the coordinates at intervals of 500 fs to optimize the induced dipoles and quantum charges iteratively for each of the transitions of interest. The calculations with frozen coordinates were done with INDIP, a specialized version of ENZYQ that also calculated the coupling factors and energy gaps for a specified set of π–π* and CT states. The induced dipoles took about 5 iterations to converge for each state.
The quantum mechanical excitation energy for a system with a particular set of induced dipoles does not include the energy required to create the dipoles. We evaluated this energy classically as
| (20) |
where the sum runs over all the induced dipoles and, as in eq. (12), the vector quantities are the induced dipole and total field at position i.35 The difference between the values of Vind for systems with dipoles optimized for the ground state and for a given excited state (ΔVind) was added to the quantum mechanical excitation energy. The energy for excitation from the ground state to excited state k on step n of an MD trajectory, with induced dipoles optimized separately for the initial and final states, then was calculated as
| (21) |
where and are the total excitation energies (including ΔVind) calculated with the induced dipoles optimized for, respectively, the ground state and state k.36 Note that the atomic coordinates always reflect the electronic state in which the MD is run, which generally is the Trp residue's lowest π–π* state, and that the coordinates are frozen when (at 500-fs intervals) we optimize the induced dipoles independently for the ground state, the π–π* states, and each of the CT states. At these points, the excitation energy of each state is calculated twice, once with the induced dipoles for that state and once with the ground-state dipoles. The environment, including induced dipoles, therefore is fully in equilibrium with the quantum subsystem only when the system is in the lowest π–π* state of the Trp. When we switch to a different state to calculate or , the induced dipoles establish a new equilibrium with the new quantum charges, while the rest of the environment finds itself out of equilibrium but unable to adjust instantaneously.
The reorganization energy associated with rearranging induced dipoles was obtained similarly as
| (22) |
Oscillator strengths and dipole moments were evaluated as similar averages of quantities calculated with the two sets of dipoles. Equations (21) and (22) assume that minima on the potential energy surfaces of the ground and excited states are displaced with respect to the magnitudes and directions of the induced dipoles, but that the two surfaces have similar curvatures as functions of these variables.
The effects of induced dipoles generally are larger and more variable for CT states than for π–π* states. This point is illustrated in Supplementary Figure S1, which shows the reorganization energies (λk,n) associated with induced dipoles for five CT excitations and the first singlet π–π* excitation of a hairpin peptide. The values for the CT excitations range from approximately 1,000 to 8,000 cm−1, while those for the π–π* excitation cluster between -50 and 200 cm−1. Induced dipoles thus can have a major influence on the calculated energy gap between a CT state and a π–π* state, as well as on the relative energies of different CT states.
We did not routinely include forces from induced dipoles explicitly in the simulations, because ENZYMIX was parameterized for simulations without these forces, and including them in ENZYQ did not improve the root-mean-squared deviations of calculated peptide structures from the starting structures. However, the induced dipoles affect the MD forcefield indirectly through their effects on the atomic charges of the quantum subsystem.
Water dipoles
Because the Trp residues in the hairpin and Trp-cage peptides are partly exposed to the solvent, it was important for ENZYQ to capture the dielectric properties of water. We therefore ran a series of MD simulations of a spherical drop of liquid water. The sphere had a radius of 21 Å and held 1419 water molecules. One molecule was used to define the center of the system, while the others were free to diffuse within the sphere. The system was equilibrated by Monte Carlo rotations of the molecules with simulated annealing from 325 to 25 K, followed by MD trajectories of 10 ps at 30 K and 20 ps at 300 K. Multiple trajectories then were propagated for 500 ps in 1-fs steps at 300 K, and the structural coordinates and atomic charges were saved every 0.5 ps for analysis with INDIP. The scaling factor for atomic polarizabilities (see above) and the van der Waals parameters for water hydrogens (AH and BH, where the energy of van der Waals interactions between atoms i and j is written AiAjrij−12 -BiBjrij−6) were varied to optimize the global agreement of a set of calculated and measured physical properties. Other parameters were standard for the ENZYMIX force field17 (atomic charges -0.80 and 0.40 for water O and H atoms, respectively, and van der Waals parameters AO = 793.0 kcal1/2mol−1/2Å6 and BO = 25.0 kcal1/2mol−1/2Å3 for water oxygens).
Supplementary Figure S2 shows the distribution of dipole moments calculated with the optimized parameter values (AH = 0.10 kcal1/2mol−1/2Å6, BH = 0.20 kcal1/2mol−1/2Å3, and polarizabilities scaled by 0.50). The calculated mean dipole moment was 2.95 debye (D), in agreement with values of 2.95 ± 0.2 D given by Gubskaya and Kusalik37 and Silvestrelli and Parrinello,38 and the value 2.9 ± 0.6 D obtained from X-ray scattering data by Badyal et al.39 Calculations of the O-H bond length, H-O-H bond angle, radial distribution functions, and diffusion coefficient of liquid water using the same parameter values are described in the Supplementary Material. The calculated properties agree well with experiment.
Simulations of peptides and 3-Methylindole
The solution NMR structures of the Ala8His/Trp10Phe β-hairpin and Tyr3Phe Trp-cage 16b peptides (Figures 1A,B and S5 and Table S3) were used to generate initial models of the other peptides listed in Tables 1 and 2. Mutations were introduced by a Monte Carlo procedure that optimized the side-chain torsional angles of the new residue while holding the backbone fixed.40 The peptide was embedded a sphere of water with a radius of 19 Å (∼1066 water molecules), and the energy was minimized by Monte Carlo rotations of the waters with simulated annealing from 325 to 25 K, followed by 10 ps of MD of the full system in the ground electronic state at 30 K. MD trajectories of 2.5 ns then were propagated at 285, 295 or 300 K in the ground electronic state. Twenty 0.5-ns trajectories in an excited state next were run for each peptide, with the first beginning by projection from the ground-state trajectory at 0.5 ns and the rest following by similar projections at 0.1-ns intervals. The Trp-cage peptides and the Phe10His and Trp1Phe/Phe10Trp hairpins were simulated at 285 K and the other hairpin peptides at 295 or 300 K. Structures of the excited system were saved every 0.5 ps, giving 20,000 structures for analysis with INDIP. The same procedure was used for simulations of 3-methylindole in a 16-Å sphere of water (681 water molecules).
Table 1.
Folding of Hairpin Peptides at 280 K. a
| Substitutions | pH | % Foldedb |
|---|---|---|
| none | 6.5 | 91.0 |
| Ala8/ε-N-acetyl-Lys 8 | 6.5 | 93.6 |
| Ala8Asn | 6.5 | 92.4 |
| Ala8Asp | 6.5 | 88.0 |
| 2.5 | 89.4 | |
| Ala8Lys | 6.5 | 91.5 |
| Ala8Cha c | 6.5 | 98.5 |
| Ala8Gln | 6.5 | 92.0 |
| Ala8Glu | 6.5 | 89.1 |
| Ala8Ser | 6.5 | 94.5 |
| Ala8Cys 8 | 6.0 | 84.5 |
| 10.5 | 48.9 | |
| Ala8Orn c | 6.5 | 92.1 |
| Ala8Tyr | 6.0 | 91.7 |
| 10.67 | 90.7 | |
| Ala8His | 7.85 | 97.7 |
| 2.5 | 94.9 | |
| Phe10Tyr | 6.5 | 90.4 |
| 10.7 | 99.0 | |
| Phe10His | 7.85 | 66.6 |
| 2.5 | 65.9 | |
| Phe10Leu | 6.5 | 59.1 |
| Trp1N-Ac-Phe / Phe10Trp | 6.5 | 41.1 |
The peptides are Ac-WVTIpGKAIFTG-NH2 with the indicated substitutions for residues in bold font. Except where indicated (last row), all the peptides had Trp at position 1.
Chemical-shift deviations of the following atoms were used to calculate the % folding: Val2 NH, Ile3 Hα, Ile4 NH, X8 Hα, Ile9 NH, and when X = Phe or Tyr, X10 Hβ3 and X10 Hδ.
Abbreviations: Cha = cyclohexylalanine, Orn = ornithine.
Table 2.
Folding of Trp-cage Peptides at 280 and 300 K.
| Peptide and Substitutions | % Folded (pH 7) a | |
|---|---|---|
| 280 K | 300 K | |
| Trp-cage 16b b | 98.9 | 96.3 |
| Arg16Cit c | 93.2 | 85.6 |
| Asp9Ala | 96.2 | 93.0 |
| Asp9Leu | 95.4 | 91.5 |
| Asp9Leu / Arg16Ile | 95.0 | 90.0 |
| Asp9Ala / Arg16Nva c | 92.8 | 89.7 |
| Trp-cage 10b d | ||
| ΔSer20 e | 99.5 | 90.9 |
| Lys8Ala | 97.2 | 83.7 |
| Asp9Glu | 97.8 | 86.2 |
| Asp9Glu / Arg16Lys | 94.4 | 80.9 |
| Asp9Arg / Arg16Glu | 94.8 | 81.5 |
| Arg16Orn e | 87.2 | 71.1 |
| Arg16Nva c | 75.0 | 52.3 |
The sum of the CSDs of the following atoms was used to calculate the % folding of each peptide: Leu7 Hα, Pro 18 Hα/Hβ3, Pro19 Hδ2/Hδ3 and Gly11 Hα2.
DAF AQWLADaGPASaRPPPS, with the indicated substitutions for one or more of the residues in bold font.
Abbreviations: Cit = citrulline, Nva = norvaline, Orn = ornithine.
DAFAQWLKDGGPASGRPPPS, with the indicated deletions or substitutions for residues in bold font.
Ser20 deleted.
Separate sets of nominal bond lengths, angles and force constants were used for the ground and excited states of the indole ring. The equilibrium geometry for the ground state was taken from a crystal structure of Trp.41. For the excited state, we used the geometry calculated by Callis et al.42 using GAUSSIAN92. As discussed by many previous workers,42–43 indoles have two overlapping excited singlet states (1La and 1Lb) with different equilibrium geometries. The 1La excited state consists predominantly of the configurations (HOMO → LUMO) and (HOMO-1 → LUMO+1) with relative amplitudes on the order of 3:1, while 1Lb consists largely of (HOMO-1 → LUMO) and (HOMO → LUMO+1). We used the geometry calculated for 1La, which has the larger oscillator strength and dominates the fluorescence under the conditions of interest here. To obtain bond-stretching force constants consistent with other parameters in the program, we fit the standard ENZYMIX force constants for C-C and C-N with various bond orders to a 2nd-order polynomial in the bond length, and used the same polynomial function for the bonds in the indole ring. Tables of the bond lengths, angles and force constants are given in Supplementary Tables S1 and S2.
For simulations of peptides, we added explicit terms for the backbone hydrogen bonds identified in the NMR structures.13b (The hairpin peptides have two H-bonds linking Val2 with Ile9 and two connecting Ile4 to Lys7; the Trp-cage peptides have H-bonds linking residues at each turn of the helix between residues 2 and 9, and bonds linking residue 6 with 11, 10 with 13, 11 with 14, and 12 with 15.) These H-bonds were assigned ideal H–O distances of 1.95 Å and N–H–O angles of 180°, bond-stretching orce constants o 20 kcal mol−1 Å−2 and bending force constants of 5 kcal mol−1. The ε-amino groups of Lys7 in the hairpins and Lys8 in the Trp-cage 10b peptides, which are located relatively far from the other groups of interest and are well solvated and presumably accompanied by counterions, were given net charges of zero; using charges of +1 had little effect on the results. Asp1 and Asp9 of the Trp-cage peptides were given charges of -1, and Arg16 a charge of +1.
We expected that differences between the classical (MM) and quantum mechanical (QM) atomic charges would need reconciling at the interface between the two parts of the program. Vivian and Callis44 found that using INDO/S-CIS (Zindo) charges with the CHARMM force field led to excessively strong interactions of water with carbons of the indole ring, shifting the calculated emission of tryptophan too far to the red. Scaling the QM charges down by 20% before sending them to the MM program gave better agreement with experiment. To establish a scaling procedure for ENZYQ, we calculated some of the spectroscopic properties of 3MI in water. The relative fluorescence (F) at wavenumber v was calculated as
| (23) |
Here Ek,n and fk,n are, respectively, the excitation energy (eq. 21) and oscillator strength of excited state k on step n of an MD trajectory; N is the total number of steps; kB, the Boltzmann constant; T, the temperature; and is a line-shape function constructed as a weighted sum of four Gaussians shifted from Ek,n by 0, -1600, -3200 and -4800 cm−1 to approximate the distribution of Franck-Condon factors for 1La emission from indole and 3MI.42, 45 Equation (23) assumes that the 1La and 1Lb states establish a Boltzmann equilibrium rapidly relative to fluorescence.
When the uncorrected QCFF-PI charges were used, the calculated energy of the emission spectrum of 3MI peaked at 28,100 cm−1, exceeding the measured value (26,900 cm−1)43d by about 4% (see Supplementary Figure S4A). Increasing the quantum charges by ∼5% brought the two values into agreement. Increasing the classical potentials from the solvent by ∼10% before they were added to the diagonal terms of the Fock matrix gave similar results (Figure S4B). With either of these adjustments, however, the calculated width of the emission spectrum was too large by about 20% (Figure S4C, D: FWHM calculated = 6,270 cm−1, observed43d = 5,200 cm−1). In addition, the CT energies calculated for both the hairpin and Trp-cage peptides sometimes were erratic and the SCF procedure occasionally failed to converge. Scaling the quantum charges down by 20% gave more consistent CT energies and better reproduced the width of the emission band. We therefore decreased the charges by this latter factor to explore whether the calculated differences between π–π* and CT energies would be informative even though the absolute emission energies were systematically too high. The potentials were not scaled.
Results
Peptide Structures and Stability
NMR structures (see Figure 1A and Supplementary Figure S5 and Table S3) were generated for the hairpin peptide Ac-WVTIpGKHIFTG-NH2 by converting NOE cross-peak intensities to distance constraints and simulated annealing using the program CNS.46 The previously determined structure14a of Trp-cage 10b sufficed as an initial structure for the two families of Trp-cage peptides. The parent Trp-cage 16b (Figure 1B) is very similar to 10b structurally, differing only in the replacement of an exposed Lys (Lys8) by Ala and substitution of D-Ala for glycines 8 and 15. NOE cross-peaks and chemical shift deviations (CSDs) were used to quantify the extent of folding of each of the peptide variants and to verify that each structure was essentially identical to the explicitly-solved structure of the prototype. With the exceptions of the Cys8, His10, Leu10 and Phe1/Trp10 hairpins and the norvaline16 Trp-cage, all the peptides in both series were 89 to 98% folded at 280 K and pH 6.5 (see Tables 1 and 2).
Fluorescence Measurements
Table 3 gives the absolute quantum yields (ϕ) of fluorescence for all the hairpin peptides at pH 6.5. With the exception of peptides containing Cys, His, Orn (ornithine) or Tyr at position 8 or 10, the other peptides with N-acetylTrp at position 1 have a remarkably constant ϕ of 0.251 ± 0.021, despite their varying charge and polarity. For comparison, 3-MI in water has a quantum yield of 0.34,2a and free tryptophan and N-acetyltryptophanamide have yields of 0.13 to 0.14.1b, 16 The strong quenching by Cys (ϕ = 0.04) and mild quenching by Tyr (ϕ = 0.13 at position 8 or 0.16 at position 10) compared to Ala (ϕ = 0.25) are consistent with Chen and Barkley's2c findings on quenching of 3MI fluorescence in solution. In contrast to their observations, however, Lys at position 8 did not quench fluorescence relative to Ala. This seems likely to reflect an unfavorable position of the ε-amino group relative to the tryptophan's indole ring because Orn, which resembles Lys in having a primary amino group in its side chain but has one fewer methylene group, quenched the fluorescence by about 50% (Table 3). Interchanging the positions of Trp1 and Phe10 in the Ala8 peptide results in strong quenching (ϕ = 0.06), even though this moves the indole ring far from any residue whose side chain is likely to donate or accept a proton or electron.
Table 3.
Fluorescence Quantum Yields and Emission Maxima of Hairpin Peptides at pH 6.5. a
| Substitutions | Temp / K | Yield b | λmax / nm c |
|---|---|---|---|
| none | 295 | 0.25 ± 0.02 | 343 |
| Ala8ε-N-AcK d | 295 | 0.25 ± 0.01 | 341 |
| Ala8Asn | 295 | 0.28 ± 0.03 | 344 |
| Ala8Asp | 295 | 0.27 ± 0.01 | 344 |
| Ala8Lys | 295 | 0.24 ± 0.01 | 343 |
| Ala8Cha d | 295 | 0.27 ± 0.01 | 340 |
| Ala8Gln | 295 | 0.23 ± 0.02 | 343 |
| Ala8Glu | 295 | 0.25 ± 0.03 | 343 |
| Ala8Ser | 295 | 0.22 ± 0.01 | 344 |
| Ala8Cys | 295 | 0.036 ± 0.001 | 347 |
| Ala8Orn d | 295 | 0.113 ± 0.005 | 345 |
| Ala8Tyr | 295 | 0.134 ± 0.003 | 343 |
| Ala8His | 295 | 0.17 ± 0.01 | 344 |
| Phe10Tyr | 295 | 0.166 ± 0.008 | 344 |
| Phe10His | 285 | 0.135 ± 0.004 | 347 |
| Phe10Leu | 285 | 0.24 ± 0.03 | 345 |
| Trp1Phe / Phe10Trp | 285 | 0.068 ± 0.005 | 345 |
The peptides are Ac-WVTIpGKAIFTG-NH2 with the indicated substitutions for residues in bold font. Except where indicated in the last row, all the peptides had Trp at position 1.
Fluorescence quantum yield (mean and standard deviation of three measurements).
Emission peak ± 1 nm.
Abbreviations: Ack = ε-N-Acetyl-lysine, Cha = cyclohexylalanine, Orn = ornithine.
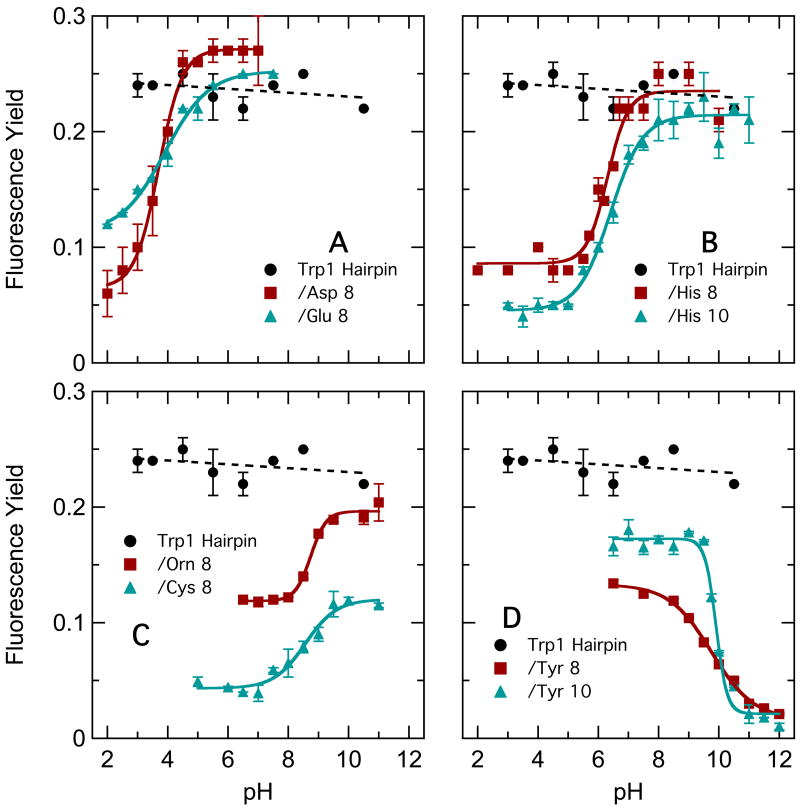
Figure 2 shows the dependence of the fluorescence yield on pH for the hairpin peptides containing an amino acid with an ionizable side chain at position 8 or 10, along with the yield for the Ala8 peptide for comparison. The fluorescence of the Ala8 peptide was essentially independent of pH. The fluorescence of the peptides containing Asp, Glu or His, however, decreased at low pH, following titration curves consistent with protonation of the side-chain carboxylic acid (Asp and Glu) or imidazole (His) group. The fluorescence of peptides containing Orn or Cys at position 8 increased at high pH where their amino or thiol side chains would be deprotonated, though the quenching relative to Ala8 remained strong in the Cys8 peptide and significant in Orn8. The fluorescence of peptides with Tyr8 or Tyr10 decreased at high pH where the phenolic side chain would be ionized. Quenching by Tyr8 was stronger than that by Tyr10 at pH 6.5, but was similar at high pH.
Figure 2.
pH dependence of yields of fluorescence from hairpin peptides with Trp in position 1 and various ionizable residues replacing either Ala8 or Phe10. A: Ala8/Phe10 (●), Asp8/Phe10 (○), Glu8/Phe10 (Δ). B: Ala8/Phe10 (●), His8/Phe10 (○), Ala8/His10 (Δ). C: Ala8/Phe10 (●), Orn8/Phe10 (○), Cys8/Phe10 (Δ). D: Ala8/Phe10 (●), Tyr8/Phe10 (○), Ala8/Tyr10 (Δ).
Although histidine, aspartate and glutamate at position 8 quenched only when protonated, replacing the solvent H2O by D2O had little effect on their quenching (Table 4). Quenching by these residues evidently involves transfer of electrons rather than protons, in accord with Chen and Barkley's2c results for 3MI in solution. In contrast, replacing H2O by D2O decreased the rate constant for quenching by Orn8 at pH 6.5 by a factor of 8, indicating that ornithine probably quenches by proton transfer. Quenching by Tyr8 and Tyr10 showed smaller, but significant isotope effects at pH 6.5, which largely disappeared at high pH even though the quenching increased in strength (Table 4). Tyr8 and Tyr10 thus appear to quench by electron transfer or resonance energy transfer at high pH, but at least partly by proton transfer or concerted transfer of a proton with an electron at pH 6.5. Cys8 also showed a small isotope effect at pH 6.5 that diminished at high pH even though the quenching remained significant.
Table 4.
Solvent Isotope Effects on Fluorescence Quenching in Hairpin Peptides. a
| Substitutions | pH | kq(H2O) / (108 s−1) b | kq(D2O) / (108 s−1) b | kq(H2O)/kq(D2O) |
|---|---|---|---|---|
| none | 6.5 | (0) c | 0.18 ± 0.02 | c |
| Ala8Asp | 3.0 | 3.85 ± 0.16 | 2.79 ± 0.23 | 1.4 ± 0.1 |
| Ala8Glu | 3.0 | 1.63 ± 0.22 | 1.63 ± 0.17 | 1.0 ± 0.2 |
| Ala8His | 3.0 | 5.09 ± 0.14 | 4.82 ± 0.62 | 1.1 ± 0.1 |
| Phe10His | 3.0 | 9.31 ± 0.41 | 5.29 ± 0.40 | 1.8 ± 0.2 |
| Ala8Orn | 6.5 | 2.63 ± 0.13 | 0.28 ± 0.03 | 9.3 ± 1.1 |
| Ala8Tyr | 6.5 | 2.09 ± 0.08 | 1.22 ± 0.08 | 1.7 ± 0.2 |
| 11.5 d | 16.1 ± 0.71 | 12.7 ± 1.1 | 1.3 ± 0.1 | |
| Phe10Tyr | 6.5 | 1.21 ± 0.08 | 0.70 ± 0.19 | 1.7± 0.2 |
| 11.5 d | 30.8 ± 1.9 | 16.5 ± 4.6 | 1.9 ± 0.6 | |
| Ala8Cys | 6.5 | 14.5 ± 0.62 | 8.02 ± 0.41 | 1.8 ± 0.2 |
| 10.0 | 2.86± 0.09 | 2.20 ± 0.09 | 1.2 ± 0.1 |
The peptides are Ac-WVTIpGKAIFTG-NH2 with the indicated substitutions for residues in bold font.
Rate constant for the pH-dependent quenching process in H2O or D2O, all at 295 K except for the Ala8/His10 peptide, which was measured at 285 K. Calculated as described in the text except for Ala 8. The entries are the mean and standard deviation of three measurements.
The fluorescence yield for Ala8 was independent of pH, and was not significantly affected by deuteration of the solvent: ϕ(H2O) was 0.25 ± 0.01 and ϕ(D2O) was 0.26 ± 0.02.
Tyr probably is not completely deprotonated at this pH.
The Trp-cage peptide DAFAQWLADaGPASaRPPPS (Trp-cage 16b with Tyr3 replaced by Phe) had a fluorescence yield of 0.01 (Table 5). Replacing Arg16 by the non-ionizable analog citrulline (Cit) increased the yield at 295 K by a factor of about 2, as did replacing Asp9 by Leu. These substitutions disrupt the electrostatic interactions between Asp9 and Arg16, and thus could affect the structure or stability of the folded peptide as well as the electric fields acting on Trp6. However, neither replacing Asp9 by Ala nor the double substitution Asp9Leu/Arg16Ile had a significant effect on the fluorescence yield. To investigate whether the increased fluorescence of some of the variant Trp-cage peptides reflected the presence of a small amount of unfolded peptide, we also measured the yields at 285 K, where the folded peptides are more stable (see Table 2). Lowering the temperature decreased the fluorescence yield slightly in the Arg16Cit peptide (Table 5), suggesting that its higher yield relative to Asp9/Arg16 at 295 K could reflect partial unfolding. Lowering the temperature had no significant effect in the Asp9Leu variant, and even increased the yield marginally in the Asp9Leu/Arg16Ile peptide. However, we cannot exclude the possibility that effects of unfolding on the fluorescence are masked by a temperature dependence of the rate of a competing electron-transfer reaction. Taken together, the relatively small effects of replacing either Asp9 or Arg16 by a non-ionizable amino acid indicate that the electric fields from the charges of these residues are strongly shielded before they reach the tryptophan.
Table 5.
Fluorescence Quantum Yields and Emission Maxima of Trp-cage peptides at pH 6.5.
| Peptide and Substitutions | Yield b | λmax / nmc | ||
|---|---|---|---|---|
| 295 K | 285 K | 295 K | 285 K | |
| Trp-cage 16b a | 0.010 ± 0.001 | 0.009 ± 0.001 | 342 | 343 |
| Arg16Cit d | 0.025 ± 0.002 | 0.016 ± 0.003 | 343 | 345 |
| Asp9Ala | 0.010 ± 0.003 | ND e | 336 | ND |
| Asp9Leu | 0.021 ± 0.004 | 0.019 ± 0.002 | 345 | 346 |
| Asp9Leu / Arg16Ile | 0.008 ± 0.003 | 0.0136 ± 0.0004 | 346 | 346 |
| Asp9Ala / Arg16Nva d | 0.014 ± 0.001 | 0.014 ± 0.001 | 343 | 343 |
| Trp-cage 10b f | ||||
| ΔSer20 | 0.023 ± 0.001 | 0.024 ± 0.001 | 348 | 349 |
| Lys8Ala | 0.0189 ± 0.0003 | 0.0168 ± 0.003 | 348 | 348 |
| Asp9Glu | 0.050 ± 0.006 | 0.043 ± 0.005 | 347 | 347 |
| Asp9Glu / Arg16Lys | 0.026 ± 0.002 | ND | 349 | ND |
| Asp9Arg / Arg16Glu | 0.033 ± 0.003 | 0.040 ± 0.002 | 347 | 346 |
| Arg16Orn | 0.037 ± 0.001 | 0.043 ± 0.001 | 349 | 348 |
| Arg16Nva d | 0.016 ± 0.002 | ND | 346 | ND |
DAFAQWLADaGPASaRPPPS, with the indicated substitutions for residues in bold font. All the Trp-cage peptides had Phe at position 3 and Trp at position 6.
Fluorescence quantum yield at the indicated temperature (mean and standard deviation of 3 measurements).
Emission peak, ± 1 nm.
Abbreviations: Cit = citruline, Nva = norvaline.
ND = Not determined.
DAFAQWLKDGGPASGRPPPS, with the indicated deletions or substitutions.
Similar results were obtained with the peptides based on Trp-cage 10b (DAFAQWLKDGGPASGRPPPS). The ΔSer20 and Lys8Ala variants of this peptide had fluorescence yields of approximately 0.02 at both 295 and 285 K (Table 5). Replacing Asp9 by Glu increased the yield about two-fold, as did the double substitution Asp9Arg/Arg16Glu (Table 5). Although the Arg16Nva and Asp9Glu/Arg16Lys variants were less well folded (Table 2), their fluorescence yields were in the same range.
In contrast to the fluorescence yield, which varied by a factor of more than 25 in different peptides, the variations of the fluorescence emission spectra were relatively small. The emission peaks of the β-hairpins ranged from 340 nm (29,400 cm−1) in the Cha8 peptide to 347 nm (28,800 cm−1) in the Cys8 and His10 peptides (Table 3), and the peaks of the Trp-cage peptides ranged from 336 (29,800 cm−1) to 346 nm (28,900 cm−1) (Table 5).
Calculated Energies and Coupling of π–π* and CT States
With the exception of the Arg16Cit variant of Trp-cage 16b, all the peptides remained well folded during simulated trajectories in either the ground state or first excited singlet state, with the root-mean-square deviation (RMSD) of the Cα atoms from their initial positions generally staying below 1.5 Å (see Supplementary Figures S6 and S7). Fluctuations about the mean positions of the Cα atoms (RMSFs) occurred mainly at the N- and C-termini (Figure S8). The Arg16Cit Trp-cage 16b peptide underwent a comparatively large excursion about 2 ns into the trajectory, but appeared to recover partly at the end. Except in this variant again, substituting a non-ionizable residue for either Asp9, Arg16, or both, did not destabilize the Trp-cage structures noticeably on the ns time scale of the simulations (see Figure S7).
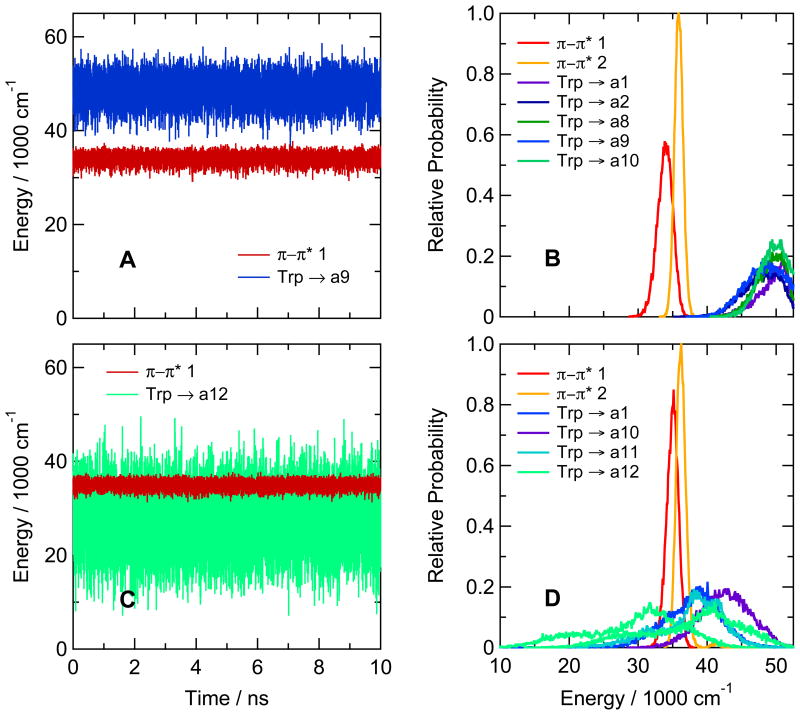
Figure 3A shows the calculated energies of the lowest excited singlet π–π* and charge-transfer (CT) states in the hairpin peptide with Trp at position 1 and Ala at position 8 (Ac-WVTIpGKAIFTG-NH2). The traces for this illustration were generated by catenating the time courses from twenty 0.5-ns trajectories in the first excited state, starting by projections from a ground-state trajectory at 0.1-ns intervals. Figure 3B shows the distributions of energies of the first two π–π* states and the first five CT states over the twenty trajectories. The CT states of the Ala8 peptide all lie well above even the second π–π* state. Similar high energies were calculated for the CT states of hairpin peptides with cyclohexyl-Ala, Ser, Lys or εN-acetyl-Lys at position 8 (see supplementary figure S9).
Figure 3.
(A) Calculated energies for excitation from the ground state to the first excited singlet π–π* state (π–π* 1, red curve) and the CT state with the lowest mean energy (Trp → a9, blue) in the hairpin peptide with Trp at position 1 and Ala at position 8 (Ac-WVTIpGKAIFTG-NH2). The traces were generated by catenating data from twenty 0.5-ns trajectories in the lowest excited singlet π–π* state, beginning by projections from a trajectory in the ground state. The first trajectory in the excited state started after 0.5 ns in the ground state, and the others followed at 0.1-ns intervals. Backbone amide groups are designated by “a” followed by a number indicating the residue that provides the amino group for the amide. The amide group between the N-terminal acetyl cap and W1 in this peptide thus is a1, and the amide between Ala8 and Ile9 is a9. CT states are designated by the side chain or amide that serve as the electron donor and acceptor, connected by an arrow. (B) Distributions of energies of the first two excited singlet π–π* states (red and orange curves) and the first five CT states (blue, green, and purple curves) of the same hairpin peptide as in A, averaged over the twenty trajectories in the excited state. In this peptide, electron transfer from the indole ring of Trp1 to backbone amides a1, a2, a8, a9 and a10 gives CT states with similar distributions of energies, all of which lie above the first two π–π* states. Various configurations (combinations of wavefunctions) give multiple CT states in which the same two groups of atoms serve as the electron donor and acceptor; this panel shows only the lowest-energy configuration for each donor-acceptor pair. (C) The same as A, but for the hairpin peptide with Phe at position 1 and Trp at position 10 (Ac-FVTIpGKAIWTG-NH2). The lowest CT state here is Trp → a12 (light green). (D) The same as B, but for the hairpin peptide with Phe at position 1 and Trp at position 10. The lowest CT states are Trp → a12 (light green), Trp → a11 (cyan), Trp → a1 (blue) and Trp → a10 (purple). Energy distributions for CT states with two different configurations are shown for Trp → a12; the second has approximately the same shape as the first, but is displaced to higher energies by about 10,000 cm−1. Only the lowest-energy configuration is shown for the other donor-acceptor pairs. The amplitudes are proportional to the relative number of times that the energy was in the corresponding bin. All bin widths are 100 cm−1, but the areas under the curves are not necessarily equal, because only the first 16 states were identified at each time point.
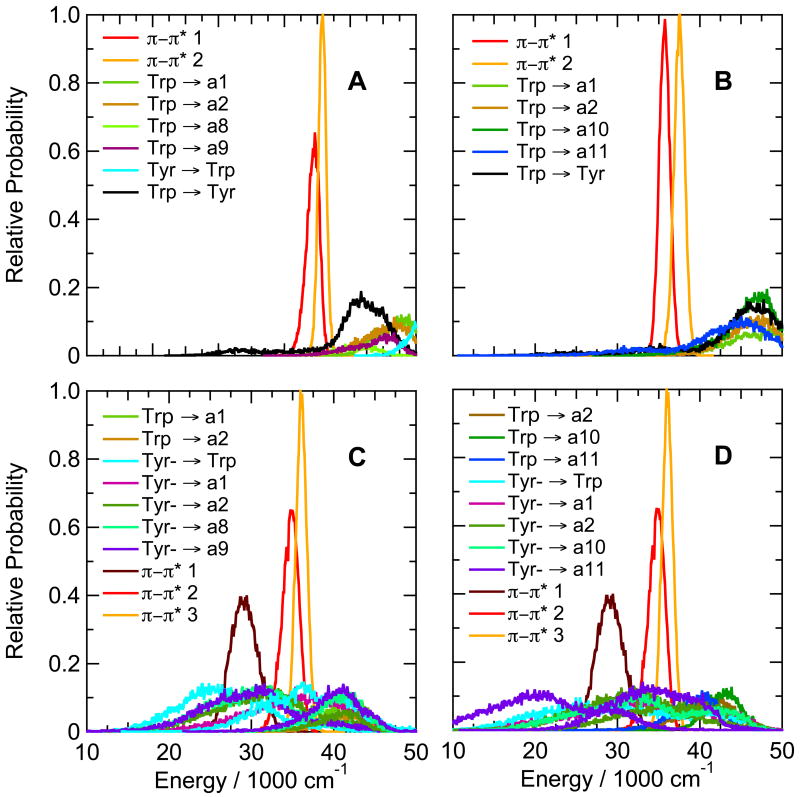
Interchanging the positions of Trp1 and Phe10 in the hairpin peptide changed the calculated energies dramatically. In the peptide with Trp at position 10, the amide between the Thr11 and Gly12 (amide a12) evidently is well positioned to act as an electron acceptor, forming a CT state whose calculated energy usually lies below the energy of the first excited π–π* state (see Figures 3C and D). A second CT state with the same donor-acceptor pair also overlaps the π–π* state extensively, as do CT states formed by electron transfer to the amide on the amino sides of Phe1 and Thr11 (amides a1 and a11) (Figure 3D).
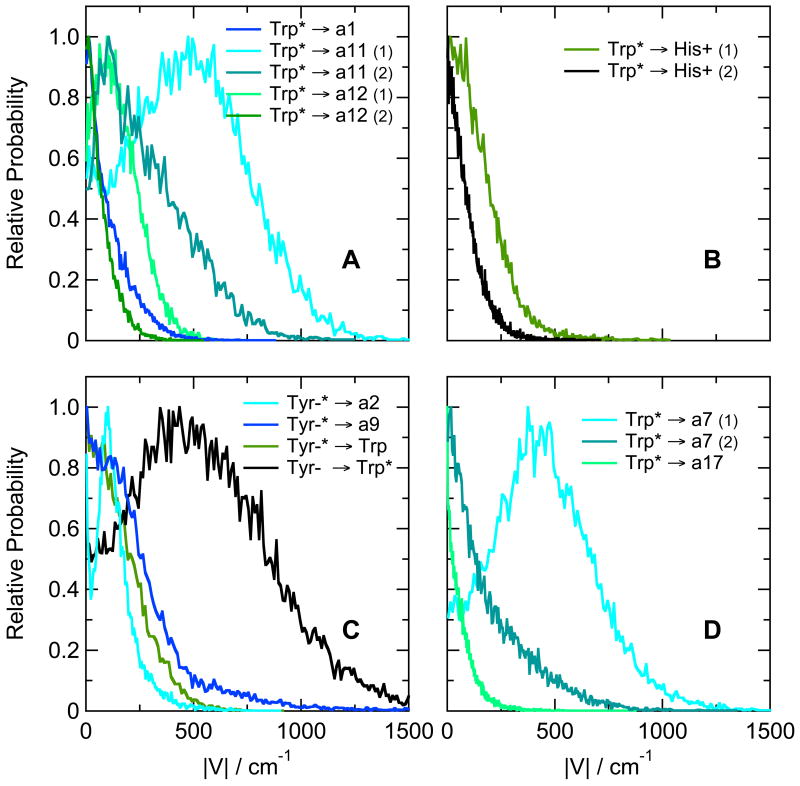
The thermodynamic favorability of electron transfer to backbone amides provides a possible explanation for the decreased fluorescence of the Trp1Phe/Phe10Trp hairpin peptide compared to the peptide with Trp at position 1 (see Table 3). However, electron transfer can compete with fluorescence only if the interaction matrix element that mixes the CT state with the π–π* excited state is sufficiently large. We evaluated the matrix elements with eqs. (5) – (10). As shown in Figure 4A, the matrix elements for electron transfer from the excited indole ring of Trp10 to amide a1, a11 or a12 are calculated to have mean absolute values in the range of 100 to 500 cm−1. These matrix elements are comparable to those calculated by Callis et al. for Trp residues in a variety of proteins.11a Given favorable energetics, they are large enough to support electron transfer on a picosecond or sub-picosecond time scale. Electron transfer to amide a10, which is less favorable energetically (Figure 3D), has a smaller matrix element with a mean absolute value of 1.4 cm−1 (not shown). The fluctuations of the matrix elements during a trajectory were largely uncorrelated with the fluctuations of the energy gaps between the π–π* and CT states.
Figure 4.
(A) Distributions of calculated matrix elements (|V|) for electron transfer from the lowest singlet π–π* excitation of the indole ring of Trp10 to amides a1, a11 and a12 in the hairpin peptide Ac-FVTIpGKHIWTG-NH2. The distributions are from the same trajectories as Figures 3C and D. Numbers in parentheses indicate two different configurations of the same electron donor and acceptor, configuration (1) having the lower energy. (B) Distributions of calculated matrix elements for electron transfer from the lowest singlet π–π* excitation of the indole ring of Trp1 to the protonated imidazole ring of His8 in the hairpin peptide Ac-WVTIpGKHIFTG-NH2. Results for two configurations are shown. The distributions are from the same trajectories as Figure 5C. (C) Distributions of matrix elements for electron transfer from the phenolate ring of ionized Tyr8 to amides a2 and a9 and the indole ring of Trp1 in the hairpin peptide Ac-WVTIpGKYIWTG-NH2. These distributions are from the same trajectories as Figure 7C. Electron transfer from Tyr8 to Trp1 can occur either from the lowest π–π* state, when the excitation is localized mainly on the Tyr phenolate ring (Tyr-* → Trp, green curve), from the second π–π* state, when the excitation is localized mainly on the Trp indole ring (Tyr- → Trp*, black), or from higher, more mixed π–π* states (not shown). (D) Distributions of matrix elements for transfer to amides a7 and a17 from the excited indole ring of Trp6 in the Trp-cage 16b peptide DAFAQWLADaGPASaRPPPS. These distributions are from the same trajectories as Figure 8A. All the distributions are normalized to 1 at their peaks.
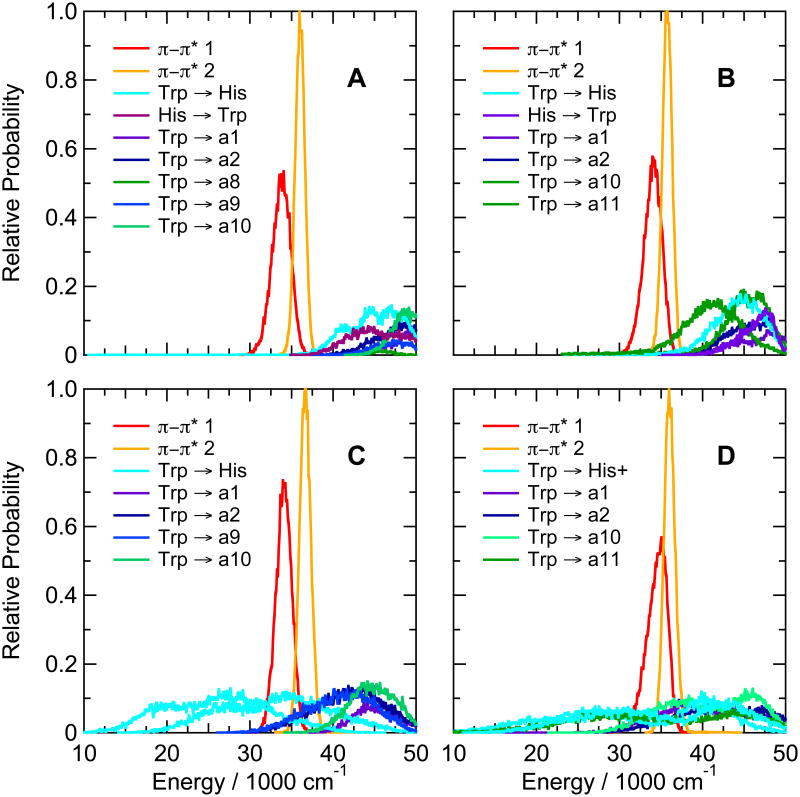
In the hairpin peptides with Trp at position 1 and neutral histidine at either position 8 or position 10, the calculations place all the CT states above the π–π* states, as in the Trp1/Ala8/Phe10 peptide (Figure 5A, B). When the His side chain is protonated, however, the mean energy of charge transfer from the indole ring to the imidazole drops below the energies of the π-π* states (Figure 5C, D). Even the second CT state of the protonated imidazole often lies below the first π–π* state. Charge transfer from the indole to backbone amide a11 also decreases substantially in energy in the peptide with protonated His at position 10 (Figure 5D), and transfer to amides a2 and a9 becomes somewhat more favorable with protonated His at position 8 (Figure 5D). The strong quenching of fluorescence seen at low pH in these peptides (Table 3 and Figure 2A) thus might be explained by electron transfer from the indole to either the protonated imidazole side chain or (at least in the peptide with His10) a backbone amide. The interaction matrix elements, however, favor transfer to the imidazole in both peptides. In the His8 peptide, the calculated matrix elements for transfer to the protonated imidazole ring, amide a2, and amide a9 had mean absolute values of 152, 16 and 12 cm−1, respectively. Figure 4B shows the distributions of the matrix elements for two configurations of transfer to the protonated imidazole. In the His10 peptide, the mean absolute value of the matrix element for electron transfer from Trp1 to the protonated imidazolole ring was 18 cm−1, while that for transfer to amide a11 was 5.3 cm−1 (not shown).
Figure 5.
Calculated distributions of excitation energies of the first two excited singlet π–π* states and the first 5 or 6 CT states of hairpin peptides with Trp at position 1 and His at either position 8 (Ac-WVTIpGKHIFTG-NH2, A, C) or position 10 (Ac-WVTIpGKAIHTG-NH2, B, D), with the His side chain either neutral (A, B) or protonated (C, D). The energy distributions were averaged over twenty 0.5-ns trajectories in the first excited singlet state. Backbone amide groups are designated as in Figure 3. CT states involving electron transfer between the indole ring of Trp1 and the imidazole ring of His are designated “Trp → His” and “His → Trp” (A and B), or (for protonated His) “Trp → His+” (C and D). CT states with two different configurations are shown for electron transfer from Trp to His+.
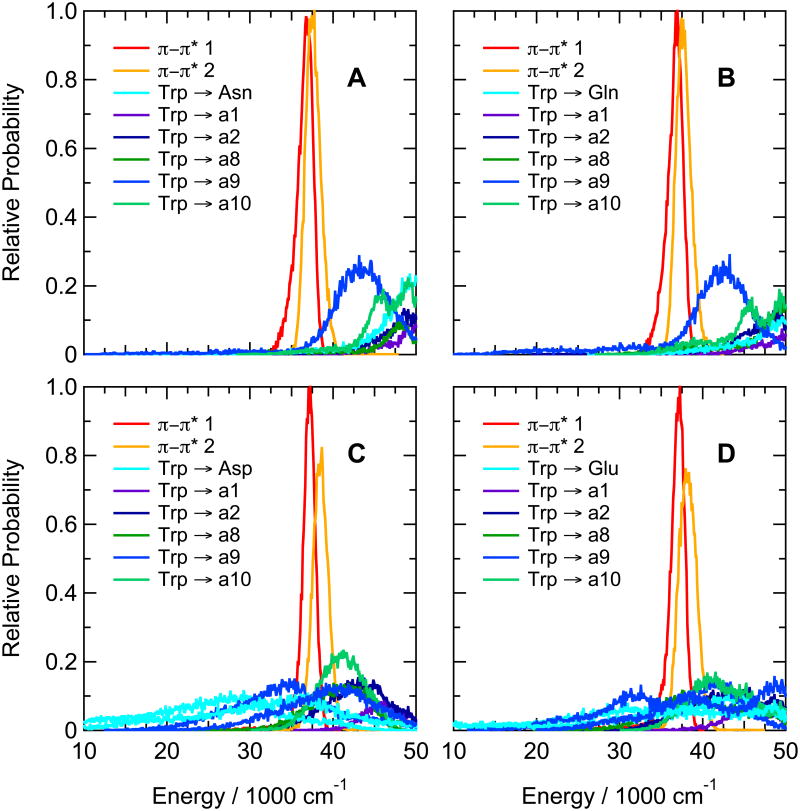
Figure 6 shows the distributions of calculated energies for hairpin peptides with Trp at position 1 and either Asn, Gln, Asp or Glu at position 8. As explained above, the simulations of peptides containing Asp or Glu could be run only with the side chains of these residues in their neutral (protonated) forms. In the peptides containing Asn or Gln, the CT states lie largely above the first two π–π* states (Figure 6A,B), while electron transfer from the indole of Trp1 to the protonated carboxylic acid side chain is highly favorable in the peptides containing Asp or Glu (Figure 6C,D). Replacing Asn by Asp or Gln by Glu also makes charge transfer from the indole to backbone amide a9 favorable. The low-lying CT states are consistent with the strong quenching of fluorescence seen in in the Asp and Glu peptides at low pH (Figure 2A), which is not seen in the corresponding peptides containing Asn or Gln.
Figure 6.
Calculated distributions of excitation energies of excited singlet π–π* and CT states of hairpin peptides with Trp at position 1 and either Asn (A), Gln (B), Asp (C) or Glu (D) in position 8 (Ac-WVTIpGKXIFTG-NH2 with X = N, Q, D or E). The energy distributions were averaged over twenty 0.5-ns trajectories in the first excited singlet state. The side-chain carboxylic acid groups of Asp and Glu were protonated. Backbone amide groups a1, a2, a8, a9 and a10 are designated as in Figure 3. CT states in which an electron moves from the indole ring of Trp1 to a side-chain carboxylic acid or amide group are designated “Trp → Asp”, “Trp → Glu”, “Trp” → “Asn” and “Trp” → “Gln” (cyan curves). CT states with two different configurations are shown for electron transfer from Trp to Asp in C, transfer to Glu in D, and transfer to a9 (blue curves) in both C and D.
In the hairpin peptides with Tyr at position 8 or 10, ionizing the phenolic side chain makes a variety of CT states favorable (Figure 7C and D), in accord with the quenching of fluorescence seen at high pH in these peptides (Figure 2D). The tyrosine's phenolate side chain acts as the electron donor in these states, with either the indole ring of the Trp or a backbone amide group acting as the acceptor. In addition, the phenolate ring has a low-lying π-π* state that mixes with the excited states of the Trp by exciton interactions (π-π*1 in Figure 7C, D). Charge-transfer states in which an electron moves from the Trp to an amide have higher calculated energies that are relatively insensitive to the ionization state of the Tyr (Figure 7A,B,C, D).
Figure 7.
Calculated distributions of excitation energies of excited singlet π–π* states and CT states of hairpin peptides with Trp at position 1 and Tyr at either position 8 (Ac-WVTIpGKYIFTG-NH2, A, C) or position 10 (Ac-WVTIpGKAIYTG-NH2, B, D), with the Tyr side chain either neutral (A, B) or ionized (C, D). The energy distributions were averaged over twenty 0.5-ns trajectories in the first excited singlet state. Backbone amide groups are designated as in Figure 3; states involving electron transfer between the indole ring of Trp and the phenol ring of Tyr are designated “Trp” → “Tyr”, “Tyr → Trp” and (for ionized Tyr) “Tyr- → Trp”. When the Tyr is ionized, the first excited π–π* state (π–π*1, dark brown) is localized mainly on the phenolate ring; the second and third π–π* states (red and orange), mainly on the indole ring of Trp1. When the Tyr is neutral (panels A and B), π–π*1 and π–π*2 (red and orange) are localized mainly on Trp1, and the first excited singlet state of the phenol group is at higher energies (not shown). CT states with two different configurations are shown for electron transfer from ionized Tyr to amides a1, a2, a8 and a9 in C, and to amides a1, a2, a10 and a11 in D.
Coupling matrix elements for some of the CT reactions of Tyr8 in the hairpin peptide are shown in Figure 4C. The coupling for transfer from the Tyr to the indole ring of Trp1 is particularly strong in π-π*2, when the excitation is located predominantly on the Trp (black curve in Figure 4C); the matrix element for this process has a mean absolute value of about 550 cm−1. In π-π*1, when the excitation is mainly on the phenolate ring, the mean value is about 160 cm−1 (green curve). The excited tyrosine in π-π*1 also can transfer an electron to amide a2 or a11 with similar matrix elements (cyan and blue curves). Resonance energy transfer from the excited Trp to the phenolate ring is coupled more weakly, with a mean matrix element of 4.8 cm−1 (not shown).
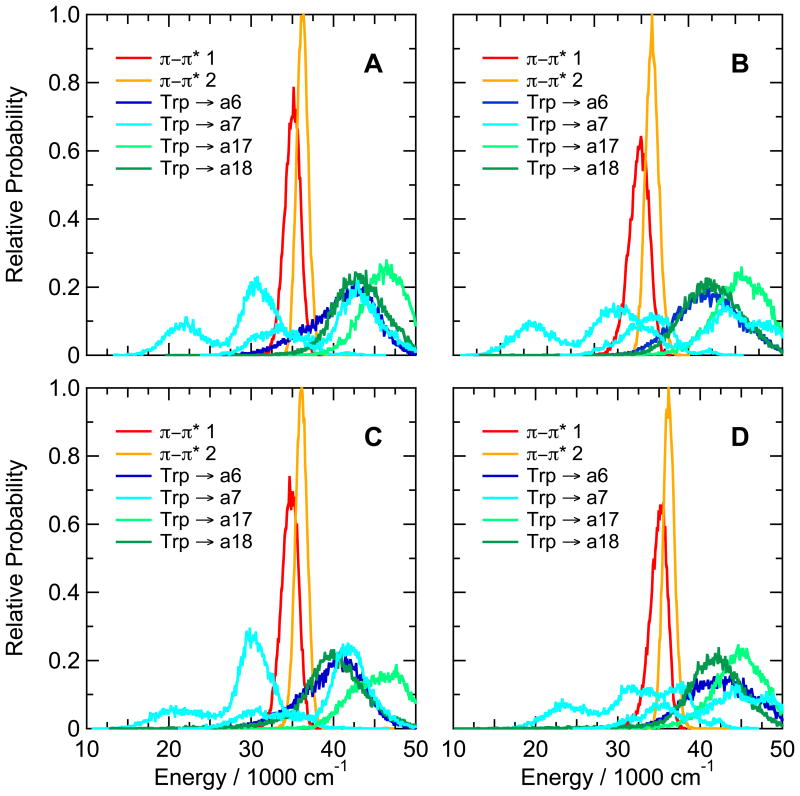
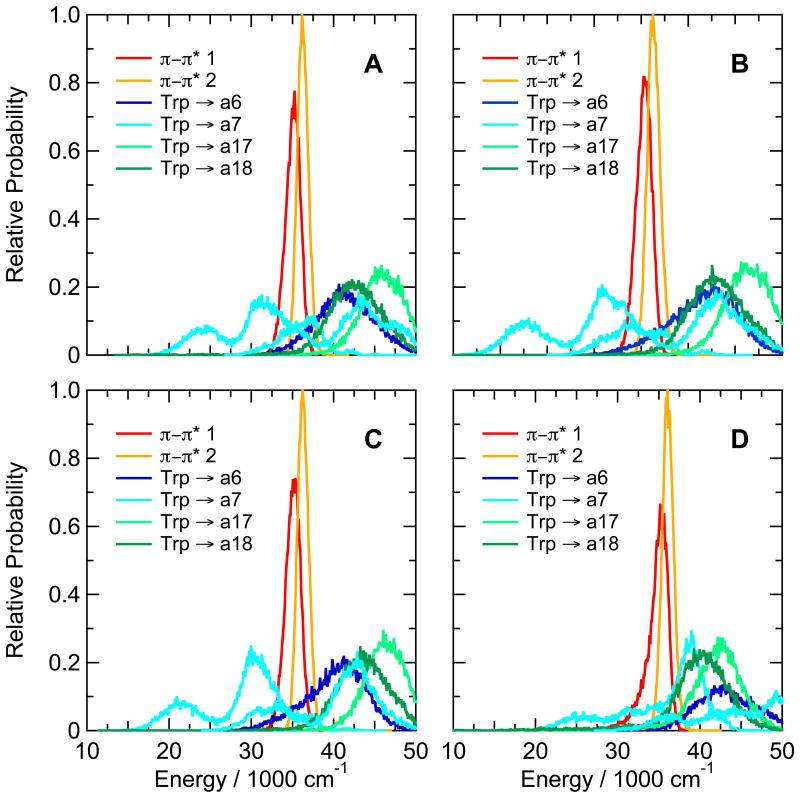
Turning to the Trp-cage peptides, Figure 8A shows calculated distributions of energies of π-π* and CT states of the prototype 16b peptide containing Trp at position 6, Asp at position 9, and Trp at position 16. The energies of electron transfer from the indole to backbone amide a7 are markedly bimodal, but are strongly favorable in both arms of the distribution. The Trp-a7 donor-acceptor pair also has a second CT state with a similar, bimodal energy distribution shifted to higher energies by about 15,000 cm−1; formation of this state is favorable in the lower arm of the distribution. Electron transfer to amide a17, which is linked to the indole N of Trp6 by a hydrogen bond, is less favorable than transfer to either a6, a7 or a18.
Figure 8.
Calculated distributions of excitation energies of the first two excited singlet π–π* states and low-lying CT states of (A) the Trp-cage 16b peptide DAFAQWLADaGPASaRPPPS, (B) the Asp9Leu variant, (C) the Arg16Cit (citrulline) variant, and (D) the Asp9Ala/R16Nva (norvaline) variant. The energy distributions were averaged over twenty 0.5-ns trajectories in the first excited singlet state. Backbone amide groups a6, a7, a17 and a18 (blue, cyan, and light and dark green curves, respectively) are designated as in Figure 3. CT states with two different configurations are shown for electron transfer to a7. See Figure S10 for similar plots for the Asp9Leu/Arg16Ile variant.
Substitutions that replaced one or both of the ionizable residues at positions 9 and 16 by a non-ionizable residue (Asp9Leu, Asp9Ala, Arg16Cit, Asp9Ala/Arg16Nva, and Asp9Leu/Arg16Ile) had surprisingly little effect on the calculated CT energies in the Trp-cage 16b peptide (see Figure 8B,C,D and Supplementary Figure S10B,C). The calculated CT energies also were very similar in the Trp-cage 10b series with Ala in place of Lys8, Glu in place of Asp 9 or Nva in place of Arg16, or with the C-terminal Ser deleted (Figures 9A,B,C and S10A). However, the double substitution Asp9Arg/Arg16Glu, which approximately interchanges the positions of the positive and negative charges of residues 9 and 16, shifted the CT states involving amide a7 to higher energies while lowering the energy of reducing a17 (Figure 9D).
Figure 9.
Calculated distributions of excitation energies of the first two excited singlet π–π* states and the low-lying CT states of (A) the Asp9Glu variant of the Trp-cage 10b peptide DAFAQWLKDGGPASGRPPPS, (B) the ΔSer20 variant, (C) the Lys8Ala variant, and (D) the Asp9Arg/Arg16Glu variant. The energy distributions were averaged over twenty 0.5-ns trajectories in the first excited singlet state. Backbone amide groups (blue, cyan, and light and dark green curves) are designated as in Figures 3 and 8. Two configurations are shown for electron transfer to a7 (cyan).
The matrix elements for electron transfer to amides a7 and a17 in the Trp-cage 16b peptide are shown in Figure 4D. Amide a7, which has the more favorable energetics, also has the larger matrix element, with a mean abolute value of 380 cm−1. Transfer to amide a6 is less well coupled, with a mean matrix element of 1.9 cm−1 (not shown).
Discussion
The experimental results presented in Tables 3-5 and Figure 2 are in accord with previous findings that electron transfer to a variety of acceptors can quench fluorescence of indole derivatives in solution.2-6 Electron transfer to protonated imidazole, thiol and carboxylic acid groups probably accounts for the pH-dependent quenching of fluorescence in β-hairpin peptides with Trp at position 1 and His, Glu, Asp or Cys at position 8 or 10 (Figure 2A, B, C), while the strong quenching in the hairpin with Trp at position 10 (Table 3) and in the Trp-cage peptides (Table 5) probably reflects transfer to a backbone amide group. We also saw strong quenching by Tyr at high pH, where the phenolate side chain likely acts as an electron donor (Figure 2D), and weaker quenching at neutral pH, where the phenol group might serve as either a donor or an acceptor. Cysteine quenched weakly at high pH, where the ionized thiol group presumably could act as an electron donor (Figure 2C). To our knowledge, quenching of tryptophan fluorescence by electron transfer to the indole ring has not been described previously. We found a large D/H isotope effect for quenching by ornithine at neutral pH (Figure 2C), corroborating the observation that protonated amines can quench by proton transfer,2a, 2c although the analog with Lys in place of ornithine did not show this behavior. Asn and Gln, which quench fluorescence of 3-methylindole relatively weakly in solution2c but are reported to quench more effectively in some proteins,7 did not quench significantly better than Ala in the hairpin peptides we studied (Table 3).
Electron-transfer processes involving Trp and Tyr residues are well known in proteins, and have been characterized by EPR and ENDOR as well as optical spectroscopy. Relatively long-lived Trp radicals have been seen in cytochrome c peroxidase,47 horseradish peroxidase,48 lignin peroxidase,49 ribonucleotide reductase,50 DNA photolyase,51 cytochrome c oxidase52 and azurin,53 and similar radicals of Tyr in ribonucleotide reductases,54 photosystem II,55 cytochrome c oxidase,56 galactose oxidase,57 prostaglandin synthase58 and cytochrome P450cam.59 The radicals in these proteins are created by oxidation of the Trp or Tyr side chain and are stabilized by deprotonation. Charge-transfer states containing these radicals probably decay rapidly by recombination. Radicals formed by reduction of a Trp or Tyr residue have never been detected directly, as far as we are aware, although indole radical anions reportedly can be generated by pulse radiolysis.60
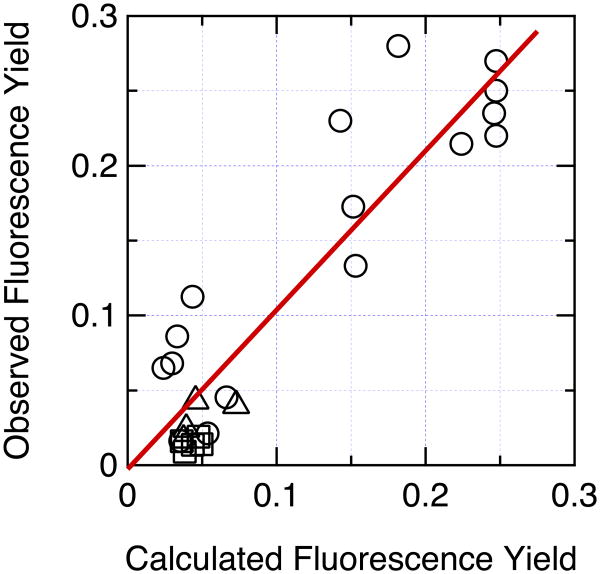
The QM-MM calculations shown in Figures 3-9 are qualitatively consistent with the measured fluorescence yields in all the peptides that were amenable to treatment by ENZYQ and INDIP. In the peptides for which we could calculate the energetics of electron transfer, and which lacked a protonated amino group that might quench by proton transfer, a low-energy CT state that is strongly coupled to excitation of the indole ring appears to be sufficient for strong quenching of fluorescence. (As noted above, ENZYQ could not treat thiols or ionized carboxyl groups.) Again, either a backbone amide group or a protonated carboxyl or imidizole group of a Glu, Asp or His residue can serve as the electron acceptor (Figures 3C, 6C,D and 7). The neutral phenol ring of Tyr apparently can act as a weak electron acceptor (Figures 7A,B), and the ionized phenolate ring as a donor (Figures 7C,D).
Replacing Asp9, Arg16, or both by non-ionizable amino acids in the Trp-cage peptides has little effect on the calculated energies of the pertinent CT states of Trp6 (Figures 8 and S10), in accord with the experimental finding that the fluorescence yield remains largely unchanged (Table 5). The fields from the charged side chains evidently are well screened by counterions, the surrounding solvent and induced dipoles. As noted above, the somewhat higher fluorescence yield in the Arg16Cit variant of Trp-cage 16B at 295 K could reflect partial unfolding. This would be difficult to reproduce quantitatively in short MD simulations, but is consistent with the increasing RMSD seen toward the end of the ground-state simulation of this peptide (Figure S7B) and with the higher RMSF throughout the peptide (Figure S8B).
The calculations also provide information on the identities of the amide groups that accept an electron in the Trp-cage peptides (Figures 8 and S10) and in the β-hairpin with Trp at position 10 (Figure 3C), which would be difficult to determine experimentally. Perhaps surprisingly, the most effective electron acceptor in the Trp-cage peptides is not a17, which is hydrogen-bonded to the indole N of Trp6, but rather a7 (Figures 4C, 8 and S10). Finally, the simulations indicate that, in addition to transferring an electron to the excited indole, ionized tyrosine residues can quench tryptophan fluorescence by resonance energy transfer (Figure 7C,D). This process probably would be followed quickly by electron transfer from the excited phenolate ring to a backbone amide.
To begin a more quantitative discussion of the competition between charge transfer, resonance energy transfer and fluorescence, it is instructive to evaluate the quantity
| (24) |
in which 〈PΔE≤0(t)〉 is the probability of finding one or more CT or exciton states degenerate with or below the indole ring's lowest singlet π–π* state at time t, the brackets denote averaging over MD trajectories of a given peptide in the excited state, and ϕ0 is the average of the measured fluorescence yields for the hairpins with Trp at position 1 and a non-quenching residue (Ala, Asn, Gln, ε-N-acetyl-Lys, Lys, cyclohexyl-Ala or Ser) at position 8 (0.2475). This simple function correlates surprisingly well with the measured fluorescence yields, considering that it covers a variety of electron donors and acceptors with no adjustable parameters (see Figure S11). However, eq. (24) is unlikely to provide reliable predictions of Trp fluorescence yields, because it would hold only if the electronic coupling matrix element (V) is always large enough to make electron transfer or resonance energy transfer much faster than radiative decay of the excited state whenever the thermodynamics are favorable. In particular, electron transfer would have to be fast even if the only available CT or exciton state lies far below the π–π* state in energy. Although tunneling to excited vibrational levels of the product state allows transfer processes to occur in this situation, the Franck-Condon factors decrease as the two states move apart, and the exact form of this decrease probably depends on the system.61 The ability of eq. (24) to predict the fluorescence yields for some of the present peptides could depend on higher-energy CT states that come into resonance with the π–π* state as the lowest CT state drops out.
A more general approach is to write the rate constant for electron transfer as
| (25) |
Here ΔE(t) is the time-dependent difference between the calculated excitation energies of diabatic reactant and product electronic states, ρFC(ΔE(t)) is the Franck-Condon-weighted density of product vibronic states that are degenerate with the reactant, and ξ is a parameter related to the rate at which coherent oscillations between the degenerate vibronic states decay by dissipation of energy to the surroundings. Equation (25) reduces to the Golden Rule expression, , when 〈|V|2〉 ≪ ħξ / 2π. It goes to the adiabatic limit, ket = 〈ξ ρFC (ΔE(t))〉, when 〈|V|2〉 ≫ ħξ / 2π. Expressions of the same general form have been discussed by Zussman and others, and have been related to models of polar solvents.62 However, when it is written simply as an average over trajectories in the reactant state, eq. (25) does not require assuming that ΔE has any particular functional dependence on the reaction coordinate. This makes it unnecessary to evaluate the complete reorganization energy of the reaction by running trajectories in the product state as well as the reactant or by analyzing the fluctuations of ΔE. In addition to treating electron transfer, eq. (25) also should apply to the rate constant for resonance energy transfer (kret) from the excited Trp to the Tyr phenolate ring in the hairpin peptides with ionized Tyr at position 8 or 10, although ρFC(ΔE) undoubtedly differs in detail for electron- and energy-transfer.
Although microscopic simulations might be used to extract ξ and ρFC for the main vibrational modes that are coupled to each CT or energy-transfer reaction, this would require calculating the quantum energies at shorter intervals than the 0.5-ps periods we used here. For the present discussion, we will treat ξ and ρFC as phenomenological parameters that are the same for all the peptides and reactions under discussion. The total rate constant for quenching in a given peptide (kq) then is just the sum of eq. (25) over all the reactions with significant values of 〈|V|2〉 and 〈ρFC〉. Assuming further that the rate constants for radiation and other nonradiative processes (kf and knr) are the same for all the peptides and are either independent of time or fluctuate randomly with respect to V and ΔE, the calculated fluorescence yield becomes
| (26) |
Figure 10 shows a plot of the measured fluorescence yields versus the yields calculated using equations (25) and (26). For these calculations, we wrote ρFC as the product of a sigmoidal function that rises steeply from 0 to 1 as ΔE becomes negative (2/[1+exp(ΔE/δ)]) and a Gaussian providing a more gradual falloff when ΔE ≪ 0:
Figure 10.
Correlation of the measured fluorescence yield with the yield calculated by eqs. (24) – (27) with ξ = 2.5×1013 cm−1s−1, σ = 1.5×104 cm−1, δ = 100 cm−1, kf = 6.11×107s−1 and knr = 1.858×108s−1. Circles, hairpin peptides; squares, Trp-cage 16b peptides; triangles, Trp-cage 10b peptides. The fluorescence yields were measured at 285 K for the Trp-cage peptides and the Phe10His and Trp1Phe/Phe10Trp hairpin peptides, and at 295 K for the other hairpins. The observed values for hairpin peptides containing either Glu, Asp, His or Tyr with the side chain in its protonated form, or containing His or Tyr with the side chain deprotonated, were obtained from the asymptotes of the sigmoidal fits to the data in Figure 2. Data for 26 peptides are shown. (The hairpins with Cys, ornithine, Lys, or ionized Glu or Asp at position 8 were not simulated because the present treatment cannot handle ionized carboxyl groups, S atoms, or quenching by proton transfer. The Phe10Leu hairpin, the Asp9Ala Trp-cage 16b peptide, and the Arg16Orn, Arg16Nva and Asp9Glu/Arg16Lys Trp-cage 10b peptides were omitted because of poor folding or lack of fluorescence data at 285 K.) The calculations for hairpin peptides containing ionized Tyr considered direct electron transfer from Trp to backbone amides, electron transfer from the phenolate ring to the excited indole ring of the Trp, and resonance energy transfer from Trp (π–π*2) to Tyr (π–π*1). Charge transfer from the Tyr to backbone amides thus does not contribute to the calculated quenching, although the resulting CT states could serve as sinks for removal of π–π*1 (see Figure 7). The straight line is a least-squares fit to all the data (R2 = 0.849, Pearson correlation coefficient = 0.922, y-intercept = -0.0026 ± 0.0124, slope = 1.053 ± 0.0906).
| (27) |
The radiative rate constant kf in eq. (26) was taken to be 6.11×107 s−1 (see Methods) and knr was set to 1.858×108 s−1 to give ϕ0 = 0.2475 as for eq. (24). Setting σ = 15,000 ± 1,000 cm−1, δ = 100 ± 100 cm−1 and ξ = (2.5 ± 0.5)×1013 cm−1s−1 gives a good linear correlation between the measured and calculated yields. The y-intercept of the plot is essentially zero and the slope is close to unity. However, the quenching in the Trp-cage16b peptides and the hairpin peptides containing ionized Tyr tends to be underestimated relative to that in the other peptides, suggesting that an individualized treatment of ρFC or ξ might lead to further improvements. The other nonradiative processes that are lumped together in knr also could vary somewhat among the different peptides.
Figure S12A shows a plot of |V|2ξ/(|V|2 + ħξ/2π) one of the two fluctuating quantities whose product contributes to the average in eq. (25). With the value of ξ given above (2.5×1013 cm−1 s), ket becomes essentially independent of |V| when |V| > 30 cm−1. Although it may seem surprising that an electron- or resonance-transfer reaction could approach the adiabatic limit when 〈|V|〉 is still much smaller than the vibronic envelopes of the reactant and product states, the more pertinent consideration here is the ratio of the electronic oscillation frequency 2|V|/h (∼1013 s−1 when |V| = 30 cm−1) to the rate at which the energy o the resonant vibronic states dissipates to the surroundings: if dissipation of vibrational energy requires a time longer than the reciprocal of the electronic oscillation frequency, the reaction should approach adiabaticity.62b-f An effective time constant on the order of 10−13 s for vibrational relaxations seems not unreasonable for the systems discussed here, considering that low-frequency vibrational modes can oscillate coherently for several picoseconds after photoexcitation of photosynthetic reaction centers,63 bacteriorhodopsin,64 heme proteins65 and photoactive yellow protein.66
Figure S12B shows the second fluctuating quantity in eq. (25), ρFC(ΔE), as given by eq. (27) with σ = 15,000 and δ = 100 cm−1. The functional form that we have used for ρFC(ΔE) is purely phenomenological, but stems conceptually from quantum mechanical expressions for electron transfer in multi-mode harmonic systems67 and is qualitatively consistent with the dependence of the rate of electron transfer on ΔE in photosynthetic reaction centers.61d-f It is expected to be asymmetrical because there are many resonant transition from the reactant to excited vibrational levels of the product when ΔE < 0, but few when ΔE > 0. Note that ΔE here is approximately the 0-0 energy difference between the two states, not the gap between the vibronic levels that must be in resonance. The large value of σ makes ρFC(ΔE) broader than we might expect, but in principle could reflect coupling to multiple high-frequency vibrational modes along with a quasi-continuum of low-frequency modes. It is important to bear in mind, however, that the values of σ and δ obtained by fitting the fluorescence data might not be physically meaningful if the calculations over- or underestimate ΔE for all the peptides. Shifting all the energy gaps in the positive direction would decrease σ and increase δ. In addition, since the calculations can over- or underestimate the quenching rate for particular types of peptides, the values of ξ,σ and δ derived here depend to some extent on the number of peptides of each type that we studied. Attempts are underway to apply the same treatment to a more diverse group of peptides and proteins.
Conclusions
Tryptophan fluorescence can be quenched by electron transfer from the excited indole ring to the side chains of protonated His, Glu and Asp residues, or to amide groups of the peptide backbone. Ionized Tyr side chains probably can quench both by resonance energy transfer from the indole to the phenolate ring, and by electron transfer from the phenolate to the excited indole ring. The quenching in all cases depends on the electronic coupling and energy gap between the reactant and product states, which fluctuate with time and can vary widely with the peptide structure. Although room clearly remains for improvements, the calculated energies and interaction matrix elements appear to account well for the measured fluorescence yields. Among the factors that we believe contribute to this agreement are MD simulations that are long enough to sample much of the pertinent conformational space, consideration of multiple CT and energy-transfer reactions, a self-consistent treatment of induced electric dipoles for the reactant and product state in each of these reactions, and the use of a rate equation that sums over competing reactions and interpolates between the extremes of adabatic and nonadiabatic processes.
Supplementary Material
Acknowledgments
This work was supported by a grant from the National Science Foundation (0641640) to W.W.P., a grant from the National Institutes of Health (GM059658) to N.H.A., and a Molecular Biophysics Training Grant (NIH 5T32-GM008268) that supported A.W.M. and B.L.K. during part of the project. We thank Dr. Arieh Warshel (University of Southern California) for providing the original versions of ENZYMIX and QCFF-PI, Kian Alden for making some of the fluorescence measurements, and Arieh Warshel, Marcel Swart and Stefan Stoll for helpful discussions.
Abbreviations
- CD
circular dichroism
- CI
configuration interaction
- Cit
citrulline
- CSD
chemical shift deviation
- CT
charge transfer
- FWHM
full width at half-maximal amplitude
- HOMO
highest occupied molecular orbital
- HPLC
high-pressure liquid chromatography
- LUMO
lowest unoccupied molecular orbital
- MD
molecular dynamics
- NOE
nuclear Overhauser effect
- NOESY
nuclear Overhauser effect spectroscopy
- Nva
norvaline
- Orn
ornithine
- QM
quantum mechanical
- RMSD
root-mean-square deviation
- RMSF
root-mean-square fluctuation. Standard 1- and 3-letter abbreviations are used for common amino acids
Footnotes
Supporting Information: Bond stretching and bending parameters for the Trp side chain in the ground and excited state (Tables S1 and S2); additional details on the MD force field; representative calculated contributions of induced dipoles to reorganization energies (Figure S1); calculated dipole moments, diffusion coefficients, and other properties of liquid water (Figures S2 and S3); calculated fluorescence properties of 3MI in water (Figure S4); NMR ensemble structures of the hairpin peptide with His at position 8 (Figure S5); coordinates of the structure of this peptide used for MD simulations and generating models of other peptides (Table S3); plots of the RMSD from ground-state simulations for 25 peptides (Figures S6 and S7); plots of the RMSF for 12 representative peptides (Figure S8); plots of calculated π–π* and CT energies for 6 peptides not shown in the main figures (Figures S9 and S10); details on calculations of fluorescence yields (Table S4 and Figure S11); and plots of the components of eq. (25). This material is available free of charge on the internet at http://pubs.acs.org.
References
- 1.(a) Hennecke J, Sillen A, Huber-Wunderlich M, Engelborghs Y, Glockshuber R. Biochemistry. 1977;36:6391–6400. doi: 10.1021/bi963017w. [DOI] [PubMed] [Google Scholar]; (b) Eftink MR, Jia Y, Hu D, Ghiron CA. J Phys Chem. 1995;99:5713–5723. [Google Scholar]; (c) Callis PR, Liu T. J Phys Chem B. 2004;108:4248–4259. [Google Scholar]
- 2.(a) Yu HT, Colucci WJ, McLaughlin ML, Barkley MD. J Am Chem Soc. 1992;114:8449–8454. [Google Scholar]; (b) Chen Y, Liu B, Yu HT, Barkley MD. J Am Chem Soc. 1996;118:9271–9278. [Google Scholar]; (c) Chen Y, Barkley MD. Biochemistry. 1998;37:9976–9982. doi: 10.1021/bi980274n. [DOI] [PubMed] [Google Scholar]
- 3.Cowgill RW. Arch Biochem Biophys. 1963;100:36–44. doi: 10.1016/0003-9861(63)90031-6. [DOI] [PubMed] [Google Scholar]
- 4.Shinitzky M, Goldman R. Eur J Biochem. 1967;3:139–144. doi: 10.1111/j.1432-1033.1967.tb19508.x. [DOI] [PubMed] [Google Scholar]
- 5.Steiner R, Kirby EP. J Phys Chem. 1969;73:4130–4135. doi: 10.1021/j100846a015. [DOI] [PubMed] [Google Scholar]
- 6.Ricci RW, Nesta JM. J Phys Chem. 1976;80:974–980. [Google Scholar]
- 7.Qiu W, Li T, Zhang L, Yang Y, Kao YT, Wang L, Zhong D. Chem Phys. 2008;350:154–164. [Google Scholar]
- 8.(a) Loewenthal R, Sancho J, Fersht AR. Biochemistry. 1991;30:6775–7669. doi: 10.1021/bi00241a021. [DOI] [PubMed] [Google Scholar]; (b) DeBeuckeleer K, Volckaert G, Engelborghs Y. Proteins. 1999;36:42–53. [PubMed] [Google Scholar]
- 9.(a) Thompson PA, Muñoz V, Jas GS, Henry ER, Eaton WA, Hofrichter J. J Phys Chem B. 2000;104:378–389. [Google Scholar]; (b) Jas GS, Eaton WA, Hofrichter J. J Phys Chem B. 2001;105:261–272. [Google Scholar]
- 10.Kubelka J, Eaton WA, Hofrichter J. J Mol Biol. 2003;329:625–630. doi: 10.1016/s0022-2836(03)00519-9. [DOI] [PubMed] [Google Scholar]
- 11.(a) Callis PR, Petrenko A, Muiño PL, Tusell JR. J Phys Chem B. 2007;111:10335–10339. doi: 10.1021/jp0744883. [DOI] [PubMed] [Google Scholar]; (b) Tusell JR, Callis PR. J Phys Chem. 2012;116:2586–2594. doi: 10.1021/jp211217w. [DOI] [PubMed] [Google Scholar]
- 12.(a) Warshel A, Sharma PK, Kato M, Parson WW. Biochim Biophys Acta. 2006;1746:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]; (b) Parson WW, Warshel A. Calculations of electrostatic energies in proteins using microscopic, semimicroscopic and macroscopic models and free energy perturbation approaches. In: Aartsma TJ, Matysik J, editors. Biophysical Techniques in Photosynthesis. Springer; Dordrecht: 2008. p. 401. [Google Scholar]
- 13.(a) Kier B, Andersen NH. J Am Chem Soc. 2008;130:14675–14683. doi: 10.1021/ja804656h. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Kier B, Shu I, Eidenschink L, Andersen NH. Proc Natl Acad Sci USA. 2010;107:10466–10471. doi: 10.1073/pnas.0913534107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.(a) Barua B, Lin JC, Williams DV, Kummler P, Neidigh JW, Andersen NH. Protein Eng Des Sel. 2008;21:171–185. doi: 10.1093/protein/gzm082. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Williams DV, Barua B, Andersen NH. Organic & Biomolec Chem. 2008;6:4273–4279. doi: 10.1039/b814314e. [DOI] [PubMed] [Google Scholar]
- 15.Gardecki JA, Maroncelli M. Appl Spectros. 1998;52:1179–1189. [Google Scholar]
- 16.(a) Chen RF. Anal Lett. 1967;1:35–42. [Google Scholar]; (b) Szabo AG, Rayner DM. J Am Chem Soc. 1980;102:554–563. [Google Scholar]
- 17.Lee FS, Chu ZT, Warshel A. J Comput Chem. 1993;14:161–185. [Google Scholar]
- 18.Beeman D. J Comput Phys. 1976;20:130–139. [Google Scholar]
- 19.(a) Warshel A, Karplus M. J Am Chem Soc. 1972;94:5612–5625. [Google Scholar]; (b) Warshel A, Lappicirella A. J Am Chem Soc. 1981;103:4664–4673. [Google Scholar]
- 20.King G, Warshel A. J Chem Phys. 1989;91:3647–3661. [Google Scholar]
- 21.Lee FS, Warshel A. J Chem Phys. 1992;97:3100–3107. [Google Scholar]
- 22.Del Re G. Theor Chim Acta. 1958;1:4031–4040. [Google Scholar]
- 23.Alden RG, Johnson E, Nagarajan V, Parson WW, Law CJ, Cogdell RG. J Phys Chem B. 1997;101:4667–4680. [Google Scholar]
- 24.(a) Moser CC, Dutton PL. Biochim Biophys Acta. 1992;1101:171–176. [PubMed] [Google Scholar]; (b) Page C, Moser CC, Chen XX, Dutton PL. Nature. 1999;402:47–52. doi: 10.1038/46972. [DOI] [PubMed] [Google Scholar]
- 25.Beratan DN, Onuchic JN, Winkler JR, Gray HB. Science. 1992;258:1740–1741. doi: 10.1126/science.1334572. [DOI] [PubMed] [Google Scholar]
- 26.Warshel A, Parson WW. J Am Chem Soc. 1987;109:6143–6152. [Google Scholar]
- 27.(a) Warshel A, Levitt M. J Mol Biol. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]; (b) Warshel A, Kato M, Pisliakov AV. J Chem Theor Comput. 2007;3:2034–2045. doi: 10.1021/ct700127w. [DOI] [PubMed] [Google Scholar]
- 28.Westbrook JD, Levy RM, Krogh-Jespersen K. Proc SPIE. 1992;1640:10–19. [Google Scholar]
- 29.Thole BT. J Chem Phys. 1981;59:341–350. [Google Scholar]
- 30.(a) Van Duijnen PT, Swart M. J Phys Chem A. 1998;102:2399–2407. [Google Scholar]; (b) Swart M, Van Duijnen PT. Mol Simul. 2006;32:471–484. [Google Scholar]
- 31.Bernardo DN, Ding Y, Krogh-Jespersen K, Levy RM. J Phys Chem. 1994;98:4180–4187. [Google Scholar]
- 32.(a) Burnham CJ, Li JL, Xantheas SS, Leslie M. J Chem Phys. 1999;110:4566–4581. [Google Scholar]; (b) Burnham CJ, Xantheas SS. J Chem Phys. 2002;116:1500–1510. [Google Scholar]; (c) Burnham CJ, Xantheas SS. J Chem Phys. 2002;116:5115–5124. [Google Scholar]
- 33.(a) Ren P, Ponder JW. J Comput Chem. 2002;23:1497–1506. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]; (b) Ren P, Ponder JW. J Phys Chem B. 2003;107:5933–5947. [Google Scholar]; (c) Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio RA, Jr, Head-Gordon M, Clark GNI, Johnson ME, Head-Gordon T. J Phys Chem B. 2010;114:2549–2564. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Elking D, Darden T, Woods RJ. J Comput Chem. 2007;28:1261–1274. doi: 10.1002/jcc.20574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Russell ST, Warshel A. J Mol Biol. 1985;185:389–404. doi: 10.1016/0022-2836(85)90411-5. [DOI] [PubMed] [Google Scholar]
- 36.(a) Hummer G, Szabo A. J Chem Phys. 1996;105:2004–2010. [Google Scholar]; (b) Warshel A, Parson WW. Quart Revs Biophys. 2001;34:563–679. doi: 10.1017/s0033583501003730. [DOI] [PubMed] [Google Scholar]; (c) Lee FS, Chu ZT, Bolger MB, Warshel A. Prot Eng. 1992;5:215–218. doi: 10.1093/protein/5.3.215. [DOI] [PubMed] [Google Scholar]
- 37.Gubskaya AV, Kusalik PG. J Chem Phys. 2002;117:5290–5302. [Google Scholar]
- 38.Silvestrelli PL, Parrinello M. J Chem Phys. 1999;111:3572–3580. [Google Scholar]
- 39.Badyal YS, Saboungi ML, Price DL, Shastri SD, Haeffner DR, Soper AK. J Chem Phys. 2000;112:9206–9208. [Google Scholar]
- 40.Alden RG, Parson WW, Chu ZT, Warshel A. J Am Chem Soc. 1995;117:12284–12298. [Google Scholar]
- 41.Takigawa T, Ashida T, Sasada Y, Kakudo M. Bull Chem Soc Japan. 1966;39:2369–2378. doi: 10.1246/bcsj.39.2369. [DOI] [PubMed] [Google Scholar]
- 42.Callis PR, Vivian JT, Slater LS. Chem Phys Lett. 1995;244:53–58. [Google Scholar]
- 43.(a) Catalán J, Diaz C. Chem Phys Lett. 2003;368:717–723. [Google Scholar]; (b) Weber G. Biochem J. 1960;75:335–345. doi: 10.1042/bj0750335. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Song PS, Kurtin WE. J Am Chem Soc. 1969;91:4892–4906. [Google Scholar]; (d) Meech SR, Phillips D. Chem Phys. 1983;80:317–328. [Google Scholar]; (e) Lami H, Glasser N. J Chem Phys. 1986;84:597–604. [Google Scholar]; (f) Ruggiero AJ, Todd DC, Fleming GR. J Am Chem Soc. 1990;112:1003–1014. [Google Scholar]; (g) Callis PR. J Chem Phys. 1991;95:4230–4240. [Google Scholar]; (h) Muiño PL, Callis PR. J Chem Phys. 1994;100:4093–4109. [Google Scholar]; (i) Rogers DM, Hirst JD. J Phys Chem A. 2003;107:11191–11200. [Google Scholar]
- 44.Vivian JT, Callis PR. Biophys J. 2001;80:2093–2109. doi: 10.1016/S0006-3495(01)76183-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.(a) Hahn DK, Callis PR. J Phys Chem A. 1997;101:2686–2691. [Google Scholar]; (b) Short KW, Callis PR. J Chem Phys. 2000;113:5235–5244. [Google Scholar]
- 46.(a) Brünger AT, Adams PD, Clore GM, DeLano WL, Gros P, Grosse-Kunstleve RW, Jiang JS, Kuszewski J, Nilges M, Pannu NS, Read RJ, Rice LM, Simonson T, Warren GL. Acta Cryst D Biol Crystallogr. 1998;54:905–921. doi: 10.1107/s0907444998003254. [DOI] [PubMed] [Google Scholar]; (b) Brünger AT. Nature Protoc. 2007;2:2728–2733. doi: 10.1038/nprot.2007.406. [DOI] [PubMed] [Google Scholar]
- 47.(a) Sivaraja M, Goodin DB, Smith M, Hoffman BM. Science. 1989;245:738–740. doi: 10.1126/science.2549632. [DOI] [PubMed] [Google Scholar]; (b) Huyett JE, Doan PE, Gurbiel R, Houseman ALP, Sivaraja M, Goodin DB, Hoffman BM. J Am Chem Soc. 1995;117:9033–9041. [Google Scholar]
- 48.Morimoto A, Tanaka M, Takahashi S, Ishimori K, Hori H, Morishima I. J Biol Chem. 1998;273:14753–14760. doi: 10.1074/jbc.273.24.14753. [DOI] [PubMed] [Google Scholar]
- 49.(a) Blodig W, Smith AT, Winterhalter K, Piontek K. Arch Biochem Biophys. 1999;370:86–92. doi: 10.1006/abbi.1999.1365. [DOI] [PubMed] [Google Scholar]; (b) Smith AT, Doyle WA, Dorlet P, Ivancich A. Proc Natl Acad Sci USA. 2009;106:16084–16089. doi: 10.1073/pnas.0904535106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Baldwin J, Krebs C, Ley BA, Edmondson DE, Huynh BH, Bollinger JMJ. J Am Chem Soc. 2000;122:12195–12206. [Google Scholar]
- 51.(a) Gurudas U, Schelvis PM. J Am Chem Soc. 2004;126:12788–12789. doi: 10.1021/ja047161d. [DOI] [PubMed] [Google Scholar]; (b) Brettel K, Byrdin M. Curr Opin Struct Biol. 2010;20:693–701. doi: 10.1016/j.sbi.2010.07.003. [DOI] [PubMed] [Google Scholar]
- 52.Wiertz FGM, Richter OMH, Ludwig B, de Vries S. J Biol Chem. 2007;282:31580–31591. doi: 10.1074/jbc.M705520200. [DOI] [PubMed] [Google Scholar]
- 53.Shafaat HS, Leigh BS, Tauber MJ, Kim JE. J Am Chem Soc. 2010;132:9030–9039. doi: 10.1021/ja101322g. [DOI] [PubMed] [Google Scholar]
- 54.(a) Larsson A, Sjoberg BM. EMBO J. 1986;5:2037–2040. doi: 10.1002/j.1460-2075.1986.tb04461.x. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Reece SY, Seyedsayamdost MR, Stubbe J, Nocera DG. J Am Chem Soc. 2007;129:13828–13830. doi: 10.1021/ja074452o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.(a) Debus RJ, Barry BA, Babcock GT, McIntosh L. Proc Natl Acad Sci USA. 1988;85:427–430. doi: 10.1073/pnas.85.2.427. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Berthomieu C, Heinerwadel R. Biochim Biophys Acta. 2005;1707:51–66. doi: 10.1016/j.bbabio.2004.03.011. [DOI] [PubMed] [Google Scholar]
- 56.(a) MacMillan F, Kannt A, Behr J, Prisner T. Biochemistry. 1999;38:9179–9184. doi: 10.1021/bi9911987. [DOI] [PubMed] [Google Scholar]; (b) Budiman K, Kannt A, Lyubenova S, Richter OMH, Ludwig B, Michel H, MacMillan F. Biochemistry. 2004;43:11709–11716. doi: 10.1021/bi048898i. [DOI] [PubMed] [Google Scholar]
- 57.(a) Whittaker JW. Arch Biochem Biophys. 2005;433:227–239. doi: 10.1016/j.abb.2004.08.034. [DOI] [PubMed] [Google Scholar]; (b) Lee YK, Whittaker MM, Whittaker JW. Biochemistry. 2008;47:6637–6649. doi: 10.1021/bi800305d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.(a) Malkowski MG, Ginell SL, Smith WL, Garavito RM. Science. 2000;289:1933–1937. doi: 10.1126/science.289.5486.1933. [DOI] [PubMed] [Google Scholar]; (b) Rogge CE, Ho B, Liu W, Kulmacz RJ, Tsai AL. Biochemistry. 2006;45:523–532. doi: 10.1021/bi051235w. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Wu G, Tsai AL, Kulmacz RJ. Biochemistry. 2009;48:11902–11911. doi: 10.1021/bi901600f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Schünemann V, Lenzian F, Jung C, Contzen J, Barra AL, Sligar SG, Trautwein A. J Biol Chem. 2004;279:10919–10930. doi: 10.1074/jbc.M307884200. [DOI] [PubMed] [Google Scholar]
- 60.Arce R, Charron M, Simpson GA. Radiation Res. 1976;68:215–228. [PubMed] [Google Scholar]
- 61.(a) Marcus RA. J Chem Phys. 1956;24:966–978. [Google Scholar]; (b) Liang N, Miller JR, Closs GL. J Am Chem Soc. 1990;112:5353–5354. [Google Scholar]; (c) Closs GL, Miller JR. Science. 1988;240:440–447. doi: 10.1126/science.240.4851.440. [DOI] [PubMed] [Google Scholar]; (d) Warshel A, Chu ZT, Parson WW. Science. 1989;246:112–116. doi: 10.1126/science.2675313. [DOI] [PubMed] [Google Scholar]; (e) Parson WW, Warshel A. Chem Phys. 2004;296:201–216. [Google Scholar]; (f) Parson WW, Warshel A. J Phys Chem B. 2004;108:10474–10483. [Google Scholar]
- 62.(a) Zusman LD. Chem Phys. 1980;49:295–304. [Google Scholar]; (b) Garg A, Onuchic JN, Ambogoakar V. J Chem Phys. 1983;83:4491–4503. [Google Scholar]; (c) Calef DF, Wolynes PG. J Phys Chem. 1983;87:33873400. [Google Scholar]; (d) Onuchic JN, Wolynes PG. J Phys Chem. 1988;92:6495–6503. [Google Scholar]; (e) Ripps I, Jortner J. J Phys Chem. 1987;87:2090–2104. [Google Scholar]; (f) Sparpaglione M, Mukamel S. J Phys Chem. 1988;91:3938–3943. [Google Scholar]
- 63.(a) Vos MH, Lambry JC, Robles SJ, Youvan DC, Breton J, Martin JL. Proc Natl Acad Sci USA. 1991;88:8885–8889. doi: 10.1073/pnas.88.20.8885. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Rischel C, Spiedel D, Ridge JP, Jones MR, Breton J, Lambry JC, Martin JL, Vos MH. Proc Natl Acad Sci USA. 1998;95:12306–12311. doi: 10.1073/pnas.95.21.12306. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Spörlein S, Zinth W, Wachtveitl J. J Phys Chem B. 1998;102:7492–7496. [Google Scholar]; (d) Streltsov AM, Vulto SIE, Shkuropatov AY, Hoff AJ, Aartsma TJ, Shuvalov VA. J Phys Chem B. 1998;102:7293–7298. [Google Scholar]
- 64.Wang Q, Schoenlein RW, Peteanu LA, Mathies RA, Shank CV. Science. 1994;266:422–424. doi: 10.1126/science.7939680. [DOI] [PubMed] [Google Scholar]
- 65.(a) Zhu L, Sage JT, Champion PM. Science. 1994;266:629–632. doi: 10.1126/science.7939716. [DOI] [PubMed] [Google Scholar]; (b) Rosca F, Kumar AT, Ye X, Sjodin T, Demidov AA, Champion PM. J Phys Chem A. 2000;104:4280–4290. [Google Scholar]; (c) Gruia F, Kubo M, Ye X, Ionascu D, Lu C, Poole RK, Yeh SR, Champion PM. J Am Chem Soc. 2008;130:5231–5244. doi: 10.1021/ja7104027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Mataga N, Chosrowjan H, Shibata Y, Imamoto Y, Kataoka M, Tokunaga F. Chem Phys Lett. 2002;352:220–225. [Google Scholar]
- 67.(a) Kubo R, Toyozawa Y. Progr Theor Phys. 1955;13:160–182. [Google Scholar]; (b) Lin SH. Theor Chim Acta. 1968;10:301–310. [Google Scholar]; (c) Sarai A. Chem Phys Lett. 1979;63:360–366. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.