Random pinning glass model

Abstract

Glass transition, in which viscosity of liquids increases dramatically upon decrease of temperature without any major change in structural properties, remains one of the most challenging problems in condensed matter physics despite tremendous research efforts in past decades. On the other hand, disordered freezing of spins in magnetic materials with decreasing temperature, the so-called “spin glass transition,” is understood relatively better. A previously found similarity between some spin glass models and the structural glasses inspired development of theories of structural glasses based on the scenario of spin glass transition. This scenario, although it looks very appealing, is still far from being well established. One of the main differences between standard spin systems and molecular systems is the absence of quenched disorder and the presence of translational invariance: it often is assumed that this difference is not relevant, but this conjecture still needs to be established. The quantities, which are well-defined and characterized for spin models, are not easily calculable for molecular glasses because of the lack of quenched disorder that breaks the translational invariance in the system. Thus the characterization of the similarity between spin and the structural glass transition remains an elusive subject. In this study, we introduced a model structural glass with built-in quenched disorder that alleviates this main difference between the spin and molecular glasses, thereby helping us compare these two systems: the possibility of producing a good thermalization at rather low temperatures is one of the advantages of this model.

Dramatic slowing of the relaxation process in almost all liquids when supercooled below the melting temperature still lacks a proper explanation (1, 2). The increase in relaxation time in deep supercooled regimes is so impressive that it becomes extremely difficult for the system to reach equilibrium in experimental time scales, and eventually the liquid falls out of equilibrium with further decreases in temperature to undergo a calorimetric glass transition. Glass temperature is defined as a temperature at which the viscosity of the liquids becomes 10¹³ poise (3, 4). It is clear that this definition is ad hoc in nature and depends crucially on the choice of parameter; the main question, which remains to be answered, is whether there is a true thermodynamic transition below this calorimetric transition or whether this is just a kinetic phenomenon (5), with the viscosity diverging only in the zero temperature limit.

Many approaches to understanding this remarkable slowing in the dynamics of supercooled liquids invoke the existence of a cooperative length scale (6) associated with the collective rearrangements of particles and its divergence at the elusive glass transition. The slowing is believed to be caused by the difficulty in rearranging sets of ever-increasing numbers of particles collectively while approaching glass transition. Progress made in recent years in identifying such a length scale has been quite encouraging. Developments include a dynamic heterogeneity length scale from the analysis of a four-point density–density correlation function (7–10), a point-to-set length scale (11), a patch length scale (12), length scales associated with non-affine displacement of particles (13), and length scales from finite size scaling of configurational entropy (10) and density of states (14), to name just a few. Unfortunately, there still is no general consensus about the importance of these length scales for glass transition and their relationship to one another. The main hurdle in reaching such a goal is that these length scales are accessible only through computer simulation studies because of the protocols needed to compute them. So, these length scales can be estimated only in a small-parameter range in which they grow very modestly, thereby making it almost impossible to see the divergence as one approaches the glass transition. To further elaborate on this lack of general consensus in the field of glass transition, it is worthwhile to mention the alternative approaches to glass transition. In one of these approaches, glass transition is described as a purely kinetic phenomenon that happens solely as a result of dynamical arrest caused by the local constraints (5). This, together with a recent study (15) in which the relevance of static length scale on the glass transition is questioned, makes the whole picture of glass transition somewhat fuzzy as well as interesting.

Despite all these caveats, there are some theories that are quite successful in explaining the observed phenomena in glass transition. One of the leading contenders among them is the random first-order transition (RFOT) theory proposed by Kirkpatrick, Thirumalai, and Wolynes, and developed further by others (16–23). This theory, which is inspired by the similarity seen between the dynamics of the p-spin glass model and those of the structural glasses (24–30), predicts the existence of a symmetry-breaking transition at the Kauzmann temperature from a supercooled liquid to an ideal glass state and allows microscopic computations of the phase transition (21). This theory, which is very much in the same spirit as the phenomenological Adam–Gibbs theory (22) proposed earlier, also suggests that p-spin glass models and structural glasses may be in the same universality class. However, there is an inherent difference between these two models, namely the existence of quenched disorder in spin glasses. Lack of quenched disorder in structural glasses makes it rather difficult to calculate quantities such as spin glass–type order parameter and susceptibility. Moreover, the whole low-temperature phase cannot be accessed by simulations. In a recent mean field and renormalization group study (31, 32), it was proposed that with random pinning one can explore the ideal glass phase, as in the temperature concentration of the frozen particle plane there exists a critical point and one can reach the glass phase from liquid phase without going through the divergence in the structural relaxation time (32, 33). Similar studies done in the mode-coupling theory (MCT) framework (34, 35) also confirm this picture. All these studies and some other recent studies (14, 21, 36–38) clearly show that exploring the glassy state in the random pinning geometry may be very insightful, with the added advantage of built-in quenched disorder. This may enable us to do replica theoretic calculations for these kinds of particle models to shed more light on the soundness of the replica approach to structural glasses.

In general, a system of particles of equal size interacting via a radially isotropic pairwise potential will have liquid-to-crystal phase transition with decreasing temperature for dimensions d ≤ 3. At higher dimensions, it was shown that crystallization is strongly suppressed (39), so to form a glass it is very important for a dimension at least smaller than 4 to introduce frustration in the system to prevent it from quickly falling into the crystalline global minimum. In spin glasses, the random interactions between the spins are the source of this frustration, and in structural glasses compositional disorder—for example, different sizes of the particles or the asymmetric interaction between different types of particles—usually generates the required frustration. Because of the presence of these extra degrees of freedom, in general glass models often are very hard to equilibrate at lower temperatures, as one also must equilibrate these extra degrees of freedom. It would be nice to have a glassy model system without extra degrees of freedom. In this article, we propose to generate the required frustrations by random pinning: we have studied a system in which there is no randomness in the interaction potential and no compositional disorder. Our model system consists of particles of equal size interacting via a purely repulsive potential (see Materials and Methods for details on the potential used) with some fraction ρ_imp of them frozen randomly in space. If a sufficient number of these particles are frozen randomly in space at some high temperature (T = 1.00 in this case; see SI Materials and Methods for details on the pinning criterion), there is enough frustration in the system to force the system to remain in disorder. As there are no other degrees of freedom to equilibrate apart from the positions of the particles, we expect that this model can be equilibrated to temperatures lower than those of the usual models to study the lower temperature phase of the supercooled liquid. With the quenched disorder, this also is a very attractive model to compare with the spin glass models. At a high density of quenched particles, no crystallization is present; however, the glass phase also is absent. We will show there is an intermediate region with a small, but not too small, fraction of quenched particles, where part of the usual structural glass phenomenology survives and the system does not crystallize, also at very low temperatures. Our construction differs from that of refs. 31 and 32 in that the quenched disorder is crucial to avoiding crystallization and finding a phase transition.

Results

It turns out that one needs to freeze around ρ_imp = 9% of particles to get a system that will not show crystallization, at least for bigger system sizes (N > 250). For smaller systems, this amount of frozen particles is found to be insufficient to prevent the crystallization. With ρ_imp = 11%, even the smaller system sizes do not show any tendency to crystallize. So for the present study, we chose to work with ρ_imp = 11% for all the system sizes studied. We restricted ourselves to small system sizes, mainly because we wanted to achieve full equilibration of the system to very low temperatures. The studied system sizes are in the range N ∈ {100, 4,000}. In Fig. 1 Upper, we show the pair correlation function for different temperatures to confirm that there is no sign of incipient crystallization in this temperature range. In Fig. 1 Upper Right, we show the self part of the average two-point density correlation function 〈Q_s(t)〉 (see Dynamics for details) for N = 512 system size for different temperatures in the range T ∈ {0.400, 1.000}. One can see the nice development of the plateau in the correlation function with decreasing temperature. In Fig. 1 Upper Right Inset, we show the temperature dependence of the α-relaxation time, and the line is the fit to the data using the Vogel–Fulcher–Tamman (VFT) formula with the estimated divergence temperature T_K ∼ 0.17 for N = 512 system size. The dynamic transition temperature or the mode-coupling cross-over temperature is estimated to be T_d ∼ 0.394 by a power fit. One should keep in mind that these extrapolated estimations of the divergence temperatures may not be very reliable as the range of the data is not very big.

Fig. 1.

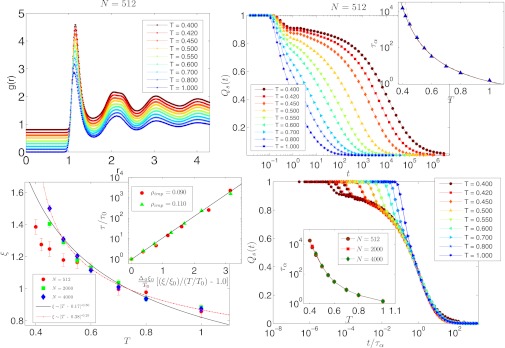
(Upper Left) Pair correlation function g(r) for N = 512 system size for different temperatures. The curves for different temperatures are shifted vertically for clarity. (Upper Right) Self part of the two-point correlation function Q_s(t) for different temperatures. (Inset) α-Relaxation time τ_α calculated as the time when Q_s(t) goes to 1/e of its initial value. The line is the fit to the data using the VFT formula with T_K ≃ 0.17. The dynamic transition temperature (MCT) is estimated to be T_d ≃ 0.394 (red dashed line). (Lower Left) Extracted static length scale from the replica overlap correlation functions (see Materials and Methods for details). The red circles, green squares, and blue diamonds are from the system with N = 512, N = 2,000, and N = 4000, respectively. The estimation of the length scale from N = 512 system size seems to have some finite size effects that almost disappear for N = 2,000 and N = 4,000 system sizes. The black line is the fit to the data using the form ξ(T) ∼ |T − T_K|^γ, with chosen T_K ≃ 0.17 and γ ≃ 0.50, and the red line with dot is the same fitting in which we allowed all the parameters to vary, and the resulting T_K ≃ 0.38 and γ ≃ 0.25. (Inset) Dependence of the relaxation time with the length scale for N = 4,000 system sizes. One can see some degree of universality in the relationship between relaxation time and length scale (see text for details). (Lower Right) Time–temperature superposition for the Q_s(t) for all system sizes N = 512, 2,000, and 4,000 for all the studied temperatures. The very nice collapse of the data confirms that this model indeed has all the usual features of a glassy system. (Inset) Temperature dependence of τ_α for different system sizes.

As our model is not translationally invariant because of the presence of the quenched disorder, defining overlap between two replicas becomes easy and unambiguous. For example, if we have a system with translational symmetry, then in defining the overlap between two replicas we must account for the fact that two replicas may be similar even though they may be translated or rotated in space (40). We defined the overlap between two replicas using the window function w(x), which is 1 if x < 0.30 and zero otherwise. We say the two replicas are similar if, for each particle at position 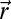in replica 1, there is a particle of replica 2 within a sphere of radius 0.30 (see Replica Overlap and Extraction of Static Length Scale for details). We also defined local overlap and calculated the corresponding spatial correlation function to extract the static length scale over which the replicas are similar. In Fig. 1 Lower Left, the extracted static correlation length of two replicas [see Replica Overlap and Extraction of Static Length Scale for details (41)]. The finite size effect seems to die out quickly once we go to N = 2,000 system size for lower temperatures. The modest growth of the static length scale in this temperature range is very similar to other glass models. Fig. 1 Lower Right Inset shows the dependence of the relaxation time with this length scale (see Relationship Between Length Scale and Relaxation Time for details). The apparent universality for the two cases with different frozen particle density also is in agreement with the recent findings for usual glass models (42, 43).

To achieve equilibration at even lower temperatures, we implemented parallel tempering simulation methods following ref. 44 but restricted ourselves to systems up to N = 250. The details of the simulation method and the parameters used are given in SI Materials and Methods, Parallel Tempering Methods. We parallelized the parallel tempering method using message-passing interface routines to speed the simulation. We ran different replicas in different computer cores and found that the system could be equilibrated to very low temperatures within reasonable CPU time (∼12 h for N = 250 particles using 16 replicas in 16 cores). We checked to make sure the system did not crystallize, even at the lowest temperature studied. We believe parallel tempering methods work so well for our model because it has only positions to equilibrate and does not have any other compositional disorder that needs further equilibration. In Fig. 2 Left, we collapsed the probability distribution of potential energy P(E, T) for different temperatures according to the ansatz Eq. S3, on the probability distribution of the reference temperature T₀ = 0.425, to ascertain whether proper equilibration is achieved in our simulations (see SI Materials and Methods, Parallel Tempering Methods for details). The nice collapse of the data indicates that the equilibration is achieved with very good accuracy. Fig. 2 Right shows the temperature dependence of the average potential energy, and the inset shows the corresponding specific heat calculated from the fluctuation of potential energy. Although average potential energy does not show strong finite size effects, one can see a somewhat strong finite size effect in the specific heat. The nicely developed peak in the specific heat seems to be a precursor to a possible second-order phase transition, as also is seen in ref. 23. The usual discontinuity in the specific heat seems to remain rounded in a volume-independent fashion. Notice that at the lowest temperatures, we have simulated the specific heat drops to the Dulong–Petit value, suggesting that harmonic degrees of freedom are the most relevant ones at these temperatures.

Fig. 2.

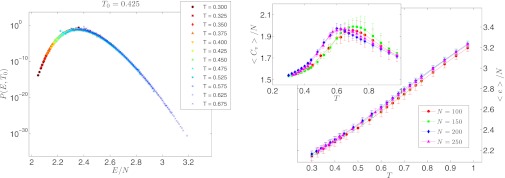
(Left) Collapse of distribution of energy P(E) for different temperatures on the distribution of P(E, T₀) with T₀ = 0.425 in the parallel tempering run for N = 100 system size according to Eq. S3 to check the equilibration. The nice collapse confirms that very good equilibration is achieved using the parallel tempering method for lower temperatures. (Right) Temperature dependence of the energy for different system sizes. One can see that the finite size effect is not very strong here. (Inset) Specific heat calculated from the fluctuation of potential energy for different system sizes. Some finite size effects may be seen here.

In Fig. 3, the temperature evolution of the distribution of overlap q is shown for six different system sizes. One clearly can see the change in distribution from Gaussian to bimodal with decreasing temperature. The distribution seems to deviate from the Gaussian one at temperatures close to the temperature at which the specific heat also shows a peak as a function of temperature for that system size. The shape of the distribution as a function of the temperature recalls what happens in mean field theory in the replica approach: below the critical temperature, a peak at higher values of q appears, whereas the low q peak has an intensity proportional to the temperature.

Fig. 3.

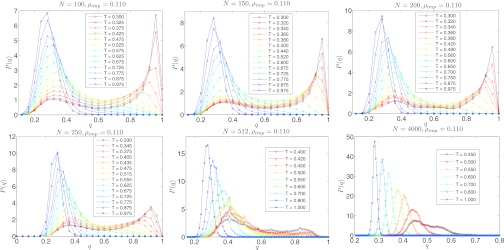
Temperature evolution of the probability distribution of overlap q for six different system sizes, N = 100, 150, 200, 250, 512, and 4,000.

In Fig. 4 Left, the temperature dependence of the overlap (see Materials and Methods for details on definition) for different system sizes is shown, and one clearly can see that for larger system sizes, the overlap seems to change more sharply. The corresponding susceptibility is given by χ_SG = (N − N_imp)[〈δq²〉], where 〈.〉 is the thermal averaging and [.] means the averaging over the different realizations of the disorder. N_imp is the number of impurity particles in the system given by N_imp = ρ_impN. In Fig. 4 Center, the susceptibility shows dramatic variation with temperature, and at lower temperatures the susceptibility also seems to change quite strongly with system size. For system size N = 250, the susceptibility changes by a factor of almost 50 compared with its high temperature value. With these data, divergence of the susceptibility at lower temperatures in the thermodynamic limit cannot be established, but the strong increase in its value with the system size is encouraging. We have tried to collapse the susceptibility data for different system sizes using the finite size scaling ansatz (L ≡ N^1/3):

Fig. 4.

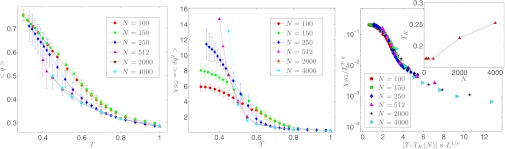
(Left) Temperature dependence of overlap for different system sizes. Bigger system sizes seem to show sharper changes of overlap q with temperature. (Center) Spin glass susceptibility is plotted as a function of temperature for the studied system sizes. The strong variation with temperature is remarkable. Notice the strong system size dependence of susceptibility at lower temperatures. Currently, we cannot say whether this susceptibility will diverge with decreasing temperature in a thermodynamic limit, as the system sizes studied here are still quite small. One must study bigger system sizes to determine the possible divergence of the spin glass susceptibility at lower temperatures. (Right) Scaling collapse of the spin glass susceptibility using the scaling ansatz Eq. 1. The exponents are η ≃ −0.1, ν ≃ 1.0 with T_K as shown in the Inset.

with rather poor results. A better collapse is shown in Fig. 4 Right, with η ≃ −0.1, ν ≃ 1.0, and T_K(L) now being a function of system size L. It is important to notice that as T_K grows with system size, it is reasonable that the divergence temperature will not go to zero in the thermodynamic limit. The data seem to indicate a possible nonzero temperature thermodynamical transition of second order in nature. The inability to collapse the data with a size-independent critical temperature may be the effect of the strong finite size-scaling corrections: the system sizes studied here are relatively small. A different scenario (in the thermodynamic limit) would be a strong increase in the susceptibility approaching the mode-coupling transition temperature followed by a cross-over to a different behavior at low temperature. We noted that the susceptibility data for N = 4,000, T ≥ 0.45 (that should have small finite size effects) are well fitted by a power law, with a critical temperature ∼0.4, i.e., the putative mode-coupling transition. Much more extensive simulations are needed to better understand the nature of the transition, if any.

These results are very similar to the one obtained for the finite range p-spin glass model in 3D in ref. 23. At this stage, one should take it only as a qualitative similarity. Further study is needed to ascertain the universality classes of these models to compare them quantitatively. These 3D p-spin glass models show a transition that is neither discontinuous [1 replica symmetry breaking (RSB) type] nor continuous (full-RSB type): the deep reasons for this behavior are not clear (45). On the other hand, structural glasses are more similar to the 1RSB-type (RFOT) transition, although first one still must pinpoint the transition in structural glasses to make any concrete statement. Therefore, it is not clear presently whether the current model is more similar to the spin glass or the structural glass models. Qualitatively, it can be seen that this model has all the typical behaviors of a usual glassy system. We hope this model will help us bridge the gap between spin glass and structural glass and shed some light on the mysteries of structural glass.

MCT calculations in similar geometry for the hard sphere system in ref. 35 suggest that for a given packing fraction, there is a critical density of the frozen particles and the time dependence of the two-point correlation function will change from two steps to one step. Although the precise pinning criterion is different from our study, we want to determine whether one can qualitatively recover some of these MCT predictions and to make sure we are not very close to the critical density. We performed similar studies for different ρ_imp for N = 100 and calculated the overlap distribution P(q). One clearly can see in Fig. 5 that there is no qualitative change in behavior with different pinning densities. Although one does not expect the MCT predictions to be strictly obeyed in real systems, it seems one must go to a higher pinning density to clarify this connection. In Fig. 5 Right, we show how 〈q〉 changes with ρ_imp as a function of temperature, and the top right inset shows the corresponding susceptibility.

Fig. 5.

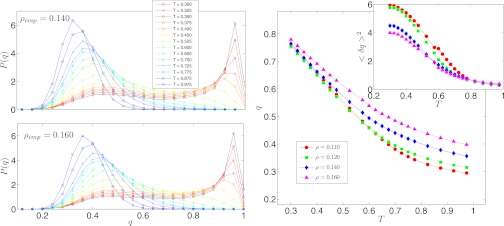
Data for N = 100. (Left) Distribution of overlap P(q) system sizes for two different concentrations of frozen particles. There is no strong qualitative difference between these distributions for two concentrations. (Right) Average overlap 〈q〉 as a function of temperature for different concentrations of frozen particles. (Right Inset) Dependence of susceptibility on concentration ρ_imp.

Conclusions

We showed how a very simple particle model with random pinning may be used to explore the glassy phase at a deep supercooled regime, as well as how this model may be used to compute different spin glass correlation functions to shed light on the relationship between spin glass transition and structural glass transition, which is the basis for most of the recent theories of structural glasses. This model also may be used to determine the relationship between different length scales, as in this model the length scale is calculated directly from the spin glass order parameter correlation function. It would be extremely interesting to arrive at a precise determination of the phase structure of the model and to compare it with accurate numerical simulations.

Materials and Methods

Simulation Details.

The interaction potential for r_ij ≤ x_c is given by

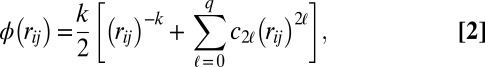whereas it is 0 for r_ij ≤ x_c, where r_ij is the distance between particles i and j, and x_c is the dimensionless length for which the potential will vanish continuously up to q derivatives. The coefficients c₂ℓ are given in ref. 14. We chose the parameters x_c = 1.3854, k = 10, and q = 2.

Dynamics.

We studied the dynamics using the two-point overlap correlation function 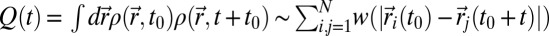, where 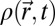is particle density at space point 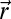at time t, and w(r) = 1, if r ≤ a and zero otherwise. Average over the time origin t₀ is assumed. The window function [a = 0.30] is used to remove the fluctuations in particle positions due to small-amplitude vibrational motion. In the definition of Q(t), the contribution due only to the self-term is denoted as Q_s(t). The structural relaxation time τ_α is the time where Q_s(τ_α) = 1/e.

Replica Overlap and Extraction of Static Length Scale.

In this section, we explain how we have extracted the growing static length scale in this system. We followed the method used in ref. 8, which is explained briefly below. We start with the following definition of overlap between two replica: 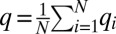, where 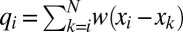with w(x) = 1 for x < 0.3 else 0. Now we define the coarse grain variable as 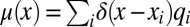and defined f(r) = 〈μ(x)μ(y)〉, where z = |x − y|. Now to remove the natural oscillation in the function f(r), we divide the function by pair correlation function g(r) to define another function c(r) =f(r)/g(r), and fit the function to 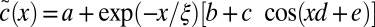to extract the length scale ξ. We extracted the correlation length scale for the N = 512, 2,000, and 4,000 system sizes, which have been equilibrated using standard molecular dynamics simulations using the Berendsen thermostat (46), and we studied the system in the temperature window T ∈ {0.400, 1.000}. We averaged the data over 20 different realizations of the disorder. For the last three temperatures, T = 0.400, 0.420, and 0.450, we averaged the data over 40 realizations of the disorder.

Relationship Between Length Scale and Relaxation Time.

We start with the ansatz for the relationship between relaxation time τ_α and the static correlation length ξ. 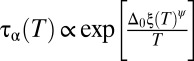, where Δ₀ is a nonuniversal coefficient that depends on the details of the glass former. Now at reference temperature T = T₀ (the highest temperature in this case), we define the typical length to be ξ₀; then, the relaxation time at that temperature is 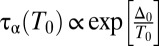. Therefore, we have the following relationship:

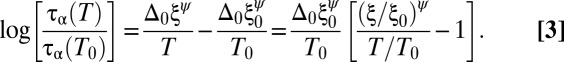As the prefactor Δ₀ is not known a priori for different models, we chose Δ₀ = 1.0, 1.11 for ρ_imp = 0.090, and 0.110, respectively in Fig. 1. We also chose ψ = 1.0 for these two cases.