Reconciling differential gene expression data with molecular interaction networks

Abstract

Motivation: Many techniques have been developed to compute the response network of a cell. A recent trend in this area is to compute response networks of small size, with the rationale that only part of a pathway is often changed by disease and that interpreting small subnetworks is easier than interpreting larger ones. However, these methods may not uncover the spectrum of pathways perturbed in a particular experiment or disease.

Results: To avoid these difficulties, we propose to use algorithms that reconcile case-control DNA microarray data with a molecular interaction network by modifying per-gene differential expression P-values such that two genes connected by an interaction show similar changes in their gene expression values. We provide a novel evaluation of four methods from this class of algorithms. We enumerate three desirable properties that this class of algorithms should address. These properties seek to maintain that the returned gene rankings are specific to the condition being studied. Moreover, to ease interpretation, highly ranked genes should participate in coherent network structures and should be functionally enriched with relevant biological pathways. We comprehensively evaluate the extent to which each algorithm addresses these properties on a compendium of gene expression data for 54 diverse human diseases. We show that the reconciled gene rankings can identify novel disease-related functions that are missed by analyzing expression data alone.

Availability: C++ software implementing our algorithms is available in the NetworkReconciliation package as part of the Biorithm software suite under the GNU General Public License: http://bioinformatics.cs.vt.edu/∼murali/software/biorithm-docs.

Contact: murali@cs.vt.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

A cell’s response to its environment is governed by an intricate network of molecular interactions. These interactions dynamically change in response to a myriad of cues. Therefore, discovering the response network, i.e. the set of molecular interactions that are active in a given cellular context is a fundamental question in computational systems biology (Ideker and Sharan, 2008). Many response network algorithms integrate molecular interaction networks with treatment-control differential expression data, which quantifies the statistical significance of the difference between the expression of genes under two conditions, e.g. diseased versus healthy cells (Beisser et al., 2010; Keller et al., 2009; Qiu et al., 2010; Ulitsky et al., 2010). Given several treatment and control samples, these methods compute a P-value for each gene that indicates the statistical significance of its differential expression between treatment and control. These approaches typically integrate such expression data with the interaction network by directly using each gene’s P-value or some transformation of the P-value as the weight of the gene in the network. Ideker et al. (2002) pioneered this type of analysis. After converting per-gene P-values into z-scores, they computed connected subgraphs with high aggregate z-scores. Beisser et al. (2010) extended the approach of Ideker et al. (2002) by solving the prize-collecting Steiner problem. Chowdhury et al. (2011) identified dysregulated subnetworks by computing state functions that indicate which combination of up- and down-regulated genes within the subnetwork can classify the disease of interest. The goal of many of these approaches is to score genes by combining their expression profiles across multiple samples and subsequently compute a (connected) subgraph such that the genes in it jointly optimize some combination of their scores. A recent trend, exemplified by BioNet (Beisser et al., 2010) and DEGAS (Ulitsky et al., 2010), is to focus on computing subgraphs with few nodes. The rationale behind these approaches is that small subnetworks enriched with dysregulated genes correspond to parts of the disease-related pathways. Such approaches were motivated by the observation that only part of a pathway is often changed by disease (Ulitsky et al., 2010) and that interpreting small subnetworks is easier than interpreting larger ones (Beisser et al., 2010). HotNet (Vandin et al., 2010) identifies significantly mutated pathways in cancer by marking mutated genes in an interaction network and propagating this information throughout the network by a method similar to the Heat Kernel (HK) (see Section 2).

While these recent methods are powerful at highlighting specific pathways and subnetworks, they have not been designed to uncover the spectrum of processes and pathways that might be perturbed in a particular experiment or disease. Applying functional enrichment tests to significantly differentially expressed genes can address this issue, but such analysis typically ignores underlying protein interactions. Top-ranking differentially expressed genes are often highly disconnected in the corresponding protein interaction network, making it difficult to discern the precise mechanisms by which enriched pathways affect the disease. Furthermore, insignificantly differentially expressed genes may represent crucial components of disease-related pathways, but such genes are often ignored by standard enrichment methods.

Motivated by these observations, rather than computing condition-specific subgraphs, we propose to use previously published approaches that reconcile differential gene expression P-values with an underlying interaction network to re-rank all genes with respect to the treatment of interest. We describe techniques developed in the machine learning and information retrieval communities (Zhu et al., 2003; Page et al., 1999; Chung, 2007; Zhou et al., 2004) to reconcile gene expression data with the interactions in the network by computing smooth functions over neighboring nodes in the underlying network. In this article, we use the negative logarithm of the per-gene P-values (which do not directly incorporate any interaction data) as prior indicators of each gene’s relevance to a particular treatment; we describe mathematical functions that allow the expression values to change so that two genes connected by an interaction have similar values, while controlling the deviation of those values from their original settings. This modification allows genes with no significant differential expression to be re-ranked highly if their products interact with the products of many significantly differentially expressed genes.

This work offers the following three novel contributions. First, we propose that such reconciliation algorithms should strive to maintain the following properties:

1. Top-ranking genes after reconciliation should participate in coherent network structures, i.e. interacting genes should receive similar scores. This property can assist in the functional evaluation of top-ranking genes.

2. Reconciled gene rankings given by different treatments should be dissimilar, especially among top-ranking genes. This requirement ensures that the process of reconciliation does not dilute the differences between the transcriptional signatures of distinct diseases or treatments.

3. Top-ranking reconciled genes should be functionally coherent.

Second, we comprehensively assess the extent to which each algorithm addresses these three properties. Third, we evaluate each approach on a large compendium of gene expression data that includes 54 diverse human diseases. We apply a state-of-the-art functional enrichment algorithm (Bauer et al., 2010) to address the functional coherence of the gene rankings provided by the reconciliation algorithms. We demonstrate that the reconciled gene rankings identify disease-related functions that would be missed by analyzing statistically significant differentially expressed genes alone.

2 METHODS

Let G(V, E) denote an undirected protein interaction graph in an organism, where V is the set of nodes and E is the set of undirected edges, in which each edge (u, v) represents an interaction between genes 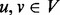. We denote the weight of an edge (u, v) by w_uv > 0. The larger the weight of an interaction, the larger is our belief that u and v indeed physically interact in the cell. Let N_u denote the set of neighbors of node u in G and let 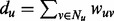denote the weighted degree of u.

Given some biological condition, let 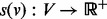be a function that maps genes in V to a non-negative real number representing their degree of perturbation in the contrast between the condition and an appropriate control (e.g. brain cells from patients diagnosed with Alzheimer’s disease (AD) and healthy brain cells). The larger the value of s(v), the more we consider the gene to be perturbed in the disease compared with the control. We compute s(v) as the negative absolute value of the base 10 logarithm of the gene’s P-value. We normalize the s(v) values so that they sum to 1. These represent the starting values for each node in V. Note that s(v) represents the degree of peturbation of gene v but does not record whether the gene is up- or down-regulated.

Interacting genes often participate in the same protein complex, are members of the same biological pathway or are controlled by the same transcription factor. Consequently, interacting gene pairs commonly display similar expression profiles. The fundamental intuition underlying our approach is that if two genes u and v are connected by a highly weighted interaction in G, then s(u) and s(v) should maintain similar values. Furthermore, the larger the value of w_uv, the closer s(u) and s(v) should be. This assumption enables the approaches presented here to elucidate highly relevant genes that may be missed by differential gene expression studies alone. For example, genes within the same complex or pathway may not be individually perturbed to a significant extent, but we may be able to exploit the interactions among them to recognize that the complex or pathway is perturbed as a whole. Guided by this intuition, we propose to compute a value p(v) between 0 and 1 for every node 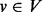. We want the value of p(v) to simultaneously balance two potentially conflicting constraints:

1. p(v) remains close to v’s initial value s(v).

2. p(v) is similar to p(u) for every neighbor .

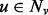We describe four different methods for computing p(v): Vanilla Algorithm (V), PageRank (PR), GeneMANIA (GM) and Heat Kernel (HK). These methods were developed previously in machine learning and information retrieval (Zhu et al., 2003; Page et al., 1999; Chung, 2007; Zhou et al., 2004) and have proven widely applicable in computational biology (Mostafavi et al., 2008; Komurov et al., 2010; Vanunu et al., 2010; Gonçalves et al., 2011; Köhler et al., 2008; Winter et al., 2012; Johannes et al., 2010; Nitsch et al., 2010; Vert and Kanehisa, 2003). Each of these algorithms appears in the literature under different names; we select the most recognizable names from the literature.

For the first three methods, we describe an energy function over the graph G that, when minimized, addresses the two constraints listed above. We then describe an iterative algorithm for each method that efficiently minimizes the energy function and provably converges to the optimum theoretical solution. We are unable to formulate a similar energy function for the fourth method, HK. However, we describe a well-known approximation to the discrete HK equation. This approximation yields a computationally efficient iterative solution similar to those used for the other three methods. We omit well-known proofs of convergence for each approach.

2.1 Vanilla algorithm

The Vanilla algorithm seeks to minimize following energy function:

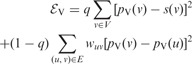When we compute the values of 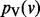that minimize 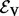, the first sum ensures that 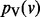remains close to s(v) for each node v in G, while the second sum ensures that 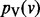remains close to 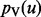for every 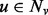. The parameter q, for 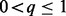, balances the contribution of each sum to the energy function. Because 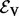is a quadratic function of the 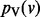values, we can minimize it by setting its partial derivative with respect to each 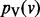to 0, obtaining the following linear system:

We compute 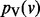using an iterative algorithm on G. We initialize the value at node v to s(v). If we use 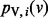to denote the value of node v at iteration i, we can write the following recurrence for :

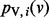As i tends to infinity, for each node v, converges to .

2.2 PageRank

In the formulation of , the contribution of a node is proportional to its weighted degree. Therefore, nodes with high weighted degree may have an unduly large influence on the solution. The PR approach (Page et al., 1999; Komurov et al., 2010; Winter et al., 2012; Johannes et al., 2010) accounts for the effect of the weighted degree of each node by minimizing a slightly different energy function on G:

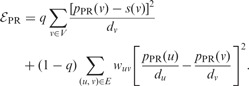In the second sum, we divide each occurrence of p_PR (v) by d_v to adjust for the weighted degree of node v. As before, the parameter q serves to balance the conflicting constraints represented by each of the two sums in . Because is a quadratic function of the values, we minimize it by setting its partial derivative with respect to each 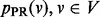to 0, obtaining the following linear system:

2.3 GeneMANIA

The GM method (Zhou et al., 2004; Mostafavi et al., 2008; Vanunu et al., 2010) is motivated by similar concern from the PR method that nodes with high weighted degree may have disproportionately large effect on the final node values. Therefore, GM seeks to minimize the following energy function on G:

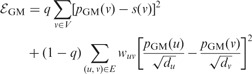In the second sum, we divide each occurrence of p_GM (v) by 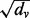(compared with dividing by d_v in PR) to adjust for the weighted degree of node v. Again, q balances the contribution from each sum in the energy function. We minimize 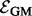by setting its partial derivative with respect to each 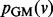to 0, achieving the following linear system:

2.4 Heat kernel

The Heat Kernel of a graph describes the dispersion of heat throughout a network over time. Here, the amount of heat corresponds to the degree of perturbation of each gene, represented by a node in the network, to the disease of interest. The HK is given by the following equation (Chung, 2007; Nitsch et al., 2010; Vert and Kanehisa, 2003):

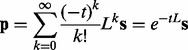(1)

where t parameterizes the rate of heat dispersion, and L describes the edges between nodes in the network. We define L = I − W, where I is the identity matrix, and W is a normalized edge weight matrix such that 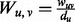. Because directly computing the matrix exponential in Equation 1 is computationally expensive, we use the approximation

which converges to Equation 1 as 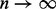. We must select n large enough such that the approximation given by 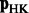is sufficiently close to Equation 1. We select n = 100, as this value performed well for Web graphs (Yang et al., 2007), which are at least an order of magnitude larger than the biological networks we used. We use the following algorithm to iteratively compute 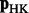. Let 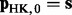and recursively define

3 DATASETS

Gene expression data.

We used gene expression data for 54 different human diseases and for the corresponding normal tissues (Suthram et al., 2010). A complete list of diseases is available in the Supplementary Text. For each disease and its corresponding control, we applied Linear Models for Microarray Data (LIMMA) (Smyth, 2005) to these DNA microarray data to compute a t-statistic and a P-value indicating the statistical significance of the differential expression of each gene in that disease, when compared with the corresponding control. We used the negative base 10 logarithm of each gene’s P-value as the initial value for each gene in the network, and we normalized these values so they summed to 1. We considered alternatively computing mutual information between each gene and the sample phenotype labels, but we were concerned that the small number of samples may not yield reliable mutual information values. Nonetheless, our methods can be readily applied to mutual information values, and we plan to investigate this extension in future research.

Interaction network.

We used the human MiMI protein interaction network (Tarcea et al., 2009) containing 11,074 proteins and 77,952 non-self interactions. We estimated the reliability of each interaction by its FS-weight (Chua et al., 2006) (see Supplementary Text).

Functional enrichment.

We annotated the genes in our network with 3272 gene sets from MSigDB version 3.0 category C2 (Subramanian et al., 2005), 1703 CORUM complexes (Ruepp et al., 2008), 223 NCI PID curated pathways (Schaefer et al., 2009) and 75 NetPath pathways (Kandasamy et al., 2010). We performed all tests for functional enrichment using Model-based Gene Set Analysis (MGSA) (Bauer et al., 2010) directly from the R Bioconductor package. We discuss our selection of MGSA in the Supplementary Text. We applied MGSA to the top 250 genes ranked only by their differential expression P-values and to the top 250 genes after applying our reconciliation algorithms.

4 RESULTS

We divide our results into five parts to address the desirable properties listed in the introduction. First, in Section 4.1, we examine topological properties of the final gene rankings given by each algorithm, providing insight on how these approaches address the first property. In Section 4.2, we simultaneously address the second and third properties by analyzing how well the gene rankings for seven diseases recover the genes in canonical pathways for those diseases. In Section 4.3, we discuss similarities between the gene rankings produced by each algorithm across all diseases. Our main concern in these evaluations is the extent to which disease-specific signals are not masked by network-based effects, directly addressing the second desirable property. In Section 4.4, we perform functional enrichment tests on the top-ranking genes reported by our reconciliation methods. This analysis further reinforces our conclusions from the previous section and addresses the final desirable property that top-ranking genes should demonstrate functional coherence. Lastly, in Section 4.5, we investigate the insulin-mediated glucose transport pathway in several diseases related to the brain. We demonstrate that network reconciliation identifies disease-related proteins from this pathway that are missed by differential expression analysis.

We performed this analysis over a wide range of values for the input parameter q; we report results for 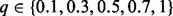. Note that the HK is parametrized by t > 0. We used the transformation q = 2^−t to determine values that covered a reasonable range of possible values for t. This transformation has the additional benefit that q tends to 0 (respectively, 1) as t tends to ∞ (respectively, 0). Because large t increases the dispersion of heat through the network, the interpretation of q remains the same for all algorithms: large q gives more weight to the starting values, while small q emphasizes network topology.

4.1 Network coherence

The first desirable property of reconciliation algorithms seeks to identify coherent network structures among top-ranking genes. Each algorithm ranks disease-related genes highly by taking into account both expression and interaction data. However, such rankings may prove difficult to interpret if the top-ranking genes are sparsely connected, inducing many small connected components. Indeed, a lack of connectivity among such components may conceal the mechanisms by which the disease-related genes interact. We computed the number of connected components induced in the MiMI network by the top k genes reported by each of the four reconciliation algorithms for .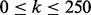

Supplementary Figure S1 illustrates the change in the number of connected components induced by the top k genes reported by each algorithm. Surprisingly, for Vanilla, the connectivity among top-ranking genes decreases when more emphasis is placed on the network. Indeed, a decrease in q results in many more connected components among top-ranking genes. Because top-ranking genes reported by Vanilla tend to be less connected as the network is given higher emphasis, we conclude that the V performs poorly with respect to the network connectivity property. However, PR, GM and HK drastically decrease the number of connected components as q decreases, indicating high network coherence for these algorithms. In Section 2.1 of the Supplementary Text, we compare these connected component counts from the true data to 100 randomized gene expression datasets, demonstrating that the ranks given by the true expression data consistently display higher network coherence.

4.2 Recovering canonical pathways

We assessed the ability of reconciliation algorithms to recover genes involved in the canonical pathway for a disease. Of the 54 diseases in our gene expression data, seven were represented in the Kyoto Encylopedia of Genes and Genomes (KEGG) (Kanehisa et al., 2008), which maintains manually curated pathways of disease mechanisms. We applied the network reconciliation algorithms to each of these seven diseases, namely, malignant melanoma, Huntington’s disease (HD), glioblastoma, endometriosis, dilated cardiomyopathy, Alzheimer’s disease (AD) and acute myeloid leukemia. We assessed how highly the genes in each disease pathway are ranked by the reconciliation process and by their initial differential expression values.

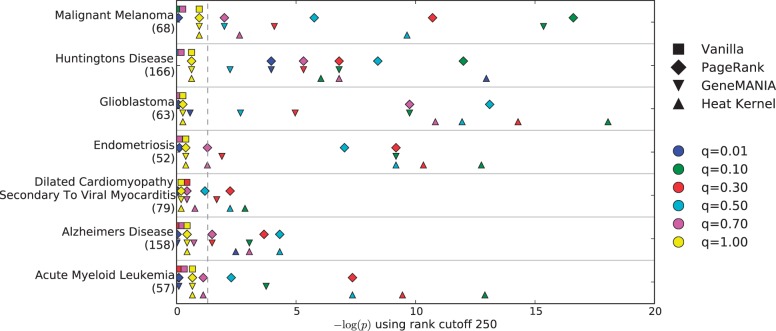
Figure 1 displays the hypergeometric P-values of the overlap between the top 250 genes ranked by each method and the set of genes in the corresponding KEGG pathway. We plot the negative logarithm of each P-value. Points to the right of the dashed gray line indicate significant findings (P < 0.05). Results using rank cutoffs of 500 and 1000 are available in the Supplementary Material and reinforce the findings presented here. Figure 1 demonstrates that an insignificant number of genes in each of the seven KEGG pathways are among the top-ranked genes when considering differential expression P-values alone (yellow points). Additionally, Vanilla does not highly rank a significant number of KEGG pathway genes for any of the seven diseases or for any value of the input parameter q. In contrast, a statistically significant number of KEGG pathway genes appear among the top 250 genes ranked by PR, GM and HK for every disease and at least one value of q. These findings indicate that reconciling gene expression values with an underlying interaction network provides insights into disease mechanisms that may be missed by expression studies alone.

Fig. 1.

Negative logarithms of the hypergeometric P-values indicating the significance of the overlap between the members of seven KEGG pathways and the top 250 genes ranked by each algorithm for the corresponding disease. The number of genes in each KEGG pathway is provided in parentheses. Points to the right of the dashed gray line indicate significant P-values (P < 0.05)

The value of q that results in the most significant overlap with the KEGG pathway varies considerably depending on the disease and the algorithm. We note that setting q = 0.5 for the PR algorithm results in the most significant P-values for two of the three brain diseases with canonical pathways in KEGG (glioblastoma and AD). Therefore, we set q = 0.5 when we perform a focused analysis of brain diseases in Sections 4.4 and 4.5, although other choices are reasonable. Because no value of q for Vanilla successfully identifies disease genes from their canonical pathways, we drop this algorithm from analysis in the remaining sections and provide results for Vanilla in the Supplementary Text.

4.3 Similarity between gene rankings

Next, we investigate how each algorithm distinguishes different diseases. Ideally, applying a reconciliation algorithm to transcriptional signatures from two diseases that affect different biological pathways should result in different gene rankings, specifically among the top-ranking genes. For PR, GM and HK, we examine the difference between the final gene rankings given by each algorithm across all 54 diseases. Because this collection of diseases affects a wide variety of organs, tissues and cell types, we expect their disease-related genes (and thus the top-ranking genes) to vary considerably.

For each algorithm, we computed the Jaccard index of the top k genes after reconciliation between every pair of diseases for 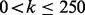. The Jaccard index measures the size of the intersection divided by the size of the union of two sets. Thus, a high Jaccard index between a pair of diseases indicates that the top k genes are highly similar between diseases, while low Jaccard index suggests the algorithm maintains disease specificity in its final rankings. Figure 2 illustrates the Jaccard indices for each algorithm. Each point indicates the average Jaccard index across all 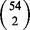pairs of diseases. As expected, the Jaccard index increases with a decrease in q for any rank cutoff. Indeed, as q decreases, the network plays a more pronounced role in each algorithm and provides the same signal regardless of the input disease. Thus, to minimize the overlap between the top k genes reported for each pair of diseases, one could simply use the initial rankings given solely by the expression data (i.e. q = 1). However, this has the obvious drawback that the connectivity of the proteins is completely ignored.

Fig. 2.

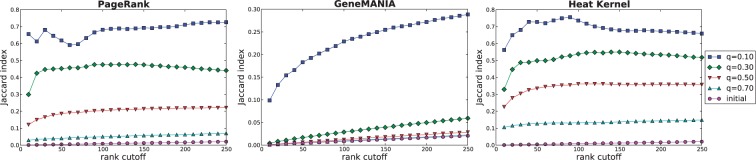
The Jaccard index of the top k genes reported by each algorithm for a pair of different diseases. Each point indicates the average Jaccard index of all 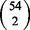pairs of diseases using a particular value of q as input to the algorithm

In general, for every value of q, the GM method results in a much lower Jaccard index than the other algorithms. Selecting q = 0.1 is clearly a bad choice, as the Jaccard index of the top k genes between any pair of disease is ∼0.7 for PR and HK. However, setting q = 0.5 or higher results in a reasonably low Jaccard index for all algorithms. For the functional enrichment analysis presented in the remaining sections, we set q = 0.5, as this parameter value jointly addresses the desirable properties for PR, GM and HK in the analyses presented thus far.

4.4 Functional enrichment analysis

Inter-disease functional similarity.

We applied functional enrichment tests to further evaluate the gene rankings. Using the gene sets and pathways described in Section 3 as protein functional annotations, we applied MGSA to the top 250 genes reported by each reconciliation method on seven diseases that affect the brain: AD, bipolar disorder, glioblastoma, HD, Rett syndrome, schizophrenia and senescence. Figure 3(a) illustrates the Jaccard index between the top k functions returned by MGSA, 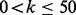, for each pair of brain disorders. While the Jaccard indices are not as low as those for the MGSA results applied to the initial gene rankings given by the expression data, there is a remarkably low overlap between the top functions reported for each pair of diseases. This result supports the findings in Section 4.3 that reconciled gene rankings maintain disease specificity. We demonstrate that enriched functions are also relevant to their corresponding diseases in Section 4.5.

Fig. 3.

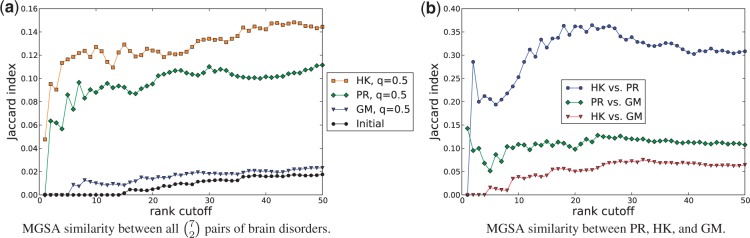
The Jaccard index of the top-ranking functions returned by MGSA on seven brain disorders. (a) MGSA similarity between all pairs of brain disorders. (b) MGSA similarity between PR, HK, and GM

Inter-algorithm functional similarity.

We also investigated the similarity between the functional results of different algorithms. In Figure 3(b), we show the average Jaccard index between the top k functions returned by MGSA for a pair of reconciliation algorithms applied to a single disease. We plot the average across the seven brain disorders. The Jaccard indices are highest for the pair of algorithms PR and HK at ∼0.3 for the first 50 functions. The small index for any pair of algorithms suggests that each algorithm probes a different space of functional annotations for the same disease. We find this to be a particularly striking finding. Because PR and HK show a high overlap (Jaccard index 0.7) between the top 250 genes reported by each algorithm on the same disease (Supplementary Fig. S4), we expected high similarity in gene rankings to translate into similar functional enrichment results. We plan to further explore this finding in future studies.

4.5 Insulin-mediated glucose transport in the brain

Finally, we further investigated how reconciliation algorithms addressed our fourth desirable property that genes involved in biological functions related to the disease of interest should be ranked highly. We were particularly interested in the effect of reconciliation algorithms on low-ranking genes (i.e., genes with insignificant differential expression between disease and control) annotated by such functions. Ideally, we hoped to see the values of such genes modified through the reconciliation process in such a way that most genes involved in relevant functions were re-ranked highly. For this analysis, we focused on the NCI PID pathway insulin-mediated glucose transport. We selected this pathway because dysregulation of insulin-mediated glucose uptake has been previously implicated in patients diagnosed with various neurodegenerative disorders, including AD and HD (Craft and Watson, 2004). After applying PR reconciliation, this function appears in the top 22 most enriched functions for four of the seven brain disorders (Table 1), including AD and HD.

Table 1.

Enrichment of the NCI pathway insulin-mediated glucose transport in the top 250 genes before and after applying PR to the expression profiles of seven brain disorders

Disease	Before PR		After PR
Alzheimer’s disease	0.0000	(3290)	0.8839	(2)
Bipolar disorder	0.0000	(1763)	0.0030	(431)
Glioblastoma	0.0000	(1963)	0.8340	(4)
Huntington’s disease	0.0060	(130)	0.3804	(22)
Rett syndrome	0.0000	(3244)	0.6333	(9)
Schizophrenia	0.0000	(3115)	0.0000	(3459)
Senescence	0.0000	(3384)	0.0067	(265)

The values are the posterior probabilities reported by MGSA, where higher value indicates a higher probability that the pathway is enriched. In parentheses, we report the rank of the pathway among 5273 gene sets.

Alzheimer’s disease.

Elderly patients diagnosed with AD show impaired glucose tolerance, often erroneously attributed to poor exercise and diet. However, reduced insulin-mediated glucose uptake is observed in early stage AD patients whose physical activity and dietary patterns do not differ from healthy adults (Craft and Watson, 2004). Thus, dysregulation of this pathway (i.e. enrichment in disease versus control) may provide an early indication of AD. For each of the seven brain diseases we studied, Table 1 reports the MGSA enrichment posterior probabilities for the NCI PID pathway insulin-mediated glucose transport in the top 250 proteins before and after applying the PR reconciliation method. This pathway was not enriched in the top 250 proteins ranked only by the differential expression of the corresponding genes. However, PR re-ranked proteins from the insulin-mediated glucose transport pathway highly, drastically increasing the enrichment of the pathway and moving this function from rank 3290 before reconciliation to 2 after applying PR. Thus, we identified a pathway whose role is highly relevant to AD but is missed using standard functional enrichment methods when only the gene expression data is used. By integrating the expression profile with a network of protein interactions, we were able to highlight this pathway by re-ranking relevant proteins whose corresponding genes are not significantly differentially expressed.

Huntington’s disease.

Figure 4(a) illustrates the subnetwork induced by proteins in the insulin-mediated glucose transport pathway. At the core of this pathway are seven proteins from the 14-3-3 protein family. The 14-3-3 proteins play a major role in cellular signal transduction, and they are known to appear abundantly throughout the brain. These proteins can bind to a wide variety of other human proteins, altering features of the target protein such as subcellular localization, functional activity and phosphorylation state (Dougherty and Morrison, 2004). Figure 4(a) demonstrates that most of the genes encoding the 14-3-3 proteins are not significantly differentially expressed in HD versus healthy samples; none of the seven genes appear in the top 250 significantly differentially expressed genes (with the first appearing only at rank 500). However, after applying network reconciliation, as Figure 4(b) illustrates, the ranks of all seven 14-3-3 proteins increased drastically (along with several additional members of the pathway). The 14-3-3 proteins were re-ranked highly because many nearby genes in the network were significantly differentially expressed, and their value propagated through the dense subnetwork of 14-3-3 proteins during the reconciliation process. Notice that the insulin-mediated glucose transport pathway was ranked highly in HD before and after applying PR (Table 1). However, 12 proteins from this pathway appeared in the top 250 proteins after reconciliation compared with just five before reconciliation. Thus, in this case, reconciliation did not identify a novel pathway related to the disease (as we discovered with AD), but reconciliation re-ranked highly relevant proteins that would be missed using differential gene expression alone. Furthermore, the role of this pathway in HD may be easier to interpret because the involvement of the 14-3-3 proteins is highlighted by reconciliation but missed otherwise.

Fig. 4.

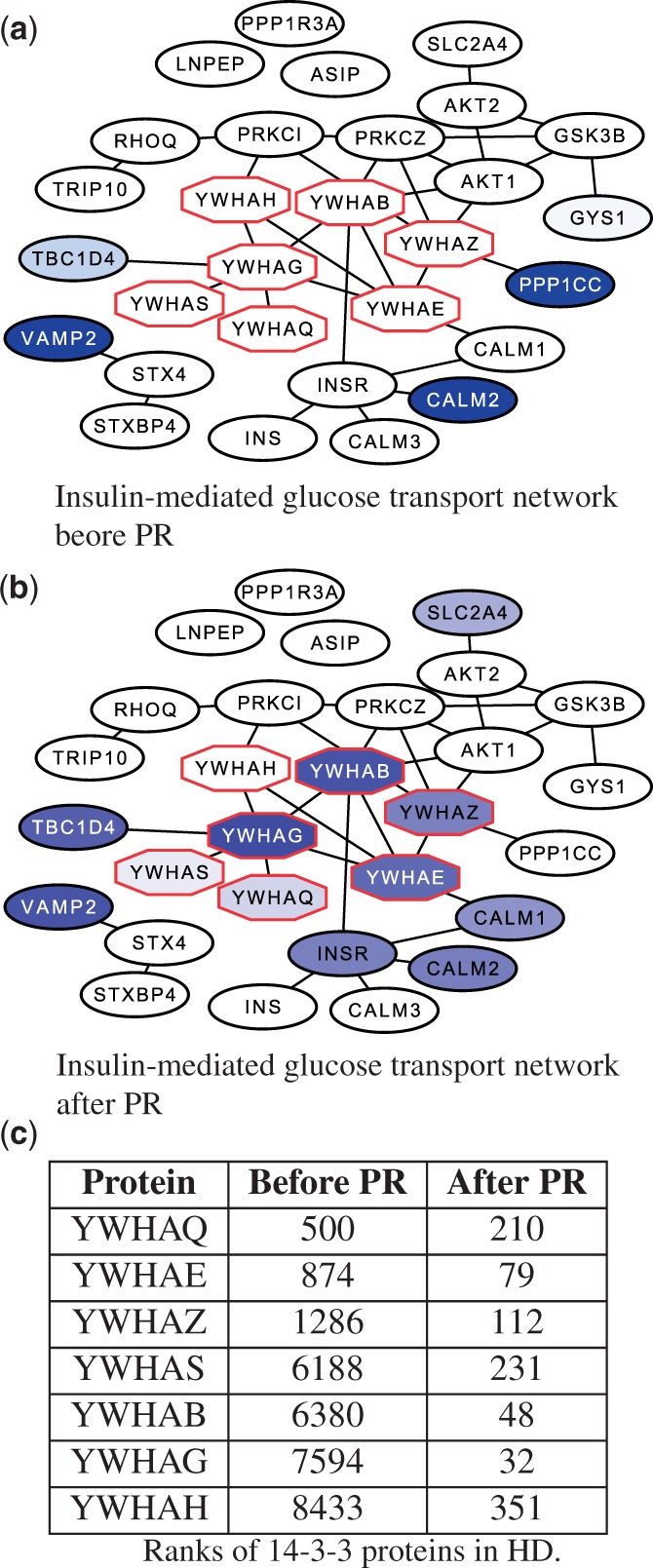
A comparison of the subnetwork induced by genes involved in the NCI PID pathway insulin-mediated glucose transport with nodes ranked by (a) differential expression P-values from patients diagnosed with HD and (b) after applying PR. Non-white nodes indicate genes ranked in the top 250, and darker nodes indicate higher ranking. Octagonal nodes indicate genes in the 14-3-3 family of proteins. Subnetwork visualizations for HK, GM and V are available in the Supplementary Text (Supplementary Fig. S6). (c) Ranks of 14-3-3 family proteins before and after applying PR to the HD expression data

High degree proteins.

One concern with our methodology is that the reconciliation approaches may overemphasize proteins with many neighbors in the network. Indeed, the reconciliation methods may be more likely to propagate value to nodes with many neighbors, and our analysis of AD and HD may be biased, as we have already mentioned that the 14-3-3 proteins are highly promiscuous. However, notice that the insulin-mediated glucose transport pathway is not found to be enriched in bipolar disorder, schizophrenia or senescence after reconciliation (Table 1). In fact, this pathway is even less enriched in schizophrenia after reconciliation, demonstrating that the enrichment results are not biased by such high degree nodes.

5 DISCUSSION

We described four approaches to integrate case-control gene expression data with molecular interaction networks. These methods actively modify gene expression measurements to match the constraints imposed by the edges in the network, while controlling the deviation of the modified values from their original settings. We enumerated three desirable biological properties that this class of algorithms should address. These properties aim to balance input from gene expression data with an underlying interaction network while maintaining that the returned gene rankings are specific to the condition being studied. Addressing any one of these properties alone may be trivial. For example, to address the first property that top-ranking genes should participate in coherent network structures, one could simply return a list of genes such that each gene in the list is connected to one of its predecessors in the list. Thus, any cutoff in the gene ranking induces a single connected component. However, addressing all three properties simultaneously is more difficult and warranted further investigation. We analyzed each algorithm using differential gene expression data from a variety of human diseases that interrogate vastly different organs and tissues. Ultimately, this work attests to the wide applicability of reconciliation algorithms and suggests reasonable values of their input parameters to address the three desirable properties. We demonstrated that i) PR, GM and HK always outperform Vanilla with respect to our primary motivating properties and ii) applying any of these three network reconciliation algorithms then analyzing the resulting gene ranks yields more interpretable results than analyzing the ranking of significantly differentially expressed genes alone.

In the future, we plan to consider other biologically relevant formulations of the energy function. An important extension is to situations that violate our assumption that two linked genes should be similarly perturbed in a condition. For instance, a transcription factor may be connected to a target gene that it down-regulates. In this situation, it seems appropriate to ensure that the transcription factor and its target have distinct values. More generally, the expression of a gene may have a complex dependence on those of its interactors. When such relationships are known, it will be useful to incorporate them into our formulation. Lastly, our methods use the significance of a gene’s differential expression while ignoring whether the gene is up- or down-regulated. Promising extensions may incorporate the direction of regulation as well as the mechanism of regulatory interactions.

Funding: This work was supported by National Science Foundation (NSF) Graduate Research Fellowship [to C.L.P.], NSF [CBET-0933225, DBI-1062380 to T.M.M.], National Institute of General Medical Sciences of the National Institutes of Health [R01GM095955 to T.M.M.] and Fralin Life Sciences Institute Summer Research Fellowship [to J.R.A.].

Conflict of interest: None declared.