Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Feb 28;3:1357. doi: 10.1038/srep01357

Enhancement of the finite-frequency superfluid response in the pseudogap regime of strongly disordered superconducting films

Mintu Mondal 1, Anand Kamlapure 1, Somesh Chandra Ganguli 1, John Jesudasan 1, Vivas Bagwe 1, Lara Benfatto 2, Pratap Raychaudhuri 1,a
PMCID: PMC3584313  PMID: 23446946

Abstract

The persistence of a soft gap in the density of states above the superconducting transition temperature Tc, the pseudogap, has long been thought to be a hallmark of unconventional high-temperature superconductors. However, in the last few years this paradigm has been strongly revised by increasing experimental evidence for the emergence of a pseudogap state in strongly-disordered conventional superconductors. Nonetheless, the nature of this state, probed primarily through scanning tunneling spectroscopy (STS) measurements, remains partly elusive. Here we show that the dynamic response above Tc, obtained from the complex ac conductivity, is highly modified in the pseudogap regime of strongly disordered NbN films. Below the pseudogap temperature, T*, the superfluid stiffness acquires a strong frequency dependence associated with a marked slowing down of critical fluctuations. When translated into the length-scale of fluctuations, our results suggest a scenario of thermal phase fluctuations between superconducting domains in a strongly disordered s-wave superconductor.

At the microscopic level, the superconducting (SC) state is characterized by two remarkable properties: (i) the pairing of electrons in bound states, i.e. Cooper pairs, leading to a gap Δ in the electronic excitation spectrum and (ii) the formation of a macroscopic phase coherent state of the Cooper pairs, responsible for the SC behavior. Based on the conventional Bardeen-Cooper-Shrieffer theory1, one expects the SC transition to happen at the temperature where Δ goes to zero2, since the energy cost of twisting the phase of the condensate, i.e. the superfluid stiffness J, is usually much larger than Δ. However, this central paradigm has been questioned within the context of underdoped high-temperature superconductors, where the pairing scale Δ, associated to the pseudogap (PG) state, is much larger than J, which gets reduced by the proximity to the Mott insulator3. More recently a series of experiments on strongly disordered s-wave superconductors4,5,6 (TiN, InOx and NbN) outlined a scenario, that bears some similarities with the case of high-temperature superconductors. Indeed, on the one hand it has been shown that a soft gap in the electronic excitation spectrum continues to persist in the tunneling density of states (t-DOS) up to a temperature T*, well above Tc. On the other hand disorder scattering reduces J, thereby rendering the system susceptible to phase fluctuations3. In addition, STS measurements revealed that at strong disorder the superconducting state becomes inhomogeneous, segregating into domains where the SC order parameter is large and regions where the order parameter is completely suppressed6,7,8. From the theoretical standpoint it is now understood that disorder contributes to maintain the paring scale finite at strong disorder, while phase fluctuations can drive the transition9,10,11. At the same time it has been suggested that strong disorder can induce a direct superconductor-insulator transition (SIT) by localization of Cooper pairs12. In such scenario several additional predictions have been made12,13 concerning the emergence of physical effects remnant of a glassy behavior, that can be evidenced for example by the statistical analysis of the inhomogenous order-parameter distribution observed by STS far below8 Tc. However, a clear picture of the relation between all these effects in the pseudogap (PG) state is still lacking, due to the inability of STS to probe the superfluid response of the system.

In this article, we address this problem through measurement of the ac complex conductivity, 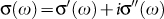Inline graphic, on NbN thin films with different levels of disorder using a broadband Corbino microwave spectrometer14,15,16 operating in the frequency range, 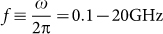Inline graphic. The advantage of this technique is that it is sensitive to superconducting correlations over finite time scales. Thus, it allows one to probe directly the remnant superfluid response of the system above Tc, that is the crucial quantity to look at in order to outline the nature of the PG state. In addition, the length scale of electron diffusion at microwave frequency is of the order of the nanometers, i.e. the same order of the inhomogeneity probed by STS. We then expect that this technique can also give us indirectly a picture of the spatial variation of the SC properties in the PG state, whose relevance below Tc has been well established by STS measurements6,7,8. In the superconducting state, where phase coherence extends over all length and time scales, the superfluid density (ns) and hence J can be determined from σ''(ω) using the relations2,3,

graphic file with name srep01357-m1.jpg

where e and m are the electronic charge and mass respectively, and a is the length scale associated with phase fluctuations, that is typically of the order of the dirty-limit coherence length, ξ0. Above Tc one can define a frequency-dependent stiffness 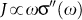Inline graphic which vanishes as 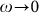Inline graphic but survives as long as SC correlations are finite on the time scale set by the inverse frequency. For ordinary Ginzburg-Landau (GL) like SC fluctuations17,18, short-lived Cooper pairs give a finite response over a small temperature and frequency range above Tc, due to the fact that the typical frequency scale of Cooper pairs 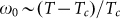Inline graphic becomes soft only near the transition. While this is indeed the case for our less disordered samples, the central observation of this study is that in strongly disordered NbN films, J becomes strongly dependent on the probing frequency below T*, signalizing an unexpected slowing down of the SC fluctuations. The persistence of the high-frequency superfluid response up to T* supports the scenario where the PG state consists of phase incoherent, slowly fluctuating domains while the superconducting state emerges at Tc when global phase coherence is established between all the domains.

Results

NbN as a model system to study the interplay of superconductivity and disorder

Samples used in this study consist of a set of epitaxial NbN thin films19 with different levels of disorder grown on single crystalline MgO substrates. The disorder is in the form of Nb vacancies in the NbN crystal lattice which is tuned by controlling the deposition conditions. Tc, defined as the temperature at which dc resistance goes below our measurable limit varies in the range Tc ≈ 15.71 – 3.14 K. The effective disorder, characterized using the product of the Fermi wave vector, kF, and electronic mean free path, l, is in the range kFl ~ 9.5 – 1.8. The thickness (t) of all films was ~50 nm which is much larger than the dirty limit coherence length20, ξ0 ~ 4−8 nm. The phase diagram of disordered NbN established earlier from STS and transport measurements on similar samples21 reveal that samples with Tc < 6 K show a pronounced PG phase with T* ~ 6–7 K.

Complex conductivity as a function of frequency and temperature

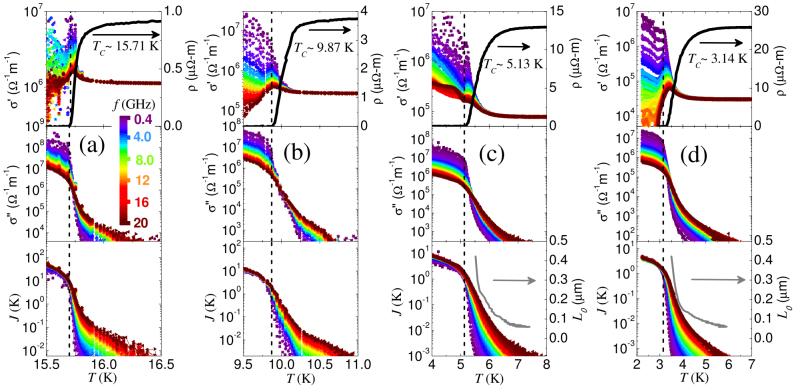
Figure 1(a)–(b) shows the representative data for σ'(ω) and σ''(ω) as a function of frequency at different temperatures for the sample with Tc ~ 3.14 K. Consistent with the expected behavior in the superconducting state, at low temperatures σ'(ω) shows a sharp peak as ω→0 whereas σ''(ω) varies as 1/ω (dashed line). Well above Tc, σ'(ω) is flat and featureless and σ''(ω) is within the noise level of our measurement consistent with the behavior in a normal metal at frequencies much smaller than the quasiparticle scattering rate, which is of the order of 1016 Hz in our NbN samples22. Figure 2(a)–(d) shows σ'(ω)-T, σ''(ω)-T and J-T at different frequencies for four samples with different Tc. All samples display a dissipative peak in σ'(ω) close to Tc. For low disordered samples σ''(ω) for all frequencies dropped below our measurement limit close to Tc. As shown later the narrow fluctuation regime in these samples is well described by GL Cooper-pairs fluctuations. On the other hand, samples with higher disorder show an extended fluctuation regime where σ''(ω) remains finite up to a temperature well above Tc. We convert σ''(ω) into J (from eqn. 1) using the experimental values of ξ0 obtained from upper critical field measurements20. For T ≪ Tc, J is frequency independent, showing that the phase rigidity is established over all time scales. However, for the samples with higher disorder (Fig. 2(c) and 2(d)), J becomes strongly frequency dependent above Tc: While at 0.4 GHz J falls below our experimental threshold, J ≤ 5*10−4 J (T = Tc), very close to Tc, with increase in frequency it acquires a long tail and remains finite well above Tc.

Figure 1. ac conductivity of NbN film with Tc ~ 3.14 K.

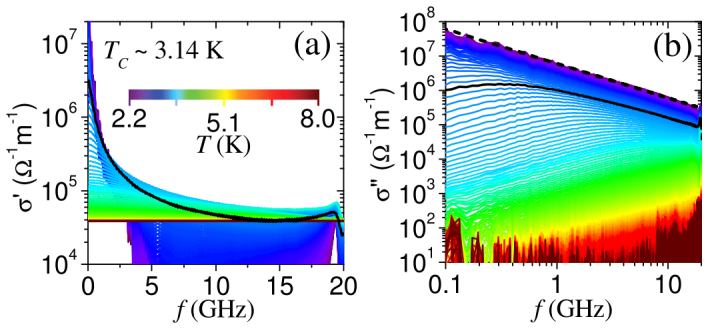
Figure 1

Open in a new tab

(a) σ' and (b) σ'' at different temperatures as a function of frequency; the solid black line shows the data at T = Tc.The color scale corresponding to the temperatures is shown in panel (a). The dashed line in (b) is a fit to σ''(ω) ∝ 1/ω for the data at 2.2 K.

Figure 2. Temperature dependence of σ and J at different frequencies.

Figure 2

Open in a new tab

Temperature dependence of σ' (upper panel), σ'' (middle panel) and J (lower panel) at different frequencies for four samples with (a) Tc ~ 15.7 K (b) Tc ~ 9.87 K (c) Tc ~ 5.13 K and (d) Tc ~ 3.14 K. The color scale showing different frequencies is displayed in (a). The solid (black) lines in the top panels show the temperature variation of resistivity (ρ). Vertical dashed lines correspond to Tc. The solid (gray) lines in the bottom panels of (c) and (d) show the variation of L0 above Tc.

Connection with the pseudogap state observed from STS measurements

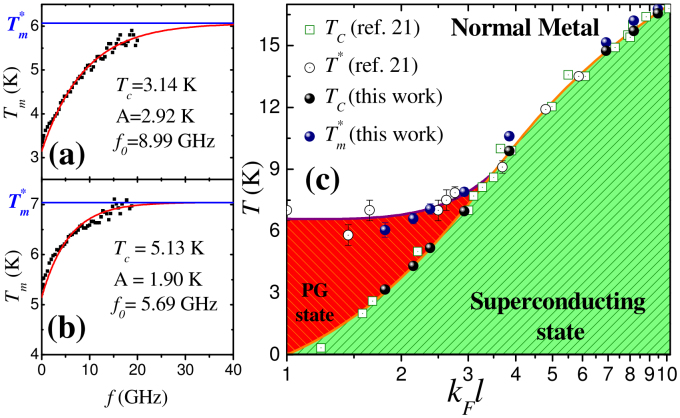
To understand the connection between these observations and the PG state observed in STS measurements21, we define 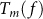Inline graphic as the temperature above which 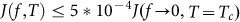Inline graphic. The variation of 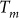Inline graphicwith frequency shows a trend which saturates at high frequencies and can be fitted well with an empirical relation of the form, 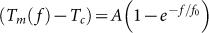Inline graphic (Fig. 3 (a–b)). Using the best fit values of A and f0, we determine the limiting value, 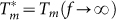Inline graphic. In Figure 3(c), we plot 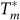Inline graphic and Tc for several samples along with the variation of T* and Tc obtained from STS measurements, as a function of kFl. Within the error limits of determining these temperatures, 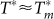Inline graphic, showing that the onset of the PG in the t-DOS coincides with the onset of finite J in the high frequency limit. Furthermore, only the samples in the disorder range where a PG state appears, show a large difference between Tc and 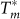Inline graphic. We therefore attribute the frequency dependence of J to a fundamental property related to the PG state.

Figure 3. Phase diagram as a function of disorder from microwave and STS measurements.

Figure 3

Open in a new tab

(a)–(b) Variation of Tm as a function of frequency, f, for the sample with Tc ~ 3.14 K and Tc ~ 5.13 K respectively. The red line shows a fit of the data with the empirical relation 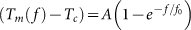Inline graphic; the best fit values of A and f0 are shown in the panels. The blue lines show 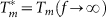Inline graphic. (c) Phase diagram showing Tc and T* obtained from STS measurements [Ref. 21] as a function of kFl along with Tc and 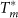Inline graphic obtained from microwave measurements. Samples with Tc < 6 K show a PG state above Tc.

Slowing down of critical fluctuations in the pseudogap regime

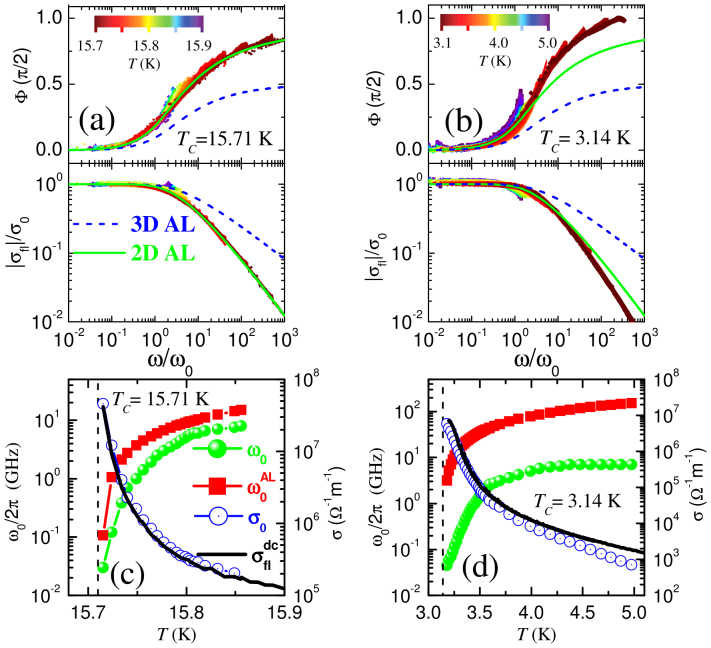
Having established the relation between the PG state and the finite high frequency phase stiffness, we now look at the fluctuation region above Tc more closely. On very general grounds, the fluctuation conductivity, σfl(ω) is predicted23 to scale at each temperature as 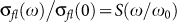Inline graphic, where ω0(T) is a characteristic fluctuation frequency. We obtain σfl(ω) from σ(ω) by subtracting the dc value of the conductivity above 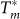Inline graphic. Since the phase angle 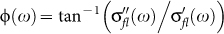Inline graphic is the same as the phase angle of S, by scaling φ(ω) at each temperature with a different ω0 one can expect a collapse of all data on a single curve. |σfl(ω)| would similarly scale when normalized by σfl(0) for the same values of ω0 at each temperature. Such a scaling works for all the samples in the frequency range 0.4 – 12 GHz as shown in Figure 4(a) and 4(b) for the samples with Tc ~ 15.71 K and 3.14 K respectively. We observe a very good agreement between the temperature variation of σfl(0) and dc fluctuation conductivity, 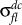Inline graphic obtained from the temperature dependence of d.c. resistivity (ρ) measured in the same run (Fig. 4(c) and 4(d)) showing the consistency of our scaling procedure. We can then have a closer look at the form of the scaling function S obtained for our films. In general, the function S is constrained by the physics of the low and high frequency limits: For ω → 0, S →1 corresponding to the normal state conductivity, and for ω→ ∞, S → c(ω/ω0)[(d − 2)/z − 1] where c is a complex constant, d is the dimension and z is the dynamical exponent, with z = 2 for models based on relaxational dynamics. This is the case for example for ordinary GL Cooper-pairs fluctuations17,18, where Aslamazov-Larkin (AL) and Maki-Thompson (MT) contributions are between the possible candidates for the observed fluctuation conductivity. Indeed, a direct comparison with the data for the sample with Tc ~ 15.71 K (Fig. 4(a)) shows that S matches very well with the AL prediction for d = 2, while MT corrections are suppressed by disorder (see Supplementary information). Observe that the 2d character of fluctuations is not surprising24: Indeed even though our films are thick as compared to the zero-temperature coherence length20 ξ0, i.e. 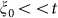Inline graphic, in the scaling regime the T-dependent GL correlation length 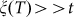Inline graphic is much larger than the film thickness, and GL fluctuations are effectively two-dimensional17 (see Supplementary information). On the other hand, the corresponding curve of S obtained for the sample with Tc ~ 3.14 K does not match at all with GL prediction, as it is better evidenced by a direct comparison between ω0 (Fig. 4(c) and 4(d)) and the expected value from 2D AL theory, i.e. 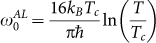Inline graphic. Whereas for both samples ω0→0 as T→Tc, showing the expected critical slowing of fluctuations as the SC transition is approached, for the film with Tc ~ 15.71 K the best scaling value of ω0 is in agreement with 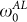Inline graphic within a factor of the order of unity, while in the film with Tc ~ 3.14 K ω0 is more than one order of magnitude smaller than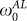Inline graphic. This effect cannot be attributed to a wrong choice of the scaling prefactor σ0, since this one still agrees very well with the measured dc fluctuation conductivity, see Fig. 4d. Instead, the lowering of ω0 with respect to 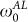Inline graphicreflects the change of the form of the scaling function S, evidenced in Fig. 4b. Moreover ω0 remains relatively small up to temperatures as large as T*, explaining why in the same range of probing frequencies the stiffness has a stronger frequency dependence in the sample with lower Tc. The emergence of such a low characteristic fluctuation frequency already below T* in the most disordered sample thus signals a fundamental breakdown of the standard Cooper-pairs fluctuation scenario, which cannot be accounted for by any simple adjustment of parameters within GL theory. We note that also recent developments aimed to account for the effect of the pseudogap on the Gaussian fluctuations cannot explain our results25. Indeed, the main result of Ref. [25] is that the pseudogap opening would lead to a faster suppression above Tc of the Gaussian fluctuations with respect to the ordinary GL case, while our experimental results show a robust persistence of the fluctuation conductivity in a wide range of temperatures above Tc.

Figure 4. Characteristic fluctuation frequency obtained from analysis of fluctuation conductivity.

Figure 4

Open in a new tab

(a)–(b) Rescaled phase (upper panel) and amplitude (lower panel) of σfl(ω) using the dynamic scaling analysis on two films with Tc ~ 15.7 and 3.14 K respectively. The solid and dashed lines show the predictions from 2D and 3D AL theory respectively. The color coded temperature scale for the scaled curves is shown in each panel. (c)–(d) Variation of ω0, 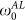Inline graphic, σ0 and 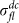Inline graphic as a function of temperature. The dashed vertical lines correspond to Tc.

Discussion

We can now put these observations in perspective. It has been shown from STS measurements that in the presence of strong disorder the spatial landscape of the superconductor become highly inhomogeneous, thereby forming domain-like structures, tens of nm in size, where the SC order parameter (OP) is finite and regions where the OP is completely suppressed8. One way to visualize the superconducting state is as a disordered network of Josephson junctions, where the domains observed in STS get coupled through Josephson coupling giving rise to the global phase coherent state. In this scenario, Tc corresponds to the temperature at which the weakest couplings are broken. Therefore, just above Tc the sample consists of large phase-coherent domains (consisting of several smaller domains) fluctuating with respect to each other. We believe that the large fluctuations at low frequency in our most disordered sample originate from fluctuations between coherent domains which gradually fragment with increasing temperature. As the temperature is increased further, the large domains progressively fragment eventually reaching the limiting size observed in STS measurements at a temperature close to T*. In such a scenario J will depend on the length scale at which it is probed. When probed on a length scale much larger than the phase coherent domains, J→0. On the other hand, when probed at length scale of the order of the domain size J would be finite. J(ω) probes the phase stiffness over a length scale set by the diffusion of the electron over one cycle of radiation which is given by L(ω) = [D/(ω/2π)]0.5. Here, D, is the electronic diffusion constant given by, 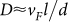Inline graphic, where vF and l are the Fermi velocity and the electronic mean free path. Therefore, for each temperature, the frequency-dependent stiffness J(ω) would vanish at a frequency such that the corresponding L(ω) becomes much larger than the size of the phase-coherent domains at the same temperature, L0(T). Using this criterion we can estimate the temperature dependence of L0(T) = L(ω), where ω corresponds to the highest frequency which J(ω) goes below our measurement resolution at temperature T (Fig 2 (c) and 2(d)). Taking d = 3 in the definition of the diffusion constant (since 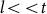Inline graphic), the limiting value of L0 at T ≈ T* is between 50–60 nm which is in the same order of magnitude as the domains observed in STS measurements8 on NbN films with similar Tc.

In summary, we have shown that in strongly disordered NbN thin films which display a PG state, J becomes dependent on the temporal and spatial length scale for Tc< T < T*. The remarkable consistency between T* determined from STS and microwave measurements, and the evident deviations from the expected behavior for GL fluctuations, suggest the notion that the superconducting transition in these systems is driven by phase disordering of a strongly inhomogeneous superconducting background. While our results bear strong similarity with the results obtained earlier on a disordered InOx film26, we would like to note that the whole fluctuation regime cannot be attributed to Berezinskii-Kosterlitz-Thouless (BKT) physics, since earlier measurements27 have shown that the BKT fluctuation regime is restricted to a narrow temperature range above Tc (see also Supplementary Material). On the other hand, the persistence far from Tc of slow relaxation processes, as characterized by the low frequency scale ω0, resembles the emergence of a glassy physics, which has been recently predicted at strong disorder12,13 and indirectly observed by STS6,8. However, an explicit connection between our findings and existing predictions, as for example the relevance of a small number of percolative paths for the current at strong disorder is still lacking13, and its formulation would certainly improve considerably our understanding of the superconductor-insulator transition.

Methods

Sample preparation

Our samples consisted of epitaxial NbN thin films grown using reactive magnetron sputtering of Nb in Ar/N2 gas mixture on (100) oriented single crystalline MgO substrates at 600°C. The thickness of all samples was measured using stylus profilometer. The disorder in the form of Nb vacancies in the NbN crystalline lattice was controlled by adjusting the Nb/N2 ratio in the plasma by controlling the Ar/N2 ratio in the gas mixture and the sputtering power. Large Nb/N2 ratio resulted in the non-superconducting Nb2N crystallographic phase. At the optimal ratio we obtained stoichiomentric NbN films with Tc ~ 16 K. Further reduction of Nb/N2 ratio resulted in progressively disordered films with Nb vacancies with gradual suppression of Tc. These samples show remarkable consistency between Tc, ρ and kFl values. Consequently, for each sample kFl was estimated from the resistivity and Tc and ρ using the universal relation between these quantities established earlier21. For broadband microwave measurements, two concentric silver pads (Fig. 5) were deposited on each sample using thermal evaporation.

Figure 5. Schematic drawing of the “Corbino” microwave spectrometer.

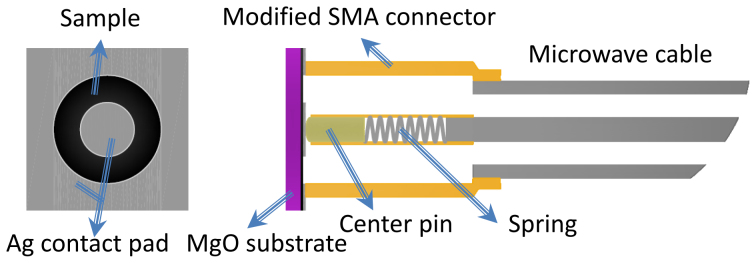
Figure 5

Open in a new tab

Schematic drawing of the superconducting film with Ag contact pads in Corbino geometry (left) and of the 50 Ω transmission line terminating with the sample (right); a specially modified microwave connector with spring loaded centre pin is used to establish the contact with the inner and outer contact pads.

Measurements

σ(ω) was measured using a home-built broadband Corbino microwave spectrometer coupled to a continuous flow 4He cryostat operating down to 2.3 K. The operating frequency range of the spectrometer was 0.1–20 GHz. However, since the σ(ω)-T data is noisy below 0.4 GHz for the samples with high Tc (> 9 K) most of the analysis in this paper is restricted to the frequency range 0.4–20 GHz. In this technique14, concentric metallic contact pads of Ag are deposited on the superconducting films in Corbino geometry such that the inner and outer electrodes on the sample mate with the inner and outer electrode of a modified microwave connector at the end of a transmission line (Fig. 5). The sample thus acts as a terminator for an open ended transmission line. The complex reflection coefficient, S11, is measured by measuring the reflected microwave signal from the sample using a vector network analyzer. Using a standard procedure28, a set of three samples with well known reflection coefficient were used to correct of extraneous reflections, damping and phase shifts in the transmission line. A thick NbN film (300 nm) with Tc ~ 16.1 K was used as a short standard (S11 = −1) at a temperature of 2.3K. A flat Teflon piece was used for open standard (S11 = 1). A NiCr evaporated film with 20 Ω resistance between the two Corbino pads was used as a standard load. The sample impedance, Zs, is obtained from the relation, 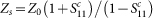Inline graphic , where 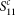Inline graphic is the corrected reflection coefficient and Z0 = 50 Ω is the characteristic impedance of our transmission line; 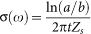Inline graphic where a and b are the inner and outer diameters of the two “Corbino” electrodes. The d.c. resistance of the sample was measured in-situ using the bias-tee of the network analyzer using a two-probe technique. The temperature independent two-probe background resistance (~7 Ω) was subtracted while calculating the resistivity.

Determination of the electronic diffusion (D) constant and probing length of NbN films

For diffusive transport, the diffusion constant is given by, D = vFl/d. Since l is much smaller than the film thickness for all our films, the electronic transport in the normal state is 3-dimensional (d = 3) even though the superconducting fluctuations show 2-dimensional character. To get the variation of D with disorder, we estimated vF and l for several NbN films with Tc ranging from 16.5 K to 0.6 K. 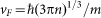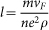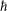vF and l were estimated22 from Hall coefficient (RH) and resisitivity (ρ) measured at 285 K using the free electron formulae, Inline graphic and Inline graphic, where Inline graphic is the Planck's constant, m is the electron mass and n is the carrier density given by n = 1/(RHe). Figure 6(a) show the variation of vF, l with Tc for 12 different films. The diffusion constant in the present work was estimated from Tc by interpolating the smooth variation of D vs. Tc (Fig. 6(b)). In Fig. 6(c) we plot the probing length given by (D/f)1/2 as a function of Tc for microwave radiation with frequency of 0.4 GHz and 20 GHz.

Figure 6. Estimation of the diffusion constant for NbN thin films.

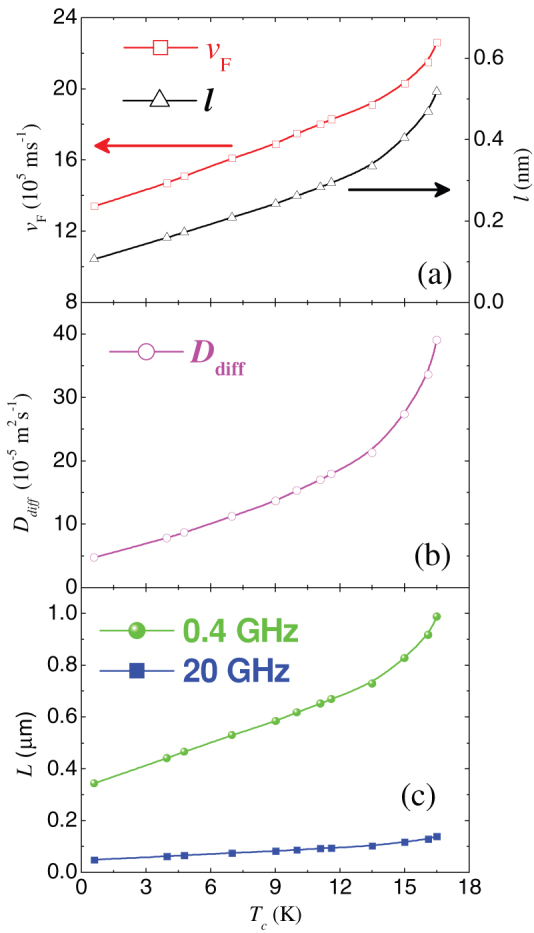
Figure 6

Open in a new tab

(a) Variation of Fermi velocity, vF, and electronic mean free path, l for NbN thin films with different Tc. (b) Variation of the diffusion constant, D, estimated using the values of vF and l in panel (a). (c) Probing length scale at 0.4 GHz and 20 GHz for samples with different Tc.

Author Contributions

M.M. designed and built the broadband microwave spectrometer and performed the experiments. M.M., P.R., L.B., A.K. and S.C.G. analyzed the data. J.J. and V.B. optimized the deposition conditions, synthesized the NbN films and measured the thickness. P.R. and L.B. wrote the manuscript. All authors contributed to the concept of the paper.

Supplementary Material

Supplementary Information

Aslamazov-Larkin and Maki-Thompson expressions for fluctuation conductivity and Comparison with the predictions from BKT theory

srep01357-s1.pdf (1.2MB, pdf)

Acknowledgments

We thank Peter Armitage for valuable suggestions regarding the experiment and analysis, and Claudio Castellani and Andrey Varlamov for useful discussions. L.B. acknowledges partial financial support by MIUR under project FIRB-RBFR1236VV.

References

  1. Bardeen J., Cooper L. N. & Schrieffer J. R. Theory of superconductivity. Phys. Rev. 108, 1175 (1975). [Google Scholar]
  2. Tinkham M. Introduction to Superconductivity (Dover Publication Inc., Mineola, New York, 2004). [Google Scholar]
  3. Emery V. J. & Kivelson S. A. Importance of phase fluctuations in superconductor with small superfluid density. Nature 374, 434 (1995). [Google Scholar]
  4. Sacépé B. et al. Localization of preformed Cooper pairs in disordered superconductors. Nature Commun. 1, 140 (2010).21266990 [Google Scholar]
  5. Mondal M. et al. Phase fluctuations in a strongly disordered s-wave NbN superconductor close to the metal-insulator transition. Phys. Rev. Lett. 106, 047001 (2011). [DOI] [PubMed] [Google Scholar]
  6. Sacépé B. et al. Localization of preformed Cooper pairs in disordered superconductors. Nature Physics 7, 239 (2011). [Google Scholar]
  7. Sacépé B. et al. Disorder-induced inhomogeneities of the superconducting state close to the superconductor-insulator transition. Phys. Rev. Lett. 101, 157006 (2008). [DOI] [PubMed] [Google Scholar]
  8. Lemarié G. et al. Universal scaling of the order-parameter distribution in strongly disordered superconductors. (unpublished, arXiv:1208.3336).
  9. Ghosal A., Randeria M. & Trivedi N. Role of spatial amplitude fluctuations in highly disordered s-wave superconductors. Phys. Rev. Lett. 81, 3940 (1998). [Google Scholar]
  10. Dubi Y., Meir Y. & Avishai Y. Nature of the superconductor–insulator transition in disordered superconductors. Nature 449, 876 (2007). [DOI] [PubMed] [Google Scholar]
  11. Bouadim K., Loh Y. L., Randeria M. & Trivedi N. Single- and two-particle energy gaps across the disorder-driven superconductor–insulator transition. Nat. Phys. 7, 884 (2011). [Google Scholar]
  12. Feigelman M. V., Ioffe L. B. & Mézard M. Superconductor-Insulator transition and energy localization. Phys. Rev. B 82, 184534 (2010). [Google Scholar]
  13. Seibold G., Benfatto L., Castellani C. & Lorenzana J. Superfluid density and phase relaxation in superconductors with strong disorder. Phys. Rev. Lett. 108, 207004 (2012). [DOI] [PubMed] [Google Scholar]
  14. Kitano H., Ohashi T. & Maeda A. Broadband method for precise microwave spectroscopy of superconducting thin films near the critical temperature. Rev. Sci. Instrum. 79, 074701 (2008). [DOI] [PubMed] [Google Scholar]
  15. Scheffler M. & Dressel M. Broadband microwave spectroscopy in Corbino geometry for temperatures down to 1.7 K. Rev. Sci. Instrum. 76, 074702 (2005). [DOI] [PubMed] [Google Scholar]
  16. Booth J. C., Wu D. H. & Anlage S. M. A broadband method for the measurement of the surface impedance of thin films at microwave frequencies. Rev. Sci. Instrum. 65, 2082 (1994). [Google Scholar]
  17. Schmidt H. The onset of superconductivity in the time dependent Ginzburg-Landau theory. Z. Phys. 216, 336 (1968). [Google Scholar]
  18. Aslamazov L. G. & Varlamov A. A. Fluctuation conductivity in intercalated superconductors. J. Low Temp. Phys. 38, 223 (1980) [Google Scholar]
  19. Chockalingam S. P., Chand M., Jesudasan J., Tripathi V. & Raychaudhuri P. Superconducting properties and Hall effect of epitaxial NbN thin films. Phys. Rev. B 77, 214503 (2008). [Google Scholar]
  20. Mondal M. et al. Phase Diagram and upper critical field of homogeneously disordered epitaxial 3-dimensional NbN films. J. Supercond Nov Magn 24, 341 (2011). [Google Scholar]
  21. Chand M. et al. Phase diagram of the strongly disordered s-wave superconductor NbN close to the metal-insulator transition. Phys. Rev. B 85, 014508 (2012). [DOI] [PubMed] [Google Scholar]
  22. Chand M. Ph.D. Thesis, Tata Institute of Fundamental Research, Mumbai, India (available at http://www.tifr.res.in/~superconductivity/pdfs/madhavi.pdf). [Google Scholar]
  23. Fisher D. S., Fisher M. P. A. & Huse D. A. Thermal fluctuations, quenched disorder, phase transitions, and transport in type-II superconductors. Phys. Rev. B 43, 130 (1991). [DOI] [PubMed] [Google Scholar]
  24. Ohashi T., Kitano H., Maeda A., Akaike H. & Fujimaki A. Dynamic fluctuations in the superconductivity of NbN films from microwave conductivity measurements. Phys. Rev. B 73, 174522 (2006). [Google Scholar]
  25. Levchenko A., Norman M. R. & Varlamov A. A. Nernst effect from fluctuating pairs in the pseudogap phase of the cuprates. Phys. Rev. B 83, 020506(R) (2011). [Google Scholar]
  26. Liu W., Kim M., Sambandamurthy G. & Armitage N. P. Dynamical study of phase fluctuations and their critical slowing down in amorphous superconducting films. Phys. Rev. B 84, 024511(2011). [Google Scholar]
  27. Mondal M. et al. Role of the vortex-core energy on the Berezinskii-Kosterlitz-Thouless transition in thin films of NbN. Phys. Rev. Lett. 107, 217003 (2011). [DOI] [PubMed] [Google Scholar]
  28. Stutzman M. L., Lee M. & Bradley R. F. Broadband calibration of long lossy microwave transmission lines at cryogenic temperatures using nichrome films. Rev. Sci. Instrum. 71, 4596 (2000). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Aslamazov-Larkin and Maki-Thompson expressions for fluctuation conductivity and Comparison with the predictions from BKT theory

srep01357-s1.pdf (1.2MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES