Energetics and Dynamics of the Low-Lying Electronic States of Constrained Polyenes: Implications for Infinite Polyenes

Abstract

Steady-state and ultrafast transient absorption spectra were obtained for a series of conformationally-constrained, isomerically pure polyenes with 5–23 conjugated double bonds (N). These data and fluorescence spectra of the shorter polyenes reveal the N dependence of the energies of six ¹B_u⁺ and two ¹A_g⁻ excited states. The ¹B_u⁺ states converge to a common infinite polyene limit of 15,900 ± 100 cm⁻¹. The two excited ¹A_g⁻ states, on the other hand, exhibit a large (~9000 cm⁻¹) energy difference in the infinite polyene limit, in contrast to the common value previously predicted by theory. EOM-CCSD ab-initio and MNDO-PSDCI semi-empirical MO theories account for the experimental transition energies and intensities. The complex, multistep dynamics of the 1¹B_u⁺ → 2¹A_g⁻ → 1¹A_g⁻ excited state decay pathways as a function of N are compared with kinetic data from several natural and synthetic carotenoids. Distinctive transient absorption signals in the visible region, previously identified with S* states in carotenoids, also are observed for the longer polyenes. Analysis of the lifetimes of the 2¹A_g⁻ states, using the energy gap law for nonradiative decay, reveals remarkable similarities in the N dependence of the 2¹A_g⁻ decay kinetics of the carotenoid and polyene systems. These findings are important for understanding the mechanisms by which carotenoids carry out their roles as light-harvesting molecules and photoprotective agents in biological systems.

1. Introduction

The discovery of the low-lying 2¹A_g⁻ state in all-trans diphenyloctatetraene by Hudson and Kohler¹ in 1972 resulted in a fundamental revision of our understanding of the photophysics and photochemistries of conjugated systems with alternating single and double bonds.^2,3 In the intervening 40 years, the 2¹A_g⁻ state has been identified and characterized in a large number of polyenes and biologically relevant carotenoids.^4–7 The seminal discovery of this state and subsequent work on other short, model polyenes was based on the analysis of fluorescence spectra obtained under conditions that provided sufficient vibronic resolution to identify the 1¹A_g⁻ ↔ 2¹A_g⁻ electronic origins. For shorter polyenes, this transition exhibits a characteristic (~3000–4000 cm⁻¹) Stokes shift relative to the electronic origin of the symmetry-allowed, 1¹A_g⁻ → 1¹B_u⁺ absorption, which is predicted to be the lowest energy singlet-singlet ππ* transition (HOMO → LUMO) in simple versions of molecular orbital (MO) theory. Theoretical explanations by Schulten, Karplus, and others^8,9 for E(2¹A_g⁻) < E(1¹B_u⁺) in all-trans polyenes indicated that interactions between the singly and doubly excited electronic configurations were required to account for electron correlation in these extended, one-dimensional π-electron systems. It also should be noted that the E(2¹A_g⁻) < E(1¹B_u⁺) state ordering applies to all polyenes with more than three conjugated double bonds.¹⁰

The initial experiments on diphenyloctatetraene¹ and other model, all-trans tetraenes,¹¹ pentaenes,¹² and hexaenes¹³ depended on their relatively large, 2¹A_g⁻ → 1¹A_g⁻ fluorescence yields and the ability of these simple systems to be incorporated into low-temperature mixed crystals (typically n-alkanes) and glasses. The spectral resolution achieved under these conditions allowed site-selective excitation of polyenes in homogeneous solvent environments and showed that the forbidden 1¹A_g⁻ ↔ 2¹Ag⁻ transitions were made allowed by Herzberg-Teller coupling involving low-frequency (~100 cm⁻¹) b_u promoting modes.¹⁴ These one-photon optical experiments were followed by investigations of the two-photon-induced fluorescence excitation spectra of octatetraene in low-temperature mixed crystals,^15,16 which preserve the center of symmetry. These studies verified the assignment of the lowest excited singlet state as 2¹Ag⁻. Subsequently, simple methyl-substituted and unsubstituted tetraenes and pentaenes were studied as isolated molecules in supersonic jets, both in one-photon and two-photon fluorescence excitation experiments.^17–20 This confirmed the earlier assignments of electronic origins and vibronic bands and the influence of symmetry on the intensities of the “forbidden” transitions. Analysis of the experiments on isolated tetraenes also showed that the oscillator strength for the Herzberg-Teller-allowed, 1¹Ag⁻ → 2¹Ag⁻ transition in all-trans octatetraene was comparable to the oscillator strength of this transition in cis isomers lacking a center of symmetry.^17–19

The early studies of the 2¹Ag⁻ state in simple model polyenes later were extended to polyenes of photobiological interest. These include the retinyl chromophores involved in vision^21,22 and carotenoids employed for light-harvesting and photoprotection in photosynthetic organisms.²³ The functioning of the photosynthetic apparatus depends on the energies and dynamics of the low-energy excited electronic states of the carotenoids and chlorophylls in antenna and reaction center pigment–protein complexes. Initial studies of the 2¹Ag⁻ states in carotenoids having relatively long π-electron conjugated chain lengths relied on the detection of fluorescence signals from the 2¹Ag⁻ state, which become vanishingly small with increasing N. For example, the 2¹Ag⁻ → 1¹Ag⁻ fluorescence yield for all-trans β-carotene (N = 11) is ≤10^−5.24,25 This makes the detection and assignment of fluorescence signals quite challenging, particularly because of the crossover to stronger 1¹B_u⁺ → 1¹Ag⁻ emissions in longer polyenes and carotenoids.²⁶ These higher energy emissions mask the inherently weak, lower energy fluorescence signals from the 2¹Ag⁻ state.

The difficulties in obtaining reliable 2¹Ag⁻ energies for carotenoids were addressed by the development of transient absorption techniques, which demonstrated the feasibility of detecting vibronically-resolved, symmetry-allowed 2¹Ag⁻ → 1¹B_u⁺ transitions of carotenoids in the near infrared (NIR) region.^27,28 The energy of the 2¹Ag⁻ state then can be calculated from the difference between the 1¹Ag⁻ → 1¹B_u⁺ and 2¹Ag⁻ → 1¹B_u⁺ vibronic origins. Both of these transitions are symmetry-allowed and relatively strong for all-trans isomers. The critical advantages of using transient absorption to determine the 2¹Ag⁻ energies of longer polyenes and carotenoids were reinforced by our recent work on the fluorescence of all-trans hexadecaheptaene (N = 7).²⁹ These studies indicated that electronic excitation of the all-trans species produced distorted, more-highly emissive trans structures and cis isomers in the 2¹Ag⁻ state and that the 2¹Ag⁻ → 1¹Ag⁻ emission could not be identified with same distribution of polyene geometries present in the ground state. Thus, earlier reports of fluorescence from longer all-trans polyenes and carotenoids must be attributed to more strongly-allowed radiative decay from less-symmetric molecules, either present as photochemical impurities, or as distorted ground state conformers, or formed on the 2¹Ag⁻ potential surface following excitation of more-symmetric, all-trans species. This scenario is supported by the apparently larger oscillator strengths in longer polyenes (N > 4) for 2¹Ag⁻ → 1¹Ag⁻ radiative decay from cis isomers and distorted trans isomers relative to the symmetry-forbidden transitions of molecules that retain C_2h geometry and selection rules.^2,30

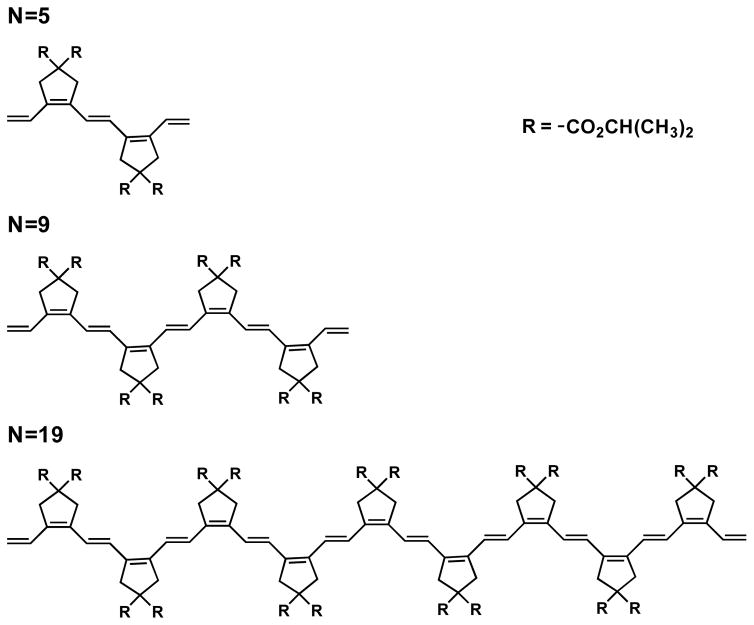
The advantages of transient absorption measurements here are combined with recent developments in synthetic techniques,^31,32 which have provided a series of stable, rigid polyenes containing five-membered rings (Fig. 1). The peripheral ester groups enhance the solubility of these molecules in a variety of organic solvents without perturbing the interior π orbitals. These molecules have planar π-electron frameworks and are resistant to conformational disorder and thermal and photochemical isomerization. This results in a more homogeneous distribution of ground and excited state geometries, giving well-resolved absorption spectra, even in room temperature solutions.

Figure 1.

Representative polyene structures.

We have carried out a systematic investigation of the electronic spectroscopy of this homologous series of polyenes, obtaining steady-state absorption spectra in the ultraviolet and visible for N = 5–23 and transient absorption spectra in the visible and NIR for N = 7–19. This has allowed the analysis of an unusually rich set of data to understand the changes in the energies and dynamics of several excited electronic states as a function of N. These experiments provide insights on the photophysics of related polyenes, including carotenoids employed in photobiology. The data also allow comparisons with theoretical predictions of the excited state properties of these molecules in the infinite polyene limit.

The molecules investigated here alternate between C_2h and C_2v symmetry, sharing a concise Abelian C₂ subgroup. Because the properties of the ππ* excited states are determined by the C₂ subgroup, which is maintained by all of these polyenes, we can provide an unambiguous discussion of the excited states by referring only to the C_2h point group. An extended point group correlation table for the C_2h and C_2v point groups is provided in the supplementary information section (Table S1). This approach allows a comparison of the present results with numerous experimental and theoretical studies on linear polyenes² and on a wide range of less symmetrical carotenoids^23,26,33 and retinyl^21,22,34 polyenes. We also designate ionic (+) versus covalent (−) states following the work of Schulten, Karplus and coworkers.^8,9,35 Linear polyenes with all-trans conformations have allowed ¹Ag⁻ → ¹B_u⁺ transitions, and the transitions from the ¹Ag⁻ state to all other states (¹B_u⁻, ¹A_g⁺, ¹Ag⁻) are symmetry forbidden or orbital parity forbidden. Cis-linkages induce oscillator strength in transitions to excited ¹A_g⁺ states, conventionally designated as “cis bands.” Polar polyenes can induce mixing of the ionic and covalent states, and transitions to the ¹B_u⁻ and ¹Ag⁻ states can gain oscillator strength, depending upon the direction and magnitude of their dipole moments.^36,37

2. Materials and Methods

Sample Purification

Polyenes were synthesized as described previously³² and were received as dried samples. Prior to spectroscopic measurements, samples were purified using a Millipore Waters 600E high-performance liquid chromatography (HPLC) system equipped with a Waters 2996 single diode-array detector. Each polyene was dissolved in methylene chloride and filtered prior to injection into a Phenomenex Ultracarb C18 column (250 × 4.6 mm, 5 μm particle size). The HPLC mobile phase was changed as a linear gradient from acetonitrile/methanol/water (42:53:5, v/v/v) to acetonitrile/methanol (30:70, v/v) over 50 or 60 minutes at a flow rate of 1 mL/min. The purified samples were collected upon elution from the HPLC, dried under a gentle stream of nitrogen gas, and stored at −80 °C until the spectroscopic measurements.

Steady-State Absorption and Fluorescence Spectroscopy

Absorption spectra in room temperature and 77 K 2-methyltetrahydrofuran (2-MTHF) were recorded on a Cary 400 spectrometer. 77 K spectra were obtained from samples slowly frozen in a 1-cm Suprasil cryogenic cuvette (NSG) suspended in a copper holder within a customized flat-windowed (Suprasil) liquid-nitrogen cryostat (Ace Glass). The liquid nitrogen was in contact with the bottom of the copper cuvette holder but did not reach the optical path in the center of the frozen sample. The low-temperature absorption spectra were corrected for the absorption and light scattering of the 2-MTHF glass and other optical components. Fluorescence and fluorescence excitation spectra were obtained on a SPEX/JY Model 212 spectrofluorimeter. All emission spectra were corrected for the wavelength dependence of the photomultiplier and other optical components using a correction file traceable to NIST standard lamps. Fluorescence spectra were subjected to mild smoothing (using Savitsky-Golay algorithms^38,39 implemented by Grams AI software) to reduce the noise inherent in these weakly emitting systems. The smoothing procedures only minimally distorted the relatively broad vibronic details in the emission spectra. In converting fluorescence spectra from wavelength to energy (cm⁻¹) scales, spectra were corrected for the differences between band-passes at constant wavelength resolution vs. constant wavenumber resolution, i.e., I(ν̃)/dν̃ = λ²I(λ)/dλ⁴⁰ Positions of the vibronic bands were determined by fitting the spectra to sums of Gaussians using Grams AI spectroscopy software. Peak positions of prominent bands were calculated as averages from a range of fits using different numbers of Gaussians and different initial guesses for the least squares fits.

Time-Resolved Absorption Spectroscopy

Time-resolved absorption spectra of the polyenes dissolved in 2-MTHF were recorded at room temperature using the femtosecond transient absorption spectrometer system previously described.⁴¹ The laser system consisted of an amplified Ti:sapphire tunable laser (Spectra-Physics Spitfire/Tsunami/Millenia) pumped at a 1 kHz repetition rate by an Evolution 15, Q-switched Nd:YLF laser (Coherent). A Spectra-Physics OPA-800C optical parametric amplifier produced a pump beam with a duration of ~60 fs, and a 3 mm Sapphire plate contained in a Helios time-resolved spectrometer (Ultrafast Systems, LLC) generated a white light continuum for probing transients in the visible and NIR spectral regions. Mutual polarization of the pump and probe beams was set at the magic angle (54.7°). The pump wavelengths used in the measurements are specified in Table 1. The pump beam had a diameter of 1 mm and an energy of ~1 μJ/pulse, resulting in a pump intensity of 2.6 to 3.3 × 10¹⁴ photons/cm² pulse. Transient absorption spectra were recorded from samples having absorbances (A) at the excitation wavelength between 0.4 and 0.6 in a 2-mm path length cell. The signals were averaged over 5 s, and the samples were stirred with a magnetic microstirrer to minimize photodegradation. To evaluate the integrity of the samples, steady-state absorption spectra were recorded before and after each transient absorption experiment. Surface Xplorer Pro v1.1.5 (Ultrafast Systems, LLC) software was used for chirp correction and to subtract scattered excitation light. Global fitting analysis of the transient absorption spectral and temporal datasets was based on a sequential decay model⁴² and carried out using a modified version of ASUFit v 3.0 software provided by Dr. Evaldas Katilius of Arizona State University. The number of kinetic components required was determined by a chi squared (χ²) test and by examination of the goodness of fit of the transient decay traces across the entire bandwidth of the spectral profiles.

Table 1.

Lifetimes of the relaxed 2¹Ag⁻ (τ₁), vibrational hot 2¹Ag⁻ (τ₁), 1¹B_u⁺ (τ₂), and other components from global fitting of the transient absorption spectra.

N	λex (nm)	τ1 (ps)a	τ′1 (ps)	τ2 (fs)b	τ3 (ps)
7	410	370 ± 10 / 340 ± 50	0.7 ± 0.1	180 ± 40 / 160 ± 40
9	400	28 ± 3 / 28 ± 5	1.0 ± 0.3	120 ± 30 / 150 ± 10
11	490	6.1 ± 0.3 / 5.3 ± 1.0	0.5 ± 0.1	120 ± 50 / 140 ±10
13	508	2.3 ± 0.2 / 2.6 ± 0.5		130 ± 30 / 100 ± 30	5.0 ± 0.5
15	517	1.1 ± 0.2 / 1.2 ± 0.1		90 ± 10 / 70 ± 10	6.9 ± 0.5
19	508	0.49 ± 0.01 / 0.50 ± 0.05		100 ± 10 / 70 ±10	0.67 ± 0.03
					2.7 ± 0.2

^a2¹Ag⁻ lifetimes derived from visible/NIR transient absorption spectra.

^b1¹B_u⁺ lifetimes derived from visible/NIR transient absorption spectra.

Theoretical Analysis

Excited state calculations were carried out using a variety of MO methods for comparative purposes. Modified neglect of differential overlap with partial single- and double-configuration interaction (MNDO-PSDCI) methods^6,43 were used to study the impact of conformational degrees of freedom on the excited states of all the polyenes. This semiempirical method includes single and double excitations within the π system and has been useful in understanding the electronic properties of short-and long-chain polyenes and carotenoids.^30,44,45 The standard Austin Model 1 (AM1) parameterization was used: Mataga repulsion integrals (rijm=2) and identical π and σ electron mobility constants of 1.7 (pimc=sigmc=1.7).^6,43 When the π system provided more than ten filled molecular orbitals, the single and double configuration interactions (CISD) were limited to the ten highest energy filled and ten lowest energy virtual π molecular orbitals. Ab-initio calculations were carried out by using configuration interaction singles (CIS),⁴⁶ equation of motion coupled cluster with singles and doubles (EOM-CCSD)^47–49 and symmetry-adapted-clustered-configuration-interaction (SAC-CI)^50,51 methods as implemented in Gaussian 09.⁵² The CIS calculations were carried out using full single configuration interactions (CI), and the SAC-CI calculations were carried out at highest precision [full single CI and extensive double CI (LevelThree selection)].^50,53 The active space of the EOM-CCSD calculations was modified for each calculation to include the entire π system minus the highest energy unfilled and lowest energy filled π orbitals. Exclusion of these “outer” π orbitals had no meaningful impact on the nine lowest energy transitions, and the EOM-CCSD methods are highly efficient and size consistent with appropriate selection of the active space.⁵⁴ Excited state properties were calculated relative to the second order Møller-Plesset (MP2) ground state.⁵⁵ All ab-initio calculations used the double-zeta D95 basis set.⁵⁶ CASSCF methods and state averaged optimization methods were used to search for conical intersections in the smaller polyenes, but no such features were found. We examine this issue in more detail in section 3.4.

3. Results and Discussion

3.1 Absorption and Dynamics of Polyene Excited States in Room Temperature Solutions

Steady-State Absorption Spectra

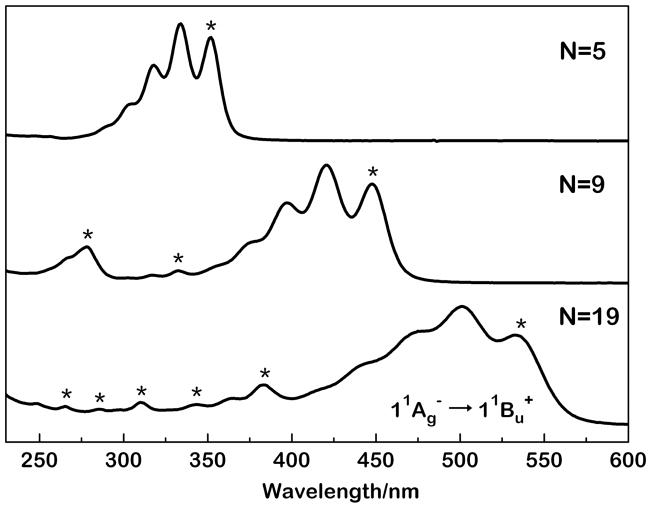
Steady-state absorption spectroscopy of polyenes with N = 5–23 lead to the identification of several “allowed” electronic transitions in these systems.³² The relatively rigid, planar structures of these polyenes result in well-resolved absorption spectra, even in room temperature solutions, as demonstrated for polyenes with N = 5, 9, and 19 in Fig. 2. The vibronic progressions reflect partially resolved combinations of totally symmetric C–C and C=C stretches, and the strongly allowed, low energy 1¹Ag⁻ → 1¹B_u⁺ transitions exhibit vibronic intervals ranging from ~1500 cm⁻¹ for N = 5 to ~1200 cm⁻¹ for N = 19. Analysis of the vibronic bands indicates an almost constant linewidth of ~1000 cm⁻¹, regardless of the energy of the electronic transition or the length of conjugation. The relatively high vibronic resolution in room temperature solutions, combined with our ability to systematically follow the shifts of spectral features as a function of the number of conjugated double bonds, greatly aids the identification and assignments of the origins ((0–0) bands) of the electronic transitions in these systems. Assignments of the weaker, higher energy transitions further are facilitated by their systematically stronger dependence on N. The electronic origins for several electronic transitions for N = 5, 9, and 19 are indicated in Fig. 2.

Figure 2.

Room temperature, steady-state absorption spectra of N = 5, 9, and 19. Asterisks indicate positions of electronic origins ((0–0) bands) for “allowed” transitions.

Transient Absorption Spectra in the Visible Region

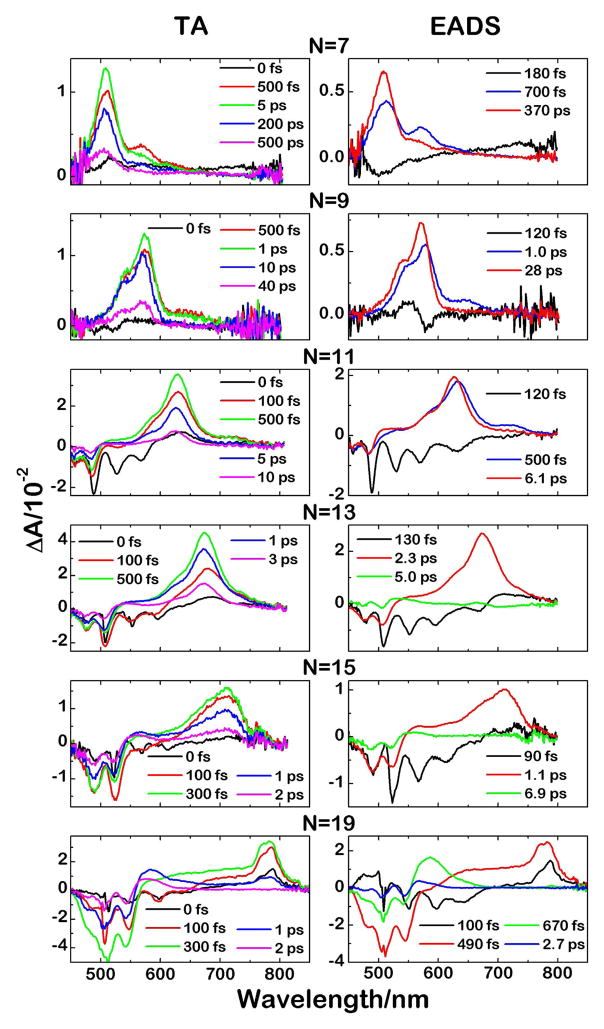
We recorded ultrafast, time-resolved, transient absorption spectra of polyenes with N = 7–19 in room temperature solutions of 2-MTHF. Spectra in the 450–800 nm wavelength region at various delay times between the pump and probe pulses are given in Fig. 3. The negative amplitudes observed between 450 and 700 nm correspond to the depletion of the ground state and bleaching of the strongly allowed 1¹Ag⁻ → 1¹B_u⁺ absorption, cf. Fig. 2. The positive transient absorption signals between 500 and 800 nm are assigned to a symmetry-allowed, 2¹Ag⁻ → n¹B_u⁺ transition.⁵⁷ In parallel with trends observed in the steady-state absorption spectra (Fig. 2), all of the transient absorption features show systematic shifts to longer wavelengths with increasing N. Also, it is significant that, for both the steady-state and transient absorption spectra, the relative transition intensities show no detectable differences for molecules with C_2h (N = 5, 9, 13, 17, 21) vs. C_2v (N = 7, 11, 15, 19, 23) symmetries. This supports the use of the C_2h symmetry labels and selection rules for describing the electronic spectroscopy of all polyenes in this series.

Figure 3.

Transient absorption (TA) spectra obtained at different time delays in the visible at room temperature in 2-MTHF. Global analysis of decays provides evolution associated difference spectra (EADS).

The components in the transient absorption spectra are revealed by a global fitting analysis of the spectral and temporal datasets according to a sequential decay model, yielding “Evolution Associated Difference Spectra” (EADS), which also are shown in Fig. 3 for N = 7–19. The lifetimes of the kinetic components are given in Table 1. Note that for N = 7–15 (Table 1), three EADS components are needed to account for the transient absorption signals in the 450–800 nm range. N = 19 requires a fourth EADS component for a good fit. For all molecules, the shortest lived of these components occurs between 90 and 180 fs and can be assigned to a combination of the bleaching of the 1¹Ag⁻ → 1¹B_u⁺ transition (λ ≈ 450–550 nm) and 1¹B_u⁺ → 1¹Ag⁻ stimulated emission (weak negative signals with λ ≈ 550–700 nm). These fast decays are typical of the 1¹B_u⁺ lifetimes of related carotenoids.^57–59 Although the instrument response time of ~100 fs precludes a more quantitative analysis, the 1¹B_u⁺ lifetime clearly decreases with increasing N, as previously noted for carotenoids.⁶⁰

For N = 7, 9 and 11, the second EADS component obtained from a fit to the transient absorption data in the visible region (Fig. 3) has a lifetime (τ₁′) of 500–1000 fs (Table 1) and can be identified with the decay of a symmetry-allowed, 2¹Ag⁻ → n¹B_u⁺ transition from a vibronically excited 2¹Ag⁻ electronic state. Similar EADS components have been assigned as “hot bands” in the 2¹Ag⁻ → n¹B_u⁺ transitions of carotenoids,^57,61,62 indicating relatively slow vibrational relaxation within the 2¹Ag⁻ states. For the shorter polyenes (N = 7–11), this spectral feature is displaced by ~1800 cm⁻¹ from the (0–0) band associated with the 2¹Ag⁻ → n¹B_u⁺ transitions from vibrationally relaxed 2¹Ag⁻ states. These vibronic spacings are consistent with significant increases in 2¹Ag⁻ of the frequencies of the totally symmetric (a_g) C=C stretching modes that dominate polyene electronic spectra, cf. vibronic spacings of ~1400 cm⁻¹ for the 1¹Ag⁻ → 1¹B_u⁺ transitions of N = 7–11 (Fig. 2). This increase, first noted in high-resolution optical spectra of model pentaenes and hexaenes,^12–14 is due to vibronic coupling between the 1¹Ag⁻ and 2¹Ag⁻ states. Similar increases have been observed in a variety of carotenoids.^57,61,62

Polyenes with N = 13, 15 and 19 lack kinetic features associated with an intermediate, vibronically hot 2¹Ag⁻ component, and for these molecules the second EADS component can be assigned to the decay of thermally equilibrated 2¹Ag⁻ (S₁) states. It should be noted that, even for N = 7, 9 and 11, the spectral features associated with vibrational relaxation in 2¹Ag⁻ are significantly weaker than those observed for carotenoids,^57,63 most likely due to the relative rigidity of these systems. The small amplitude EADS components in the shorter polyenes, identified with 2¹Ag⁻ vibrational relaxation, may be due to larger geometry changes (and larger Franck-Condon factors) when the smaller molecules are excited into their 1¹B_u⁺ and 2¹Ag⁻ states. This would give rise to larger transient populations of vibrational states involving C–C and C=C stretches. For N = 7, 9, and 11, the lifetime of the vibrationally relaxed 2¹Ag⁻ state (τ₁) decreases from 370 to 28 to 6.1 ps. The trend continues for N = 13, 15 and 19 (second EADS components), with 2¹Ag⁻ lifetimes (τ₁) of 2.3, 1.1, and 0.49 ps, respectively (Table 1). We note that the 2¹Ag⁻ lifetimes for this series primarily reflect the rates of nonradiative decay, since for long (N ≥ 7) polyenes the radiative decay rates for the symmetry-forbidden 2¹Ag⁻ → 1¹Ag⁻ transitions (≤10⁷/s) are much smaller than the rates of nonradiative relaxation.^64,65 As will be discussed in section 3.4, the 2¹Ag⁻ lifetimes can be related to the systematic decrease in the energy of the 2¹Ag⁻ state with increasing conjugation length, following the energy gap law for radiationless decay.^57,66

The transient absorption spectra and EADS components of these constrained polyenes are remarkably similar to those of a wide variety of less rigid, less symmetric, biologically relevant carotenoids.^{45,57,59,67–70} These similarities include the presence of longer decay components, observed exclusively in polyenes with N = 13, 15, and 19, which are particularly prominent for N=19. These components (the third EADS with lifetimes of 5.0, 6.9, and 2.7 ps for N = 13, 15 and 19) have weak absorptions on the blue side of the main 2¹Ag⁻ → n¹B_u⁺ absorption band. Following previous discussions of the transient absorption spectra of longer carotenoids such as spirilloxanthin (N = 13),⁵⁷ these features are assigned to what have been labeled as “S* states.” In N = 19 there is a fourth EADS component with τ = 0.67 ps (Fig. 3, Table 1) with a spectrum similar to that of the S* state, suggesting that multiple S* signals may be present in the longest polyene. This also is consistent with what has been reported for long carotenoids.⁵⁷

The S* state has been the subject of significant discussion and controversy.⁷¹ An early explanation for the S* signals, first reported for a β-carotene analog with N = 19, was that they were due to 1¹Ag⁻ → 1¹B_u⁺ absorptions from vibrationally excited 1¹Ag⁻ states,²⁵ which later were attributed to population by impulsive stimulated Raman scattering (ISRS) during the excitation pulse.⁶⁹ The complexity of interpreting S* signals for a wide range of carotenoids and the current polyenes is illustrated by recent work on β-carotene. The ISRS hypothesis was explored by Jailaubekov et al.,⁷² who compared narrow- and broad-band excitation of room temperature β-carotene solutions and demonstrated that even excitation with narrow band pulses generated the S* signal, ruling out the ISRS mechanism. Lenzer et al.⁷³ consequently assigned the S* features in β-carotene in n-hexane as absorption from vibrationally excited 1¹Ag⁻, directly populated via internal conversion from 2¹Ag⁻, as originally proposed by Gillbro et al.²⁵ However, these conclusions have been challenged by recent broadband 2D electronic spectroscopy of β-carotene in a 77 K glass,⁷⁴ which demonstrated that ISRS can be important when conformational flexibility is limited. Similar geometric restrictions may apply to these constrained polyenes, even in room temperature solutions.

One of several competing explanations associates S* with distorted or twisted conformers on the 2¹Ag⁻ potential surface, populated via 1¹B_u^+.45,67 For example, for ground state spirilloxanthin (N = 13), torsional motions around the single and double bonds have been proposed to lead to a more compact, corkscrew structure with a small dipole moment, which stabilizes the interactions of the 1¹Ag⁻ state with the solvent. Excitation into the 2¹Ag⁻ state can unravel this corkscrew geometry, leading to additional channels for relaxation and potentially complex, time-dependent signals associated with absorption from 2¹Ag^−.57 The presence of S* signals in N = 13 and N = 15 (Fig. 3) suggests a similar explanation, though it is important to emphasize that the ground and excited states of these relatively planar and highly constrained polyenes offer a much more restricted set of twisting coordinates than those available to carotenoids.⁵⁷ These polyenes cannot undergo large amplitude motions and have a more limited number of conformational minima on the 1¹Ag⁻ and 2¹Ag⁻ potential surfaces. For example, under the same thermal and photochemical conditions that convert all-trans β-carotene (N = 11) into equilibrium mixtures of cis and trans isomers, the corresponding N = 11 polyene in this series is essentially unreactive.⁷⁵ The observation of relatively strong and characteristic S* signals in these geometrically constrained polyenes thus significantly narrows the range of motions required to account for similar transient absorption signals in the carotenoids.

Another important observation regarding the origin of the S* signals is the excited state dynamics of the N = 19 polyene. Analysis of the transient absorption spectra shown in Fig. 3 (bottom right panel) shows that the second EADS component (red) exhibits strong 2¹Ag⁻ → n¹B_u⁺ absorption at 780 nm but no S* signals. This absorption decays in 490 fs to form a third EADS component (green) with relatively strong S* signals at 580 nm. As shown in Fig. S1, the rise times of the S* signals in N = 19 equal the decay time of the 2¹Ag⁻ state, indicating that S* is directly populated from 2¹Ag⁻. These kinetics have not been seen in previous studies of carotenoids and suggest that the N=19 S* signals are due to 1¹Ag⁻ → 1¹B_u⁺ absorption from excited vibrational levels of the ground state (1¹Ag⁻), as previously suggested for β-carotene.⁷³ However, this model cannot explain the dynamics of the N = 13 and 15 polyenes or of the S* signals in spirilloxanthin (N=13) or rhodoxanthin (N=14).^76–78 For all of these molecules, S* signals appear within 200–500 fs, well in advance of the > 1 ps decay times of the 2¹Ag⁻ states. (See the transient absorption traces for N=13 and 15 in Fig. 3.) The 490 fs component in N=19 also might be explained by S* as a twisted 2¹Ag⁻ excited state that is generated within the 490 fs 2¹Ag⁻ lifetime. Additional experimental and theoretical studies of the dynamics of this constrained polyene series (N = 5–23) promise to provide further insights on the role of molecular structure, conjugation length, and the ultrafast excitation conditions on the S* signals in a wide range of polyenes and carotenoids in different solvent environments. However, further refinement and integration of the different models for the S* signals remain significant challenges and fall outside the scope of this paper.

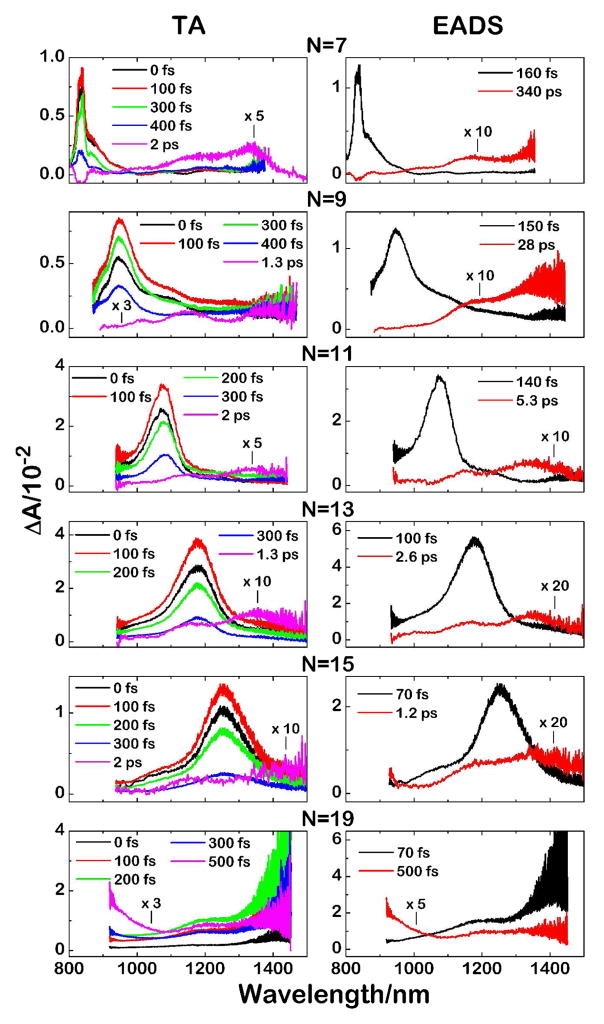
Transient Absorption Spectra in the NIR Region

Time-resolved, transient absorption spectra of the N = 7–19 polyenes in the NIR (~850–1400 nm) in room temperature 2-MTHF are given in Fig. 4. These signals can be accounted for by two EADS components as indicated. The short-lived (70–160 fs, cf. ~100 fs instrument response) components in the NIR transient absorptions can be identified with a symmetry-allowed, 1¹B_u⁺ → n¹Ag⁻ absorption. As expected, these transitions show a systematic shift to longer wavelength with increasing conjugation (~840 nm for N = 7; ~1400 nm for N = 19). The lifetimes of these components are in good agreement with the 1¹B_u⁺ lifetimes (90–180 fs) from the EADS analysis of the transient absorption spectra in the visible region (Table 1). The energies of 1¹Ag⁻ → 1¹B_u⁺ (0–0) bands can be added to the 1¹B_u⁺ → n¹Ag⁻ transition energies to calculate the energy of the n¹Ag⁻ state as a function of conjugation length. The transient absorption experiments thus provide detailed data on a second, higher energy “dark state,” which cannot be detected in the steady-state absorption spectra (Fig. 2).

Figure 4.

Transient absorption (TA) spectra obtained at different time delays in the NIR at room temperature in 2-MTHF. Global analysis of decays provides evolution associated difference spectra (EADS).

The NIR spectra also lead to the determination of the energies of the lowest energy single state (2¹Ag⁻). For shorter, model systems (4 ≤ N ≤ 7), the 2¹Ag⁻ state can be observed in fluorescence experiments,^5,29 but the dominance of nonradiative decay processes makes it difficult to detect 2¹Ag⁻ → 1¹Ag⁻ transitions in longer (N > 7) polyenes and carotenoids. It now is clear that previously reported 2¹Ag⁻ → 1¹Ag⁻ fluorescence in all-trans carotenoids and long polyenes most likely can be attributed to cis impurities and/or conformationally distorted all-trans species, either present in distributions of 1¹Ag⁻ geometries or formed on 2¹Ag⁻ potential surfaces.²⁹ The measurement of the energies and dynamics of 2¹Ag⁻ states in carotenoids and polyenes thus is more reliably accomplished by detecting the symmetry-allowed 2¹Ag⁻ → 1¹B_u⁺ transition, as originally demonstrated by Polívka and Sundström.²⁷

The long-lived EADS components shown in Fig. 4 display weak 2¹Ag⁻ → 1¹B_u⁺ absorptions in the 1000–1400 nm range, but there is sufficient signal and vibronic resolution to analyze these features and to assign vibronic bands. As with the other electronic transitions in the steady-state and transient absorption spectra, our ability to compare spectra of molecules over a wide range of conjugation lengths is an indispensible tool in assigning the vibronic bands. In addition, previous work on the 2¹Ag⁻ → 1¹B_u⁺ absorptions in a variety of carotenoids is crucial in understanding similar signals in these constrained systems. The lifetimes of the longest-lived EADS components in the NIR are in excellent agreement with those obtained for the much stronger 2¹Ag⁻ → n¹B_u⁺ transitions in the visible region (Table 1). We thus can be assured that the weak absorptions detected in the NIR correspond to transitions from thermally relaxed 2¹Ag⁻ states. No components corresponding to the S* signals were observed in the NIR, as noted in a previous study on the carotenoid spirilloxanthin.⁷⁹

3.2 Energies of the Low-Lying Electronic States

Fluorescence Spectroscopy of N = 5 and N = 7

An understanding of the low-lying 2¹Ag⁻ states in linear polyenes, including carotenoids, initially emerged from analysis of the low temperature absorption and emission spectra of short model systems.^3,10 Simple all-trans polyenes with N = 4–7 have detectable fluorescence and exhibit spectra with sufficient vibronic resolution to allow the identification of the electronic origins and other vibronic bands of the lowest energy singlet to singlet transitions (1¹Ag⁻ → 1¹B_u⁺ and 2¹Ag⁻ → 1¹Ag⁻).^5,80 The canonical fluorescence characteristics of polyenes are well illustrated by the N = 5 and N = 7 members of the current series. However, the rigid, planar geometries of these molecules result in negligible 2¹Ag⁻ → 1¹Ag⁻ (S₁ → S₀) fluorescence yields for N > 7, and we must rely on transient absorption experiments to determine the energies and dynamics of the lowest lying singlet states for polyenes with larger N. Fortunately, for N = 7, we can compare the electronic transition energies obtained from fluorescence spectra (2¹Ag⁻ → 1¹Ag⁻) with those deduced from transient absorption (2¹Ag⁻ → 1¹B_u⁺). The overlap of the two complementary techniques for N = 7 proved to be crucial in assigning the weak 2¹Ag⁻ → 1¹B_u⁺ vibronic bands in the NIR absorption spectra (Fig. 4), allowing the determination of the 2¹Ag⁻ (S₁) energies for polyenes with N > 7.

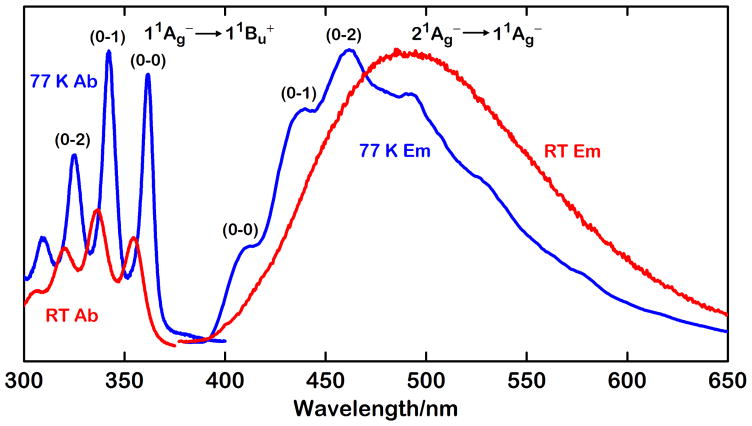
The N = 5 polyene displays the signature absorption and fluorescent spectra of short, model polyene systems (Fig. 5). The room temperature and 77 K absorption spectra (1¹Ag⁻ → 1¹B_u⁺) both exhibit well-resolved vibronic bands at ~1500 cm⁻¹ intervals, which can be assigned to overtones and combinations of totally symmetric carbon–carbon single and double bond stretching vibrations. The degree of vibronic resolution in the room temperature absorption spectra suggests a relatively homogeneous distribution of ground state polyene geometries with essentially coplanar, π-conjugated, double and single bonds. Cooling the sample to 77 K results in a ~500 cm⁻¹ shift to lower energy of the strongly allowed 1¹Ag⁻ → 1¹B_u⁺ absorption, and also results in a significant narrowing of the vibronic bands and a concomitant increase in absorbance. The increase in absorbance and the bathochromic shift in part are due to the increases in solute concentration and the larger refractive index of the higher density, low temperature glass, but the shift to longer wavelengths and the spectral narrowing also can be attributed to an increase in conformational order, resulting in an even narrower distribution of approximately planar molecular geometries.

Figure 5.

Room temperature and 77 K absorption and fluorescence spectra of N = 5 in 2-MTHF. For room temperature emission, λ(excitation) = 354 nm; for 77 K emission, λ (excitation) = 360 nm.

The N = 5 fluorescence spectra exhibit the classic Stokes shift between the strongly allowed (ε > 10⁵ L/mole cm) absorption (1¹Ag⁻ → 1¹B_u⁺) and the symmetry-forbidden emission (2¹Ag⁻ → 1¹Ag⁻). The low temperature emission spectrum has sufficient vibronic resolution to allow the identification of the 2¹Ag⁻ → 1¹Ag⁻ (0–0) band at 24,450 ± 20 cm⁻¹ (409 nm), giving a 1¹B_u⁺ – 2¹Ag⁻ energy gap of ~ 4,800 cm⁻¹ at 77 K. These data agree well with the 2¹Ag⁻ (S₁) energies of simpler N = 5 polyene hydrocarbons. For example, all-trans dodecapentaene has an 2¹Ag⁻ energy of ~24,200 cm⁻¹ in room temperature, nonpolar hydrocarbon solvents,⁵ which reinforces the observation that the 1¹Ag⁻ ↔ 2¹Ag⁻ transition energies of polyenes primarily depend on the conjugation length N and are relatively insensitive to the details of substitution and solvent environment. 1¹Ag⁻ ↔ 1¹B_u⁺ transition energies, on the other hand, are much more dependent on the molecular structure and solvent, primarily due to the much larger (~100x) transition dipole of this strongly allowed transition.²⁶

It is important to note that, while the 1¹Ag⁻ → 1¹B_u⁺ absorption of the N = 5 polyene shifts to lower energy upon cooling to 77 K, the Franck–Condon envelope of the 2¹Ag⁻ → 1¹Ag⁻ emission shifts to higher energy with cooling (Fig. 5). The lack of vibronic resolution in the room temperature emission spectrum makes this shift difficult to quantify, but the combination of the ~500 cm⁻¹ red shift in absorption and a comparable blue shift in the emission suggests a substantially larger (~5,800 ± 300 cm⁻¹) 1¹B_u⁺ – 2¹Ag⁻ energy gap in the room temperature solution for N = 5. The shift of the 2¹Ag⁻ → 1¹Ag⁻ transition to higher energy upon cooling to 77 K can be rationalized by the inability of the relatively short-lived 2¹Ag⁻ state to relax its geometry in the rigid low-temperature glass. There is evidence for similar blue shifts in the 2¹Ag⁻ → 1¹Ag⁻ emissions in several other polyenes. For example, we previously noted increases of ~500 cm⁻¹ in the 2¹Ag⁻ → 1¹Ag⁻ (0–0) bands in dimethyl polyenes with N = 4–7 upon cooling these molecules from room temperature to 77 K in n-alkane solvents.⁸¹ These changes, in combination with the red shifts in the 1¹Ag⁻ → 1¹B_u⁺ absorptions, decrease the 1¹B_u⁺ – 2¹Ag⁻ gaps by ~1,200 cm⁻¹ when these model polyenes are immobilized in 77 K matrices. A ~500 cm⁻¹ red shift of the 1¹Ag⁻ → 1¹B_u⁺ absorption and a ~400 cm⁻¹ blue shift of the 2¹Ag⁻ → 1¹Ag⁻ (S₁ → S₀) emission spectrum upon cooling room temperature samples to 77 K also was observed in a model N = 7 open-chain carotenoid,⁶⁴ and comparable blue shifts are noted in the broad, unresolved S₁ → S₀ (2¹Ag⁻ → 1¹Ag⁻) emissions of the N = 7 and N = 8 analogues of β-carotene.⁶⁵

The room temperature and 77 K absorption and fluorescence spectra of N = 7 (Fig. 6) reveal similar patterns, though the fluorescent yield of N = 7 is significantly smaller than that of N = 5. The longer polyene exhibits both 1¹B_u⁺ → 1¹Ag⁻ and 2¹Ag⁻ → 1¹Ag⁻ emissions, and the overlap of these two spectra presents some challenges in assigning the S₁ → S₀ (0–0) band. Using the N = 5 spectra as a guide, we note that the vibronic bands of the well-resolved 1¹Ag⁻ → 1¹B_u⁺ absorption and the 1¹B_u⁺ → 1¹Ag⁻ emission show parallel shifts (~500 cm⁻¹) to longer wavelengths upon cooling. The 2¹Ag⁻ → 1¹Ag⁻ fluorescence spectrum undergoes a 500–1000 cm⁻¹ shift to shorter wavelengths in the 77 K glass. Using sums of Gaussian fits, the 2¹Ag⁻ → 1¹Ag⁻ vibronic origin for N = 7 at 77 K was determined to be 19,900 ± 100 cm⁻¹ (503 nm). This compares with 19,600 cm⁻¹ for hexadecaheptaene (N = 7) in a 77 K EPA glass⁸¹ and ~19,200 cm⁻¹ in various hydrocarbon solvents at room temperature.⁵ These energies also can be compared with a 2¹Ag⁻ energy of 18,540 ± 40 cm⁻¹ for an N = 7 open-chain carotenoid in 77 K EPA.⁶⁴ As for N = 5, the N = 7 spectra thus show a significant narrowing of the 1¹B_u⁺ – 2¹Ag⁻ energy gap when room temperature solutions are frozen into 77 K rigid matrices. Other important features to note in the N = 7 spectra are the characteristic vibronic progressions, which facilitate the precise measurement of the (0–0) transition energies in all but the room temperature fluorescence spectra.

Figure 6.

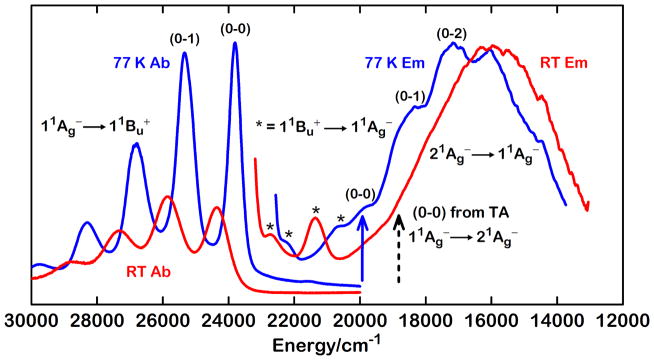
Room temperature and 77 K absorption and fluorescence spectra of N = 7 in 2-MTHF. For room temperature emission, λ(excitation) = 408 nm; for 77 K emission, λ(excitation) = 416 nm. The blue and black arrows correspond to the (0–0) bands of 1¹Ag⁻ ↔ 2¹Ag⁻ transitions obtained from the 77 K fluorescence spectrum and calculated from the room temperature transient absorption (TA) measurements.

The N = 9 polyene has extremely weak fluorescence signals, which are dominated by 1¹B_u⁺ → 1¹Ag⁻ emission. A crossover from 2¹Ag⁻ → 1¹Ag⁻ (S₁ → S₀) emission to 1¹B_u⁺ → 1¹Ag⁻ emission is a common feature of longer polyenes (N ≥ 7)^26,82 and precludes the detection of the 2¹Ag⁻ → 1¹Ag⁻ (0–0) band for N = 9. Our inability to detect S₁ → S₀ emission in N = 9 is consistent with earlier work on the temperature dependence of the S₁ → S₀ fluorescence of all-trans hexadecaheptaene (N = 7),²⁹ which suggested that the previously reported fluorescence from longer polyenes and carotenoids most likely is due to subsets of cis impurities and/or higher energy, distorted/twisted all-trans species formed in the 2¹Ag⁻ states following excitation of symmetric, all-trans molecules. The rigid, planar structures induced by the framework of five-member rings in the current polyenes preclude large amplitude distortions or trans ↔ cis isomerization⁷⁵ and likely result in 1¹Ag⁻ and 2¹Ag⁻ potential surfaces with fewer distorted conformational minima that can be populated in room temperature solutions or 77 K glasses. This can explain the vanishing 2¹Ag⁻ → 1¹Ag⁻ fluorescence signals from these samples compared to their more flexible carotenoid and polyene counterparts with N > 7. It is important to stress that for N = 7 of the current polyene series, the comparison of 1¹Ag⁻ ↔ 2¹Ag⁻ (0–0) bands estimated from fluorescence and from transient absorption measurements should relate sets of molecules with very similar, relatively homogeneous distributions of ground and excited state geometries.

Assignment of Vibronic Bands in 2¹Ag⁻ → 1¹B_u⁺ Transient Absorption Spectra

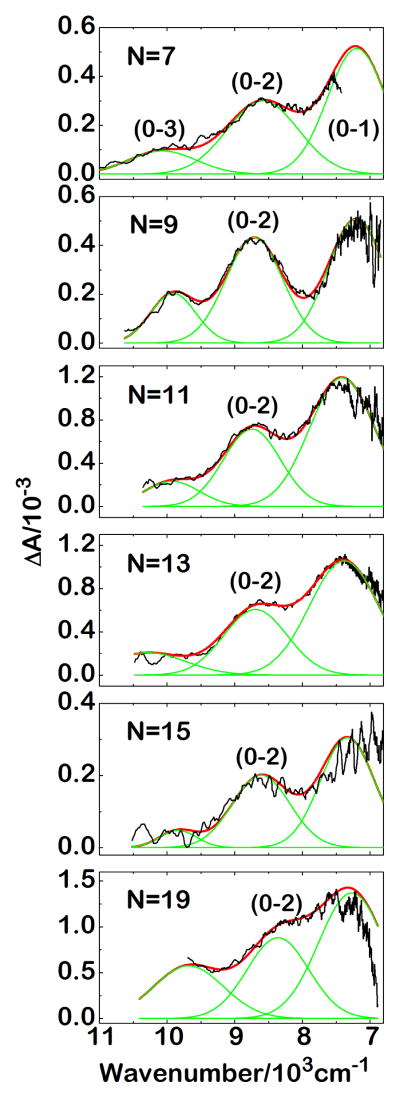
Our analysis of the room temperature and 77 K absorption and emission spectra of the N = 5 and N = 7 polyenes was essential in interpreting the 2¹Ag⁻ → 1¹B_u⁺, NIR transient absorption measurements on N = 7–19, which were carried out in room temperature, 2-MTHF solutions. These spectra are presented in Fig. 7, along with representative sums of Gaussian fits to spectra obtained from global fitting (EADS). The 2¹Ag⁻ → 1¹B_u⁺ vibronic spacings calculated from the Gaussian fits (~1450 cm⁻¹ for N = 7; ~1200 cm⁻¹ for N = 19) are in good agreement with those observed in the room temperature 1¹Ag⁻ → 1¹B_u⁺ spectra (~1500 cm⁻¹ for N = 7; ~1200 cm⁻¹ for N = 19 (Fig. 2)). The dependence of the 1¹B_u⁺ vibronic energies on N parallels the decrease in the frequencies of the 2¹Ag⁻ C–C and C=C vibrational modes with increasing N in tertiary-butyl capped polyenes.⁸³ Sums of Gaussian fits to the “raw” 2¹Ag⁻ → 1¹B_u⁺ transient absorption data in the NIR are in excellent agreement with fits made to the EADS spectra. The analyses of these fits are greatly simplified by the remarkable consistency of the NIR absorbance features for N = 7, 9, 11, 13, 15, and 19 (Fig. 7), which indicates an almost constant 1¹B_u⁺ – 2¹Ag⁻ energy difference in this series. Our interpretation of these spectra also builds on previous vibronic analyses of the NIR, 2¹Ag⁻ → 1¹B_u⁺ transient absorption spectra of several carotenoids.^27,57,71

Figure 7.

Representative sum of Gaussian fits to NIR transient absorption spectra (2¹Ag⁻ → 1¹B_u⁺).

The limit of our spectral range in the NIR (7,000 – 11,000 cm⁻¹) precludes the direct observation of transient absorption features that can be identified with the 2¹Ag⁻ → 1¹B_u⁺ electronic origins ((0–0) bands). We thus considered several options for the assignments indicated in Fig. 7. Our analysis of the room temperature and 77 K fluorescence spectra for N = 7 forces the assignment of the 2¹Ag⁻ → 1¹B_u⁺ vibronic bands indicated in Fig. 7. Comparison of the 2¹Ag⁻ → 1¹B_u⁺ (0–2) and 1¹Ag⁻ → 1¹B_u⁺ (0–2) energies for N = 7 then allows the direct calculation of the room temperature 2¹Ag⁻ zero-point energy as 18,800 ± 90 cm⁻¹ (532 nm). Figure 6 compares this estimate of the room temperature (0–0) band with the electronic origin observed in the 77 K S₁ → S₀ fluorescence (19,900 cm⁻¹, 503 nm). The approximately 1000 cm⁻¹ difference is consistent with the shift between the 77 K and room temperature emissions seen in Fig. 5 and Fig. 6 and shifts noted in other polyenes (see above). The relatively broad N = 7 fluorescence spectrum at room temperature precludes the accurate measurement of the S₁ → S₀ (0–0), but the shift in the vibronic envelope of the room temperature emission relative to the 77 K emission supports the assignments of the vibronic bands in the 2¹Ag⁻ → 1¹B_u⁺ spectrum given in Fig. 7. No other choice for these assignments can be reconciled with the N = 7 fluorescence spectra, and the central vibrational band that occurs ~8500 cm⁻¹ for N = 7–19 thus can be safely assigned to the (0–2) vibrational band of the 2¹Ag⁻ → 1¹B_u⁺ transition. Comparisons between the (0–2) bands for the 2¹Ag⁻ → 1¹B_u⁺ and 1¹Ag⁻ → 1¹B_u⁺ transitions lead to the 2¹Ag⁻ energies presented in Table 2. As anticipated from Fig. 7, the 1¹B_u⁺ – 2¹Ag⁻ energy difference is essentially constant (5900 ± 200 cm⁻¹) for N = 7–19 and also agrees well with our estimate (5,800 ± 300 cm⁻¹) for the energy gap for N = 5, based on its room temperature absorption and emission spectra (see above). Measurements of the 1¹B_u⁺ – 2¹Ag⁻ energy gap for a series of dimethyl polyenes indicated a small, systematic increase with conjugation length, i.e. the gap increases from ~4500 cm⁻¹ for N = 4 to ~6000 cm⁻¹ for N = 7 in room temperature hexane.⁵ Previous studies on natural and synthetic carotenoids with N = 7–13 suggest that this gap approaches an asymptotic limit for large N, so the current results are consistent with the considerable amount of data on the excited state energies of short, model polyenes and carotenoids.^27,45

Table 2.

State and transition energies (cm⁻¹) of polyene excited states in 2-MTHF.^a

N	11Bu+b	21Ag−c	21Ag− → 11Bu+d	21Ag− → 11Bu+	11Bu+ → n1Ag−
7	24400	18800	5600	19700	11900
9	22100	16300	5800	17500	10600
11	20700	14700	6000	16000	9300
13	19800	13800	6000	14900	8500
15	19200	13100	6100	14100	8000
19	18400	12600	5800	~12800	< 7100

^aEstimated uncertainties (±1σ) are ~100 cm⁻¹ for the energies indicated.

^b(0–0) band from sum of Gaussian fits to the 1¹Ag⁻ → 1¹B_u⁺ steady-state absorption.

^cCalculated from the difference between the (0–2) band of the 1¹Ag⁻ → 1¹B_u⁺ steady-state absorption and the (0–2) band of the 2¹Ag⁻ → 1¹B_u⁺ component from transient absorption. Peak positions were obtained from sum of Gaussian fits.

^dDifference between 1¹B_u⁺ and 2¹Ag⁻ energies.

3.3 Electronic Energies of ¹Ag⁻ and ¹B_u⁺ States: Dependence of Transition Energies on Conjugation Length

Assignments of Electronic Transitions

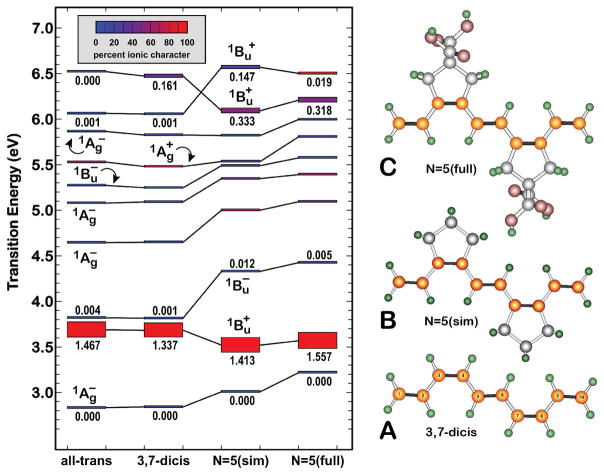
The polyenes under study are constrained to planar, multi-cis structures by five-membered rings which include a cis double bond and have two polar R substituents, where R=CO₂CH(CH₃)₂ (Fig. 1). When these groups were included in our calculations, we simplified R as R′=COOH. The structural and electronic influences of the polar R′ groups and the five-membered rings were studied for the N = 5 polyenes using MNDO-PSDCI^6,43 theory (Fig. 8) and EOM-CCSD^47–49 theory (Fig. S2). As shown in Fig. 8, the backbone of rings has an important impact on the transition energies and oscillator strengths of all electronic transitions. However, the ordering of levels is not affected except in the higher energy regions. The R′ group also has an effect, but in more subtle ways that likely would be masked by the polar solvent (2-MTHF) used to record the spectra. Because our primary interests in this study are the energies and intensities of polyene electronic transitions, we included the rings but excluded the R′ groups in subsequent calculations.

Figure 8.

The impact of geometry and substituents on the calculated properties of the N = 5 polyene. The insert shows the calculated excited state level ordering based on MNDO-PSDCI calculations for the unsubstituted all-trans polyene, the unsubstituted 3,7-di-cis polyene (A), the 3,7-di-cis polyene with a simplified backbone (B), and the full N = 5 polyene including the ring substituents (C). Oscillator strengths for selected transitions and the relative ionic versus covalent character of each electronic state are indicated. Results for these four models based on EOM-CCSD methods are presented in Fig. S2.

We started our examination of the excited state level ordering by studying the absorption spectrum of the N = 9 polyene, which provides a viable target for both our semiempirical and ab-initio methods. Comparisons of MNDO-PSDCI, SAC-CI and EOM-CCSD calculations are presented in Fig. S3. Although the SAC-CI calculations were carried out at the highest standard level (LevelThree),^50,53 a ¹B_u⁺ state is calculated to be the lowest-lying singlet state. This prediction is not consistent with the experimental results, which give strong evidence for a lowest-excited ¹A_g⁻ state. All the other methods predict 2¹A_g⁻ as the lowest excited singlet. Nevertheless, the SAC-CI calculations provide a good description of the electronic properties of the ionic ¹B_u⁺ states.

The EOM-CCSD calculations represent the highest-level of theory employed in this study and serve as the reference to which the other calculations should be compared. In most respects, the EOM-CCSD calculations are in excellent agreement with experiment. These methods predict a lowest excited 2¹Ag⁻ state and allowed ¹B_u⁺ states in all regions for which bands are observed in the room temperature absorption spectra. However, all transition energies are consistently underestimated by ~0.4 eV. Because the EOM-CCSD and MNDO-PSDCI calculations are in excellent agreement regarding transition energies and oscillator strengths, we used the computationally faster MNDO-PSDCI methods to explore possible origins of the differences in the calculated versus observed transition energies. One possible source of error might be the assumption of planar C_2h (or C_2v) geometries. For example, these polyenes may be distorted slightly in polar solution around the single bonds to generate a corkscrew conformation, which creates a dipole moment along the polyene chain. This conformation previously was shown to be an important contributor to the absorption spectra of carotenoids.⁵⁷ A corkscrew conformation was generated for the N = 9 polyene by using B3LYP/6-31G(d) methods and solvent optimization utilizing the Polarizable Continuum Model (PCM)^84–86 in acetonitrile. The resulting conformation exhibited small (4–6 degrees) dihedral distortions of the single bonds and generated a small blue shift in the transition energies (Fig. S3). Agreement with the experimental transition energies improved only slightly, and we concluded that the formation of corkscrew conformations is possible, but of minimal importance in understanding the spectra of these conformationally constrained molecules.

All the theoretical treatments are in agreement that the only electronic transitions with detectable oscillator strength originating in the ground state are 1¹Ag⁻ → ¹B_u⁺ (Fig. 9). It may surprise the observer that transitions to ¹A_g⁺ states, which are responsible for the distinctive “cis-bands” in polyene and carotenoid electronic spectra,^30,87,88 do not have observable intensities in these systems. However, the cis linkages in these molecules are symmetrically placed and do not generate mixing between the gerade and ungerade excited states to yield oscillator strength in the 1¹Ag⁻ → ¹A_g⁺ transitions. The inherent simplicity of the absorption spectra of these polyenes thus is associated, in large part, with the lack of participation of ¹A_g⁺ states in absorption.

Figure 9.

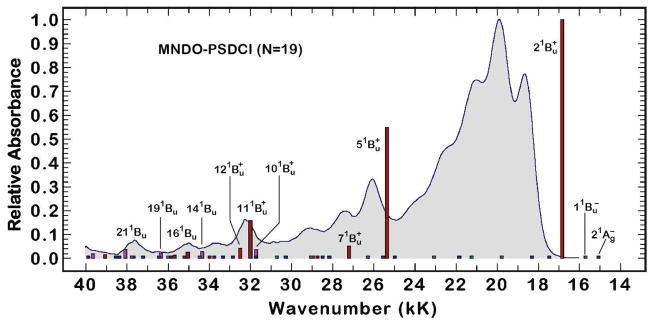
The electronic transitions predicted by MNDO-PSDCI molecular orbital theory are superimposed on the absorption spectrum of the N = 19 polyene. (1 kK = 10³ cm⁻¹) The heights of the vertical bars are proportional to the calculated oscillator strengths of the transitions. The calculations included the simplified backbone system (Fig. 8B) and included full single and double configuration interaction within the π-system. Note that all of the allowed states are ¹B_u⁺ states. The ionic (+) versus covalent (−) character of these states is mixed at higher energies to such an extent that assignment of ionic versus covalent character is not possible.

The MNDO-PSDCI calculations on N = 19 (Fig. 9) also indicate the possible presence of a second “dark” state (¹B_u⁻) below the ¹B_u⁺ state responsible for the major absorption in these molecules. A low-energy ¹B_u⁻ state was predicted in early calculations on longer polyenes by Tavan and Schulten,⁸⁹ and in more recent theoretical studies.^30,90–92 Although Raman excitation studies^91,92 and two-photon polarization studies⁶ have reported evidence for this state, the ¹B_u⁻ state has not been observed in direct UV–visible absorption experiments. Nor is there any compelling evidence for the ¹B_u⁻ state in the excited state dynamics of these polyenes or corresponding carotenoids.

Dependence of Electronic Energies on Conjugation Length: Implications for the Excited State Energies of Infinite Polyenes

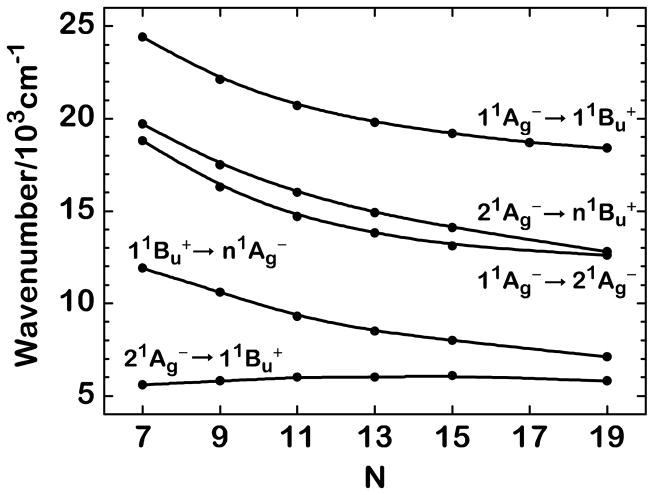
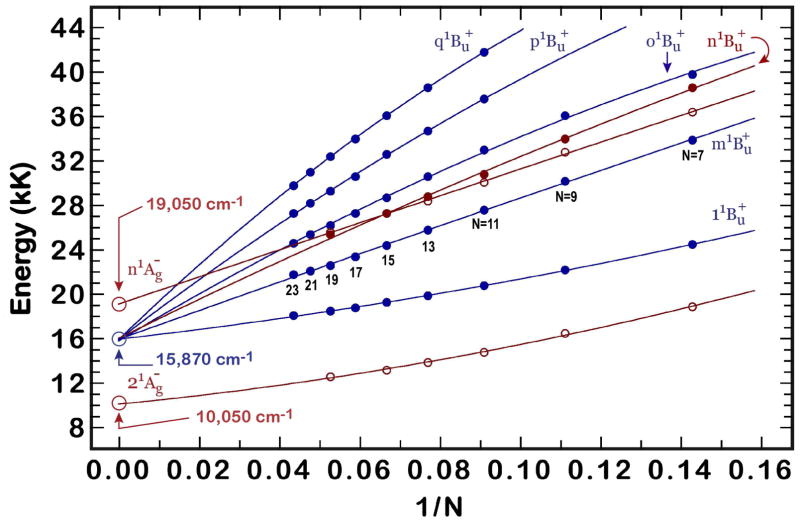
The lowest energy electronic transitions in the visible and NIR transient absorption experiments for N = 7–19 are summarized in Table 2 and in Fig. 10. Based on these transition energies and the energies of the 1¹Ag⁻ → 1¹B_u⁺ transition, the energies of additional excited electronic states can be calculated and compared with the “allowed” electronic states seen directly in absorption, e.g., 1¹Ag⁻ → 1¹B_u⁺. The current studies, combined with the transition energies observed in the unusually well-resolved steady-state absorption spectra (Fig. 2 and Scriban et al.³²), provide an unusually rich set of data (Table S2) on the low-lying singlet states (¹Ag⁻ and ¹B_u⁺) of this homologous series of polyenes over a wide range of conjugation lengths (N = 5–23). The data summarized in Fig. 11 (and Table 2 and Table S2) offer some straightforward challenges for improving theoretical descriptions of polyene excited states, including understanding the electronic structures in the infinite polyene limit.

Figure 10.

Polyene transition energies in room temperature 2-MTHF. Data from Table 2. Energies of the 1¹Ag⁻ → 1¹B_u⁺ transition (0–0) were obtained from sum of Gaussian fits. Energies of the 2¹Ag⁻ → n¹B_u⁺ and 1¹B_u⁺ → n¹Ag⁻ transitions correspond to the wavelengths of maximum absorption of EADS components from the transient absorption spectra. The 1¹Ag⁻ → 2¹Ag⁻ transition energy was calculated from the difference between the (0–2) band of the 1¹Ag⁻ → 1¹B_u⁺ steady-state absorption and the (0–2) band of the 2¹Ag⁻ → 1¹B_u⁺ transient absorption. Peak positions were obtained from sum of Gaussian fits.

Figure 11.

Electronic transition energies of N = 7–23 polyenes in room temperature 2- MTHF (data from Table S2). (1 kK = 10³ cm⁻¹) Data points and lines in blue correspond to absorption measurements, and data points and lines in red are derived from transient absorption measurements. Open circles designate measurements of ¹A_g⁻ state energies and solid circles designate measurement of ¹B_u⁺ states energies. Lines are from quadratic fits (E = A +B/N +C/N²) as explained in the text. Parameters of the fits are presented in Table S3.

The assignments of the absorption spectra are supported by MNDO-PSDCI, SAC-CI and EOM-CCSD calculations on N = 5 and N = 9 (Fig. 8, S2, and S3) and on the MNDO-PSDCI calculations on N = 19 (Fig. 9). All the transitions in the steady-state, room temperature absorption spectra, including the strongly allowed transition that dominates all polyene spectra, are assigned to 1¹Ag⁻ → x¹B_u⁺ transitions. As discussed above, the weak 1¹Ag⁻ → 1¹A_g⁺ transitions (“cis bands”) observed in the absorption spectra of carotenoids and cis-polyenes do not have detectable oscillator strengths in these symmetric, alternating, cis-trans polyene systems. The oscillator strengths of the “symmetry-allowed” transitions to ¹B_u⁺ states systematically decrease for transitions into higher energy states, and this pattern is supported by the calculations. The transient absorption spectra also involve symmetry-allowed transitions: 2¹Ag⁻ → 1¹B_u⁺, 2¹Ag⁻ → n¹B_u⁺, and 1¹B_u⁺ → n¹Ag⁻. In combination with the 1¹Ag⁻ → 1¹B_u⁺ transition energies, the transient absorption spectra thus allow calculations of the energies of 2¹Ag⁻, n¹Ag⁻, and the state labeled as n¹B_u⁺. The electronic energies obtained by combining the steady-state absorption data of Scriban et al.³² and the data from the transient absorption experiments are summarized in Fig. 11, Table 2, and Table S2.

The data presented in Fig. 11 show remarkably simple patterns, which allow extrapolation of energies to large N. All of the ¹B_u⁺ states, including the ¹B_u⁺ state detected in the transient absorption spectra exhibit a systematic nonlinear dependence with respect to 1/N. Deviations from a linear dependence, previously assumed for the electronic energies of shorter polyenes and carotenoids, are most obvious in this series, due to the large range of N values and the number of electronic states we have been able to detect and assign. The curvature in the data (Fig. 11) can be accounted for by including an additional term in the least squares fits. Separate quadratic fits to each of the ¹B_u⁺ states suggested a common asymptotic limit of 15,000 ± 1000 cm⁻¹. We thus did a global fit to all of the ¹B_u⁺ energies, assuming a common, unspecified value at 1/N = 0. This global fit established an extrapolated ¹B_u⁺ energy of 15,870 ± 94 cm⁻¹. Including this value in individual fits to each ¹B_u⁺ state resulted in the quadratic fits indicated in Fig. 11 and summarized in Table S3. This asymptotic limit is remarkably consistent with the vibronically-resolved 77 K absorption spectrum of a related polyene polymer (1/N ≈ 0), containing a mixture of five- and six-membered rings, which shows a single, prominent absorption (1¹Ag⁻ → 1¹B_u⁺) with an electronic origin at 15,800 cm^−1.93 As discussed previously,⁹³ the convergence of all of the “allowed” transition energies in the infinite polyene limit accounts for the very simple, well-resolved absorption spectrum of the unpurified polymer. It is important to note that this convergence was predicted by the early multi-reference double-excitation configuration-interaction (MRDCI) calculations of Tavan and Schulten,⁸⁹ which indicate a common energy for all “ionic” states (¹B_u⁺ and ¹A_g⁺) for N = ∞. The current studies cannot detect any ¹A_g⁺ states, due to the vanishingly small ¹Ag⁻ → n¹A_g⁺ transition dipoles (“cis bands”) in these polyene systems.

Tavan and Schulten⁸⁹ also predicted a similar convergence of the excited “covalent” states (¹Ag⁻ and ¹B_u⁻), but a common asymptotic limit clearly is not supported by the data for the 2¹Ag⁻ and n¹Ag⁻ states shown in Fig. 11. The two ¹Ag⁻ states are separated by ~9000 cm⁻¹ in the infinite polyene. We explored both theoretically and experimentally the possibility that the difference in the transition energies of the two ¹Ag⁻ states could be due to the different spectroscopic methods used to assign the state energies. Note that the higher energy n¹Ag⁻ state was observed via transient absorption spectroscopy from the first excited ¹B_u⁺ state. We examined the possibility that an evolved 1¹B_u⁺ state would decrease in energy relative to the higher n¹Ag⁻ state to yield a blue-shifted transition energy. Although EOM-CCSD and MNDO-PSDCI calculations predict that an evolved ¹B_u⁺ state indeed shifts to lower energy, the calculations indicate that the higher ¹Ag⁻ state, which is optically coupled to the ¹B_u⁺ state, drops by a comparable amount. In our simulations, the largest ¹B_u⁺ → ¹Ag⁻ shift induced by excited state evolution was a 300 cm⁻¹ blue shift calculated for N = 5 (Fig. S4), which is negligible compared to the observed separation of ~9000 cm⁻¹. Furthermore, the relative shifts of these states decrease as the conjugation length increases. Our calculations show that the rigid structures of these polyenes is partially responsible for preventing excited state evolution from creating significant shifts in the measured absolute state energies.

The theoretical analysis is supported by the time independence of the 1¹B_u⁺ → n¹Ag⁻ transient absorption profiles during the 100–200 fs lifetime of the 1¹B_u⁺ state (Fig. 4). Additional experimental support for the viability of the ~9000 cm⁻¹ separation between the ¹Ag⁻ states is that one of the six ¹B_u⁺ states included in the extrapolations (n¹B_u⁺) also was observed via transient absorption. This state, designated by closed red circles and a red line in Fig. 11, extrapolates to the same infinite polyene limit as for the ¹B_u⁺ states detected in the steady-state absorption spectra. We conclude with confidence that the two ¹Ag⁻ states assigned in this study extrapolate to significantly different infinite polyene limits and that the 9000 cm⁻¹ separation is intrinsic to the energies of the manifold of ¹Ag⁻ states rather than an experimental artifact.

3.4 Energy Gap Law Analysis of 2¹Ag⁻ Lifetimes

Comparisons with Carotenoids

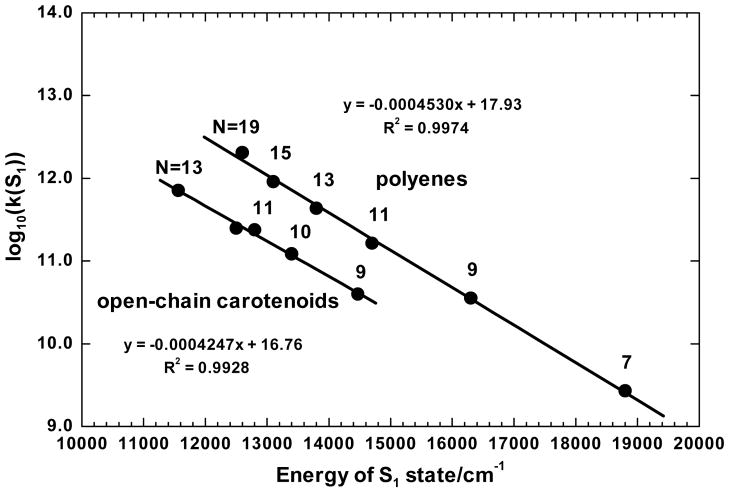
The lifetimes (τ₁) of the 2¹Ag⁻ states of these polyenes are dominated by nonradiative decay to the ground state and show a significant decrease with conjugation length, ranging from 370 ps for N = 7 to 0.50 ps for N = 19 (Table 1). The energy gap law⁶⁶ predicts that the rate of nonradiative decay depends approximately exponentially on the 2¹Ag⁻–1¹Ag⁻ energy difference, which in turn depends approximately inversely on the conjugation length (Fig. 11). A simple application of the energy gap law for the current series is presented in Fig. 12 and compared with a similar analysis of 2¹Ag⁻ lifetimes and energies for several open-chain, all-trans carotenoids (Table S4). Both sets of molecules exhibit linear relationships between the log of the 2¹Ag⁻ decay constant and the 2¹Ag⁻ energy determined from transient absorption experiments. Although additional data on 2¹Ag⁻ energies and lifetimes is available from fluorescence measurements, previous work²⁹ has shown that the fluorescence of longer (N > 7), all-trans polyenes is dominated by emission from less symmetric cis impurities or by distorted trans isomers, either present in the ground state or formed in the 2¹Ag⁻ state following the excitation of more symmetric, all-trans species. Steady-state and time-resolved fluorescence experiments of longer polyenes thus may favor the detection of nonrepresentative subsets of 2¹Ag⁻ conformers and geometric isomers, even for highly-purified samples with relatively narrow distributions of all-trans ground state conformers. Measurements of the 2¹Ag⁻ energies and lifetimes by detection of the symmetry allowed, 2¹Ag⁻ → 1¹B_u⁺ and 2¹Ag⁻ → n¹B_u⁺ transitions thus provide a more reliable set of data for exploring the connections between 2¹Ag⁻ decay rates and energies.

Figure 12.

Simplified energy gap law analysis of 2¹Ag⁻ lifetimes for constrained polyenes and open-chain carotenoids. k is 1/τ₁ from Table 1 and Table S4. Parameters for the linear fits are indicated.

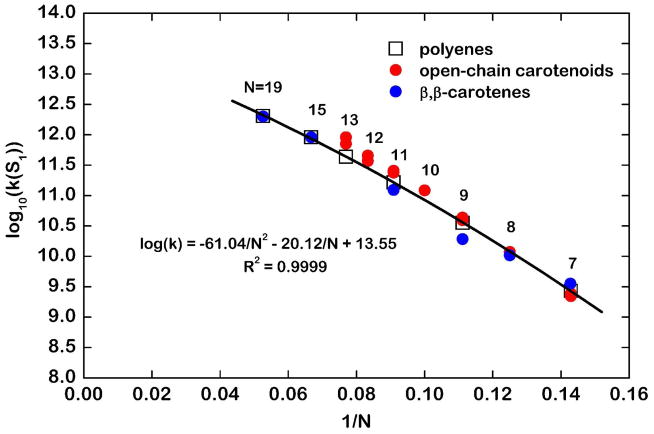
Figure 12 shows excellent fits to the energy gap law for the open-chain carotenoids (N = 9–13) and the polyenes (N = 7–19). This figure illustrates the uniformly lower 2¹Ag⁻ energies (~2,000 cm⁻¹) for carotenoids with a given N. The nonradiative decay rates also are systematically smaller for the carotenoids, and these counteracting effects result in 2¹Ag⁻ lifetimes that are quite comparable for polyenes and open-chain carotenoids with the same conjugation length, cf. τ₁ = 4.5 ps for lycopene vs. τ₁ = 6.1 ps for the N = 11 polyene. Comparison between these two series (Fig. 13) illustrates the very similar nonradiative decay rates for molecules with a given N. Longer open-chain carotenoids tend to have slightly shorter lifetimes than their polyene counterparts, but the 2¹Ag⁻ dynamics are rather similar. To underscore this point, we also include data for β-carotene and its synthetic analogues (N = 9–19). Note (Table S4) that the 2¹Ag⁻ lifetimes for the N = 15 and N = 19 analogues of β-carotene are identical to the 2¹Ag⁻ lifetimes measured for the polyene series, i.e., 1.1 and 0.5 ps.²⁵ The data for the three series (Fig. 13, Table S4) reinforce the conclusion that the length of conjugation is the primary determinant of 2¹Ag⁻ dynamics for a wide range of polyenes and carotenoids. The decay rates with the largest deviations from this simple pattern (corresponding to β-carotene analogues with N = 7, 8, and 9) are those whose lifetimes were determined using fluorescence techniques, rather than by transient absorption. This further emphasizes that the weak, symmetry-forbidden fluorescent signals detected in these systems likely are not representative of the all-trans conformers that dominate the distributions of ground state geometries.

Figure 13.

log₁₀(k(S₁)) versus 1/N for constrained polyenes, open-chain carotenoids, and β,β^-carotenes. k is 1/τ₁ from Table 1 and Table S4. Red data points are open-chain carotenoids with N = 7–13; blue data points are β,β-carotenes with N = 7–19. Quadratic fit is to data for constrained polyenes.

We explored the possibility that the 2¹Ag⁻ state converts to the ground state via population of a conical intersection. Theoretical studies suggest that such features are present in many polyenes^94–96, and we investigated this for the N=5 and N=7 polyenes using CASSCF methods as implemented in Gaussian 09. Our tentative conclusion is that the rigid backbone of rings (Fig. 1) provides structural constraints that prevent the adiabatic formation of conical intersections, but the observation of nearly degenerate avoided crossings indicates that such features may be present in the larger polyenes. The relatively long lifetimes of the 2¹Ag⁻ states in the N=5 and 7 polyenes (Table 1) suggest that, while conical intersections might well be part of the excited state landscape, the population of these features is not kinetically favorable. The much shorter lifetimes of the 2¹Ag⁻ states in the longer polyenes implies that conical intersections may play roles in 2¹Ag⁻ → 1¹Ag⁻ internal conversions for polyenes with N>7. However a more detailed analysis of the potential of conical intersections to account for the data summarized in Figures 12 and 13 is beyond the purview of this paper.

Excited State Dynamics of Infinite Polyenes

The data summarized in Fig. 11–13 also allow us to speculate on the excited state dynamics of infinite polyenes. As discussed in the previous section, extrapolation of the energies of the symmetry allowed transitions (~15,900 cm⁻¹ in the infinite polyene limit) is in good agreement with the (0–0) energy for the 1¹Ag⁻ → 1¹B_u⁺ transition in a related polymer (DEDPM) with 1/N ≈ 0.⁹³ Extrapolation of the 2¹Ag⁻ energies gives a limiting energy of at ~10,000 cm⁻¹, consistent with the constant, ~5,900 cm⁻¹ 1¹B_u⁺ – 2¹Ag⁻ energy gap noted in Fig. 7 and Table 2.

The 2¹Ag⁻ lifetime data (τ₁) data for N = 7–19 (Fig. 13) extrapolates to a 2¹Ag⁻ lifetime of ~30–40 fs for the infinite polyene. However, we expect limits to the time scales in which these molecules convert electronic energy into vibrational energy, which raises the question whether a <100 fs 2¹Ag⁻ lifetime can be realized. The convergence of the 2¹Ag⁻ and 1¹B_u⁺ lifetimes (τ₁ and τ₂, Table 1) for polyenes with large N complicates the analysis of the excited state kinetics and the transient absorption spectra. Nevertheless, comparison of the data presented here for the N = 7–19 polyenes with recent femtosecond pump–probe experiments on the DEDPM polymer in room temperature THF narrows the range of the 2¹Ag⁻ lifetime in the limit of infinite N.⁹⁷ The molar mass and polydispersity of the DEDPM sample translates into polymers with 3300 ± 760 double bonds. Synthetic defects in the polymerization reactions, chemical and photochemical degradation, and conformational disorder, especially in room temperature solutions, most likely result in distributions of considerably shorter conjugated segments, but the absorption spectra appear to be dominated by molecules with conjugation lengths >50.⁹³ The transient absorption spectra of DEDPM thus should be representative of species with 1/N ≈ 0, especially for samples excited on the red edge of the broad absorption band. Antognazza et al.⁹⁷ in ultrafast pump–probe experiments (10 fs time resolution) on room temperature THF solutions of DEDPM isolated decay components of 17, 50, 175 and 1200 fs. The first two components were assigned to the depopulation of the 1¹B_u⁺ state (17 fs) to a hot 2¹Ag⁻ state via an intermediate state denoted S_x (50 fs). Vibrational relaxation of the 2¹Ag⁻ state was associated with the 175 fs component, and the 1200 fs component was assigned to radiationless decay from the zero-point level of 2¹Ag⁻ into the ground state. Our analysis of the kinetic components of polyenes with N = 7–19 (Table 1), however, makes it is unlikely that a polyene with 1/N ≈ 0 could have a 2¹Ag⁻ lifetime longer than 1 ps. Thus, the 1200 fs feature observed by Antognazza et al.⁹⁷ most likely is due to the decay of the S* signal, an hypothesis that also is supported by the shape of the species-associated spectrum of this component. The 500 fs 2¹Ag⁻ lifetime of the N = 19 polyene then makes it is plausible to assign the 175 fs component in DEDPM to decay of the relaxed 2¹Ag⁻ state, which is considerably longer than the 30–40 fs lifetime predicted by the linear extrapolation presented in Fig. 13.

4. Conclusions

1. We have carried out detailed experimental and theoretical studies on the low-lying electronic states of a series of synthetic, constrained polyenes with 5–23 conjugated double bonds (N). The rigid geometries of these molecules result in vibronically-resolved electronic spectra, even in room temperature solutions.³² This has allowed a systematic investigation of the energies of several allowed (¹B_u⁺) and forbidden (¹Ag⁻) electronic states as a function of conjugation length.

2. We have recorded steady-state UV and visible absorption spectra for N = 5–23 and ultrafast transient absorption spectra for N=7–19 in the visible and NIR spectral regions. Absorption and fluorescence spectra of the N = 5 and N = 7 polyenes, both in room temperature solutions and in 77 K glasses, proved critical in assigning the vibronic bands of the symmetry-allowed, 2¹Ag⁻ → 1¹B_u⁺ transitions detected in the NIR transient absorption experiments. The energies of the 2¹Ag⁻ → 1¹B_u⁺ transitions from the time-resolved absorption measurements were subtracted from the energies of the strongly-allowed, 1¹Ag⁻ → 1¹B_u⁺ transitions obtained from steady-state absorption spectra to yield the 2¹Ag⁻ energies for N = 7–19 (Table 2). We find that the 1¹B_u⁺ – 2¹Ag⁻ energy gap of 5900 ± 200 cm⁻¹ is invariant to polyene length for N = 7–19 in room temperature 2-MTHF.

3. EOM-CCSD ab-initio and MNDO-PSDCI semi-empirical MO calculations facilitated the assignments of six ¹B_u⁺ states and two excited ¹Ag⁻ states in the steady-state and transient absorption spectra. Both theories account for the experimental transition energies and intensities, provided the aliphatic rings are included in the calculations, and predict that only the 1¹Ag⁻ → ¹B_u⁺ transitions have sufficient oscillator strength to be observed in the steady-state absorption spectra.

   1. Analysis of the N dependence of the ¹B_u⁺ energies indicates that the six “ionic” states extrapolate to an infinite polyene energy of ~15,900 cm⁻¹ (Fig. 11). This energy is in excellent agreement with the electronic origin of the 1¹Ag⁻ → 1¹B_u⁺ transition of a related conjugated polymer (DEDPM) with very large N.⁹³ The convergence of the ¹B_u⁺ states to a common, infinite polyene limit agrees with the early theoretical predictions of Tavan and Schulten.⁸⁹

   2. The two excited ¹Ag⁻ states exhibit a substantial (~9000 cm⁻¹) energy difference in the infinite polyene limit (Fig. 11), in contrast to the common limit for “covalent” states (¹Ag⁻ and ¹B_u⁻) predicted by previous theoretical treatments.⁸⁹ The EOM-CCSD calculations indicate that this energy difference cannot be associated with the time-evolution of the relevant excited states.

4. The ultrafast transient absorption experiments provide detailed information on the dynamics of the excited states following photo-excitation into the 1¹B_u⁺ state. The kinetic data confirm the assignments of transitions originating from both the 2¹Ag⁻ and the 1¹B_u⁺ states and provide insights on the decay pathways of these states. The transient absorption spectra, EADS components, and excited state lifetimes of these constrained polyenes are remarkably similar to those of less rigid, less symmetric, biologically relevant carotenoids with comparable conjugation lengths.^45,57,71 These similarities include the longer-lived “S*” components observed in polyenes with N = 13, 15, and 19. Comparisons with previous ultrafast studies of the dynamics of the low-lying excited states of carotenoids are important for elucidating the mechanisms by which naturally-occurring polyenes carry out their light-harvesting and photoprotective roles in biological systems.

5. The 2¹Ag⁻ lifetimes are well-accounted for by the 2¹Ag⁻ –1¹Ag⁻ energy differences, following the energy gap law for radiationless decay. As shown in Fig. 13, the decay kinetics of these rigid polyenes as a function of N are in remarkable agreement with N dependence of the 2¹Ag⁻ decay rates of both open-chain carotenoids and analogues of β-carotene. For example, for the N = 11 polyene, lycopene (N = 11) and β-carotene (N = 11), the 2¹Ag⁻ lifetimes are 6.1, 4.0, and 8.1 ps, respectively.^98,99

6. The excited state dynamics for the N = 7–19 polyenes also have allowed us to revisit previous ultrafast experiments on the “infinite polyene,” the related DEDPM polymer.⁹⁷ Extrapolation of the 2¹Ag⁻ lifetimes for the polyene series suggests a 30–40 fs lifetime in the infinite polyene limit. However, our analysis of the DEDPM kinetic data⁹⁷ points to a 175 fs 2¹Ag⁻ lifetime and a 1200 fs component that we assign to the decay of the S* state.

7. Transient signals assigned to S* states in previous studies of long carotenoids are observed for the N = 13, 15, and 19 polyenes. Similar signals in the long carotenoids have been ascribed to conformational twisting within 2¹Ag^−.45,57,67 However, the restricted range of torsional motions available to these highly-constrained polyenes on their 2¹Ag⁻ potential surfaces significantly limits the rearrangements required to account for the prominent S* signals in both sets of molecules. For the N = 19 polyene, the rise of S* parallels the decay of the 2¹Ag⁻ state, suggesting that these S* signals may be due to 1¹Ag⁻ → 1¹B_u⁺ absorption from excited vibrational levels of the ground state (1¹Ag⁻), as originally proposed by Gillbro et al.²⁵ However, this model cannot explain the dynamics of the N = 13 and 15 polyenes or the S* signals in spirilloxanthin (N=13) or rhodoxanthin (N=14).^76–78 For all of these molecules, the S* signals appear well in advance of the > 1 ps decay times of the 2¹Ag⁻ states. Understanding which of the two models for the S* signals is appropriate under what conditions will require more extensive experimental and theoretical efforts on this polyene series. Further studies should result in the development of a more comprehensive kinetic model for the excited state decays of both synthetic and naturally-occurring polyenes as a function of their conjugation lengths, structural features, and solvent environments.