Controlled reflectance surfaces with film-coupled colloidal nanoantennas

Abstract

Efficient and tunable absorption is essential for a variety of applications, such as the design of controlled emissivity surfaces for thermophotovoltaic devices¹; tailoring of the infrared spectrum for controlled thermal dissipation²; and detector elements for imaging³. Metamaterials based on metallic elements are particularly efficient as absorbing media, because both the electrical and the magnetic properties of a metamaterial can be tuned by structured design⁴. To date, metamaterial absorbers in the infrared or visible range have been fabricated using lithographically patterned metallic structures^2,5–9, making them inherently difficult to produce over large areas and hence reducing their applicability. We demonstrate here an extraordinarily simple method to create a metamaterial absorber by randomly adsorbing chemically synthesized silver nanocubes onto a nanoscale thick polymer spacer layer on a gold film –making no effort to control the spatial arrangement of the cubes on the film– and show that the film-coupled nanocubes provide a reflectance spectrum that can be tailored by varying the geometry. Each nanocube is the optical analog of the well-known grounded patch antenna, with a nearly identical local field structure that is modified by the plasmonic response of the metal dielectric function, and with an anomalously large absorption efficiency that can be partly attributed to an interferometric effect¹⁰. The absorptivity of large surface areas can be controlled using this method, at scales out of reach of lithographic approaches like e-beam lithography otherwise required to manipulate matter at the nanometer scale.

To enhance the light absorbed within a medium, both the reflectance as well as the transmittance of the medium must be minimized. While any opaque material, such as a metal, can essentially eliminate transmittance, eliminating the reflectance is more difficult. For a material defined by its electric permittivity ε and magnetic permeability μ, the Fresnel reflection coefficient for the s polarization has the form

$$r_s=\frac{z_{2}cos{\theta }_i-z_{1}cos{\theta }_t}{z_{2}cos{\theta }_i+z_{1}cos{\theta }_t}$$ (1)

where $z_j=\sqrt{\frac{{\mu }_j}{{\epsilon }_j}}$ is the wave impedance for medium j, and θ_i and θ_t are the incident and transmitted angle of the wave with respect to the surface normal. For normal incidence, for which θ_i = θ_t = 0, Eq. (1) shows that if z₁ = z₂, reflection is eliminated. Since the impedance of vacuum has the value $z_0=\sqrt{{\mu }_0/{\epsilon }_0}$, Eq. (1) suggests that any medium whose wave impedance has the value z₀ will be reflectionless. An opaque, impedance matched structure can be considered an ideal absorber, since all incident light (at least normally) must be absorbed.

Because magnetic response is far more limited in naturally occurring materials, especially beyond frequencies of a few terahertz, impedance-matching a medium by introducing higher permeability materials is not generally feasible. In contrast, artificially structured metamaterials can have controlled magnetic as well as electric properties at nearly any wavelength in the electromagnetic spectrum (including the visible)¹¹; metamaterials have thus been suggested as a venue for ideal absorbers⁴. It has been shown that a metamaterial composite comprising lithographically patterned resonant conducting elements on top of a conducting back plane can be made reflectionless for light incident over a broad range of incident angles^2,12. To achieve the requisite magnetic response at infrared and visible wavelengths, a variety of metallic metamaterial structures have been used, such as cut-wire pairs^13,14. By combining different types of metamaterial elements together into a single composite, more complicated reflectance spectra can be engineered, achieving the level of control needed in certain spectroscopy and energy harvesting applications^7,12.

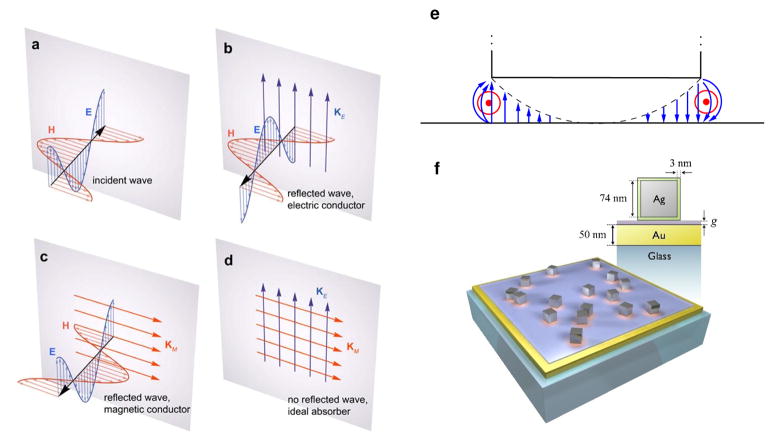
Because an absorbing structure does not require any significant volume, the appropriateness of defining bulk constitutive parameters such as ε and μ that are rigorously defined over a volume only can be called into question; thus, alternative descriptions have been proposed⁸. Here, we similarly find it instructive to adopt a related model of reflection, as illustrated in Fig. 1. We view the metamaterial surface, or metasurface^15–17, as supporting both electric as well as fictitious magnetic surface current densities that are excited by the incident wave. Because both currents produce reflected waves that are exactly out-of-phase with each other, their sum can cancel out entirely if the total induced effective magnetic current exactly balances the total induced electric current¹⁷.

FIG 1.

Forming an ideal absorber. (a) Light incident on a conductor reflects due to either b, the excitation of electric surface current densities K_E or c, fictious magnetic surface current densities K_M. If both are excited, the back reflected wave represents the sum of the waves in b and c, for which the electric and magnetic fields can exactly cancel, leaving the current to be absorbed as in d. f An ideal absorber can be formed by adding resonant nanoantennas atop a conducting film for which e the enhanced electric field (blue) is equivalent to effective magnetic currents (red).

Although magnetic conductors do not physically exist, many devices are commonly described as scattering waves via the excitation of effective magnetic currents. One example is that of the grounded patch antenna, which consists of a conducting metallic patch positioned above a conducting (ground) plane, as illustrated in Fig. 1e. The patch antenna supports a series of cavity-like resonances in which the electromagnetic field is localized within the gap between ground plane and patch element. For modes in which the electric field is maximum at the patch edges, the patch can be equivalently described as having a magnetic surface current density K_M that flows along the periphery of the patch, with magnitude given by 2 E × n, where the field is determined at the patch edge and n is a unitary vector normal to the surface. Thus, adding a population of patch antennas at some critical density to an otherwise conducting sheet can generate enough fictitious magnetic surface current density that will offset the electric surface current density of an incident wave.

The underlying mode description of the patch is extensible to any wavelength as long as the patch and surface behave as conductors. While metals are often described as lossy dielectric materials at optical wavelengths, they nevertheless support currents and can be used to form the optical equivalent of patch antennas¹⁸. Note that the particular arrangement of antennas on the surface should not matter for an isotropic absorber, since it is only necessary to introduce enough magnetic current to offset the electric current. Thus, an artificially structured ideal absorber should not be reliant on any sort of patterning methods, and we can make use of colloidal self-assembly processes to very simply produce a randomized patch antenna geometry.

In plasmonic systems, field localization is generally correlated with local field enhancement $f=\frac{E_l}{E_0}$, where f is the ratio between the local electric field and the electric field of the incident wave. In the present context, the enhancement serves to increase the effective magnetic surface current that flows in response to the applied field. Equivalently, the resonance can be viewed as enhancing the coupling between the gap modes and the incident field, enabling the incident fields to penetrate into the gap region. In the latter interpretation, the enhanced absorption in the nanocube system can be considered closely related to the extraordinary enhanced transmission in very thin slit arrays¹⁹ and the large absorption that can be obtained with extremely shallow metallic gratings²⁰.

As a means of demonstrating the proposed colloidal approach to an ideal optical absorber, we consider nanocubes with edge length ℓ, separated by a nanometer-scale distance from a gold film by a dielectric spacer layer with a 1.54 optical index. To estimate the absorption efficiency of the nanoantennas, we perform numerical simulations over a domain containing a single absorber, and apply either periodic (Fourier Modal Method²¹) or absorbing (COMSOL) boundary conditions. As has been noted previously, square patches exhibit scattering behaviour very similar to strips⁸ because they share the same underlying mechanisms^7,18; we are thus able to run two-dimensional simulations in many cases to perform quick optimizations, followed by fewer confirming three-dimensional simulations.

A gap-plasmon guided mode, whose profile is shown Fig. 2, is supported under the cube. The constructive interferences of this mode, reflected back and forth at the edges of the cube, creates a cavity resonance as in a Fabry-Perot interferometer. This mechanism makes the resonance insensitive to the angle of incidence as well as to the polarization of the incident wave (see Supplementary Information for a detailed analysis).

FIG 2.

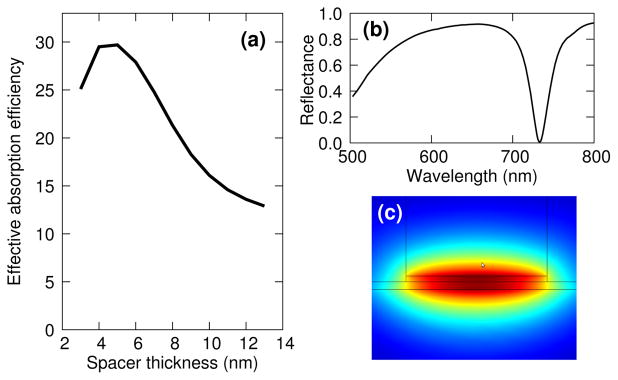
Theoretical absorption efficiency of the nanocubes. (a) Effective absorption efficiency as a function of the spacer thickness, defined as the ratio of the absorption cross-section for a single nanocube to its physical cross-section. The absorption cross-section is computed as the ratio of the energy absorbed over the illumination intensity. (b) Reflectance spectrum for cubes that are 70 nm large, periodically (350 nm) distributed, spaced from the metallic film by a 8 nm thick dielectric layer (c) Modulus of the magnetic field for the mode that is guided under the cube (out of plane wavevector).

When the thickness of the spacer layer is decreased, the effective index n_e of the mode increases, reaching arbitrarily large values. Since the relation between the resonance wavelength and the cavity size ℓ is roughly $\ell \simeq \frac{\lambda }{2n_e}$, resonances can thus be excited under cubes that are only a tenth of the wavelength, especially for very thin spacer layers. Fig. 2 shows that the effective absorption efficiency–defined as the power absorbed by the nanocube divided by the incident intensity and normalized to the actual surface occupied by a cube–is maximum for a spacer layer that is between 5 and 10 nm thick. For larger spacer thicknesses, the resonance is not as well formed, the reflection coefficient of the mode being relatively low. For extremely thin layers, the resonance is poorly excited by the incident field. The effective absorption efficiency can be as large as 30, meaning that around 3% of the surface needs theoretically to be covered with cubes to reach an almost complete absorption (see Fig. 2).

Since the cavity is excited uniformly on either side of the cube in normal incidence, it constitutes a perfect example of an interferometrically controlled absorption¹⁰: the field amplitude is twice as large as if the cavity was excited from one side only, and the absorption is thus four times larger (especially compared to a structure like the shallow grating described in²⁰ where the absorption mechanism is very similar). This phenomenon contributes to the very large absorption efficiency and explains why second-order resonances are not likely to be excited (see Supplementary Information).

Having evaluated the underlying mechanisms of the nanoparticle-based ideal absorber, we next seek to experimentally implement the concept using chemically synthesized metal nanocubes that are randomly adsorbed on an organic insulating spacer layer (of precisely controlled thickness) above a gold film. Because the synthetic chemistry for nanocubes favors silver rather than gold, silver nanocubes with an edge length of 74 nm were synthesized according to previously published protocols^22,23. Electron microscopy images of the cubes are shown in Fig. 3. It should be noted that a periodic arrangement of nanocubes would entirely suppress scattering, which is not the case for the random distributions considered here. Significant scattering can thus be expected to occur from the nanoantennas, as confirmed by the dark field optical images shown in Fig. 3c. The scattering places an upper limit on the reflectivity away from the absorption dip, as well as a lower limit on the reflectivity at the peak absorption.

FIG 3.

Silver nanocubes. Scanning electronic microscopy image of the silver nanocubes (a) as fabricated and (b) deposited on the gold film with a 17.1% surface coverage showing the remarkably uniform spacing; (c) dark-field images of the nanocubes adsorbed randomly adsorbed on a nanoscale polymer spacer –ranging in thickness from 3.6 nm to 17 nm–on a gold film showing the light scattered by the individual nanocubes for less than 1% surface coverage.

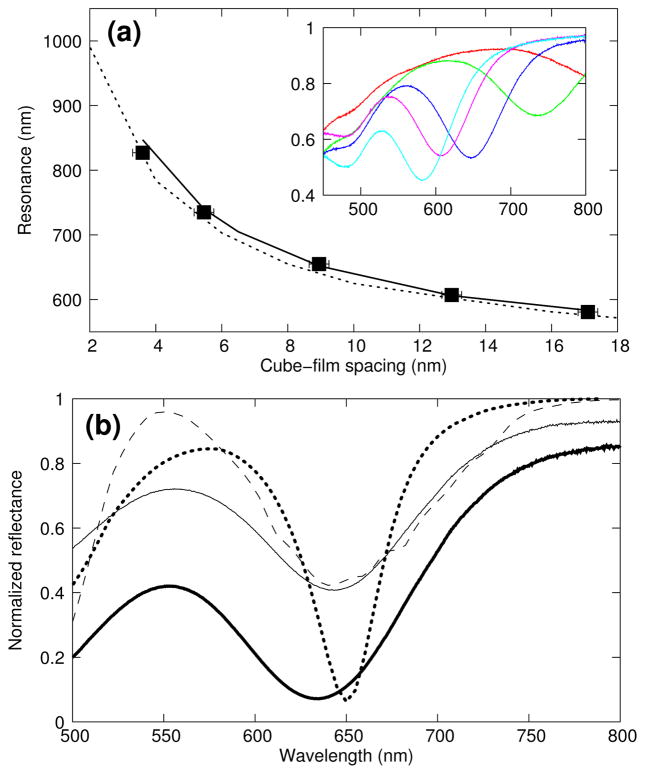
Reflectance spectra were obtained from samples where 4.2% of the gold film surface was occupied by nanocubes and the nanocube-film separation distance was modulated by polyelectrolyte (PE) molecular spacer layers of increasing thicknesses^24–28. Figure 4a shows the position of the measured resonance as a function of the overall thickness under the cubes –assuming the nanocube-film separation distance is the sum of the PE spacer layer thickness and a 3 nm thick stabilizer coating that surrounds the cubes. The position of the resonances can be accurately determined by 3D simulations²¹ if the coating and the rounded corners of the cubes are taken into account (by using a somewhat smaller cube dimension of 62 nm). Again, as is typical with nanoplasmonic systems, the resonance properties are crucially sensitive to the thickness and dielectric properties of the spacer layer, making the reflectance properties of the surface easily tunable by just changing slightly the gap dimension.

FIG 4.

Tunability of the reflectance. (a) Position of the resonance as a function of the spacer thickness. Measured positions (black squares) from 4.18% cube density surface agree with 3D simulations (solid line) and 2D simulations (dotted line) for 74 nm wide gold nanorods surrounded with air. The inset shows the corresponding experimental reflectances for a 25°angle of incidence. (b) Experimental reflectance in normal incidence, normalized to the gold film, for a 7.3% (thin curve) and 17.1% (thick curve) surface coverage, compared with simulations of uniform cubes (dotted line, 4.2% surface coverage) and a model including size dispersion (dashed line, See Supplementary Information).

Based on our 3D simulations, which utilized a perfectly uniform population of cubes, we would expect a small reflectance even for such a small surface coverage. However, the silver cubes as prepared varied in dimension. This size variation contributes to a broader and shallower absorption dip in the reflectance. In order to experimentally achieve very low reflectance, in the absence of preparing a more uniform population of silver nanocubes, the concentration of cubes on the surface had to be increased. Figure 4b shows the relative reflectance observed from nanocube-film samples with 7.3% and 17.1% surface coverage of these imperfect cubes spaced from the gold film by a 6 nm PE layer and also simulated reflectance for both perfectly uniform cubes and for cubes having a similar size distribution as seen experimentally. A reflectance smaller than 7% is observed in normal incidence at 637 nm from samples with 17.1% surface coverage, further demonstrating the ease and extent to which the reflectance can be controlled.

For many applications, a narrow absorption band may be desirable. Size dispersion appears to be the primary limitation on achieving much more narrow spectroscopic features. This limitation can likely be overcome either with more controlled fabrication processes or by nanoparticle separation techniques^29,30. The very small size and highly efficient optical response of the cubes suggests that mixed cube populations with controlled sized dispersion could be used to further tailor the absorption at will. While those structures can be designed to operate in the infrared, we envision introducing alternative materials which would have better thermal properties. It is however worth underscoring that the extreme sensitivity of the resonant modes supported by the nanocubes can be leveraged for immediate biosensor applications³⁰. The gap-dependent cavity resonances have a completely different character than the classical resonances of spherical nanoparticles coupled to a film²⁸, so that in addition to their higher sensitivity, they can be excited very conveniently with normal incidence.

The spectral control available from absorbing metasurfaces forms the basis for a growing number of promising applications, including thermal detectors, light sources, energy harvesting systems and even biosensors. To date, structured absorbers have been successfully demonstrated across the entire electromagnetic spectrum, relying on top-down lithographic pattering as the fabrication approach. While such patterning can produce highly uniform arrays of structures with tight tolerances, it does not scale well to large areas as would likely be needed in most applications of interest. By contrast, the bottom-up, colloidal approach described here is simple, rapid, inexpensive and easily scalable, potentially opening the door to the eventual cost-effective manufacture of large area metasurfaces with controlled reflectance.

Methods Summary

A 5nm Chromium adhesion layer and 50 nm thick gold film was deposited by electron beam evaporation onto a Nexterion Glass B slide. The surface of the gold film was then treated with a layer-by-layer (LBL) deposition²⁸ of poly (allylamine) hydrochloride (PAH) and polystyrene sulfonate (PSS) to create a controlled polyelectrolyte (PE) spacer layer thickness²⁴. The thickness of the PE layer was measured prior to deposition of the nanocubes using a J.A. Woolam Co., Inc., M-88 spectroscopic ellipsometer. The silver nanocubes were immobilized on the PE surface by a brief exposure to the colloidal solution followed by rinsing with water and drying under a stream of nitrogen. In an effort to limit the number of aggregates accumulating on the surface of the film, the exposure to the colloidal solution was carried out with the gold film facing down so that aggregates would theoretically sink away from the surface. The coverage density of nanocubes on the gold film was controlled by varying the concentration of colloids in solution and the time that the surface was exposed to the solution. Scanning electron microscope (SEM) images were used to determine both the surface density of the cubes and their size distribution; which were found to have a standard deviation of the order of 10 nm (see Supplementary Information). To measure the normal incidence reflectance properties of the samples, white light from a 75 W Xenon source was directed at the sample through a 0.13 numerical aperture 5x magnification microscope objective while the reflected signal was collected by the same objective and directed though a 50-50 beamsplitter to a spectrometer. For off-normal specular reflectance, 1mm diameter multimode fibers terminated with collimating lens adapters formed both the excitation (light source to sample) and collection (reflected signal from sample to spectrometer) paths.

Methods

A 50 nm thick gold film was deposited by electron beam evaporation (CHA Industries), at 2 Angstroms/sec onto a Nexterion Glass B slide (Schott North America, Inc.), including a 5 nm Chromium adhesion layer (deposited at 1 Angstrom/sec). The surface of the gold film was then treated with a layer-by-layer (LBL) deposition²⁸ of poly (allylamine) hydrochloride (PAH, kDa, Aldrich) and polystyrene sulfonate (PSS, kDa, Aldrich) to create a controlled polyelectrolyte (PE) spacer layer thickness²⁴. For each deposition step, the gold-coated glass slides were immersed in 0.003 moles-of-monomer/L (monomol/L) PE and 1 M NaCl for 30 min, rinsed thoroughly with a gentle stream of ultra-pure water (18 MΩ, used throughout), and immersed in fresh ultra-pure water for 1 min, after which the substrates were either immersed in 1 M NaCl for 30 s before repeating the same steps for deposition of the oppositely charged PE or dried with a stream of high-purity nitrogen for analysis. All LBL depositions were initiated and terminated with the cationic PAH layer to facilitate both the attachment of the first PE layer to the gold film through amine-gold interactions^25–27 and the electrostatic immobilization of the silver nanocubes. The silver nanocubes, which were made following a previously published protocol²², were immobilized on the PE surface by a brief exposure to the colloidal solution followed by rinsing with water and drying under a stream of nitrogen. In an effort to limit the number of aggregates accumulating on the surface of the film during this attachment process, the nanocube solution was sonicated briefly and the slide was lowered gold side down onto a coverslip containing a 30 μl droplet of the colloidal solution, whereupon the coverslip was picked up by the slide using the capillary force of the droplet spreading onto the film surface. Under these conditions, aggregates would theoretically sink away from the surface of the gold film during the incubation. The density of coverage of nanocubes on the surface of the gold film was controlled by varying the concentration of colloids in solution and the time that the surface was exposed to the colloidal solution. Scanning electronic microscope (SEM) images were used to determine both the surface density of the cubes after deposition on the LBL layers and the size distribution of the cubes; which were found to have a standard deviation of the order of 10 nm (see Supplementary Information). The thickness of the PE layer was measured prior to deposition of the nanocubes using a J.A. Woolam Co., Inc., M-88 spectroscopic ellipsometer. To measure the normal incidence specular reflectance properties of the samples, white light from a 75 W Xenon source (ORIEL) was directed at the sample through a 0.13 numerical aperture 5x magnification microscope objective (NIKON) while the reflected signal was collected by the same objective and directed though a 50-50 beamsplitter to a spectrometer (ACTON 2300i). For off-normal (25°) specular reflectance, 1 mm diameter multimode fibers terminated with collimating lens adapters formed both the excitation (light source to sample) and collection (reflected signal from sample to spectrometer) paths. With this technique, the beam diameter at the surface of the sample is approximately 3 mm. In all of the presented data, the cube covered film reflectivity is normalized by the reflectance spectrum of the bare gold film.