Recent Explosive Human Population Growth Has Resulted in an Excess of Rare Genetic Variants

Abstract

Human populations have experienced recent explosive growth, expanding by at least three orders of magnitude over the past 400 generations. This departure from equilibrium skews patterns of genetic variation and distorts basic principles of population genetics. We characterized the empirical signatures of explosive growth on the site frequency spectrum and found that the discrepancy in rare variant abundance across demographic modeling studies is mostly due to differences in sample size. Rapid recent growth increases the load of rare variants and is likely to play a role in the individual genetic burden of complex disease risk. Hence, the extreme recent human population growth needs to be taken into consideration in studying the genetics of complex diseases and traits.

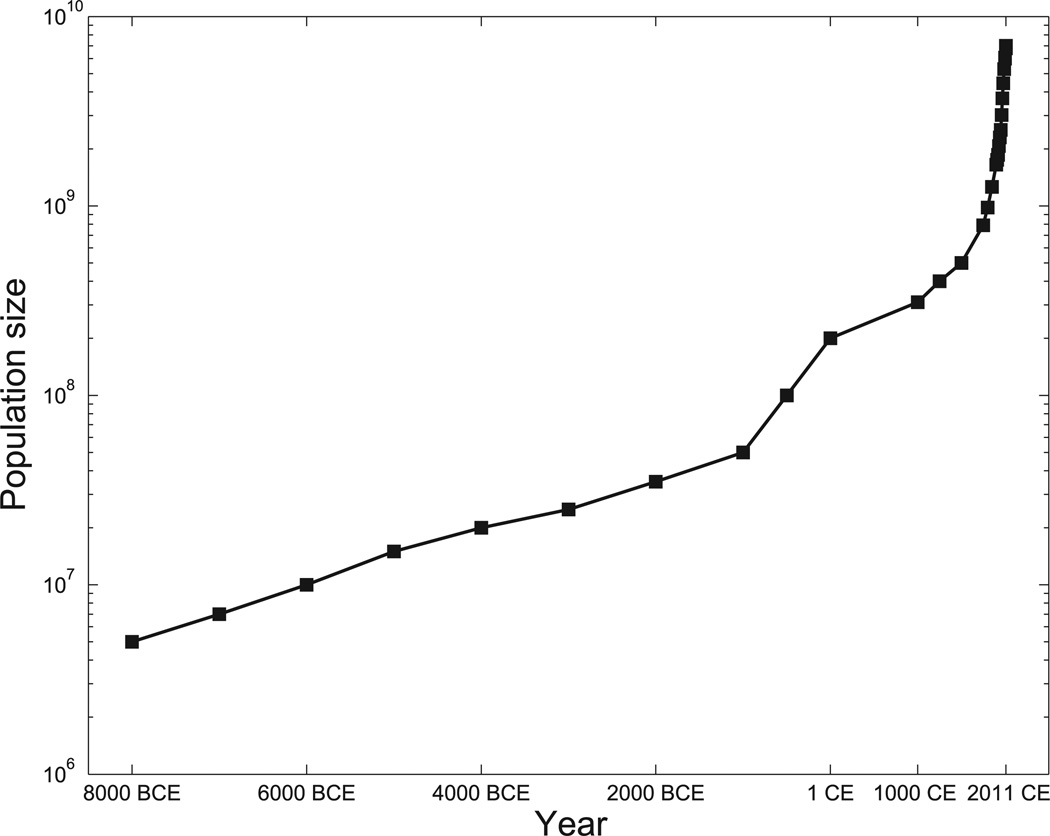
The human global population has recently grown (1) from a few million people roughly 10,000 years ago to an estimated 7 billion today (2, 3). The extent of this growth—more than three orders of magnitude within fewer than 400 generations—can be divided into one epoch of moderate exponential growth followed by accelerated explosive growth starting fewer than 100 generations ago (Fig. 1). This situation implies massive departures from population genetic equilibrium. In particular, rapid recent growth generates a load of rare variation, due to recent mutations, which may play a role in complex disease risk.

Fig. 1.

Census (rather than effective) population size is presented on a logarithm scale over the past 10,000 years, from about 5 million at 8000 BCE to about 7 billion today from data in (1, 3, 30, 31). The depicted linear increase (on the log scale) through most of the presented epoch denotes exponential growth of relatively constant percentage increase in population size per year. An acceleration of that increase starting in the Common Era is evident.

Studies modeling the demographic history of human populations from genetic data have considered a recent epoch of exponential growth of effective population size [effective population size, which is typically smaller than the real population size, determines the genetic properties of a population (4)]. Earlier studies used small amounts of data or had ascertainment biases toward an excess of common variants—which tend to be due to less recent mutations— and did not observe population growth. Recent studies (5, 6) observed an excess of rare variants in resequencing data and modeled past population growth by comparing the prediction of a model with the observed site frequency spectrum (SFS). For European history, these studies estimated as much as 0.5% growth in effective population size per generation since the split of the ancestors of Europeans and East Asians ~1000 generations ago, resulting in an effective population size of a few tens of thousands today (Table 1). However, these studies did not capture the full scope of human expansion, which may be due to the models not allowing for a recent acceleration in growth rate (5). We hypothesize, however, that the limited sample size of these studies (at most 60 individuals), which only allowed capturing variants of frequency as low as ~1% in the sample, has provided a limited view of rare variants in the population. Rare variation adds information on mutations that have occurred during recent epochs of accelerated explosive growth and that may be identified from sequencing larger sample sizes (7–10). Several ongoing projects are sequencing ever-larger numbers of individuals genome-wide (11, 12).

Table 1.

Genetic estimates of recent exponential growth in Europe.

Study	Sample size (n)*	Time growth started (years ago)†	Initial Ne‡	Growth per generation (%)
Gravel et al. (5)	60	23,000§ (21,000–27,000)	1032 (677–1290)	0.48 (0.30–0.75)
Gutenkunst et al. (6) (including New World modeling)	22	26,400§ (21,700–30,700)	1500 (900–2200)	0.23 (0.16–0.34)
Gutenkunst et al. (6) (excluding New World modeling)	22	21,200§ (17,600–23,900)	1000 (500–1500)	0.4 (0.26–0.57)
Schaffner et al. (29)	62	8750‖	7700	0.73‖
Coventry et al. (18)	10,422	1400 (900–2800)	7700#	9.4 (4.5–14.5)

^*Number of individuals of European ancestry used for inference.

^†Number of years ago, on the basis of 25 years per generation. All studies assumed growth to continue into the present.

^‡Effective population size (N_e) before the start of the exponential growth phase.

^§Time of growth was assumed in these studies to coincide with the split of the ancestors of Europeans and East Asians, hence the split and growth were estimated as a single parameter.

^‖Fixed parameters that were not estimated from the data, and which are hence not considered in the discussion in the main text. (Growth is instantaneous to a fixed value of N_e = 100,000, which is approximately equivalent to exponential growth of 0.73% per generation.)

^#A fixed parameter, following (29).

Learning from the frequencies of genetic variants about the demographic history during the past 10,000 years requires capturing variants that entered the population in that time span. Many such variants are likely to be rare in the population as a whole (i.e., frequency <0.1%; see below), requiring sequencing of a larger sample of individuals than previously considered in demographic studies. Although it is now economically feasible to sequence a sufficiently large number of individuals, such an effort introduces a new scale to the problem of false positives among newly identified variants such as single-nucleotide polymorphisms (SNPs). Specifically, the ability to easily distinguish SNPs present only once in the sample (singletons) from sequencing errors decreases as the sample size increases.

Despite an improvement in the accuracy of sequencing technologies, some errors remain unavoidable. For example, with a sequencing error rate of 1 in 10,000 bases, in a sample of 10,000 individuals, each base pair will exhibit two errors on average across the sample and the majority of monomorphic sites will appear polymorphic (most often as a singleton or a doubleton; i.e., with the rare allele present in one or two copies in the sample). On the other hand, strict filtering of the data will lead to missing many rare variants because they are not observed as reliably. Hence, any analysis of large sample sizes must account for the uncertainty inherent in sequencing by considering the variant calls probabilistically, and secondary validation of rare variants by an alternate sequencing procedure is essential.

For accurate analysis of human genetic data, it is also necessary to address how assumptions underlying most population genetic analysis tools are violated with samples of thousands or more individuals (13). This may require generalizations of population genetics theory to cases in which the sample size is not necessarily smaller than the historical effective population size (13–17).

A recent study (18) analyzed a large sample size through Sanger resequencing data for two genes (KCNJ11 and HHEX) in 10,422 European Americans from the Atherosclerosis Risk in Communities (ARIC) study (19). They estimated the fraction of variants that are validated by Roche/454 sequencing, which in turn recalibrated the probabilities of genotype calls and accuracy of calling rare variants. The entire SFS was considered probabilistically, with a total expected number of 262 and 317 SNPs in the two genes, respectively (18). Considering a sample of 10,000 individuals, the number of singletons estimated was at least 5 times that predicted by the standard Wright-Fisher model (18). Similarly, the expected number of doubletons was at least 3 times the prediction. Sub-samples of the data show that the number of singletons increases almost linearly with sample size. As a result, in the collection of all SNPs in this sample, more than 50% are singletons. Qualitatively similar results have been reported from sequencing of 202 genes in 15,000 individuals from different populations (20) and whole exomes of 2440 individuals of European and African ancestry (12).

By focusing on “neutral” sites—defined in (18) as synonymous SNPs and sites at least 30 base pairs from a coding region—the authors estimated a model of European demographic history from comparison of the model-predicted SFS with the probabilistically observed SFS (18) while allowing for the sample size to exceed the effective population size (13). The model estimates pointed to a recent extreme growth of 9.4% per generation [95% Bayesian credible interval (CI), 4.5 to 14.5%], starting 1400 years ago (95% CI, 900 to 2800 years ago) (Table 1). [The current global human population growth rate is estimated at 1.1% per year, equivalent to about 30% per generation (3).] The present effective population size of Europeans as estimated by the model is 1.1 million (95% CI, 0.3 to 1.9 million) (18), compared to the present effective population size of only a few tens of thousands estimated by previous models that incorporated recent exponential growth (5, 6) (Table 1).

There are several differences between the models of population history assumed by the different studies that considered recent population growth—as well as between the inference methods used—that can potentially explain the differences in results (Table 1). However, we hypothesize that the very different results are mostly due to differences in sample size. A larger sample size allows identification of rarer polymorphisms that are, on average, due to more recent mutations. Singletons in studies of 20 to 60 individuals have a frequency on the order of 1% and are due to much older mutations than the singletons of 0.005% frequency in a sample of 10,000. In the latter sample, 80% of the variants were observed in fewer than 10 copies (<0.05%), with the vast majority of these being due tomutations that arose in the past 2500 years, according to the estimated model (18). In contrast, the majority of common SNPs with frequency greater than 5% have been segregating for several tens of thousands of years. For neutral SNPs of 5% frequency, fewer than one is expected to have arisen across the entire genome during the past 2500 years, and only ~8% during the past 10,000 years (18). Thus, the larger the sample size, the more recent the epoch it probes.

The excess of rare variants found with a large sample size predicts a growth of 5 to 14% per generation over the past 900 to 2800 years, compared to models of smaller sample size that predicted growth of between 0.2 and 0.7% over a longer period of 20,000 to 30,000 years (5, 6). A demographic history consistent with the archaeological and historical records of Europe (Fig. 1) emerges by bringing together the different models: The human population has been expanding for at least hundreds of generations, and the excess of very rare variation indicates that the rate of expansion has accelerated substantially over at least the last several dozen generations (18) (Table 1). Additional data and future modeling with additional parameters are required to estimate more accurately these different phases of population growth.

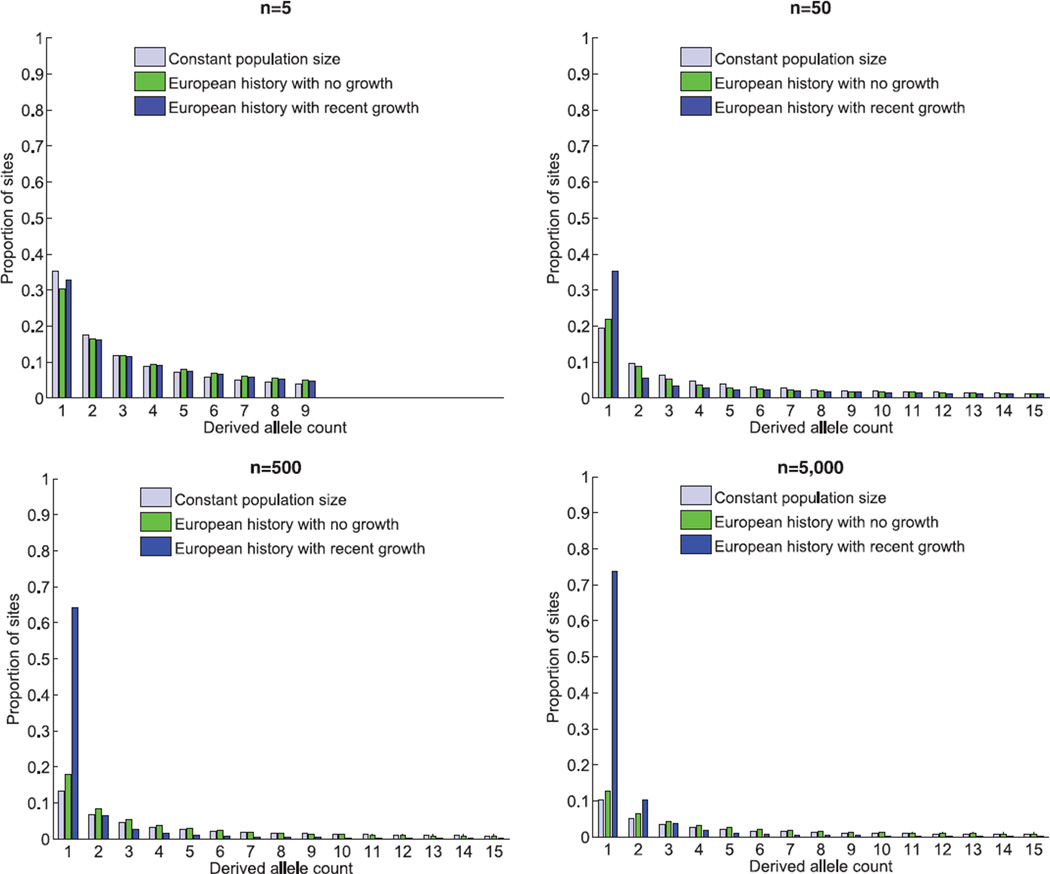
We contrasted three simplified models of population history to exemplify the general effects of recent explosive growth and sample size on the SFS: (i) a population of constant size throughout history, (ii) a model of European history with two population bottlenecks (21), and (iii) a variant of the second model that adds recent exponential growth, as supported by previously estimated parameters (Table 1) and the archaeological record (Fig. 1). The expected SFS under the three models (Fig. 2) points to considerable inflation in the fraction of variants that are singletons when recent growth is introduced in model 3: For a sample of 500 individuals, where a singleton corresponds to a frequency of 0.1%, model 1 predicts 13% of variants to be singletons, whereas the addition of the population bottlenecks in model 2 inflates this percentage to 18%. The addition of recent exponential growth in model 3 results in an increase to 64% (Fig. 2). The effect of recent explosive growth, as captured in model 3, seems restricted to an inflation of singletons (Fig. 2). However, the observed deflation of other rare frequency categories is due to the inflation in the proportion of singletons and the SFS capturing relative proportions from all variants. Indeed, after removal of singletons and renormalization of other frequency categories (accounting for the possibility of filtering singletons from data because of rare variants having not been validated), the SFS exhibits inflation in doubletons and other rare variants (fig. S1).

Fig. 2.

The expected site frequency spectrum (SFS) of the derived allele (the new mutation arisen in the population) for three different demographic models: (i) a population that has been of constant size throughout history; (ii) a model previously fit to the derived allele frequency spectrum of Europeans, which includes an out-of-Africa population bottleneck and a second, more recent, population bottleneck (21); and (iii) the same two-bottleneck model of European history with the addition of recent exponential growth from a population size of 10,000 at the advent of agriculture to an extant effective population size of 10,000,000, which amounts to 1.7% growth per generation during the last 400 generations. The results presented are based on sequences of 5, 50, 500, and 5000 diploid individuals. Figures are from 10 million coalescent simulations (32); the expectation of models 1 and 2 were also validated analytically (21). In all panels, the proportions of all possible derived allele counts, ranging from 1 to 2n − 1, sum up to 1, although only those for 1 through 15 are presented. See fig. S1 for a version of this figure in which singletons are excluded and the SFS renormalized.

The simulated SFS supports the conclusion that differences between previously estimated models of population expansion (Table 1) can be explained by differences in sample size. The inflation in singletons in model 3 relative to model 2 ranges from only 8% (which can easily be missed in model fitting) for a very small sample size to almost 500% for a large sample (Fig. 2). This relative increase is compounded by the fact that the proportion of singletons decreases as sample size increases (in the absence of explosive growth) and that the proportion of singletons for model 3 is actually increasing as a function of sample size, from 33% to 74%, because in a larger sample singletons represent rarer variants due to more recent mutations (Fig. 2). As a result, a standard sample size of 50 to 100 only provides a glimpse into the inflation in singletons. In our models, a sample size of 50 individuals identifies a quarter of the inflation relative to a sample size two orders of magnitude larger (Fig. 2). This effect of sample size is even more pronounced for rare variants that are not singletons (fig. S1).

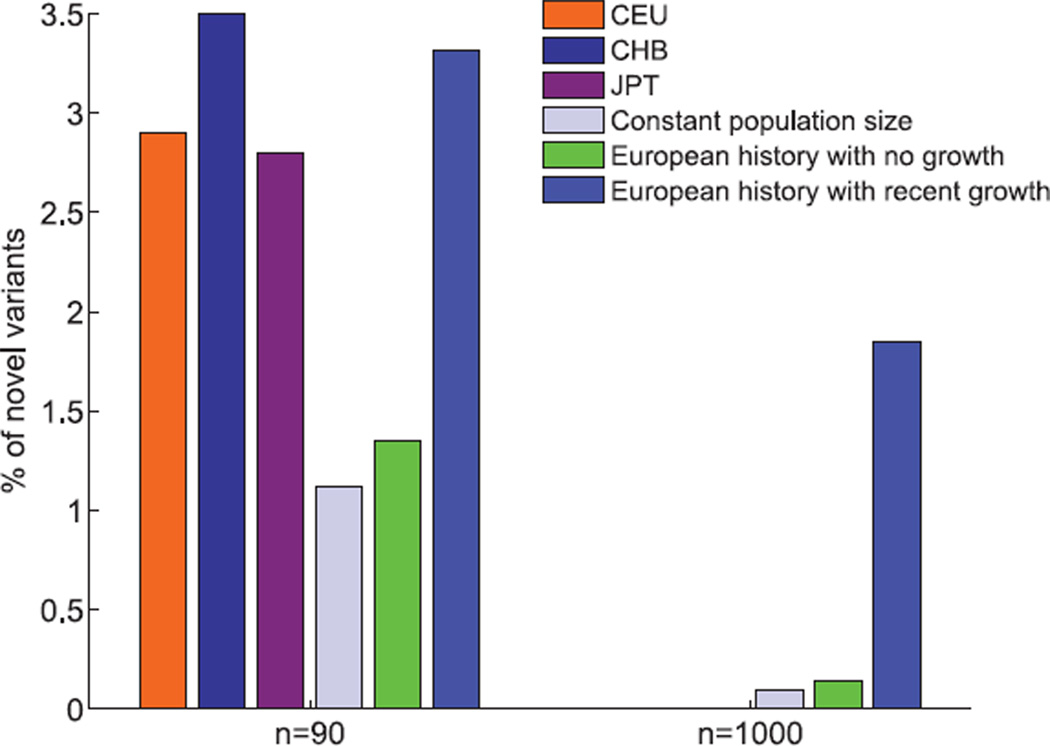
The inflation in the number of rare variants due to explosive growth implies that, even in large samples, many variants will be restricted to a single individual. We thus examined the individual burden of mutations, defined here as the proportion of heterozygote variants in each newly sequenced individual that are novel (i.e., completely absent from a previously sequenced large sample from the same population).We estimated the expectation of this quantity in the three idealized demographic models described above and measured this quantity in populations of European and East Asian ancestry on the basis of ENCODE regions from HapMap 3 (22). Model 2 predicts that 1.3% of heterozygous positions in a new individual are otherwise completely monomorphic in a population sample of 90 individuals (Fig. 3). This percentage underpredicts the empirically observed 2.9% in a sample of European ancestry (Fig. 3), and its prediction is almost as poor as that of a model of constant population size (1.1%). Adding recent explosive growth changes the prediction to 3.3% of heterozygous positions and provides a much better fit to the observed data in European and East Asian populations (Fig. 3).

Fig. 3.

Percentage of novel variants in a sequenced individual. Bars denote the fraction, out of all sites for which a given individual is heterozygous, that are also monomorphic in a separate sample of 90 (left) or 1000 (right) individuals from the same population. Expected fraction is presented for the same three demographic models as in Fig. 2. For n = 90—a value chosen on the basis of availability of empirical data—the observed fraction for three populations of European (CEU), Chinese (CHB), and Japanese (JPT) ancestry is also provided, from resequencing data of ENCODE regions from the HapMap 3 Project (22). We averaged over all possible choices of an individual out of each sample in these data. The empirical results are inconsistent with the two models excluding growth, and they match a simplistic model that includes recent exponential expansion. We note that the empirical estimates are likely slight underestimates due to stringent quality control filters (22). No empirical data are available for a sample of size 1000.

The fraction of novel variants discovered in each sequenced genome decreases in all models as more individuals are sequenced (Fig. 3), because increasing sample size results in a greater likelihood that a variant has already been ascertained. Interestingly, though, the discrepancy between the prediction of models with and without population growth increases as more individuals are sequenced: Whereas explosive growth predicts a 150% increase in the proportion of unique mutations for 90 previously sequenced genomes (3.3% versus 1.3%), in the case of 1000 previously sequenced genomes it predicts a 1200% increase (Fig. 3). The model predicts that even in the 1001st genome sequenced, about 1.9% of the variants (which number about 57,000) would be novel. These models are limited to neutral mutations, and deleterious mutations would likely exhibit an even larger percentage of novel rare variants (23).

With disease-gene association studies moving in the direction of exome and whole-genome sequencing, models of the genetics of complex traits need to accommodate recent, rapid human population growth. The medical implications of an excess of rare genetic variation and increased individual mutational load are of particular interest in light of the limited success of genome-wide association studies at explaining the genetic basis of complex human diseases (24–27). Some degree of genetic risk for complex disease may be due to this recent rapid expansion of rare variants in the human population. A better understanding of the population genetic consequences of such recent, explosive growth for how genetic variation will be structured in populations is needed for optimal sampling designs that most efficiently identify disease risk variants. The extraordinary growth implies a massive departure from equilibrium, such that populations will continue to accumulate genetic variability until a new equilibrium is reached. Our models showed a skewed SFS, with nearly normal counts of SNPs in all frequency classes other than the very rarest classes, which are highly inflated. These rare variants are so recent that they appear as novel mutations, with relatively little time for natural selection to operate.

Explosive growth also results in a haplotype structure that deviates from the prediction of standard population genetics because recombination will not have broken down linkage disequilibrium between rare mutations and neighboring common variants. This results in a deviation in the distribution of haplotypes that contain both common variants with deep evolutionary history and recent mutations. However, it presents an opportunity for mapping methods that are based on the structure of haplotypes or that aggregate signals from multiple variants according to their inferred biological impact (so-called burden tests). Furthermore, the skewed genealogical structure when the sample size exceeds the historical effective population size can result in excess sharing of identical-by-descent blocks among affected individuals, which can be used for associating rare variants (13). Optimization of association-testing methods will clearly benefit from expanding our understanding of the population genomic variation in rapidly expanding populations.

To shed further light on recent epochs in the history of modern humans, large-scale sequencing of many thousands of individuals is needed (28), together with more elaborate demographic modeling. The sequenced population should exhibit as little substructure as possible because sequencing several closely related populations—while optimizing other criteria of variant discovery (11)—does not accurately capture the frequency of rare variants due to mutations that postdate population split. It is also imperative to understand the impact of natural selection during the phase of explosive growth, an aspect that our models did not attempt to capture.