Effects of mutation, truncation and temperature on the folding kinetics of a WW domain

Abstract

The purpose of this work is to show how mutation, truncation and change of temperature can influence the folding kinetics of a protein. This is accomplished by principal component analysis (PCA) of molecular dynamics (MD)-generated folding trajectories of the triple β-strand WW domain from the Formin binding protein 28 (FBP) [PDB: 1E0L] and its full-size, and singly- and doubly-truncated mutants at temperatures below and very close to the melting point. The reasons for biphasic folding kinetics [i.e., coexistence of slow (three-state) and fast (two-state) phases], including the involvement of a solvent-exposed hydrophobic cluster and another delocalized hydrophobic core in the folding kinetics, are discussed. New folding pathways are identified in free-energy landscapes determined in terms of principal components for full-size mutants. Three-state folding is found to be a main mechanism for folding FBP28 WW domain and most of the full-size and truncated mutants. The results from the theoretical analysis are compared to those from experiment. Agreements and discrepancies between the theoretical and experimental results are discussed. Because of its importance in understanding protein kinetics and function, the diffusive mechanism by which FBP28 WW domain and its full-size and truncated mutants explore their conformational space is examined in terms of the mean-square displacement, (MSD), and PCA eigenvalue spectrum analyses. Subdiffusive behavior is observed for all studied systems.

Introduction

In order to perform their vital functions in every cell, proteins must fold into their biologically-active three-dimensional structure. Starting from the famous experiments¹ of Anfinsen and colleagues in 1961, an active question still remains as to how proteins attain their biologically active conformations. Protein folding is a rapid and complex process that is difficult to characterize because folding does not refer to the progressive pathway of a single conformation. Instead, it pertains to interconversions among ensembles of conformations in a back-and-forth progression from the non-native to the native state. In addition, the non-native and native states themselves may consist of a large ensemble of conformations, interconverting at a rapid rate, and characterized by basins with many minima in each state.

The two-state model of protein folding kinetics,^2,3 consisting of the denatured and the native state separated by the energetically unfavorable transition state, successfully used for description of the folding dynamics of many proteins, is not the only possible model. Proteins can also fold through intermediate states^4,5 or undergo one-state downhill folding.^4,6 Each protein folds by one of these mechanisms. Hence, it is still an important and challenging problem^7-14 to select a correct model for protein folding kinetics and the coordinates of the free-energy landscape (FEL),^15-17 in order to identify intrinsic pathways along which proteins fold. Recent experimental studies^5,18-22 show that protein folding kinetics can be altered by selected point mutation, by truncation or by changing the temperature/solvent conditions.

In this work, we examine how mutation, truncation, and change of temperature may alter the folding kinetics of the 37-residue triple-β-stranded WW domain from the Formin binding protein 28 (FBP) (PDB: 1E0L).²³ Because of the small size, fast-folding kinetics and biological importance, the formation of intermolecular β-sheets is thought to be a crucial event in the initiation and propagation of amyloid diseases such as Alzheimer's disease²⁴ and spongiform encephalopathy,²⁵ FBP28 WW domain and other WW domain proteins (e.g., CA150, Pin1, FiP35) have been the subjects of extensive theoretical^10,26-32 and experimental^{5,18-22,33,34} studies. By using tryptophan-fluorescence-decay measurements, Gruebele and coworkers^5,18 concluded that the folding of wild-type FBP28 WW domain and of most of its mutants involves intermediates (three-state folding), while other mutants fold according to a two-state mechanism. The conclusion regarding three-state folding was later challenged by Fersht and coworkers²⁰ who found that FBP28 WW domain and its mutants studied, in ref. 5, undergo ultrafast aggregation and, consequently, the deviation from non-single-exponential kinetics reported by Gruebele and coworkers⁵ could be attributed to early oligomerization stages. By using fluorescence measurements, Fersht and coworkers²⁰ found single-exponential kinetics in clear contradiction of the work of the other group.⁵

It should be noted, though, that different measurements (fluorescence decay⁵ and fluorescence intensity,²⁰ respectively, at various folding times) were used in the two studies. Because fluorescence decay times are more sensitive to the local environment, it is possible that both intermediates and the native state are seen as two distinct species in fluorescence-decay measurements but as a single species in fluorescence measurements. On the other hand, the sensitivity to local environment can also result in the detection of low-degree oligomers by the fluorescence-decay technique. In their study,⁵ Gruebele and coworkers did not, however, observe a concentration dependence of the folding rates which is an argument against oligomerization. Moreover, the fluorescence decay experiments performed by Gruebele and coworkers to determine the kinetics of FBP28 WW domain folding were carried out at protein concentrations ranging from 10 to 100 μM,⁵ and the upper boundary of the time interval of data acquisition was 500 μs.⁵ Thus, while the aggregation of FBP28 WW domain is an ultra-fast process, as demonstrated in ref. 20, it seems that, only for the highest protein concentration, could the measurements performed in ref. 5 be influenced by aggregation at the very end of the data-collection time window. This observation does not, however, exclude the possibility of formation of oligomers with size too small to be detectable by light-scattering measurements. It should also be noted that, for the related protein, Pin1 WW domain and its mutants, Gruebele and coworkers³⁵ observed a two-state folding mechanism. For the Pin1 WW domain and its mutants, they also observed residual non-single-exponential kinetics. However, the kinetics tended toward single exponential as the protein concentration decreased; consequently, as opposed to the FBP 28 WW domain and its mutants,⁵ deviation from non-single-exponential kinetics could be attributed to aggregation.

In this work, we studied three full-size mutants of FBP28 WW domain (Y11R, Y19L, W30F), and three shortened mutants: an N-terminal truncated one (ΔN Y11R) and two N- and C-terminal truncated ones (ΔNΔC Y11R, and ΔNΔC Y11R/L26A). For each mutant and for the wild-type (WT) protein, we ran multiplexed replica exchange molecular dynamics (MREMD) simulations to determine their folding-transition temperatures and, finally, production simulations consisting of 32 canonical molecular dynamics (MD) trajectories for each protein at temperatures close to the folding-transition temperatures. All simulations were carried out with the coarse-grained united-residue (UNRES) force field.^{13, 36-44} The mutation sites (red color) and ΔN/ΔC truncations (green color) are illustrated in Figure 1. They were chosen as in the experimental work of Nguyen et al.⁵

Figure 1.

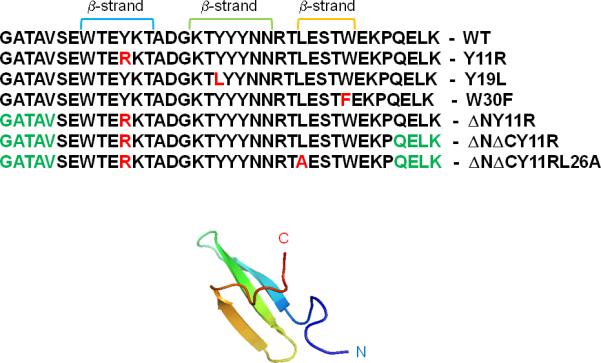
Experimental NMR structure of triple β-strand WW domain from the Formin binding protein 28 (FBP) [PDB: 1E0L]. The sequences of the WT, all full-size and truncated mutants of FBP28 WW domain with mutated residues (in red color) and ΔN/ΔC truncations (in green color), are shown.

The folding dynamics of FBP28 WW domain and its mutants are studied here by constructing FELs along the principal components (PCs) obtained from a covariance-matrix-based mathematical technique, called principal component analysis (PCA),⁴⁵ which typically captures most of the total displacement from the average protein structure with the first few PCs during a simulation. We also investigate the diffusive behavior along the first five lower-indexed PCs for all systems by using the mean-square displacement (MSD) and PCA eigenvalue spectrum.⁴⁶

The purpose of this work is to determine how mutation, truncation and change of temperature affect the folding mechanism of FBP28 WW domain. Therefore, we considered four selected trajectories (in total about 2 μs formal time and effectively 2 ms), exhibiting folding/unfolding events, for each system, at each temperature, and performed PCA.

Results and Discussion

In order to determine the melting temperature of each system and the temperatures at which to carry out canonical MD runs, we first performed a multiplexed replica exchange (MREMD) simulation⁴⁷ of WT FBP28 WW domain and its mutants. The folding-transition temperatures are collected and compared with the experimental values of ref. 5 in Table 1.

Table 1.

Calculated and experimental melting temperatures of wild type FBP28 WW domain and its mutants.

Name	TM, K (Calculated)	TM, K (Experiment)5
WT	339	337
Y11R	343	339
Y19L	319	328
W30F	335	339
ΔN Y11R	334	339
ΔNΔC Y11R	331	328
ΔNΔC Y11R/L26A	327	329

Earlier theoretical studies^27,28 have shown that, below the melting temperature, WT FBP28 WW domain folds with biphasic kinetics, the origin of which was found to be the independence of the formation of loop 2 contacts with respect to the remainder of the protein. Therefore, the complexity of the folding kinetics, caused by coexistence of three- and two-state folding pathways, makes FBP28 WW domain a very interesting system to study.

In order to make a comparison with some experimental results, the mutations and truncations in the present work were selected as in the experiments of ref. 5.

Wild type FBP28 WW domain

We recently showed^10,12 that the folding dynamics of WT FBP28 WW domain at temperatures below the melting point demonstrated a three-state folding mechanism, which is in agreement with the experimental results of ref. 5. Therefore, in the present work, we investigated the folding dynamics for WT FBP28 WW domain only at 340K, very close to the melting point, to determine whether WT FBP28 WW domain still follows a three-state folding mechanism with unfolded, intermediate, and folded states, or is a collection of partially unfolded (“residually folded”) structures at the melting point, as was observed for protein A.¹⁴

Figure 2 illustrates the one-dimensional FELs [also called free energy profiles, FEPs, μ_i(q_i) = –RT ln P_i(q_i), where P_i(q_i), T and R are the probability density function (pdf), the absolute temperature, and the universal gas constant, respectively] of the first five PCs (panel a) of the MD trajectories for WT FBP28 WW domain at 340K (1° above the melting temperature). In order to avoid overlapping, the FEPs are shifted upward by 2×(i – 1) units (i is the index of the PC) along the ordinate. Panel b of Figure 2 illustrates the two-dimensional FEL along the first two PCs (q₁, q₂), μ(q₁,q₂ ) –RT ln P(q₁,q₂), at the temperature 340K. Panel c shows the percentages of the fluctuations captured by the first 30 PCs.

Figure 2.

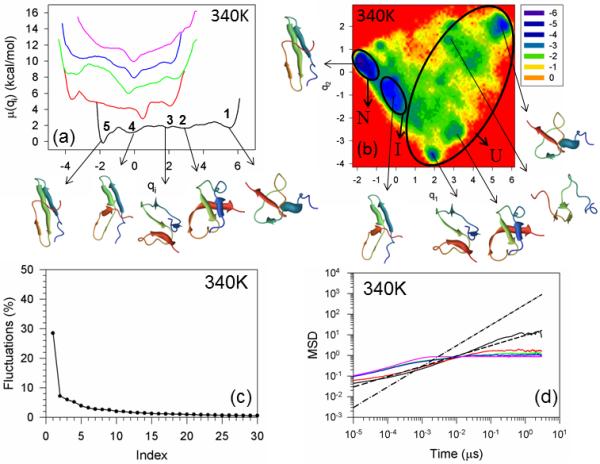
Free energy profiles of the first five principal components for folding MD trajectories for FBP28 WW domain at 340K (panel a). The black, red, green, blue and pink solid lines in panel (a) correspond to FEPs along the first (with representative structures at the minima), second, third, fourth, and fifth PCs, respectively. The free-energy landscape (in kcal/mol) along the first two PCs with representative structures at the minima for folding MD trajectories at 340K for FBP28 WW domain is shown in panel b. The letters “U”, “I”, and “N” correspond to unfolded, intermediate (with 4.0Å < RMSD < 6.0Å of representative structures), and native states, respectively. The percentages of the total fluctuations captured by the first 30 PCs for FBP28 WW domain is shown in panel (c). The mean square displacement (MSD) as a function of time of the first five PCs for FBP28 WW domain at 340K is shown in panel (d). The black, red, green, blue and pink solid lines in panel d correspond to MSDs along the first, second, third, fourth, and fifth PCs, respectively. The black dashed and dash-dot lines correspond to t^0.5 and t¹, respectively.

Both the FEPs and FELs of WT FBP28 WW domain and its mutants (see below) are highly rugged having many local minima located in broad basins. In order to define the unfolded, intermediate and native states, we, first, examined the root-mean-square deviation (RMSD) from the native structure for all structures found in each minimum, and then selected one or several representative structures for each minimum; after that we used the following criterion: (i) if the RMSD of a representative structure of a minimum is less than 4.0 Å, then the minimum corresponds to the native state; (ii) If the RMSD is 4.0Å < RMSD < 6.0Å, then the minimum corresponds to the intermediate state; (iii) if the RMSD is greater than 6.0Å, then the minimum corresponds to the unfolded state.

As in our previous studies,^10,12 the free energy profiles of WT FBP28 WW domain along only the first PC (black solid line in panel a of Figure 2) can be characterized as multiply-hierarchical (i.e., they contain more than one major basin of minima).⁴⁸ Three states (unfolded, intermediate and native) can be identified at 340K; however, the intermediate state is not as prominent (deep) as at lower temperature (330K).^10,12 The unfolded state contains three shallow local minima (1, 2, 3 in panel a). Although some representative structures in the minima of the unfolded state exhibit partially or fully formed strands or loops, none of them has a formed hairpin. The representative structure of the intermediate state (minimum 4) has a formed hairpin 1 composed of strands 1 and 2; however, strand 3 does not have a complete β-structure and hairpin 2 is not formed. For an alternative demonstration of the differences between representative structures of the native, intermediate and unfolded states, (ϕ, ψ) scatter plots [and also the (θ, γ) scatter plots, because UNRES employs these coarse-grained angle] have been constructed [Figure S1 (Supplementary Materials)], in which we can clearly see how the local conformations in the plots for the representative structure of the unfolded state are spread over almost the entire plane, whereas the conformations in the plots for representative structures of the intermediate and native states are more concentrated in the regions of β-sheets. It should be noted that these (ϕ,ψ) scatter plots may not be as accurate as those for all-atom MD simulations, which is not surprising because the ψ and ϕ angles are subject here to errors inherent in the conversion from the coarse-grained (UNRES) to the all-atom representation.

With the increase of temperature, the barriers between the unfolded (1, 2, 3), intermediate (4), and native states (5) are lowered by ~ 40% compare to those at lower temperatures^10,12 and, consequently, the interconversion rate between these states is increased. Also, the local minima of the unfolded (1, 2, 3) and intermediate (4) states are more shallow than those at lower temperatures,^10,12 which indicates that the protein spends less time in unfolded and intermediate states with increasing temperature. The rest of the FEPs, along the second, third, fourth, and fifth PCs, belong to either singly-hierarchical (characterized by a number of local minima arranged within a single coarse-grained minimum) or harmonic categories;⁴⁸ however, it should be noted that some tendency toward multiply-hierarchy can be observed for the FEP of the second PC, and the fluctuations captured by the first PC lowered to ~ 30% of the total fluctuations at the temperature very close to the melting point (see panel c) [the first PC usually captured more than 40% of the total fluctuations at lower temperatures^10,12]; hence, the two-dimensional FEL along the first two PCs is necessary for a correct description of the protein folding dynamics. The FELs illustrate that WT FBP28 WW domain folds with three-state kinetics. All states (unfolded, intermediate and native) along with a few new minima in the unfolded basin can be identified on the FEL (panel b). These findings are not in agreement with the experimental results of ref. 5, in which WT FBP28 WW domain becomes a two-state folder at the melting temperature. One of the reasons for this discrepancy may be the fact that the intermediate state is not as prominent at 340K as at lower temperatures, and the experiment was not able to detect it. On the other hand, the reason for the discrepancy can be an inaccuracy of the UNRES force field. Moreover, in spite of the fact that there are no other literature reports, to the best of our knowledge, in which WT FBP28 WW domain was folded by canonical MD simulations, with which to compare our results (it is still difficult to fold proteins with ~ 30μs folding time with the all-atom force fields, excluding some exceptions³¹), all theoretical investigations that studied folding of WT FBP28 WW domain by replica exchange MD simulations,^27-29 reported three-state folding. Besides, the theoretical studies^30-32 of other WW domain proteins (Pin1, FiP35) illustrate quite rugged free-energy landscapes leading to multi-state dynamics.

Apart from the folding kinetics, it is also interesting to explore how mutation, truncation and change of temperature influence the diffusive behavior of the system. Therefore, we have studied the diffusive behavior of WT FBP28 WW domain, and its mutants by using two different methods: MSD analysis and PCA eigenvalue spectrum. Panel d of Figure 2 illustrates the MSDs of the first five PCs at 340K. Since the global motions along the first PC contain a major part of the total fluctuation in FBP28 WW domain, our interest was focused on the diffusive behavior of the system along this PC (black solid line). For easy visualization of the kind of diffusive behavior along the first five PCs, the black dashed and dash-dot lines corresponding to t^0.5 and t¹, respectively, are drawn. It is clear from the results illustrated in panels a and b that WT FBP28 WW domain at 340K behaves subdiffusively [see the Hölder exponent (defined in the Materials and Methods section) H_D < ½] because the barrier heights on the folding pathway are low, and the system does not need to make long jumps to overcome the barriers. These findings are consistent with earlier results obtained by Yang et al. from single-molecule experiments.⁴⁹ It should be noted, that WT FBP28 WW domain at lower temperatures showed normal and even superdiffusive behavior in certain regions of time,¹⁰ which was caused by high barrier heights on the folding pathways. Another method, which can determine the diffusive behavior of a protein, the PCA eigenvalue spectrum, also revealed subdiffusion for WT FBP28 WW domain at 340K [with a Hurst parameter (defined in the Materials and Methods section) H = 0.379] (not shown).

The full-size mutants of FBP28 WW domain: Y11R, Y19L, and W30F

In this work, certain residues, whose side chains are part of a solvent-exposed hydrophobic cluster, were mutated to determine whether the Tyr-11/Tyr-19/Trp-30 hydrophobic cluster is associated with biphasic kinetics.

The FEPs of the first five PCs, and the FELs along the first two PCs of MD trajectories for the Y11R full-size mutant at temperatures below and close to the melting point are shown in panels a and b of Figure S2 (Supplementary Materials) and Figure 3, respectively. Panel c of Figure S2 (Supplementary Materials) illustrates the percentages of the total fluctuations captured by the first 30 PCs at 335K and 345K. The substitution of the nonpolar amino acid (Tyr) by the polar amino acid (Arg), in general, does not change the folding mechanism (three-state folding) at both temperatures; however, the mutation results in an additional folding pathway [U → I(2) → N] at 345K along which Y11R folds differently, as shown below.

Figure 3.

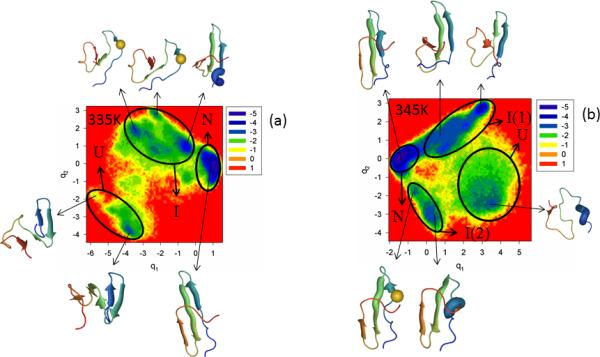
The free-energy landscape (in kcal/mol) along the first two PCs with representative structures at the minima for folding MD trajectories for the Y11R full-size mutant at 335K is shown in panel (a) and for 345K in panel (b). The letters “U”, “I”, and “N” correspond to unfolded, intermediate and native states, respectively. The mutated residue is shown in spherical representation in some representative structures (panels a and b).

Both FEPs along the first PC [panel a of Figure S2 (Supplementary Materials)] and the FEL along the first two PCs (panel a of Figure 3) at 335K, below the melting point, illustrate only one folding pathway with three states: unfolded (minimum 1 in FEP and “U” in FEL), intermediate (minima 2, 3, 4 in FEP and “I” in FEL), and native (minimum 5 in FEP and “N” in FEL); however, it should be noted that hairpin 1 in representative structures of minima 2 and 3 in FEP [panel a of Figure S2 (Supplementary Materials)] and in corresponding minima of the intermediate state in FEL (panel a of Figure 3) at 335K is distorted, and strands 1 and 2 do not have β-structure. This deformation of the hairpin is caused by the mutation (see the spherical representation of a residue in the representative structures), although the most shifted residue is a neighboring residue (GLU-10). It should be noted that the second WW domain, the CA150 protein, which is identical in sequence with FBP28 WW domain, forms amyloid fibrils in vitro,³³ and the conformers causing the aggregation are very similar to those found in minima 2 and 3 of the FEP [panel a of Figure S2 (Supplementary Materials)].

With increase of temperature (to 345K), the influence of the mutation increases and makes the system fold along two different pathways (panel b of Figure 3). The mutant Y11R folds along the first folding pathway [U → I(1) → N], which is the most probable folding pathway (according to the color shades), similarly to WT FBP28 WW domain, i.e., hairpin 1 forms first in the intermediate state and then the protein jumps to the native state. The second folding pathway [U → I(2) → N] indicates a different order of formation of hairpins (different structural pattern), i.e., hairpin 2 forms first in the intermediate state before the protein reaches the native state. Panel b of Figure 3 clearly illustrates the distortion of hairpin 1 by the mutation [see the spherical representation of a residue in the representative structures of the intermediate state I(2)], which is the reason for inducement of the second folding pathway. The second folding pathway was not identified by the FEP along the first PC at 345K [panel b of Figure S2 (Supplementary Materials)], which is not surprising because the percentage of the total fluctuations captured by the first PC [panel c of Figure S2 (Supplementary Materials)] is even lower (~ 24%) than it was for WT FBP28 WW domain at 340K and, for a correct description of the folding dynamics, a multiply-hierarchical shape of a PC is not always enough,¹² i.e., the percentage of captured fluctuations should be ~ 40%.¹² The mutation loosened the protein structure, which caused the decrease of the percentage of the captured fluctuations.¹² This effect of mutation can be observed even in representative structures of the native state at both temperatures, which still have a low RMSD (~ 3.5 Å) but not all strands have a fully formed β-structure, and consequently, the turns become larger.

As in WT FBP28 WW domain, the mutant Y11R exhibits subdiffusive behavior [H_D < ½ (at both temperatures), and the Hurst parameters at 335K and 345K are 0.132 and 0.086, respectively]. Such behavior, which is a consequence of distributions of waiting times on a random walk leading to a significant number of steps with long trapping times, implies that the diffusive motion of the protein covers less volume in configurational space than if the motion were Brownian.⁵⁰

Our results showed that the mutation (Tyr11Arg) does not change the three-state folding mechanism. However, the mutation influences the formation of hairpin 1, which, consequently, induces an extra folding pathway at 345K.

The next mutant investigated is Y19L. The results shown in Figure S3 (Supplementary Materials) and Figure 4 indicate that the replacement of an aromatic amino acid (Tyr) by a very nonpolar branched aliphatic amino acid (Leu) destabilizes the folding pathway more than that in the Tyr-11 → Arg mutation. In particular, the Tyr → Leu mutation results in the appearance of an additional folding pathway, even at T = 315 K, which is below the melting point (panel a of Figure 4). Also, most of the representative structures of the intermediate state, illustrating the first formation of hairpin 1, are partially deformed [minima 1, 3 in the FEP [panel a of Figure S3 (Supplementary Materials)], and minima in I(1) in the FEL (panel a of Figure 4)]. All of them lack the fully-formed strands and are distorted because of the mutation (see the spherical representation of a residue in the representative structures). Almost all strands (i.e., strands 2 and 3) forming hairpin 2 of representative structures in the second intermediate state I(2) at 315K have the β-structure, and hairpin 1 in these representative structures is completely deformed (panel a of Figure 4). The probability of folding through the first formation of a hairpin 1, [U → I(1) → N], is still higher than that [U → I(2) → N] at 315K. It should be noted that both FEPs and FELs at the temperature (315K) below the melting point (319K) [panel a of Figure S3 (Supplementary Materials) and panel a of Figure 4] are more rugged than those for WT FBP28 WW domain and the Y11R mutant. The FEP along the second PC clearly exhibits the multiply-hierarchical shape [red solid line in panel a of Figure S3 (Supplementary Materials)]; hence, a two-dimensional FEL along the first two PCs is necessary for correct description of the folding dynamics. Moreover, some minima (3, 4, 5) of the FEP along the first PC at 315K have two different representative structures (panel a of Figure S3 (Supplementary Materials)], which is another indication of the need for two-dimensional (sometimes even higher^11-13) FELs.

Figure 4.

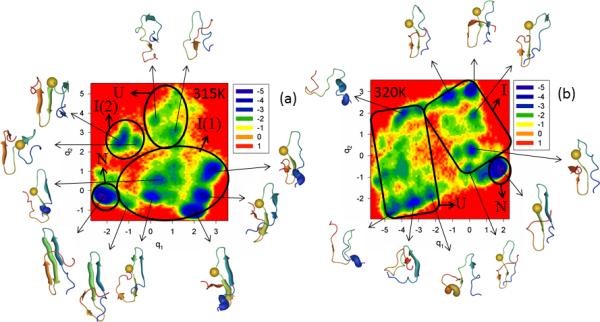
Same as in Figure 3 but for the Y19L full-size mutant at 315K and 320K.

The influence of mutation is increased with increasing temperature. Panel b of Figure S3 (Supplementary Materials) and panel b of Figure 4 show FEPs and FEL of Y19L, respectively, at 320K very close to the melting point, 319K. None of the representative structures of the intermediate state exhibits a formed hairpin 1; this structural element is present as an irregular chain reversal. Even a representative structure of the native state, the RMSD of which slightly exceeds the threshold (4.0Å) determined above for being in the native state, displays partially-deformed hairpins [see representative structures of minimum 6 in FEP [panel b of Figure S3 (Supplementary Materials)], and native state “N” (panel b of Figure 4)]. The folding mechanism of mutant Y19L is still quantitatively the same (three-state folding); however, from a structural point of view, the system folds completely differently, i.e., hairpin 2 (which is less stable than hairpin 1 for the WT FBP28 WW domain) starts forming first in the intermediate state and then the protein jumps to the native state. This suggests that the stability of hairpin 1 is strongly decreased, which is confirmed by the fact that the melting temperature of the Y19L mutant (328 K and 319 K from experiment and our simulations, respectively) is remarkably lower than that of the wild-type protein (337 K and 339 K from experiment and simulations, respectively). A possible reason for the decrease of the stability of the N-terminal hairpin and the change of folding order is the fact that leucine is a branched residue, as opposed to tyrosine and, consequently, cannot approach the aromatic nonpolar residues across the N-terminal β-sheet sufficiently closely for the β-hairpin hydrogen bonds to form. Both FEP and FEL at 320K are quite rugged, as are those at 315K. The percentage of fluctuations captured by the first PCs is ~ 30%. Based on the MSD and PCA eigenvalue spectrum analyses, the system behaves subdiffusively at both temperatures (Hölder exponent H_D < ½, and Hurst parameters at 315K and 320K are 0.021 and 0.066, respectively).

Our results indicate that the (Tyr19Leu) mutation has a stronger influence on the folding pathways than the Y11R mutation, although the folding mechanism remains the same, i.e., three-state folding.

The last full-size mutant of FBP28 WW domain investigated in this work is W30F. Trp-30, which is located close to the C-terminus, was replaced by Phe; in other words, one aromatic nonpolar amino acid was replaced by another aromatic nonpolar amino acid. The FEPs of the first five PCs, and the FELs along the first two PCs of the MD trajectories for the W30F mutant are illustrated in Figure S4 (Supplementary Materials) and Figure 5, respectively, at temperatures below (panels a – c of both Figures) and at the melting point (335K) for this mutant (panel d of both Figures). Panel e of Figure S4 (Supplementary Materials) shows the percentages of the total fluctuations captured by the first 30 PCs at 320K, 325K, 330K and 335K. Based on the results shown on these panels, the W30F mutant is a three-state folder at all temperatures. Both FEPs and FELs show only one folding pathway at all temperatures, in which hairpin 1 forms first in the intermediate state before jumping to the native state. Strands 1 and 2 of most of the representative structures in the intermediate states and all the strands of the representative structures in the native states are either fully or partially formed. The percentage of the total fluctuations captured by the first PC increases with decreasing temperature, which is in agreement with our previous studies of FBP28 WW domain.^10,12 Thus, we can say that, among all full-size mutants studied in this work, the Trp-30 → Phe mutation has the least influence on the folding mechanism and structural pattern. These results are not surprising, because of the following: (i) both tryptophan and phenylalanine are very nonpolar, aromatic amino acids, and (ii) in the folding pathway of FBP28 WW domain, hairpin 1 always forms first and strand 3 forms last; hence, the substitution made in strand 3 with the same type of amino acid should not be expected to influence the structural pattern or folding mechanism. In order to influence the structural pattern, Trp probably should be replaced by other types of amino acids (e.g. polar, nonpolar aliphatic, etc).

Figure 5.

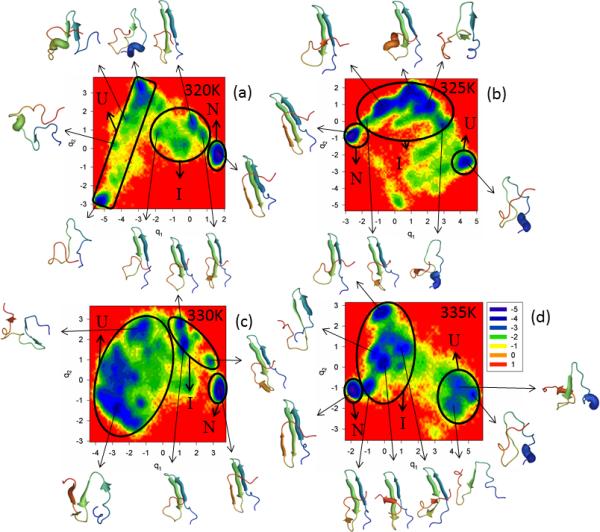
Same as in Figure 3 but for the W30F full-size mutant at 320K, 325K, 330K and 335K.

Although our findings regarding the folding model differ from the experimental results (two-state folding),^5,19,20 there is a consistency with experiments^19,20 regarding the folding rate enhancement. In other words, the W30F mutant folds faster than WT FBP28 WW domain (not shown here), which is in agreement with earlier experimental^19,20 and theoretical²⁶ studies, caused by mutation which may perturb the non-native (unfavorable) interactions, formed by the residues of the third β-strand involving W30.

Based on the MSD and PCA eigenvalue spectrum, W30F exhibits subdiffusive behavior at all temperatures. However, it should be noted that the Hölder exponent (< ½) and Hurst parameter (~ 0.45) are higher at low temperatures (320K and 325K) than those at higher temperatures. The increase of H_D and H at low temperatures might be due to the fact that, with the decrease of temperature, the system explores less conformational space, and spends a longer time in the minima before escaping from the minima and overcoming the barrier over which the protein makes longer jumps. The results are in agreement with an earlier study of coordinate-, time- and temperature-dependent diffusion dynamics in protein folding,⁵¹ which illustrates how the kinetic traps become more prominent and the kinetics slow down with the decrease of temperature.

Thus, we can conclude that the full-size hydrophobic core mutants (Y11R, Y19L and W30F) retain a three-state folding mechanism at temperatures below and very close to the melting point, and are not associated with biphasic kinetics. These findings are partially in agreement with experiment.⁵ The point is that a three-state folding mechanism in experiments⁵ was observed only for the Y11R and Y19L mutants at temperatures below their melting points. Both Y11R and Y19L became two-state folders at their melting temperatures, and the third mutant, W30F, exhibited single-exponential kinetics (two-state folding) at all temperatures (below and at its melting point).⁵ Moreover, we found that the Y11R and Y19L mutations influence the structural pattern along the folding pathways and at, certain temperatures, induce extra folding pathways, while the W30F mutation has the least influence on the folding pathway.

Truncated mutants of FBP28 WW domain: ΔNY11R, ΔNΔCY11R, and ΔNΔCY11R/L26A

Since no evidence for involvement of the solvent-exposed hydrophobic cluster (involving residues 11, 19, and 30) in a three-state folding mechanism was found, the next step to explain the reason for biphasic kinetics is to consider mutations combined with truncations.

The FEPs of the first five PCs, and the FELs along the first two PCs of the MD trajectories for the N-terminal truncated mutant ΔNY11R are illustrated in Figure S5 (Supplementary Materials) and Figure 6, respectively, at the temperatures below (panel a of both Figures) and very close to the 334K melting point (panel b of both Figures). Panel c of Figure S5 (Supplementary Materials) shows the percentages of the total fluctuations captured by the first 30 PCs at 330K and 335K. Both the FEP and FEL at these two temperatures indicate that ΔNY11R is a three-state folder; in other words, ΔN truncation has almost no effect on the biphasic kinetics. This finding can be explained by inspection of 10 NMR structures,²³ which illustrates that the truncated N-terminal sequence does not interact with the rest of the protein in WT FBP28 WW domain.

Figure 6.

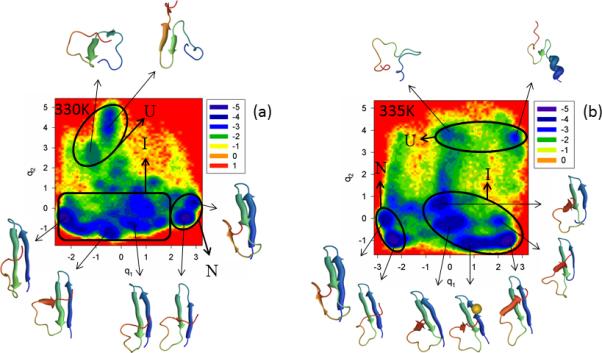
Same as in Figure 3 but for the ΔNY11R truncated mutant at 330K and 335K.

It should be noted from Figure 6 that, at both temperatures, ΔNY11R folds along the same pathway, i.e., the representative structures of the unfolded state do not contain any fully-formed strands or loops, the representative structures of the intermediate state have a formed hairpin 1, strand 3 does not have a β-structure and hairpin 2 is not formed. Even after jumping into the native state, hairpin 2 does not become fully formed (strand 3 never forms a β-structure completely); consequently, the RMSD of folded ΔNY11R slightly exceeds the threshold (4.0Å) determined above for the native state. Neither the FEP nor the FEL at both temperatures illustrates the extra folding pathway observed in the Y11R mutant (panel b of Figure 3), which indicate that N-terminal truncation may have no effect on the folding mechanism, but it certainly influences the folding pathways. In other words, with truncation of the N-terminal sequence, the influence induced by substitution of the nonpolar amino acid (Tyr) by the polar amino acid (Arg) on formation of hairpin 1 has disappeared. We do not explore the reasons for this effect, which are beyond the scope of this paper.

Not only do the FEPs along the first PC exhibit the multiply-hierarchical shape at both temperatures, but the FEPs along the second PC also belong to the multiply-hierarchical category. In addition, the percentages of the total fluctuations captured by the first PC lower to ~ 23% and 19% at 330K and 335K, respectively [panel c of Figure S5 (Supplementary Materials)]. All these results indicate that (i) at least a two-dimensional FEL is necessary for a correct description of the folding dynamics, and (ii) truncation of the N-terminal sequence loosened (slightly) the protein structure.

Slow diffusion (subdiffusion) is revealed at both temperatures, in particular, the Hurst parameter H is 0.064 (330K) and 0.018 (335K), and the Hölder exponent H_D is < ½ (330K, 335K).

Since N-terminal truncation did not simplify the folding mechanism, the Y11R mutant was truncated at both termini. The point is that one of the C-terminal residues, Leu-36, is part of a delocalized hydrophobic core (Trp-8/Tyr-20/Pro-33/Leu-36) conserved among WW domain sequences.²³

Figure S6 (Supplementary Materials) and Figure 7 show the FEPs of the first five PCs and FELs along the first two PCs, respectively, of the MD trajectories for the N and C-termini truncated mutant ΔNΔCY11R at temperatures below (panel a of both Figures) and very close to the 331K melting point (panel b of both Figures). Panel c of Figure S6 (Supplementary Materials) shows the percentages of the total fluctuations captured by the first 30 PCs at 325K and 330K. The FEP along the first PC at 325K is very rugged; however, based on the representative structures of each minimum, three states (unfolded, intermediate, and native) can be identified. It should be noted that the FEPs along the first two PCs exhibit a multiply-hierarchical shape, and the FEP along the third PC has some features of the multiply-hierarchical category [panel a of Figure S6 (Supplementary Materials)], which indicate the necessity of at least a two-dimensional FEL for a correct description of the folding kinetics. The FEL along the first two PCs (panel a of Figure 7) illustrates a three-state folding mechanism. The folding pathway is very similar to that in ΔNY11R. Thus, double truncation eliminates the effect of mutation on hairpin formation observed in the full-size mutant Y11R. It should be noted that hairpin 2 of ΔNΔCY11R is more formed in the native state than in ΔNY11R, and strand 3 has the β-structure.

Figure 7.

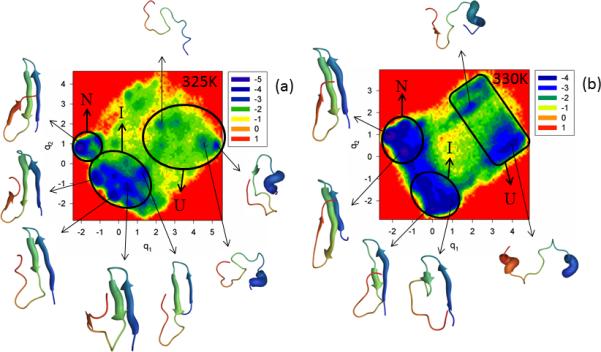
Same as in Figure 3 but for the ΔNΔCY11R truncated mutant at 325K and 330K.

The increase of temperature very close to the melting point lowered the barriers in the FEP along the first PC, and the states cannot be identified clearly [panel b of Figure S6 (Supplementary Materials)]. However, based on the representative structures at the minima, three-state folding is identified. Also, the FEPs along the first three PCs exhibit a multiply-hierarchical shape, which indicates the need for a three-dimensional FEL. A two-dimensional FEL is shown in panel b of Figure 7 [a three-dimensional FEL (not shown) did not reveal any important changes in the folding pathway]; in the two-dimensional FEL, one large-size basin and two medium-size sub-basins can be identified. The large basin contains two sub-basins (states). Based on the representative structures at the minima found in these sub-basins, they correspond to intermediate and native states. The other two medium-size sub-basins are parts of another large basin corresponding to the unfolded state. As at 325K, ΔNΔCY11R at the temperature very close to the melting point folds along the pathway in which hairpin 1 forms first in the intermediate state; however, β-structures of strands 1 and 2 are not as formed, as at 325K. Only after jumping into the native state do all strands become fully-formed, but hairpin 2 appears to be a bit deformed. It should be noted that, because of the unavailability of the experimental native structure of ΔNΔCY11R, we are unable to discuss how much hairpin 2 is deformed in the native state (perhaps it is not deformed at all). The results illustrated in panel c of Figure S6 (Supplementary Materials) are similar to those for ΔNY11R, which indicates that C-terminal truncation has no effect on the concerted motions in this mutant. As for most of the other mutants, ΔNΔCY11R also behaves subdiffusively.

Our finding of three-state folding for ΔNΔCY11R is not in agreement with the experimental results ref. 5, in which C-terminal truncation restored a two-state folding mechanism over the entire temperature range. However, it should be noted that the experimental folding mechanism of ref. 5 was determined by an exponential-function fitting of the observed relaxation kinetics, which is very different from our approach. Therefore, it is hard to say how much the exponential fit⁵ reflects all the minima, observed in the FEPs and FELs. If the exponential fitting of the relaxation kinetics corresponds to the coarse-grained picture of the FEL, then the free-energy landscape plotted in panel b of Figure 7 corresponds to two-state folding, because of two major basins.

The last doubly truncated and doubly mutated mini-protein studied in this work is ΔNΔCY11R/L26A. The main reason for this extra mutation⁵ is that loop 2 (Arg-24, Thr-25) might be involved in stabilization of nonnative states, and, indeed, previous experimental studies¹⁸ indicated a contribution of loop 2 in the protein-folding mechanism. Figure S7 (Supplementary Materials) and Figure 8 illustrate the FEPs of the first five PCs and FELs along the first two PCs, respectively, of the MD trajectories for the N- and C-terminally-truncated mutant ΔNΔCY11R/L26A at the temperatures below (panel a of both Figures) and above the melting point of 327K for this mutant (panel b of both Figures). The replacement of the very nonpolar amino acid (Leu) by the smaller nonpolar amino acid (Ala) [both being aliphatic amino acids] slightly influenced the folding scenario at 325K. It is still three-state folding, but both the FEP and FEL of ΔNΔCY11R/L26A illustrate a much more convincing picture of three-state folding [with three states (unfolded, intermediate and native) and a high barrier between the unfolded and intermediate states] than was obtained for ΔNΔCY11R (Figure 7). This finding is in harmony with the experimental results of ref. 5, in which the Leu26Ala mutation partially restored biexponential kinetics (three-state folding) in the two-state folder mini-protein ΔNΔCY11R at a temperature below the melting point. Moreover, unlike ΔNY11R and ΔNΔCY11R, hairpin 2 of a representative structure for ΔNΔCY11R/L26A in the native state is fully formed. As in ΔNΔCY11R, only one folding pathway can be identified here. The results of the FEPs (exhibiting a multiply-hierarchical shape along the 1^st, 2^nd and 4^th PCs) [panel a of Figure S7 (Supplementary Materials)] and the percentages of the total fluctuations captured by the PCs [panel c of Figure S7 (Supplementary Materials)], indicate that the Leu26Ala mutation makes the concerted motions in the protein less prominent, and slightly loosens the structure of the mini-protein.

Figure 8.

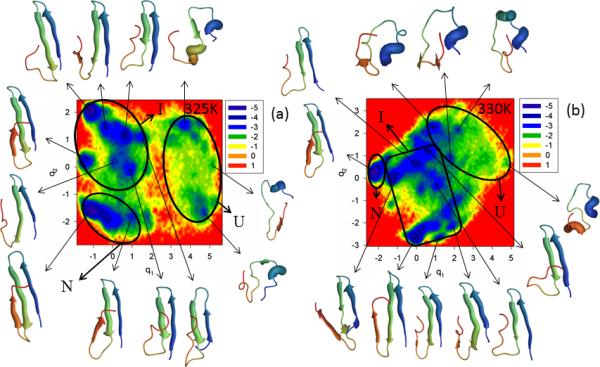
Same as in Figure 3 but for the ΔNΔCY11R/L26A truncated mutant at 325K and 330K.

Increasing temperature from 325K to 330K decreases the barrier between the unfolded and intermediate basins [panel b of Figure S7 (Supplementary Materials)]. Based on representative structures at the minima of the FEP along the first PC [panel b of Figure S7 (Supplementary Materials)] and the FEL along the first two PCs (panel b of Figure 8), ΔNΔCY11R/L26A is still a three-state folder at 330K; however, only two basins with many minima can be clearly identified. Some minima of the unfolded state merged with the intermediate state, and the native state is part of a large basin separated by a low barrier. If we consider the coarse-grained picture of the FEL, as was discussed above, then we have two-state folding at 330K, which coincides with the experimental results of ref. 5. Subdiffusive behavior was revealed at both temperatures for the ΔNΔCY11R/L26A mini-protein [H_D < ½ (at both temperatures), H = 0.017 (325K), H = 0.007 (330K)].

Conclusions

Protein folding trajectories were generated with the coarse-grained UNRES force field for the triple β-strand WW domain from the Formin binding protein 28 (FBP28 WW domain) and its full-size, singly- and doubly-truncated mutants at temperatures below and very close to the melting point. The molecular dynamics of these trajectories was analyzed by application of PCA, MSD and PCA eigenvalue spectrum to determine how mutation, truncation and change of temperature can influence the folding kinetics and diffusive behavior of a protein. The mutations and truncations were the same as those implemented by the experimental results of ref. 5. These experimental findings provided an impetus to investigate folding mechanisms by molecular dynamics simulations, an already proven method for elucidating the microscopic aspects of folding, and then to compare them to the experimental results. In this respect, it should be noted that the methods for determining folding mechanisms are different in the experimental and in the present theoretical work, and direct comparison of the results is impossible. Therefore, based on our observations on all full-size and truncated mutants, we assumed that the exponential fitting of relaxation kinetics used in the experiment of ref. 5 corresponds to the coarse-grained picture of the FEL. In other words, if the state is not sufficiently prominent on the FEL it cannot be detected by the experimental approach.

The main findings of this work are as follows:

1. Unlike protein A,¹⁴ according to computations, WT FBP28 WW domain adopts a three-state folding mechanism at the melting temperature, although the intermediate state is not as prominent as it was at a lower temperature (330K).^10,12,13 This might be one of the reasons for the discrepancy with experiment,⁵ in which single exponential (two-state) folding was observed for WT FBP28 WW domain at the melting temperature.

2. By mutating the residues of the solvent-exposed hydrophobic cluster and analyzing the MD trajectories of each mutant at temperatures below and very close to the melting point, it was found that the strand-crossing (11, 19, 30) hydrophobic cluster does not lead to three-state folding kinetics, i.e., it is not associated with biphasic kinetics.^27,28 In other words, replacement of residues in the hydrophobic cluster by other residues does not change the folding mechanism, except for W30F, which surprisingly exhibits single exponential kinetics over the entire temperature range,⁵ and contradicts our findings (three-state folding). In other words, the substitution of one amino acid with the same type of amino acid probably should not have a crucial influence on the structural pattern or folding mechanism.

3. Tyr11Arg and Tyr19Leu mutations (two members of the hydrophobic cluster ensemble) clearly influence the formation of hairpin 1, and induce an extra folding pathway, which exhibits a different order of formation of the hairpins.

4. The representative structures of the intermediate state of the Y11R mutant with deformed hairpin 1 are very similar to conformers causing the aggregation in the folding experiment³³ of the second WW domain of CA150 which is identical in sequence to FBP28 WW domain.

5. N-terminal truncation had no effect on the folding mechanism of the Y11R mutant, but it certainly influenced the folding pathways by suppressing the extra folding pathway induced by the Tyr11Arg mutation. The reasons of this effect have yet to be elucidated.

6. Additional C-terminal truncation had no effect on either the folding mechanism or the structural pattern along the folding pathway, which eliminated the involvement of the delocalized hydrophobic core (Trp-8/Tyr-20/Pro-33/Leu-36) in the folding kinetics. However, the Leu26Ala mutation slightly influenced the folding mechanism at 325K by providing a clearer picture of three-state folding. This finding is in agreement with experiment,¹⁸ in which the involvement of loop 2 (Arg-24, Thr-25) in stabilizing non-native states was shown.

7. Neither mutation nor truncation could change the diffusive behavior of WT FBP28 WW domain at temperatures close to the melting point. Only a significant change of temperature may influence the diffusive behavior of a protein. Slow diffusion (subdiffusion), caused by trapping of the protein in shallow minima, was revealed for all systems studied here indicating a strong suppression of diffusion. This finding is in agreement with experiment.⁴⁹

Materials and Methods

UNRES model and simulations details

PCA was applied here to the MD trajectories generated with the coarse-grained UNRES^13,36-44 force field. In the UNRES force field, a polypeptide chain is represented as a sequence of α-carbon (C^α) atoms linked by virtual C^α...C^α bonds with united peptide groups halfway between the neighboring C^α's, and united side chains, whose sizes depend on the nature of the amino acid residues, attached to the respective C^α's by virtual C^α...SC bonds.

The effective energy is expressed by Eq. 1.^13,36-44

$$U=w_{SC}\sum _{i<j}{f}_{S{C}_{i}S{C}_j}\left(T\right)U_{S{C}_{i}S{C}_j}+w_{SCp}\sum _{i\ne j}{U}_{S{C}_i{p}_j}+w_{pp}{f}_2\left(T\right)\sum _{i<j-1}{U}_{p_i{p}_j}+w_{tor}{f}_2\left(T\right)\sum _i{U}_{tor}\left({\gamma }_i\right)+w_{tord}{f}_3\left(T\right)\sum _i{U}_{tord}({\gamma }_i,{\gamma }_{i+1})+w_b\sum _i{U}_b\left({\theta }_i\right)+w_{rot}\sum _i{U}_{rot}({\alpha }_{S{C}_i},{\beta }_{S{C}_i},{\theta }_i)+w_{bond}\sum _i{U}_{bond}\left(d_i\right)+\sum _{m=3}^6{w}_{corr}^{\left(m\right)}{f}_m\left(T\right)U_{corr}^{\left(m\right)}+w_{SS}\sum _i{U}_{SS;i}$$ (1)

with⁴¹

$$f_m\left(T\right)=\frac{\ln (e+e^{-1})}{\ln \left\{\text{exp}\left[{\left(\frac{T}{T_0}\right)}^{m-1}\right]+\text{exp}\left[-{\left(\frac{T}{T_0}\right)}^{m-1}\right]\right\}};T_0=300K$$ (2)

where the successive terms represent side chain-side chain, side chain-peptide, peptide-peptide, torsional, double-torsional, bond-angle bending, side-chain local, distortion of virtual bonds, multi-body (correlation) interactions, and formation of disulfide bonds, respectively. The w's are the relative weights of each term. The correlation terms arise from a cumulant expansion³⁸ of the restricted free energy function of the simplified chain obtained from the all-atom energy surface by integrating out the secondary degrees of freedom. The temperature-dependent factors of Eq. 2 account for the fact that the UNRES effective energy function is a free-energy function.⁴² In this study we used the force field⁴⁴ parameterized with 1ENH and 1E0L.

The molecular dynamics implementation of UNRES (UNRES/MD)^52,53 and its multiplexed replica exchange extension^47,54 were used for the calculations. In replica-exchange molecular dynamics (REMD), N trajectories are run at N different temperatures. After M MD steps, two neighboring trajectories are selected at random and an exchange of temperature between trajectories is attempted with a Boltzmann probability. This modification enables us to perform a walk in energy space and, consequently, a more thorough exploration of conformational space compared to canonical MD. Multiplexed replica exchange molecular dynamics (MREMD) differs from REMD in that multiple trajectories are run at each temperature. For both canonical and MREMD simulations, the size of the time step was 4.89 fs.

In order to determine the melting temperature for each system studied, we initially carried out a 60,000,000 MD-step MREMD simulation (about 0.3 μs formal time; effectively 0.3 ms⁵³) at 20 temperatures (T = 250, 260, 270, 280, 290, 300, 310, 320, 330, 335, 340, 345, 350, 360, 380, 400, 420, 440, 460, and 500 K) with two trajectories per temperature (40 trajectories total). Constant temperature was maintained with the Berendsen thermostat,⁵⁵ the coupling constant being τ = 48.9 fs. To compute thermodynamic quantities, including the heat-capacity profile, we used the weighted histogram analysis method (WHAM),⁵⁶ as implemented in our previous work.⁴²

After determining the melting temperatures, we ran 32 canonical trajectories for each system, for about 100,000,000 MD steps (about 0.5 μs formal time) at selected temperatures below and very close to the melting point for each system. The Langevin thermostat was used in these simulations and the viscosity of water was scaled by the factor of 0.01, as in our previous work.⁵³

Principal component analysis

A detailed description of the PCA method is available in our previous papers^10-13 and in an earlier reference.⁴⁵ PCA is a covariance-matrix-based mathematical technique, and is an effective method for representing the conformational space explored in MD simulations of proteins. PCA rotates the Cartesian or internal coordinate space to a new space with new coordinates, PCs, a few of which are sufficient to describe a large part of the fluctuations of a protein.

MSD analysis and PCA eigenvalue spectrum

The mean-square displacement (MSD), a measure of the overall motion present in a protein, is found to be proportional to t^2H_D, where the quantity H_D is the Hölder exponent which, in the case of simple Brownian motion, has the value ½ (normal diffusion). The values of H_D > ½ and < ½ correspond to superdiffusion and subdiffusion, respectively.⁵⁰ When the value H_D = 1, superdiffusive behavior is called collision-less (ballistic).⁵⁷ In the language of proteins, subdiffusion indicates that a system is trapped in local minima in conformational space, and superdiffusion emerges when the system makes long jumps in conformational space.

The PCA eigenvalue spectrum is based on the following conjecture proposed by Gao et al.⁴⁶ When the number of degrees of freedom is large, the PCA eigenvalue spectrum (λ_i) of fractional Brownian motion (fBm) with parameter H (Hurst parameter) decays as a power law of the index i,

$${\lambda }_i\sim i^{-(2H+1)}$$ (3)

When H = ½, fBm reduces to standard Brownian motion. It was argued that H < ½ and H > ½ correspond to subdiffusion and superdiffusion, respectively.⁴⁶