Cortical energy demands of signaling and nonsignaling components in brain are conserved across mammalian species and activity levels

Abstract

The continuous need for ion gradient restoration across the cell membrane, a prerequisite for synaptic transmission and conduction, is believed to be a major factor for brain’s high oxidative demand. However, do energy requirements of signaling and nonsignaling components of cortical neurons and astrocytes vary with activity levels and across species? We derived oxidative ATP demand associated with signaling (P_s) and nonsignaling (P_ns) components in the cerebral cortex using species-specific physiologic and anatomic data. In rat, we calculated glucose oxidation rates from layer-specific neuronal activity measured across different states, spanning from isoelectricity to awake and sensory stimulation. We then compared these calculated glucose oxidation rates with measured glucose metabolic data for the same states as reported by 2-deoxy-glucose autoradiography. Fixed values for P_s and P_ns were able to predict the entire range of states in the rat. We then calculated glucose oxidation rates from human EEG data acquired under various conditions using fixed P_s and P_ns values derived for the rat. These calculated metabolic data in human cerebral cortex compared well with glucose metabolism measured by PET. Independent of species, linear relationship was established between neuronal activity and neuronal oxidative demand beyond isoelectricity. Cortical signaling requirements dominated energy demand in the awake state, whereas nonsignaling requirements were ∼20% of awake value. These predictions are supported by ¹³C magnetic resonance spectroscopy results. We conclude that mitochondrial energy support for signaling and nonsignaling components in cerebral cortex are conserved across activity levels in mammalian species.

The brain is one of the most energy demanding tissues in the body (1). ¹³C magnetic resonance spectroscopy (MRS) in the rat has shown that, in the resting awake state, ∼80% of cortical energy consumption is used to support signaling as reflected by the rate of glutamate neurotransmitter release and astroglial uptake (2, 3). Cerebral energy demand is also positively correlated with the rate of pyramidal neuron firing in rat cortex (4, 5). ¹³C MRS findings in the human cortex have been generally consistent with the rat results (6). However, there remain questions as to how well the energy costs of specific subcellular processes needed to support synaptic transmission and conduction are conserved over different activity levels and/or across species.

Recent bottom-up energy budgets for gray matter in the mammalian brain have attempted to understand the energetic costs of neuronal and glial electrical and neurotransmission events occurring in the neuropil (7, 8) by calculating the ATP used per neuron for signaling (P_s) and nonsignaling (P_ns) events. In the awake cortex, the total ATP used per unit cortical volume per unit time (E_tot; in units of ATP/s per centimeter³) was determined by multiplying the P_s (in units of ATP/neuron per spike) and P_ns (in units of ATP/neuron per second) parameters with cellular densities (η) and average cortical firing rates (<f>) to give signaling (Es) and nonsignaling (Ens) components,

where the summation spans for neurons and astrocytes. These studies agreed with in vivo measurements in that the majority of brain energy consumption was used to support signaling and also concluded that both signaling and nonsignaling events in human were about two to three times more costly on a per neuron basis than in the rat. However, these budgets have limitations (7, 8); most notably, the histological and biophysical parameters used disagree with recent values, heterogeneity across cortical lamina was disregarded (9–11), and the comparison was made with only one the resting awake state.

Here, we use a top-down as opposed to a bottom-up approach to assess the fundamental links between electrical and chemical events at the neuropil. We tested the hypotheses that the energy requirements per cell for signaling (P_s) and nonsignaling (P_ns) are independent of the state of neuronal activity (e.g., sensory activation, awake, asleep, or anesthetized) and are conserved across species (i.e., rat and human). We used layer-specific morphologic, neurophysiologic, and metabolic data in rat brain to calculate P_s and P_ns, which were then tested on human data. In contrast to views highlighting differences between rat and human brain neurometabolic couplings (7, 8), our results suggest that, on a per cellular basis, the mitochondrial energy support for mammalian cortical functions during signaling and nonsignaling are conserved.

Calculations

Energetics of Signaling and Nonsignaling Components.

We did not sum bottom-up contributions to total oxidative ATP demand as previously done in other budgets (7, 8) but rather, tested whether unchanging values of P_s and P_ns can account for measured in vivo results over a range of cortical activity levels (SI Text, section 1 and Tables S1 and S2). Although the E_s term in Eq. 1 encompasses function of both neurons and astrocytes, we base our budget to neuronal activity data due to limited ability to quantify astrocytic signaling. Given that neuronal firing is statistically representative of neuropil activity (12), we used spike rate as a quantitative measure of cortical function as has been done before (7, 8). In Eq. 1, <f> is given in units of spike.neuron/s per centimeter³ and η_N and η_A are given in units of cells/cm³. Tables S1 and S2 list values of neuronal activity and glucose consumption in rat and human, respectively (SI Text, section 1). Recordings of cortical signaling were reflected by layer-specific microelectrodes in rats and EEG in humans, whereas metabolic measurements were made by 2-deoxyglucose (2DG) autoradiography in rats and fluoro-deoxyglucose PET in humans.

Energetics of Signaling from Layer-Specific Neuronal Recordings in the Rat Somatosensory Cortex.

Cortical signaling involves events like dendritic depolarization, axonal propagation, vesicular endocytosis and exocytosis, neurotransmitter cycling, ionotropic and metabotropic receptor activity, etc. To determine E_s in Eq. 1, we first multiplied the spike rate of the ith cortical layer (f_i in units of spike/s) by the cortical density in the same layer (η_N,i in units of neurons/cm³) to obtain the number of firing events per unit volume (f_i η_N,i in units of spike.neuron/s per centimeter³). Next, we estimated the fraction of the ith cortical layer in relation to the entire cortical thickness (δ_i/Σδ_j). On multiplying, these two terms and summing across all layers gives <f> in Eq. 1 (in units of spike.neuron/s per centimeter³):

Using values of δ, η, and f from recent studies, we then determined if Eq. 1 was able to fit results from experimentally measured regional metabolism across different activity levels.

Energetics of Nonsignaling Events from Isoelectric Condition in the Rat Somatosensory Cortex.

We assigned the nonsignaling energy primarily to ion movement associated with maintaining neuronal and glial resting potentials described by Eq. 1. To separately calculate P_ns,A and P_ns,N, we needed input resistances of neurons (R_in,N) and astrocytes (R_in,A), which describe the energy demand of leaky cell membranes at rest (SI Text, section 2, and Fig. S1) and the average neuronal (η_N) and astrocytic (η_A) densities in the cerebral cortex (Table 1). Because recent R_in,x and η_x measurements in the rat show that values for neurons and astrocytes are quite similar (13–16), the calculations were slightly simplified by assuming that R_in,N ∼ R_in,A and η_N ∼ η_A (Table 1 and SI Text, section 2). To determine P_ns, we needed the metabolic demand for nonsignaling, which was possible for the rat, because state of deep pentobarbital anesthesia in Table S1 induces an isoelectric condition and thus, just contains the E_ns term. Because neuronal recordings do not show any significant cortical activity in the pentobarbital state, the nonsignaling energy described was uniform across all layers. By multiplying P_ns (in units of ATP/cell per second) with η_x (in units of cells/cm³), we get E_ns in Eq. 1 (in units of ATP/s per centimeter³). This empirically derived E_ns was held constant for all other states.

Table 1.

Energy budget parameters in rat and human brains

Source	ηN	ηA	Rin,N	Rin,A	Pns,N	Pns,A	Ps
This study (rat)	4.75*	4.75*	74†	74†	9.20‡	6.85‡	4.81§
This study (human)	1.83*	1.83*	74†	74†	9.20‡	6.85‡	4.81§
Ref. 7 (rat)	9.2	9.2	200	500	3.42	1.02	0.71
Ref. 8 (human)	4.0	3.8	79	163	8.6	3.1	2.4

Average values of cortical density of neurons (η_N; ×10⁷ neuron/cm³) and astrocytes (η_A; ×10⁷ astrocyte/cm³) densities, input resistances of neurons (R_in,N; MΩ) and astrocytes (R_in,A; MΩ), rate of ATP use for nonsignaling per neuron (P_ns,N; ×10⁸ ATP/neuron per second) and astrocyte (P_ns,A; ×10⁸ ATP/astrocytes per second), and ATP use per signaling event per neuron (P_s; ×10⁹ ATP/spike per neuron).

*Table 2 in ref. 15 shows average cortical neuronal density in rat brain, figure 2 in ref. 16 shows neuron vs. astrocyte densities are similar, and figure 2 in ref. 17 shows rat and human neuronal densities differ by ∼2.6.

^†Estimated from Fig. S1A.

^‡Calculated from Eq. S1 and Eq. 5 (details in Fig. S1B).

^§Calculated from Eqs. 1–6.

Converting Calculated Total ATP Production Rate to Cerebral Glucose Oxidation Rate.

We used the following formula to convert E_tot in Eqs. 1 to rate of glucose oxidation [calcCMR_glc(ox)],

where k depends on the oxygen-to-glucose index (OGI), which is given by the ratio of cerebral metabolic rates of oxygen (CMR_O2) and glucose (CMR_glc) consumption, and k itself is given by 10⁷/(A_vo ρ OGI), where ρ is the tissue density (1.05 g/mL) and A_vo is the Avogadro constant (6.023 × 10²³/mol). Similarly, the measured glucose oxidation [measCMR_glc(ox)] was given by

where measCMR_glc was obtained from 2DG autoradiography in rats and fluoro-deoxyglucose PET in humans (Tables S1 and S2); it is given by sum of oxidative [CMR_glc(ox)] and nonoxidative [CMR_glc(nonox)] terms, whereas CMR_glc(ox) itself has neuronal [CMR_glc(ox),N] and astrocytic [CMR_glc(ox),A] components. Thus, it is possible to obtain calculated forms of CMR_glc(nonox), CMR_glc(ox),N, and CMR_glc(ox),A across all activity states. Finally, we compared calcCMR_glc(ox) with measCMR_glc(ox) by least-square fitting to determine P_s and P_ns:

where summation was over all states (Tables S1 and S2).

Calculating Signaling and Nonsignaling Energetics in the Human Visual Cortex.

To test whether P_ns,N, P_ns,A, and P_s derived from the rat (Table 1) were representative of those values in human cerebral cortex, we calculated E_ns in the human by simply multiplying the P_ns,N and P_ns,A terms with η_N and η_A, respectively [i.e., cellular density is about 2.6 times lower in human vs. rat (17)]. Neuronal activity for each state in the human was represented by EEG-measured bispectral index (BIS) values ranging from 0 to 100 (Table S2) as used intraoperatively (18). We calculated the E_s term in the human similarly as in the rat, but because the neuronal activity data in the human originated from EEG recordings (SI Text, section 3), additional steps were needed to represent Eq. 2 to convert the BIS into units similar to the rat data (i.e., in units of spike.neuron/s per centimeter³):

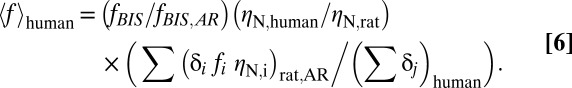f_BIS and f_BIS,AR are BIS values for a given state and the awake condition (Table S2), η_N,human and η_N,rat are the average neuronal densities in the human and rat cortices (Table 1), Σ(δ_i f_i η_N,i)_rat,AR is the numerator of Eq. 2 for the awake condition in the rat (Table 2), and (Σδ_j)_human is the cortical thickness in the human (Table 3). This conversion, from f_BIS scale in humans to <f> scale in rats, accounts for differences in average neuronal density and cortical thickness between rat somatosensory and human visual cortices (15–17, 19).

Table 2.

Calculated CMR_glc(ox) derived from neuronal activity in rat somatosensory cortex for OGI of 5.6

Behavioral state*	PR	UR1†	US1†	AR†	AS†	UR2‡	US2‡	CR‡	CS‡	HR‡	HS‡
Σ(δi fi ηN,i) (×103 spike.neuron.cm/s per centimeter3)	0.00	7,051	9,393	8,858	9,090	6,024	8,629	4,233	6,677	5,213	5,533
Σ(δi fi ηN,i)/Σδj (×107 spike.neuron/s per centimeter3)	0.00	3.71	4.95	4.67	4.79	13.36	19.13	9.39	14.80	11.56	12.27
Ens = Σ Pns,x × ηN,x (×1017 ATP/s per centimeter3)	0.76	0.76	0.76	0.76	0.76	0.76	0.76	0.76	0.76	0.76	0.76
Es = Ps × Σ(δi fi ηN,i)/Σδj (×1017 ATP/s per centimeter3)	0.00	1.79	2.38	2.24	2.30	1.53	2.19	1.07	1.69	1.32	1.40
Etot = Ens + Es (×1017 ATP/s per centimeter3)	0.76	2.55	3.14	3.01	3.07	2.29	2.95	1.84	2.45	2.08	2.16
calcCMRglc(ox) (μmol/g per minute)	0.22	0.72	0.89	0.85	0.87	0.65	0.83	0.52	0.69	0.59	0.61
measCMRglc(ox) (μmol/g per minute)	0.20	0.63	0.90	0.82	0.91	0.63	0.90	0.49	0.68	0.61	0.63

Details in Calculations. The calculated CMR_glc(ox) [calcCMR_glc(ox)] was determined from Eq. 3. The measured CMR_glc(ox) [measCMR_glc(ox)] was determined from Eq. 4 assuming OGI of 5.6. AR, awake rest; AS, awake stimulation; CR, α-chloralose rest; CS, α-chloralose stimulation; HR, halothane rest; HS, halothane stimulation; PR, pentobarbital; UR1, urethane rest; UR2, urethane rest; US1, urethane stimulation; US2, urethane stimulation.

*Details in SI Text, section 1 and see Fig. 1A for comparison between calcCMRglc(ox) and measCMRglc(ox).

^†Σδ_j was 1.90 mm (with P_s = 4.81 × 10⁹ ATP/spike per neuron; see red circles in Fig. 1A).

^‡Σδ_j was 0.45 mm [with P_s′ = (0.45/1.90) × P_s; see orange circles in Fig. 1A].

Table 3.

Calculated CMR_glc(ox) derived from neuronal activity in human visual cortex for OGI of 5.6

Behavioral state*	VGP	VGA	PRO	SEV	HAL	SLP	AWK
Σ(δi fi ηN,i) (×103 spike.neuron.cm/s per centimeter3)	282	1,192	1,317	1,306	1,959	2,674	3,407
Σ(δi fi ηN,i)/Σδj (×107 spike.neuron/s per centimeter3)	0.12	0.51	0.56	0.56	0.83	1.14	1.45
Ens = Σ Pns,x × ηN,x (×1017 ATP/s per centimeter3)	0.29	0.29	0.29	0.29	0.29	0.29	0.29
Es = Ps × Σ(δi fi ηN,i)/Σδj (×1017 ATP/s per centimeter3)	0.06	0.24	0.27	0.27	0.40	0.55	0.70
Etot = Ens + Es (×1017 ATP/s per centimeter3)	0.35	0.54	0.56	0.56	0.69	0.84	0.99
calcCMRglc(ox) (μmol/g per minute)	0.10	0.15	0.16	0.16	0.20	0.24	0.28
measCMRglc(ox) (μmol/g per minute)	0.08	0.14	0.15	0.14	0.18	0.24	0.31

Details in Calculations. To convert the EEG data in Table S2 into units of Σ(δ_i f_i η_N,i)/Σδ_j, simple conversions were needed with Eq. 6. The calculated CMR_glc(ox) [calcCMR_glc(ox)] was determined from Eq. 3. The measured CMR_glc(ox) [measCMR_glc(ox)] was determined from Eq. 4 assuming OGI of 5.6. AWK, awake; HAL, halothane; PRO, propofol; SEV, sevoflurane; SLP, non-REM sleep; VGA, acute vegetative; VGP, persistent vegetative.

*Details in SI Text, section 1 and see Fig. 1A for comparison between calcCMRglc(ox) and measCMRglc(ox).

Results

P_s in the Rat Somatosensory Cortex.

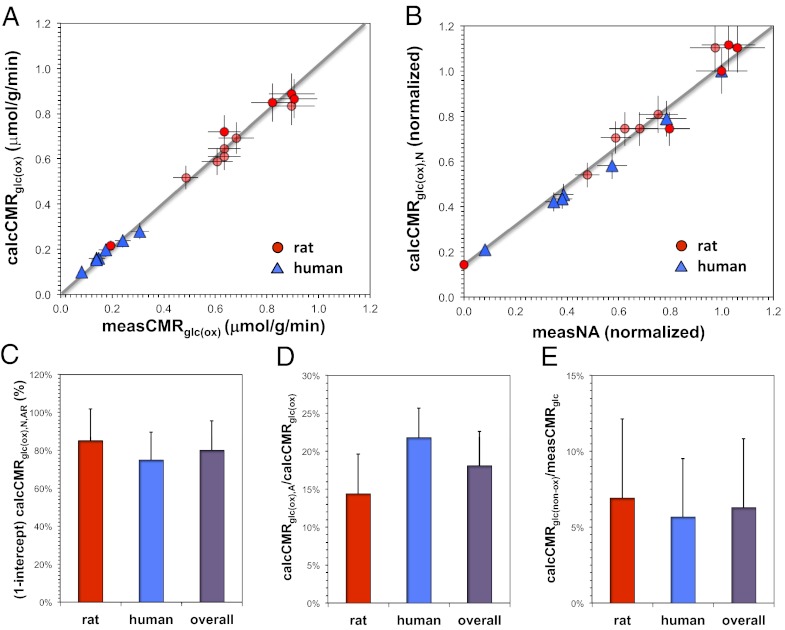
The averaged representation of normalized activity of neurons across all states showed dominant activity in the bottom two-thirds of cortical layers (Fig. S2 and Table S1), which is in good agreement with prior studies that investigated layer-specific representation of neuronal activity, 2DG autoradiography, and functional MRI (fMRI) data (9–11). The laminar activity was then used with Eqs. 1–6 to derive calcCMR_glc(ox) and compared with measCMR_glc(ox) by least-square fitting to determine P_s and P_ns. An average P_s value of 4.81 × 10⁹ ATP/spike per neuron was calculated by fitting Eq. 5 for all activity states in the rat, which is shown in Table 1. Because the neuronal activity data for some states in Table S1 were not available for all layers, P_s was estimated for those specific layers only [i.e., (0.45/1.90) × 4.81 × 10⁹ ATP/spike per neuron) (Table 2). Although the current P_s value is derived for the entire cortex, layer-specific P_s values are unlikely to vary by more than 50% of the average value. Fig. 1A shows the goodness of fit for Eq. 5 to the rat data (red circles) for an OGI of 5.6 with an R² value of 0.96 (gray line with σ² = 0.0182 for 11 states), indicating that the assumption of a constant value of P_s over the full activity range is well-supported.

Fig. 1.

Relationship between glucose oxidation [CMR_glc(ox)] and neuronal activity as a function of OGI. (A) Comparison between calculated CMR_glc(ox) [calcCMR_glc(ox)] and measured CMR_glc(ox) [measCMR_glc(ox)] values. Values of measCMR_glc(ox) were derived from 2DG autoradiography in rat brain and PET in human brain, whereas values of calcCMR_glc(ox) were derived for an OGI of 5.6. The goodness of fit between measCMR_glc(ox) and calcCMR_glc(ox) for the rat data (red circles) is indicated by the gray line with an R² value of 0.96 (σ² = 0.0182 for 11 states). The human data (blue triangles) also showed a strong correlation (R² = 0.91 and σ² = 0.0023 for seven states). (B) Comparison between measured NA (measNA) and calculated glucose oxidation in neurons [calcCMR_glc(ox),N] in rat (red circles) and human (blue triangles) brains shows good correlation [R² = 0.98, where calcCMR_glc(ox),N = 0.90measNA + 0.12]. Because the data were normalized to the awake resting state values, the intercept on the vertical axis is about ∼20% of calcCMR_glc(ox),N in the awake state for both species. (C–E) Comparison of calculated total glucose oxidation [calcCMR_glc(ox)], calculated glucose oxidation in neurons [calcCMR_glc(ox),N], calculated glucose oxidation in astrocytes [calcCMR_glc(ox),A], calculated nonoxidative glucose consumption [calcCMR_glc(nonox)], and measured total glucose consumption (measCMR_glc), where calcCMR_glc(ox) = calcCMR_glc(ox),N + calcCMR_glc(ox),A and calcCMR_glc(nonox) = measCMR_glc − calcCMR_glc(ox). Ratios in rat brain (red), human brain (blue), and overall (purple) for (C) the value of the calcCMR_glc(ox),N in B for the nonanesthetized awake resting state [calcCMR_glc(ox),N,AR] minus the value of the intercept [i.e., (1-intercept)calcCMR_glc(ox),N,AR] and the values of (D) calcCMR_glc(ox),A/calcCMR_glc(ox) and (E) calcCMR_glc(nonox)/measCMR_glc measured across all activity levels. All error bars indicate SDs from the mean. All calculations were obtained with P_s = 4.81 × 10⁹ ATP/spike per neuron, P_ns,N = 9.20 × 10⁸ ATP/neuron per second, and P_ns,A = 6.85 × 10⁸ ATP/astrocytes per second). Details are in Tables 1, 2, and 3.

P_ns in the Rat Somatosensory Cortex.

The measured CMR_glc(ox) for the pentobarbital state in the rat (Table S1) was fitted to the E_ns term (Table 2). The constant E_ns term for all activity states was 0.76 × 10¹⁷ ATP/s per centimeter³, leading to average P_ns,N and P_ns,A values of 9.20 × 10⁸ ATP/neuron per second and 6.85 × 10⁸ ATP/astrocytes per second, respectively, for an OGI range of 5.1–6.0 (20). These values of P_ns corresponded to an average R_in value of 74 MΩ (SI Text, section 2), which is well within the in vivo range measured for neurons and astrocytes (13, 14). As shown in Table 1, despite identical cortical densities of neurons and astrocytes, P_ns,N and P_ns,A were dissimilar, because slightly different Nernst potentials for Na⁺ and K⁺ and resting membrane potentials were used for neurons and astrocytes (SI Text, section 2), which has been done before (7, 8). However, similarity of contributions of astrocytes and neurons to nonsignaling energy consumption is in good agreement with measurements by ¹³C MRS made under isoelectric pentobarbital anesthesia, supporting the accuracy of the derived values (2, 21).

E_s and E_ns in the Human Visual Cortex.

At present, there are insufficient studies in which electrical signaling in the human cerebral cortex (e.g., by single-unit recording) has been measured over a range of activity states to empirically derive P_s and P_ns, which was done for the rat cerebral cortex. To assess how different these values might be in the human, we used Eq. 1 with values for neuronal and glial densities determined for human and P_s and P_ns derived from the rat data, which required normalizing the awake BIS scale in humans to rat neuronal activity scale in the awake state (Eq. 6). Laminar firing rates in the human are not available, but according to the difference of <f> between rats and humans (Tables 2 and 3), we expect the cortical neuronal firing rate in humans to be lower than in rats. Although instantaneous neuronal firing rates in the awake human cerebral cortex can be quite variable from moment to moment (22), average rates estimated from steady-state measurements (23) are about 30–40% of the highest firing rates typically observed in the awake rat (Table S1). Firing rate measurements in the awake primate cortex are slightly higher than values found in human brain (24). Given that CMR_glc in awake primate cortex is about 0.5 μmol/g per minute (25), which is between awake CMR_glc in rat and human (i.e., 0.8 vs. 0.3 μmol/g per minute, respectively), we expect that similar budget calculations can be made for primate cortex with the same P_s and P_ns values based on cellular density variations across the species (17). Although neuronal recordings in primate brain do not usually report quantitative firing rates (26), basic features of action potentials in the human cerebral cortex are quite similar to those features typically found in other animals, including rats and primates (27–29). Fig. 1A shows the goodness of fit for Eq. 5 to the human data (blue triangles) for an OGI of 5.6 with an R² value of 0.91 (gray line with σ² = 0.0023 for seven states), indicating that the assumption of a constant value of P_s derived from the rat is well-supported over the full activity range in the human.

Relative Contributions of E_s and E_ns in the Resting Awake State.

To represent the magnitude of E_ns vs. E_s in the resting awake state, we plotted the calcCMR_glc(ox),N vs. the measured neuronal activity in a normalized scale (Fig. 1B). Because the intercepts on the calcCMR_glc(ox),N vertical axis—which indicates the isoelectric condition—were ∼0.1 and ∼0.05 μmol/g per minute for the rat and human, respectively (Fig. S3), or 15–20% of the calcCMR_glc(ox),N in the awake state (Fig. 1B), the results suggest that a significant fraction of neuronal glucose oxidation in the awake state is dedicated for maintaining resting membrane potentials (Fig. 1C). Similarly, glial glucose oxidation is about ∼20% of total glucose oxidation in the awake state (Fig. 1D). Based on reported OGI values (20), nonoxidative glucose consumption is about ∼6% of total glucose consumption (Fig. 1E).

Comparison with ¹³C MRS Studies.

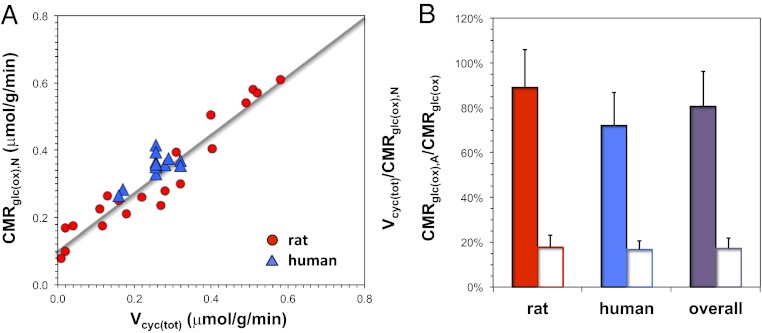
A similar linear relationship between neuronal activity and energy metabolism has been shown by results from ¹³C MRS—a method that simultaneously measures rates of total neurotransmitter cycling [V_cyc(tot)] and neuronal [CMR_glc(ox),N] as well as astrocytic [CMR_glc(ox),A] oxidative demand (2, 3). Fig. 2A shows the most up-to-date results from in vivo ¹³C MRS studies in rats and humans (Tables S3 and S4), which illustrate nearly a 1:1 relationship between ΔV_cyc(tot) and ΔCMR_glc(ox),N just beyond the isoelectric point when V_cyc(tot) approaches zero [i.e., gray line indicates an R² value of 0.92, CMR_glc(ox),N = 0.87 V_cyc(tot) + 0.10]. Moreover, the in vivo ¹³C MRS results of V_cyc(tot)/CMR_glc(ox),N and CMR_glc(ox),A/CMR_glc(ox) ratios in the awake state for both species, shown in Fig. 2B, show that neurons and astrocytes in the awake state demand about ∼20% of oxidative ATP for nonsignaling factors. These results are similar to our budget calculations in Fig. 1.

Fig. 2.

In vivo ¹³C MRS experiments reporting rates of neurotransmitter cycling [V_cyc(tot)] and glucose oxidation in neurons [CMR_glc(ox),N] and astrocytes [CMR_glc(ox),A]. (A) Values of V_cyc(tot) and CMR_glc(ox),N for rat (red circles) and human (blue triangles) cerebral cortex. The rat data represented many activity levels in the somatosensory cortex, whereas the human data were from the awake resting state in the visual cortex with varying degrees of gray vs. white matter partial volume (Table S3). Linear trends between changes in V_cyc(tot) and CMR_glc(ox),N suggest strong coupling between neurotransmitter activity and energy metabolism [R² = 0.92, where CMR_glc(ox),N = 0.87 V_cyc(tot) + 0.10], where the finite intercept ranging between 0.05 and 0.15 μmol/g per minute indicates energy consumption for nonsignaling conditions. (B) Ratios of V_cyc(tot)/CMR_glc(ox),N in the nonanesthetized awake resting state (filled bars) (Table S3) and CMR_glc(ox),A/CMR_glc(ox) for all conditions above isoelectricity (open bars) (Table S4) in rat (red), human (blue), and overall (purple). Similarity between the V_cyc(tot)/CMR_glc(ox),N ratios (filled bars) in rat and human suggests that the relationship between V_cyc(tot) and CMR_glc(ox),N in both species may be conserved. Likewise, correspondence between the CMR_glc(ox),A/CMR_glc(ox) ratios (open bars) suggests that the relationship between CMR_glc(ox),A and CMR_glc(ox) across species could be similar.

Discussion

Comparison of Derived P_ns and P_s with Prior Calculations.

There are large differences between P_ns,N and P_ns,A estimates for the rat by Attwell and Laughlin (7) and our empirically derived values (Table 1). Values of P_ns,N and P_ns,A are susceptible to starting assumptions (SI Text, section 2 and Fig. S1). This difference principally occurs, because Attwell and Laughlin (7) assumed R_in,N and R_in,A to be around 200 and 500 MΩ, respectively, based on in vitro recordings (30, 31). However, our estimates of R_in,N and R_in,A values of 74 MΩ are in close agreement with in vivo measurements (13, 14). Because P_ns depends on the reciprocal of R_in (SI Text, section 2), the higher R_in,N and R_in,A values by Attwell and Laughlin (7) are the main basis for their lower P_ns,N and P_ns,A estimates. Additionally, however, in the case of P_ns,N, there could also be differences in average neuronal density, which in the study by Attwell and Laughlin (7), were based on the mouse cortex (32), whereas our values were obtained from the rat cortex (15). The P_ns,N and P_ns,A values estimated by Lennie (8) for the human are approximately similar to our values, despite large differences in cell densities across species (Table 1). There are similar differences between P_s values for the rat by Attwell and Laughlin (7) and the human by Lennie (8) as discussed in detail below. However, in a recent ³¹P MRS study of the human brain, Zhu et al. (33) estimated a P_s value of 4.7 × 10⁹ ATP/neuron per second from measured cerebral metabolic rates of high-energy phosphate reactions catalyzed by ATPase. Assuming that, within 1 s, there is one spike in the awake brain, this value agrees well with P_s estimated in the current budget (Table 1).

Glial Energy Demand and Excitatory Vs. Inhibitory Neuronal Energy Requirements.

The calculated astrocytic energy demand (Fig. 1D) is consistent with ¹³C MRS results (Fig. 2B) but significantly higher than estimates from prior budgets (7, 8). The higher E_ns,A values are because of using more recent values of astrocyte input resistances (14). The in vivo results were fit well with the assumption of the major energetic changes with activity being in the neurons. Relatively constant astrocytic energetics (compared with neurons) as a function of overall cortical activity may reflect the energetics associated with maintaining the high astrocyte K⁺ conductance dominating over additional functional demands (e.g., transporting glutamate and/or dealing with Ca²⁺ waves) as suggested by recent studies (34–37). ¹³C MRS results, in support of these observations, show that energy demand of astrocytes changes considerably less than neuronal energy demand over wide activity levels (Table S4). However, the glial data are relatively limited compared with neuronal data, and future studies are needed to better understand glial functional energy requirements.

As in previous bottom-up calculations (7, 8), to derive P_s and P_ns, we could not separately include energy demand of inhibitory neurons, because the electrophysiological studies only included measurements of pyramidal neurons. Because CMR_glc(ox),N contains the oxidative energy requirements of both excitatory and inhibitory neurons (15), the value of P_s likely reflects glutamatergic neurons working in conjunction with an ensemble of GABAergic neurons. Electrophysiological and ¹³C MRS studies have found that, over the range of activity that we examined, both function and energy demand of GABAergic neurons is proportional to activity/demand of glutamatergic neurons (38, 39), consistent with the fractional contribution of excitatory and inhibitory neurons to P_s being constant throughout the activity range and similar to glutamatergic and GABAergic neuronal fractions measured morphologically (15).

Constancy of P_s and P_ns Across Activity Levels and Species.

Previously, Karbowski (40) suggested that basal metabolic cortical differences across species could be described on allometric rationale. However, Herculano-Houzel (17) pointed out that absolute metabolic difference across species could be explained by neuronal number variations. Both Karbowski (40) and Herculano-Houzel (17) dealt with only the awake state values and the total metabolic rate (i.e., only E_tot in Eq. 1). In the current study, we partitioned E_tot for each activity level examined in terms of signaling (E_s) and nonsignaling (E_ns) components to test if P_s and P_ns are constant across species). Thus, neither E_s nor E_ns was assumed for any given state. E_s was derived based on the neuronal firing for a given state in each cortical layer for the rat and across the cortex in the human, whereas E_ns was based on leakiness of the cell membrane. To derive P_s, we fitted E_tot to measured CMR_glc(ox) data for each state, whereas to derive P_ns, we fitted E_ns to measured CMR_glc(ox) data for pentobarbital. Because barbiturates may also inhibit mitochondrial respiration (41) and if so, could lead to an overestimate of P_ns, we fitted the data in Fig. 1B with and without the isoelectric pentobarbital data and found negligible differences in the slope, intercept, and goodness of fit [rat data: CMR_glc(ox) = 0.92 neuronal activity (NA) + 0.13, R² = 0.97 with pentobarbital and CMR_glc(ox) = 0.94 NA + 0.11, R² = 0.93 without pentobarbital]. A fixed P_ns does not necessitate a constant P_s. As shown in Fig. 1 A and B, a constant value of P_s gave an excellent fit to the data. A nonconstant P_s, most likely a decrease at higher firing rates, would have shown itself as a deviation from the best linear fit. It should be recalled that bottom-up energy budgets predict that P_s and P_ns differ significantly across species (Table 1), and moreover, constancy of P_s and P_ns beyond the awake state had not been tested (7, 8).

The finding of a constant P_s across activity levels suggests that energy-consuming subcellular processes of the neuropil (e.g., ion fluxes associated with action potentials, pre- and postsynaptic potentials, vesicular exocytosis/endocytosis, neurotransmitter release/uptake, etc.) are all tightly coupled, ensuring that the fidelity of impulse trafficking across a synapse is maintained independent of signaling frequency. Although the mechanisms upholding this neurometabolic linearity are not understood, the rapid rate with which surrounding astrocytic end feet clear synaptic glutamate is probably a critical component (3). The similarity of energetic efficiency with regard to electrical (Fig. 1) and chemical (Fig. 2) events across different activity levels suggests that there are physiological factors that limit the energy associated with cortical signaling (42) and that, within the normal physiological range of neuronal signaling, the electrical and chemical events are complimentary (3). Assuming a constant energetic cost of Na⁺ and K⁺ pumping, there is a direct relationship between synaptic strength (i.e., average current induced by a signaling event at a synapse, which can be increased through either induced conductivity or higher probability of presynaptic glutamate release) and energy consumption at the synapse.

The stability of P_s and P_ns across species suggests that, early in evolution, the mammalian brain reached an optimum tradeoff between energy consumption and computational power at a cellular level (43). This constancy differs from most other tissues, where there is a decrease in cellular metabolic rate by a power of relative animal size (1). These findings imply that relative energy costs of fundamental features of cortical communication (e.g., action potentials, pre- and postsynaptic potentials, glial neurotransmitter and K⁺ clearance, etc.) as well as physiological mechanisms for supplying mitochondrial energy for neuropil operations (e.g., hemoglobin, voltage-gated ion channels, glutamate and GABA receptors, and glucose and oxygen transport) are well-preserved through evolution (17, 28, 29, 44–49). A constant interspecies ATP demand of cortical activity emphasizes the relevance of animal testing in experimental neuroscience studies. However, the approximately twofold difference in total cortical energy consumption between rats and humans may reflect limitations in blood flow in the human to supply oxygen and glucose and remove waste products and heat in relation to the number of cells that comprise each brain (50, 51).

Implications for fMRI and Resting Awake State Neuronal Activity.

fMRI has become a major tool for mapping neuronal activity in humans and animals. An important question in fMRI studies is whether the change in signal during tasks, which is produced by changes in blood flow, blood volume, and oxygen consumption, directly reflects changes in neuronal activity (52). Our finding that a constant P_s fits experimental data both within and across species supports that measurements of the oxygen consumption component of fMRI can provide a quantitative measure of changes in neuronal activity. This conclusion is consistent with experimental studies using calibrated fMRI and multiunit recordings that have found a linear relationship between the average pyramidal cell signaling and regional oxygen consumption (4, 5, 36, 37). Our findings also show that the high level of neuronal activity in the resting awake state by ¹³C MRS is consistent with metabolic measurements of 2DG and PET as well as electrical activity measurements (spanning from EEG to extracellular recordings) for the rat and human, supporting proposals that resting state activity be incorporated into fMRI models of brain function (53). Because these results are relating macroscopic energy measurements to microscopic electrical events, we expect that the empirically derived values of P_s and P_ns can better guide bottom-up budgets of subcellular processes representing mammalian cortical function.

Materials and Methods

Tables S1 and S2 list values of neuronal activity and glucose consumption in rat and human for 11 and 7 different states, respectively, over a range of excitability (SI Text, section 1). In summary, the measured neuronal activity data were used to calculate CMR_glc(ox) and then compared with measured CMR_glc(ox) to determine values of P_s and P_ns (Tables 1, 2, and 3). The budget is described in Calculations (SI Text, section 2).