Dual-band selective double cross polarization for heteronuclear polarization transfer between dilute spins in solid-state MAS NMR

Abstract

A sinusoidal modulation scheme is described for selective heteronuclear polarization transfer between two dilute spins in double cross polarization magic-angle-spinning nuclear magnetic resonance spectroscopy. During the second N → C cross polarization, the ¹³C RF amplitude is modulated sinusoidally while the ¹⁵N RF amplitude is tangent. This modulation induces an effective spin-lock field in two selective frequency bands in either side of the ¹³C RF carrier frequency, allowing for simultaneous polarization transfers from ¹⁵N to ¹³C in those two selective frequency bands. It is shown by experiments and simulations that this sinusoidal modulation allows one to selectively polarize from ¹⁵N to its covalently bonded ¹³Cα and ¹³C′ carbons in neighboring peptide planes simultaneously, which is useful for establishing the back-bone connectivity between two sequential residues in protein structural elucidation. The selectivity and efficiency were experimentally demonstrated on a uniformly ¹³C,¹⁵N-labeled β1 immunoglobulin binding domain of protein G (GB1).

1. Introduction

In the past decade, solid-state magic-angle-spinning (MAS) NMR has rapidly emerged as a powerful technique for studying insoluble proteins such as membrane proteins, amyloid proteins, and supramolecules. Resonance assignment is an essential step in the structural determination of uniformly ¹⁵N and ¹³C labeled proteins. In this regard, sequential assignments have been commonly used to extract structural constraints [1–12] via through-spaced dipolar couplings in well designed multi-dimensional experiments based on heteronuclear [13,14] and homonuclear dipolar recoupling [15–25] techniques in solid-state MAS NMR. While the heteronuclear correlation between ¹³C and ¹⁵N is one of the most important experiments in such sequential assignments, due to the fact that each backbone nitrogen covalently bonds with the Cα and carbonyl (C′) carbons in neighboring peptide planes, thus providing useful through-bond links between two sequential residues.

The heteronuclear polarization transfer between ¹³C and ¹⁵N can be achieved by the so-called double cross polarization, i.e. DCP [13,26,27], in which ¹⁵N is first polarized from the abundant ¹H spins and then transferred to ¹³C via a second cross polarization from ¹⁵N to ¹³C. Whereas the ¹H–¹⁵N or ¹H–¹³C CP are relatively mature, most of the issues regarding DCP are primarily focused on the second N → C CP involving polarization transfer, in terms of selectivity, efficiency, and the influence of RF instability, between two low-γ nuclear species [28–42]. For example, SPECIFIC CP [31], a DCP experiment with carefully adjusted offsets and RF amplitudes on both the ¹³C and ¹⁵N channels, leads to selective polarization transfer from ¹⁵N to one of its bonded ¹³Cs (either ¹³Cα or ¹³C′), known as the two-dimensional (2D) NCA and NCO experiments, respectively. With the two NCA and NCO spectra, the connectivity between the Cα[i] and C′ [i–1] in the adjacent peptide planes can thus be established through N[i]. Alternatively, in the CANCO experiments [43], the ¹³Cα[i] is first selectively polarized from ¹H, and then sequentially transferred to ¹³C′ [i–1] through two-step selective polarization transfers (i.e. from ¹³Cα [i] → ¹⁵N[i] and then from ¹⁵N[i] → ¹³C′[i–1]). However, such three-dimensional (3D) experiments (if including the ¹⁵N chemical shift dimension) suffer from very low sensitivity due to the multistep polarization transfers among the dilute spins. The efficiency for each heteronuclear polarization transfer between ¹³C and ¹⁵N is around 30–40%. Therefore, there is only 10–15% polarization transfer efficiency from ¹³Cα[i] to ¹³C′[i–1] [43].

In this work, we propose a dual-band selective double cross polarization to simultaneously polarize the ¹³Cα[i] and ¹³C′[i–1] from ¹⁵N[i], which allows one to establish the backbone ¹³Cα[i]–¹⁵N[i]–¹³C′[i–1] connectivity in a single 2D ¹⁵N–¹³C correlation spectrum, rather than in the two NCA and NCO spectra or in a low-sensitive CANCO spectrum, provided that there is a sufficient resolution in the ¹⁵N dimension. In this new scheme, the RF amplitude of the ¹³C channel is modulated sinusoidally while that of the ¹⁵N channel is kept constant or tangent-modulated during the second N → C CP. This sinusoidal modulation [44,45] directly applies the RF amplitude onto the Cα and C′ chemical shift regions simultaneously, even if the carrier frequency is away from those regions. The modulation period needs not to be commensurate with the period of sample rotation. We refer to this new method as sine-modulated double cross polarization (smDCP). It will be shown by experiments and simulations that smDCP can be effectively used for the dual-band selective heteronuclear polarization transfer using low RF amplitudes, thus improving selectivity and relaxing the demand on ¹H decoupling power. The advantages of this new scheme will be illustrated by using a uniformly ¹³C,¹⁵Nlabeled β1 immunoglobulin binding domain of protein G (GB1) in the following sections.

2. Materials and experiments

The 56-residue β1 immunoglobulin binding domain of protein G (GB1) was expressed in E. coli BL21 (DE3) and minimal media (1.0 g/L ¹⁵N NH4Cl, 2.0 g/L ¹³C glucose), induced with 1.0 mM isopropyl β-D-thiogalactoside (IPTG) for 4 h. The cell pellet was resuspended in PBS buffer (50 mM Phosphate, 150 mM NaCl, pH 8.0) and incubated at 80 °C for 5 min. After centrifugation at 10,000 rpm for 30 min, the supernatant was purified by ion exchange (AKTA purifier 10.0), gelfiltration (Sephadex 100) and following desalination (AKTA purifier 10.0) with phosphate buffer (pH 8.0). The precipitation of GB1 was incubated over night at 4 °C in precipitation solution of 33% isopropanol (IPA) and 67% 2- methylpentane-2,4-diol (MPD). The final microcrystals were centrifuged at 5000 rpm for 2 min and transferred into a 4 mm rotor.

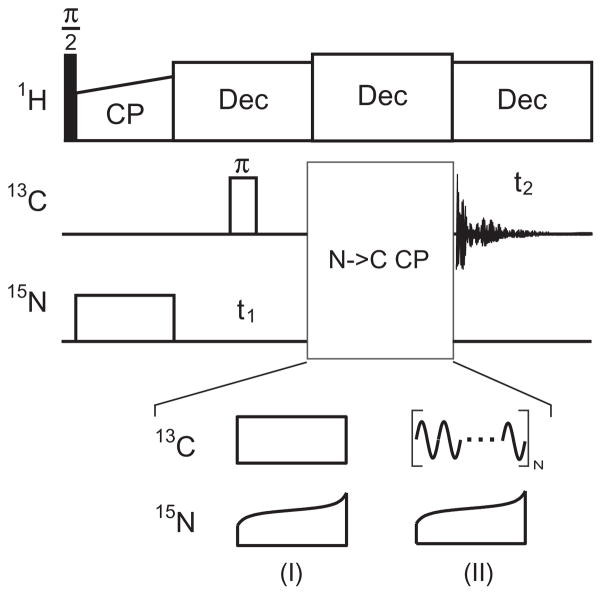
All the NMR experiments were performed on a wide-bore Varian 600 MHz NMR spectrometer of VNMRS system, equipped with a 4 mm triple-resonance T3-HXY MAS probe, at a temperature of 283 K (calibrated in separate experiments using the lead nitrate sample [46]). The sample spinning rate was set to 11 kHz ± 2 Hz. Fig. 1 shows the pulse sequences used in our experiments. The ¹H π/2 pulse was 3.3 μs, while the ¹³C π pulse length of 7.2 μs was used for decoupling in the ¹⁵N chemical shift dimension (i.e., t₁ dimension). During the first ¹H–¹⁵N CP with a contact time of 1.2 ms, the ¹⁵N RF amplitude was about 37 kHz and the ¹H RF-field was ramped from 90% to 110% of 57 kHz. The contact time for the second N → C CP was set to 5 ms, while the ¹⁵N and ¹³C RF amplitudes were varied depending upon the experimental schemes and will be described in their corresponding figures. The SPINAL-64 [47] sequence with 71 kHz RF amplitude and a 7.9 μs flip pulse was applied during both t₁ and t₂ dimension for ¹H decoupling, while an 83 kHz CW decoupling was used during the ¹⁵N–¹³C contact. The ¹³C chemical shifts were referenced to adamantane at 40.48 ppm of the downfield signal [48] and the ¹⁵N reference was calculated based on the gyromagnetic ratio as recommended by IUPAC [49]. The RF amplitudes were calculated based on several measured amplitudes with the GB1 sample and the linearity of Varian linear amplifiers.

Fig. 1.

Pulse sequences used in 2D ¹⁵N–¹³C heteronuclear correlation experiments in solid-state MAS NMR. (I) The standard ¹⁵N–¹³C CP where the ¹⁵N RF amplitude is tangent but the ¹³C RF amplitude remains constant. (II) The sine modulated scheme where the ¹⁵N RF amplitude is tangent while the ¹³C RF amplitude is sinusoidally modulated at a given modulation frequency ω_m.

Fig. 1(I) shows the standard N → C CP scheme where the ¹⁵N RF amplitude is tangent while the ¹³C RF amplitude remains constant, or vice versa, to enhance the CP efficiency [30,50]. For comparison, we use the rectangular ¹³C RF amplitude in our standard DCP experiments and refer it as ‘rectangular DCP’ in the following discussions. While in the smDCP scheme, the ¹⁵N RF amplitude is tangent while the ¹³C RF amplitude ω_1C is sinusoidally modulated, as shown in Fig. 1(II):

$${\omega }_{1\text{C}}(t)={\omega }_{1\text{C}}^{max}sin({\omega }_{\text{m}}t),$$ (1)

where, ${\omega }_{1\text{C}}^{max}$ and ω_m represent the maximum RF amplitude and the modulation frequency, respectively. Mathematically, such a sine-wave modulation induces a spin-lock field in two frequency bands positioning at distances of ±ω_m away from the carrier frequency, which allows for polarization transfers from ¹⁵N to ¹³C in these two frequency bands. While the effective RF amplitude applied on these two frequency bands is just about half of the maximum RF amplitude ${\omega }_{1\text{C}}^{max}$.

3. Results and discussion

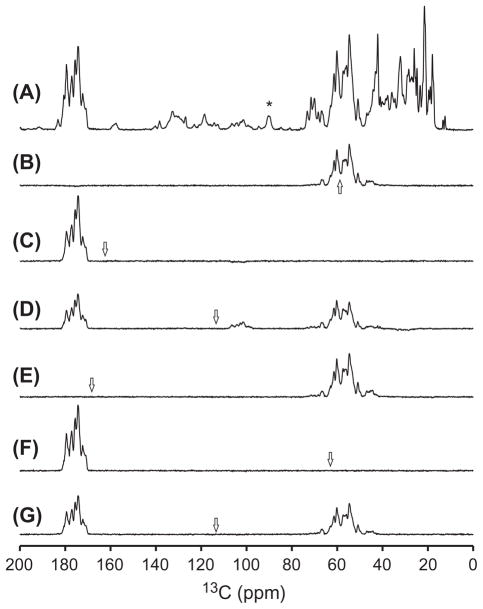
Fig. 2 shows the one-dimensional (1D) ¹³C spectra of the GB1 sample spinning at 11 kHz recorded under different N → C polarization conditions. With the direct CP from ¹H to ¹³C, all ¹³C resonances were observed, as shown in Fig. 2A. Fig. 2B and C show the SPECIFIC CP spectra using the rectangular DCP scheme (e.g. Fig. 1I) with the selective polarization pathway from ¹⁵N to ¹³Cα and ¹³C′, respectively. In these experiments, the ¹³C carrier frequency was set closely to either Cα or C′ region and its RF amplitude was chosen to be low in order to achieve the required selectivity. The efficiency for these SPECIFIC CP experiments was ~50% as compared to the direct CP from ¹H to ¹³C. If the ¹³C carrier frequency was set to the mid way between the Cα and C′ regions, the rectangular DCP experiment could also select both the ¹³Cα and ¹³C′ region simultaneously with a carefully adjusted RF amplitude [13,30,51], as shown in Fig. 2D. However, both simulations (not shown) and experiments indicate that higher ¹³C RF amplitude is needed for such a dual-band selectivity. Unfortunately, using the higher RF amplitude compromises the selectivity. As can be seen in Fig. 2D, small aliphatic carbon resonances (from 15 to 40 ppm), as well as the spinning sidebands at around 100 ppm, appear to be visible. Moreover, for the glycine ¹³Cα region (~42 ppm), the signal intensities seem to be much smaller than that in the SPECIFIC CP spectrum. The efficiency for this dual-band selectivity was ~34%, as compared to the spectrum in Fig. 2A.

Fig. 2.

1D ¹³C CP/MAS spectra of uniformly ¹³C,¹⁵N-labeled GB1 protein: (A) ¹³C spectrum directly polarized from ¹H. The asterisk indicates the signal of a spacer used to provide a better sealing of the rotor. (B–G) Double cross polarized ¹³C spectra using different N → C polarization conditions, normalized with the spectrum in (A) to illustrate their polarization efficiency. The arrows in the spectra indicate the ₁₃C carrier position in the experiments. The single-band selective SPECIFIC CP NCA (B) using ω_1N = 9.0 kHz with 10% tangent ramp and ω_1C = 3.0 kHz, and NCO (C) spectra using ω_1N = 7.0 kHz with 15% tangent ramp and ω_1C = 4.4 kHz. The dual-band rectangular DCP ¹³C spectrum (D) using ω_1N = 7.0 kHz with 11% tangent ramp and ω_1C = 16.0 kHz. The NCA (E) and NCO (F) spectra using the sine modulated ¹³C RF field with the amplitude of ${\omega }_{1\text{C}}^{max}=6.0\text{kHz}$ and ω_m = 16.667 kHz and ω_1N = 9.0 kHz with 10% and 17% tangent ramp, respectively. The dual-band selective ¹³C smDCP spectrum (G) using the sine modulated ¹³C RF field with the amplitude of ${\omega }_{1\text{C}}^{max}=6.0\text{kHz}$ and ω_m = 8.889 kHz and ω_1N = 9.0 kHz with 13% tangent ramp. The nominal RF amplitudes were calculated assuming a fine linearity of the Varian linear amplifier, which should have an accuracy of 0.5 kHz. In all experiments, 64 transients were used to accumulate the signals with a recycle delay of 3.5 s.

On the other hand, for the sine modulation scheme, even if the ¹³C carrier is set far away from the targeted region, the modulation effectively compensates the carrier offset, such that low RF amplitude can be used to achieve the needed selectivity. As shown in Fig. 2E and F, the ¹³C carrier frequency was set to ±16.667 kHz away from the Cα and C′ regions, respectively. With the sine modulation frequency of 16.667 kHz and a low ¹³C RF amplitude of 6.0 kHz, the Cα and C′ resonances were selectively polarized. As shown in the figures, the smDCP spectra are almost identical to their respective SPECIFIC CP spectra, with an efficiency of ~50% as compared to the spectrum in Fig. 2A. This implies that both frequency bands induced by the sine modulation in either side of the carrier frequency can be used for the efficient N → C polarization transfer. When the ¹³C carrier was set to the mid way between the Cα and C′ regions and the modulation frequency matched 8.889 kHz (half of the distance between the Cα and C′ regions), both the ¹³Cα and ¹³C′ regions were selected simultaneously with the efficiency of 37%, as shown in Fig. 2G. Apparently, the selectivity was comparable with that in the SPECIFIC NCO and NCA experiments, while the unwanted signals appearing in Fig. 2D was not observed in the spectrum, owing to the use of the low ¹³C RF amplitude.

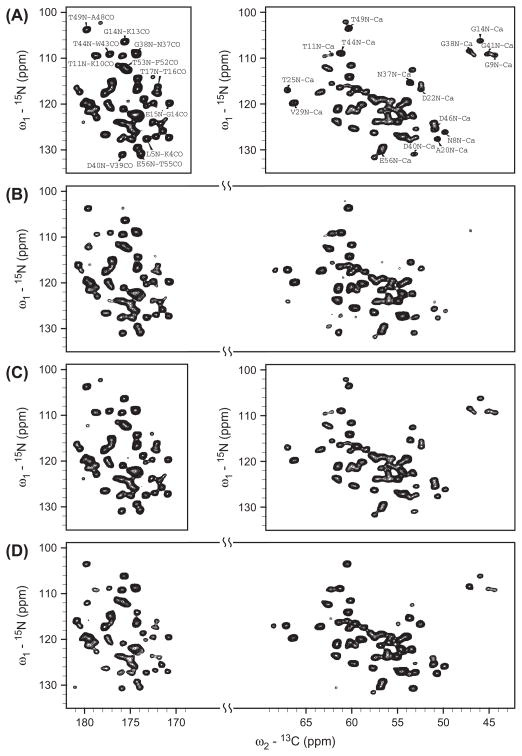
Fig. 3 shows the 2D ¹⁵N–¹³C heteronuclear correlation spectra of the uniformly ¹³C,¹⁵N-labeled GB1 under different polarization conditions. Fig. 3A shows the SPECIFIC NCO (left) and NCA (right) spectra recorded in the separate experiments where the ¹³C carrier frequency was set closely to the C′ and Cα regions, respectively. Since our sample was prepared at pH 8.0, different from pH 5.5 used in the GB1 sample preparation in the literature [52], the protein’s nano-crystalline form might be different. Thus, it is not surprising that the GB1 samples at different pHs gave rise to slightly different resonance patterns in the NCO and NCA spectra. However, their spectral resolution in both ¹³C and ¹⁵N dimensions are comparable [52], confirming that our sample was well prepared. It is worth noting that the slight difference in the resonance patterns resulting from the sample preparations should not affect any conclusion derived in this paper. Fig. 3A shows some partial assignments. Fortunately many resonances could be recognized based on the GB1 assignments as reported in the literature[53], despite the fact that there exist some additional peaks, such as the ones near the T49N-Cα and T49N-A48CO resonances. Fig. 3B shows the dual-band ¹⁵N–¹³C′/¹³Cα rectangular DCP spectrum using the rectangular ¹³C RF field during the N → C contact. Overall, the ¹⁵N–¹³C resonance patterns are similar to their respective SPECIFIC NCO and NCA spectra in Fig. 3A. However, some resonances such as the Gly ¹⁵N–¹³Cα resonances (G9N–Cα, G14N–Cα, G38N–Cα, and G41N–Cα) become very weak, while other resonances that did not appear in the SPECIFIC CP spectra started to show up in the spectrum (such as the peak in the left side of the T25N–Cα resonance), implying that the selectivity over the dual bandwidths is hardly uniform, which was also seen in 1D spectrum (e.g. Fig. 2D). It is worth noting that additional cross-peaks around (115 ppm, 103 ppm) and (141 ppm, 41 ppm) (not shown in the spectrum) should belong to the sidebands of ¹³C′ and ¹⁵N and to the folded-in aliphatic ¹³C and ¹⁵N in sidechains. Thus, the selectivity for the dual-band rectangular DCP is poor owing to the use of the required large ¹³C RF amplitude during the N → C contact.

Fig. 3.

2D ¹⁵N–¹³C heteronuclear correlation spectra of uniformly ¹³C,¹⁵N-labeled GB1 protein using different N → C polarization conditions. (A) Single-band SPECIFIC ¹⁵N–¹³Cα (Right) and ¹⁵N–¹³C′ (Left) spectra recorded in two separate experiments with the same experimental parameters as in Fig. 2B and C, respectively. (B) Dual-band rectangular DCP ¹⁵N–¹³Cα/¹³C′ spectrum using the same parameters as in Fig. 2D. (C) Single-band selective ¹⁵N–¹³Cα (Right) and ¹⁵N–¹³C′ (Left) smDCP spectra recorded in two separate experiments with the same experimental conditions as in Fig. 2E and F, respectively. (D) Dual-band selective ¹⁵N–¹³Cα/¹³C′ smDCP spectrum using the same parameters as in Fig. 2G. The spectra were processed by nmrPipe [54] and plotted with Sparky [55]. In all experiments, 40 transients were used to accumulate the signals for each t₁ increment with a recycle delay of 3.5 s.

Fig. 3C shows the single-band ¹⁵N–¹³C′ (left) and ¹⁵N–¹³Cα (right) smDCP spectra using the sine modulated ¹³C RF amplitude during the N → C contact. It can be clearly noted that these spectra are almost identical to those in Fig. 3A, except for the one appearing at (112 ppm and 179 ppm) (below the T11 N-K10CO resonance), again implying that the frequency bandwidths induced by the sine modulation in both sides of the carrier frequency can be used for selective N → C polarization transfer. Fig. 3D shows the dual-band selective ¹⁵N–¹³C′/¹³Cα smDCP spectrum when the two frequency bandwidths induced by the sine modulation fell into the C′ and Cα regions simultaneously. Clearly, the resonance patterns in both the ¹⁵N–¹³C′ and ¹⁵N–¹³Cα regions are almost the same as in the single-band selective ¹⁵N–¹³C′and ¹⁵N–¹³Cα spectra as shown in Fig. 3A and C, despite the fact that a few additional peaks, such as (130 ppm and 180 ppm), (130 ppm and 61 ppm) and (118 ppm and 68 ppm), start to appear or gain in intensity. However, the Gly resonances, which almost disappeared in Fig. 3B, were as intensive as in the single-band selective ¹⁵N–¹³C′ and ¹⁵N–¹³Cα spectra as shown in Fig. 3A and C. On the other hand, those unwanted resonances appearing at around (115 ppm, 103 ppm) and (141 ppm, 41 ppm) in Fig. 3B completely disappeared in the dual-band selective ¹⁵N–¹³C′/¹³Cα smDCP spectrum. Thus, it is concluded that this sine modulation scheme provides an excellent selectivity.

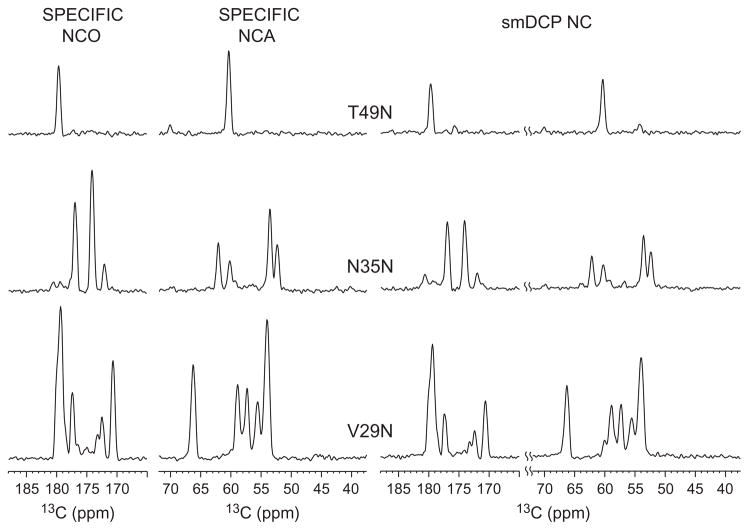
Fig. 4 shows the three 1D slices taken along T49N (Top), N37N (Middle), and V29N (Bottom) from the 2D SPECIFIC NCO/NCA spectra in Fig. 3A and from the smDCP NC spectrum in Fig. 3D, respectively. From their relative intensities, it can be noticed that the signal-to-noise (S/N) ratio for the dual-band selective smDCP is about 68–74% of that for the SPECIFIC NCO/NCA, which is consistent with the observation of the efficiency in the 1D spectra (c.f. Fig. 2). Therefore, the S/N for a single dual-banded smDCP spectrum (in the same overall time by doubling the number of scans) should be comparable to the two separate SPECIFIC NCO/NCA spectra. Our experimental result is beyond what is expected from the fact that the S/N for the dual-banded smDCP is considered to be half of that for SPECIFIC CP since the ¹⁵N magnetization is transferred to both carbon sites in the former scheme as compared to only one site in the latter scheme. However, one has to realize that such an expectation holds only when the ¹⁵N magnetization is completely transferred to the ¹³C and/or there exhibits the same spin dynamics during the N → C CP. Due to the fact that the C–N dipolar coupling is very small (~ a few kHz), the polarization transfer rate from N to C is rather slow. A few millisecond CP contact time (e.g. 5 ms in our experiments) can hardly transfer the ¹⁵N magnetization completely to ¹³C. On the other hand, the spin dynamics during the N → C CP may be different in these two schemes since they exhibit different spin systems during CP (N–C for SPECIFIC CP and C–N–C for the dual-banded smDCP). Such a difference might lead to different spin dynamics, as been observed in different ¹H–S systems [56–58].

Fig. 4.

1D slices taken from the SPECIFIC NCO/NCA spectra in Fig. 3A and from the smDCP NC spectrum in Fig. 3D along T49 N (Top), N37N (Middle), and V29N (Bottom).

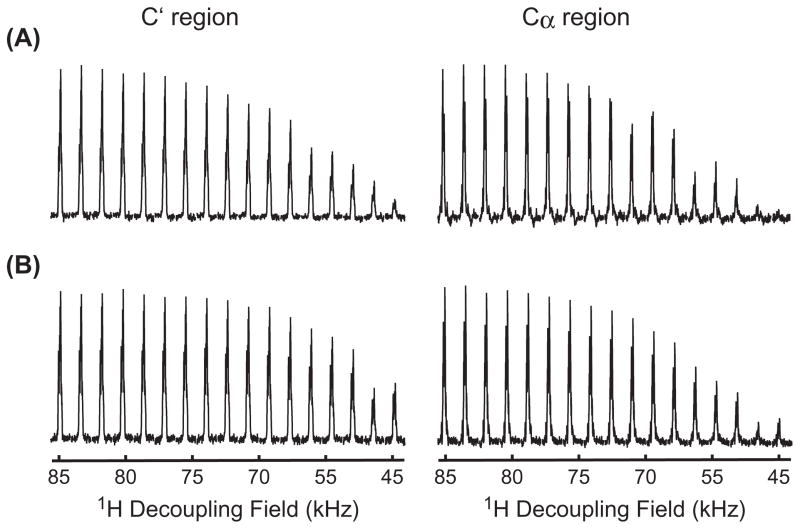
In the DCP experiments, low ¹³C RF amplitude in the N → C polarization transfer will relax the demand on the ¹H decoupling field during the N → C contact. In our experiments, the maximum ¹³C RF amplitude ${\omega }_{1\text{C}}^{max}$ used in the dual-band selective smDCP experiments (e.g. Fig. 2G) was about one-third of that used in the dual-band rectangular DCP experiments (e.g. Fig. 2D). Fig. 5 shows the dependence of the N → C polarization efficiency as a function of the applied ¹H decoupling power during the N → C contact. As the ¹H decoupling power decreasing from 85 to about 71 kHz, the polarization efficiency from N → Cα dropped to about 60% and 80% for the rectangular and sine modulated DCP schemes, respectively, while the efficiency from N → C′ decreased to ~75% and 90% in their respective spectra. It appears that the ¹H decoupling power is more influential on the Cα carbons, probably owing to the strength of dipolar interactions between ¹H and ¹³C as well as the difference between the applied ¹H decoupling and the ¹³C RF amplitude during the N → C contact. A large difference between the ¹H decoupling and ¹³C RF amplitude during the N → C contact is needed to provide sufficient mismatch between the ¹H and ¹³C spins to avoid potential spin exchange between the two spins, especially when they possess a stronger dipolar coupling. Therefore, this might be the reason why the ¹⁵N → ¹³Cα polarization efficiency for the Gly residues was much worse in the dual-band rectangular DCP (e.g. Fig. 3B) than in the dual-band smDCP experiments (e.g. Fig. 3D). Indeed, the former experiment required five times higher ¹³C RF amplitude than the latter one under the same ¹H decoupling power of 83 kHz during the N → C contact.

Fig. 5.

Dependence of the N → C polarization efficiency as a function of the ¹H decoupling amplitude during the N → C contact time in different N → C polarization schemes. (A) The dual-band rectangular DCP using the parameters in Fig. 2D. (B) The dual-band smDCP using the parameters in Fig. 2G.

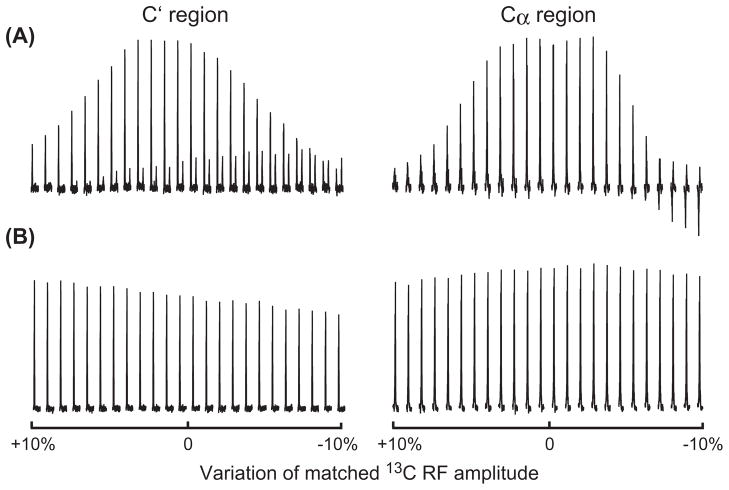
It had been reported that the parameters in the DCP experiments were sensitive to experimental settings, such as MAS speed, frequency offset and RF fields [33,38,39]. The influence of instability of ¹³C RF-field on the N → C polarization efficiency is also investigated for the dual-band polarization transfers, as shown in Fig. 6. It can be seen in Fig. 6A that the ¹⁵N → ¹³Cα and ¹⁵N → ¹³C′ polarization efficiencies for the rectangular DCP scheme suffer severely from the variation of ¹³C RF amplitude and decrease to about 30– 50% with about 10% variation. On the other hand, for the smDCP scheme the efficiency from ¹⁵N → ¹³Cα was just slightly affected by the ¹³C RF variation, while about 70% efficiency from ¹⁵N → ¹³C′ was preserved. Thus, there is an advantage to use this sine modulation scheme in long duration experiments.

Fig. 6.

Instability effect of ¹³C RF field on the N → C polarization efficiency in different schemes. The ¹³C RF amplitude was varied by ±10% of the optimized values (set to 0) in Fig. 2D and G.

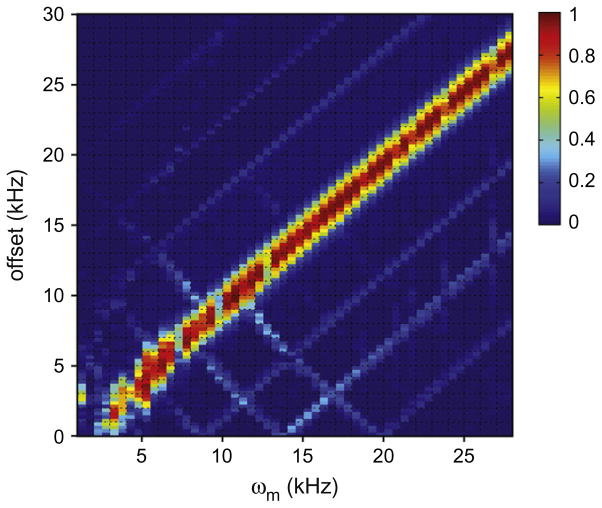
Fig. 7 shows the simulated selectivity for the sine modulation scheme (e.g. Fig. 1II) as a function of offset and modulation frequency ω_m. In the simulations, the experimental parameters of ω_1N = 9 kHz, ${\omega }_{1\text{C}}^{max}=6\text{kHz}$, and the MAS rate of 11 kHz were used. Clearly, the frequency selective bandwidth (i.e. the offset range within which the polarization efficiency is above 60%) was about ω_m ± 2 kHz, apparently independent of the spinning rate. In other words, the selective bandwidth is about ±2 kHz at distances of ±ω_m away from the carrier frequency. This bandwidth is independent of spinning rate but depends on the RF amplitude ${\omega }_{1\text{C}}^{max}$ used in the experiments. For a better selectivity, low-power RF amplitude is always preferable. Our simulations (not shown here) suggest that the dual-banded smDCP scheme should be effective at the magnetic field B₀ up to 18.8 T with the spinning rate of 25 kHz. However, at very high fields where the chemical shift anisotropy (CSA) interactions become significant, there is a potential that the efficiency and selectivity could be compromised when using low-power RF amplitude which becomes unable to spin-lock the magnetization during the N → C CP. It has been demonstrated recently [60] that low-power symmetry-based band-selective sequences appear to be an effective approach for applications in high fields and fast sample spinning.

Fig. 7.

Simulated selectivity of the sine modulated scheme (e.g. Fig. 1II) as a function of offset and modulation frequency ω_m. The SPINEVOLUTION [59] was used for the simulations. For simplicity, a constant ¹⁵N RF-field was utilized, and the spin system was ¹⁵N–¹³C, with a distance of r_C–N = 1.448 Å. The chemical shift parameters for ¹³C were δ_iso = 0 ppm, δ_aniso = 24 ppm, η = 0.92; for ¹⁵N, δ_iso = 0 ppm, δ_aniso = 100 ppm, η = 0.8. In the simulations, ω_1N = 9 kHz, ${\omega }_{1\text{C}}^{max}=6\text{kHz}$, and the MAS rate of 11 kHz were used. The maximum intensity in this plot was normalized to 1.

4. Conclusion

We have demonstrated that sinusoidal modulation of the ¹³C RF amplitude during the second N → C cross polarization in double cross polarization (DCP) MAS NMR spectroscopy provides an effective spin-lock field in two selective frequency bands in either side of the ¹³C RF carrier frequency, allowing for simultaneous polarization transfers from ¹⁵N to ¹³C in those two selective frequency bands. When the two frequency bands fall into the C′ and Cα regions, the dual-band selective heteronuclear polarization transfer from ¹⁵N to both ¹³C′ and ¹³Cα can be achieved simultaneously in one experiment, rather than in two separate SPECIFIC NCO and NCA experiments or in a low-sensitive CANCO experiment, which is useful for establishing the backbone connectivity between two sequential residues in protein structural elucidation. It should be recognized that this information about the sequential Cα[i]–N[i]–C′[i–1] topology alone is not sufficient to obtain sequential resonance assignments. It has to be combined with other 2D or 3D experiments such as NCACX/NCOCX and/or ¹³C–¹³C correlation experiments. With the ability of selecting both the backbone Cα and C′ carbons, some elaborate 2D or 3D experiments could be designed to simplify crowded resonances typically observed in ¹³C–¹³C correlation spectra of biological samples being studied and to help assigning resonances, especially when combined with specific labeling approaches such as glycerol labeling strategy. For the dual-band selective polarization transfer, this new scheme greatly relaxes the demand on both ¹³C and ¹H decoupling amplitudes. As compared to standard DCP experiments, this sine modulated scheme is also less sensitive to the instability of the ¹³C RF field. Moreover, such a modulation could also be applicable for dual-band selective heteronuclear polarization transfer between other spin pairs, as mentioned by Baldus et al. [31], such as ¹⁹F, ³¹P and even ¹H in paramagnetic systems, with the use of a moderate RF amplitude when applied to the spin that has a large chemical shift distribution, especially under fast MAS condition [45].