Abstract
Utilizing multiple biomarkers is increasingly common in epidemiology. However, the combined impact of correlated exposure measurement error, unmeasured confounding, interaction, and limits of detection (LODs) on inference for multiple biomarkers is unknown. We conducted data-driven simulations evaluating bias from correlated measurement error with varying reliability coefficients (R), odds ratios (ORs), levels of correlation between exposures and error, LODs, and interactions. Blood cadmium and lead levels in relation to anovulation served as the motivating example, based on findings from the BioCycle Study (2005–2007). For most scenarios, main-effect estimates for cadmium and lead with increasing levels of positively correlated measurement error created increasing downward or upward bias for OR > 1.00 and OR < 1.00, respectively, that was also a function of effect size. Some scenarios showed bias for cadmium away from the null. Results subject to LODs were similar. Bias for main and interaction effects ranged from −130% to 36% and from −144% to 84%, respectively. A closed-form continuous outcome case solution provides a useful tool for estimating the bias in logistic regression. Investigators should consider how measurement error and LODs may bias findings when examining biomarkers measured in the same medium, prepared with the same process, or analyzed using the same method.
Keywords: biomarkers, cadmium, environmental epidemiology, lead, measurement error; reliability
Accurately identifying health effects from chemical exposures among populations is essential, as chemical exposures are widespread and discordant conclusions complicate risk assessment. Although issues concerning exposure timing are increasingly being addressed in the environmental epidemiologic literature, the biomarker measurement process and limits of detection (LODs) are often overlooked as sources of bias. Assessing interactions between biomarkers of chemical exposure is increasingly common, yet bias in interaction parameters from correlated error has not been quantified. Such correlations could arise between chemical exposures stemming from similar sources or subject to a common cause, or during the measurement process if the biomarkers were measured in the same medium and were subject to LODs.
Imperfect measurement complicates inference (1). With 1 continuous biomarker and independent random measurement error, effect estimates are usually biased toward the null (2, 3). Independent random measurement error in the context of confounding between exposures can induce bias in either direction (4). Less well studied is correlated exposure measurement error, which may occur when biomarkers are measured using the same collection, preparation, and measurement methods. When only 1 variable is truly associated with the outcome, correlated measurement error between exposure and a confounder tends to induce less bias than correlation between exposures (5), and it can bias results upward when odds ratio (OR) > 1.00 and downward when OR < 1.00 (6). Measurements are limited by values below the laboratory LOD. Appropriate substitution for values below the LOD can minimize bias (7–10). Bias in settings with multiple correlated variables subject to LODs, which are measured with correlated error, has yet to be explored.
The effects of varying levels of correlation between covariates, interaction, and circumstances subject to LODs are unknown. Therefore, we assessed bias in main effects and interactions between biomarkers under data-driven scenarios. Our example was motivated by the BioCycle Study (11) and is specific to cadmium and lead exposures measured in blood in relation to anovulation (12). This example is broadly applicable to settings with binary outcomes, and we provide the closed-form solution for linear outcomes.
MATERIALS AND METHODS
Motivation
Evidence suggests that exposure to cadmium (13, 14) and lead (15, 16) may affect ovulation. Among 259 healthy premenopausal women in the BioCycle Study (2005–2007), we observed (nonsignificant) associations between elevated blood levels of cadmium and lead and anovulation (OR = 1.29 (95% confidence interval: 0.20, 8.47) and OR = 1.20 (95% confidence interval: 0.62, 2.34), respectively) (12). Could measurement error have biased these results? We sought to describe the effect of correlated measurement error and LODs, with and without effect modification, on the association between cadmium and lead exposures and anovulation via simulation. Cadmium and lead levels were simulated using the measured mean and variance from the BioCycle Study. Cadmium and lead levels measured in the BioCycle Study were approximately lognormally distributed, had arithmetic means of 0.34 µg/L and 1.02 µg/dL and variances of 0.05 and 0.40, and were positively correlated (Pearson's ρ = 0.12; P = 0.04). The observed correlation is a function of the underlying true exposure correlation as well as measurement error correlation. Our simulations explored a variety of correlation scenarios. The prevalence of anovulation was 8%.
Directed acyclic graph
The causal relation between 2 continuous biomarkers X1 and X2, such as cadmium and lead; measured levels of those biomarkers,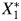 
and 
; and 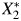a binary outcome Y, such as anovulation, is expressed in the directed acyclic graph (DAG) shown in Web Figure 1 (available at http://aje.oxfordjournals.org/). DAGs are useful tools for describing the structure of measurement error (17). True cadmium and lead exposure levels are associated via an antecedent, unmeasured confounding factor (U1), inducing correlation, ρx, between X1 and X2. Results pertaining to ρx will be applicable to bias in situations with unmeasured confounding. While the exposures to environmental toxicants may cause the outcome, we make inference using measured exposures. The measurement process induces error, and we obtain 
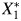and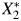 
, not X1 and X2. Because cadmium and lead are measured from the same specimen collection using the same preparation methods and the same equipment, the measurement process may introduce additional correlation. U2 represents the measurement error process, creating measurement error correlation, ρε, between 
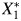and 
.
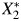Measurement error
True biomarker values X are often measured with some error, ε, such that the measured biomarker values can be expressed as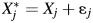 
, where j indicates the biomarker. Classical, normally distributed, mean-zero measurement error was assumed for εj.
We characterized the relative magnitude of measurement error by means of the reliability coefficient, R, in terms of biomarker and error variances, such that
 |
An R of 1 indicates a biomarker with no measurement error, while an R close to 0 is almost entirely error. Plausible values for R between 0.5 and 1.0 were based upon laboratory estimates and literature review (18, 19). Measurement error variances for cadmium and lead were a function of their respective variances and R,
 |
Limit of detection
Biomarker measurements may be censored by LODs, leading to missing values. Lead and cadmium in the BioCycle Study were subject to LODs. The laboratory-reported LODs were 0.20 μg/L for cadmium (25% < LOD) and 0.25 μg/dL for lead (0% < LOD). Because nearly all lead values were above the LOD in simulations, we simulated a case where the lead LOD was 0.50 μg/dL, resulting in approximately 25% of values being less than the LOD.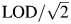 
was used for values below the LOD, to reflect common practice (9).
Simulations
We conducted a simulation study to evaluate bias to inference under several data-driven scenarios of varying sample sizes, R's, odds ratios, ρx, and ρε. For each realization of the data, vectors of true cadmium (Cd) and lead (Pb) blood levels,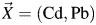 
, were simulated, assuming lognormal distributions via component-wise exponentiating vectors generated from a multivariate normal distribution,
 |
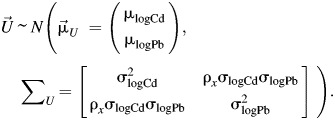Parameter values were chosen on the basis of observed levels in the BioCycle Study, with consideration given to varying levels of measurement error,
 |
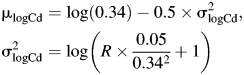and
 |
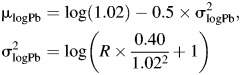(see Web Appendix for details). We constructed cadmium and lead exposures measured with multivariate normally distributed error, such that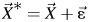 
, where
 |
, and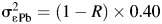 
. We applied LODs to the simulated measured exposure levels. Application of LODs to our previously simulated values resulted in
 |
Levels of the correlations ρX and ρε varied between −0.6 and 0.6 by increments of 0.1, independently, for a total of 169 different combinations (132 = 169). Sample sizes ranged from 100 to 1,000. For parsimony, results for n = 200 are presented. Results reflect a mean of 5,000 iterations for each combination of parameters. Findings for lead and cadmium apply to other lognormally distributed biomarker measurements. Cadmium had a smaller mean and wider variance, with approximately 25% of values below the LOD, while lead had a larger mean and smaller variance and was not affected by values below the LOD.
Models for anovulation
A range of effect sizes for the relation of the two exposure biomarkers, cadmium and lead, with anovulation was simulated using true odds ratios of 0.75, 1.00, 1.25, and 1.75. We used 3 models to estimate the odds of anovulation for main effects only and where an interaction term was 1.5 times the log odds of the main effects. We added measurement error as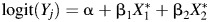 
for main effects and 
with an interaction. LODs and measurement error were added as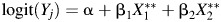 
for main effects and 
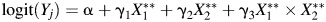with an interaction.
Simulation results
We quantified bias as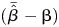 
and relative percent bias as 
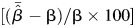to describe how estimates deviated from the truth. Mean squared error (MSE), calculated as 
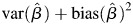, described variability in our results. Relative percent bias and MSE were determined for each of 3 models with and without an interaction: 1) no measurement error, 2) measurement error, and 3) LOD with measurement error. Simulations were performed with R statistical software (R Foundation for Statistical Computing, Vienna, Austria, 2010).
RESULTS
We present results with minimal, moderate, and severe measurement error, corresponding to R values of 0.95, 0.80, and 0.50, and for odds ratios of 0.75 and 1.75, because minimal bias was observed for OR = 1.00 and bias for OR = 1.25 was comparable to that for OR = 0.75, though in the opposite direction. Notably with regard to interpretation, negative relative percent bias indicates bias toward OR = 1.00 (β = 0) for both OR = 0.75 (true β = −0.29) and OR = 1.75 (true β = 0.56), whereas the corresponding absolute bias would be upward and downward, respectively.
Main-effects models
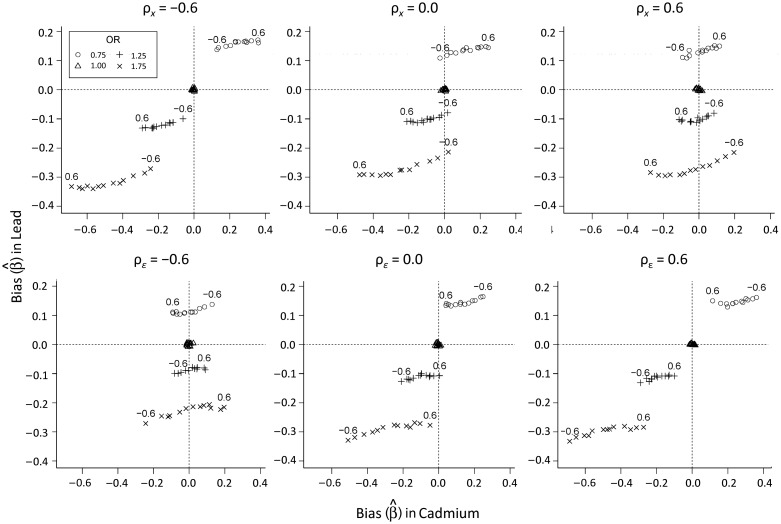
Minimal bias was observed at low levels of measurement error (R = 0.95) (Table 1). Bias and MSE increased as the magnitude of measurement error increased (R = 0.80) (Web Table 1). Bias and MSE were highest under severe measurement error (R = 0.50), with most cases having negative relative percent bias (Table 2). Figure 1 demonstrates that the bias in effect estimates observed in our simulations (in both magnitude and direction) is a function of both ρx and ρɛ, as well as the marginal exposure distributions. Figure 1 and the tables demonstrate that the magnitude of bias varied by levels of ρx and ρɛ, with the greatest levels of bias occurring with the greatest levels of measurement error (R = 0.50), and that the direction of the bias could be affected for cadmium but not for lead. Under those conditions, strongly positively correlated biomarkers (ρx = 0.6) with OR = 1.75 were biased downward for ρɛ > 0 and upward for ρɛ < 0 for cadmium, while for lead, bias from OR = 1.75 was consistently downward. For ρx = −0.6 (upper left panel in Figure 1), bias from OR = 1.75 was downward, with minimal bias for ρɛ = −0.6, increasing in magnitude as ρɛ increased to 0.6. The lower middle panel of Figure 1 shows that uncorrelated errors (ρε = 0) led to downward bias for OR = 1.75, with bias increasing in magnitude as ρx increased for cadmium but not for lead. The biases for OR = 0.75 and OR = 1.25 displayed the same patterns for lead and cadmium with regard to ρɛ but were of a lesser magnitude and in the opposite directions for OR = 0.75. When ρε = 0 and ρx = −0.6, the downward bias was decreased, with estimates of the bias of lead remaining relatively unchanged. The effect of bias from uncorrelated measurement error (ρε = 0) on uncorrelated biomarkers (ρx = 0) is shown in Tables 1 and 2. The percent bias increased with increasing measurement error and was generally lower than bias for correlated biomarkers and errors.
Table 1.
Relative Percent Bias (and Mean Squared Error) in the Associations Between Cadmium and Lead Levels and Anovulation Under Low Levels of Measurement Error (R = 0.95) for OR = 0.75 and OR = 1.75 in Main-Effects Models (n = 200), With Varying Levels of Correlation Between Biomarkers and Error Correlation, BioCycle Study, 2005–2007
| ρɛ = −0.6 |
ρɛ = 0.0 |
ρɛ = 0.6 |
||||
|---|---|---|---|---|---|---|
| Cadmium | Lead | Cadmium | Lead | Cadmium | Lead | |
| OR = 0.75 | ||||||
| ρx = −0.6 | 2.82 (0.55)a | −1.12 (0.08) | −10.04 (0.56) | −3.97 (0.07) | −22.44 (0.55) | −5.12 (0.07) |
| ρx = −0.2 | 10.39 (0.46) | −5.53 (0.06) | −1.84 (0.47) | −3.62 (0.06) | −18.97 (0.44) | −3.69 (0.06) |
| ρx = 0.0 | 14.53 (0.46) | 3.53 (0.07) | −2.14 (0.47) | 1.19 (0.06) | −12.05 (0.46) | −3.37 (0.06) |
| ρx = 0.2 | 14.72 (0.47) | 1.13 (0.06) | 7.11 (0.46) | −0.28 (0.06) | −13.30 (0.46) | −2.01 (0.07) |
| ρx = 0.6 | 31.86 (0.70) | −6.58 (0.08) | 7.17 (0.65) | −5.82 (0.09) | 7.36 (0.69) | −3.46 (0.09) |
| OR = 1.75 | ||||||
| ρx = −0.6 | 1.60 (0.58) | −2.62 (0.09) | −5.72 (0.59) | −3.43 (0.08) | −24.05 (0.58) | −7.65 (0.08) |
| ρx = −0.2 | 3.99 (0.48) | −0.34 (0.07) | −7.93 (0.48) | −4.18 (0.07) | −11.89 (0.73) | −2.74 (0.07) |
| ρx = 0.0 | 6.49 (0.47) | −0.87 (0.07) | −3.38 (0.50) | −2.89 (0.07) | −5.55 (0.49) | −2.93 (0.07) |
| ρx = 0.2 | 4.34 (0.51) | −1.42 (0.07) | −1.98 (0.52) | −3.02 (0.07) | −7.38 (0.50) | −3.27 (0.07) |
| ρx = 0.6 | 12.38 (0.70) | −5.40 (0.10) | 8.97 (0.73) | −2.51 (0.11) | 0.65 (0.75) | −4.06 (0.10) |
Abbreviation: OR, odds ratio.
a Numbers in parentheses, mean squared error.
Table 2.
Relative Percent Bias (and Mean Squared Error) in the Associations Between Cadmium and Lead Levels and Anovulation Under High Levels of Measurement Error (R = 0.50) for OR = 0.75 and OR = 1.75 in Main-Effects Models (n = 200), With Varying Levels of Correlation Between Biomarkers and Error Correlation, BioCycle Study, 2005–2007
| ρɛ = −0.6 |
ρɛ = 0.0 |
ρɛ = 0.6 |
||||
|---|---|---|---|---|---|---|
| Cadmium | Lead | Cadmium | Lead | Cadmium | Lead | |
| OR = 0.75 | ||||||
| ρx = −0.6 | −51.74 (0.68)a | −47.39 (0.12) | −105.71 (0.66) | −58.64 (0.12) | −129.57 (0.73) | −54.97 (0.11) |
| ρx = −0.2 | −8.47 (0.54) | −36.50 (0.09) | −56.85 (0.50) | −51.24 (0.10) | −97.04 (0.64) | −50.49 (0.10) |
| ρx = 0.0 | 3.66 (0.49) | −37.63 (0.08) | −55.53 (0.47) | −46.75 (0.09) | −83.74 (0.60) | −50.55 (0.10) |
| ρx = 0.2 | 11.39 (0.49) | −36.41 (0.08) | −28.49 (0.47) | −44.78 (0.09) | −75.08 (0.59) | −49.19 (0.11) |
| ρx = 0.6 | 34.54 (0.47) | 36.71 (0.08) | −3.53 (0.50) | −44.73 (0.10) | −42.04 (0.72) | −51.26 (0.08) |
| OR = 1.75 | ||||||
| ρx = −0.6 | −37.85 (0.75) | −47.27 (0.22) | −93.44 (1.02) | −59.90 (0.29) | −126.10 (1.43) | −58.47 (0.27) |
| ρx = −0.2 | −5.70 (0.51) | −39.12 (0.16) | −63.15 (0.70) | −52.97 (0.23) | −98.69 (1.07) | −53.22 (0.24) |
| ρx = 0.0 | 4.61 (0.50) | −40.78 (0.17) | −44.53 (0.57) | −50.08 (0.22) | −88.62 (0.97) | −49.48 (0.22) |
| ρx = 0.2 | 12.26 (0.47) | −37.89 (0.15) | −36.27 (0.51) | −47.99 (0.20) | −79.82 (0.93) | −48.01 (0.21) |
| ρx = 0.6 | 36.71 (0.54) | −39.66 (0.16) | −8.95 (0.48) | −48.39 (0.21) | −49.88 (0.82) | −50.54 (0.25) |
Abbreviation: OR, odds ratio.
a Numbers in parentheses, mean squared error.
Figure 1.
Bias in the associations between cadmium and lead levels and anovulation under high levels of measurement error (R = 0.50) in main-effects models, with varying levels of true correlation between biomarkers (ρx) and error correlation (ρɛ), BioCycle Study, 2005–2007. The upper 3 panels show fixed levels of ρx and ρɛ values varying from −0.6 to 0.6, while the lower 3 panels show fixed levels of ρɛ and varying ρx values. (OR, odds ratio).
The direction and degree of bias depended upon levels of error correlation (Figure 1). Strongly positively correlated errors (ρε = 0.6) resulted in bias toward the null, which could cause a statistically significant finding to become nonsignificant, as shown in the lower right panel of Figure 1. For cadmium, downward bias was observed for OR < 1.00 and upward bias for OR > 1.00, with positively correlated or uncorrelated biomarkers (ρx = 0.6 or ρx = 0.0) and negatively correlated measurement error (ρɛ < 0).
These results show that bias in effect estimates for a dichotomous outcome is a function of the level of measurement error, R, and that the degree to which error correlations might play a role depends on the marginal distribution of the biomarkers. Evidence of the latter is that varying ρε had little to no effect on the bias of lead estimates but considerable effect on the bias of cadmium estimates. Lack of a closed-form solution for the bias here hinders us from making general statements regarding these relations. However, a similar scenario with a continuous outcome can further illustrate the relations between correlations and bias in effect estimates. Assume that Y in Web Figure 1 is a continuous outcome variable, while the remainder of the DAG is unchanged. Standard linear regression could be employed here rather than the logistic regression considered previously. The closed forms for effect estimates in standard linear regression will lead to a bias from the use of a measured exposure, X*, instead of the true exposure, X, that can be expressed as: Bias (β) = β − βt = [(cov(X) + cov(ε))−1 − (cov(X))−1]cov(X,Y) (details are provided in the Web Appendix). Using the same levels of exposure and effect size from the dichotomous cases above, this closed form for linear regression provides a reasonable approximation of the expected bias in a logistic framework from confounded effect estimates subject to correlated measurement error. Our simulation results are nearly identical to this closed-form solution (Web Figure 2). Researchers could quantify potential bias from correlated measurement error using this formula. This sensitivity analysis could be performed for a known or estimated amount of correlated measurement error through cov(ε) or for a range of potential levels and correlations of errors. Where it was previously possible to conduct sensitivity analyses to quantify effects of uncorrelated measurement error, this solution enables straightforward evaluation of similar cases with correlated exposure measures and errors.
Interaction models
Interaction models were substantially more biased than main effects. Minimal bias was observed with minimal error (R = 0.95) (Table 3). At moderate levels of measurement error (R = 0.80), bias and MSE were typically lowest for the main effects of lead, higher for cadmium, and highest for the interaction (Web Table 2). Under severe measurement error (R = 0.50), γ3 was almost exclusively strongly biased toward the null, possibly because of less compensation between the main effects and interaction (Table 4). MSE increased with increasing levels of error and correlation, with the highest MSEs observed for strong positively correlated errors.
Table 3.
Relative Percent Bias (and Mean Squared Error) in the Associations Between Cadmium and Lead Levels and Anovulation Under Low Levels of Measurement Error (R = 0.95) for OR = 0.75 and OR = 1.75 in Interaction Models (n = 200), With Varying Levels of Correlation Between Biomarkers and Error Correlation, BioCycle Study, 2005–2007
| ρɛ = −0.6 |
ρɛ = 0.0 |
ρɛ = 0.6 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Cadmium | Lead | Cadmium × Lead | Cadmium | Lead | Cadmium × Lead | Cadmium | Lead | Cadmium × Lead | |
| OR = 0.75 | |||||||||
| ρx = −0.6 | 43.49 (1.53)a | 11.52 (0.19) | −41.07 (2.29) | 37.30 (1.61) | 13.31 (0.20) | −60.46 (2.48) | 39.61 (1.70) | 12.48 (0.21) | −73.34 (2.61) |
| ρx = −0.2 | 18.53 (2.04) | 5.00 (0.24) | −4.57 (2.11) | 18.60 (2.11) | 4.35 (0.27) | 16.70 (2.34) | −1.97 (2.16) | −1.64 (0.25) | −10.50 (2.11) |
| ρx = 0.0 | 5.48 (2.21) | −0.23 (0.26) | 6.93 (1.94) | −22.97 (2.25) | −8.11 (0.27) | 17.31 (1.94) | −10.01 (2.22) | −2.91 (0.27) | 5.28 (1.94) |
| ρx = 0.2 | −24.71 (2.50) | −11.75 (0.29) | 33.49 (1.95) | −50.07 (2.42) | −19.20 (0.28) | 41.51 (1.90) | −57.74 (2.41) | −18.42 (0.28) | 36.46 (1.89) |
| ρx = 0.6 | −104.01(3.16) | −43.05 (0.37) | 83.17 (2.08) | −107.17(3.03) | −37.03 (0.34) | 76.57 (1.89) | −122.24 (3.08) | −45.46 (0.36) | 81.20 (1.94) |
| OR = 1.75 | |||||||||
| ρx = −0.6 | 37.68 (1.74) | 10.68 (0.23) | −40.89 (2.83) | 37.86 (1.84) | 12.19 (0.24) | −62.82 (3.17) | 37.06 (1.92) | 13.50 (0.25) | −82.50 (3.64) |
| ρx = −0.2 | 31.21 (2.34) | 8.10 (0.29) | 17.24 (2.59) | 25.99 (2.92) | 5.99 (0.28) | −26.63 (2.58) | 16.53 (2.28) | 6.77 (0.28) | −33.14 (2.63) |
| ρx = 0.0 | 8.16 (2.74) | 0.12 (0.34) | 2.43 (2.73) | −1.12 (2.62) | −2.37 (0.32) | −1.34 (2.60) | 7.11 (2.60) | −1.17 (0.33) | −8.58 (2.65) |
| ρx = 0.2 | −2.28 (2.97) | −5.16 (0.36) | 14.21 (2.73) | −22.55 (3.05) | −9.73 (0.36) | 15.51 (2.73) | −37.22 (2.96) | −14.02 (0.36) | 17.84 (2.63) |
| ρx = 0.6 | −38.03 (3.94) | −26.39 (0.49) | 46.98 (3.32) | −70.83 (4.11) | −34.56 (0.51) | 59.48 (3.44) | −94.69 (4.45) | −33.87 (0.52) | 58.84 (3.46) |
Abbreviation: OR, odds ratio.
a Numbers in parentheses, mean squared error.
Table 4.
Relative Percent Bias (and Mean Squared Error) in the Associations Between Cadmium and Lead Levels and Anovulation Under High Levels of Measurement Error (R = 0.50) for OR = 0.75 and OR = 1.75 in Interaction Models (n = 200), With Varying Levels of Correlation Between Biomarkers and Error Correlation, BioCycle Study, 2005–2007
| ρɛ = −0.6 |
ρɛ = 0.0 |
ρɛ = 0.6 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Cadmium | Lead | Cadmium × Lead | Cadmium | Lead | Cadmium × Lead | Cadmium | Lead | Cadmium × Lead | |
| OR = 0.75 | |||||||||
| ρx = −0.6 | 40.82 (1.65)a | −18.87 (0.20) | −108.39 (1.81) | −13.58 (1.68) | −32.17 (0.22) | −131.23 (2.08) | −26.00 (1.76) | −25.76 (0.22) | −147.37 (2.23) |
| ρx = −0.2 | 65.51 (1.81) | −12.37 (0.21) | −82.49 (1.64) | −3.28 (1.84) | −33.27 (0.23) | −95.22 (1.78) | −48.02 (1.99) | −32.78 (0.24) | −103.06 (1.81) |
| ρx = 0.0 | 59.88 (1.94) | −18.50 (0.23) | −62.26 (1.56) | −18.60 (1.91) | −40.99 (0.25) | −65.01 (1.58) | −58.81 (2.04) | −39.18 (0.26) | −83.52 (1.66) |
| ρx = 0.2 | 57.45 (2.03) | −22.64 (0.24) | −44.70 (1.48) | −20.32 (1.94) | −43.87 (0.26) | −50.02 (1.46) | −80.11 (2.12) | −49.69 (0.27) | −51.80 (1.39) |
| ρx = 0.6 | 49.87 (2.13) | −30.30 (0.26) | −19.74 (1.37) | −66.29 (2.13) | −64.91 (0.31) | 1.89 (1.34) | −112.22 (2.31) | −70.78 (0.32) | −8.58 (1.15) |
| OR = 1.75 | |||||||||
| ρx = −0.6 | 25.37 (1.60) | −25.30 (0.24) | −102.76 (2.84) | −14.82 (1.73) | −34.17 (0.28) | −128.39 (3.73) | −32.12 (1.92) | −28.49 (0.28) | −145.25 (4.56) |
| ρx = −0.2 | 48.86 (1.99) | −21.33 (0.25) | −78.22 (2.36) | −7.23 (1.82) | −34.09 (0.30) | −96.92 (2.80) | −36.72 (2.07) | −34.53 (0.31) | −110.28 (3.18) |
| ρx = 0.0 | 57.00 (2.09) | −21.71 (0.26) | −64.93 (2.10) | −12.11 (1.97) | −38.55 (0.33) | −76.80 (2.36) | −46.92 (2.19) | −41.30 (0.29) | −89.67 (2.59) |
| ρx = 0.2 | 60.30 (2.22) | −22.35 (0.27) | −55.99 (1.96) | −21.78 (1.95) | −45.54 (0.37) | −57.01 (1.92) | −55.98 (2.30) | −45.59 (0.38) | −72.33 (2.17) |
| ρx = 0.6 | 39.96 (2.38) | −36.83 (0.36) | −20.99 (1.73) | −40.85 (2.34) | −61.25 (0.49) | −21.35 (1.59) | −102.16 (2.91) | −68.73 (0.55) | −21.53 (1.41) |
Abbreviation: OR, odds ratio.
a Numbers in parentheses, mean squared error.
Limit of detection
Results for biomarkers subject to LODs and measurement error were similar (data not shown). Models subject to LODs had modestly decreased bias for cadmium and were very similar for lead. MSE was improved for values below the LOD, as expected because substitution of a correctly specified constant did not induce bias and artificially reduced the variance estimator (8). We additionally simulated a higher LOD for lead of 0.5 (corresponding to approximately 25% of values below the LOD) and observed diminished bias in comparison with models for measurement error alone. Incorrect specification of the substitution value would probably be prone to greater bias (20).
Example: anovulation in the BioCycle Study
Our results suggest that studies finding no association between continuous exposure biomarkers and dichotomous outcomes may be subject to bias and may miss harmful associations. Previously, we found no statistically significant association between cadmium, lead, and anovulation (12). Based on simulation results, under reasonable levels of exposure measurement error and positive correlation, the observed odds ratios, 1.29 and 1.20, probably reflect a stronger association which was biased toward the null. Presuming a true odds ratio of 1.75, moderate levels (R = 0.80) of measurement error resulted in observed odds ratios between 1.43 and 1.93 under conditions where the correlation between cadmium and lead was low (ρx = 0.2). Under severe measurement error (R = 0.50), the observed odds ratio was severely biased towards the null (OR = 1.12) with strong positively correlated errors (ρɛ = 0.6). Our simulations show that under reasonable levels of measurement error and correlation, this observed odds ratio could reflect a stronger association affected by downward bias or a weaker association biased upward under negatively correlated errors.
DISCUSSION
We evaluated the effects on inference of several factors not previously considered jointly: varying levels of measurement error (generally leading to attenuation of effects), correlation between exposures (confounding bias due to a common cause of the exposures and outcome), correlated measurement error (collider bias), LODs (measurement error as a function of exposure level), and statistical interaction. Our simulations, using cadmium and lead biomarker values in the BioCycle Study and a range of plausible values of correlation and measurement error, showed that results are biased toward the null in most settings with moderate levels of measurement error (R = 0.50) and association, which could produce underestimation of risks to public health. Bias was negligible across all levels of correlation when the true odds ratio was 1.00 (and where the odds ratio for cadmium equaled that for lead), indicating that correlated measurement error would not be responsible for type 1 error; type 2 error is more likely. The interaction parameter was consistently more biased toward the null than the main effects, which could complicate detection of interactions. The interaction parameter was often biased in the direction opposite that of the main effects. Murad and Freedman (21) demonstrated in the linear regression setting that the errors in interaction parameters do not follow a normal distribution, as they are the product of 2 normal distributions. Moreover, the error of the interaction parameter is also a function of X1 and X2, which is not the case for the main effects, where the error is independent of X. Because of the dependence on the values of X1 and X2, the interaction parameter error can bias the results in either direction. Our findings underscore the difficulty of detecting both main effects and interaction effects and highlight the importance of caution in interpretation of findings, as bias toward the null is likely. Investigators should learn about the measurement process to understand the levels and directions of correlation between exposures and error.
Biomarker measurement error can bias results and complicate risk assessment. Confounding and selection bias are more frequently discussed in the epidemiologic literature, despite the fact that adjustment for confounding may minimally affect inference (22). There is a robust body of literature focusing on correction techniques in nutritional epidemiology (3, 23–25). However, laboratory processes remain a black box, despite increasing reliance on biomarkers. For inductively coupled plasma mass spectroscopy, specimen processing with mass calibration, nebulizer gas flow, external calibrator preparation, or deviations during the quality control process represent potential sources of error (18, 26). Errors introduced in this process would probably cause positive correlation, which might produce underestimation of risk. Our findings translate to biologic variability or other sources of error, provided that such errors are random and approximately normal.
Our findings of strong bias from correlated measurement error are in line with previous findings that nondifferential measurement error may bias findings toward the null (27, 28). We observed bias in simulated lead levels to point consistently downward for OR > 1.00 and upward for OR < 1.00. However, bias for simulated cadmium levels was seen in both directions for a given odds ratio, depending on the correlations. This was due to differences in their distributions, specifically relative differences in their variances. As the findings here demonstrate, this bias can be magnified if those errors are correlated. The closed-form approximation in the Web Appendix shows the amount of bias likely to be present based on specific data on the distributions of the biomarkers and anticipated measurement errors for the given assay. Web Figure 2 displays a linear approximation for the bias based on our simulations. A comparison shows that the linear case (Web Figure 2) can provide insight into the anticipated biases for correlated measurement errors in logistic regression (Figure 1). There is a robust body of literature on calibration methods for known quantities of measurement error in relation to a gold standard (29–32) but less on assessment of the effects of correlated error (25, 33). Such corrections assume independent error and underestimate the bias. Correlated errors with weak confounding factors can reverse the direction and positively or negatively bias the true association, whereas correlated errors and strong risk factors do not lead to appreciable bias with independent measurement error (5). We extended these findings to the case of 2 correlated variables associated with the outcome, subject to correlated error, interactions, and LODs, and observed upward and downward bias.
Our results confirmed that power to detect an interaction was diminished in the presence of measurement error (34, 35). Interactions between biomarkers of exposure assessed as nonlinear responses are often explored. If the primary goal of a study is to assess the interaction between biomarkers of exposure, it is likely that reduced power from measurement error could obscure an interaction. Nondifferential correlated measurement error can induce bias in interaction estimates, causing severe underestimation of interaction effects.
Measurements subject to LODs were less biased and had smaller MSEs than comparable scenarios not subject to LODs, because we selected statistically valid substitution values. This approach may not always be feasible, since the true distribution of the data may be unknown. Previous work demonstrated that the direction and magnitude of bias depends upon the distribution of the exposure and the substitution method, and that the level of bias tends to be lower than that in settings not subject to a LOD (7). Our findings agreed with prior findings of more modest bias in settings with LODs and extended those findings to settings with correlated exposures and correlated error. Simulations with alternate substitutions are an important next step.
Our work was novel in that we simultaneously considered unmeasured confounding, interactions between exposures, LODs, and correlated measurement error. Heretofore, studies involving biomarker measurement have not considered the role of measurement error, as biomarker values are considered gold standards in many settings (36). Not only are the levels of error we simulated plausible, they are commonly encountered. As biomarker measures become ubiquitous, understanding correlations, the measurement process, and the extent of errors will be critical in order to appropriately interpret results.
In conclusion, it is critical to consider measurement error as it relates to biomarkers with LODs and interactions. This includes involvement during the data collection and measurement process and recognition that bias from measurement error may obscure important health effects from chemical exposures. Obtaining replicates or quality control information from the laboratory can aid in understanding the direction and magnitude of bias. Epidemiologists’ involvement in the measurement process will be a crucial step toward understanding the extent to which measurement error may affect our findings.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Epidemiology Branch, Division of Epidemiology, Statistics, and Prevention Research, Eunice Kennedy Shriver National Institute of Child Health and Human Development, Bethesda, Maryland (Anna Z. Pollack, Neil J. Perkins, Sunni L. Mumford, Aijun Ye, Enrique F. Schisterman); and Department of Epidemiology, Bloomberg School of Public Health, Johns Hopkins University, Baltimore, Maryland (Anna Z. Pollack).
This research was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development and by the Long-Range Research Initiative of the American Chemistry Council.
This paper was a finalist for the 2011 Reuel A. Stallones Student Prize Paper, awarded by the Congress of Epidemiology.
Conflict of interest: none declared.
REFERENCES
- 1.Wald A. The fitting of straight lines if both variables are subject to error. Ann Math Stat. 1940;11(3):284–300. [Google Scholar]
- 2.Armstrong BG. The effects of measurement errors on relative risk regressions. Am J Epidemiol. 1990;132(6):1176–1184. doi: 10.1093/oxfordjournals.aje.a115761. [DOI] [PubMed] [Google Scholar]
- 3.Thomas D, Stram D, Dwyer J. Exposure measurement error: influence on exposure-disease relationships and methods of correction. Ann Rev Public Health. 1993;14:69–93. doi: 10.1146/annurev.pu.14.050193.000441. [DOI] [PubMed] [Google Scholar]
- 4.Marshall JR, Hastrup JL. Mismeasurement and the resonance of strong confounders: uncorrelated errors. Am J Epidemiol. 1996;143(10):1069–1078. doi: 10.1093/oxfordjournals.aje.a008671. [DOI] [PubMed] [Google Scholar]
- 5.Marshall JR, Hastrup JL, Ross JS. Mismeasurement and the resonance of strong confounders: correlated errors. Am J Epidemiol. 1999;150(1):88–96. doi: 10.1093/oxfordjournals.aje.a009922. [DOI] [PubMed] [Google Scholar]
- 6.Thoresen M. A note on correlated errors in exposure and outcome in logistic regression. Am J Epidemiol. 2007;166(4):465–471. doi: 10.1093/aje/kwm107. [DOI] [PubMed] [Google Scholar]
- 7.Richardson DB, Ciampi A. Effects of exposure measurement error when an exposure variable is constrained by a lower limit. Am J Epidemiol. 2003;157(4):355–363. doi: 10.1093/aje/kwf217. [DOI] [PubMed] [Google Scholar]
- 8.Lubin JH, Colt JS, Camann D, et al. Epidemiologic evaluation of measurement data in the presence of detection limits. Environ Health Perspect. 2004;112(17):1691–1696. doi: 10.1289/ehp.7199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schisterman EF, Vexler A, Whitcomb BW, et al. The limitations due to exposure detection limits for regression models. Am J Epidemiol. 2006;163(4):374–383. doi: 10.1093/aje/kwj039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cole SR, Chu H, Nie L, et al. Estimating the odds ratio when exposure has a limit of detection. Int J Epidemiol. 2009;38(6):1674–1680. doi: 10.1093/ije/dyp269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schisterman EF, Gaskins AJ, Mumford SL, et al. Influence of endogenous reproductive hormones on F2-isoprostane levels in premenopausal women: the BioCycle Study. Am J Epidemiol. 2010;172(4):430–439. doi: 10.1093/aje/kwq131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pollack AZ, Schisterman EF, Goldman LR, et al. Cadmium, lead, and mercury in relation to reproductive hormones and anovulation in premenopausal women. Environ Health Perspect. 2011;119(8):1156–1161. doi: 10.1289/ehp.1003284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Saksena SK. Cadmium: its effects on ovulation, egg transport and pregnancy in the rabbit. Contraception. 1982;26(2):181–192. doi: 10.1016/0010-7824(82)90086-5. [DOI] [PubMed] [Google Scholar]
- 14.Godowicz B, Pawlus M. Effect of cadmium chloride on the ovulation and structure of ovary in the inbred KP and CBA mice strains. Folia Histochem Cytobiol. 1985;23(4):209–216. [PubMed] [Google Scholar]
- 15.Foster WG, McMahon A, Rice DC. Subclinical changes in luteal function in cynomolgus monkeys with moderate blood lead levels. J Appl Toxicol. 1996;16(2):159–163. doi: 10.1002/(SICI)1099-1263(199603)16:2<159::AID-JAT326>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- 16.Kolesarova A, Roychoudhury S, Slivkova J, et al. In vitro study on the effects of lead and mercury on porcine ovarian granulosa cells. J Environ Sci Health A Tox Hazard Subst Environ Eng. 2010;45(3):320–331. doi: 10.1080/10934520903467907. [DOI] [PubMed] [Google Scholar]
- 17.Hernan MA, Cole SR. Invited commentary: causal diagrams and measurement bias. Am J Epidemiol. 2009;170(8):959–962. doi: 10.1093/aje/kwp293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Palmer CD, Lewis ME, Geraghty CM, et al. Determination of lead, cadmium and mercury in blood for assessment of environmental exposure: a comparison between inductively coupled plasma-mass spectrometry and atomic absorption spectrometry. Spectrochim Acta Part B At Spectrosc. 2006;61(8):980–990. [Google Scholar]
- 19.Massadeh A, Gharibeh A, Omari K, et al. Simultaneous determination of Cd, Pb, Cu, Zn, and Se in human blood of Jordanian smokers by ICP-OES. Biol Trace Elem Res. 2010;133(1):1–11. doi: 10.1007/s12011-009-8405-y. [DOI] [PubMed] [Google Scholar]
- 20.Nie L, Chu H, Liu C, et al. Linear regression with an independent variable subject to a detection limit. Epidemiology. 2010;21(suppl 4):S17–S24. doi: 10.1097/EDE.0b013e3181ce97d8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Murad H, Freedman LS. Estimating and testing interactions in linear regression models when explanatory variables are subject to classical measurement error. Stat Med. 2007;26(23):4293–4310. doi: 10.1002/sim.2849. [DOI] [PubMed] [Google Scholar]
- 22.Blair A, Stewart P, Lubin JH, et al. Methodological issues regarding confounding and exposure misclassification in epidemiological studies of occupational exposures. Am J Ind Med. 2007;50(3):199–207. doi: 10.1002/ajim.20281. [DOI] [PubMed] [Google Scholar]
- 23.Kuha J. Corrections for exposure measurement error in logistic-regression models with an application to nutritional data. Stat Med. 1994;13(11):1135–1148. doi: 10.1002/sim.4780131105. [DOI] [PubMed] [Google Scholar]
- 24.Spiegelman D, Schneeweiss S, McDermott A. Measurement error correction for logistic regression models with an “alloyed gold standard.”. Am J Epidemiol. 1997;145(2):184–196. doi: 10.1093/oxfordjournals.aje.a009089. [DOI] [PubMed] [Google Scholar]
- 25.Spiegelman D, Zhao B, Kim J. Correlated errors in biased surrogates: study designs and methods for measurement error correction. Stat Med. 2005;24(11):1657–1682. doi: 10.1002/sim.2055. [DOI] [PubMed] [Google Scholar]
- 26.Centers for Disease Control and Prevention. Fourth National Report on Human Exposure to Environmental Chemicals. Atlanta, GA: Centers for Disease Control and Prevention; 2009. [Google Scholar]
- 27.Chavance M, Dellatolas G, Lellouch J. Correlated nondifferential misclassifications of disease and exposure—application to a cross-sectional study of the relation between handedness and immune disorders. Int J Epidemiol. 1992;21(3):537–546. doi: 10.1093/ije/21.3.537. [DOI] [PubMed] [Google Scholar]
- 28.Gladen B, Rogan WJ. Misclassification and the design of environmental studies. Am J Epidemiol. 1979;109(5):607–616. doi: 10.1093/oxfordjournals.aje.a112719. [DOI] [PubMed] [Google Scholar]
- 29.Rosner B, Willett WC, Spiegelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Stat Med. 1989;8(9):1051–1069. doi: 10.1002/sim.4780080905. [DOI] [PubMed] [Google Scholar]
- 30.Spiegelman D, McDermott A, Rosner B. Regression calibration method for correcting measurement-error bias in nutritional epidemiology. Am J Clin Nutr. 1997;65(4 suppl):1179S–1186S. doi: 10.1093/ajcn/65.4.1179S. [DOI] [PubMed] [Google Scholar]
- 31.Spiegelman D, Valanis B. Correcting for bias in relative risk estimates due to exposure measurement error: a case study of occupational exposure to antineoplastics in pharmacists. Am J Public Health Nations Health. 1998;88(3):406–412. doi: 10.2105/ajph.88.3.406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Freedman LS, Fainberg V, Kipnis V, et al. A new method for dealing with measurement error in explanatory variables of regression models. Biometrics. 2004;60(1):172–181. doi: 10.1111/j.0006-341X.2004.00164.x. [DOI] [PubMed] [Google Scholar]
- 33.Fewell Z, Davey SG, Sterne JA. The impact of residual and unmeasured confounding in epidemiologic studies: a simulation study. Am J Epidemiol. 2007;166(6):646–655. doi: 10.1093/aje/kwm165. [DOI] [PubMed] [Google Scholar]
- 34.Wong MY, Day NE, Luan JA, et al. Estimation of magnitude in gene-environment interactions in the presence of measurement error. Stat Med. 2004;23(6):987–998. doi: 10.1002/sim.1662. [DOI] [PubMed] [Google Scholar]
- 35.Greenwood DC, Gilthorpe MS, Cade JE. The impact of imprecisely measured covariates on estimating gene-environment interactions. BMC Med Res Methodol. 2006;6(1):21. doi: 10.1186/1471-2288-6-21. doi:10.1186/1471-2288-6-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Spiegelman D. Approaches to uncertainty in exposure assessment in environmental epidemiology. Annu Rev Public Health. 2010;31:149–163. doi: 10.1146/annurev.publhealth.012809.103720. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.