Abstract
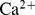 sparks and
sparks and 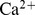 waves play important roles in calcium release and calcium propagation during the excitation-contraction (EC) coupling process in cardiac myocytes. Although the classical Fick’s law is widely used to model
waves play important roles in calcium release and calcium propagation during the excitation-contraction (EC) coupling process in cardiac myocytes. Although the classical Fick’s law is widely used to model 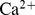 sparks and
sparks and 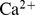 waves in cardiac myocytes, it fails to reasonably explain the full-width at half maximum(FWHM) paradox. However, the anomalous subdiffusion model successfully reproduces
waves in cardiac myocytes, it fails to reasonably explain the full-width at half maximum(FWHM) paradox. However, the anomalous subdiffusion model successfully reproduces 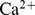 sparks of experimental results. In this paper, in the light of anomalous subdiffusion of
sparks of experimental results. In this paper, in the light of anomalous subdiffusion of 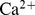 sparks, we develop a mathematical model of calcium wave in cardiac myocytes by using stochastic
sparks, we develop a mathematical model of calcium wave in cardiac myocytes by using stochastic 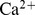 release of
release of 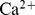 release units (CRUs). Our model successfully reproduces calcium waves with physiological parameters. The results reveal how
release units (CRUs). Our model successfully reproduces calcium waves with physiological parameters. The results reveal how 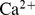 concentration waves propagate from an initial firing of one CRU at a corner or in the middle of considered region, answer how large in magnitude of an anomalous
concentration waves propagate from an initial firing of one CRU at a corner or in the middle of considered region, answer how large in magnitude of an anomalous 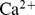 spark can induce a
spark can induce a 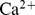 wave. With physiological
wave. With physiological 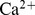 currents (2pA) through CRUs, it is shown that an initial firing of four adjacent CRUs can form a
currents (2pA) through CRUs, it is shown that an initial firing of four adjacent CRUs can form a 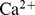 wave. Furthermore, the phenomenon of calcium waves collision is also investigated.
wave. Furthermore, the phenomenon of calcium waves collision is also investigated.
Introduction
Nomenclature
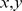 spatial coordinates,
spatial coordinates, 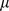 m
m
 time, ms
time, ms
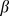 fractional order of the spatial derivative.
fractional order of the spatial derivative.
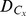 ,
, 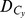
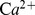 diffusion coefficients along
diffusion coefficients along  -axis and
-axis and 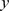 -axis,
-axis, 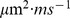
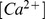 free
free 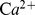 concentration,
concentration, 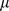 M
M
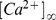 resting
resting 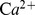 concentration,
concentration, 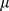 M
M
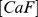 Ca-bound fluo-3 concentration,
Ca-bound fluo-3 concentration, 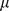 M
M
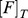 total fluo-3 concentration,
total fluo-3 concentration, 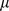 M
M
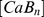 Ca-bound endogenous buffer concentration,
Ca-bound endogenous buffer concentration, 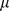 M
M
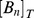 total endogenous buffer concentration,
total endogenous buffer concentration, 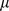 M
M
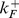 ,
, 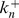 forward rate constants for dye and endogenous buffer reactions,
forward rate constants for dye and endogenous buffer reactions, 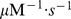
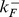 ,
, 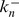 reverse rate constants for dye and endogenous buffer reactions,
reverse rate constants for dye and endogenous buffer reactions, 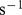
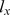 ,
, 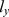 spatial separation of CRUs along
spatial separation of CRUs along  -axis and
-axis and 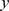 -axis,
-axis, 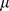 m
m
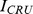 current through the CRU, pA
current through the CRU, pA
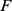 Faraday’s constant,
Faraday’s constant, 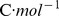
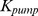 SR pump Michaelis constant,
SR pump Michaelis constant, 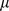 M
M
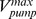 maximum SR pump rate,
maximum SR pump rate, 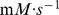
 SR pump Hill coefficient
SR pump Hill coefficient
 CRU Hill coefficient
CRU Hill coefficient
 molar flux of a clustered RyR channel,
molar flux of a clustered RyR channel, 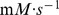
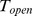 open time of CRU, ms
open time of CRU, ms
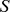 stochastic switching function equaling either 0 or 1
stochastic switching function equaling either 0 or 1
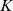
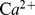 sensitivity parameter,
sensitivity parameter, 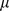 M
M
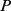 probability of
probability of 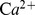 spark occurrence,/calcium release unit/ms
spark occurrence,/calcium release unit/ms
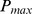 maximum probability of
maximum probability of 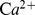 spark occurrence,/calcium release unit/ms
spark occurrence,/calcium release unit/ms
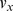 wave velocity along
wave velocity along  -axis,
-axis, 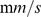
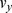 wave velocity along
wave velocity along 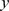 -axis,
-axis, 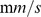
In the endoplasmic or sarcoplasmic reticulum(SR) of cardiac cells, there stores plenty of 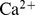 , the concentration of which is 2–3 orders of magnitude greater than that in the cytosol. During the excitation-contraction(EC) coupling process, triggered by L-type
, the concentration of which is 2–3 orders of magnitude greater than that in the cytosol. During the excitation-contraction(EC) coupling process, triggered by L-type 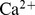 channels,
channels, 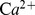 is released from SR through ryanodine receptors(RyRs) on the z-lines [1]–[4], where RyR is one kind of
is released from SR through ryanodine receptors(RyRs) on the z-lines [1]–[4], where RyR is one kind of 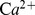 release units(CRUs). This event is called “
release units(CRUs). This event is called “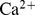 spark”.
spark”. 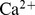 -induced
-induced 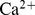 release(CICR) makes RyRs fire in succession such that
release(CICR) makes RyRs fire in succession such that 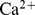 concentration rises [1], [5], the process of which is called calcium transient. Physiologically, calcium homeostasis is important for the contraction and relaxation of the heart muscle. However, in some pathological conditions, spontaneous propagating wave of
concentration rises [1], [5], the process of which is called calcium transient. Physiologically, calcium homeostasis is important for the contraction and relaxation of the heart muscle. However, in some pathological conditions, spontaneous propagating wave of 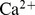 may occur, which is called “calcium wave”. The occurrence of calcium wave can affect the heart’s normal function, and may induce some disease, such as ventricular arrhythmias [6].
may occur, which is called “calcium wave”. The occurrence of calcium wave can affect the heart’s normal function, and may induce some disease, such as ventricular arrhythmias [6].
The model of 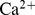 spark using Fick’s Law failed to reproduce the full-width at half maximum(FWHM) of experimental results for
spark using Fick’s Law failed to reproduce the full-width at half maximum(FWHM) of experimental results for 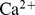 sparks. Simulated results for
sparks. Simulated results for 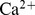 spark based on Fick’s Law presented a lower FWHM (∼1.0 μm), which was only half the width of experimental result (∼2.0 μm). Izu et al. [7] tried to increase the current through RyR to get larger FWHM, however, the spark amplitude also increased (∼10 times), which is far beyond experimental results and physiological conditions. In contrast, the results obtained with the anomalous subdiffusion model of
spark based on Fick’s Law presented a lower FWHM (∼1.0 μm), which was only half the width of experimental result (∼2.0 μm). Izu et al. [7] tried to increase the current through RyR to get larger FWHM, however, the spark amplitude also increased (∼10 times), which is far beyond experimental results and physiological conditions. In contrast, the results obtained with the anomalous subdiffusion model of 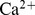 spark were found to be in close agreement with the experimental ones so that the “FWHM Paradox” was successfully explained [8]–[10]. Therefore, it is confirmed that diffusion of
spark were found to be in close agreement with the experimental ones so that the “FWHM Paradox” was successfully explained [8]–[10]. Therefore, it is confirmed that diffusion of 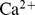 in cytoplasm obeys no longer Fick’s Law, but the anomalous subdiffusion.
in cytoplasm obeys no longer Fick’s Law, but the anomalous subdiffusion.
A 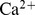 wave is formed from propagation of
wave is formed from propagation of 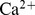 sparks. According to the results for
sparks. According to the results for 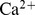 sparks,
sparks, 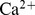 wave should also obey the anomalous subdiffusion. However, all previous work on
wave should also obey the anomalous subdiffusion. However, all previous work on 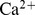 waves were based on Fick’s Law [11]–[14]. Anisotropic
waves were based on Fick’s Law [11]–[14]. Anisotropic 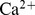 diffusion was studied by Girard et al. [11]. Keizer and Smith [12] investigated
diffusion was studied by Girard et al. [11]. Keizer and Smith [12] investigated 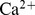 waves under stochastic firing of CRUs. Izu et al. [13] combined large CRU currents [7], stochastic firing of CRUs, asymmetric distribution of CRUs and anisotropic
waves under stochastic firing of CRUs. Izu et al. [13] combined large CRU currents [7], stochastic firing of CRUs, asymmetric distribution of CRUs and anisotropic 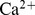 diffusion to investigate the propagation of
diffusion to investigate the propagation of 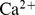 waves. Lu et al. [14] studied the effect of rogue RyRs on
waves. Lu et al. [14] studied the effect of rogue RyRs on 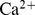 waves in ventricular myocytes with heart failure.
waves in ventricular myocytes with heart failure.
In this work, we develop a mathematical 2D model based on anomalous subdiffusion of 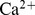 sparks. The anomalous subdiffusion model is used to study
sparks. The anomalous subdiffusion model is used to study 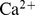 waves propagation from an initial firing of one CRU at a corner or in the middle of the considered region. We reproduce wave velocities of experimental results using a small current through CRUs which is close to the physiological conditions. The phenomenon of calcium waves collision is also investigated. With physiological
waves propagation from an initial firing of one CRU at a corner or in the middle of the considered region. We reproduce wave velocities of experimental results using a small current through CRUs which is close to the physiological conditions. The phenomenon of calcium waves collision is also investigated. With physiological 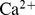 currents(2pA) through CRUs, an initial firing of four adjacent CRUs is shown to form a
currents(2pA) through CRUs, an initial firing of four adjacent CRUs is shown to form a 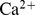 wave. Furthermore, study on how the system becomes unstable is also performed by changing the transverse distance of CRUs.
wave. Furthermore, study on how the system becomes unstable is also performed by changing the transverse distance of CRUs.
Methods
0.1 Anomalous Diffusion Model for Calcium Waves
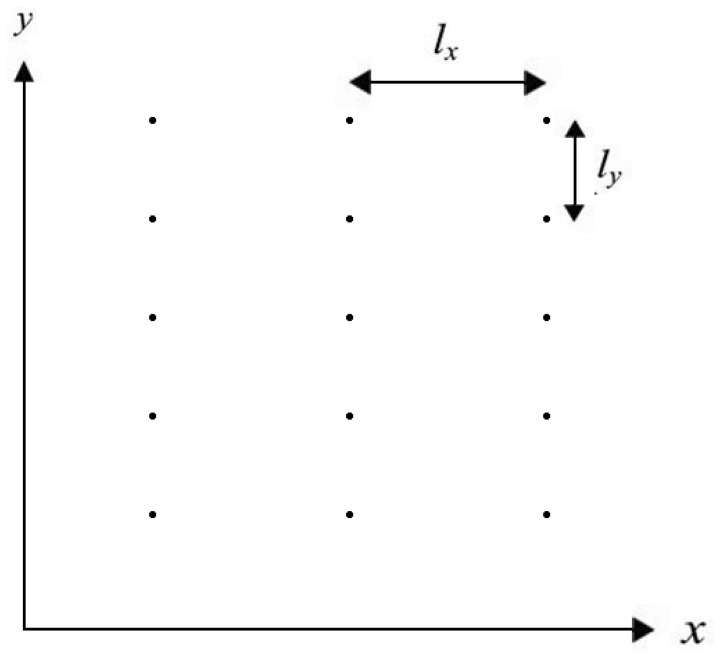
Figure 1 shows a 2-dimensional schematic of a cardiac myocyte(establishing line resources along  -axis [13]) which contains plenty of CRUs. The regular intervals of CRUs are
-axis [13]) which contains plenty of CRUs. The regular intervals of CRUs are  along
along  -axis and
-axis and 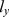 along
along 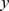 -axis. The governing equation for
-axis. The governing equation for 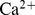 waves based on the anomalous subdiffusion model can be expressed as
waves based on the anomalous subdiffusion model can be expressed as
Figure 1. The 2D model of a cardiac myocyte.
The black dots represent CRUs which distribute regularly spaced 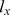 along
along  -axis and
-axis and 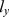 along
along 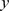 -axis.
-axis.
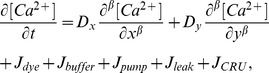 |
(1) |
where 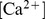 is the free
is the free 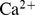 concentration;
concentration; 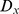 and
and 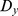 are diffusion coefficients for anisotropic diffusion with
are diffusion coefficients for anisotropic diffusion with 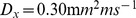 and
and 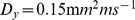 [15];
[15]; 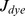 and
and 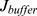 are fluxes due to
are fluxes due to 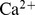 fluorescent indicator dye and endogenous stationary buffers;
fluorescent indicator dye and endogenous stationary buffers; 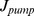 is pumping rate of SR
is pumping rate of SR 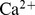 -ATPase, and
-ATPase, and 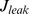 is a SR leak that is to balance
is a SR leak that is to balance 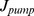 ; The expressions of
; The expressions of 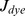 ,
, 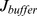 ,
, 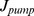 , and
, and 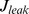 are
are
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where  identifies each of buffer species.
identifies each of buffer species. 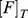 and
and 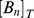 represent total concentration of the indicator and buffers, respectively.
represent total concentration of the indicator and buffers, respectively. 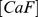 and
and 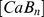 are concentration of the
are concentration of the 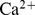 -bound complexes.
-bound complexes. 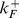 ,
, 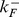 ,
, 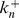 and
and 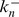 are reaction kinetics.
are reaction kinetics. 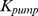 is the affinity constant for SR pumps,
is the affinity constant for SR pumps,  the Hill constant, and
the Hill constant, and 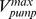 the maximum rate. SR leak is used to balance
the maximum rate. SR leak is used to balance 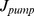 in resting state.
in resting state.
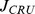 is the flux of
is the flux of 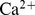 release from CRU, the expression of which is the same as that of Izu et al. [13],
release from CRU, the expression of which is the same as that of Izu et al. [13],
| (8) |
where 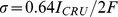 is a molar flux of a clustered RyR channel(
is a molar flux of a clustered RyR channel(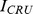 is current through the CRU and F is Faraday’s constant), and
is current through the CRU and F is Faraday’s constant), and  the Dirac delta function, S a stochastic function which controls the firing of the CRU, and
the Dirac delta function, S a stochastic function which controls the firing of the CRU, and 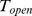 the firing time. Within a time interval
the firing time. Within a time interval 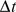 , the probability that the CRU fires is
, the probability that the CRU fires is 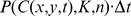 , where
, where 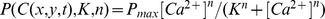 with
with 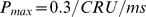 the maximum probability of
the maximum probability of 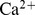 spark occurrence,
spark occurrence, 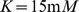
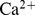 the sensitivity parameter and
the sensitivity parameter and 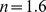 the Hill coefficient.
the Hill coefficient.
The anomalous space diffusion is model used in Eq.(1), where 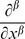 is the Riemann-Liouville operators which is defined as
is the Riemann-Liouville operators which is defined as
| (9) |
| (10) |
where 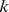 is an integer with
is an integer with 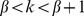 (
(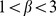 ). In Eq.(1), when
). In Eq.(1), when 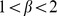 , anomalous space superdiffusion occurs, while anomalous space subdiffusion occurs when
, anomalous space superdiffusion occurs, while anomalous space subdiffusion occurs when 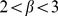 . Particularly, our model reduces to Fick’s Law when
. Particularly, our model reduces to Fick’s Law when 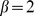 . According to Li et al. [10], calcium sparks follow the anomalous space subdiffusion of
. According to Li et al. [10], calcium sparks follow the anomalous space subdiffusion of 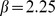 , so we only consider the space subdiffusion in the following sections.
, so we only consider the space subdiffusion in the following sections.
0.2 Numerical Methods
Our simulation is performed on a rectangular region with size of 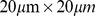 , which is meshed with a uniform grid size of
, which is meshed with a uniform grid size of 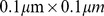 . The time-step size is 0.005ms.
. The time-step size is 0.005ms.
For the fractional differential term, we used the right-shifted Gr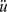 nwald formula to make a finite difference approximation [16].
nwald formula to make a finite difference approximation [16].
| (11) |
| (12) |
where 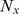 and
and 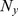 are positive integers, and
are positive integers, and 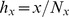 ,
, 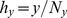 .
.  denotes the gamma function. The shifted Gr
denotes the gamma function. The shifted Gr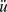 nwald approximation for fractional order derivative has been shown to be unconditionally stable [16].
nwald approximation for fractional order derivative has been shown to be unconditionally stable [16].
Considering simple impermeability of the cell boundary to the diffusing ions, reflecting boundary conditions 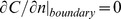 are taken on all edges [14]. The scale of our computation time is 200–500ms so that a CRU would not reopen after firing and closing.
are taken on all edges [14]. The scale of our computation time is 200–500ms so that a CRU would not reopen after firing and closing.
Standard values of parameters used in the current study are listed in Table 1 and Table 2. 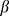 ,
, 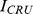 and
and 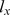 are changeable parameters whose effects on the results will be investigated.
are changeable parameters whose effects on the results will be investigated.
Table 1. Standard parameter values.
| Parameter | Value |
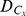
|
0.30 |
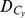
|
0.15 |
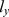
|
0.8 |
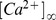
|
0.1 |
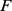
|
96500 |
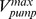
|
208 |
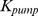
|
0.184 |
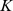
|
15 |

|
3.9 |

|
1.6 |
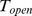
|
10 |
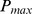
|
0.3 |
Table 2. Standard parameter values for dye and endogenous buffers.
| buffers | k+ | k | [B]T |
| dye | 80 | 90 | 50 |
| Calmodulin | 100 | 38 | 24 |
| Troponin | 39 | 20 | 70 |
| SR | 115 | 100 | 47 |
| SL | 115 | 1000 | 1124 |
Results and Discussion
Modeling a 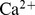 wave from a Single
wave from a Single 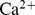 Spark
Spark
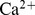 waves have been shown to be initiated and sustained by
waves have been shown to be initiated and sustained by 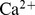 sparks [17]. Under pathological conditions,
sparks [17]. Under pathological conditions, 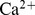 sparks fire spontaneously and stochastically, so whether a single spark can trigger a
sparks fire spontaneously and stochastically, so whether a single spark can trigger a 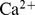 wave is important to the stability of cardiac myocytes [4]. Simulations based on Fick’s Law reveal that large currents through CRUs and high calcium concentrations are needed to trigger a
wave is important to the stability of cardiac myocytes [4]. Simulations based on Fick’s Law reveal that large currents through CRUs and high calcium concentrations are needed to trigger a 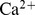 wave [13]. In this work, based on the anomalous subdiffusion model, we find the current which can trigger a normal
wave [13]. In this work, based on the anomalous subdiffusion model, we find the current which can trigger a normal 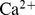 wave initiating from a single
wave initiating from a single 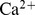 spark at the corner of considered region.
spark at the corner of considered region.
According to Li et al. [10], calcium sparks follow the anomalous space subdiffusion of 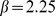 , so this subdiffusion order is also taken in our simulation. In our model, initial source is a 10ms opening of one CRU, the longitudinal intervals are
, so this subdiffusion order is also taken in our simulation. In our model, initial source is a 10ms opening of one CRU, the longitudinal intervals are 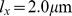 . When we take
. When we take 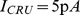 , the longitudinal wave velocity (
, the longitudinal wave velocity (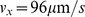 initiating from the corner) is in good agreement with the experimental result(
initiating from the corner) is in good agreement with the experimental result(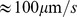 [17]).
[17]).
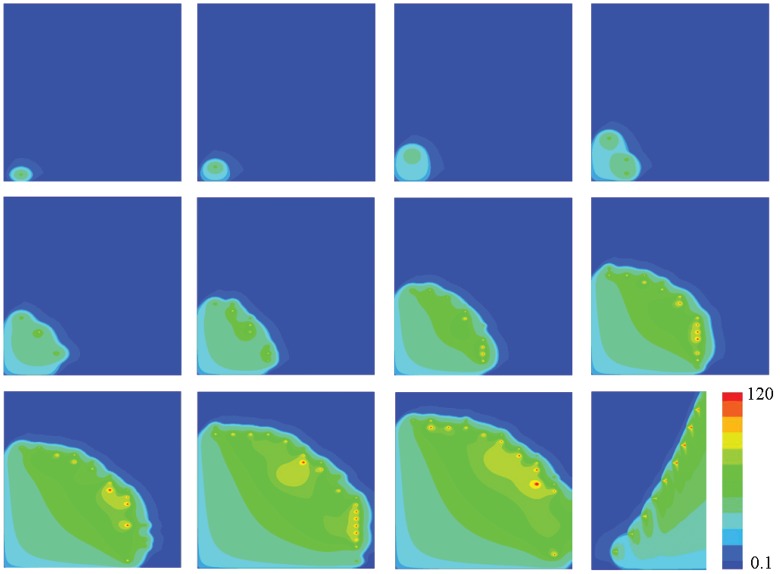
Figure 2 shows 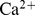 waves propagating on a discrete rectangle lattice initiating from a 10ms opening of the CRU at point (2,0.8). The snapshots are the
waves propagating on a discrete rectangle lattice initiating from a 10ms opening of the CRU at point (2,0.8). The snapshots are the 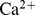 concentration distribution at 10, 30, 50, 70, 90, 110, 130, 150, 170, 190 and 200ms (left to right, top to bottom). From image to image, we can see CRUs fire stochastically by turns while
concentration distribution at 10, 30, 50, 70, 90, 110, 130, 150, 170, 190 and 200ms (left to right, top to bottom). From image to image, we can see CRUs fire stochastically by turns while 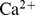 concentration wave propagates to the points of CRUs. At the beginning, CRUs fire one by one, and the amplitude(maximum of
concentration wave propagates to the points of CRUs. At the beginning, CRUs fire one by one, and the amplitude(maximum of 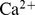 concentration in a region) is not very large; but with the increase of time, some of CRUs fire simultaneously in a short time so that
concentration in a region) is not very large; but with the increase of time, some of CRUs fire simultaneously in a short time so that 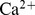 sparks influence each other, and the amplitudes of
sparks influence each other, and the amplitudes of 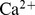 sparks become larger and larger. For example, the CRU at (2,1.6) fires at
sparks become larger and larger. For example, the CRU at (2,1.6) fires at 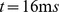 , the CRU at (2,2.4) fires at
, the CRU at (2,2.4) fires at 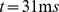 ; at
; at 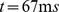 , the CRUs at (4,0.8) and (4,2.4) fires simultaneously, in a short time interval, at
, the CRUs at (4,0.8) and (4,2.4) fires simultaneously, in a short time interval, at 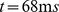 the CRU at (2,4.8) fires. In image 10, sparks occur at (18,4.0), (18,4.8), (18,5.6), (18,6.4), (18,7.2), (18,8.0), (18,8.8) and (18,9.6) in rapid succession, which may trigger a calcium transient. Image 11 shows that the boundary limits the propagation of
the CRU at (2,4.8) fires. In image 10, sparks occur at (18,4.0), (18,4.8), (18,5.6), (18,6.4), (18,7.2), (18,8.0), (18,8.8) and (18,9.6) in rapid succession, which may trigger a calcium transient. Image 11 shows that the boundary limits the propagation of 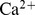 wave, but in an actual cardiac myocyte with size
wave, but in an actual cardiac myocyte with size 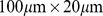 , calcium transient will be observed. In addition, though the space intervals of CRUs along y-axis are more compact than along x-axis, transverse wave velocity
, calcium transient will be observed. In addition, though the space intervals of CRUs along y-axis are more compact than along x-axis, transverse wave velocity 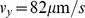 is smaller than that along x-axis
is smaller than that along x-axis 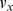 (because the diffusion coefficient along
(because the diffusion coefficient along 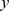 -axis
-axis 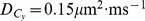 is smaller than that along
is smaller than that along  -axis
-axis 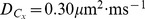 ).
).
Figure 2. Snapshots of 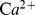 waves initiating from a 10ms opening of the CRU at the point (2,0.8).
waves initiating from a 10ms opening of the CRU at the point (2,0.8).
Snapshots are taken at 10, 30, 50, 70, 90, 110, 130, 150, 170, 190 and 200ms (left to right, top to bottom). Image 12 is the longitudinal linescan images along 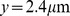 . The value of parameters are
. The value of parameters are 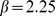 ,
, 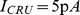 and
and 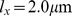 . The concentration is from
. The concentration is from 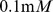 to
to 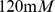 .
.
Our numerical results show that a single 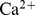 spark can trigger a normal
spark can trigger a normal 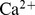 wave under the pathological condition of
wave under the pathological condition of 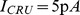 which is consistent with the experimental results(longitudinal wave velocity
which is consistent with the experimental results(longitudinal wave velocity 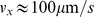 ). Physiological current through CRUs is about 2pA. However, the current may be increased (but not so large as 20pA [7], [13]) by external or internal factors, such as some disease or some electroneurographic signals. Our model present that a spontaneous
). Physiological current through CRUs is about 2pA. However, the current may be increased (but not so large as 20pA [7], [13]) by external or internal factors, such as some disease or some electroneurographic signals. Our model present that a spontaneous 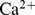 spark can form a
spark can form a 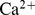 wave. The physical reason is, subdiffusion of
wave. The physical reason is, subdiffusion of 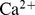 is slower than that for Fick’s diffusion. When an event of
is slower than that for Fick’s diffusion. When an event of 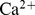 spark occurs, high value of
spark occurs, high value of 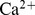 concentration may stay in a larger region around the firing CRU (for one
concentration may stay in a larger region around the firing CRU (for one 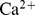 spark, FWHM is
spark, FWHM is 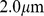 for subdiffusion and
for subdiffusion and 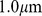 for Fick’s diffusion ), the firing probability of adjacent CRUs becomes higher. Then the fire-diffuse-fire process can be initiated and sustained, a
for Fick’s diffusion ), the firing probability of adjacent CRUs becomes higher. Then the fire-diffuse-fire process can be initiated and sustained, a 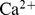 wave can propagate. So a smaller current and fewer sparks are needed to form a
wave can propagate. So a smaller current and fewer sparks are needed to form a 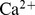 wave with our model than that using Fick’ Law.
wave with our model than that using Fick’ Law.
Because of the large FWHM for one spark due to anomalous subdiffusion, one firing CRU will trigger a 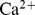 wave. Then we prohibit the event of another spontaneous spark so that it will not affect the initial
wave. Then we prohibit the event of another spontaneous spark so that it will not affect the initial 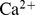 wave. In other words, when local
wave. In other words, when local 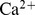 concentration is larger than resting
concentration is larger than resting 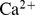 concentration,
concentration, 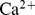 sparks may occur. So the “wall” of high
sparks may occur. So the “wall” of high 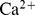 concentration spreads from the left corner to the top of cardiac myocyte. Image 12 shows the sequence of CRU firing along
concentration spreads from the left corner to the top of cardiac myocyte. Image 12 shows the sequence of CRU firing along 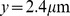 (the longitudinal linescan). The horizontal axis denotes time
(the longitudinal linescan). The horizontal axis denotes time  (from left to right,200ms), and the vertical axis denotes spatial coordinate
(from left to right,200ms), and the vertical axis denotes spatial coordinate  (20
(20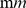 ). Except for initial two sparks, CRUs fire at nearly regular intervals, and the “wall” of high
). Except for initial two sparks, CRUs fire at nearly regular intervals, and the “wall” of high 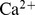 concentration is nearly a straight line. Here, from the initial spark to the second spark, it takes more time than those of the subsequent sparks, which is different from the results by Izu et al. [13](in their simulation, the transverse linescan is adopted, but the qualitative profile must be the same). It is because the subsequent sparks are triggered by two or more adjacent sparks, and the longitudinal wave velocity approaches to a constant value, but it takes more time to trigger the next CRUs from the initial signal spark.
concentration is nearly a straight line. Here, from the initial spark to the second spark, it takes more time than those of the subsequent sparks, which is different from the results by Izu et al. [13](in their simulation, the transverse linescan is adopted, but the qualitative profile must be the same). It is because the subsequent sparks are triggered by two or more adjacent sparks, and the longitudinal wave velocity approaches to a constant value, but it takes more time to trigger the next CRUs from the initial signal spark.
Effect of the Anomalous Subdiffusion Order
The anomalous diffusion order 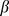 , which determines the diffusion mode of
, which determines the diffusion mode of 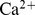 waves, was shown to affect the wave velocity considerably in last subsection(comparing with Fick’s Law). When
waves, was shown to affect the wave velocity considerably in last subsection(comparing with Fick’s Law). When 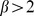 , a large value of
, a large value of 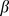 means a wild spread of initial concentration, but with the increase of time, the remanent concentration at initial point will be smaller due to the wild spread of calcium concentration. So the anomalous diffusion order
means a wild spread of initial concentration, but with the increase of time, the remanent concentration at initial point will be smaller due to the wild spread of calcium concentration. So the anomalous diffusion order 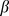 affects not only the wave velocity, but also the amplitude of each CRU, and further the average amplitude of a
affects not only the wave velocity, but also the amplitude of each CRU, and further the average amplitude of a 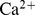 wave. Here,
wave. Here, 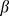 is taken to be 2.00, 2.05, 2.15 and 2.25 in order to figure out whether the amplitudes of
is taken to be 2.00, 2.05, 2.15 and 2.25 in order to figure out whether the amplitudes of 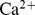 waves will change obviously with the variation of wave velocities. The initial condition is still a 10ms opening of the CRU at the point (2,0.8).
waves will change obviously with the variation of wave velocities. The initial condition is still a 10ms opening of the CRU at the point (2,0.8).
Table 3 presents the effect of anomalous fractional order 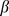 on the longitudinal wave velocity
on the longitudinal wave velocity 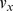 and the average amplitude, respectively. Comparing with the results based on Fick’s law, velocities of
and the average amplitude, respectively. Comparing with the results based on Fick’s law, velocities of 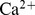 waves increase considerably when anomalous subdiffusion order
waves increase considerably when anomalous subdiffusion order 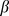 becomes bigger. For
becomes bigger. For 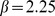 , the wave velocity(
, the wave velocity(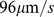 ) is almost twice as big as that based on Fick’s law(
) is almost twice as big as that based on Fick’s law(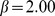 ,
, 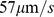 ). It is because FWHM along
). It is because FWHM along  -axis for
-axis for 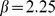 (
(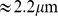 ) is almost twice as large as that for
) is almost twice as large as that for 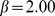 (
(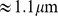 ). Here, in
). Here, in 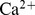 waves, FWHM for one CRU is affected by adjacent sparks, so it is a little bigger than FWHM of a single
waves, FWHM for one CRU is affected by adjacent sparks, so it is a little bigger than FWHM of a single 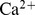 spark(
spark(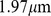 [10]). In contrast to wave velocity, the variation of amplitudes is not very considerable. For
[10]). In contrast to wave velocity, the variation of amplitudes is not very considerable. For 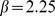 , amplitude is 81% as that for
, amplitude is 81% as that for 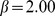 . The physical reason is that although for
. The physical reason is that although for 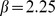 , FWHM along
, FWHM along  -axis is twice as big as that for
-axis is twice as big as that for 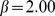 , the full duration at half maximum(FDHM) along
, the full duration at half maximum(FDHM) along  -axis for one spark still has a obvious decrease. So when the total release of
-axis for one spark still has a obvious decrease. So when the total release of 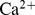 concentration is almost the same, under the expansion of spatial affection and the decrease of temporal continuity, amplitude of
concentration is almost the same, under the expansion of spatial affection and the decrease of temporal continuity, amplitude of 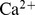 waves does not decreases obviously. In addition, wave velocities and amplitudes do not vary linearly with
waves does not decreases obviously. In addition, wave velocities and amplitudes do not vary linearly with 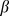 . When
. When 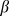 is larger, the effect of subdiffusion on
is larger, the effect of subdiffusion on 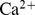 waves is greater. It is because when the variation of
waves is greater. It is because when the variation of 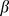 is small, the other parameters, such as the speed of diffusion
is small, the other parameters, such as the speed of diffusion 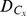 and the release strength of sparks
and the release strength of sparks 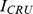 , play important roles in
, play important roles in 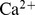 waves. When
waves. When 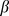 becomes bigger, replacing the primary position of the diffusion speed and release strength, diffusion mode affects
becomes bigger, replacing the primary position of the diffusion speed and release strength, diffusion mode affects 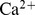 waves significantly(wave velocities).
waves significantly(wave velocities).
Table 3. The effect of anomalous fractional order β to longitudinal wave velocity 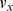 and amplitude.
and amplitude.
| β | 2.00 | 2.05 | 2.15 | 2.25 |
| νx | 57 | 62 | 75 | 96 |
| amplitude | 135 | 128 | 118 | 110 |
Effect of Initial Location
Propagation of a 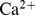 wave from a corner of the cardiac myocyte has been studied. It is found that the reflecting boundaries increase the amplitude of the initial spark, then further promote the propagation of the
wave from a corner of the cardiac myocyte has been studied. It is found that the reflecting boundaries increase the amplitude of the initial spark, then further promote the propagation of the 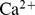 wave. In order to figure out the boundaries determine the propagation of the
wave. In order to figure out the boundaries determine the propagation of the 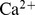 wave or just affect the wave velocity, we change the location of the initial
wave or just affect the wave velocity, we change the location of the initial 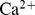 spark and study how the reflecting boundaries affect
spark and study how the reflecting boundaries affect 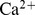 waves. In general, the process in which more than two sparks firing together, then several
waves. In general, the process in which more than two sparks firing together, then several 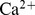 waves propagating, meeting and dissipating is very common in cardiac myocytes. This event is called
waves propagating, meeting and dissipating is very common in cardiac myocytes. This event is called 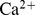 waves collision, and it was observed in experiments [17]. We will discuss in the following the interaction of several
waves collision, and it was observed in experiments [17]. We will discuss in the following the interaction of several 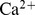 waves.
waves.
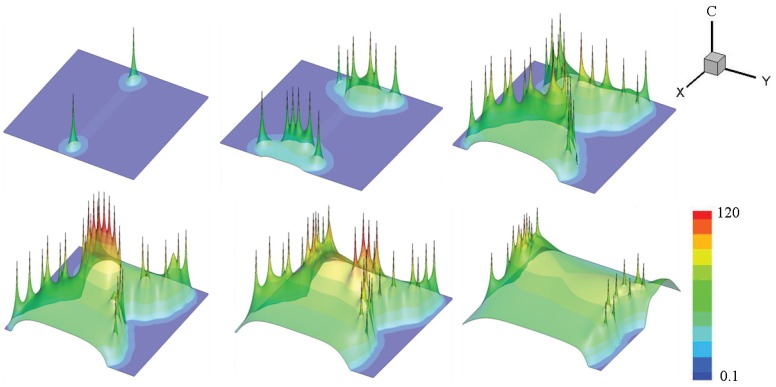
As shown in Fig. 3, it takes only 120ms for a 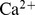 wave initiating from a 10ms opening of the CRU at a middle point (10,9.6) to propagates to the left and the bottom boundaries. Triggering from the middle of the region, the “walking distance” of a
wave initiating from a 10ms opening of the CRU at a middle point (10,9.6) to propagates to the left and the bottom boundaries. Triggering from the middle of the region, the “walking distance” of a 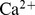 wave becomes shorter, and it will spread more quickly to the boundary. Due to the shorter “walking distance”, less sparks will occur simultaneously, and it will not make the
wave becomes shorter, and it will spread more quickly to the boundary. Due to the shorter “walking distance”, less sparks will occur simultaneously, and it will not make the 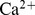 wave develop sufficiently; but trigger from the corner, while the
wave develop sufficiently; but trigger from the corner, while the 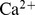 wave spreads wildly, large amount of sparks will fire together in a small region(Figure 2, right corner of Image 10). Comparing with the
wave spreads wildly, large amount of sparks will fire together in a small region(Figure 2, right corner of Image 10). Comparing with the 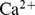 wave initiating from a corner without the effect of the boundaries, the initial concentration of the region will be smaller, then the probability of CRUs firing will be lower, so the events of
wave initiating from a corner without the effect of the boundaries, the initial concentration of the region will be smaller, then the probability of CRUs firing will be lower, so the events of 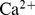 sparks are more stochastic and irregular. Affected by the absence of the reflecting boundaries and the shorter “walking distance”, longitudinal wave velocity
sparks are more stochastic and irregular. Affected by the absence of the reflecting boundaries and the shorter “walking distance”, longitudinal wave velocity 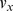 reduces to
reduces to 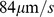 , and
, and 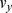 reduces to
reduces to 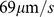 . So
. So  waves are easier to occur at the boundaries of cardiac myocytes, whcih can be compared with the experimental results [17], [18], [19]. Initiation of Free
waves are easier to occur at the boundaries of cardiac myocytes, whcih can be compared with the experimental results [17], [18], [19]. Initiation of Free  waves [18] and spontaneous
waves [18] and spontaneous  waves [19] is kinetically favored near the boundaries, and the waves initialing from the boundaries are also easier to propagate. In ref. [17], though the results are obtained by line-scan, initiation of the waves is always near the endpoints of the line, and the waves are always triggered near the boundaries of cardiac myocytes. However, the amplitude is smaller than that of the wave from the corner though the change is not obvious. It is because the initial condition is an opening of only one spark, the reflecting effects of the boundaries are not sufficiently obvious. So the reflecting boundaries can increase the propagating probability of
waves [19] is kinetically favored near the boundaries, and the waves initialing from the boundaries are also easier to propagate. In ref. [17], though the results are obtained by line-scan, initiation of the waves is always near the endpoints of the line, and the waves are always triggered near the boundaries of cardiac myocytes. However, the amplitude is smaller than that of the wave from the corner though the change is not obvious. It is because the initial condition is an opening of only one spark, the reflecting effects of the boundaries are not sufficiently obvious. So the reflecting boundaries can increase the propagating probability of 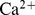 waves, though they are not the crucial factor for the propagation of
waves, though they are not the crucial factor for the propagation of 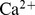 waves. In contrast, the anomalous subdiffusion mode of
waves. In contrast, the anomalous subdiffusion mode of 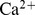 concentration is the decisive factor for whether the
concentration is the decisive factor for whether the 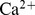 wave can be formed by a single
wave can be formed by a single 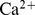 spark.
spark.
Figure 3. Snapshots of 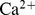 waves initiating from a 10ms opening of the CRU at the point (10,9.6).
waves initiating from a 10ms opening of the CRU at the point (10,9.6).
Snapshots are taken at 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110 and 120ms (left to right, top to bottom). The value of parameters are 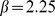 ,
, 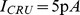 and
and 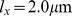 . The concentration is from
. The concentration is from 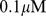 to
to 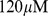 .
.
Figure 4 presents the event of two 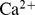 waves collision(3D images). The initial condition is 10ms opening of CRUs at points (2,9.6) and (18,9.6), and they will form two
waves collision(3D images). The initial condition is 10ms opening of CRUs at points (2,9.6) and (18,9.6), and they will form two 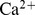 waves. Two
waves. Two 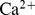 waves will meet at the middle as shown in Image 4, at
waves will meet at the middle as shown in Image 4, at 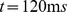 . Several sparks fire at the same time, and local
. Several sparks fire at the same time, and local 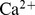 concentration reaches a peak value. With increasing time,
concentration reaches a peak value. With increasing time, 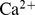 concentration will return to a lower value under the effect of buffers and pump, and no sparks will occur because of the CRUs’ “refractory period”. The 2D linescan image shows the process of two
concentration will return to a lower value under the effect of buffers and pump, and no sparks will occur because of the CRUs’ “refractory period”. The 2D linescan image shows the process of two 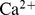 waves collision and vanishment(Fig. 8 in [17]), but it cannot show how the propagating direction changes. When
waves collision and vanishment(Fig. 8 in [17]), but it cannot show how the propagating direction changes. When 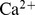 concentration reaches a peak value in the middle, CRUs along
concentration reaches a peak value in the middle, CRUs along  -axis(
-axis(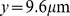 ) are closed, but CRUs along
) are closed, but CRUs along 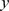 -axis(
-axis(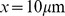 ) have never been opened before. Therefore,
) have never been opened before. Therefore, 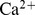 waves can propagate along the line of
waves can propagate along the line of 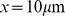 . Finally, all CRUs are closed and will not reopen.
. Finally, all CRUs are closed and will not reopen.
Figure 4. Snapshots of 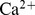 waves collision.
waves collision.
Snapshots are taken at 10, 70, 110, 120, 130 and 150ms (left to right, top to bottom). The value of parameters are 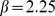 ,
, 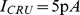 and
and 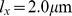 . The concentration is from
. The concentration is from 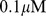 to
to 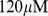 .
.
Modeling 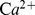 Waves Under a Physiological Current
Waves Under a Physiological Current
To reproduce the feature of calcium waves found in experiments(primary result is wave velocity), a large current through CRU has been used in the former subsection. However, physiological value of 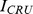 is about 2pA. So in the following discussion,
is about 2pA. So in the following discussion, 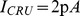 is adopted to study how many adjacent normal
is adopted to study how many adjacent normal 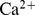 sparks can trigger a
sparks can trigger a 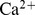 wave and find out the longitudinal interval of CRUs which could make a single
wave and find out the longitudinal interval of CRUs which could make a single 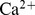 spark trigger a normal
spark trigger a normal 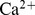 wave. Because of the small value of
wave. Because of the small value of 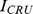 , wave velocity and amplitude will be smaller. In order to make
, wave velocity and amplitude will be smaller. In order to make 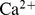 waves spread all over the region, the computation time is prolonged to 500ms. To diminish the effect of the reflecting boundaries, the initial location is chosen at the middle of the region.
waves spread all over the region, the computation time is prolonged to 500ms. To diminish the effect of the reflecting boundaries, the initial location is chosen at the middle of the region.
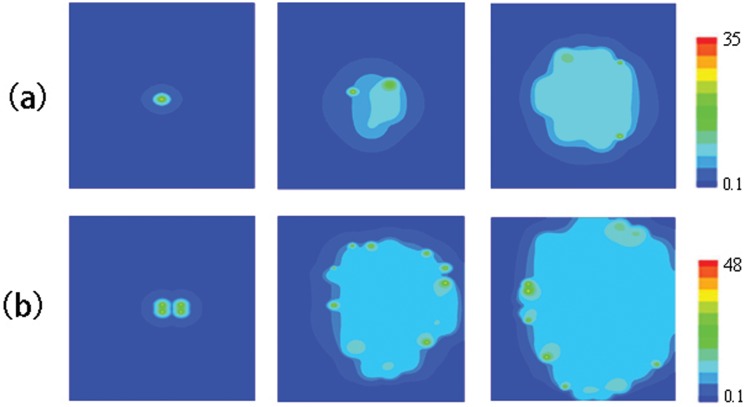
Figure 5a shows whether a 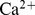 wave can be triggered by one spark at the middle of the region for
wave can be triggered by one spark at the middle of the region for 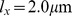 . When
. When 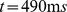 , the wave only spreads through half the region, and the events of
, the wave only spreads through half the region, and the events of 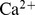 sparks are almost isolate. Under physiological conditions, even considering anomalous subdiffusion, high value of
sparks are almost isolate. Under physiological conditions, even considering anomalous subdiffusion, high value of 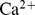 concentration may stay in a larger region around the firing CRU. For a small current, the amplitude of one spark is still small, the
concentration may stay in a larger region around the firing CRU. For a small current, the amplitude of one spark is still small, the 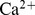 wave cannot propagate to the whole region, so the cardiac myocyte is stable when a normal spontaneous spark occurs.
wave cannot propagate to the whole region, so the cardiac myocyte is stable when a normal spontaneous spark occurs.
Figure 5. Illustration of. 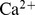 waves induced by physiological
waves induced by physiological 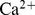 sparks.
sparks.
(a)Snapshots of 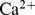 waves initiating from a 10ms opening of the CRU at the point (10,9.6), snapshots are taken at 10, 330 and 490ms. The value of parameters are
waves initiating from a 10ms opening of the CRU at the point (10,9.6), snapshots are taken at 10, 330 and 490ms. The value of parameters are 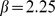 ,
, 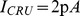 and
and 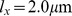 . (b)Snapshots of
. (b)Snapshots of 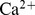 waves initiating from 10ms opening of the CRUs at the point (10,9.6), (12,9.6), (10,10.4) and(12,10.4), snapshots are taken at 10, 330 and 490ms. The value of parameters are
waves initiating from 10ms opening of the CRUs at the point (10,9.6), (12,9.6), (10,10.4) and(12,10.4), snapshots are taken at 10, 330 and 490ms. The value of parameters are 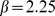 ,
, 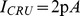 and
and 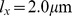 .
.
The initial number of firing sparks is changed to study how many adjacent normal 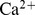 sparks can trigger a
sparks can trigger a 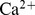 wave. The result is shown in Fig. 5b. It can be seen that four CRUs firing simultaneously at the middle will form a “weak”
wave. The result is shown in Fig. 5b. It can be seen that four CRUs firing simultaneously at the middle will form a “weak” 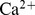 wave in the region. At
wave in the region. At 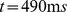 , the wave reaches the top, bottom and right boundaries, and several sparks can be found at the same time. However, three adjacent normal
, the wave reaches the top, bottom and right boundaries, and several sparks can be found at the same time. However, three adjacent normal 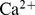 sparks can only form a local
sparks can only form a local 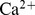 wave. So with the computation time of 500ms, for
wave. So with the computation time of 500ms, for 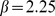 ,
, 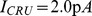 and
and 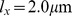 , four adjacent CRUs firing together is the critical initial condition to trigger a
, four adjacent CRUs firing together is the critical initial condition to trigger a 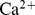 wave. However, wave velocity and amplitude here is very small(
wave. However, wave velocity and amplitude here is very small(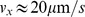 ), and the
), and the 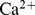 concentration of the whole region is much smaller than that in Figs. 2, 3, 4.
concentration of the whole region is much smaller than that in Figs. 2, 3, 4.
In Figure 6a, the longitudinal interval is changed. For the case of 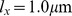 , it takes only 110ms for the wave to reach the left boundary. With the simultaneous firing of several CRUs, an obvious
, it takes only 110ms for the wave to reach the left boundary. With the simultaneous firing of several CRUs, an obvious 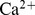 concentration wave is observed. Although the amplitude is smaller, longitudinal wave velocity(
concentration wave is observed. Although the amplitude is smaller, longitudinal wave velocity(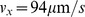 ) is comparative with the case of
) is comparative with the case of 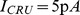 ,
, 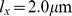 . The physical reason for such a significant change which happens by changing
. The physical reason for such a significant change which happens by changing 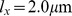 to
to 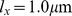 is that FWHM for
is that FWHM for 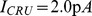 is about
is about 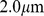 , and if the interval between two CRUs reduces to
, and if the interval between two CRUs reduces to 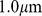 , the half maximum value of a spark can “reach” adjacent CRUs easily. In addition, less interval makes more CRUs fire together, and the wave will be easier to propagate.
, the half maximum value of a spark can “reach” adjacent CRUs easily. In addition, less interval makes more CRUs fire together, and the wave will be easier to propagate.
Figure 6. With smaller longitudinal intervals, the effect of initial 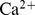 sparks numbers.
sparks numbers.
(a)Snapshots of 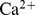 waves initiating from a 10ms opening of the CRU at the point (10,9.6), snapshots was taken at 10, 60 and 110ms. (b)Snapshots of
waves initiating from a 10ms opening of the CRU at the point (10,9.6), snapshots was taken at 10, 60 and 110ms. (b)Snapshots of 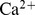 waves initiating from a 10ms opening of the CRUs at the point (9,9.6), (10,9.6), (9,10.4) and(10,10.4), snapshots are taken at 10, 50 and 90ms. (c)Snapshots of
waves initiating from a 10ms opening of the CRUs at the point (9,9.6), (10,9.6), (9,10.4) and(10,10.4), snapshots are taken at 10, 50 and 90ms. (c)Snapshots of 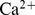 waves initiating from 10ms opening of the CRUs at the point (9,9.6), (10,9.6), (11,9.6), (9,10.4), (10,10.4), (11,10.4), (9,11.2), (10,11.2), (11,11.2),snapshots are taken at 10, 40 and 70ms. The value of parameters for a, b and c are
waves initiating from 10ms opening of the CRUs at the point (9,9.6), (10,9.6), (11,9.6), (9,10.4), (10,10.4), (11,10.4), (9,11.2), (10,11.2), (11,11.2),snapshots are taken at 10, 40 and 70ms. The value of parameters for a, b and c are 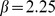 ,
, 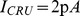 and
and 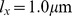 .
.
Our results have revealed that two factors(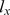 and number of firing CRUs) can both make a
and number of firing CRUs) can both make a 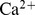 wave propagate. But which the effect is more significant? Figure 6 shows when
wave propagate. But which the effect is more significant? Figure 6 shows when 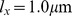 , three
, three 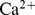 waves trigger from one, four, and nine initial adjacent
waves trigger from one, four, and nine initial adjacent 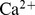 sparks, respectively. From 6a to 6c, both longitudinal wave velocity and amplitude become larger (
sparks, respectively. From 6a to 6c, both longitudinal wave velocity and amplitude become larger (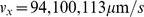 , amplitudes are
, amplitudes are 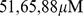 ), but the difference is not obvious as that between Figs. 5a and 6a. So the longitudinal interval of CRUs affects
), but the difference is not obvious as that between Figs. 5a and 6a. So the longitudinal interval of CRUs affects 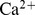 waves more significantly than the number of firing CRUs. If the longitudinal interval of CRUs becomes smaller due to some reasons, such as cardiac myocytes deformation,
waves more significantly than the number of firing CRUs. If the longitudinal interval of CRUs becomes smaller due to some reasons, such as cardiac myocytes deformation, 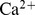 waves will easily occur, then cardiac myocytes will be unstable.
waves will easily occur, then cardiac myocytes will be unstable.
Conclusion
In this work, we present a mathematical model based on anomalous subdiffusion of 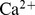 concentration in the process of
concentration in the process of 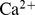 wave triggered by
wave triggered by 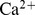 sparks.
sparks. 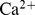 waves propagating from an initial firing of one single CRU at a corner or in the middle of a 2D rectangular region is numerically simulated. Our results can reproduce wave velocities of experimental results using a small current. We show that
waves propagating from an initial firing of one single CRU at a corner or in the middle of a 2D rectangular region is numerically simulated. Our results can reproduce wave velocities of experimental results using a small current. We show that 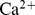 waves can be triggered by one single
waves can be triggered by one single 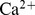 spark under a small CRU current(
spark under a small CRU current(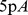 ). When anomalous subdiffusion order
). When anomalous subdiffusion order 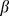 becomes bigger, velocities of
becomes bigger, velocities of 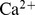 waves increase obviously, but the variation of amplitude is not very considerable. The phenomenon of calcium waves collision is also simulated. Under physiological
waves increase obviously, but the variation of amplitude is not very considerable. The phenomenon of calcium waves collision is also simulated. Under physiological 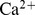 currents(
currents(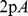 ) through CRUs, an initial firing of four adjacent CRUs is shown to form a
) through CRUs, an initial firing of four adjacent CRUs is shown to form a 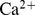 wave. When
wave. When 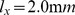 , an isolated spark cannot trigger a
, an isolated spark cannot trigger a 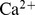 wave, so the system is stable under physiological condition. Then the longitudinal interval of CRUs is changed to study how the system becomes unstable and how an obvious
wave, so the system is stable under physiological condition. Then the longitudinal interval of CRUs is changed to study how the system becomes unstable and how an obvious 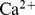 wave is formed. Our work is based on a more realistic diffusion model of
wave is formed. Our work is based on a more realistic diffusion model of 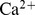 sparks with the parameters close to physiological values. The simulation results may be useful in further studies about
sparks with the parameters close to physiological values. The simulation results may be useful in further studies about 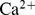 waves.
waves.
Funding Statement
This work was supported by the National Natural Science Foundation of China (Grant No. 11272014 and No. 10825208), and National Key Basic Research Program of China (Grant No. 2013CB531200). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Cheng H, Lederer W, Cannell M (1993) Calcium sparks: elementary events underlying excitationccontraction coupling in heart muscle. Science 262: 740–744. [DOI] [PubMed] [Google Scholar]
- 2. Cheng H, Lederer M, Xiao R, Gomez A, Zhou Y, et al. (1996a) Excitation-contraction coupling in heart: new insights from ca2+ sparks. Cell Calcium 20: 129–140. [DOI] [PubMed] [Google Scholar]
- 3. Cannell M, Cheng H, Lederer W (1995) The control of calcium release in heart muscle. Cell Calcium 268: 1045–1049. [DOI] [PubMed] [Google Scholar]
- 4. Lopez-Lopez J, Shacklock P, Balke C, Wier W (1995) Local calcium transients triggered by single l-type calcium channel currents in cardiac cells. Science 268: 1042–1045. [DOI] [PubMed] [Google Scholar]
- 5. Fabiato A (1985) Time and calcium dependence of activation and inactivation of calcium-induced release of calcium from the sarcoplasmic reticulum of a skinned canine cardiac purkinje cell. J Gen Physiol 85: 247–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Lakatta E, Guarnieri T (1993) Spontaneous myocardial calcium oscillations: Are they linked to ventricular fibrillation. J Cardiovasc Electrophysiol 44: 73–89. [DOI] [PubMed] [Google Scholar]
- 7. Izu L, Mauban J, Balke C, Wier W (2001a) Large currents generate cardiac ca2+ sparks. Biophys J 80: 88–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Tan W, Fu C, Xie W, Cheng H (2007) An anomalous subdiffusion model for calcium spark in cardiac myocytes. Appl Phys Lett 91: 183901. [Google Scholar]
- 9. Cheng H, Lederer W (2008) Calcium sparks. Physiol Rev 88: 1491–1545. [DOI] [PubMed] [Google Scholar]
- 10. Li K, Fu C, Cheng H, Tan W (2011) Anomalous subdiffusion of calcium spark in cardiac myocytes. Cell Mol Bioeng 4: 457–465. [Google Scholar]
- 11. Girard S, Luckhoff A, Lechleiter J, Sneyd J, Clapham D (1992) Two-dimensional model of calcium waves reproduces the patterns observed in xenopus oocytes. Biophys J 61: 509–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Keizer J, Smith G (1998) Spark-to-wave transition: saltatory transmission of calcium waves in cardiac myocytes. Biophys Chem 72: 87–100. [DOI] [PubMed] [Google Scholar]
- 13. Izu L, Gil W, William B (2001b) Evolution of cardiac calcium waves from stochastic calcium sparks. Biophys J 80: 103–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Lu L, Xia L, Ye X, Cheng H (2010) Simulation of the effect of rogue ryanodine receptors on a calcium wave in ventricular myocytes with heart failure. Phys Biol 7: 026005. [DOI] [PubMed] [Google Scholar]
- 15. Baylor S, Hollingworth S (1998) Model of sarcomeric ca2+ movements, including atp ca2+ binding and diffusion, during activation of frog skeletal muscle. J Gen Physiol 112: 297–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Charles T, Mark M, Hans-Peter S (2006) A second-order accurate numerical approximation for the fractional diffusion equation. J Comput Phys 213: 205–213. [Google Scholar]
- 17. Cheng H, Lederer M, Lederer W, Cannell M (1996b) Calcium sparks and [ca2+]i waves in cardiac myocytes. Am J Physiol 39: C148–C159. [DOI] [PubMed] [Google Scholar]
- 18. John C, Lionel F, Ellis B, George T (1978) A free calcium wave tranverses the activating egg of the medaka, oryzias latipes. J Cell Biology 76: 448–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Takamatsu K, Wier W (1990) Calcium waves in mammalian heart: quantification of origin, magnitude, waveform, and velocity. J Cell Biology 4: 1519–1525. [DOI] [PubMed] [Google Scholar]