LoopWeaver: Loop Modeling by the Weighted Scaling of Verified Proteins

Abstract

Modeling loops is a necessary step in protein structure determination, even with experimental nuclear magnetic resonance (NMR) data, it is widely known to be difficult. Database techniques have the advantage of producing a higher proportion of predictions with subangstrom accuracy when compared with ab initio techniques, but the disadvantage of also producing a higher proportion of clashing or highly inaccurate predictions. We introduce LoopWeaver, a database method that uses multidimensional scaling to achieve better, clash-free placement of loops obtained from a database of protein structures. This allows us to maintain the above-mentioned advantage while avoiding the disadvantage. Test results show that we achieve significantly better results than all other methods, including Modeler, Loopy, SuperLooper, and Rapper, before refinement. With refinement, our results (LoopWeaver and Loopy consensus) are better than ROSETTA, with 0.42 Å RMSD on average for 206 length 6 loops, 0.64 Å local RMSD for 168 length 7 loops, 0.81Å RMSD for 117 length 8 loops, and 0.98 Å RMSD for length 9 loops, while ROSETTA has 0.55, 0.79, 1.16, 1.42, respectively, at the same average time limit (3 hours). When we allow ROSETTA to run for over a week, it approaches, but does not surpass, our accuracy.

1. Introduction

In the loop modeling problem, one is given a target protein structure with a gap. This gap is a region of consecutive residues in which the protein structure is missing atomic coordinates.

The goal is to generate a realistic loop in order to fill in the gap and obtain a protein structure model with no break in the backbone. The edges of the gap are called stems. The Euclidean distance between these two stems is called the span of the gap, while the number of residues missing is the length of the gap.

Loop regions, the regions of the protein that cannot be classified as a well-defined secondary structure (helices and extended structures), are highly flexible due to the lack of long distance atomic bonds that characterize the well-defined secondary structures. This freedom of movement makes them hard to model compared to more rigid regions (Kryshtafovych et al., 2005). So, while the loop modeling problem is not strictly limited to the actual loop regions of a protein structure, in practice, these are the regions where it will be applied.

Such gaps arise frequently in predictive protein models built using a template-based approach, where a protein's structure is predicted using one or more templates (proteins with similar sequence and known structure). Any region that does not have at least one template match covering it must be modeled separately, so loop modeling may be required to connect multiple templates together. Additionally, even with very good template matches, there can be regions where the one-to-one correspondence of residues between the input sequence and template match does not hold, because there has been an insertion-or-deletion (indel) mutation between the two sequences. Without such a correspondence, the known atomic coordinates of the template cannot be directly converted into coordinates for the protein being modeled, so these regions must be modeled afterward. These mutations occur most often in or around loop regions since the high conformational flexibility of these regions allows them to accept such changes.

Gaps can also occur in experimental protein models, especially nuclear magnetic resonance (NMR) models. In an NMR experiment, protein structure is modeled by examining the way in which a protein interacts with strong magnetic fields. The more a region moves while in solvent, the more noise that results when examining that particular region. Since loops can move around much more than other regions, loop NMR data tends to be very noisy. This makes it very difficult to model loops based on NMR data alone, so loop modeling must be used in conjunction with the NMR data.

One category of loop modeling techniques is called statistical, de novo, or ab initio. This category of methods works by sampling loops from a statistical model and ensuring they fit properly into the gap. The statistical model is usually in the form of probability distributions for phi,psi torsion angle pairs. There are a number of ways that one can use such models in order to generate closed loops (meaning loops that connect properly to both stems of the gap).

One such way is used in the ModLoop package of MODELLER (Fiser and Sali, 2003; Fiser et al., 2000). This program starts with a straight loop connecting the two end points, which is then adjusted and refined using several methods so that it takes on a more realistic shape while maintaining closure. So, angles are not directly sampled from the statistical model, but existing angles are adjusted to make them more probable under the model. This method also means that if one already has a good guess (possibly from another tool) ModLoop can start from there rather than from the very unrealistic straight line model.

Another technique is that used in the Loopy program (Xiang et al., 2002), which generates loops by sampling torsion angle pairs, regardless of whether or not this results in loops that fit into the gap, and then adjusts the loops to fit properly after. This generation is very rapid, allowing thousands of loops to be generated in a very short time frame. From here the loops are closed using the random tweak method (Shenkin et al., 1987), which randomly adjusts torsion angles in order to improve the loop with respect to constraints. The best loops are then split apart and recombined to form new loops, with this recombination also done using the random tweak method.

The RAPPER tool (de Bakker et al., 2003) builds a fragment starting at one stem and working toward the other. Angles are sampled, and the fragment is extended with these sampled angles. If at any point a fragment is obtained that cannot be closed (the distance to the far stem cannot physically be reached using the number of atoms that are still unplaced), then the fragment is discarded and the procedure restarted. This allows for the rapid generation of sampling loops from the statistical model without the lengthy refinement used by tools such as ModLoop, while still allowing the sampled angles to be used exactly as they are sampled instead of requiring modification to ensure closer as is done with tools such as Loopy.

The Kinematic Closure (KIC) algorithm, used as part of ROSETTA's loop modeling package (Mandell et al., 2009), can be used to create close loops by altering only six of the angles involved. The algorithm, if given an initially closed loop, is able to maintain closure while setting all but six of the torsion angles to any desired angle. This means that all but six angles can be sampled statistically, thought he other six angles are set in order to maintain closure and may not be consistent with the statistical model. ROSETTA can then sample some or most of the angles (depending on the length of the loop), and accept or reject the solution based on how poor the other six angles are. ROSETTA uses KIC to obtain realistic loops by repeated application of the algorithm, accepting or rejecting the moves by simulated annealing.

Another category of loop modeling techniques is the knowledge based or database category. These methods work by finding existing loops that can be placed into the gap. One example is the Loops in Proteins (LIP) database (Michalsky et al., 2003). When introduced, the LIP database demonstrated that there are cases in which a very close match from the database can be used to obtain a very accurate prediction. A more recent version of the LIP database is used by the SuperLooper server (Hildebrand et al., 2009). LIP and SuperLooper work by finding matches within a database of known protein structures. Matches are found by superimposing the stems of that gap to be filled with atoms the same length apart (length refers to the number of residues between them, rather than physical distance), and selecting those with low root mean squared deviation (RMSD). If the stem RMSD is low enough, then not only must the database loop have very similar span, but it also must have similar orientation. Matches are ranked both by the stem RMSD and by sequence similarity.

Another knowledge-based loop modeler is FREAD (Deane and Blundell, 2001), which recently has been reevaluated with newer data (Choi and Deane, 2010) and improved methodology, giving improved accuracy at the cost of being less likely to produce a match. FREAD finds matches based on sequence similarity and filters them to fit by requiring a very similar C_α to C_α span. Although this distance filter is less restrictive than the stem RMSD ranking used by SuperLooper, FREAD has a very strict sequence similarity filter, so if a match is found that passes the filters, it will be highly accurate.

When compared to statistical methods, database methods have the advantage that, should a very similar loop exist in the database, the prediction based on that similar loop will be very accurate. As the protein databank continues to grow, database techniques become more accurate, with no changes to the technique itself. On the other hand, if no match fits into the gap, or all matches that do fit clash with the rest of the protein, then the database technique will be unable to produce a result. Even with low stem RMSD scores, there will often be unrealistic torsion angles at the edges of the loop, and even a few bad angles can cause serious problems with many energy-potential functions.

Some tools, such as ROSETTA—when using the cyclic coordinate descent, or CCD, algorithm (Wang et al., 2007) (as opposed to the KIC algorithm mentioned above)-and FALC (Lee et al., 2010), can be viewed as a hybrid between statistical and knowledge-based methods. In both tools, loops are generated statistically, but based on sequence-specific models derived from fragment matches rather than generic models. Both tools search a database of protein structures to find very short but very similar matches called fragments. These fragments are then used to create statistical models of the torsion angles that are unique for each position in the loop. This allows for statistical sampling with a much reduced search space. ROSETTA samples from the fragment-based models, which generate unclosed loops. These loops are then closed using CCD, where a random angle is changed in order to bring the loop as close to closed as possible. This is a greedy algorithm that can result in bad angles, so moves are accepted and rejected based on how consistent the new angle is with the statistical model, using a simulated annealing procedure.

2. Method Overview

We have developed a new database-based method, which we call LoopWeaver (Loop modeling by the Weighted Scaling of Verified proteins). Matches are found in a database of known structures using the RMSD of the stem regions. These matches are then placed into the gap and ranked. Our method for placing these loops into the gap is substantially different from that used in existing database methods such as SuperLooper and FREAD. Rather than using the RMSD of the stems to determine the placement, we formulate the problem as an instance of the Weighted Multi-Dimensional Scaling problem (de Leeuw, 1977), and solve it using established heuristics. This improves the orientation by reducing the unreasonable angles at the edges of the loop, which means that energy functions are better able to rank our results. Additionally, this method fixes chain-breaks introduced if there are no matches with sufficiently low stem RMSD and can be extended to fix most of the clashes that occur when placing the loop into the gap. A chain-break is when there is an unrealistic bond length the loop connects with either stem (or internally within the loop). On a 2.2 GHz Opteron, it takes roughly 5 minutes to find and close 500 database matches for a length 10 loop. We use the DFIRE (Zhou and Zhou, 2002) energy potential function to rank the final loop candidates. As this is an all-atom potential function, the results must have accurate side-chains built. Side-chains are built using the TreePack tool (Xu, 2005; Xu and Berger, 2006). This adds an average of 5 minutes to the running time. Side-chain packing involves all of the atoms surrounding the region being packed, so this step is also mostly independent of the length of the loop. For some tests, our best candidate is then refined using the KIC refinement protocol included in ROSETTA 3.3.

Figure 1 illustrates two example LoopWeaver results. In Figure 1a we have a case demonstrating the strengths of database methods, where the database loop is nearly identical to the native loop, global RMSD 0.62 Å. Meanwhile, both the ModLoop and Loopy candidates are pulled to the right, with global RMSD 4.37 Å and 3.10 Å, respectively. In Figure 1b, we have a more difficult case for database-based methods. With no good match in the database, selecting from the medium-quality matches is difficult, and without scaling we would select the orange loop (4.06 Å global RMSD). Multidimensional scaling improves the torsion angles and bond lengths where the loop connects to the anchors, allowing for better candidate ranking using an energy potential function, and LoopWeaver selects the blue loop (1.47 Å).

FIG. 1.

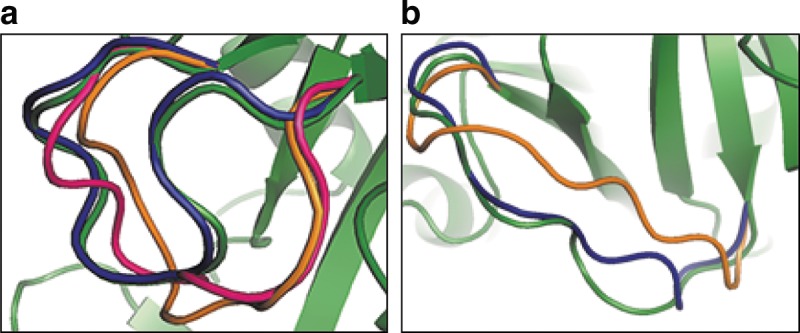
Example Loop Weaver results: (a) Loop Weaver (blue) compared with ModLoop (orange), Loopy (magenta), and native structure (green). Protein T0513, loop length 10, loop B. (b) Loop Weaver (blue) compared with unmodified database loop placement (orange) and native structure (green). Protein T0533, loop length 11, loop A.

3. Results

3.1. Test Sets

As LoopWeaver is a database-driven tool, it cannot be benchmarked using the same target proteins as used in older loop modeling papers. Doing so either puts the database tool at substantial advantage by using a current database (because even if the exact matches are excluded, there still may be many similar matches in the database, so loops that were once difficult may now be considered easy loops to model), or substantial disadvantage by using a database from the same time as the test set, which negates the advantage of rapidly expanding coverage in the protein data bank (PDB). Therefore, we tested our tool against others using more recent test sets. Specifically, we have selected all loop regions [identified by DSSP (Kabsch and Sander, 1983)] of length 6 through 11 from the x-ray targets presented at the CASP8 and CASP9 experiments, while excluding NMR models. The target proteins' native structures were obtained from Zhang Lab at the University of Michigan (http://zhanglab.ccmb.med.umich.edu/). To ensure fairness, our database consists of only protein structures released to the PDB prior to the start of the CASP8 experiments. The Method Details section contains the specifics of the database composition and selection.

Although the CASP targets mostly have full domain template matches available (since their purpose is to test template-based protein modeling), they are selected by hand to be difficult, meaning that although there is a full domain template match, it is not identical to the actual tertiary structure. Since most of such deviations occur in the flexible loop regions, few of our loop targets can be modeled using the full domain template match.

3.2. Details of other methods used

We compare our results to those of several top loop modeling applications. The approaches used by these methods are described in the Introduction section. Here we describe the specific parameters used in order to test these methods. First, we compare with the ModLoop program from the MODELLER package (Fiser et al., 2000). ModLoop was run with refinement set to “fast” and used to generate 50 loops. The candidates returned from MODELLER were then re-ranked according to their DFIRE (Zhou and Zhou, 2002) energy potential, which improves MODELLER's performance over the default DOPE energy function. When evaluating RAPPER, we generated 1000 candidates as described in their article. As with MODELLER, we ranked the RAPPER results by the DFIRE energy potential since this substantially improves their accuracy for all test sets when compared to the default RAPDF energy function. The statistical tool Loopy was run with all parameters left to default and with the number of initial models set to 2000 for loops shorter than length 10, and 4000 otherwise. These are the recommended number of candidates for loops of these lengths (Xiang et al., 2002). While RAPPER and MODELLER take an average of 3 hours (on a 2.2 GHz Opteron) per length 9 loop modeled, Loopy takes around 20 minutes. Finally, we test against version 3.3 of ROSETTA (Mandell et al., 2009). This version uses the KIC algorithm to generate closed loops where all but six torsion angles can be exactly equal to the statistically sampled angle.

ROSETTA is often excluded from benchmarks, as although it produces very accurate predictions, the Monte Carlo simulation required to do so is very time consuming. For example, while it may take 20 minutes for Loopy to generate a prediction for a given loop, ROSETTA can take upward of 5 days to do the same (if one uses the recommended settings). If the number of candidates generated is lowered drastically, ROSETTA can complete in time comparable with other tools, but is no longer accurate, at least when using the CCD algorithm for loop closure. However, the new KIC loop-closing algorithm, although slower than the older CCD algorithm, is accurate even with a greatly reduced running time, where CCD was not. ROSETTA tests used the parameters as described in their online guide (Mandell and Pache, 2011) and generated 10 candidate structures. Additionally, we used the “-loops::fix_natsc” flag to prevent ROSETTA from refolding the native sidechains. By default, ROSETTA will refold any native sidechains that lie within a certain distance (14 Å by default) of a portion of the loop that was remodeled. This may be more realistic for many loop modeling situations, but since other tools do not do this, it would result in ROSETTA solving a much harder problem and being at a disadvantage. Not enabling this option resulted in a longer running time and less accurate predictions, as expected.

We do not compare our method with FALC (Lee et al., 2010), a recent fragment assembly loop modeling server. As with the CCD closure protocol from ROSETTA, FALC is a statistical technique that samples angles from a position-specific phi,psi distribution built using fragment matches. We submitted the CASP8 portion of our length 10 test set to the FALC server and observed an average score of 2.36 local RMSD, and 4.55 global RMSD. This is significantly larger than all other tools on this same subset, so we elected to cease submitting to their server.

Our tables also do not compare our results with those of SuperLooper or FREAD as neither tool returns results for all loops, and it is meaningless to compare averages for different sets. For example, out of the 60 length 10 loops, FREAD (using the same database as LoopWeaver) returned matches for only 6 loops, and SuperLooper (using LIP from 2007) returned 45. For the six results returned by FREAD, the average score was 0.94 Å local RMSD. Over the same six loops, LoopWeaver returns an average score of 0.44 Å. With so few results, there is no significance to this difference, which is the result of one single error in FREAD's selection of database matches. For the other five loops, both tools make predictions based on the same database matches.

Finally, as the ROSETTA KIC paper (Mandell et al., 2009) claims results to those of molecular mechanics refinement as used in PLOP (Zhu et al., 2006), we have not examined molecular mechanics–based solutions or the LoopBuilder (Soto et al., 2007) protocol that uses PLOP for the refinement of Loopy-generated loop candidates.

3.3. Scores

Table 1 shows the results of running our tool, as well as Loopy, MODELLER, and RAPPER, on the various test sets. The “Loops” column indicates the number of targets in the given test set. Note that the longer the gap, the fewer loops of that size there are to test against. There were too few loops of length 12 or longer to justify inclusion. At length 5 and below, all tools make highly accurate predictions that are for the most part indistinguishable, so these sets are also not included.

Table 1.

Average RMSD Scores for Tested Tools

Length	Loops	LoopWeaver	ModLoop	Loopy	Rapper
6	205	0.73/1.27	0.78/1.52	1.00/1.89	1.02/1.83
7	171	1.02/1.85	1.16/2.13	1.21/2.23	1.25/2.19
8	118	1.38/2.59	1.39/2.63	1.42/2.36	1.64/2.77
9	101	1.68/2.91	1.80/3.32	1.85/3.10	1.90/3.31
10	60	1.88/3.33	2.22/3.99	1.95/3.34	2.09/3.53
11	43	2.08/3.37	2.25/3.90	2.45/3.80	2.52/4.16

The first value is the minimum (or local) RMSD, the second value is the unminimized (or global) RMSD.

Included are both the local and global RMSD averages. The local RMSD captures the similarity of the overall shape of a loop without being dependent on its orientation. (A small twist can have a very small effect on the local RMSD, but a huge effect on the global RMSD.) The global RMSD captures both the shape and the orientation of the loop. In both instances, all heavy backbone atoms are used in the calculation. LoopWeaver performs quite well when compared with Loopy, MODELLER, and RAPPER.

ROSETTA results are not included in this table. The reason for this exclusion is that ROSETTA includes a final refinement stage that the other tools lack. While all tools, ROSETTA included, start by generating loop candidates, closing those loop candidates if needed and possibly making small adjustments to improve the energy of the candidates, ROSETTA then goes on to do a thorough refinement of its results using Monte Carlo simulation. Any comparison to ROSETTA should involve results that have undergone similar refinement efforts.

In Table 2, we present the LoopWeaver results after applying ROSETTA's KIC refinement tool, as well as the ab initio ROSETTA results. In both cases, we generate a total of 10 candidates. When generating candidates for the refined LoopWeaver results, we generated all 10 refined loops based on the top LoopWeaver candidate rather than generating one each for the top 10 candidates. We made this decision as the top result is almost always better than the next results, so it would be better to make multiple attempts at refining the leading candidate instead of making only one attempt, which may degrade the quality of the model. LoopWeaver's refined results are better than both the unrefined results and the final ROSETTA results. The ROSETTA team recommends generating 1000 candidates for loop modeling of longer loops, and the extensive simulation involved is very CPU intensive (Mandell and Pache, 2011). Generating 1000 candidates for a single length 9 loop takes an average of 10 days on a 2.2 GHz Opteron, and almost all of this running time is used by the refinement stage. The ROSETTA team also notes that shorter loops may require fewer models. By generating 10 candidates, the same number as we generate while refining LoopWeaver candidates, we attain an average running time of 2.5 hours, comparable to the running time of MODELLER or RAPPER. Even with this restriction, the final ROSETTA results are substantially better than MODELLER and RAPPER, so this restriction is not unreasonable. Nevertheless, in the next section we also run ROSETTA for the recommended time and show that it does not catch up to our final results.

Table 2.

Average RMSD Scores with ROSETTA Refinement

Length	Loops	LoopWeaver	ROSETTA
6	205	0.46/0.87	0.55/1.05
7	171	0.73/1.38	0.79/1.55
8	117	1.00/1.76	1.16/2.17
9	101	1.22/2.25	1.42/2.73
10	60	1.43/2.43	1.67/3.09
11	43	1.72/2.94	1.90/3.38

The first value is the minimum (or local) RMSD, the second value is the unminimized (or global) RMSD.

3.4. Consensus scores

Because knowledge-based and statistical methods work in very different ways, there are many cases in which one yields an accurate prediction and the other does not. It is therefore desirable for us to combine LoopWeaver and one of the ab initio methods.

In Table 3, we present several consensus results. Consensus is done by employing the DFIRE energy potential function to select between the top results of the methods being combined.

Table 3.

Average RMSD Scores for Consensus Results

Length	Loops	LoopWeaver	Loopy + LoopWeaver	ModLoop + LoopWeaver	Loopy + ModLoop
6	205	0.71/1.36	0.69/1.30	0.77/1.48	0.80/1.54
7	171	1.02/1.85	0.96/1.76	1.01/1.84	1.11/2.06
8	118	1.38/2.59	1.21/2.19	1.34/2.53	1.32/2.51
9	101	1.68/2.91	1.61/2.72	1.56/2.90	1.73/3.19
10	60	1.88/3.33	1.81/3.11	2.03/3.59	2.14/3.81
11	43	2.08/3.37	1.96/3.18	2.03/3.53	2.16/3.65

The first value is the minimum (or local) RMSD, the second value is the unminimized (or global) RMSD.

For all test sets, the combination of Loopy and LoopWeaver yields an average score lower than either tool alone. For other combinations, this is not always the case, and we often end up with a score that is somewhere between the two tools rather than superior to both. This is because of the method of selection. None of the methods used optimizes its results against the DFIRE potential. So, although this function is accurate when selecting between candidates generated by the same method, it becomes less accurate when selecting between techniques. Because Loopy results have better DFIRE potential than MODELLER results with similar accuracy, they tend to be selected more often, even in cases when they are substantially worse.

We can improve our results by applying the ROSETTA KIC refinement step to our results, just as we have done before. In Table 4, we show the results of applying KIC refinement to the Loopy and LoopWeaver consensus results. We selected these two tools for the refined consensus step because they had the best combined score prior to refinement. Additionally, running both tools takes a total of less than 30 minutes (average for the length 10 set on a 2.2 GHz Opteron), while RAPPER and MODELLER both take several hours to complete on average. To obtain these results, we make two KIC refinement calls, one for each tool's candidate, with each generating 5 candidates so that we are still generating a total of 10 and are not doubling the refinement step's running time. The top refined candidate is selected by ROSETTA, not by DFIRE as was the case for the unrefined consensus results.

Table 4.

Average RMSD Scores for Refined Consensus Results

Length	Loops	LoopWeaver	Loopy + LoopWeaver	ROSETTA
6	205	0.46/0.87	0.42/0.79	0.55/1.05
7	171	0.73/1.38	0.64/1.15	0.79/1.55
8	118	1.00/1.76	0.81/1.37	1.16/2.17
9	101	1.22/2.25	0.98/1.76	1.42/2.73
10	60	1.43/2.43	1.12/1.92	1.67/3.09
11	43	1.72/2.94	1.43/2.42	1.90/3.38

The first value is the minimum (or local) RMSD, the second value is the unminimized (or global) RMSD.

ROSETTA's KIC refinement makes substantial improvements to the average scores for all of our test sets, allowing us to attain much lower scores than ROSETTA alone while on a similar timescale. These results even hold if we allow the ROSETTA ab initio execution substantially more time. We only have completed numbers for length 9 due to the large amount of CPU time required, but for length 9 and 1000 candidates generated, the average ROSETTA score is 1.01 for the local RMSD and 1.82 for the global. So, if we allow ROSETTA 100 times the running time as our Loopy and LoopWeaver consensus method, ROSETTA approaches but does not overtake our results. Further increases to the number of ROSETTA candidates will result in only minor improvements, since almost all loops have converged by this point. It is also important to note that our own consensus results can be improved by increasing the amount of refinement effort.

4. Method Details

4.1. Database matches

We use a database comprising roughly 14,400 protein chains, selected using PISCES (Wang and Dunbrack, 2003), with the cutoff values being 3.0 resolution, 90% identity, and 1.0 R value. Because our test sets include targets from CASP8, we only allowed PISCES to select from proteins with a release date prior to the start of CASP8 (May 2008). This database is used for all tests, even those involving targets from CASP9 rather than CASP8.

We examine the database of known protein structures and look for appropriately spaced residues that are similar to the stems of the target gap. The metric used for determining the similarity between the stems is RMSD_stem, the RMSD for the C, Cα, and N atoms in each stem. Once we have obtained this large set of matches, we sort according to the stem RMSD and take the top 500 matches. Where SuperLooper takes only matches that have a very low stem RMSD (otherwise the match will potentially introduce a large chain break), our method of fitting the loop can resolve chain breaks, so we take the best matches regardless of quality.

4.2. Fitting the loop

Once suitable loop candidates have been selected from the database, they must be placed into the gap in order to connect to the protein backbone correctly. Because we are selecting matches based on the stem RMSD, this can be done by using the superposition matrix used for computing the minimum stem RMSD and applying it to the rest of the match. If we restrict ourselves to matches with a very low stem RMSD, this will always fill the gap without having unreasonable bond lengths. If we are less strict with regard to the stem RMSD, then the loop will not necessarily fill the gap without having unrealistic atomic distances where the loop connects to the rest of the protein backbone.

One can view the placement of the loop into the gap as an attempt to satisfy two contradictory requirements. The first requirement is that the stems remain the same. The second requirement is that the loop we place should be the same shape as the database match, including the stem region of the database match. This requirement cannot be fully satisfied if we are not allowed to change the stems in the target protein. Using the superposition of the stems is not optimal. The inserted loop does not match the database loop because it has different stems, and although these differences are quite minor, they can have a large impact on the orientation of the loop. Our goal is then to satisfy these two sets of requirements in a more optimal way. This will hopefully not only improve the orientation of the loop, but also resolve any unrealistic bond lengths caused by a less restrictive RMSD cutoff value.

We have chosen to solve these requirements by formulating them as an instance of weighted multidimensional scaling as described in de Leeuw (1977). Weighted multidimensional scaling is a problem often used in statistics, as it can be used to turn high-dimensional data into two or three dimensional data suitable for graphing. It has also been used in MUFOLD (Zhang et al., 2010) as a method for assembling protein fragments. For a given dimension d and n points of data, we have D, a symmetric n × n matrix, as well as W, also a symmetric n × n matrix, and wish to find 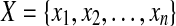where x_i is a coordinate in d-space, such that we minimize the stress, defined as 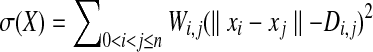. For our problem instances, d = 3 and n is the total number of heavy backbone atoms in both the loop and the stems.

4.2.1. Formulating the problem

The matrix D is defined as

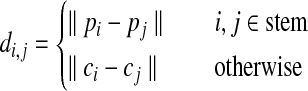(1)

Where 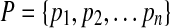is the set of atomic coordinates in the protein being modeled (1 being the first heavy atom in the C-terminus stem, and n being the last atom in the N-terminus stem), and 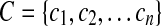is the set of atomic coordinates in the loop candidate using the same numbering system.

The atoms are listed in the order N Cα C O, so atom 0 will be the first N atom in the C-stem.

The reason we use the weighted version of this problem is that not all of the desired distances are equally important. Primarily, we do not want to make any changes to the stem atom, so the pairwise weights between two stem atoms should be very large. Beyond this, atoms that are closer together should be given higher weights. If two atoms pass within a few angstrom of each other within the loop, then they should remain close to this distance regardless of other changes, especially if they are adjacent atoms within the backbone. On the other hand, atoms that are far apart are free to move around a fair bit without changing the overall shape of the protein (if we ignore the effects of that movement on all of the other atoms, that is). Traditionally, a default weight assignment of d^−α is used when the distance values do not have an intrinsic or obvious weight, where d is the corresponding distance and α is often a value between 1 and 2. A value of 2 is recommended (Cohen, 1997) if you want more emphasis on close points than on distant points, which is the case here. We tested a small number of length 8 loops that are not part of our test set and tried exponents ranging from −1 to −3 in increments of 0.1. The best results were achieved at exactly −2. We define the matrix W as

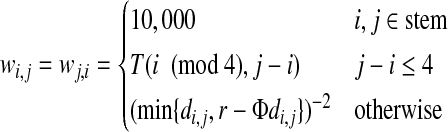(2)

where 0 ≤ i < j < n, T is a 4 × 4 lookup table, r is the diameter of the database match (the largest pairwise distance between any two atoms in the loop), and Φ is the golden ratio conjugate ().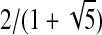

The lookup table T is used to give very high weights to atoms in the same or adjacent residues. In particular, any atoms only one bond apart have very high weights. The weights for corresponding atoms in adjacent residues (Cα to Cα⁺¹ for example) are also quite high so that torsion angles are not changed too much. T is reproduced here in Figure 2. For all atoms, the j − i = 4 cell will be the weight for the distance from that atom to the corresponding atom in the next residue. For the j − i = 1 cell, this will be the weight for the next atom in the protein backbone, with the exception of O. These values are the reciprocals of the variance of the corresponding distances in all loops of our protein structure database. The reasoning for this is that we want a move of one standard deviation to carry the same weight for any pair of atoms. Since the objective function involves squared distances, we use the variance of the distances rather than the standard deviations. This results in the Cα to Cα⁺¹ weight being higher than the N to N⁺¹ or C to C⁺¹, for example, which is to be expected given that the omega torsion angle should change less than the phi and psi angles. Since the higher weight will make this angle less likely to be changed, this is a desirable outcome.

FIG. 2.

Matrix T used for short-distance weights: The rows correspond to the type of the first atom. The columns correspond to how many atoms ahead the second atom is, in the same ordering. So, row 2 column 3 corresponds to the distance between a Cα atom and the N atom in the next residue.

We have the golden ratio term in the last case of the piecewise equation, rather than simply using d_i,j, because we want to preserve the overall shape of the loop as much as possible. Part of this is keeping the diameter of the loop roughly the same. The weight of a distance represents how much a pair of atoms are allowed to move relative to each other while still having a minor effect on that pair's contribution to the stress function. The reason we made the weight equal to d⁻² is that the farther the atoms are apart, the less their exact distance apart matters. However, if they are near to the desired diameter of the loop and we wish to keep the diameter approximately the same, they should not be given as much freedom to move. So, we want the weights to start increasing again as d approaches r. The value Φ, which we use to make the weights increase after a certain point, was selected empirically. We selected target loops from the database, and for each target loop, found the matching loops with RMSD less than 1.5 Å—that is, loops that are fairly similar in shape though not identical. Then, we created bins with a width of 0.5 Å, and for every pair of atoms within the loop, we populated the corresponding bin with the squared deviation of all corresponding pairs of atoms. So if a pair of atoms was 9.4 Å apart in base loop, and we found a database match in which the same atoms were 10.1 Å apart, we would add (9.4 – 10.1)² to the bin for the range 9.25 through 9.5 Å. For most loops tested, the standard deviation roughly follows the equation (min{d_i,j,r – Φd_i,j})². Again, we set the weights to the reciprocal of this value, so that a difference of one standard deviation will contribute equally to the objective function regardless of where that distance occurs.

4.2.2. Solving the problem

We use the SMACOF algorithm (de Leeuw, 1977) for solving the weighted multidimensional scaling problem. This algorithm works by minimizing a simple function that majorizes the stress function, yielding a fast, deterministic heuristic. This algorithm produces a good trade-off between speed and accuracy (Basalaj, 2001) and is also very simple to implement.

4.3. Clashes

The problem formulation does not address the issue of collisions. As the algorithms for solving the problem rely on applying matrix functions to the working set of atomic coordinates, no care is, or can be, paid to making sure the solution will not clash with the rest of the protein.

For resolving clashes, we keep track of all solutions that clash with the rest of the protein. Here, clash is defined as coming within 2.4 Å rather than a more complex method. After using SMACOF to close the database matches, we are left with a list of residues from the protein that clashed with one or more solution. For all of these residues, we evaluate the pairwise DFIRE energy potential between the clashing residues and the loop candidate residues. We then keep only those clashing residues whose average contribution to the energy potential is positive over all of the loop candidates. After discarding these residues, we will be left with residues that clash with, or at least are unfavorably close to, many of the candidates rather than residues that clashed with only a few database matches. The Cα atoms from the central residue of each remaining clashing residue (if any) are then included in the matrices. As these atoms are from the input structure, they are fixed just like the stem atoms and so treated the same. The desired distance d between clash atom a and loop atom b is computed by taking the average of d_a,b for all loop candidates where the total DFIRE potential between a and the loop is negative (negative is good for energy potential functions), as long as the candidate did not clash with a. If the candidate clashed with another atom, it is still included in the average so that these distances can be computed even if there were no clash-free candidates.

This approach is almost always able to resolve clashes. Even in instances where over 90% of the database matches clash after the first round of scaling, we are able to resolve almost all clashes. In most cases, this second round results in less accurate predictions, but a less accurate candidate is more desirable than a clashing candidate.

4.4. Ranking and selection

After we have obtained closed loops through weighted multidimensional scaling, we must determine which is the most likely loop to fill the target gap. We chose the DFIRE (Zhou and Zhou, 2002) energy function, as others have had good results using this function to rank loop candidates (Deane and Blundell, 2001; Zhang et al., 2004). Because DFIRE is an all-atom model, we require the additional step of adding side-chain atoms to the protein backbone. We used the TreePack program (Xu, 2005; Xu and Berger, 2006) to do so.

5. Conclusions

In summary, we have created a new knowledge-based loop modeling tool, LoopWeaver, which extends existing knowledge-based techniques by placing the database loops into the gap region using weighted multidimensional scaling. This improved method of placement not only allows us to use matches with less similar stems without causing breaks in the protein backbone but also improves the quality of the candidate ranking using an energy potential function. These improvements require only a few minutes of running time in order to place 1000 database matches.

We have shown that on its own, LoopWeaver performs better than existing methods, with the exception of ROSETTA. However, LoopWeaver is also able to best ROSETTA when both tools make use of ROSETTA's extensive Monte Carlo refinement protocol. Finally, the combined results from LoopWeaver and Loopy, also using ROSETTA's refinement protocol, are better than using either tool alone, and also better than the ROSETTA results when ROSETTA is allowed 100 times the total running time, which includes both the loop modeling and loop refinement stages.

Acknowledgments

We would like to thank Dong Xu for introducing us to the multi dimensional scaling problem and its applications in protein structure prediction (Zhang et al., 2010).

This work was made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: www.sharcnet.ca) and Compute/Calcul Canada.

Daniel Holtby's research is funded in part by an NSERC PGS D scholarship. Ming Li's research is supported in part by NSERC Grant OGP0046506, Canada Research Chair program, an NSERC Collaborative Grant, OCRiT, Premier's Discovery Award, and the Killam Prize.

Disclosure Statement

No competing financial interests exist.