Charge Group Partitioning in Biomolecular Simulation

Abstract

Molecular simulation techniques are increasingly being used to study biomolecular systems at an atomic level. Such simulations rely on empirical force fields to represent the intermolecular interactions. There are many different force fields available—each based on a different set of assumptions and thus requiring different parametrization procedures. Recently, efforts have been made to fully automate the assignment of force-field parameters, including atomic partial charges, for novel molecules. In this work, we focus on a problem arising in the automated parametrization of molecules for use in combination with the gromos family of force fields: namely, the assignment of atoms to charge groups such that for every charge group the sum of the partial charges is ideally equal to its formal charge. In addition, charge groups are required to have size at most k. We show 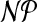-hardness and give an exact algorithm that solves practical problem instances to provable optimality in a fraction of a second.

1. Introduction

In the context of drug development, biomolecular systems such as protein-peptide (Yang et al., 2010), protein-ligand (Sharma et al., 2009), and protein-lipid interactions (Boggara et al., 2010) can be studied with the use of molecular simulations (Allen and Tildesley, 1987; van Gunsteren et al., 2006) using a force-field model that describes the interatomic interactions. Many biomolecular force fields are available, including amber (Cornell et al., 1995), charmm (Brooks et al., 2009), opls (Jorgensen et al., 1996), and gromos (Scott et al., 1999; Oostenbrink et al., 2004; Schmid et al., 2011). These force fields have in common that the nonbonded intermolecular interactions are represented in terms of interatomic pair potentials.

Typically, the number of atoms in biomolecular systems are in the range of 10⁴ to 10⁶. To observe relevant biological phenomena, time scales in the order of nano- to milliseconds need to be simulated. For such large-scale systems, evaluating all atom–atom interactions is practically infeasible. One way of dealing with this is to only consider interactions of atoms whose distance is within a pre-specified cutoff radius. Since not all interactions are considered, an error is introduced. The magnitude of the error due to omitting atom–atom interactions is inversely proportional to the distance between the atoms. More problematically, there are discontinuities as atoms move in and out of the cutoff radius.

Errors and discontinuities are reduced by combining atoms into charge groups, for which individual centers of geometry are determined. If the distance between two centers of geometry lies within the cutoff distance then all interactions between the atoms of the involved charge groups are considered. Ideally, charge groups should be neutral as interactions are then reduced to dipole–dipole interactions that scale inversely proportional to the cubed interatomic distance. Charge groups should not be too large. This is because the effective cutoff distance of an individual atom in a given charge group is given by the cutoff distance minus the distance to the center of geometry of the charge group. If the distance of an atom to the center of geometry becomes large, the effective cutoff becomes small, leading to errors and discontinuities as described above. For the same reason, charge groups should be connected as interatomic bonds impose spatial proximity.

To simulate a molecule, a force field requires a specific topology, which includes the atom types, bonds and angles, the atomic charges, and the charge group assignment. Most biomolecular force fields come with a set of topologies for frequently simulated molecules such as amino acids, lipids, nucleotides, and cofactors. Unparametrized molecules, however, require the construction of their topologies. Such a situation occurs, for instance, when assessing the binding affinity of a novel druglike compound to a certain protein.

Manually building topologies for new compounds is a tedious and time-consuming task, especially when a large chemical library needs to be screened, for example, when determining binding affinities for large sets of potential drug compounds to a newly discovered protein target. Therefore, automated approaches are needed.

Here, we focus on the gromos family of force fields, which has been specifically tailored to simulate biochemical processes, including protein-drug binding and peptide folding. A widely used topology generator for the gromos force field is prodrg (Schüttelkopf and van Aalten, 2004). However, the charge group assignment by prodrg for amino acid topologies contained several large charge groups comprising disconnected atoms, which is inconsistent with gromos (Lemkul et al., 2010). The Automated Topology Builder (atb) is a recent method for automated generation of gromos topologies (Malde et al., 2011). The assignment of atomic charges and charge groups by the atb proceeds in three consecutive stages. Firstly, partial charges are computed using quantum calculations. Subsequently, the symmetry of the molecule is exploited to ensure that symmetric atoms have identical charges. Finally, the molecule is partitioned into charge groups using a greedy algorithm. The atb method was experimentally verified for a set of biologically relevant molecules (Malde et al., 2011). For some large molecules, such as the cofactor adenosine-5’-triphosphate (ATP), however, the atb assigns too large charge groups, which leads to instabilities during simulation as described above.

As existing automated procedures such as prodrg and the atb fail in assigning appropriate charge groups, we have investigated the problem in detail. Our contribution is threefold: (1) We introduce the charge group partitioning problem and give a sound mathematical problem definition resulting in charge groups of small size and zero charge. We prove 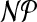-hardness of the problem and identify important special cases, for which we give polynomial time algorithms. (2) Exploiting the properties of molecular structures enables us to present a tree decomposition-based algorithm that solves typical practical problem instances to optimality within fractions of a second. (3) We evaluate the performance of our method by running simulations using the resulting charge group assignments of amino acid side chains, which yield results consistent with experimentally known values. Moreover, for large, highly charged molecules such as ATP, we obtain charge groups that are both suitable for use in simulations as well reasonable from a chemical perspective.

2. Problem Statement and Complexity

In this section, we give a formal definition of the problem associated with assigning appropriate charge groups within a molecule. Our aim is to capture the two important aspects of chemical intuition discussed above: (1) The number of atoms in a charge group should not exceed a given integer k and (2) the sum of partial and formal charges of a charge group is ideally equal. Mathematically, the latter condition is equivalent to requiring the sum of differences of formal and partial charges in a charge group to be close to zero. We prove 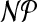-hardness of the problem even if we take into account special characteristics of graphs representing a molecular structure. For the special case k = 2, we obtain a polynomial-time algorithm by reducing the problem to a minimum-cost perfect-matching problem.

A molecular structure can be modeled as a degree-bounded graph G = (V, E), where the nodes correspond to atoms and the edges to chemical bonds. In addition, we consider node weights 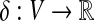, where δ(v) corresponds to the difference between formal and partial charge of the atom v. A formal definition of the charge group partitioning problem is as follows:

Definition 1

(Charge group partitioning, cgp). Given a graph G = (V, E), node weights 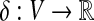, and an integer 2 ≤ k ≤ |V|−1, find a partition 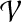of V such that for all 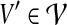it holds |V′| ≤ k, the subgraph G[V′] induced by V′ is connected, and which has minimal total error

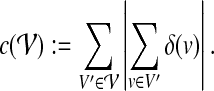Each subset 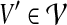of the nodes in the partition corresponds to a charge group. The following theorem shows 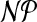-hardness of the problem, even for the restricted case where G is planar. As we will discuss in Section 3, most molecular graphs are planar.

Theorem 1

cgp is 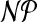-hard, even in the restricted case where G is planar, k = 4, the maximum degree of a node in the graph is 4, and the node weights are .

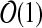Proof

Clearly, the problem belongs to 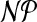. Consider the following problem.

Definition 2

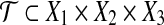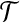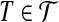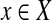(Planar three-dimensional matching, planar 3DM). Given disjoint sets X₁, X₂, X₃ with |X₁| = |X₂| = |X₃| = m and a set of n triples . The bipartite graph B, with as its one color class and X = X₁ ∪ X₂ ∪ X₃ as its other color class and an edge between and if and only if 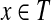, is planar. Each element of X appears in 2 or 3 triples only. Does there exist a perfect matching in 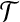(i.e., a subset 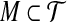of m triples such that each element of X occurs uniquely in a triple in )?

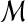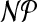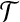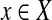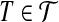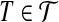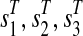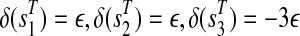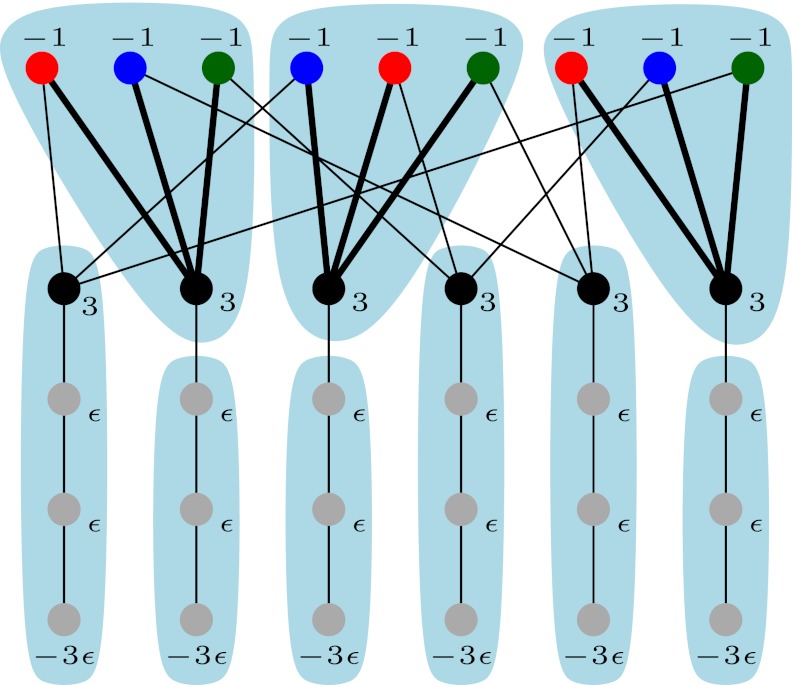
This problem has been shown as -complete by Dyer and Frieze (1985). We reduce it to cgp in polynomial time. Take the bipartite graph B in the definition of Planar 3DM with and X as color classes. Give each a weight δ(x) = −1 and each a weight δ(T ) = 3. For each we introduce three extra vertices with weights , for an arbitrary 0 < ε < 1, and connect them by the path 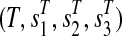, which we call the tail of T. See Figure 1 for an example. Clearly, the resulting graph G remains planar (and bipartite). Since each 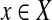is in at most three triples, it is easy to see that G has bounded degree 4.

FIG. 1.

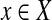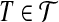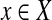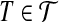Reduction from planar 3dm (see Definition 2): every corresponds to a node with weight δ(x) = −1, whereas every corresponds to a node with weight δ(T) = 3. There is an edge between nodes and if and only if 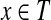. In addition to every 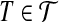, a path (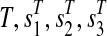) is attached with weights 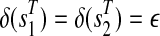and .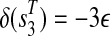

Given a feasible partition to the cgp-instance, we say a group is of type i if it contains exactly i nodes from 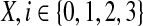and exactly one node from 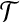. Notice that, for i = 1, 2, 3, each type i group contributes error (3−i) by itself, and because it covers a 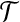-node and therefore leaves a tail-path, it contributes indirectly an extra error ε (the alternative of including one of the tail nodes into the group with the triple node does not decrease the sum of the two errors). A type 0 group consists of a 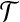-node only and therefore will be combined with its tail to yield an error of 3 − ε. Let y_i denote the number of type i groups, 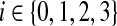. Let y denote the number of X-vertices that form a group on their own. Then the feasible solution has total error

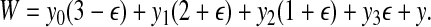(1)

We show that there exists a perfect matching if and only if G admits a partition with total error

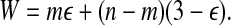Suppose 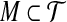is a perfect matching. For every triple 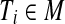, we create a type 3 group consisting of the corresponding vertex T_i in G and the three vertices corresponding to its three elements. Hence y₃ = m. By the properties of the matching all X-vertices of G are now covered, and n − m triple-vertices of G remain uncovered. The latter necessarily form n − m type 0 groups: y₀ = n − m. Insertion in Equation (1) yields W = mε + (n − m)(3 − ε).

Now assume that no perfect matching exists. First, note that in any optimal solution to the cgp-instance y = 0. Assume y > 0 and let 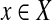be such a vertex. Then every neighbor of x in 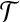is contained in a group of type i, with i ≤ 2. Therefore, adding x to any such group would decrease the cost of the solution by at least 2(1−ε). Furthermore, every group that contains two nodes from 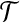can be split into two groups without increasing the cost of the solution. Now, since there exists no perfect matching, we need m + c groups of type 1, 2, or 3, for some c ≥ 1, to cover all vertices in X. Using equations

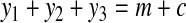(2)

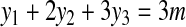(3)

we get

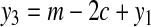(4)

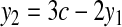(5)

and the cost contributed to Equation (1) by type 1, 2, and 3 groups becomes equal to mε + c(3 + ε). Together with the remaining n − m − c groups of type 0, the total weight becomes

   ■

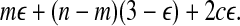Using the same reduction but extending the tails to length k − 1 paths with ε weight on the internal vertices and − (k−1)ε weight on the leaf proves the problem to be hard for any k ≥ 4.

cgp with k = 2 can be solved by formulating a minimum-cost perfect-matching problem. Starting from G = (V, E), we assign a weight to the edges that is equal to the error that the pair of vertices will contribute if chosen as a group of the partition. For each vertex 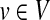creates a shadow vertex v′ with δ(v′) = 0. The weight on the edge {v, v′} is then |δ(v)|, the error if v is chosen as a single vertex group. Additionally, we insert an edge {u′, v′} of weight 0 if and only if 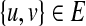. It is not difficult to see that a minimum-cost perfect-matching in this graph corresponds to an optimal partition, where an edge in the matching between a vertex and its shadow vertex signifies a single vertex group in the partition.

For k = 3 and for general, non-planar graphs, cgp is 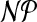-hard by reduction from ordinary 3DM. Intriguingly, for planar graphs and k = 3 the complexity is still unknown.

3. Dynamic Programming for Bounded Treewidth

While problem cgp is 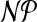-hard in general, as shown in the previous section, we can solve it by a dynamic program in polynomial time if the molecule graph is a tree. Starting from the leaves, we proceed toward an arbitrarily chosen root node. At a given node i we guess the group V′ that contains i in the optimal solution to the subproblem induced by the subtree rooted at i and recurse on the subtrees obtained when removing V′. Due to the size restriction |V′| ≤ k, we only have to consider a polynomial number of groups.

Although the structural formula of biomolecules is not always a tree, as we will see later, it is usually still treelike, which has already been exploited in Dehof et al. (2011). Formally, this property is captured by the treewidth of a graph (Robertson and Seymour, 1986). The definition is as follows.

Definition 3

A tree decomposition (T, X) of a graph G = (V, E) consists of a tree T and sets X_i for all 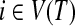, called bags, satisfying the three following properties:

• 1. Every vertex in G is associated with at least one node in

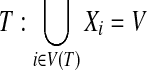
• 2. For every edge 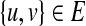, there is an 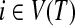such that {u, v} ⊆ X_i.

• 3. The nodes in T associated with any vertex in G define a subtree of T.

The width of a tree decomposition is max_i|X_i| − 1. The treewidth of G is the minimum width of any tree decomposition of G.

In this section, we propose a tree decomposition-based dynamic program for problem cgp, whose running time grows exponentially with the treewidth of G. Therefore, a tree decomposition of small width is crucial for the efficiency of our approach. Unfortunately, computing a tree decomposition of minimum width is 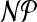-hard (Arnborg et al., 1987). However, for the class of r-outerplanar graphs, an optimal tree decomposition can be determined in time 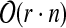(Alber et al., 2005). A graph is r-outerplanar if, after removing all vertices on the boundary face, the remaining graph is (r − 1)-outerplanar. A graph is 1-outerplanar if it is outerplanar, that is, if it admits a crossing-free embedding in the plane such that all vertices are on the same face. Interestingly enough, most molecule graphs of biomolecules are r-outerplanar for some small integer r. For example, Horváth et al. (2010) have observed that 94.3% of the molecules in the National Cancer Institute (NCI) database (http://cactus.nci.nih.gov/) are 1-outerplanar. Even more, every r-outerplanar graph has treewidth at most 3r − 1 (Bodlaender, 1998). Therefore, not surprisingly, Yamaguchi et al. (2003) observed that out of 9,712 chemical compounds in the kegg ligand database (Goto et al., 2002), all but one had treewidth between 1 and 3, with a single molecule having treewidth 4. In fact, among the molecules considered here, the maximal treewidth was 2. As a result, our tree decomposition-based dynamic program found an optimal charge group partitioning in well under one second.

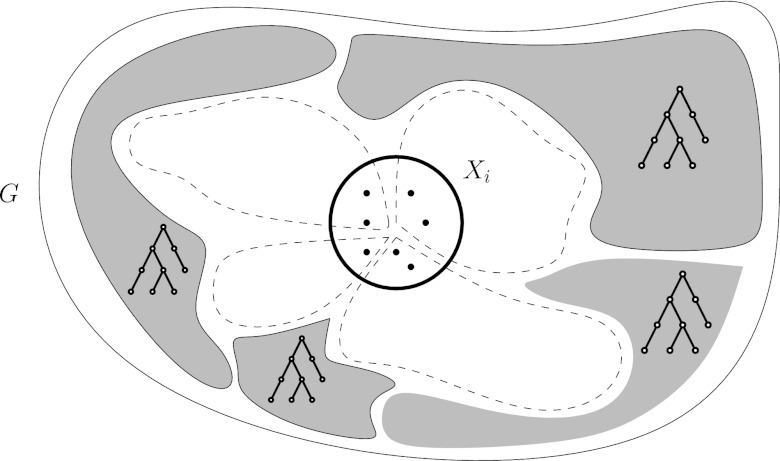
Let (T, X) be a tree decomposition of width ℓ for graph G = (V, E). The high-level idea of the algorithm is as follows (Fig. 2). For an arbitrarily chosen root i of the tree decomposition, we guess the groups that intersect X_i, denoted by the dashed lines in the figure. After removing these groups, G falls apart into connected components, denoted by the filled regions in the figure. By the properties of a tree decomposition, these connected components will correspond one-to-one to the subtrees of the tree decomposition obtained by removing bags that became empty. Recursing on the roots of these new subtrees yields the overall optimal solution.

FIG. 2.

Illustration of the tree decomposition-based dynamic programming algorithm. A graph G falls apart into connected components (gray regions) by removing the groups (dashed lines) that intersect bag X_i.

Without loss of generality we assume that T has at most n := |V | vertices and depth 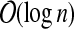(Bodlaender, 1989), with r being the root of T. In the following, we let 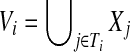, where T_i denotes the subtree rooted at i, and write V(T_i) for the set of nodes in T_i. We define an extension of a partition of a vertex set V₁ ⊆ V with nodes in V₂\V₁ into connected subgraphs of G of size k at most:

Definition 4

For vertex sets V₁ ⊆ V₂ ⊆ V, set 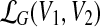contains all sets 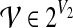with 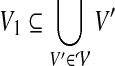, all sets in 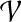being disjoint, and all 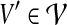satisfying: (i) G[V′] is connected, (ii) |V′| ≤ k, and (iii) V₁ ∩ V′ ≠ ∅.

Furthermore, by r(S) we denote the root of a subtree S of T, and for any node i in T and any vertex set A ⊆ V we denote by 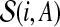the set of trees, corresponding to the connected components of 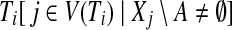whose roots are not a descendant of another subtree in 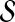(i.e., there are no 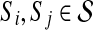for which 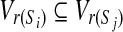). With a slight abuse of notation, for sets A ⊆ V and 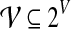we will write 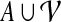instead of 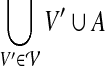, when the meaning is clear from the context. Then for any node i of T and any subset A ⊆ V, the cost of an optimal solution to cgp on graph G[V_i\A], denoted by cgp(i, A), can be described by the recurrence

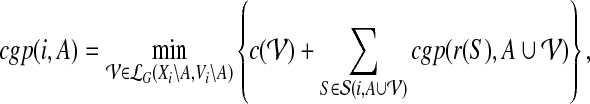(6)

which also holds in the base case where 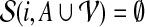, in particular when i is a leaf of T. The optimal partition has cost cgp(r, ∅). We can solve the recurrence relation (Eq. 6) using dynamic programming.

Theorem 2

The cost of an optimal solution to cgp on a graph of treewidth ℓ and maximum degree d can be computed in time .

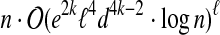Proof

Let (T, X) be a tree decomposition of G of width k and depth 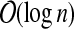. Consider an arbitrary node i in T and a subset A ⊆ V, for which X_i\A ≠ ∅. We first observe that

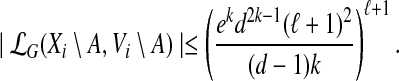(7)

Indeed, for each partition 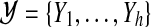of X_i\A, the number of possible extensions in 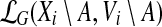can be bounded as follows. For 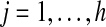, let B_j be the set of vertices at distance at most k − 1 from Y_j in the graph G_j = G[V_i\(A ∪ X_i) ∪ Y_j] (this set can be found by contracting Y _j to a single vertex y_j and performing BFS in G_j starting from y_j). Each possible extension is then given by a family of pairwise-disjoint sets 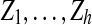, where Z_j ⊆ B_j, G[Z_j ∪ Y_j] is connected and |Y_j ∪ Z_j| ≤ k. Since the degree of each vertex is at most d, it follows that |B_j| ≤ |Y_j|d^k−1. Consequently, the total number of choices of sets Z_j is at most (ℓ + 1)e^kd^2k−1/(k(d−1)) (and all these choices can be enumerated in time 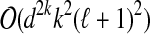and space 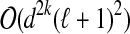) (see Uehara, 1999). Since h ≤ ℓ + 1, the overall number of choices we consider is bounded by Equation (7).

Since every 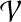considered in Equation (6) intersects X_i\A (requirement 3), and due to the properties of a tree decomposition and the connectivity of all parts 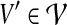(in G), the induced subgraph 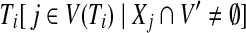, for all 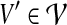, is a subtree of T_i rooted at i. Keeping this crucial observation in mind, let us focus our attention on a particular node i in T, and bound the number of sets A that we need to consider on the left-hand side of Equation (6). To this end, it is convenient to consider the computation tree T for Equation (6) (that is, the recursion tree obtained when solving Eq. (6)) in a top-down fashion. We can label each node in this tree by (j, A), where j is a node in T and A is a subset of V. The root of T is (r, ∅), and the children of node (j, A) are labeled by the elements of the set .

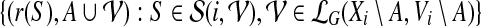Consider node (i, A) in T, and let 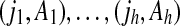be its ancestors. It is clear that every vertex 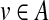belongs to exactly one connected component (group) V′ that originated at some ancestor 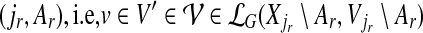; we say, in this case, that ancestor (j_r, A_r) contributes to (i, A). Since X_i\A ≠ ∅ [by our assumption that (i, A) appears in the computation tree], it follows by our observation above that the number of ancestors that contribute to (i, A) is at most ℓ (since each such ancestor contributes at least one component that has a nonempty intersection with X_i). In other words, A can be partitioned into at most ℓ parts, such that each part belongs to a connected component that originated at some ancestor of (i, A), and hence, |A| ≤ kℓ. The number of choices for the contributing ancestors is at most depth(T )^ℓ. Using an argument similar to the one used to derive Equation (7), we can conclude that for each vertex v in one of the chosen ancestors, the number of connected components originating at v is at most e^kd^2k−1/(k(d−1)), and thus we obtain 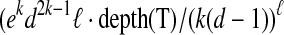for the total number of choices for A. For each such choice we have to evaluate a number of sets bounded by Equation (7), whose properties 1–3 can be verified in time . Determining the roots of subtrees in takes time .   ■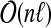

Additionally storing, along with each entry cgp(i, A), the partition 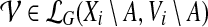minimizing the right-hand side in Equation (6), allows us to finally reconstruct a charge group partition that gives the optimal cost.

4. Experimental Evaluation

We implemented the dynamic programming method for bounded treewidth in C++ using the lemon graph library (http://lemon.cs.elte.hu). We used libtw (www.treewidth.com/) to obtain bounded treewidth decompositions of the input molecules. In our implementation, we solve the dynamic programming recurrence Equation (6) in a top-down fashion by employing memoization.

4.1. Hydration-free energy of amino acid side chains

We tested the quality of charge group assignments by comparing the calculated free energies of solvation in water of a set of 14 charge-neutral amino acid side chain analogs to experimental values, which are denoted by ΔG_hyd,exp (Gerber, 1998; Oostenbrink et al., 2004). For each analog, we used the gromos 53A6 covalent and van der Waals parameters (Oostenbrink et al., 2004) and partial atomic charges symmetrized by the atb (Malde et al., 2011). A united-atom representation is used for aliphatic carbon groups. For comparison, we also include the manually parametrized solution that the gromos 53A6 force field provides (Oostenbrink et al., 2004). The topologies are derived from the amino acid structures by truncating at the C_α–C_β bond. For simplicity, we refer to these analogs by their parent amino acid.

Using the gromacs 4.5.1 package (Berendsen et al., 1995), we computed the free energy of hydration ΔG_hyd,calc using the thermodynamic integration method (Beveridge and DiCapua, 1989). A series of simulations were performed at a constant pressure of p = 1 bar and a constant temperature T = 298.15 K. The free energy was calculated for the process A → B, which involved switching off all nonbonded interactions of the solute in water and in the gas phase. The hydration-free energy is calculated as ΔG_hyd,calc = ΔG_AB,solution−ΔG_AB,gas (Villa and Mark, 2002). The simulations were performed in cubic periodic boxes of length L ≈ 3 nm. Depending on the analog, the solvated system contained approximately 900 SPC (Villa and Mark, 2002) water molecules.

As described in the introduction, neutral charge groups lead to more accurate simulation results. In our problem definition, we aim to identify a charge group assignment in which the constituent charge groups have small residual error, which is the absolute difference between the sum of the formal charges and the sum of the partial charges of the atoms in the charge group. To ensure neutral charge groups where possible, we adjust the partial charges slightly by redistributing the residual error of every charge group over its atoms.

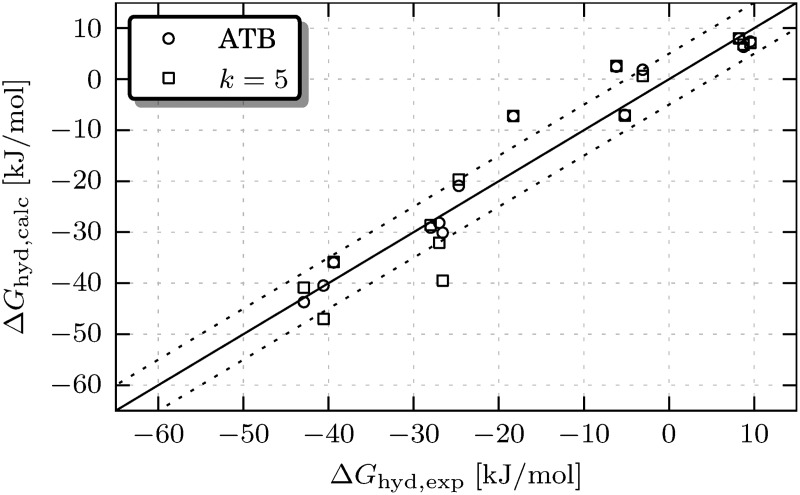
The results are presented in Table 1 and Figure 3. The gromos 53A6 simulation results (ffG53A6 in Table 1) for the studied analogs show good agreement with experiment, which is not surprising as the force field has been parametrized to reproduce the hydration-free energy (Oostenbrink et al., 2004). Using the atb charge group assignment solution (ATB in Table 1) leads to slightly larger deviations from experiment, but the average deviation is also within the experimental error of approximately 5 kJ/mol (Malde et al., 2011). Although the current method leads to values close to those obtained experimentally, they deviate slightly more from experiment than the atb values.

Table 1.

Comparison of Hydration-free Energies ΔG_hyd of Amino Acid (AA) Analogs

		ΔGhyd,calc
AA analog	ΔGhyd,exp	ffG53A6		ATB		k = 5
Asn	−40.6	−42.7	(2.1)	−40.5	(0.1)	−47.0	(6.4)
Asp	−28.0	−30.1	(2.1)	−29.1	(1.1)	−28.6	(0.6)
Cys	−5.2	−4.9	(0.3)	−7.0	(1.8)	−7.1	(1.9)
Gln	−39.4	−40.4	(1.0)	−35.9	(3.5)	−35.9	(3.5)
Glu	−27.0	−27.0	(0.0)	−28.2	(1.2)	−32.1	(5.1)
His	−42.9	−44.8	(1.9)	−43.7	(0.8)	−40.9	(2.0)
Ile	8.7; 8.8	9.1	(0.3)	6.3	(2.5)	6.7	(2.1)
Leu	9.4; 9.7	10.8	(1.2)	7.4	(2.2)	7.1	(2.5)
Lys	−18.3	−18.1	(0.2)	−7.2	(11.1)	−7.2	(11.1)
Met	−6.2	−7.4	(1.2)	2.5	(8.7)	2.6	(8.8)
Phe	−3.1	−1.3	(1.8)	1.8	(4.9)	0.6	(3.7)
Trp	−24.7	−25.9	(1.2)	−20.9	(3.8)	−19.7	(5.0)
Tyr	−26.6	−26.9	(0.3)	−30.1	(3.5)	−39.5	(12.9)
Val	8.2	8.5	(0.3)	8.0	(0.2)	8.0	(0.2)
Average			(1.1)		(3.2)		(4.7)

All free-energy values are given in kJ/mol. When two values separated by a semicolon are given, two experimental values were found. The absolute free-energy differences between simulation outcomes and the experimental values are given in parentheses. The average values of these differences are given in the bottom line. “ffG53A6” denotes results using the default gromos force field parameters for the analog, “ATB” denotes those using the atb charge group assignment, “k = 5” denotes those using our method. We performed a two-tailed paired Student's t-test between the distributions given in column 6 (ATB) and column 8 (k = 5) resulting in a p-value of 0.2867. The difference in hydration-free energy differences is thus not statistically significant.

FIG. 3.

Calculated ΔG_hyd values versus experimental ones, showing the effect of the charge group assignment on the simulated hydration-free energy. The labels in the legend are the same as in Table 1. The solid line represents perfect agreement with experiment, dotted lines indicate the ±5 kJ/mol approximate experimental error.

4.2. Adenosine tri-phosphate

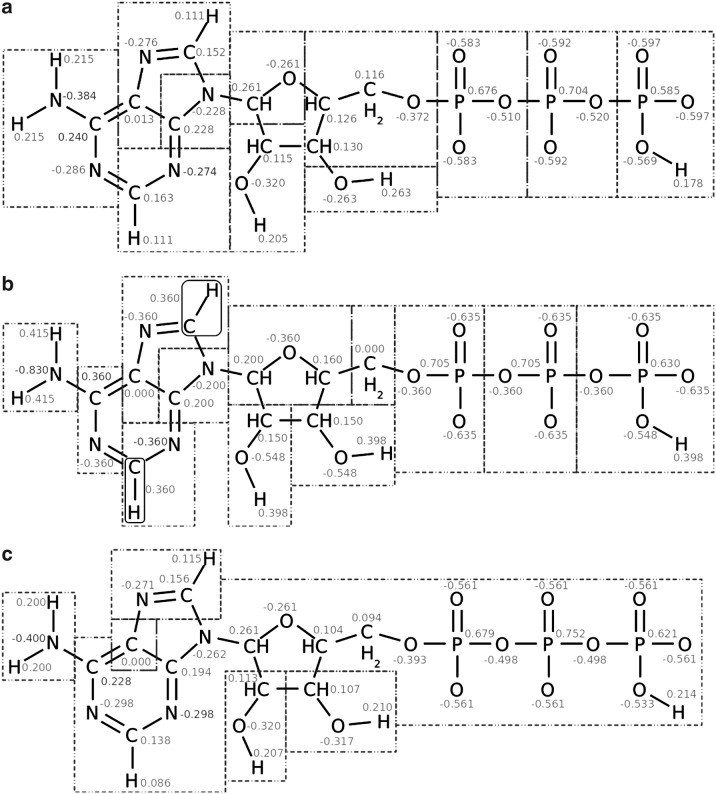
Although showing good performance on the amino acid side chains, the atb method may lead to unacceptably large charge groups, in particular for large highly charged molecules. An example is the cofactor ATP, for which the atb combined all phosphate groups and part of the ribose and nucleotide ring systems into a single charge group (Fig. 4c). In Figure 4b, the gromos 53A6 charge group assignment is given. For comparison, our solution is presented in Figure 4a and shows that the phosphate groups have been sorted in separate charge groups in agreement with the 53A6 assignment and in line with chemical intuition where one expects functional group such as phosphate, amino, and hydroxyl moieties to form separate charge groups.

FIG. 4.

Charge group assignments for adenosine tri-phosphate (ATP) at pH 5.0. The total molecular charge is −3. The partial charges are shown in gray. (a) Our optimal assignment according to Definition 1, obtained with k = 5, (b) gromos 53A6 assignment, and (c) assignment by the atb. Note that the C–H segments indicated by the rounded boxes are considered as single atom types in the gromos assignment, whereas they comprise two atoms in the other assignments.

5. Discussion

In this work, we have formally introduced the charge group partitioning problem that arises in the development of atomic force fields, and more generally, in the identification of functional groups in molecules. The problem is to assign atoms to charge groups of size at most k and such that for every charge group the sum of its partial charges is close to the sum of its formal charges. We showed 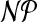-hardness for k ≥ 4 and proposed and implemented an exact algorithm capable of solving practical problem instances to provable optimality. With this combination of rigorous definition and exact solution approach, we have made a first step toward formalizing and quantifying some of the aspects that make up “chemical intuition”.

Algorithmically, we showed that the case k = 2 is solvable in polynomial time. In addition, we have presented a polynomial-time algorithm for bounded charge group size in cases where the molecular graph is a tree. Based on the observation that molecular graphs have bounded treewidth in practice and exploiting further properties such as outerplanarity and bounded degree, we developed a practical dynamic programming algorithm, which is based on a tree decomposition of the graph corresponding to the chemical structure of interest. An interesting open question is to settle the complexity status for the case k = 3.

Since our method relies on point charges obtained from quantum mechanical calculations, the quality of charge group assignments and subsequently of simulation outcomes depends on the accuracy of these calculations. However, our experiments have shown that taking into account charge group size and neutrality already gives good results, especially for large highly charged molecules such as ATP, where other methods fail to produce meaningful solutions. Still, the greedy partitioning algorithm built into the atb performs better on the set of smaller amino acid side chain molecules, which is due to the fact that this method exploits additional chemical knowledge. It is thus able, for instance, to deal with a symmetric molecule such as the tyrosine side chain, where the charge group assignment of our new method resulted in a large deviation because we do not consider symmetry in our problem definition. We will, therefore, investigate how to incorporate symmetry into our approach, which is not trivial as symmetry may interfere with the optimal substructures required by the dynamic program. In addition to symmetry, we plan to integrate other aspects of chemical intuition. For example, we will investigate the effect of bounding the error per charge group. Additionally, we plan to integrate constraints that take spatial geometry into account rather than using the number of atoms as a measure for charge group size. We would like to stress that only through a proper problem definition, together with a method capable of obtaining provably optimal solutions, one is able to make progress in answering the question how a good charge group partition should look like.

Acknowledgments

We thank SARA Computing and Networking Services (www.sara.nl) for their support in using the Lisa Compute Cluster. In addition, we are grateful to the referees for helpful comments. The research leading to these results has received support from the Tinbergen Institute as well as from the Innovative Medicines Initiative Joint Undertaking under grant agreement no. 115002 (eTOX), resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/20072013) and EFPIA companies in-kind contribution.

Author Disclosure Statement

The authors declare that no competing financial interests exist.