Abstract
Cilia and flagella are microtubule-based organelles that protrude from the cell body. Ciliary assembly requires intraflagellar transport (IFT), a motile system that delivers cargo from the cell body to the flagellar tip for assembly. The process controlling injections of IFT proteins into the flagellar compartment is, therefore, crucial to ciliogenesis. Extensive biochemical and genetic analyses have determined the molecular machinery of IFT, but these studies do not explain what regulates IFT injection rate. Here, we provide evidence that IFT injections result from avalanche-like releases of accumulated IFT material at the flagellar base and that the key regulated feature of length control is the recruitment of IFT material to the flagellar base. We used total internal reflection fluorescence microscopy of IFT proteins in live cells to quantify the size and frequency of injections over time. The injection dynamics reveal a power-law tailed distribution of injection event sizes and a negative correlation between injection size and frequency, as well as rich behaviors such as quasiperiodicity, bursting, and long-memory effects tied to the size of the localized load of IFT material awaiting injection at the flagellar base, collectively indicating that IFT injection dynamics result from avalanche-like behavior. Computational models based on avalanching recapitulate observed IFT dynamics, and we further show that the flagellar Ras-related nuclear protein (Ran) guanosine 5'-triphosphate (GTP) gradient can in theory act as a flagellar length sensor to regulate this localized accumulation of IFT. These results demonstrate that a self-organizing, physical mechanism can control a biochemically complex intracellular transport pathway.
Keywords: Chlamydomonas, self-organization, nuclear import, long flagella mutants, power spectrum
Cilia and flagella generate fluid flows and mediate cell signaling (1), and ciliary length defects cause a wide range of congenital human diseases. Many of these defects arise from mutations in intraflagellar transport (IFT) proteins, which are required to build and maintain the length of cilia and flagella (2). The IFT proteins form complexes called IFT trains that haul cargo to the ciliary tip for assembly (3–7). IFT trains first localize to the basal body (8) and then enter the cilium as a group in an injection event. Understanding the IFT injection process is critical to understanding ciliary length control because the injection rate sets the overall amount of transport that in turn determines the rate of steady-state flagellar assembly (9).
A previous report indicated that entry of new IFT trains is periodic (10), suggesting that a biochemical oscillator may regulate IFT injection. However, the biochemical components of this hypothetical oscillator are currently unknown. Components of the gate controlling entry into the cilium are being identified (4, 5), but identifying the oscillating components themselves could be an extremely difficult biochemical problem because it is not obvious how to determine whether any given protein is part of the oscillator. In fact, it is not even clear whether there must be a biochemical oscillator at all. An alternative mechanism known as avalanching can produce nearly periodic behavior without needing any extra regulatory components.
Avalanches are spontaneous transfers of energy or material that propagate through a system to varying degrees such that event magnitude is determined by degree of propagation (11–13). Avalanche-like behavior occurs in wide-ranging examples in nature, from sand piles (13) and magnetic turbulence in plasmas (14) to solar flares (15), earthquakes (16), and neuronal activity (17), and has even been described in microtubule dynamics (18) and neuronal growth cone motility (19). Avalanching systems share the common feature that they are driven toward an unstable state by an input of energy or material that accumulates until an avalanche returns the system to a more stable state. The underlying mechanism of avalanching (11) produces several characteristic features that can be detected by time series analysis, such as bursting and long memory, which occur because individual events can propagate and influence future events, and a fat-tailed event size distribution, which occurs because there is no characteristic event size due to the propagating nature of avalanches.
Results and Discussion
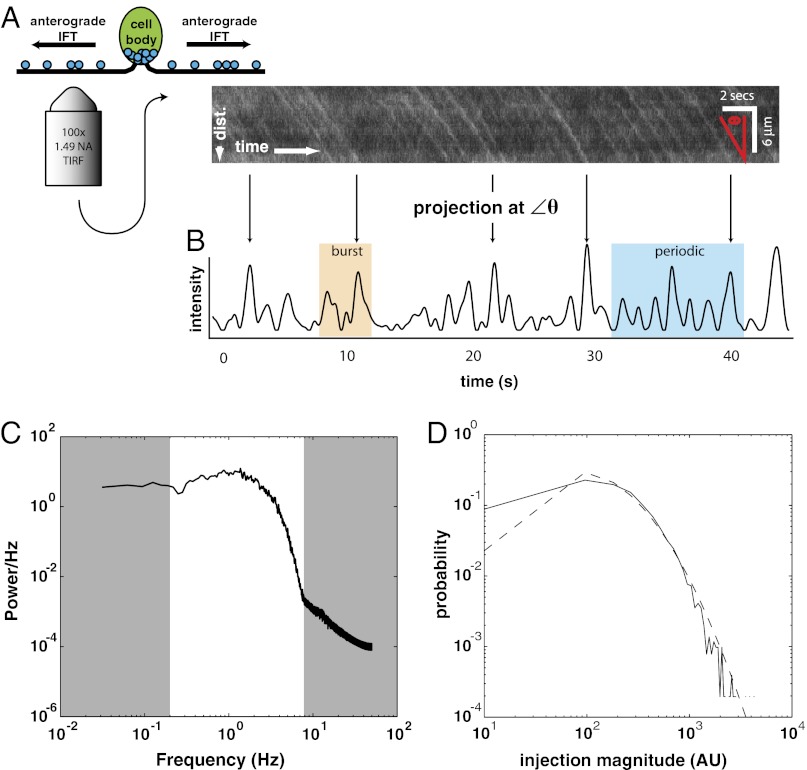
To explore the possibility that IFT injection dynamics are produced by avalanche-like events, we examined time series of IFT injections into the cilium. We used total internal reflection fluorescence (TIRF) microscopy of green fluorescent protein (GFP)-tagged IFT proteins in Chlamydomonas reinhardtii flagella (6, 20) because of the availability of genetic mutants with abnormal flagellar length and the ease of flagellar imaging in this system (Fig. 1A). Preliminary visual examination of the time series revealed some apparent periodicity as previously noted (10) (Fig. 1B) but also significant bursting activity (confirmed as described in Fig. S1, P = 0.001, 11/40, binomial statistic) as well as long-memory behavior as judged by the Hurst exponent = 0.61, SEM = 0.03 (see SI Materials and Methods for additional analysis of long-memory behavior), which indicates positive correlation between events over time, so that when one event has occurred it makes further events more likely to occur. These observations suggest that IFT injections are not completely independent random events but rather are influenced by event history, as is the case in avalanching systems.
Fig. 1.
The IFT train injector produces avalanche-like behavior. (A) TIRF microscopy produces movies of KAP-GFP (44) IFT train movement, which are then converted to kymographs of movement along the flagellar axis. (B) A median projection across the kymograph at angle θ (red on kymograph), the predominant angle of train movement (6), produces a smoothed time series of injections. Behaviors such as bursting (orange) and periodicity (blue) are evident. Details of the kymograph analysis are given in SI Materials and Methods. (C) The injector shows quasiperiodicity. We used the time series with a length >50 s (n = 37) to compute the averaged power spectrum. The average is representative of the individual power spectra. The white region highlights the portion of the spectrum that reflects the dwell times between successive injections. The gray regions correspond to nonadjacent injections (low frequency) and shape of individual peaks in the time series (high frequency). The broad peak in the power spectrum results from transient periodicity as indicated in Fig. S3. (D) The IFT injection size distribution (solid line) indicates a fat-tailed distribution (n = 2,537 injections). A lognormal distribution was fitted to the data (dashed line). We removed the smallest injections and fitted the remaining tail of the distribution (n = 1,435 injections) to a power law (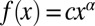 ). We found α = 2.85 with P = 0.018, using methods of Clauset et al. (49).
). We found α = 2.85 with P = 0.018, using methods of Clauset et al. (49).
To quantify the periodicity of IFT trains, we computed the power (squared amplitude) in the signal at each frequency (Fig. 1C and Fig. S2A). Power is concentrated in the low frequencies (centered around 1 Hz) but drops off at high frequencies. The broad peak in the power spectrum indicates that the injections are quasiperiodic (periodic but not strictly so). To determine the origin of the broad peak, we examined the power spectrum in a rolling window across each time series to determine whether the periodicity is a transient phenomenon (21) (Fig. S3). In 100% of our kymographs, significant periodicity (P < 0.05) occurs at 1 Hz for at least 71.5% of the time [robust Fisher’s G-test (22); SI Materials and Methods]. More specifically, we observe onset and decay of periodicity in the individual time series, showing that injections transition continuously between periodic and aperiodic regimes (Fig. S3). Simple biochemical clocks, which are subcellular systems of biomolecules, also produce oscillations (23). However, clocks work via time lags in the activity of sequential components and hysteresis in component states. Thus, biochemical clocks, like real clocks, produce robust oscillations (24) in contrast to the bursts of activity and transient episodes of periodicity that we observe. In contrast, avalanche-like systems are known to spontaneously exhibit such transient episodes of periodicity (25–27). Thus, avalanching can provide a simpler explanation for the observed periodicity. Further consistent with avalanching, we observe a fat-tailed injection size distribution that falls off according to a power law (Fig. 1D), characteristic of the broad distribution of event sizes seen in other avalanching systems (11). On the basis of comparison with previous stepwise photobleaching experiments in Engel et al. (20), we estimate that one kinesin-associated protein on the heterotrimeric kinesin-2 complex (KAP)-GFP molecule corresponds to ∼33 normalized intensity units in our measurements (SI Materials and Methods); hence the injection events appear to correspond to avalanches involving on the order of 1–30 IFT particles.
Next, we asked how, in principle, avalanche-like behavior could be generated in the IFT injection system by examining several computational models that have been applied to avalanching systems (Fig. S4): sandpiles (28), coupled sliding blocks (29), and traffic jams (30). The sandpile model showed the closest agreement with the experimental observations (Fig. S4 A and B), but sandpiles are a highly abstract concept to apply to living cells, and sandpile model components do not directly match the components of the IFT system. Therefore, we developed a quantitative model of the IFT injection system, initially derived from the sandpile model but mapping the grains onto jammed IFT particles in the flagellar pore (Figs. S5 and S6). In this model, the accumulation of sand above the angle of repose in a sand pile (13) (Fig. 2A) is replaced by accumulation of potential energy generated by collections of motors acting against cytoskeletal networks (31). This simple model recapitulates the key features of the observed IFT data (Fig. S6), including the power spectrum and the Hurst exponent. It also predicted a positive correlation between injection size and time interval between injections governed by the accumulation of material at the basal body.
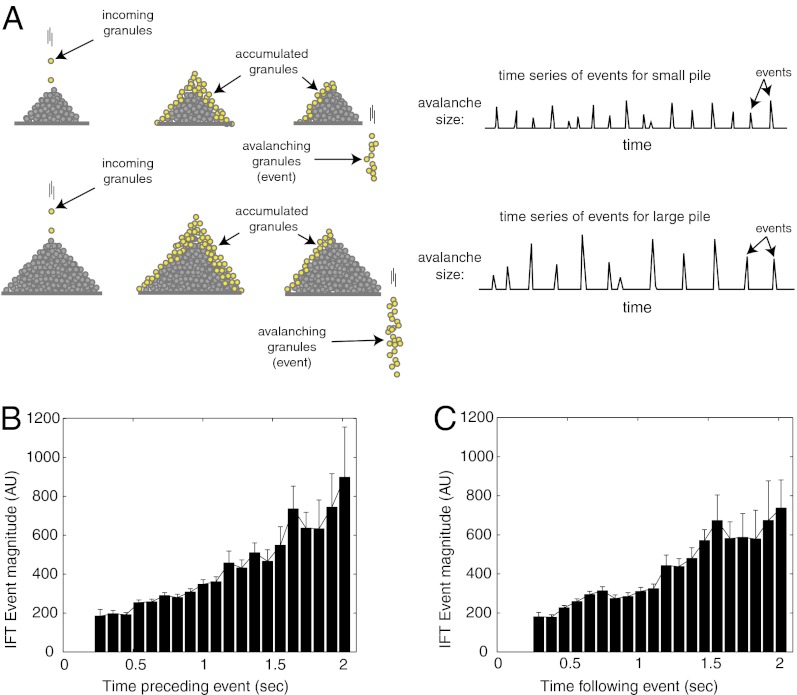
Fig. 2.
IFT injection dynamics match dynamics of avalanching systems. (A) In an experimental sandpile, a continuous incoming feed of sand grains produces a quasiperiodic, discontinuous series of avalanches. In a larger pile, the avalanches are larger and less frequent (13). (B) Mean IFT injection magnitude vs. the time since the previous injection shows that longer time intervals are associated with larger injections. (C) Mean IFT injection magnitude vs. the time until the next injection shows that longer times after an injection are associated with larger injections. Error bars are SEM.
Because material must accumulate to be released, many avalanching systems (27, 32, 33), including our model, show a correlation between the amount of strain or material released and the time intervals between release events. We found that this trend was evident in actual IFT injections measured in living cells (Fig. 2 B and C and Figs. S2 B and C and S6B). In IFT the correlation is stronger for the time interval preceding an event, suggesting that the system has more variability in accumulation of material than in release of material (34). In comparing average behaviors of different flagella, an increase in average injection size correlates with an increase in the average time interval between adjacent injections, corresponding to a decrease in injection frequency (Fig. S7A; injection size, 147 vs. 463 normalized intensity units, n = 77, P = 8.9 × 10−14, two-tailed t test; mean injection frequency, 1.4 Hz vs. 0.87 Hz, P = 3.1 × 10−6, two-tailed t test.) Injection size and intervals were determined directly from the time series. At first glance from a biological perspective, the trend of larger injection sizes with decreasing injection frequency is somewhat surprising because the decrease in IFT frequency counteracts some of the increase in size. However, for an avalanching pile, increasing the input rate of material can increase the size of the accumulated load, which results in larger but less-frequent releases of material (27) (Fig. 2A). Again consistent with avalanching, it appears the injection dynamics we observe arise as a natural consequence of a simple physical system rather than as a directly regulated process.
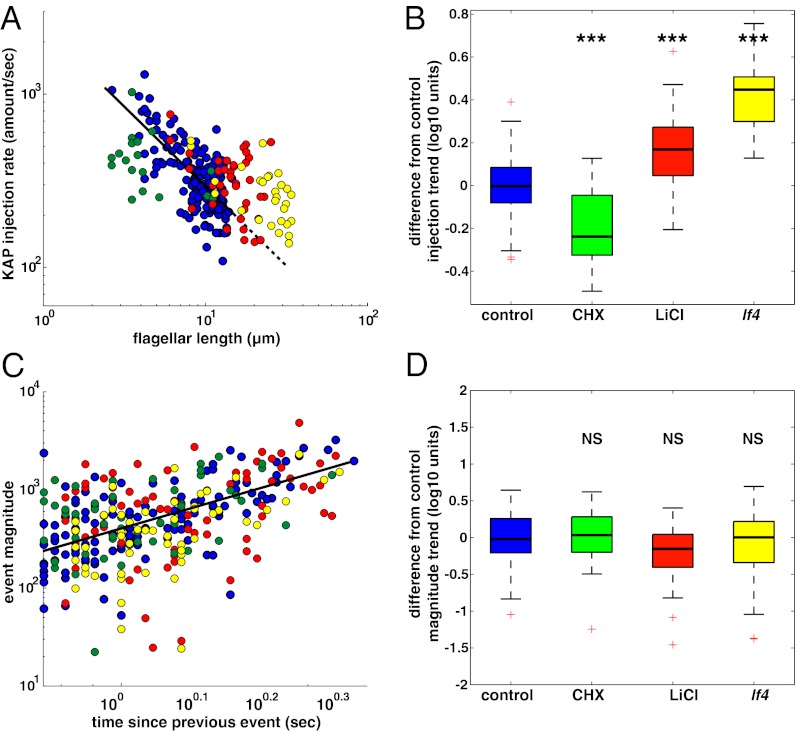
To examine the role of this process in flagellar length control, we measured the injection dynamics (i.e., timing and magnitude) under three distinct biochemical and genetic perturbations that alter flagellar length. We considered two perturbations that increase average flagellar length (the lf4 mutant and lithium treatment) and one that decreased average length (cycloheximide treatment). In wild-type cells, the injection rate decreases with increasing flagellar length (20) (Fig. 3A), matching the kinetics of flagellar regeneration: Short flagella grow rapidly and the growth rate decreases as flagella become longer. When we perturbed flagellar length, we saw that the injection rate appears to set flagellar length rather than vice versa: Perturbations that lengthened flagella (lf4, lithium) showed increased injection at any given length, and a perturbation that shortened flagella (cycloheximide) reduced injection for any given length (Fig. 3 A and B). This behavior is opposite what we would expect if the injector were correcting for the perturbed length; thus the IFT injection rate appears crucial to flagellar length control.
Fig. 3.
Pharmacological and genetic perturbations modify the length-dependent injection rate but do not change injection dynamics. We used the lf4 mutation (50) (kinase) and lithium treatment (51) [GSK3 inhibitor (47)] to study the effects of long flagella on the IFT injector, and we used cycloheximide (52) (protein synthesis inhibitor) to study the effects of short flagella. (A) Examining the injection rate as a function of flagellar length showed a drastic effect on the normal length-dependent injection rate: Control trend (n = 168 flagella; blue circles, black solid line with extrapolation dashed) shows a decrease in the injection rate for longer flagella. Cycloheximide (n = 18 flagella; CHX, green circles) decreases the injection rate below the control trend. Lithium chloride (n = 38 flagella; LiCl, red circles) and the lf4 mutation (n = 29 flagella; lf4, yellow circles) increase the injection rate above the control trend. (B) A box and whisker plot of the residual for each dataset to the control (blue) trend line shows a significant decrease in CHX (green) and a significant increase in LiCl (red) as well as with the lf4 mutation (yellow) by multiple pairwise comparison using Bonferroni’s correction for α (***P < 0.0001). (C) Despite the significant change in the amount of injected material per second, we found no effect on the relationship between individual injection size and the time between events. We plotted the magnitude of each injection event, measured by GFP intensity, vs. the time since the previous injection event. The control trend line (solid black) for injection magnitude as a function of accumulation time represents all of the datasets well: control, n = 130 events, blue circles; CHX, n = 55 events, green circles; LiCl, n = 72 events, red circles; and lf4, n = 57 events, yellow circles. (D) Box and whisker plot of the residual in event magnitude from the control trend line shows no significant difference (NS) in injection dynamics due to the perturbations. Box and whicker plots: top and bottom of each colored box represent the 25th and 75th percentiles, respectively. The horizontal line within the box is the median. Whiskers extend to the last data point within 1.5× the interquartile range. Red crosses represent outlier values.
Under perturbation, injection rates were still consistent with avalanching: Perturbations did not alter the relation between event size and time interval compared with that seen in wild-type cells (Fig. 3 C and D and Table S1). If instead a clock were to regulate the injector, then to make a longer flagellum the clock would either have to open the injection pore more frequently or allow more material to be injected for each event. Either way, the relation between event size and time interval should be changed. However, an avalanche-like system has a natural relation between event size and time interval because the driving input accumulates during the time interval between events. Therefore, increasing a given time interval should increase the resulting event magnitude. Thus, a perturbation could alter the average injection rate by changing the rate of driving input to the system, but would not alter the dependence of injection magnitude on time interval. These observations could be explained in a clock-based system only if one added additional assumptions about separate control of clock period and injector magnitude in response to the clock and assumed that both parameters were under the control of length-altering perturbations in a manner that happened to maintain the magnitude–time interval relation. Avalanche-like behavior thus provides a more parsimonious explanation for the results of these perturbation experiments.
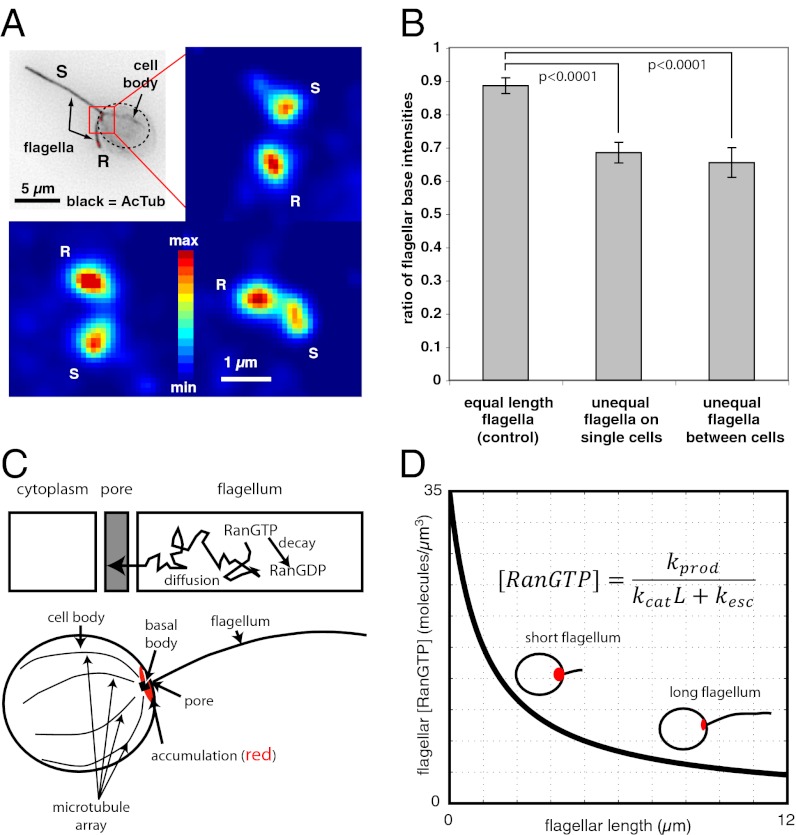
Avalanching suggests another important prediction: The injection dynamics should depend on the size of the accumulated load of IFT material (i.e., small, frequent injections arise from small accumulated loads, whereas large, infrequent injections arise from large accumulated loads; Fig. 2A). Therefore, we examined the amount of IFT material accumulated at the flagellar base (8) to determine whether we could detect evidence for such a relationship. We compared rapidly regenerating vs. full-length flagella, which have large, infrequent injections and small, frequent injections, respectively (20) (Fig. 4 A and B and Figs. S2 D and E and S8). Consistent with an avalanching system, we found that more material accumulates at the base of the regenerating flagella. This observation indicates that the injection dynamics are proportional to the recruitment of material to the flagellar base. Thus, to achieve length control, the system may regulate just the accumulation of material at the flagellar base, rather than regulating each individual IFT train injection as some reports suggest (4, 5, 10, 20). We note that this finding indicates that two biochemical processes are actually at work: (i) entry licensing (4, 5) and (ii) accumulation of IFT material at the flagellar base (8) in a length-dependent manner.
Fig. 4.
IFT dynamics are linked to IFT train localization intensity at the flagellar base. (A) An enlarged view of the flagellar base region shows that higher-intensity staining for kinesin-II occurs at the base of the regenerating flagella (R) in cells that have one steady-state-length flagellum (S) and one regenerating flagellum. Color bar indicates stain intensity ranging from lowest (blue) to highest (dark red). Inset (Upper Left) gives the cellular context for the magnified views. (B) The ratio of integrated kinesin-II staining between the flagellar bases of regenerating and steady-state-length flagella was quantified in 22 control cells with two equal-length flagella (ratio in control cells is the lower-intensity base to the higher-intensity base), in 23 single cells with unequal-length flagella (ratio in unequal-length flagella is the longer flagellum base to the shorter flagellum base), and in 15 view frames comparing one cell with two regenerating flagella to another cell with two steady-state-length flagella (ratio is the mean steady-state base to the mean regenerating base). Error bars are SEM. In every single case, the short regenerating flagella had higher-intensity staining at their bases compared with full-length flagella (38/38, P < 1 × 10−12, binomial statistic). (C) Diagram illustrating how the RanGTP gradient can act as a length sensor. The model assumes RanGTP is produced at constant rate, degrades with first-order kinetics, and can diffuse out through the flagellar pore (for details and derivation of model see SI Appendix). (D) A graph of the model illustrates variation in RanGTP concentration at the flagellar base as a function of flagellar length. The model predicts that longer flagella should have a lower RanGTP concentration and therefore less IFT accumulation than shorter flagella, as seen experimentally in B. Parameters used for the plot: RanGTP production rate (53) of 10 molecules per second, RanGTP decay constant (54) of 10/s, RanGTP diffusion constant (54) of 3 µm2/s, flagellar cross-sectional area = 0.02 µm2, and pore length = 0.2 µm. For effect of parameter variation see Fig. S12.
We next asked whether our finding that accumulation of heterotrimeric kinesin II and IFT20 is length dependent can be consistent with existing biochemical data. Dishinger et al. (4) presented the intriguing result that nuclear import machinery licenses homodimeric kinesin-2 [osmotic avoidance abnormal-3 (OSM-3)/kinesin family member-17 (KIF-17)] for ciliary entry. On the basis of those findings, we developed a theoretical model to predict how the ciliary Ras-related nuclear protein (Ran) guanosine 5'-triphosphate (GTP) gradient would be expected to change as a function of flagellar length. The results of this model show that RanGTP-stimulated recruitment of IFT motors to the basal body should be a decreasing function of flagellar length (Fig. 4 C and D and SI Appendix). In this model the length dependence arises because a given RanGTP molecule will spend more time inside a longer flagellum, thus giving it more time to hydrolyze before being sensed. Although the model is completely theoretical, all of the parameters can be estimated on the basis of published literature (SI Appendix). The model predicts realistic length dependence and reasonable concentrations of molecules when given the real parameter values (Fig. 4D and SI Appendix). This model provides a key missing element in previous organelle size control models, which showed that a constant quantity of IFT material per flagellum could lead to a simple mechanism to maintain a fixed size, but did not address how a constant amount of IFT material was achieved in the flagella in the first place (9, 20, 35). Furthermore, because the model depends on production and decay of RanGTP, it suggests that mutations affecting flagellar length, such as lf and shf mutants (36), could potentially alter length by affecting RanGTP production or by affecting transmission of the length-dependent RanGTP signal that selectively recruits IFT proteins to the transitional fibers of the basal body (8). We note that this type of model could be extended to any compartmentalized organelle as a general size sensor.
Conclusions
Our findings explain a previous problem for flagellar length control, which was how a constant amount of IFT material could be maintained in the flagellum (9, 35). The answer appears to be that controlling the amount of IFT material localized at the flagellar base in a length-dependent manner imparts a length dependence on injection via avalanching, such that as flagellar length increases, the injection rate decreases, leading to a roughly constant amount of IFT material in the flagellum. Our findings also explain why the injection frequency counteracts the injection magnitude when the injection rate increases. We previously suggested the decreased injection frequency for large particles was due to increased time to remodel larger trains (20); however, we see a large variation in particle sizes (Fig. S7 B and C) and a correlation between the particle size and the time following an injection (Fig. 2C and Fig. S7C), which conflicts with this explanation. The behaviors, including the observed variation, can be parsimoniously explained as a natural consequence of avalanching, as directly confirmed by a simple computational model for IFT (Fig. S6). This simple model gives a consistent explanation of diverse data on IFT dynamics (7, 10, 20), accumulation of material at the flagellar base (8), a constant amount of IFT material in the flagellum (9, 35), and overall length control (9, 35). It also makes the important prediction that length is controlled by a length-dependent accumulation of IFT particles at the basal body, which we suggest arises from the inherent length dependence of the ciliary RanGTP gradient (Fig. 4D). Given the similarities between ciliary and nuclear import (4, 37, 38), we expect that avalanche-like behavior also may have relevance to the study of nuclear import dynamics (39–41).
Our data show that IFT exhibits avalanche-like qualities, indicating that some of the fundamental organization of cells is in fact self-organizing. Avalanching systems often show “1/f” noise (12), evidenced by a power spectrum with a slope of −1. Such behavior is predicted by theoretical models of avalanching, most notably the model of “self-organized criticality” (12). We did not observe such 1/f dependence in the power spectra of IFT (Fig. 1C); hence IFT does not seem to be an instance of self-organized criticality. In fact, physical models of avalanche-like systems often fail to exhibit a 1/f spectrum (27, 42) due to a variety of factors. Finite-size effects are one such factor (13). By comparing fluorescent intensities between individual particles and the accumulation at the flagellar base, we estimate that the IFT injector holds on the order of 100 trains and thus falls in the realm of finite size effects. Furthermore, the 1/f behavior in the power spectrum will hold only when both the event size distribution and the event interval distribution have similar power-law distributions. In our case, as in other cases described (42), only the event size distribution has a fat tail that could be fitted with a power law, but not the distribution of time intervals between events (Fig. S9), thus explaining why the power spectrum need not show a clear power-law shape. In any case, we suggest only that our data fit the general class of avalanche-like systems, rather than the specific class of models described by the self-organized criticality model.
We also note that because such avalanche-like systems have the potential for periodic behavior, they offer the cell a spontaneous mechanism by which to generate regularity and could therefore serve as the evolutionary starting point for a biochemical oscillator. Oscillators are ubiquitous in cells, regulating such diverse functions as the cell cycle, cardiac muscle contraction, and diverse aspects of metabolism (43). Although oscillators are ubiquitous, they are often composed of many coordinated parts, raising the question of how they can arise in evolution. Our findings suggest that avalanching oscillators arise spontaneously in a cell by a simple physical mechanism.
Materials and Methods
The KAP-GFP rescue of the flagellar assembly mutant-3 (fla3) mutant was described previously by Mueller et al. (44), and an lf4/KAP-GFP/fla3 strain was produced by mating and PCR-based genotyping. The lf4 strain used was allele lf4-V86, obtained by Gregory Pazour in a screen for phototaxis mutants (45). An IFT20-GFP rescue of the null IFT20 mutant was produced as described previously (46). All strains were grown on Tris-acetate-phosphate (TAP) agar plates and then transferred to M1 liquid media under continuous light before fixation or live cell imaging. LiCl (Sigma) was used as described (47). Cycloheximide (Sigma) was prepared as a 10-mg/mL stock in ethanol and diluted to a 10-µg/mL working concentration. Cells were deflagellated by passing log-phase culture through an insulin syringe (28 gauge, 1 cc).
Live cell imaging was performed on a Nikon te2000 microscope with a 100× 1.49 NA TIRF oil lens and 488-nm laser illumination with a 514-nm dichroic mirror and a 525-nm filter. Images were recorded at 29.7 frames per second on a Photometrics QuantEM EMCCD camera with 0.156 μm per pixel. The calibration technique is described in SI Materials and Methods. Kymographs were made using Nikon elements (v3.1) and converted to IFT injection time series, using custom MATLAB software as described previously (6) with specific parameters for smoothing and background subtraction that are indicated in SI Materials and Methods. Kymograph analysis performance given in Fig. S10. Kymographs were used to compute power spectra (Fig. S11) and further analyzed as described in SI Materials and Methods.
Methanol fixation was as described previously (48). Fixed samples were imaged on a Deltavision microscope at 100×. Z-stacks were acquired with a 0.2-μm z-step. Deconvolution was performed using Deltavision software. Custom software was written in MATLAB to delineate and quantify the area at the flagellar base. Samples were compared by one-way ANOVA and then multiple pairwise comparisons were made using Bonferroni’s correction for α.
Statistical tests were performed in MATLAB, using the Statistical Analysis Toolbox.
Supplementary Material
Acknowledgments
We thank C. Tang and J. Sethna for many helpful discussions and advice about avalanching systems; J. Azimzadeh, L. Holt, H. Madhani, W. Shou, J. Burton, D. Mullins, M. Chan, S. Rafelski, H. Ishikawa, E. Kannegaard, P. Crofts, B. Engel, Z. Apte, and M. Slabodnick for helpful comments on the manuscript; and M. Porter and C. Dieckmann for providing strains. We also thank K. Thorn, A. Thwin, and the Nikon Imaging Center at University of California, San Francisco for technical expertise on microscopy. Funding for this work was provided by National Institutes of Health Grant R01 GM097017 (to W.F.M.). W.B.L. was supported by a National Science Foundation (NSF) Graduate Research Fellowship. Some of the initial stages of this work were supported by the Santa Fe Institute through NSF Grant 0200500 entitled “A Broad Research Program in the Sciences of Complexity.”
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1217354110/-/DCSupplemental.
References
- 1.Badano JL, Mitsuma N, Beales PL, Katsanis N. The ciliopathies: An emerging class of human genetic disorders. Annu Rev Genomics Hum Genet. 2006;7:125–148. doi: 10.1146/annurev.genom.7.080505.115610. [DOI] [PubMed] [Google Scholar]
- 2.Pazour GJ, Rosenbaum JL. Intraflagellar transport and cilia-dependent diseases. Trends Cell Biol. 2002;12(12):551–555. doi: 10.1016/s0962-8924(02)02410-8. [DOI] [PubMed] [Google Scholar]
- 3. Cole DG, Snell WJ (2009) SnapShot: Intraflagellar transport. Cell 137(4):784–784e1. [DOI] [PubMed]
- 4.Dishinger JF, et al. Ciliary entry of the kinesin-2 motor KIF17 is regulated by importin-beta2 and RanGTP. Nat Cell Biol. 2010;12(7):703–710. doi: 10.1038/ncb2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Craige B, et al. CEP290 tethers flagellar transition zone microtubules to the membrane and regulates flagellar protein content. J Cell Biol. 2010;190(5):927–940. doi: 10.1083/jcb.201006105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ludington W, Marshall W. Automated analysis of intracellular motion using kymographs in 1, 2, and 3 dimensions. Proc SPIE. 2009;7184:71840Y–71840Y-9. [Google Scholar]
- 7.Hao L, et al. Intraflagellar transport delivers tubulin isotypes to sensory cilium middle and distal segments. Nat Cell Biol. 2011;13(7):790–798. doi: 10.1038/ncb2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Deane JA, Cole DG, Seeley ES, Diener DR, Rosenbaum JL. Localization of intraflagellar transport protein IFT52 identifies basal body transitional fibers as the docking site for IFT particles. Curr Biol. 2001;11(20):1586–1590. doi: 10.1016/s0960-9822(01)00484-5. [DOI] [PubMed] [Google Scholar]
- 9.Marshall WF, Rosenbaum JL. Intraflagellar transport balances continuous turnover of outer doublet microtubules: Implications for flagellar length control. J Cell Biol. 2001;155(3):405–414. doi: 10.1083/jcb.200106141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dentler W. Intraflagellar transport (IFT) during assembly and disassembly of Chlamydomonas flagella. J Cell Biol. 2005;170(4):649–659. doi: 10.1083/jcb.200412021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sethna JP, Dahmen KA, Myers CR. Crackling noise. Nature. 2001;410(6825):242–250. doi: 10.1038/35065675. [DOI] [PubMed] [Google Scholar]
- 12.Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of the 1/f noise. Phys Rev Lett. 1987;59(4):381–384. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
- 13.Jaeger HM, Liu Ch, Nagel SR. Relaxation at the angle of repose. Phys Rev Lett. 1989;62(1):40–43. doi: 10.1103/PhysRevLett.62.40. [DOI] [PubMed] [Google Scholar]
- 14.Politzer PA. Observation of avalanchelike phenomena in a magnetically confined plasma. Phys Rev Lett. 2000;84(6):1192–1195. doi: 10.1103/PhysRevLett.84.1192. [DOI] [PubMed] [Google Scholar]
- 15.Lu E, Hamilton R, McTiernan J, Bromund KR. Solar flares and avalanches in driven dissipative systems. Astrophys J. 1993;412:841–852. [Google Scholar]
- 16.Sornette A, Sornette D. Self-organized criticality and earthquakes. EPL. 1989;9(3):197–202. [Google Scholar]
- 17.Teramae JN, Fukai T. Local cortical circuit model inferred from power-law distributed neuronal avalanches. J Comput Neurosci. 2007;22(3):301–312. doi: 10.1007/s10827-006-0014-6. [DOI] [PubMed] [Google Scholar]
- 18.Odde DJ, Buettner HM, Cassimeris L. Spectral analysis of microtubule assembly dynamics. AIChE J. 1996;42(5):1434–1442. [Google Scholar]
- 19.Odde DJ, Tanaka EM, Hawkins SS, Buettner HM. Stochastic dynamics of the nerve growth cone and its microtubules during neurite outgrowth. Biotechnol Bioeng. 1996;50(4):452–461. doi: 10.1002/(SICI)1097-0290(19960520)50:4<452::AID-BIT13>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- 20.Engel BD, Ludington WB, Marshall WF. Intraflagellar transport particle size scales inversely with flagellar length: Revisiting the balance-point length control model. J Cell Biol. 2009;187(1):81–89. doi: 10.1083/jcb.200812084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schaffer WM, Kendall BE, Tidd CW, Olsen LF. Transient periodicity and episodic predictability in biological dynamics. IMA J Math Appl Med Biol. 1993;10(4):227–247. doi: 10.1093/imammb/10.4.227. [DOI] [PubMed] [Google Scholar]
- 22. Ahdesmaki M, Lahdesmaki H, Yli-Harja O (2007) Robust Fisher’s test for periodicity detection in noisy biological time series. Genomic Signal Processing and Statistics, 2007. GENSIPS 2007. IEEE International Workshop on (Tuusula, Finland), pp 1–4.
- 23.Kim J, Winfree E. Synthetic in vitro transcriptional oscillators. Mol Syst Biol. 2011;7:465. doi: 10.1038/msb.2010.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pomerening JR, Sontag ED, Ferrell JE., Jr Building a cell cycle oscillator: Hysteresis and bistability in the activation of Cdc2. Nat Cell Biol. 2003;5(4):346–351. doi: 10.1038/ncb954. [DOI] [PubMed] [Google Scholar]
- 25.Julian B. Period doubling and other nonlinear phenomena in volcanic earthquakes and tremor. J Volcanol Geotherm Res. 2000;101(1–2):19–26. [Google Scholar]
- 26.Shelly DR. Periodic, chaotic, and doubled earthquake recurrence intervals on the deep San Andreas fault. Science. 2010;328(5984):1385–1388. doi: 10.1126/science.1189741. [DOI] [PubMed] [Google Scholar]
- 27.Jaeger HM, Nagel SR. Physics of the granular state. Science. 1992;255(5051):1523–1531. doi: 10.1126/science.255.5051.1523. [DOI] [PubMed] [Google Scholar]
- 28.Hwa T, Kardar M. Avalanches, hydrodynamics, and discharge events in models of sandpiles. Phys Rev A. 1992;45(10):7002–7023. doi: 10.1103/physreva.45.7002. [DOI] [PubMed] [Google Scholar]
- 29.Huang J, Turcotte D. Evidence for chaotic fault interactions in the seismicity of the San Andreas fault and Nankai trough. Nature. 1990;348:234–236. [Google Scholar]
- 30.Chowdhury D, Schadschneider A, Nishinari K. Physics of transport and traffic phenomena in biology: From molecular motors and cells to organisms. Phys Life Rev. 2005;2:318–352. [Google Scholar]
- 31.Mahadevan L, Matsudaira P. Motility powered by supramolecular springs and ratchets. Science. 2000;288(5463):95–100. doi: 10.1126/science.288.5463.95. [DOI] [PubMed] [Google Scholar]
- 32.Shimazaki K, Nakata T. Time-predictable recurrence model for large earthquakes. Geophys Res Lett. 1980;7(4):279–282. [Google Scholar]
- 33.Baiesi M, Paczuski M, Stella AL. Intensity thresholds and the statistics of the temporal occurrence of solar flares. Phys Rev Lett. 2006;96(5):051103. doi: 10.1103/PhysRevLett.96.051103. [DOI] [PubMed] [Google Scholar]
- 34.Weldon R, Scharer K, Fumal T, Biasi G. Wrightwood and the earthquake cycle: What a long recurrence record tells us about how faults work. GSA Today. 2004;14:4–10. [Google Scholar]
- 35.Marshall WF, Qin H, Rodrigo Brenni M, Rosenbaum JL. Flagellar length control system: Testing a simple model based on intraflagellar transport and turnover. Mol Biol Cell. 2005;16(1):270–278. doi: 10.1091/mbc.E04-07-0586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Lefebvre P (2009) Flagellar length control. The Chlamydomonas Sourcebook: Cell Motility and Behavior, The Chlamydomonas Sourcebook, ed Witman GB (Academic, Elsevier, Oxford), 2nd Ed, Vol 3, pp 115–129.
- 37.Kee HL, et al. A size-exclusion permeability barrier and nucleoporins characterize a ciliary pore complex that regulates transport into cilia. Nat Cell Biol. 2012;14(4):431–437. doi: 10.1038/ncb2450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fan S, et al. Induction of Ran GTP drives ciliogenesis. Mol Biol Cell. 2011;22(23):4539–4548. doi: 10.1091/mbc.E11-03-0267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kubitscheck U, et al. Nuclear transport of single molecules: Dwell times at the nuclear pore complex. J Cell Biol. 2005;168(2):233–243. doi: 10.1083/jcb.200411005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yang W, Musser SM. Nuclear import time and transport efficiency depend on importin beta concentration. J Cell Biol. 2006;174(7):951–961. doi: 10.1083/jcb.200605053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Montpetit B, Weis K. Cell biology. An alternative route for nuclear mRNP export by membrane budding. Science. 2012;336(6083):809–810. doi: 10.1126/science.1222243. [DOI] [PubMed] [Google Scholar]
- 42. Sethna JP, Dahmen KA, Perkovic O (2004) Random-field Ising models of hysteresis. arXiv preprint cond-mat/0406320.
- 43.Brandman O, Meyer T. Feedback loops shape cellular signals in space and time. Science. 2008;322(5900):390–395. doi: 10.1126/science.1160617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mueller J, Perrone CA, Bower R, Cole DG, Porter ME. The FLA3 KAP subunit is required for localization of kinesin-2 to the site of flagellar assembly and processive anterograde intraflagellar transport. Mol Biol Cell. 2005;16(3):1341–1354. doi: 10.1091/mbc.E04-10-0931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pazour GJ, Sineshchekov OA, Witman GB. Mutational analysis of the phototransduction pathway of Chlamydomonas reinhardtii. J Cell Biol. 1995;131(2):427–440. doi: 10.1083/jcb.131.2.427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lechtreck K-F, et al. The Chlamydomonas reinhardtii BBSome is an IFT cargo required for export of specific signaling proteins from flagella. J Cell Biol. 2009;187(7):1117–1132. doi: 10.1083/jcb.200909183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wilson NF, Lefebvre PA. Regulation of flagellar assembly by glycogen synthase kinase 3 in Chlamydomonas reinhardtii. Eukaryot Cell. 2004;3(5):1307–1319. doi: 10.1128/EC.3.5.1307-1319.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Feldman JL, Marshall WF. ASQ2 encodes a TBCC-like protein required for mother-daughter centriole linkage and mitotic spindle orientation. Curr Biol. 2009;19(14):1238–1243. doi: 10.1016/j.cub.2009.05.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Clauset A, Shalizi C, Newman M (2007) Power-law distributions in empirical data. arXiv eprint:0706.1062.
- 50.Berman SA, Wilson NF, Haas NA, Lefebvre PA. A novel MAP kinase regulates flagellar length in Chlamydomonas. Curr Biol. 2003;13(13):1145–1149. doi: 10.1016/s0960-9822(03)00415-9. [DOI] [PubMed] [Google Scholar]
- 51.Nakamura S, Takino H, Kojima MK. Effect of lithium on flagellar length in Chlamydomonas reinhardtii. Cell Struct Funct. 1987;12:369–374. [Google Scholar]
- 52.Rosenbaum JL, Moulder JE, Ringo DL. Flagellar elongation and shortening in Chlamydomonas. The use of cycloheximide and colchicine to study the synthesis and assembly of flagellar proteins. J Cell Biol. 1969;41(2):600–619. doi: 10.1083/jcb.41.2.600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Klebe C, Prinz H, Wittinghofer A, Goody RS. The kinetic mechanism of Ran—nucleotide exchange catalyzed by RCC1. Biochemistry. 1995;34(39):12543–12552. doi: 10.1021/bi00039a008. [DOI] [PubMed] [Google Scholar]
- 54.Becskei A, Mattaj IW. The strategy for coupling the RanGTP gradient to nuclear protein export. Proc Natl Acad Sci USA. 2003;100(4):1717–1722. doi: 10.1073/pnas.252766999. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.