Linear Transforms for Fourier Data on the Sphere: Application to High Angular Resolution Diffusion MRI of the Brain

Abstract

This paper presents a novel family of linear transforms that can be applied to data collected from the surface of a 2-sphere in three-dimensional Fourier space. This family of transforms generalizes the previously-proposed Funk-Radon Transform (FRT), which was originally developed for estimating the orientations of white matter fibers in the central nervous system from diffusion magnetic resonance imaging data. The new family of transforms is characterized theoretically, and efficient numerical implementations of the transforms are presented for the case when the measured data is represented in a basis of spherical harmonics. After these general discussions, attention is focused on a particular new transform from this family that we name the Funk-Radon and Cosine Transform (FRACT). Based on theoretical arguments, it is expected that FRACT-based analysis should yield significantly better orientation information (e.g., improved accuracy and higher angular resolution) than FRT-based analysis, while maintaining the strong characterizability and computational efficiency of the FRT. Simulations are used to confirm these theoretical characteristics, and the practical significance of the proposed approach is illustrated with real diffusion weighted MRI brain data. These experiments demonstrate that, in addition to having strong theoretical characteristics, the proposed approach can outperform existing state-of-the-art orientation estimation methods with respect to measures such as angular resolution and robustness to noise and modeling errors.

1. Introduction

We consider the design of linear transformations that can be applied to Fourier data sampled on the surface of a sphere. In particular, we assume that we observe values of the three-dimensional Fourier transform of an unknown real-valued function $f\left(\mathbf{x}\right)\in {\mathcal{L}}_1\left({\mathbb{R}}^3\right)$ ( where ${\mathcal{L}}_1(\cdot )$ denotes the space of absolutely integrable functions):

$$E\left(\mathbf{q}\right)={\int }_{{\mathbb{R}}^3}f\left(\mathbf{x}\right)\exp \left(-i2\pi {\mathbf{q}}^T\mathbf{x}\right)d\mathbf{x}.$$ (1)

We assume that E (q) is only observed at points q from the 2-sphere of radius ρ, i.e., $\mathbf{q}\in {\mathcal{S}}_{\rho }^2$, where ${\mathcal{S}}_{\rho }^2=\{\mathbf{q}\in {\mathbb{R}}^3:\mid \mid \mathbf{q}\mid {\mid }_{{\ell }_2}=\rho \}$. We additionally assume that f (x) originates from a class of functions with real-valued and non-negative Fourier transforms (i.e., it is necessary that f (x) = f (−x)).

We specifically consider the family of linear transforms R_G that map such spherical Fourier data onto ${\mathcal{S}}_1^2$ according to

$$R_G\left\{E\right(\mathbf{q}\left)\right\}\left(\mathbf{u}\right)={\int }_{\mathbf{q}\in {\mathcal{S}}_{\rho }^2}E\left(\mathbf{q}\right)G\left({\mathbf{u}}^T\mathbf{q}\right)d\mathbf{q},$$ (2)

where $\mathbf{u}\in {\mathcal{S}}_1^2$ is an orientation parameter of the transform. The choice of the transform kernel G (·) determines the characteristics of the transforms from this family, and is the main focus of the present work. While the design of signals and filters on the sphere has been considered previously in other contexts (e.g. Wei et al., 2011, and its references), the specific inverse problem setting of (1) leads to a design problem that is quite distinct.

Spherical Fourier sampling is an accurate model of the data acquisition procedure in high angular resolution magnetic resonance diffusion imaging (HARDI), and a special case of (2), known as the Funk-Radon Transform (FRT), has been previously proposed by Tuch et al. in this context (Tuch, 2002; Tuch et al., 2003; Tuch, 2004). In particular, the FRT uses G(u^Tq) = δ(u^Tq), where δ(·) denotes the Dirac delta function. In this notation, the delta function is being used to define a contour integral around the equator of ${\mathcal{S}}_{\rho }^2$ that is perpendicular to u. The FRT is useful in the context of HARDI data because it allows computation of an approximate diffusion orientation distribution function (ODF), which quantifies information about the amount of diffusion along any given orientation u. This diffusion orientation information can be valuable in the study of anisotropic structures like white matter fibers in the central nervous system (CNS), because the diffusion ODF for a given voxel is often similar in shape to the distribution of white matter fibers within that voxel (Seunarine and Alexander, 2009; Assemlal et al., 2011). The combination of the FRT with HARDI data is also known as Q-ball imaging (QBI) (Tuch, 2004).

Many alternatives to the FRT have been proposed in recent years for estimating orientation information from the same kind of HARDI data, including multi-tensor models (Alexander et al., 2001; Tuch et al., 2002; Hosey et al., 2005; Kreher et al., 2005; Peled et al., 2006; Behrens et al., 2007; Jian et al., 2007; Ramirez-Manzanares et al., 2007; Pasternak et al., 2008; Melie-García et al., 2008; Leow et al., 2009; Tabelow et al., 2012), higher-order generalizations of tensor models (Alexander et al., 2002; Frank, 2002; Özarslan and Mareci, 2003; Liu et al., 2004; Schultz and Seidel, 2008; Barmpoutis et al., 2009; Liu et al., 2010; Florack et al., 2010), directional function modeling (Kaden et al., 2007; Rathi et al., 2009, 2010), spherical polar Fourier expansion (Assemlal et al., 2009, 2011), independent component analysis (Singh and Wong, 2010), sparse spherical ridgelet modeling (Michailovich and Rathi, 2010), diffusion circular spectrum mapping (Zhan et al., 2004), deconvolution (Tournier et al., 2007; Anderson, 2005; Descoteaux et al., 2009; Patel et al., 2010; Yeh et al., 2011; Reisert and Kiselev, 2011), the diffusion orientation transform (Özarslan et al., 2006; Canales-Rodríguez et al., 2010), estimation of persistent angular structure (Jansons and Alexander, 2003), generalized q-sampling imaging (Yeh et al., 2010), and orientation estimation with solid angle considerations (Tristán-Vega et al., 2009; Aganj et al., 2010; Tristán-Vega et al., 2010). However, the FRT has a unique combination of useful characteristics: it does not require a strict parametric model of the diffusion signal, it is linear and its theoretical characteristics can be explored analytically, and it can be computed very quickly using efficient algorithms (Anderson, 2005; Hess et al., 2006; Descoteaux et al., 2007; Kaden and Kruggel, 2011). Despite this, a significant disadvantage has been that FRT-based orientation estimates can have lower resolution/accuracy relative to some of the alternative processing methods (Alexander, 2005; Anderson, 2005; Jian et al., 2007; Ramirez-Manzanares et al., 2007; Schultz and Seidel, 2008; Barmpoutis et al., 2009; Descoteaux et al., 2009; Tournier et al., 2008; Rathi et al., 2009; Aganj et al., 2010; Tristán-Vega et al., 2009; Michailovich and Rathi, 2010; Yeh et al., 2011; Canales-Rodríguez et al., 2010; Yeh et al., 2010; Tristán-Vega et al., 2010; Assemlal et al., 2011), partly because the approach is based on a sub-optimal definition of the ODF (Barnett, 2009; Aganj et al., 2010; Tristán-Vega et al., 2009).

In this work, we show that by generalizing the FRT with (2), it is possible to significantly enhance performance while maintaining the desirable characteristics of the FRT. A preliminary account of this work was presented in Haldar and Leahy (2012).

1.1. Diffusion MRI and the Funk-Radon Transform

1.1.1. Diffusion MRI Basics

The statistical characteristics of molecular diffusion within a single MR imaging voxel can be coarsely summarized using a probability density function P (x, Δ) known as the ensemble average diffusion propagator (EAP) (Callaghan, 1991). The EAP quantifies the average probability that a water molecule, undergoing a random walk over a time period of length Δ, will be found at a spatial displacement of $\mathbf{x}\in {\mathbb{R}}^3$ relative to its starting position. Under the assumptions of pure diffusion and that the system is at thermal equilibrium, the EAP will be symmetric (i.e., P (x, Δ) = P (−x, Δ)) and have zero-mean. Under the q-space formalism (Callaghan, 1991), the ideal measured DW-MRI data is modeled as (1), where the q-space function E (q) corresponds to the signal observed from the MR scanner as a function of diffusion gradient parameters q, and f (x) ∝ P (x, Δ).

In practice, the diffusion signal E (q) is measured over a finite set of different q values, and a variety of different q-space sampling schemes have been proposed. One approach is to densely sample q-space. For example, assuming the EAP is support-limited and the sampling density satisfies the Nyquist criterion, then reconstruction of the full EAP is possible via Fourier inversion (Wedeen et al., 2005). However, this kind of encoding can be demanding on MR hardware, and can also be time consuming since experiment time is proportional to the number of samples. At the other extreme, parametric models for the EAP can be used to reduce q-space sampling requirements significantly. For example, the conventional diffusion tensor imaging (DTI) model (Basser et al., 1994) is equivalent to modeling the EAP as a zero-mean Gaussian distribution, and estimation of the corresponding 3 × 3 positive semidefinite covariance matrix can be achieved with as few as 7 different q-space samples. However, it has become widely recognized that a simple Gaussian model is insufficient to accurately model diffusion in complex biological tissues. In the CNS, this is due in part to the fact that the simple Gaussian model can have at most one dominant orientation, and is thus incapable of representing the EAPs that are observed when a single voxel contains partial volume contributions from multiple crossing white matter fiber bundles.

HARDI sampling, in which diffusion data is sampled densely on the surface of a sphere, enables a more reasonable balance between data acquisition speed/complexity and the capability to resolve crossing fibers. It has been shown that approaches using HARDI sampling have only incrementally lower performance compared to Nyquist-rate Fourier encoding, but have significantly enhanced performance over DTI (Kuo et al., 2008; Zhan and Yang, 2006).

1.1.2. Orientation Distribution Functions and the Funk-Radon Transform

An important objective in DW-MRI is to derive fiber orientation information from HARDI data, and there are different ways to define an ODF to quantify the orientations associated with an EAP. In QBI (Tuch, 2004), an ideal ODF was defined as¹

$$\begin{array}{cc}\hfill OD{F}_{\mathrm{QBI}}\left(\mathbf{u}\right)& ={\int }_0^{\infty }f\left(\alpha \mathbf{u}\right)d\alpha \hfill \\ \hfill & =\frac{1}{2}{\int }_{-\infty }^{\infty }f\left(\alpha \mathbf{u}\right)d\alpha \hfill \\ \hfill & =\frac{1}{2}{\int }_{-\infty }^{\infty }{\tilde{f}}_{\mathrm{u}}(0,0,z)dz\hfill \end{array}$$ (3)

for orientation vectors $\mathbf{u}\in {\mathcal{S}}_1^2$. The function ${\tilde{f}}_{\mathbf{u}}(\cdot )$ expresses f (·) in a rotated coordinate system in which the orientation vector u is parallel to the z-axis. This definition of the ODF computes radial projections of the EAP, which Tuch showed can be approximated by the FRT. In particular, it can be verified that the FRT satisfies

$$\begin{array}{cc}\hfill & {\int }_{\mathbf{q}\in {\mathcal{S}}_{\rho }^2}E\left(\mathbf{q}\right)\delta \left({\mathbf{u}}^T\mathbf{q}\right)d\mathbf{q}\hfill \\ \hfill & =\rho {\int }_0^{2\pi }{\tilde{E}}_{\mathbf{u}}(\rho \cos \theta ,\rho \sin \theta ,0)d\theta \hfill \\ \hfill & 2\pi \rho \int \int {\int }_{{\mathbb{R}}^3}{\tilde{f}}_{\mathrm{u}}(x,y,z)J_0\left(2\pi \rho \sqrt{x^2+y^2}\right)dxdydz\hfill \end{array}$$ (4)

where ${\tilde{E}}_{\mathbf{u}}(\cdot )$ is the coordinate-rotated version of E (·) (cf. ${\tilde{f}}_{\mathbf{u}}(\cdot )$ and f (·)), and J₀ (·) is the zeroth-order Bessel function of the first kind. Given that J₀ (·) has most of its energy concentrated at the origin, (4) can be viewed as a coarse approximation of (3), with the approximation quality improving for larger values of the sampling radius ρ.

While the QBI definition of the ODF has been used with great success, an improved ODF definition is given by (Wedeen et al., 2005; Barnett, 2009; Aganj et al., 2010; Tristán-Vega et al., 2009)

$$\begin{array}{cc}\hfill ODF\left(\mathbf{u}\right)& ={\int }_0^{\infty }f\left(\alpha \mathbf{u}\right){\alpha }^{2}d\alpha \hfill \\ \hfill & =\frac{1}{2}{\int }_{-\infty }^{\infty }f\left(\alpha \mathbf{u}\right){\alpha }^{2}d\alpha \hfill \\ \hfill & =\frac{1}{2}{\int }_{-\infty }^{\infty }{\tilde{f}}_{\mathrm{u}}(0,0,z)z^{2}dz.\hfill \end{array}$$ (5)

Physically, this corresponds to radial integration of the EAP over a cone of constant solid angle, and differs from (3) by including the appropriate volume element for radial integration in spherical coordinates. And unlike (3), this ODF is proportional to the probability distribution that would be obtained by marginalizing over the radial component of the EAP. While (5) has better theoretical and practical characteristics than the QBI ODF (Barnett, 2009; Aganj et al., 2010; Tristán-Vega et al., 2009; Assemlal et al., 2011), existing methods to compute (5) from sampled data have either required additional modeling assumptions (Tristán-Vega et al., 2009; Aganj et al., 2010; Tristán-Vega et al., 2010; Canales-Rodríguez et al., 2010; Assemlal et al., 2011), the application of nonlinear operators (e.g., logarithmic-transformations) to the diffusion data (Tristán-Vega et al., 2009; Aganj et al., 2010; Tristán-Vega et al., 2010; Canales-Rodríguez et al., 2010), or more complicated non-spherical q-space sampling (Wedeen et al., 2005; Canales-Rodríguez et al., 2009).

2. Materials and Methods

2.1. Linear Transforms of the Fourier 2-Sphere

By definition, any function f (x) proportional to a valid probability density belongs to ${\mathcal{L}}_1\left({\mathbb{R}}^3\right)$. As a result, the associated q-space function E (q) will always be bounded and uniformly continuous (Katznelson, 1968), and linear transformations obtained using (2) will be well defined for transform kernels satisfying $G({\mathbf{u}}^T\cdot )\in {\mathcal{L}}_1\left({\mathcal{S}}_{\rho }^2\right)$. This occurs if and only if $G\left(t\right)\in {\mathcal{L}}_1\left(\right[-\rho ,\rho \left]\right)$.

For any $G({\mathbf{u}}^T\cdot )\in {\mathcal{L}}_1\left({\mathcal{S}}_{\rho }^2\right)$, the action of (2) applied to noiseless data can be expressed as

$$\begin{array}{cc}\hfill & R_G\left\{E\right(\mathbf{q}\left)\right\}\left(\mathbf{u}\right)\hfill \\ \hfill & ={\int }_{\mathbf{q}\in {\mathcal{S}}_{\rho }^2}\left({\int }_{{\mathbb{R}}^3}f\left(\mathbf{x}\right)\exp \left(-i2\pi {\mathbf{q}}^T\mathrm{x}\right)d\mathbf{x}\right)G\left({\mathbf{u}}^T\mathbf{q}\right)d\mathbf{q}\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^3}f\left(\mathbf{x}\right)\left({\int }_{\mathbf{q}\in {\mathcal{S}}_{\rho }^2}G\left({\mathbf{u}}^T\mathbf{q}\right)\exp \left(-i2\pi {\mathbf{q}}^T\mathrm{x}\right)d\mathbf{q}\right)d\mathbf{x}\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^3}f\left(\mathbf{x}\right)g(\mathbf{u},\mathbf{x})d\mathbf{x},\hfill \end{array}$$ (6)

where we have introduced

$$g(\mathbf{u},\mathbf{x})\equiv {\int }_{\mathbf{q}\in {\mathcal{S}}_{\rho }^2}G\left({\mathbf{u}}^T\mathbf{q}\right)\exp \left(-i2\pi {\mathbf{q}}^T\mathbf{x}\right)d\mathbf{q}.$$ (7)

The function g (u, x) can be interpreted like a point-spread function, and through (6), provides a direct relationship between the transformed data, the EAP, and the kernel function G (·).

Using the same unitary coordinate transformation as before to define ${\tilde{g}}_{\mathbf{u}}(\cdot )$ in terms of g (u, ·), we can also express (7) in rotated coordinates as

$${\tilde{g}}_{\mathrm{u}}(x,y,z)={\int }_{-\rho }^{\rho }G\left(\tau \right)B(x,y,\tau )\exp (-i2\pi \tau z)d\tau ,$$ (8)

with

$$B(x,y,\tau )=2\pi \rho J_0\left(2\pi \sqrt{{\rho }^2-{\tau }^2}\sqrt{x^2+y^2}\right).$$ (9)

The derivations leading up to (8) and (9) are shown in the appendix. Note that the integral in (8) can be viewed as a combination of a Hankel transform and a Fourier transform, though we will not use this fact in what follows.

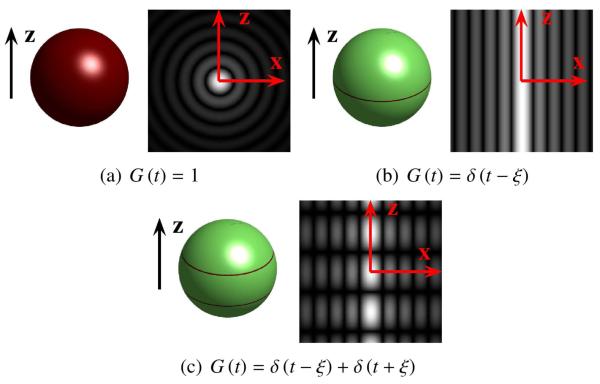
As can be seen from (8) and (9), the functions ${\tilde{g}}_{\mathbf{u}}(x,y,z)$ resulting from (2) can be expressed as a linear combination of Bessel functions modulated by complex sinusoids and possess axial symmetry about the z-axis. We list a few important ${\tilde{g}}_{\mathbf{u}}(x,y,z)$ and G (t) pairs in Table 1, and illustrate G(u^Tq) and ${\tilde{g}}_{\mathbf{u}}(x,y,z)$ in Fig. 1. Note that while the transform kernels involving delta functions are not in ${\mathcal{L}}_1\left({\mathcal{S}}_{\rho }^2\right)$, the contour integrals they imply are still well defined.

Table 1.

Some Transform Kernel Pairs

Kernel Function G(t)	Corresponding ${\tilde{g}}_{\mathrm{u}}(x,y,z)$	Notes
1	4π sinc(2ρ(x2+y2+z2))	See Bracewell (2000) and Fig. 1(a)
δ(t-ξ) with fixed parameter ξ ∈ [−ρ, ρ]	$2\pi \rho J_0\left(2\pi \sqrt{{\rho }^2-{\xi }^2}\sqrt{x^2+y^2}\right)\exp (-i2\pi \xi z)$	ξ = 0 yields the FRT, see Fig. 1(b)
δ(t-ξ) + δ(t+ξ) with fixed parameter ξ ∈ [−ρ, ρ]	$4\pi \rho J_0\left(2\pi \sqrt{{\rho }^2-{\xi }^2}\sqrt{x^2+y^2}\right)\cos \left(2\pi \xi z\right)$	See Fig. 1(c)

Figure 1.

Illustration of the function pairs listed in Table 1. In each subfigure, the left image shows G(u^Tq) for q on the sphere, and the right image shows the magnitude of ${\tilde{g}}_{\mathbf{u}}(x,0,z)$ in the x-z plane, both for the case where u is oriented along the z-axis. Note that ${\tilde{g}}_{\mathbf{u}}(x,y,z)$ is axially symmetric about the z-axis. The function pairs are shown with (b) ξ = 0 and (c) ξ = 0.36ρ.

Since f (x) is real-valued and symmetric, we can further restrict attention to functions g (u, x) that are also real-valued and symmetric with respect to x. In turn, this restricts attention to real-valued and symmetric kernel functions G (·), so that all of the interesting g (u, x) that can be obtained with (2) can equivalently be expressed as linear combinations of cosine-modulated Bessel functions in the form of the last entry of Table 1.

2.1.1. Fast Computation

The previous subsection described the class of interesting transforms that can be obtained from (2). In this subsection, we will show that the computation of this transform can be performed easily by making use of spherical harmonics. The spherical harmonics form an orthonormal basis for ${\mathcal{S}}_1^2$, and are frequently defined as (Descoteaux et al., 2007)

$$Y_{\ell }^m\left(\mathbf{u}\right)=\sqrt{\frac{2\ell +1}{4\pi }\frac{(\ell -m)!}{(\ell +m)!}}{P}_{\ell }^m\left(\cos \theta \right)\exp \left(im\varphi \right),$$ (10)

where the harmonic degree ℓ = 0, 1, … , ∞, and the harmonic order m = −ℓ, … , 0, … , ℓ. In this expression, τ ∈ [0, π] is the polar angle and φ ∈ [0, 2π] is the azimuthal angle for the vector u, and $P_{\ell }^m(\cdot )$ is the associated Legendre function of degree ℓ and order m.

Use of spherical harmonic representations is common in the HARDI literature, partly due to the observation that the spherical harmonics are eigenfunctions of the FRT (Anderson, 2005; Hess et al., 2006; Descoteaux et al., 2007; Kaden and Kruggel, 2011). Thus, if E (q) is represented through its coefficients {c_ℓm} in the spherical harmonic basis as

$$E\left(\mathbf{q}\right)=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{c}_{\ell m}{Y}_{\ell }^m\left(\mathbf{q}\right),$$ (11)

then we can efficiently compute the FRT through simple rescaling of each spherical harmonic coefficient by the corresponding eigenvalue. While there are several methods of deriving the eigenfunction relationship for the FRT, Descoteaux et al. (2007) used the Funk-Hecke theorem as the basis for their derivations.

For this paper, we observe that the Funk-Hecke theorem indicates that spherical harmonics will be eigenfunctions of (2) for most choices of the transform kernel G (t):

Theorem (Funk-Hecke, adapted from Freeden and Schreiner (2009)): Suppose that $G\left(t\right)\in {\mathcal{L}}_1\left(\right[-\rho ,\rho \left]\right)$. Then for any $\mathbf{u}\in {\mathcal{S}}_1^2$,

$${\int }_{\mathbf{q}\in {\mathcal{S}}_{\rho }^2}G\left({\mathbf{u}}^T\mathbf{q}\right)Y_{\ell }^m\left(\mathbf{q}\right)d\mathbf{q}={\lambda }_{\ell }^G{Y}_{\ell }^m\left(\mathbf{u}\right),$$ (12)

where the eigenvalue ${\lambda }_{\ell }^G$ is given by

$${\lambda }_{\ell }^G=2\pi {\rho }^2{\int }_{-1}^1{P}_{\ell }\left(t\right)G\left(\rho t\right)dt.$$ (13)

P_ℓ(t) in (13) is the Legendre polynomial of degree ℓ.

It follows from this theorem that (2) can be equivalently written for $G\left(t\right)\in {\mathcal{L}}_1\left(\right[-\rho ,\rho \left]\right)$ in terms of the spherical harmonic coefficients {c_ℓm} as

$$R_G\left\{E\right(\mathbf{q}\left)\right\}\left(\mathbf{u}\right)=\sum _{\ell =0}^{\infty }{\lambda }_{\ell }^G\sum _{m=-\ell }^{\ell }{c}_{\ell m}{Y}_{\ell }^m\left(\mathbf{u}\right).$$ (14)

It should be noted that G(t) = δ(t–ξ) (e.g., as used by the FRT) is not an element of ${\mathcal{L}}_1\left(\right[-\rho ,\rho \left]\right)$. However, an eigenfunction relationship is also valid for the circular contour integrals implied by these transform kernels. In particular, the eigenvalues corresponding to the transform kernel G(t) = δ(t–ξ) are

$${\lambda }_{\ell }^G=2\pi \rho P_{\ell }(\xi ∕\rho ).$$ (15)

This result was proven for ξ = 0 in (Anderson, 2005; Hess et al., 2006; Descoteaux et al., 2007) for use with the FRT, and the proof technique of Descoteaux et al. (2007) extends in a straightforward manner for nonzero ξ.

2.2. The Funk-Radon and Cosine Transform

Based on the general class of transforms introduced in the previous section, we propose the FRACT, which we define by the transform kernel

$$G\left(t\right)=\frac{1}{8{\pi }^3{\xi }^2\rho }\left(2\delta \right(t)-\delta (t+\xi )-\delta (t-\xi \left)\right),$$ (16)

for some ξ with 0 < ξ < ρ. The results of the previous section imply that the FRACT has

$$\begin{array}{cc}\hfill {\tilde{g}}_{\mathrm{u}}& (x,y,z)=\hfill \\ \hfill & \frac{1}{2{\pi }^2{\xi }^2}{J}_0\left(2\pi \rho \sqrt{x^2+y^2}\right)\hfill \\ \hfill & -\frac{1}{2{\pi }^2{\xi }^2}{J}_0\left(2\pi \sqrt{{\rho }^2-{\xi }^2}\sqrt{x^2+y^2}\right)\cos \left(2\pi \xi z\right),\hfill \end{array}$$ (17)

with spherical harmonic eigenvalues given by

$${\lambda }_{\ell }^G=\frac{1}{4{\pi }^2{\xi }^2}\left(2P_{\ell }\right(0)-P_{\ell }(\xi ∕\rho )-P_{\ell }(-\xi ∕\rho \left)\right).$$ (18)

An important characteristic of the FRACT is the behavior of ${\tilde{g}}_{\mathbf{u}}(0,0,z)$ as a function of z. In particular, for small values of ξz, the FRACT satisfies

$$\begin{array}{cc}\hfill {\tilde{g}}_{\mathrm{u}}(0,0,z)& =\frac{1}{2{\pi }^2{\xi }^2}(1-\cos (2\pi \xi z\left)\right)\hfill \\ \hfill & \approx z^2,\hfill \end{array}$$ (19)

where the approximation is obtained by neglecting the higherorder terms in the Taylor series expansion of the cosine. Substituting (19) into (6), we observe that the FRACT can be used to compute an approximation of the ODF defined in (5), similar to the way in which the FRT was used to compute an approximation of the alternative ODF defined in (3). It should also be noted that, as with the FRT, the signal leakage associated with the finite width of the Bessel functions in the response function of the FRACT will diminish with increasing sampling radius ρ. However, it is important to keep in mind that using very large values of ρ places significant demands on the gradient system of an MR scanner, and that the SNR of E(q) typically decays exponentially as ρ increases. Note also that, while the relationship between (19) and (5) has no explicit dependence on ρ, the interval over which (19) accurately approximates (5) will diminish as ρ increases if ξ is chosen in proportion to ρ.

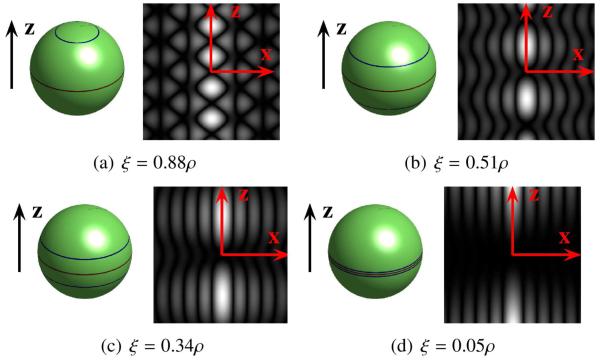
For a given ρ, the FRACT has a single parameter ξ that controls its behavior. The FRACT is not very sensitive to small variations in ξ, due to the fact that the FRACT spherical harmonic eigenvalues in (18) vary smoothly as a function of ξ because of the smoothness of the Legendre polynomials, though larger changes in ξ can lead to FRACTs with different characteristics. Examples of G(u^Tq) and ${\tilde{g}}_{\mathbf{u}}(x,y,z)$ for different choices of ξ are illustrated in Fig. 2. As can be seen, the ability of the FRACT to approximate z² improves as ξ decreases towards 0. However, it should also be noted that as ξ decreases towards 0, the energy of ${\tilde{g}}_{\mathbf{u}}\left(x\right)$ is being distributed further and further from the origin. Since EAPs typically have concentrated signal energy at the origin, this frequently implies that the signal-to-noise ratio for the FRACT also diminishes as ξ decreases. However, the value of the EAP in the region farther from the origin will typically provide more information regarding oriented anisotropic diffusion. For comparison, note that ${\tilde{g}}_{\mathbf{u}}\left(x\right)$ for the FRT was illustrated in Fig. 1(b), and that unlike the FRACT, the signal from the FRT will generally be dominated by the region of the EAP near the origin. As a result, the FRT would be expected to have higher SNR than the FRACT, but could be less sensitive to tissue orientation due to signal leakage from regions near the origin in the plane orthogonal to u. In the remainder of this paper, we will frequently use the heuristic choice of ξ = 0.34ρ, since it yielded a reasonable balance between resolution and SNR for the datasets we worked with, though other values of ξ might be preferred for these and other datasets. Further examples of the impact of ξ are shown in the supplementary material.

Figure 2.

Illustration of FRACT for different choices of ξ. In each subfigure, the left image shows G(u^Tq) for q on the sphere, and the right image shows the magnitude of ${\tilde{g}}_{\mathbf{u}}(x,0,z)$ in the x-z plane, both for the case where u is oriented along the z-axis.

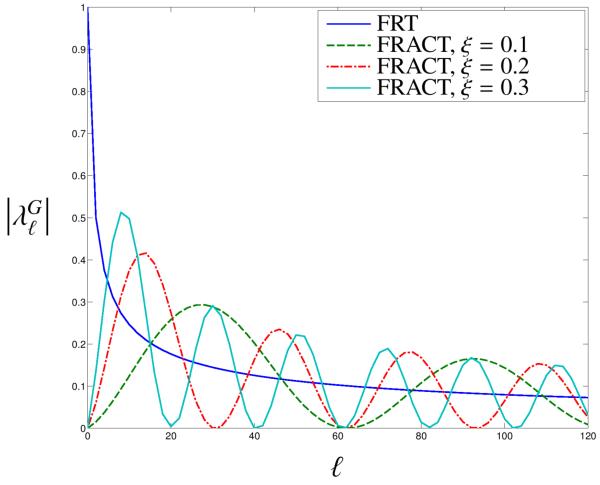
Further perspective can be obtained by looking at the spherical harmonic eigenvalues for different ξ, as shown in Fig. 3. Spherical harmonics have the property that higher ℓ values correspond to more oscillatory $Y_{\ell }^m\left(\mathbf{u}\right)$. As a result, Fig. 3 indicates that the FRT can be viewed as a form of low-pass filter, with a tendency to emphasize the smooth and/or isotropic components of the spherical data. On the other hand, the FRACT family of transforms can be viewed as bandpass filters that emphasize the higher-frequency aspects of the data. This kind of filtering would be expected to enhance the angular resolution of FRACT. It should also be noted that the FRACT nullifies the 0th-order spherical harmonic coefficient, which corresponds to the isotropic component of the spherical function. While this implies that the FRACT does not accurately estimate isotropic ODFs, the suppression of the isotropic component can help to make the anisotropic ODF components more visible. This aspect is explored in more detail in the supplementary material. Note also that as ξ decreases, the FRACT tends to reduce the contribution of the low-degree spherical harmonics. In addition, it is possible to obtain a more uniform high-pass eigenvalue curve (with reduced eigenvalue oscillations) through the linear combination of two or more FRACTs with different values of ξ.

Figure 3.

Magnitudes of the spherical harmonic eigenvalues for different transforms as a function of the spherical harmonic degree. Note that all of the eigenvalues in this plot are 0 for odd ℓ, and that these values are not shown. The eigenvalues for the FRACT transforms have been scaled by 2πξ² for better comparison with the FRT, and ρ was assumed to be 1.

2.3. Practical Implementation

The transforms considered so far have all been derived under the assumption that we have access to E (q) for all $\mathbf{q}\in {\mathcal{S}}_{\rho }^2$. However, practical HARDI data only provides the value of E (q) on a finite set of N points. This discrepancy requires the use of special data processing approaches. A common approach in the literature has been to assume that the true E (q) is relatively smooth, such that it can be approximated by a truncated spherical harmonic series with a maximum degree of L (Descoteaux et al., 2007; Anderson, 2005; Hess et al., 2006):

$$E\left(\mathbf{q}\right)\approx \sum _{\ell =0}^L\sum _{m=-\ell }^{\ell }{c}_{\ell m}{Y}_{\ell }^m\left(\mathbf{q}\right).$$ (20)

Given this signal model, the harmonic coefficients can be estimated, e.g., by least-squares fitting to the sampled data. In practice, this inverse problem can be ill-posed, and Descoteaux et al. (2007) introduced a linear regularization scheme that uses the Laplace-Beltrami operator to regularize the solution. The Laplace-Beltrami operator provides a natural smoothness measure for functions on the sphere, and is efficient to use in this context because its eigenfunctions are the spherical harmonics. In this work, we make use of the same regularization framework with the same parameters suggested by Descoteaux et al. (2007) to estimate the spherical harmonic coefficients. In addition, we also modify the spherical harmonics to be symmetric and realvalued as described by Descoteaux et al. (2007) to ensure that the estimated E (q) also has these properties. This modified spherical harmonic basis has the same eigenvalues as the original spherical harmonic basis. See Descoteaux et al. (2007) for further details.

Given the fitted spherical harmonic coefficients, any of the transforms described in this paper can be computed efficiently using (14). However, it is also important to consider how truncation of the spherical harmonic series and finite sampling of ${\mathcal{S}}_{\rho }^2$ influence the characteristics of the transforms, and in particular, the shape of g (u, x). While the effects of truncating the spherical harmonic series have been investigated in previous work (Descoteaux et al., 2007; Anderson, 2005; Hess et al., 2006; Kaden and Kruggel, 2011), we are not aware of any existing work that characterizes these effects in terms of g (u, x).

Fortunately, because we use a linear estimation technique to obtain spherical harmonic coefficients from the sampled data and (13) also represents a linear operation, it is straightforward to compute the response function g (u, x) for linear transforms of the sampled data. In particular, after expressing the estimated spherical harmonic coefficients as a linear combination of the measured data

$${\widehat{c}}_{\ell m}=\sum _{n=1}^N{b}_{n\ell m}E\left({\mathbf{q}}_n\right)$$ (21)

for some coefficients {b_nℓm}, we have that the transformed data

$$\begin{array}{cc}\hfill {\widehat{R}}_G\left\{E\right(\mathbf{q}\left)\right\}& \left(\mathbf{u}\right)\hfill \\ \hfill & =\sum _{\ell =0}^L{\lambda }_{\ell }^G\sum _{m=-\ell }^{\ell }{Y}_{\ell }^m\left(\mathbf{u}\right)\sum _{n=1}^N{b}_{n\ell m}E\left({\mathbf{q}}_n\right)\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^3}f\left(\mathbf{x}\right)g(\mathbf{u},\mathbf{x})d\mathbf{x}\hfill \end{array}$$ (22)

with

$$g(\mathbf{u},\mathbf{x})=\sum _{\ell =0}^L\sum _{m=-\ell }^{\ell }\sum _{n=1}^N{\lambda }_{\ell }^G{b}_{n\ell m}\exp \left(-i2\pi {\mathbf{q}}_n^T\mathbf{x}\right)Y_{\ell }^m\left(\mathbf{u}\right).$$ (23)

Equation (23) can be viewed as a discrete three-dimensional non-Cartesian Fourier transform, which we efficiently approximate using convolution gridding (Jackson et al., 1991).

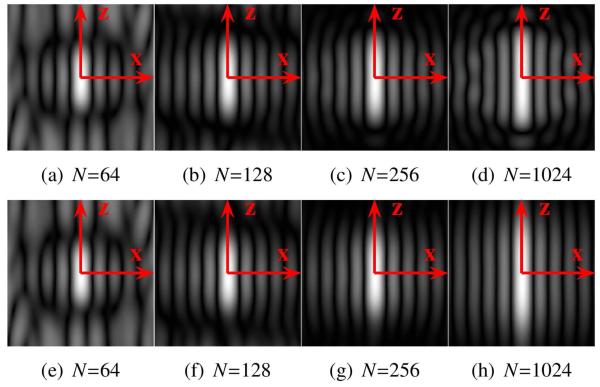
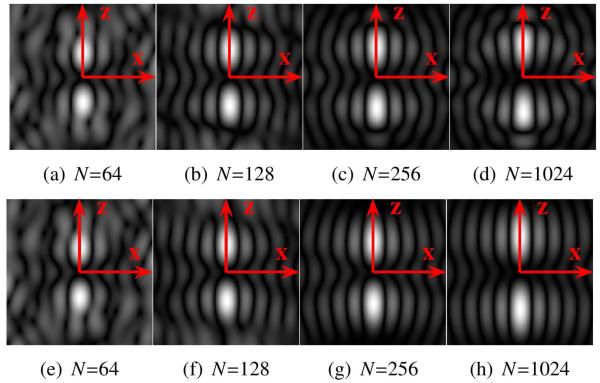
To analyze the effects of sampling and spherical harmonic truncation, we computed (23) for a variety of different sampling schemes and a variety of different values of L. In the results that follow, we will report findings for the four different sampling schemes shown in Fig. 4. These sampling patterns were obtained using a model of electrostatic repulsion to distribute the sampling locations as evenly as possible on the surface of the sphere (Jones et al., 1999). Profiles illustrating typical behaviors for g (u, x) for the FRT and the FRACT are shown in Figs. 5 and 6, respectively. As can be seen, both limited L and limited N can distort the shape of g (u, x) for both transforms, though the response functions still maintain most of the important features of the ideal FRT and FRACT when L is 8 or larger and N is larger than 64.

Figure 4.

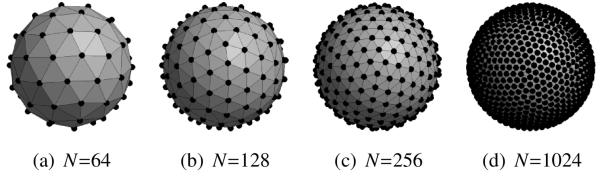
Sampling patterns with different numbers N of total measurements.

Figure 5.

Images showing the magnitude of ${\tilde{g}}_{\mathbf{u}}(x,0,z)$ in the x-z plane for the FRT, in the presence of finite sampling of the sphere and truncation of the spherical harmonic series. (a)-(d) Results using L = 8. (e)-(h) Results using L = 32. Results can be compared to the ideal response function shown in Fig. 1(b).

Figure 6.

Images showing the magnitude of ${\tilde{g}}_{\mathbf{u}}(x,0,z)$ in the x-z plane for the FRACT with parameter ξ = 0.51ρ, in the presence of finite sampling of the sphere and truncation of the spherical harmonic series. (a)-(d) Results using L = 8. (e)-(h) Results using L = 32. Results can be compared to the ideal response function shown in Fig. 2(b).

3. Results

Based on the theoretical results presented in the previous sections, we expect that the FRACT could have significantly improved performance in resolving multiple orientations from HARDI data. In the following subsections, we confirm this expectation using both simulations and real experimental data. In all results, we show ODFs that have been min-max normalized to enhance visualization (Tuch, 2004).

3.1. Simulations

A range of different numerical simulations was performed to compare the FRT and the FRACT in a variety of practical situations. In all of the numerical simulations, data was synthesized by modeling the EAP as the linear combination of multiple diffusion tensor models, though similar behavior would be expected under alternative models of a multi-fiber EAP (as will be shown later using real data). Each diffusion tensor component was given the same relative volume fraction, and diffusion tensor eigenvalues of λ₁ = 1400 × 10⁻⁶ mm²/s and λ₂ = λ₃ = 350×10⁻⁶ mm²/s (fractional anisotropy = 0.71). The relative orientations of the principal eigenvectors of the different tensors were systematically varied to establish the capabilities of each transform for resolving crossing fibers. Simulations were performed for several different b-values (a DW-MRI parameter proportional to ρ²). Pseudorandom Gaussian noise with mean zero and variance σ² was added to the data for different values of σ, and we report results for different SNR values, which we define as SNR= E (0)/σ. Due to the approximately exponential decay of E (q) with respect to ||q||_ℓ2, the SNR for each of the simulated DW data samples will be significantly lower than our reported SNR value. To match practical implementations, all processing methods were applied after discarding the phase of the simulated noisy signal, resulting in a Rician signal distribution.

Figures 7 and 8 present representative comparisons between the FRT and the FRACT at b-values of 1000 s/mm² and 2000 s/mm², respectively, with the other simulation parameters explained in the figure captions. As can be seen the FRACT can provide higher angular-resolution than the FRT, as evidenced by the fact that the FRACT is able to successfully resolve crossing fibers (i.e., the transform profile is multimodal, with maxima oriented along the direction of the true tensor orientations) in several cases where the FRT only found a single orientation maximum. As expected, the performance of both the FRACT and the FRT improved with increasing b-value (i.e., increasing ρ). The simulations also verified that the FRACT was relatively more sensitive to noise than the FRT. However, it is observed that the FRACT is still significantly more capable of resolving tensor orientations compared to the FRT, particularly when using larger b-values.

Figure 7.

Qualitative comparison between the FRT and the FRACT at a b-value of 1000 s/mm², in a two-tensor simulation with SNR=20, N =256 directions, ξ = 0.34ρ, and L = 8. Each image shows the mean ODF (solid) and the mean ODF plus two standard deviations (transparent). Results are shown for the (a)-(d) FRT and (e)-(h) FRACT, for crossing angles of (a,e) 47°, (b,f) 57°, (c,g) 76°, and (c,g) 90°.

Figure 8.

Qualitative comparison between the FRT and the FRACT at a b-value of 2000 s/mm², in a two-tensor simulation with SNR=20, N =256 directions, ξ = 0.34ρ, and L = 8. Each image shows the mean ODF (solid) and the mean ODF plus two standard deviations (transparent). Results are shown for (a)-(d) the FRT and (e)-(h) the FRACT, for crossing angles of (a,e) 47°, (b,f) 57°, (c,g) 76°, and (c,g) 90°.

Quantitative results using this same two-tensor simulation setup are shown in Figs. 9-11, where each figure explores a different region of the simulation parameter space. In each of these figures, both the FRT and the FRACT were computed 1000 times with different noise realizations for each of 20 different angular separations between the two simulated tensors. Histograms were subsequently computed for the locations of the local maxima of the ODFs in the plane spanned by the principal eigenvalues of the two simulated tensors.

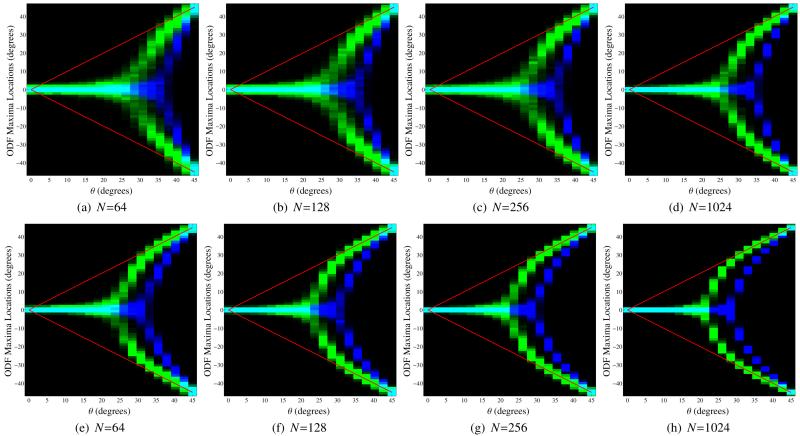
Figure 9.

Histograms for the locations of local maxima extracted from the FRT profiles (in blue) and the FRACT profiles (in green) for two simulated tensors in the x-y plane with orientation angles of −θ and +θ in polar coordinates. The color scale is set to saturate at 250 counts in a single histogram bin for improved visualization. The true orientations of the two tensors are also indicated using red lines. All simulations used SNR=80, ξ = 0.34ρ, and L = 8. The images from left to right show results for different numbers N of q-space samples. Results are shown for (a)-(d) a b-value of 1000 s/mm² and (e)-(h) a b-value of 2000 s/mm².

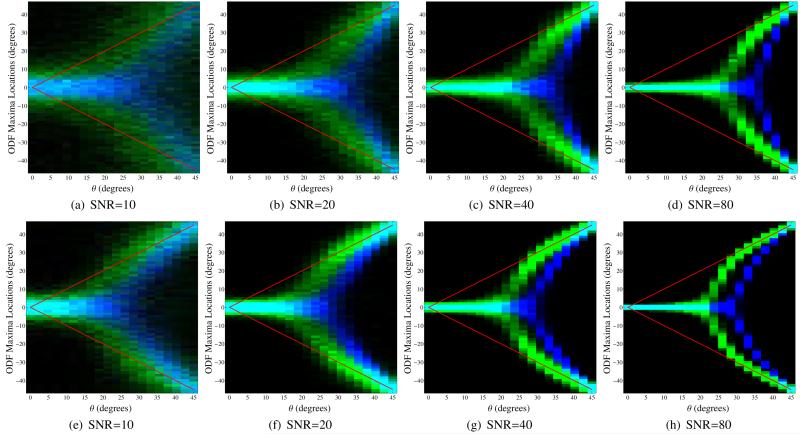
Figure 11.

Histograms for the locations of local maxima extracted from the FRT profiles (in blue) and the FRACT profiles (in green) for two simulated tensors in the x-y plane with orientation angles of −θ and +θ in polar coordinates. The color scale is set to saturate at 250 counts in a single histogram bin for improved visualization. The true orientations of the two tensors are also indicated using red lines. All simulations used ξ = 0.34ρ, N = 256, and L = 8. The images from left to right show results for different SNRs. Results are shown for (a)-(d) a b-value of 1000 s/mm² and (e)-(h) a b-value of 2000 s/mm².

Figure 9 illustrates the performance of the FRT and the FRACT as a function of the number N of q-space samples. As can be seen, the FRACT successfully identifies the existence of two different dominant orientations for a wider range of angular separations than the FRT for all four q-space sampling patterns and both b-values, indicating that the higher angular resolution of FRACT is not very sensitive to the data acquisition scheme, though it should still be noted that both methods are more accurate when using the higher b-value. In addition, the FRACT shows significantly less bias in the estimated locations of ODF maxima compared to the FRT.

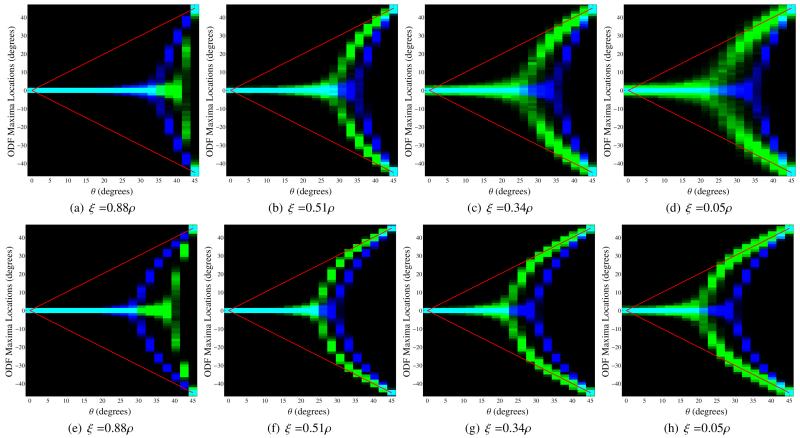
Figure 10 demonstrates the effect of ξ on the performance of the FRACT. As predicted, the choice of ξ has a profound impact. In particular, relatively large values of ξ are relatively ineffective, and the FRACT can be significantly outperformed by the FRT when ξ is not chosen appropriately. These simulations also confirm the prediction that the capability of the FRACT to resolve multiple orientations improves as ξ decreases to zero, since the FRACT histogram is multimodal over the largest range when ξ takes the smallest value. However, this figure also confirms that the FRACT with small values of ξ is more sensitive to noise than it is with large values of ξ, as indicated by the increased width of the histogram peaks.

Figure 10.

Histograms for the locations of local maxima extracted from the FRT profiles (in blue) and the FRACT profiles (in green) for two simulated tensors in the x-y plane with orientation angles of −θ and +θ in polar coordinates. The color scale is set to saturate at 250 counts in a single histogram bin for improved visualization. The true orientations of the two tensors are also indicated using red lines. All simulations used SNR=80, N = 256, and L = 8. The images from left to right show results for different values of the FRACT parameter ξ. Results are shown for (a)-(d) a b-value of 1000 s/mm² and (e)-(h) a b-value of 2000 s/mm².

Figure 11 compares the effect of SNR on the FRACT and the FRT. These results illustrate that the FRACT has higher accuracy (i.e., reduced bias and better ability to resolve multiple orientations) but lower precision (i.e., larger variance around the different modes of the histogram) than the FRT across a wide range of different SNR levels.

In sum, the two-tensor simulations shown in Figs. 9-11 validate the predicted characteristics of the FRACT, and indicate that the FRACT leads to significantly improved orientation estimates compared to the standard FRT. The supplementary material accompanying this paper includes additional results that further examine the characteristics of the FRACT involving: the harmonic order L, the fractional anisotropy and volume fraction parameters in simulated multi-tensor data, the SNR and number of samples N, and the FRACT parameter ξ.

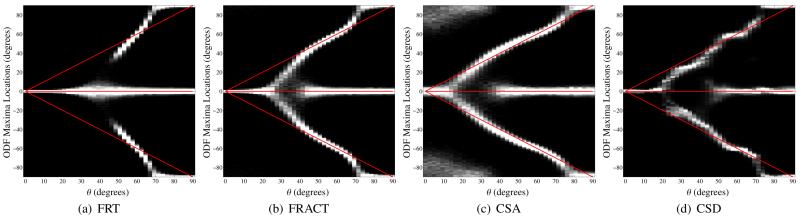
Figures 12 and 13 show comparisons between the performance of the FRT and the FRACT with previously-proposed state-of-the-art nonlinear ODF estimation methods. In particular, we compare with the nonlinear constant solid angle (CSA) QBI method (Aganj et al., 2010), and the nonlinear non-negativity constrained spherical deconvolution (CSD) method (Tournier et al., 2007). In these results, the FRT was implemented with L = 8, and the FRACT was implemented with L = 8 and ξ = 0.34ρ. The nonlinear CSA method is appropriate for estimating both isotropic and anisotropic diffusion ODFs, and computes the ODF definition of Eq. (5) under the modeling assumption that the diffusion signal along each direction decays exponentially as a function of b-value. We implemented CSA as described by Aganj et al. (2010), using L = 8 and flexible thresholding parameters of δ₁ = δ₂ = 0.001. The CSD method assumes that the measured diffusion data can be modeled as the spherical convolution of a fiber orientation distribution with an ideal fiber response (i.e., the diffusion signal that would be observed from an ideal isolated fiber bundle). We implemented CSD with L = 12, and used a previously-described iterative approach to enforce non-negativity constraints (Tournier et al., 2007). Following Tournier et al. (2007), we chose CSD parameters of τ = 0.1 and λ = 10. For these simulation examples, the ideal fiber response used in CSD matched perfectly with the diffusion tensor used to generate the data. This represents a best case scenario for CSD, since there would generally always be some amount of mismatch between the assumed fiber response and the observed diffusion signal in real applications.

Figure 12.

Histograms for the locations of local maxima extracted from the (a) FRT profiles, (b) the FRACT profiles, (c) the CSA profiles, and (d) the CSD profiles for two simulated tensors in the x-y plane with orientation angles of −θ and +θ in polar coordinates. The gray scale is set to saturate at 40 counts in a single histogram bin for improved visualization. The true orientations of the two tensors are also indicated using red lines. All simulations used SNR=40, N = 256, and a b-value of 1500 s/mm². Note that due to periodicity and symmetry relationships, the histogram for θ ∈ [45°, 90°) is a reversed and circularly-shifted version of the histogram for θ ∈ [0°, 45°).

Figure 13.

Histograms for the locations of local maxima extracted from the (a) FRT profiles, (b) the FRACT profiles, (c) the CSA profiles, and (d) the CSD profiles for three simulated tensors in the x-y plane with orientation angles of −θ, 0, and +θ in polar coordinates. Note that, unlike the previous histograms, the separation angle for these histograms is θ rather than 2θ. The gray scale is set to saturate at 100 counts in a single histogram bin for improved visualization. The true orientations of the three tensors are also indicated using red lines. All simulations used SNR=80, N = 256, and a b-value of 5000 s/mm².

Figure 12 shows simulation results for a two-tensor model at a b-value of 1500 s/mm² with SNR=40 and N = 256. As before, the FRACT has lower bias than the FRT. The FRACT also demonstrates similar bias to the CSA method, but with lower variance. In addition, the CSA method demonstrates a number of spurious ODF maxima, far away from the actual tensor orientations (spurious signal variations occur along all orientations, but these variations are more likely to become maxima along directions where the magnitude of the noiseless ODF is small). This is likely the result of low SNR, combined with modeling inaccuracies from the exponential decay assumption that underlies the CSA method, but which is not valid for a multi-tensor diffusion model. These spurious peaks can be reduced by applying additional regularization in the CSA method, though at the expense of angular resolution. As expected, the CSD method performs very well in this case, because the estimation procedure incorporated perfect knowledge of the ideal fiber response for this simulation scenario. However, it is also notable that the CSD method only has slightly improved angular resolution compared to the FRACT.

Digital animations of these comparisons are included as supplementary material accompanying the paper. The supplementary video clips use the MPEG-2 video format. All videos show ODFs estimated using the FRT, FRACT, CSA, and CSD methods from simulated data at a b-value of 1500 s/mm² with N = 256, using the same parameters described above. The true fiber orientations are indicated using red lines. Clip1.mpg shows results for a very high-SNR case (SNR=10⁶), while Clip2.mpg shows results for a case with SNR=40. Clip3.mpg is identical to Clip2.mpg, except that we augmented the CSA method with Laplace-Beltrami regularization (λ = 0.03) to smooth the ODF and reduce spurious peaks (Descoteaux et al., 2007). While the spurious peaks are significantly reduced for the CSA method, this comes at the expense of a loss in angular resolution.

An even more challenging simulation using a three-tensor model is shown in Fig. 13. Since the estimation of three distinct coplanar orientations can be very challenging, we show results for a large b-value of 5000 s/mm². As can be seen, the FRACT is more successful than the FRT in identifying and localizing the three different dominant orientations. In this case, the CSA method yields somewhat higher resolution than the FRACT, though with slightly higher variance in the estimated orientation, and a considerable number of spurious ODF maxima. As in the two-tensor case, the CSD method is very accurate due to the use of prior information, though is not substantially more accurate than the FRACT.

3.2. FiberCup Experiment Data

In this section, we demonstrate the performance of the FRACT when applied to real data acquired from an experimental phantom. We made use of the publicly-available FiberCup data (Fillard et al., 2011; Poupon et al., 2008). Briefly, the FiberCup data was acquired by scanning a custom-built phantom with a 3T MRI magnet. The phantom was built using thousands of water-filled acrylic fibers, which were organized into bundles and arranged to have complex crossing structure. Our results make use of two different scans of this phantom, one with a b-value of 1500 s/mm² and the other with a b-value of 2650 s/mm². Both datasets were acquired with 6 mm isotropic resolution and N = 64 measured diffusion directions, and edge-preserving filtering of the images (Haldar et al., 2012) was applied prior to applying the FRT, the FRACT, CSA, and CSD methods. The fiber response for CSD was derived by averaging diffusion profiles fitted from single fiber voxels demonstrating the highest anisotropy (Tournier et al., 2007). Due to the uniformity of the acrylic fibers used to construct the phantom, this estimated fiber response is expected to be very accurate.

Figure 14 shows the ODFs reconstructed by these methods from a region of the phantom where fibers cross at a 90° angle. As can be seen, the FRACT unequivocally demonstrates the presence of multiple distinct orientations in the voxels where the fibers cross for both b-values. In contrast, the ODFs obtained from the FRT do not demonstrate such prominent separations between the two groups of crossing fibers, particularly for the b = 1500 s/mm² data. Similar to previous simulations, the CSA method succesfully identifies distinct orientations, though also demonstrates spurious ODF peaks that do not correspond to true fiber orientations. As expected, the CSD method performs well for this dataset, and results are comparable to those obtained with the FRACT.

Figure 14.

ODFs reconstructed by applying (a)-(b) the FRT and (c)-(d) the FRACT to the FiberCup data. (a),(c) show results for the b = 1500 s/mm² data, while (b),(d) show results for the b = 2650 s/mm² data. The ODFs are color-coded by orientation.

3.3. In Vivo Data

Finally, we illustrate the performance of the FRACT on real in vivo human brain data. DW-MRI data was acquired using a 3T MRI scanner equipped with a 12-channel head coil. The acquisition sampled N = 144 directions at a b-value of 2500 s/mm². The acquisition covered the whole brain at 2 mm isotropic resolution with a standard multi-slice single-shot EPI readout, an echo time of 109 ms, and a repetition time of 7.9 seconds. Data was collected in accordance with the Institutional Review Board of the University of Southern California.

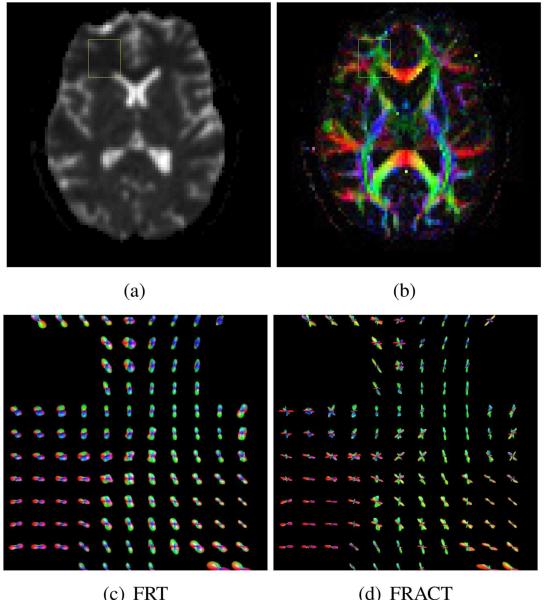
Representative results from this dataset are shown in Fig. 15. While there is no gold standard to compare to, these results are visually similar to the previous simulations and experiments, and suggest that the FRACT can offer significantly sharper ODF profiles than the FRT, enabling better identification of crossing fiber structure in regions of complicated tissue architecture.

Figure 15.

Application of the FRT and the FRACT to in vivo human brain data. (a) A b = 0 s/mm² image from a slice of interest. (b) The corresponding DTI fit, where image intensity corresponds to the fractional anisotropy of the tissue, while the image color corresponds to the orientation of the principal eigenvector of the estimated diffusion tensor. The yellow boxes in (a) and (b) indicate a region of interest (ROI) from the white matter core of the frontal lobe in which complicated fiber crossing patterns are known to occur. ODFs from the ROI are shown for (c) the FRT and (d) the FRACT.

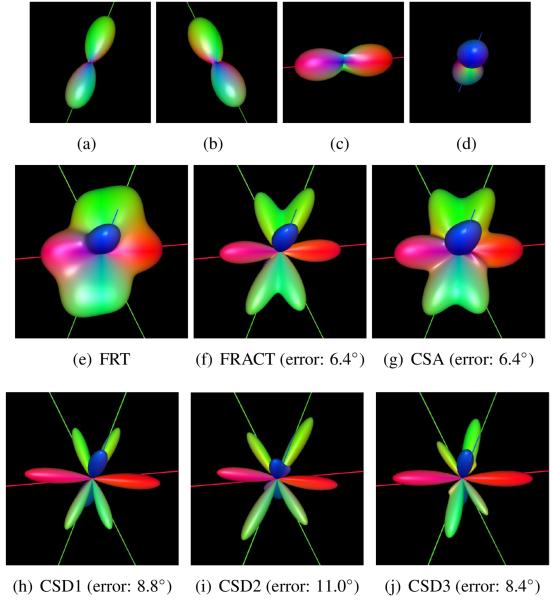
To illustrate the difference between the FRT, the FRACT, CSA, and CSD in the context of realistic data with complicated structure, a crossing fiber dataset was synthesized through the linear combination of real brain data from four different voxels demonstrating simple single-orientation structure. CSD was evaluated using fiber responses estimated in three different ways: CSD1 estimated the fiber response by averaging diffusion tensor profiles fitted independently from each of the original single-orientation voxels shown in Fig. 16(a)-(d); CSD2 and CSD3 estimated the fiber response from diffusion tensor fits to the single-voxel data shown in Figs. 16(a) and (b), respectively. In contrast to previous cases, in which the fiber response was expected to be very accurate due to the uniformity of the fiber populations, fiber bundles in the brain can be more heterogeneous, with different distributions of axon radii and different microstructural characteristics. As a result, the tensors estimated for each voxel were slightly different from one another, and none of the estimated fiber responses used for CSD perfectly match the data.

Figure 16.

Application of the FRT, the FRACT, CSA, and CSD to a mixture of fibers from in vivo human brain data. Data was combined from image voxels displaying a single dominant diffusion orientation, as shown in (a-d). FRT ODFs are shown for voxels corresponding to (a,b) forceps major, (c) genu of the corpus callosum, and (d) corticospinal tract. Reconstructions of the multi-fiber combined dataset are shown for (e) the FRT, (f) the FRACT, (g) CSA, (h) CSD1, (i) CSD2, and (j) CSD3. The lines shown in each image correspond to the dominant orientations estimated from (a-d). The figure captions show the maximum angular error between the estimated ODF maxima from the combined data and the ODF maxima from the original single-orientation data (this is not shown for the FRT, since the FRT fails to resolve all of the ODF peaks).

The results of applying the different methods to this data are shown in Fig. 16. Consistent with the previous results, the FRACT is able to accurately untangle the orientation information from this complicated dataset, while the FRT is more limited and does not resolve all of the four original orientations. For this case, the FRACT and CSA demonstrate similar angular accuracy in the estimation of the ODF maxima, though the FRACT has sharper ODF peaks. While all of the CSD results qualitatively appear to be very sharp, they are somewhat sensitive to the choice of the fiber response function, and the estimated orientations are slightly worse than those of the FRACT and CSA; this can be attributed to the relative inaccuracy of the assumed spherical convolution model in this kind of realistic case with heterogeneous fiber structures. The sensitivity of the CSD method to the fiber response function is also consistent with simulations based on synthetic data (not shown).

4. Discussion and Conclusion

This work introduced a new family of transforms for data sampled on the Fourier 2-sphere. Compared to existing methods for processing such data, these transforms are linear, flexible, and can be computed efficiently. We showed that the transforms have analytic characteristics for continuous data, and introduced new mathematical machinery for evaluating these kinds of transforms in the context of sampled data.

We also discussed one special case of this family of transforms, the FRACT, which can be applied to HARDI data to estimate oriented diffusion. Compared to the existing FRT, the FRACT has significant advantages in its ability to accurately resolve the angular orientation of anisotropic structures from DW-MRI data. These advantages were confirmed with extensive simulations and real MR data. The FRACT was also compared to state-of-the-art nonlinear ODF estimation methods. Results demonstrated that the FRACT can be as useful or even more useful than these alternative approaches for estimating orientation information. In addition, unlike the nonlinear approaches, the FRACT has analytic theoretical properties and does not require the use of unrealistic modeling assumptions. This makes FRACT-based ODF estimation attractive for practical in vivo applications, where strong modeling assumptions are unlikely to be satisfied.

Despite demonstrating significantly improved results using the FRACT, there still remain a variety of unexplored directions. The FRACT is one of the most simple extensions of the FRT, and we anticipate that more complicated choices of the G (·) kernel function could lead to even better performance. For example, by using more than just one cosine-modulated Bessel function, it would be possible to more accurately approximate z², or to synthesize functions to, e.g., approximate z^p for some value of p. The latter type of function could enable characterizable linear transform methods to estimate the higher-order moments of the EAP from HARDI data. In addition to considering alternate members of the family of transforms that can be expressed by (2), it would also be of interest to explore families of linear transforms that are more general than (2). For example, FRACT results could potentially be even further improved by employing a deconvolution-based ODF-sharpening approach that was previously proposed to improve the FRT (Descoteaux et al., 2009). As a final example, there can be interesting generalizations of our family of transforms to the case where diffusion data is sampled on the surface of multiple spheres (Wu and Alexander, 2007; Khachaturian et al., 2007).

We expect that the proposed transforms, and the associated theoretical tools that were introduced for their analysis, will prove useful for future studies in this area.

Appendix A

Derivation of (8) and (9)

The surface integral in (7) can be expressed in spherical coordinates as in (A.1). When u is aligned with the z-axis, this integral reduces to (A.2). Under the change of variables τ = ρ cos φ, and noting that $\rho \sin \varphi =\sqrt{{\rho }^2-{\tau }^2}$, (A.2) can be expressed as (A.3), which matches the expressions in (8) and (9).

$${\int }_0^{\pi }{\int }_0^{2\pi }G\left(u_x\rho \cos \theta \sin \varphi +u_y\rho \sin \theta \sin \varphi +u_z\rho \cos \varphi \right)\cdot \exp (-i2\pi (x\rho \cos \theta \sin \varphi +y\rho \sin \theta \sin \varphi +z\rho \cos \varphi \left)\right){\rho }^2\sin \varphi d\theta d\varphi .$$ (A.1)

$${\int }_0^{\pi }{\int }_0^{2\pi }G\left(\rho \cos \varphi \right)\exp (-i2\pi (x\rho \cos \theta \sin \varphi +y\rho \sin \theta \sin \varphi +z\rho \cos \varphi \left)\right){\rho }^2\sin \varphi d\theta d\varphi .$$ (A.2)

$$\begin{array}{cc}\hfill {\int }_{-\rho }^{\rho }{\int }_0^{2\pi }G\left(\tau \right)\exp & (-i2\pi (x\sqrt{{\rho }^2-{\tau }^2}\cos \theta +y\sqrt{{\rho }^2-{\tau }^2}\sin \theta +z\tau \left)\right)\rho d\theta d\tau \hfill \\ \hfill & =\rho {\int }_{-\rho }^{\rho }G\left(\tau \right)\exp (-i2\pi z\tau ){\int }_0^{2\pi }\exp \left(-i2\pi \left(x\sqrt{{\rho }^2-{\tau }^2}\cos \theta +y\sqrt{{\rho }^2-{\tau }^2}\sin \theta \right)\right)d\theta d\tau \hfill \\ \hfill & =2\pi \rho {\int }_{-\rho }^{\rho }G\left(\tau \right)\exp (-i2\pi z\tau )J_0\left(2\pi \sqrt{{\rho }^2-{\tau }^2}\sqrt{x^2+y^2}\right)d\tau ,\hfill \end{array}$$ (A.3)