Semiparametric estimation of the covariate-specific ROC curve in presence of ignorable veri cation bias

Summary

Covariate-specific ROC curves are often used to evaluate the classification accuracy of a medical diagnostic test or a biomarker, when the accuracy of the test is associated with certain covariates. In many large-scale screening tests, the gold standard is subject to missingness due to high cost or harmfulness to the patient. In this paper, we propose a semiparametric estimation of the covariate-specific ROC curves with a partial missing gold standard. A location-scale model is constructed for the test result to model the covariates’ effect, but the residual distributions are left unspecified. Thus the baseline and link functions of the ROC curve both have flexible shapes. With the gold standard missing at random (MAR) assumption, we consider weighted estimating equations for the location-scale parameters, and weighted kernel estimating equations for the residual distributions. Three ROC curve estimators are proposed and compared, namely, imputation-based, inverse probability weighted and doubly robust estimators. We derive the asymptotic normality of the estimated ROC curve, as well as the analytical form the standard error estimator. The proposed method is motivated and applied to the data in an Alzheimer's disease research.

1. Introduction

The receiver operating characteristic (ROC) curve is a useful tool to evaluate the classification ability of a medical diagnostic test or biomarker. The ROC curve is a plot of test's sensitivity versus its 1-specificity as one varies the decision threshold for test positivity. In the ROC analysis, covariates may impact the magnitude of the diagnostic test and/or the diagnostic accuracy. Lack of covariate adjustment may not only bias the result, but also impair the generalizability of the study results to other different populations. Thus the covariate-specific ROC curve is widely used to evaluate the classification accuracy within some particular sub-population. One may consider a stratified analysis and estimate the ROC curve for each sub-population specified by the covariates. However, regression type analysis is often preferred so that the covariates’ effect is estimated in a parsimonious fashion. Zhou et al. (2002) and Pepe (2003) both give a detailed review of the existing methods in estimating a covariate-specific ROC curve. Many methods require the true condition status of each patient to be determined by the “gold standard”. In many large cohort studies, however, the gold standard may not be available to everybody because it is expensive and/or invasive. Deleting the subjects with missing gold results in biased estimators, which is referred to as the “verification bias” (Begg and Greenes, 1983).

Using the missing data framework, we call the verification process to be missing at random (MAR) if the probability of disease verification is only affected by the observed variables. Under the MAR assumption, many existing methods are available for the verification bias problem for binary tests (Begg and Greenes, 1983) and ordinal tests (Gary et al., 1984; Zhou, 1996; Zhou, 1998; Rodenberg and Zhou, 2000). Recently, Zheng el al. (2005) proposed to use a weighted estimating equation (WEE) approach to estimate the covariate specific ROC curve for ordinal tests. They considered a parametric binormal form of the ROC curve. The theory of their WEE approach originated from Lipsitz et al. (1999). The weighted estimating equations utilize a model of missing mechanism as well as a model of disease probability in order to estimate the parameters in the binormal ROC curve. The advantage of their method is the robustness to some model mis-specification: either the disease model or the verification model being correct guarantees the consistency of the ROC curve estimator, which is called “doubly robust” property. Alonzo and Pepe (2005) considered the continuous test result and proposed several empirical ROC curve estimators. Their ROC curve estimators are empirical step functions, and could not incorporate the covariates effect on ROC curves.

Although covariate-specific ROC curve estimators for continuous test have been extensively discussed in the literature, not much work has been done on the verification bias correction for covariate-specific ROC curves. Page and Rotnitzky (2009) is the only published paper so far, who proposed a fully parametric model for estimating the covariate-specific ROC curve under verification bias. However, their binormal ROC curve assumption is often too restrictive in practice, so we wish to estimate the “baseline shape” of the ROC curve instead. A subgroup analysis is an option when the covariates are categorized. For example, Punglia et al. (2003) studied the ROC curve for prostate-specific antegen (PSA) measurement in detecting prostate cancer. They reported the bias corrected ROC curve stratified by age group and digital rectal examination results. When some of the covariates are continuous, however, subgroup analysis may not be feasible. In this paper, we propose a new semiparametric regression model for the covariate-specific ROC curve and the weighted estimating equations to adjust for the verification bias, which extends the results in Alonzo and Pepe (2005) and Page and Rotnitzky (2009).

We consider a continuous-scale diagnostic test and propose several semiparametric covariate-specific ROC curve estimators. A location-scale model is constructed on the diagnostic test to model the covariates effect, but the residual distributions are left unspecified. This location-scale framework is commonly used in regression settings as well. The baseline and link function of the ROC curve both have flexible shapes. Pepe (1998) first proposed and compared several regression methods to estimate the ROC curve without missing data, and showed that the location-scale model is the most efficient. With missing gold standard, we employ the weighted estimating equations for the location-scale parameters, similarly as in Zheng el al. (2005) and Page and Rotnitzky (2009). The unspecified residual distributions are estimated by the weighted kernel estimating equations, which yields the smooth ROC curve estimators. We discuss three forms of weighting techniques based on imputation and inverse probability weighting. The covariate-specific ROC curve is then estimated as a function of the location-scale parameters and the residual distribution/quantile functions. We also show the central limit theorem for the estimated ROC curve and derive the asymptotic variance formula. Compared to Alonzo and Pepe (2005), our approach can incorporate covariates, and we derive analytical variance formula; compared to Zheng el al. (2005) and Page and Rotnitzky (2009), the form of our ROC curve is more flexible, as we do not specify the baseline shape of the curve.

The paper is organized as follows. Section 2 outlines the location-scale model framework and other basic model assumptions. Section 3 presents the weighted estimating equations for the finite and infinite dimensional parameters. The limit theorems are also presented. Section 4 reports some simulation results to examine the finite sample performance of our proposed method. Section 5 applies our method to a real data example in an Alzheimer's disease research, followed by discussions in Section 6.

2. Location-scale model

Let T_i, D_i, V_i and X_i be the continuous test result, the gold standard, the verification indicator, and the covariates for the ith subject, respectively, where i = 1, 2, , n. Let a larger value of T indicate more likely to be diseased; let D = 1 denote a diseased subject (case) and 0 denote a healthy subject (control); let V = 1 denote observed gold standard and 0 denote missing gold standard. We sometimes suppress the subscript i when there is no confusion.

We assume a location-scale model for T_i:

$$T_i=\mu (X_i,D_i;\beta )+\sigma (X_i,D_i;\gamma )\times {∊}_i\left(D_i\right),$$

where μ(X_i, D_i; β) and σ(X_i, D_i; γ) are the mean and standard deviation for T_i given the values of the covariates and disease status, respectively, and ε_i(D_i) is the residual. We may also use μ_i and σ_i as an abbreviation. Let G₀ and G₁ be the unknown distribution functions for ε_i(0) and ε_i(1), respectively, with mean 0 and variance 1. Our setting of the location-scale model slightly extended the model in Section 2 of Pepe (1998), in that we allow the two distribution functions to be different. Page and Rotnitzky (2009) also used this location-scale model, but assumed the residual ε_i(D_i) to follow standard normal distribution. As we will see in the example in Section 5, the cases and controls can have quite different test distributions, both of which are far from normal.

We could then write out the covariate-specific sensitivity and specificity at some cutoff point c:

$$\begin{array}{cc}\hfill Sen{s}_x& =\mathrm{Pr}(T\ge c\mid D=1,X=x)\hfill \\ \hfill & =1-G_1\left(\frac{c-\mu (x,1;\beta )}{\sigma (x,1;\gamma )}\right),\hfill \\ \hfill 1-Spe{c}_x\left(c\right)& =\mathrm{Pr}(T\ge c\mid D=0,X=x)\hfill \\ \hfill & =1-G_0\left(\frac{c-\mu (x,0;\beta )}{\sigma (x,0;\gamma )}\right).\hfill \end{array}$$

The ROC curve is expressed as follows:

$$RO{C}_x\left(t\right)=1-G_1\left[\frac{\sigma (x,0;\gamma )}{\sigma (x,1;\gamma )}{G}_0^{-1}(1-t)+\frac{\mu (x,0;\beta )-\mu (x,1;\beta )}{\sigma (x,1;\gamma )}\right].$$

Sometimes we call G₁ and $G_0^{-1}$ the link function and the baseline of the ROC curve, respectively. Allowing the link and baseline to be unspecified grants the ROC curve more flexibility. As a comparison, Pepe (1998), and Cai and Pepe (2002) both proposed a direct regression method for estimating the covariate-specific ROC curve; the former assumes both G₁ and $G_0^{-1}$ have known parametric forms, while the latter assumes G₁ to be known and leaves $G_0^{-1}$ to be unspecified. Pepe (1998) also mentioned that the location-scale model tends to be more efficient than the direct regression method. Another advantage of the location-scale model is that its extension to missing gold standard situation is more straightforward.

3. Estimation procedures

3.1 Complete data estimating equations

In the ROC curve expression, the unknown quantities to be estimated are finite dimensional parameters β and γ, and infinite dimensional curves $G_0^{-1}$ and G₁. When the gold standard is observed for each subject, the estimation of β and γ is easily obtained via the following estimating functions:

$$\begin{array}{cc}\hfill U_1& \equiv \sum _i{U}_{1i}\equiv \sum _i{\left(\frac{\partial {\mu }_i}{\partial \beta }\right)}^T\frac{(T_i-{\mu }_i)}{{\sigma }_i^2},\hfill \\ \hfill U_2& \equiv \sum _i{U}_{2i}\equiv \sum _i{\left(\frac{\partial }{\partial \gamma }{\sigma }_i^2\right)}^T\frac{{(T_i-{\mu }_i)}^2-{\sigma }_i^2}{\text{var}\left[{(T_i-{\mu }_i)}^2\right]},\hfill \end{array}$$

where μ_i and σ_i are short for μ(X_i, D_i; β) and σ(X_i, D_i; γ) defined in the location-scale model. Substituting the estimated $\widehat{\beta }$ and $\widehat{\gamma }$ into μ_i and σ_i, we denote ${\widehat{∊}}_i\left(D_i\right)=\frac{(T_i-{\widehat{\mu }}_i)}{{\widehat{\sigma }}_i}$ to be the fitted residual. For each fixed s, the two distribution functions, G₁(s) and G₀(s), can then be estimated with the following kernel smoothing estimators:

$$\begin{array}{cc}\hfill U_3\left(s\right)& \equiv \sum _i{U}_{3i}\left(s\right)\equiv \sum _i{D}_i\left[K\left(\frac{s-{\widehat{∊}}_i\left(D_i\right)}{h}\right)-G_1\left(s\right)\right],\hfill \\ \hfill U_4\left(s\right)& \equiv \sum _i{U}_{4i}\left(s\right)\equiv \sum _i(1-D_i)\left[K\left(\frac{s-{\widehat{∊}}_i\left(D_i\right)}{h}\right)-G_0\left(s\right)\right],\hfill \end{array}$$

where K(·) is some distribution function and h is the bandwidth. In order to obtain the 1 – t quantile of G₀, $G_0^{-1}(1-t)$, we solve the following estimating function for every fixed t:

$$U_5\left(t\right)\equiv \sum _i{U}_{5i}\left(t\right)\equiv \sum _i(1-D_i)\left[K\left(\frac{G_0^{-1}(1-t)-{\widehat{∊}}_i\left(0\right)}{h}\right)+t-1\right].$$

Although t may take infinitely many values between 0 and 1, we set finite grid points to get good approximation for the smooth ROC curve. In the example, we choose t = 0.01, 0.02, · · · , 0.99 with linear extrapolation between the adjacent grid points. When the kernel $K\left(x\right)=I(x\le 0)$, we obtain the empirical estimators of G₀ and G₁. However, it is usually desired that the ROC curve is a smooth curve rather than a step function. Therefore, we use some continuous distribution function K(·), such as standard normal distribution Φ. The estimated Ĝ₀ and Ĝ₁ have the same $\sqrt{n}\text{-consistency}$ as the empirical distribution function, as long as the bandwidth is sufficiently small (Nadaraya, 1964).

3.2 Weighted estimating equations under verification bias

As the gold standard is only available for a portion of the subjects, we reweight the estimating equations. Let ρ_i = Pr(D_i = 1|T_i, X_i) = Pr(D_i = 1|T_i, X_i, V_i = 1) be the disease probability, and π_i = Pr(V_i = 1|T_i, X_i) be the verification probability. With the MAR assumption, the two probabilities can be estimated separately, where logistic regressions would be a convenient approach. We then construct the weighted estimating equations with the estimated ${\widehat{\rho }}_i$ and ${\widehat{\pi }}_i$. Three types of estimating methods are considered, namely, doubly robust (DR), inverse probability weighting (IPW) and imputation based (IB) approaches.

Let

$$S_k^{DR}\equiv \sum _i{S}_{ki}^{DR}\equiv \sum _i\left\{\frac{V_i}{{\widehat{\pi }}_i}{U}_{ki}+\left(1-\frac{V_i}{{\widehat{\pi }}_i}\right)E_{D_i\mid T_i,X_i}{U}_{ki}\right\},$$ (1)

$$S_k^{IPW}\equiv \sum _i{S}_{ki}^{IPW}\equiv \sum _i\frac{V_i}{{\widehat{\pi }}_i}{U}_{ki},$$ (2)

$$S_k^{IB}\equiv \sum _i{S}_{ki}^{IB}\equiv \sum _i\{V_i{U}_{ki}+(1-V_i\left)E_{D_i\mid T_i,X_i}{U}_{ki}\right\},$$ (3)

for k = 1, 2, 3, 4, 5. We abbreviate the superscript and use S_k to denote the general weighted estimating functions in the text below. The conditional expectation E_Di|Ti,Xi can be written as weighted summations, as D_i takes the value of 0 or 1. For example,

$$\begin{array}{cc}\hfill E_{D_i\mid T_i,X_i}{U}_{1i}& =\sum _{d=0}^1\mathrm{Pr}(D_i=d\mid T_i,X_i){\left(\frac{\partial \mu (X_i,d;\beta )}{\partial \beta }\right)}^T\frac{(T_i-\mu (X_i,d;\beta \left)\right)}{{\sigma }^2(X_i,d;\gamma )}\hfill \\ \hfill & =(1-{\rho }_i){\left(\frac{\partial \mu (X_i,0;\beta )}{\partial \beta }\right)}^T\frac{(T_i-\mu (X_i,0;\beta \left)\right)}{{\sigma }^2(X_i,0;\gamma )}+{\rho }_i{\left(\frac{\partial \mu (X_i,1;\beta )}{\partial \beta }\right)}^T\frac{(T_i-\mu (X_i,1;\beta \left)\right)}{{\sigma }^2(X_i,1;\gamma )}.\hfill \end{array}$$

The DR estimating functions (1) enjoy the “doubly robust” property: as long as either ${\widehat{\rho }}_i$ or ${\widehat{\pi }}_i$ is consistently estimated, the DR estimator is consistent; the IPW estimating equations (2) require that the verification probability, π_i, is consistently estimated; the IB estimating equations (3) require that the disease probability, ρ_i, is consistently estimated. In practice, our understanding of the missing mechanism or the disease risk may not be accurate enough, so the DR estimator allows two shots for the model specification, while IPW and IB estimators rely on a single model assumption.

All these weighted estimating equations can be solved by Newton-Raphson method. With the estimated $\widehat{\beta }$, $\widehat{\gamma }$, ${\widehat{G}}_0^{-1}$ and Ĝ₁, we could estimate the covariate-specific ROC curve as follows:

$${\widehat{ROC}}_x\left(t\right)=1-{\widehat{G}}_1\left[\frac{\sigma (x,0;\widehat{\gamma })}{\sigma (x,1;\widehat{\gamma })}{\widehat{G}}_0^{-1}(1-t)+\frac{\mu (x,0;\widehat{\beta })-\mu (x,1;\widehat{\beta })}{\sigma (x,1;\widehat{\gamma })}\right].$$

3.3 Asymptotic normality

First we examine the asymptotic behavior of the location-scale parameters. Let $B_1\left({\alpha }_1\right)={\sum }_i{B}_{1i}\left({\alpha }_1\right)$ and $B_2=\left({\alpha }_2\right)={\sum }_i{B}_{2i}\left({\alpha }_2\right)$ be the estimating functions for modelling ρ and π, respectively. Let ${\theta }_1\equiv \left(\begin{array}{c}\hfill \beta \hfill \\ \hfill \gamma \hfill \end{array}\right)$ be the location-scale parameters, and ${\widehat{\theta }}_1$ be its estimated version. Let $U_{12,i}\equiv \left(\begin{array}{c}\hfill U_{1i}\hfill \\ \hfill U_{2i}\hfill \end{array}\right)$ and $S_{12,i}\equiv \left(\begin{array}{c}\hfill S_{1i}\hfill \\ \hfill S_{2i}\hfill \end{array}\right)$. Define $I\equiv -\frac{\partial }{\partial {\theta }_1^T}E{S}_{12,i}$, $J_1=-\frac{\partial }{\partial {\alpha }_1^T}E{S}_{12,i}$, $J_2=-\frac{\partial }{\partial {\alpha }_2^T}E{S}_{12,i}$, $K_1=-\frac{\partial }{\partial {\alpha }_1^T}E{B}_{1i}$, $K_2=-\frac{\partial }{\partial {\alpha }_2^T}E{B}_{2i}$. Let $Q_i=U_{12,i}-J_1{K}_1^{-1}{B}_{1i}-J_2{K}_2^{-1}{B}_{2i}$. The asymptotic distribution of ${\widehat{\theta }}_1$ is stated in the following theorem:

Theorem 1: Under the standard regularity conditions stated in the Web Appendix,

$$\sqrt{n}\left({\widehat{\theta }}_1-{\theta }_1\right)\stackrel{d}{\to }N(0,{\Omega }_1),$$

where

$${\Omega }_1=I^{-1}\text{var}\left(Q_i\right)I^{-1}.$$

The proof of this theorem is sketched in the Web Appendix. Note that Ω₁ can be estimated by replacing all the parameters θ, α₁ and α₂ with their estimates, and replacing all the expectations in I, J₁, J₂, K₁ and K₂ with the sample mean.

Our primary interest is not to estimate the location and scale model, but to construct the ROC curve. Before studying the asymptotic property of the estimated ROC curve, we first take a look at the variances for Ĝ₁ and ${\widehat{G}}_0^{-1}$. The influence functions of ${\widehat{G}}_0^{-1}(1-t)$ and Ĝ₁(s) are stated in the following lemma.

Lemma 1: When n → +∞, h → 0 and nh⁴ → 0, both ${\widehat{G}}_0^{-1}(1-t)$ and Ĝ₁(s) are asymptotic linear for any t ∈ (0, 1) and s ∈ (–∞, +∞), :

$$\begin{array}{cc}\hfill \sqrt{n}\left({\widehat{G}}_0^{-1}(1-t)-G_0^{-1}(1-t)\right)& =\frac{1}{\sqrt{n}}\sum _i{A}_{1i}\left(t\right)+o_p\left(1\right),\hfill \\ \hfill \sqrt{n}\left({\widehat{G}}_1\left(s\right)-G_1\left(s\right)\right)& =\frac{1}{\sqrt{n}}\sum _i{A}_{2i}\left(s\right)+o_p\left(1\right)\hfill \end{array}$$

where

$$A_{1i}\left(t\right)={\left(-\frac{\partial }{\partial s}E{S}_{5i}\right)}^{-1}\left[S_{5i}+\left(\frac{\partial }{\partial {\theta }_1^T}E{S}_{5i}\right)I^{-1}{Q}_i+\left(\frac{\partial }{\partial {\alpha }_1^T}E{S}_{5i}\right)K_1^{-1}{B}_{1i}+\left(\frac{\partial }{\partial {\alpha }_2^T}E{S}_{5i}\right)K_2^{-1}{B}_{2i}\right]$$

,and

$$A_{2i}\left(s\right)={\left(-\frac{\partial }{\partial G_1\left(s\right)}E{S}_{3i}\right)}^{-1}\left[S_{3i}+\left(\frac{\partial }{\partial {\theta }_1^T}E{S}_{3i}\right)I^{-1}{Q}_i+\left(\frac{\partial }{\partial {\alpha }_1^T}E{S}_{3i}\right)K_1^{-1}{B}_{1i}+\left(\frac{\partial }{\partial {\alpha }_2^T}E{S}_{3i}\right)K_2^{-1}{B}_{2i}\right].$$

As the estimated ROC curve can be written as functions Ĝ₁, ${\widehat{G}}_0^{-1}$, and $\widehat{\theta }$, the point-wise asymptotic variance of ${\widehat{ROC}}_x\left(t\right)$ is shown in the following theorem:

Theorem 2: As the conditions for Theorem 1 and Lemma 1 hold, for any t ∈ (0, 1),

$$\sqrt{n}\left({\widehat{ROC}}_x\left(t\right)-RO{C}_x\left(t\right)\right)\stackrel{d}{\to }N(0,{\Omega }_2)$$

where the expression of Ω₂ is given in the Appendix.

The proof of Lemma 1 and Theorem 2 is sketched in the Web Appendix. According to the proof of Theorems 1 and 2, both asymptotic variances consist of two sources of variability: one from the estimating functions S_k (k = 1, · · · , 5), the other from plugging in the estimated probabilities ${\widehat{\rho }}_i$ and/or ${\widehat{\pi }}_i$. However, a nice property for the DR estimator is that the second source of variability may vanish under some special cases. In other words, the estimated ROC curves with estimated ${\widehat{\rho }}_i$ and ${\widehat{\pi }}_i$ have a similar variance as the estimated ROC curve with the true probabilities ρ_i and π_i. This property is stated in the following Corollary 1, which is proved in the Web Appendix:

Corollary 1: In the DR estimator, if ${\widehat{\rho }}_i$ is estimated with $\sqrt{n}$ consistency, the variances Ω₁ and Ω₂ do not contain the variability of estimating ${\widehat{\pi }}_i$; if ${\widehat{\pi }}_i$ is estimated with $\sqrt{n}$ consistency, Ω₁ and Ω₂ do not contain the variability of estimating ${\widehat{\rho }}_i$.

4. Simulation studies

We conducted extensive simulation studies and only report the primary results in this section. More results are shown in the Web Appendix. The first simulation compared the performance of the proposed DR, IPW and IB estimators with the estimator in Page and Rotnitzky (2009). The second simulation compares the smooth ROC curve with the empirical estimator in Alonzo and Pepe (2005), when the covariates are not associated with the test result. The impact of different bandwidth selections is also investigated. Simulation three investigate the model misspecification.

4.1 Simulation one: comparison to the parametric estimator

In this simulation, we compare our proposed methods to the doubly robust estimator in Page and Rotnitzky (2009), denoted by PR estimator. Two covariates X₁ and X₂ are generated from Bernoulli(0.5) and Uniform(–1, 1), respectively. The true disease status, D, is generated from the conditional distribution, D| X₁, X₂ ~ Bernoulli(ρ), where logit(ρ) = –0.25+0.5X₁+0.8X₂. The test result is generated from T = μ(D, X)+σ(D, X)×ε(D), where μ = 1+0.4D+0.2X₁+0.7X₂+X₁D+0.5X₂D and σ = 0.8D+1.2(1 – D). Two scenarios for the residual distribution are simulated: (A) ε(D) ~ N(0, 1), (B) (4.5 + 3ε(0)) ~ χ²(4.5) and (8 + 4ε(1)) ~ χ²(8). Apparently, the test distribution is symmetric in scenario A and skewed in scenario B. The verification indicator is generated from the conditional distribution, V|T, X₁, X₂ ~ Bernoulli(π), where logit(π) = 1 + 0.5T + 0.4X₁ + 0.6X₂. This simulation setup results in about 50% missingness of the gold standard.

We set the sample size to be 1000. From the data generation, we can see that the disease probability ρ = Pr(D = 1|T, X₁, X₂) is jointly determined by D|X₁, X₂ and T|D, X₁, X₂, i.e., $\rho =\frac{\mathrm{Pr}(D=1\mid X_1,X_2)f_{T\mid D=1,X_1,X_2}\left(t\right)}{\mathrm{Pr}(D=0\mid X_1,X_2)f_{T\mid D=0,X_1,X_2}\left(t\right)+\mathrm{Pr}(D=1\mid X_1,X_2)f_{T\mid D=1,X_1,X_2}\left(t\right)}$. This is a complex function of T, X₁ and X₂, and a linear logistic regression may not estimate the true disease probability well enough. Therefore we also include quadratic terms of T and X₂, as well as pairwise interactions between T, X₁ and X₂. Indeed, under our data generation procedure in scenario A, the quadratic form is exactly the correct model. With χ² residual, this disease model still closely approximates the true disease probability. We use the correct verification model to estimate π. The bandwidth is chosen to be 0.05. We see in simulation study two that the bandwidth has little effect on the performance of our estimators, as long as they are kept small. The results of 500 simulations are reported in Tables 1 and 2. Note that the PR estimator for the location-scale parameters are exactly the same as the DR estimator. We can see from Table 1 that the estimated location and scale parameters always have low bias and close-to-nominal coverage rate. The scale parameters are not as well estimated as the location parameters, which we would expect for most regression analysis.

Table 1.

The bias (in percentage to the true value), empirical standard deviation (SD), average standard error (SE), and the CI coverage rate for the location and scale parameters.

			Location						Scale
			Intercept	D	X 1	X 2	X1 × D	X2 × D	Intercept	D
Normal	Bias (%)	DR	-0.5	2.3	1.9	-0.8	-0.8	-0.1	-3.0	-1.2
		IPW	0.1	0.3	4.6	-0.8	-1.1	-0.4	-10.5	1.8
		IB	-0.4	1.6	1.9	-0.9	-0.7	0.6	-3.2	-0.3
	SD	DR	0.091	0.151	0.130	0.112	0.187	0.164	0.035	0.064
		IPW	0.132	0.176	0.206	0.191	0.242	0.216	0.067	0.085
		IB	0.086	0.138	0.124	0.105	0.172	0.145	0.035	0.059
	SE	DR	0.085	0.138	0.123	0.109	0.174	0.157	0.035	0.058
		IPW	0.126	0.163	0.196	0.171	0.225	0.199	0.057	0.074
		IB	0.083	0.133	0.120	0.105	0.165	0.147	0.034	0.055
	Coverage (%)	DR	95.0	92.2	94.2	94.0	93.6	93.6	93.6	93.0
		IPW	94.2	93.2	94.0	91.4	94.2	93.2	87.4	91.4
		IB	95.6	93.6	94.6	93.6	95.2	94.2	93.2	93.6
χ 2	Bias (%)	DR	0.3	-1.6	-7.2	-1.2	2.1	0.9	-2.4	-1.5
		IPW	1.1	-3.5	-10.9	-1.6	2.8	1.1	-4.2	-0.7
		IB	0.1	-0.3	-0.2	-0.1	-0.8	-1.0	-5.2	5.6
	SD	DR	0.083	0.130	0.117	0.105	0.157	0.149	0.052	0.072
		IPW	0.114	0.150	0.169	0.148	0.195	0.177	0.055	0.074
		IB	0.082	0.128	0.119	0.105	0.161	0.146	0.052	0.074
	SE	DR	0.082	0.126	0.120	0.106	0.162	0.147	0.050	0.070
		IPW	0.105	0.140	0.164	0.145	0.192	0.172	0.055	0.074
		IB	0.081	0.124	0.119	0.105	0.162	0.144	0.050	0.071
	Coverage (%)	DR	95.0	94.4	96.0	95.6	95.0	94.2	93.4	94.4
		IPW	92.4	93.4	94.2	93.4	94.6	94.4	95.0	94.6
		IB	94.2	94.8	95.6	95.2	95.2	94.6	93.0	91.8

Table 2.

The bias (in percentage to the true value), empirical standard deviation (SD), average standard error (SE), and the CI coverage rate for the estimated ROC curves by DR, IPW and IB estimators.

			ROCx (0.1)				ROCx (0.2)				ROCx (0.4)
			x = (0,0)	(0,0.5)	(1,0)	(1,0.5)	(0,0)	(0,0.5)	(1,0)	(1,0.5)	(0,0)	(0,0.5)	(1,0)	(1,0.5)
Normal	Bias (%)	DR	6.8	4.4	0.0	-0.1	2.8	2.0	0.3	-0.0	0.9	0.6	-0.1	-0.1
		IPW	6.7	4.9	-0.3	-0.5	3.2	2.2	0.0	-0.5	0.8	0.4	-0.2	-0.3
		IB	6.4	4.6	0.4	0.3	2.6	2.2	0.3	0.1	0.6	0.5	-0.1	-0.1
		PR	6.1	4.6	1.0	0.6	3.2	2.2	0.4	0.1	1.1	0.6	0.0	-0.1
	SD	DR	0.031	0.044	0.073	0.082	0.056	0.068	0.059	0.055	0.084	0.073	0.030	0.021
		IPW	0.034	0.053	0.091	0.107	0.062	0.082	0.078	0.078	0.092	0.087	0.037	0.030
		IB	0.030	0.043	0.069	0.075	0.054	0.066	0.056	0.050	0.076	0.070	0.027	0.019
		PR	0.029	0.042	0.063	0.072	0.056	0.065	0.055	0.050	0.075	0.066	0.026	0.017
	SE	DR	0.032	0.046	0.069	0.078	0.057	0.070	0.060	0.056	0.074	0.070	0.031	0.023
		IPW	0.037	0.056	0.087	0.099	0.066	0.084	0.075	0.072	0.087	0.085	0.039	0.030
		IB	0.030	0.044	0.065	0.072	0.054	0.066	0.055	0.051	0.070	0.066	0.028	0.020
		PR	0.030	0.044	0.058	0.068	0.056	0.067	0.049	0.048	0.068	0.063	0.022	0.017
	Coverage (%)	DR	94.4	95.4	93.4	94.2	95.2	94.4	95.4	95.6	91.2	93.2	95.6	97.6
		IPW	96.8	96.4	93.2	94.6	95.6	95.2	94.6	95.2	93.6	93.8	96.6	96.8
		IB	94.4	94.6	93.6	94.6	95.2	93.8	94.0	96.0	92.4	93.6	94.8	97.4
		PR	95.2	95.0	92.6	93.8	95.0	94.4	92.0	95.0	92.8	93.6	91.4	94.6
χ 2	Bias (%)	DR	3.9	3.4	4.3	4.2	1.3	1.3	1.4	0.5	-0.1	-0.5	-0.3	-0.0
		IPW	4.1	4.0	4.7	4.7	1.2	1.7	1.7	0.6	-0.2	-0.6	-0.3	-0.1
		IB	10.2	10.1	7.3	6.1	8.5	7.4	2.0	-0.2	1.2	-0.6	-1.9	-0.9
		PR	-0.7	14.5	29.7	24.2	-9.0	-3.7	-4.5	-7.0	-13.2	-13.1	-7.9	-4.5
	SD	DR	0.030	0.041	0.074	0.092	0.060	0.074	0.077	0.066	0.082	0.077	0.009	0.003
		IPW	0.031	0.044	0.080	0.102	0.066	0.083	0.086	0.075	0.092	0.088	0.009	0.003
		IB	0.032	0.043	0.074	0.090	0.061	0.074	0.068	0.058	0.073	0.069	0.012	0.006
		PR	0.035	0.050	0.073	0.078	0.061	0.072	0.056	0.051	0.067	0.062	0.021	0.016
	SE	DR	0.031	0.042	0.081	0.098	0.060	0.074	0.075	0.067	0.077	0.073	0.013	0.005
		IPW	0.033	0.045	0.090	0.110	0.067	0.084	0.086	0.075	0.087	0.083	0.015	0.005
		IB	0.032	0.043	0.078	0.092	0.006	0.072	0.065	0.057	0.069	0.065	0.014	0.007
		PR	0.023	0.035	0.051	0.063	0.043	0.056	0.045	0.046	0.060	0.059	0.023	0.017
	Coverage (%)	DR	95.0	95.4	92.6	93.2	95.2	94.8	95.0	96.2	93.4	95.4	91.3	-
		IPW	94.4	94.0	94.6	93.6	94.4	93.6	96.0	97.4	93.8	93.6	95.6	-
		IB	94.2	92.4	92.4	92.0	93.4	93.8	93.4	96.2	94.0	94.8	31.2	-
		PR	80.4	82.6	46.0	58.4	83.4	88.6	84.2	69.4	69.4	56.0	0.0	-

Table 2 only reports the ROC curve at three 1-specificity levels: 0.1, 0.2 and 0.4 because of two reasons: first, the left end of the ROC curve may be more interesting as those correspond to thresholds with good specificities; second, in our simulation, the ROC curve may be too close to 1 when 1-specificity is greater than 0.4. It is shown that with the normal residual, the bias of the estimated covariate-specific ROC curve is generally small for all the four methods and the coverage rate is close to 95%. However, if the residual distribution is χ², the binormal assumption does not hold for the PR estimator. Therefore, the PR estimator is seriously biased and the coverage is much lower than 95%, while the proposed estimators still work well. We notice that if the the true sensitivity is close to 1, the estimated standard errors are not accurate. This is because the data is sparse in estimating the tail probability of the residual distribution.

As for the comparison between the three proposed approaches, the IB estimator has the smallest standard error in general; the DR estimator gains robustness at the cost to efficiency; the IPW estimator is the least efficient among the three, as the estimating functions only use the complete cases. More simulations and discussions on the efficiency issues are given in the Web Appendix. In practice, when the risk factors of disease are well understood, we would recommend the IB estimator; otherwise, the DR estimator is preferable because of its robustness.

We also try smaller sample size (n = 200) or lower verification proportion (30%), which suggests that the proposed estimators still perform well with higher than 90% CI coverage rates. These results are similar to Tables 1 and 2, and are omitted here.

4.2 Simulation two: empirical vs. smooth ROC curve

When the covariates are not related to the test results, our proposed estimators should be close to that in Alonzo and Pepe (2005), which we refer to as the AP method. The only difference is that we use the kernel smoothing method to estimate the test distribution while they use empirical estimators. In this simulation study, we compare our proposed estimators with the AP method in terms of the mean squared error of the estimated ROC curve. The data generation is similar to scenario A of simulation one, but the mean test result is generated by μ = 1 + 0.8D, which is not affected by the covariates. We only compared the DR estimator here.

Table 3 shows that our proposed estimator generally has comparable RMSE as the AP estimator. When the bandwidth is very small, two methods lead to almost identical results. It is also shown that the proposed estimator is not sensitive to the bandwidth selection: for all the bandwidth from 0.01 to 0.2, the bias is small and the RMSE remains at the same magnitude.

Table 3.

The comparison of our proposed DR estimator and the AP estimator in terms of bias (in percentage of the true value), 100 times empirical standard deviation (SD), and 100 times root mean squared error (RMSE).

		Bias(%)		SD		RMSE
		ROC (0.1)	ROC(0.2)	ROC(0.1)	ROC(0.2)	ROC(0.1)	ROC(0.2)
DR	h = 0.01	0.4	–0.1	5.0	4.4	5.0	4.4
	h = 0.05	0.4	–0.1	4.9	4.3	4.9	4.3
	h = 0. 1	–0.1	–0.2	4.8	4.2	4.8	4.2
	h = 0.2	–1.5	–0.9	4.5	4.0	4.6	4.1
AP		0.1	–0.2	5.0	4.4	5.0	4.4

4.3 Simulation three: model misspecification

In this subsection, we conduct further simulations to examine the model misspecification. First we consider the misspecification of the disease and verification models. Aside from the DR, IPW and IB estimators in simulation one, we consider five additional estimators: DR-V (correct disease model and incorrect verification model), DR-D (correct verification model and incorrect disease model), DR-DV (incorrect disease and verification models), IPW-V (incorrect verification model), and IB-D (incorrect disease model) estimators. The misspecified verification model ignores the test result, while the misspecified disease model ignores the interactions and quadratic terms. The data generation settings are the same as Scenario A in simulation one.

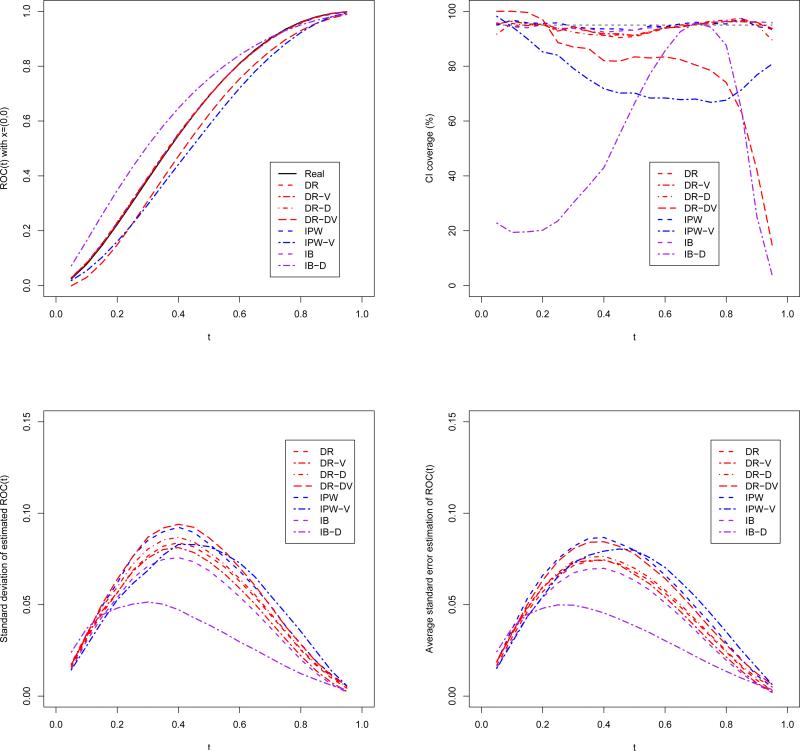
The simulation results are shown in Figure 1, which plots the ROC curve estimators with covariates (0, 0). The results for other covariates levels look similar in general, so we omit the redundant figures. As we expect, the averaging DR, IPW and IB estimators line up with the true ROC curve pretty well. When either the disease model or the verification model is incorrect, DR-D and DR-V estimators are still unbiased, but IB-D and IPW-V estimators both have serious bias. DR-DV estimator is also biased, but the magnitude of bias seems to be a bit smaller. For the CI coverage, all the estimators except DR-DV, IPW-V and IB-D have around 95% coverage rate for the whole range of t. The average standard error is close to the standard deviation of the estimates, suggesting that the asymptotic variance estimator captures the true variability very well.

Figure 1.

The true and estimated ROC curve, empirical standard deviation, average standard error, and the CI coverage rate for the estimated ROC curves using DR, DR-D, DR-V, DR-DV, IPW, IPW-V, IB and IB-D estimators.

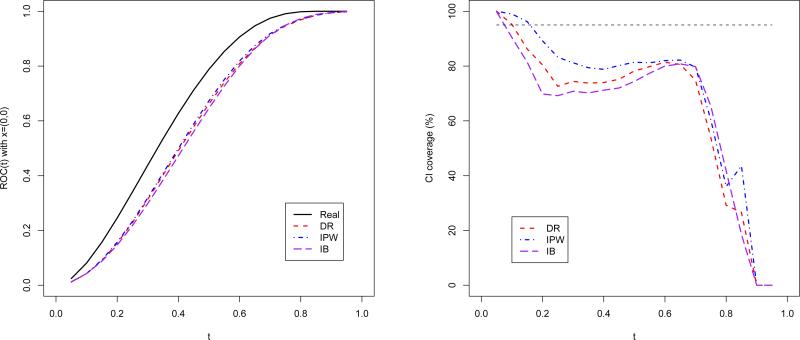
Furthermore, we check the misspecification of the location-scale model. The data is generated from a transformation model: take $S=1.6\times sign\left(T\right)\times \sqrt{\mid T\mid }$ as the test result instead, where T is the same as in simulation study one. The verification model uses S as a covariate correspondingly. The results for ROC_(0;0)(t) are shown in Figure 2. As the location-scale assumption does not hold any more, it is not surprising that all the three proposed estimators are seriously biased.

Figure 2.

The true and estimated ROC curve and the CI coverage rate for the DR, IPW and IB estimators under transformation model.

From the above three sets of simulation studies, we conclude that (1) our proposed methods perform reasonably well in finite sample settings; (2) the PR estimator is seriously biased as the test results do not follow normal distribution; (3) the proposed methods are not sensitive to the bandwidth selection; (4) the DR estimator is more preferable than the IPW and IB estimators as it protects misspecification of either the disease model or the verification model; (5) our proposed method is sensitive to the location-scale model assumption.

5. Example: NACC data

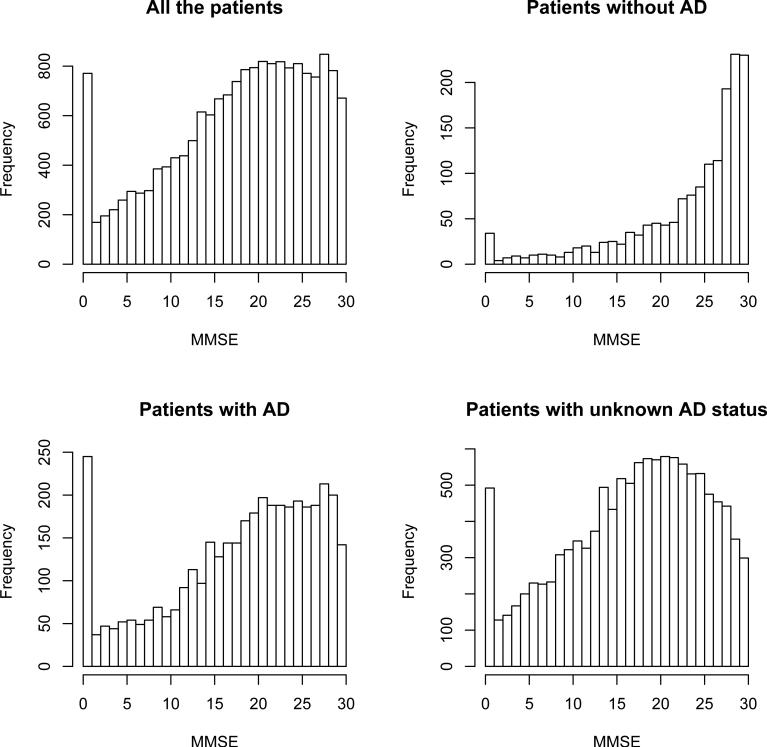
Our proposed method is illustrated using the data collected by National Alzheimer's Coordinating Center (NACC). We included a total of 17,403 deceased patients for our analysis. The test under evaluation is the Mini Mental State Examination (MMSE), which is a brief 30-point questionnaire test used to screen for cognitive impairment. The MMSE score can range from 0 to 30, with lower score indicating more severe impairment. The gold standard ascertainment of AD, based on brain autopsy, is only available for about 31% of the cohort. The missingness may be due to the patients’ or their family's decision. We believe that their decision of disease verification may be associated with the demographic characteristics (such as age, gender, race, etc.), but is unlikely to be correlated with their true AD status. So the ignorable missingness assumption seems to be reasonable here. Other covariates extracted from the database are age (continuous variable indicating age at the MMSE test), gender (binary variable with 1 indicating male), race (binary variable with 1 indicating white people), marital status (binary variable with 1 indicating married); clinical diagnosis of AD (binary variable with 1 indicating clinical diagnosed with AD), stroke (binary variable with 1 indicating having stroke before), Parkinson's disease (binary variable with 1 indicating presence of the disease), and depression (binary variable with 1 indicating presence of the disease). Figure 3 displays the distribution of the MMSE score for all the patients and for stratified verification and disease status. The distribution of the test result seems to be irregular, so it is hard to assume any parametric distribution. The test distributions for the cases and controls are very different too.

Figure 3.

MMSE distribution by AD status and verification.

We transformed the MMSE score using (30 – T)/5 so that a diseased subject tends to have larger test result, and transform the age using (age – 70)/10 so that the reported coefficients are in the appropriate magnitude. All the aforementioned covariates, as well as the MMSE score are included in the verification model. The disease model also includes the quadratic term of the test score, as well as the interaction between the test and the covariates. For modelling the MMSE score, the location model has the main effects of D and X, as well as their interactions, while the scale model only has the main effect of D with log link. The estimated coefficients of the location and scale model are given in Table 4 using DR, IPW and IB approaches. The results from the three methods generally coincide with each other. The DR estimator identifies main effects of race, clinical AD, and true disease status to be significant, indicating that these variables affects the magnitude of the test score. The race × D interaction is significant, while gender, clinical AD and depression have marginally insignificant interactions with D.

Table 4.

The estimated location and scale parameters with the associated standard errors for the NACC data.

	DR	IPW	IB
Intercept	1.394 (0.125)	1.452 (0.199)	1.408 (0.131)
Age	-0.064 (0.039)	-0.114 (0.051)	-0.054 (0.032)
Gender	-0.049 (0.079)	0.046 (0.096)	-0.028 (0.074)
Race	-0.303 (0.131)	-0.525 (0.203)	-0.304 (0.128)
Marital status	0.083 (0.086)	0.219 (0.102)	0.031 (0.076)
Clinical AD	1.120 (0.077)	1.160 (0.097)	1.128 (0.070)
Stroke	0.129 (0.095)	0.100 (0.125)	0.129 (0.083)
Parkinson's	0.186 (0.138)	0.228 (0.153)	0.292 (0.124)
Depression	-0.007 (0.108)	0.144 (0.156)	-0.006 (0.083)
D	0.984 (0.167)	1.090 (0.250)	0.982 (0.170)
D × Age	0.049 (0.052)	0.085 (0.063)	0.035 (0.041)
D × Gender	-0.146 (0.099)	-0.065 (0.119)	-0.180 (0.090)
D × Race	-0.322 (0.158)	-0.339 (0.240)	-0.330 (0.152)
D × Marital status	0.039 (0.108)	-0.090 (0.127)	0.110 (0.094)
D × Clinical AD	-0.150 (0.106)	-0.154 (0.127)	-0.166 (0.095)
D × Stroke	-0.124 (0.120)	-0.082 (0.156)	-0.115 (0.105)
D × Parkinson s	0.074 (0.172)	0.012 (0.190)	-0.058 (0.155)
D × Depression	-0.225 (0.135)	-0.119 (0.180)	-0.153 (0.102)
Intercept	0.301 (0.024)	0.391 (0.028)	0.310 (0.022)
D	0.120 (0.027)	0.149 (0.031)	0.109 (0.025)

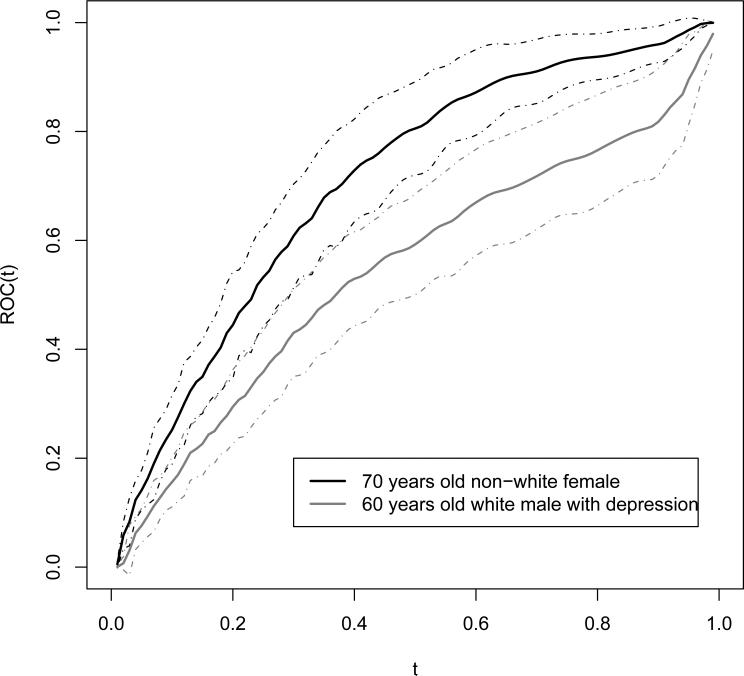
We take the bandwidth to be 0.02 in estimating the ROC curve. Hence the covariatespecific ROC curve could be plotted for every covariate level. For example, Figure 4 shows the DR estimates of the two specific ROC curves: one for 70 years old non-white female with other covariates being 0, the other for 60 years old white male with depression and other covariates being 0. The 95% CI's are also plotted. The results show that the classification ability of the MMSE test could be very different according to the covariates stratification. Although the test result can only take integer values from 0 to 30, the estimated ROC curve is smooth as the kernel estimating equations are used for the distributions. The empirical version of the ROC curve is more coarse, which could have at most 31 jumps.

Figure 4.

The covariate-specific ROC curves.

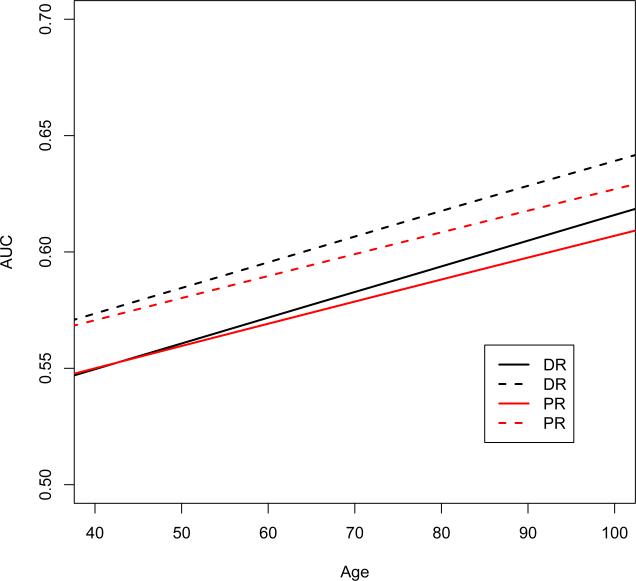
In Figure 5, we plot the DR and PR estimators of the area under ROC curve (AUC) as a function of age, with other binary covariates fixed. The solid line is for a white married male with clinical AD diagnosis and no other diseases; the dashed line is for a white not-married female with clinical AD diagnosis and no other diseases. These two covariates groups are the most prevalent in the NACC data set. We can see that the AUC is increasing by age with almost linear trend. We also find some discrepancy between DR and PR estimators, especially for older patients.

Figure 5.

DR and PR estimators for the covariate-specific AUC as a function of age: the solid line is for a white married male with clinical AD diagnosis and no other diseases; the dashed line is for a white not-married female with clinical AD diagnosis and no other diseases.

In screening for dementia or mild cognitive impairment (MCI), previous literatures suggest that the AUC for MMSE score is usually above 0.7 (Kim, et al., 2005; Isella, et al., 2006; McDowell, et al., 1997). However, we found that the MMSE score is not as promising in detecting AD, especially in younger patients. This motivates for further study of new biomarkers or combined biomarkers to improve early diagnosis of Alzheimer's disease. On the other hand, given the simplicity and low cost of the MMSE test, it is still of great use in screening for cognitive impairment in practice.

6. Discussion

In this paper, we have proposed to estimate the covariate-specific ROC curve semiparametrically when the gold standard is subject to missingness. The form of the ROC curve is flexible as both the link and the baseline functions are unknown and estimated from data. Three approaches are proposed to adjust for the verification bias: DR, IPW and IB estimators, which use different weights in the estimating equations. The disease probability and the verification probability are the key components in constructing the weighted estimating equations. The DR estimator only requires that either disease or verification model is correctly specified to have a consistent ROC curve estimator. The doubly robust property allows two shots to assume the correct model, and is favorable in practice. Otherwise, if the disease probability could be modelled correctly, the IB estimator is the most efficient. The IPW estimator is the least efficient among the three estimators. Our estimating procedures are based on the location-scale model framework, where the link and baseline functions of the ROC curve are just a distribution function and a quantile function. The location-scale parameters as well as the unspecified residual distributions are estimated, which determine the estimated ROC curve together.

Although we are focusing on the MAR verification process in this paper, the extension to nonignorable missingness (NI) is straightforward. Under the NI assumption, the observed data likelihood involves both π_i and ρ_i, that usually need to be estimated together. We can adopt the likelihood-based estimation of the nonignorable selection model in Liu and Zhou (2010). Or as in Rotnitzky et al. (2006) and Fluss et al. (2009), we specify the odds ratio of verification given disease, and then estimate π_i and ρ_i separately. With the estimated disease and verification probabilities, our proposed weighted estimating functions still work with slight modifications: for DR and IB approach, we replace ρ_i with ρ_i0 ≡ Pr(D_i = 1|V_i = 0, T_i, X_i). The resultant asymptotic variances take the similar form as the MAR case.

An alternative method might be a transformation model, i.e., we assume that h(T ) follows the distribution F (usually specified up to some parameters), where the smooth transformation h is left unspecified. The direct ROC curve estimation method in Cai and Pepe (2002) is in fact a special case of the transformation model. They assume that h is the distribution function of the test result for the controls. The direct estimation has the advantage of easy interpretation of model parameters, i.e., the effects of covariates on the ROC curve. The indirect estimation is relatively easy in modelling the location and scale of the test result. Pepe (1998) pointed out that the indirect estimation yields more efficient estimators than the direct estimation. Indeed, our proposed estimating equations for the location-scale parameters are just the gaussian score equations. Therefore, when the test distribution is close to normal, the location-scale model would be the most efficient. For highly skew data, the performance of direct and indirect ROC curve estimation is worthwhile for further exploration.

It follows from Nadaraya (1964) that the bias of the kernel CDF estimator is negligible relative to its variance, as long as the bandwidth is kept small enough. This property guarantees the $\sqrt{n}$ consistency of the estimated case and control distributions, and hence the $\sqrt{n}$ consistency of the estimated ROC curve. Another advantage of kernel smoothing is that it gives smooth ROC curve estimates as often desired.