Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Mar 15;3:1461. doi: 10.1038/srep01461

Selective modulation of cell response on engineered fractal silicon substrates

Francesco Gentile 1, Rebecca Medda 2,7, Ling Cheng 2,7, Edmondo Battista 3, Pasquale E Scopelliti 4, Paolo Milani 4,5, Elisabetta A Cavalcanti-Adam 2,7,8, Paolo Decuzzi 1,6,8,a
PMCID: PMC3598004  PMID: 23492898

Abstract

A plethora of work has been dedicated to the analysis of cell behavior on substrates with ordered topographical features. However, the natural cell microenvironment is characterized by biomechanical cues organized over multiple scales. Here, randomly rough, self-affinefractal surfaces are generated out of silicon,where roughness Ra and fractal dimension Df are independently controlled. The proliferation rates, the formation of adhesion structures, and the morphology of 3T3 murine fibroblasts are monitored over six different substrates. The proliferation rate is maximized on surfaces with moderate roughness (Ra ~ 40 nm) and large fractal dimension (Df ~ 2.4); whereas adhesion structures are wider and more stable on substrates with higher roughness (Ra ~ 50 nm) and lower fractal dimension (Df ~ 2.2). Higher proliferation occurson substrates exhibiting densely packed and sharp peaks, whereas more regular ridges favor adhesion. These results suggest that randomly roughtopographies can selectively modulate cell behavior.

Cells can sense the local microenvironment and respond to biochemical and mechanical cues by altering their morphology and biological functions1,2,3. Although the regulating mechanisms are still incompletely understood, it is well accepted that cell adhesion, migration, proliferation, differentiation as well as susceptibility to pharmacological treatments are influenced by the mechanical stiffness and geometrical features embedded in the surrounding microenvironment4,5. Also, it is becoming clear that alterations in the microenvironment contribute to the development of malignant phenotypes and constitute a potential target for the treatment of several diseases, including cancer and cardiovascular6,7. Therefore, analyzing the cell response to different topographical cues, acting over multiple temporal and spatial scales, is central to understanding and guiding several biological functions.

Nano- and micro-fabrication techniques, including optical and electron beam lithography, soft lithography and stereolithography, are available for generating substrates with ordered topographical features on which cells can be cultured and proliferate. Typically, these structures include arrays of grooves, ridges, pillars and pits and come in a variety of materials8,9,10. A few, well controlled geometrical features characterize uniquely these substrates such as the height and width, or radius of a ridge, pillar and pit; the separation distance between adjacent features or their surface density; and the orientation. Depending on the fabrication technique, the size of these features can be finely adjusted from the nano to the micron scale thus allowing for a systematic analysis of cell response. More recently, techniques for fabricating a topographical library comprising a multitude of variously organized, micron-sized features have been also proposed11. It has been shown that ridges can guide the migration of cells and affect their velocity12,13; cell adhesion and proliferation are generally impaired on nano-topographies with geometric features larger than 100 nm, as compared to nominally flat surfaces. This is can be ascribed to differences between the dimension of molecules which are responsible for adhesion and proliferation, including integrins, paxillin and focal adhesion kinase; and the geometric features that can possibly stimulate these molecules. This behavior strictly depends on cell type as it has been demonstrated, among the others, for the control of adhesion of primary human osteoblasts14 and of differentiation of human mesenchymal cells15. Furthermore, surface topographies were used for screening adhesion16 and response17 of human fibroblasts, as well as for modulating the proliferation of corneal epithelial cells and corneal fibroblasts18.

In their microenvironment, adherent cells are embedded in the extracellular matrix (ECM), a complex network of fibrils and fiber bundles hierarchically organized over multiple length scales, to provide both mechanical and biochemical cues19. The few and, unfortunately, scantelectron and atomic force microscopy studiesperformed on tissue samples confirm this picture. For instance, the basement membrane on which endothelial cells adhere and proliferate exhibits a complex topography consisting of nanoscale pores, intertwining fibers and elevationswhose characteristic size varies with the body partand animal species20,21,22,23. For example, the elevations of porcine aortic heart valve with an average height of a approx 3 nm nanometer is significantly less in comparison to the ones of the Descemet's membrane and in humans or corneal epithelium in macaque monkeys (130 nm)20,23, whereas pore size and fiber diameter are in the same order of magnitude. For tissues of mesenchymal origin, bone represents another example of hierarchically structured tissues with nanoscale organization. In fact, the ECM secreted by bone lining cells is composed mostly of collagen type I fibrils with 200 to 400 nm length and 66 nm axial periodicity24. These characteristic features are believed to be tightly correlated to the structure and load bearing properties of bone25, however what determines the fine control of their spatial organization remains to be elucidated. From these in vivo observations, it can be concluded that the single geometrical features of the tissue are intimately connected and brought together into a complex and yet undefined structure in terms of roughness and more in general topography, ranging from a few to several tens of nanometers.

Machining, sand blasting, plasma spraying, and acid etching are used to prepare substrates with randomly distributed topographical features, over multiple length scales. Traditionally, these substrates have been characterized through one sole geometrical parameter: the average surface roughness, Ra. Indeed, this is an oversimplification in that randomly rough substrates present roughness over multiple scales and their precise characterization requires the knowledge of additional parameters, including the short- and long-distance cut-off, and roll over wave lengths and, most importantly, the fractal dimension Df20,26,27. Unfortunately, most of the studies on cell adhesion and proliferation over randomly rough substrates provide only the value of Ra and the results are often conflicting. For instance, some studies documented a decrease in proliferation and adhesion with an increase in surface roughness28,29,30,31, whereas others have shown the opposite32,33. Interestingly, a few studies, including those from the authors, have reported on an optimal roughness that would maximize adhesion. This has been demonstrated for fibroblasts34, neural cells35, and different cell lines, including primary human endothelial cells (HUVECs), human epithelial cancer cell lines (A549 and HeLa cells), and one mouse mesenchymal normal cell line (NIH-3T3)36.

In this manuscript, silicon is electrochemically etched under different conditions to generate substrates with controlled geometrical parameters on which fibroblasts are cultured up to 7 days. Atomic force microscopy and surface fractal analysis are used to extract all the relevant geometrical information, including the average surface roughness Raand the fractal dimension Df. Cell morphology, adhesion and proliferation are monitored as a function of the geometrical parameters (Ra, Df) over time. Size, organization and distribution of adhesive structures are characterized via fluorescent microscopy.

Results

Silicon substrates with controlled roughness

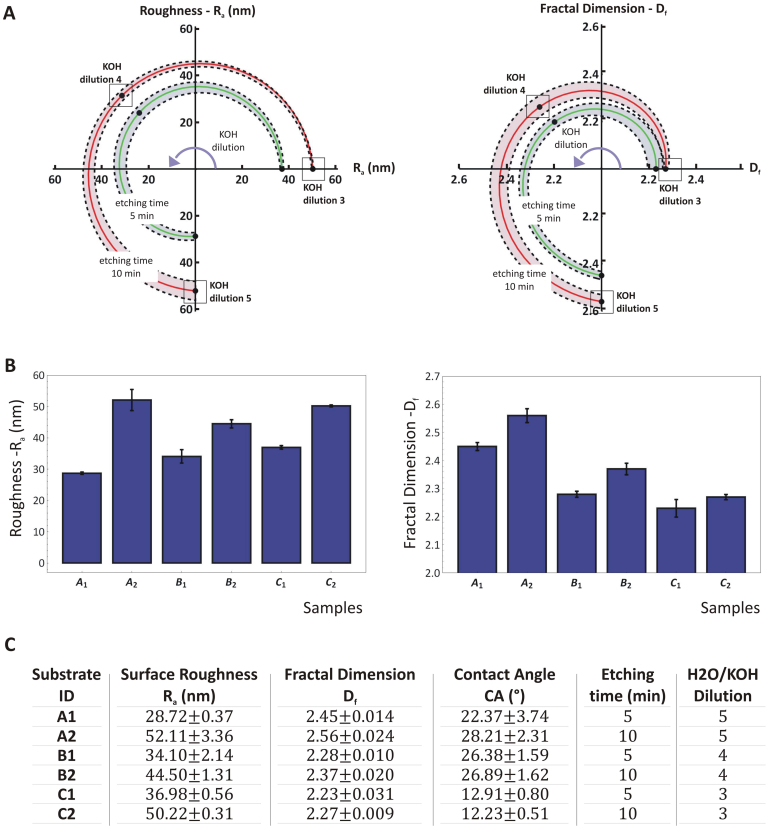
Silicon substrates with nanoscale roughness were obtained via electrochemical etching in a KOH solution, using (111)-oriented silicon wafers36. Different etching conditions were considered by changing systematically the characteristic etching time (5 and 10 min) and the dilution of the etchant in solution (1:3; 1:4 and 1:5 KOH). Hence, six different morphological properties of the silicon substrates were produced with Ra and Dfcontrolled independently. The first parameter (Ra) was observed to vary from ~30 to 50 nm, with an unetched silicon wafer exhibiting a surface average roughness of ~2 nm. The fractal dimension Dfvaried between ~2.2 and 2.6, being 2.2 the value for a nominally flat, unetched silicon wafer.

The two parameters Ra and Dfwere observed to grow with both the etching timeτ and concentration of the etching agent (KOH). This is shown in the chart of Figure 1A where the green and red lines are for a 5 and 10 min etching time, respectively. The KOH dilution increases from 1:3 to 1:5, moving along the curves in a counterclockwise direction. The chart on the left is for the surface roughness Ra, whereas the chart on the right presents data on the fractal dimension Df. The dotted lines identify the standard deviations for each tested condition. Assuming that the system evolves continuously as the KOH dilution increases, the charts in Figure 1A would provide design maps for generating substrates with different combinations of Ra and Df, within the considered ranges. The values of Ra and Dffor the six different types of substrates are also plotted in the bar charts of Figure 1B and listed in a tabular form in Figure 1C, together with the values of the operating parameters used for the etching. The resulting six surface profiles are uniquely identified with an alphanumerical code where the letter is related to the etchant dilution (A is for 1:5; B is for 1:4 and C is for 1:3) and the index is associated with the etching time (1 is for 5 min, 2 is for 10 min).

Figure 1. Modulating the topographical parameters Ra and Df by KOH etching.

Figure 1

Open in a new tab

(A) Polar plots showing the variation of the surface average roughness Ra and fractal dimension Df as a function of the KOH concentration (dilution X: H2O:KOH = X:1) and etching time. (B) The surface average roughness Ra and fractal dimension Df for the six silicon substrates. (C) The table presents for each of the six silicon substrates the corresponding values of the surface average roughness Ra; fractal dimension Df, contact angle CA; and processing parameters.

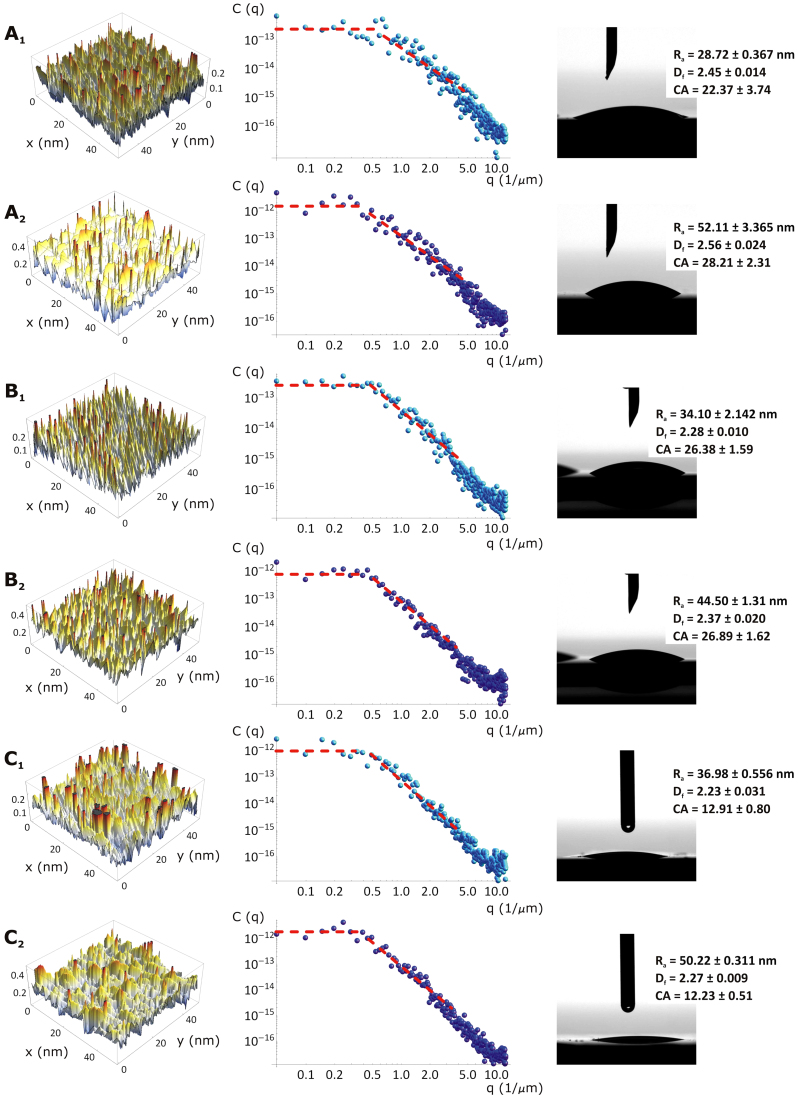
The geometrical data presented in Figure 1 derive from a topological analysis conducted with an atomic force microscope (AFM) on the six substrates. Representative AFM images of the surface profiles are presented in the first column of Figure 2. Differences among the six samples in the intensity and surface density of the peaks are readily evident. For instance, the substrate B2 as compared to C2 is characterized by thinner and more uniformly distributed peaks. The substrates B1 and C1 exhibit a surface profile similar to that obtained for B2. From these surface profiles, quantitative topological data can be extracted by performing a power spectrum density (C(q)) analysis which, by decomposing the surface profile into its spatial wavelengths, allowsfor a comparison of roughness measurements over different length scales. This is shown in the second column of Figure 2, where the quantity C(q) is plotted over multiple length scales 1/q, ranging from 0.1 to 10.0 μm−1. From the fitting of the C(q) curves, the surface roughness Ra and the fractal dimension Dfcan be extracted. Differences are readily observed among the six substrates for the C(q) curves. Note that the C(q) curves follow the classical form of the power spectrum of randomly rough natural surfaces with a short-distancecut-off wave vector (q1 ~ 10.0 μm−1), a roll-off wave vector(q0 ~ 0.5 μm−1), and a long-distance cut-off wave vector (qL ~ 0.01 μm−1). The power spectrum is linear within q1 and q0, with a slope that is related to Df, and is constant within q0 and qL. This also demonstrates that the silicon substrates under consideration are randomly rough and behave as self-affine fractal surfaces (Dfranges between 2 and 3)27. The last column of Figure 2 is related to the measurement of the contact angle (CA). All six substrates are very hydrophilic exhibiting a CA varying only between 12 and 28°. Thus, using the classical Young-Dupré relation, the interfacial energy of adhesion is γ = γLG(1 + cos(CA)) ~ 144.0 mJ/m2, this would vary within 5% among all six substrates (γLG ~ 72.8 mJ/m2 being the air/water interfacial energy).

Figure 2. Surface characterization of the six silicon substrates.

Figure 2

Open in a new tab

(A1–C2) Each line presents the Atomic Force Microscopy surface profile, the power spectrum and the contact angle measurement for a silicon substrate. In the last column, the contact angle (CA) is shown together with the Ra, Df and CA values for each analyzed substrate.

Following the approach proposed here, a set of substrates with roughness over multiple length scales can be precisely generated to replicate biologically relevant topographies.

Cell adhesion and proliferation on nanorough silicon substrates

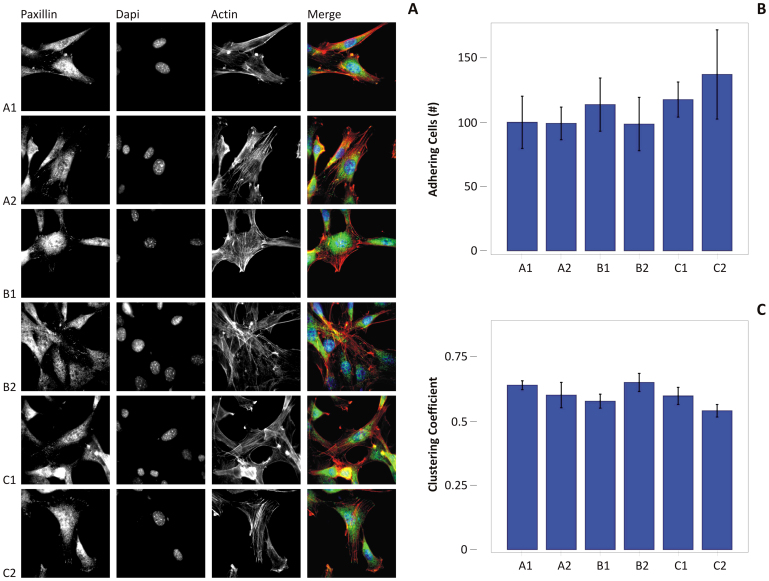
Possible differences in cell adhesion and proliferation rates were investigated by culturing 3T3 murine fibroblasts on the six substrates. The number of adhering cells and the fraction of proliferating cells were quantified using fluorescent microscopy at three different time points, namely 1, 3 and 7 days post seeding. Cell proliferation was assessed using EdU (5-ethynyl-2′-deoxyuridine)labeling, whereas the total number of cells was quantified by nuclear labeling with DAPI. Cells were also stained for F-actin and paxillin to better characterize their adhesive behavior on the nanorough substrates. The resulting data are summarized in the panels of Figure 3.

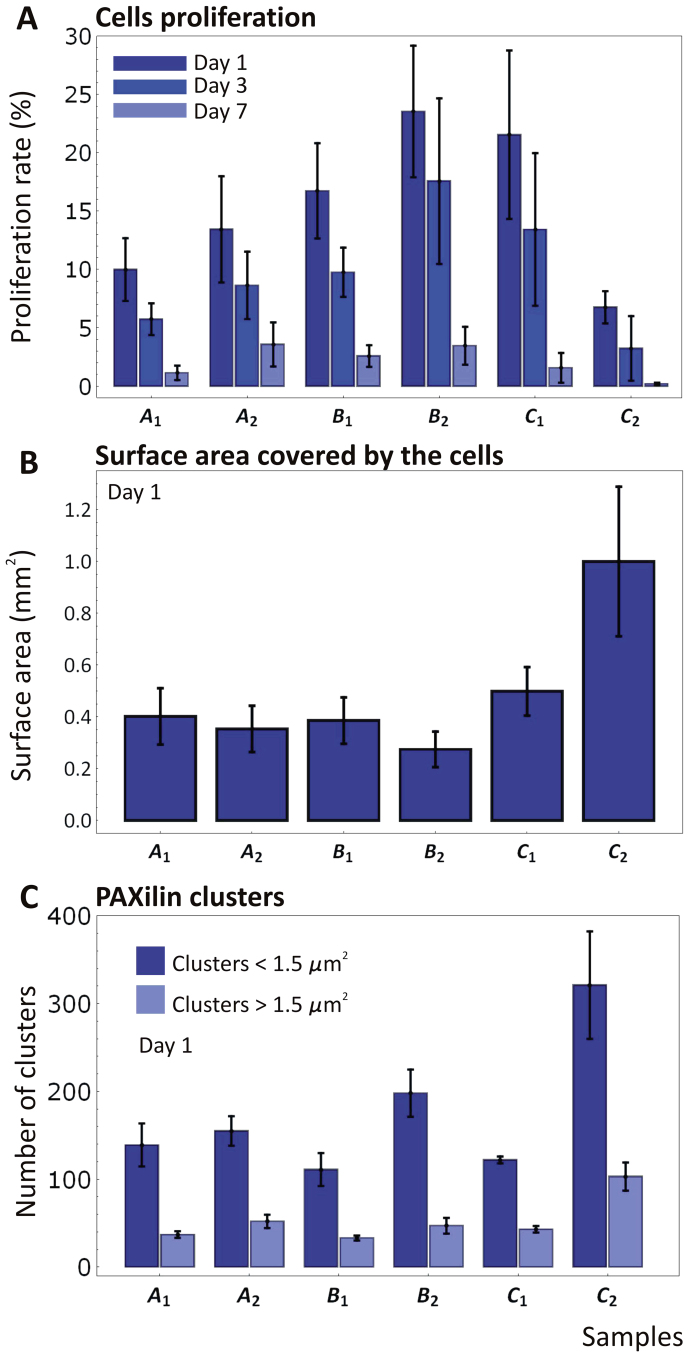
Figure 3. Cell proliferation and adhesion analysis on the six silicon substrates.

Figure 3

Open in a new tab

(A) The proliferation rate of mouse 3T3 fibroblasts is measured on the six substrates at 1, 3 and 7 days post seeding, using EdU labeling. The proliferation rate was measured as the percentage of area occupied by the cells to the total surface area. (B) The surface area covered by the cell at day 1 post seeding measured on the six substrates. (C) The number of paxillin clusters measured via widefield fluorescent microscopy.

The proliferation rates on the six substrates are presented in Figure 3A as a function of the incubation time. As expected, cell proliferation decreases monotonously, almost linearly with time, due to the interaction among adjacent cells in a monolayer tending to full confluence. More interestingly, the bar chart of Figure 3A shows a continuous increase in proliferation as moving from the substrate A1 to B2, followed by a sudden drop for C2. This trend is observed at the day 1 and day 3 time points and demonstrates the occurrence of a maximum in the percentage of proliferating cells on the substrate B2. Notice that at day 7 the proliferation on different substrates is instead similar, possibly due to the cells reaching full confluency and inhibiting any further growth (Supplementary Table 1A).

The fibroblasts growing on B2 show a proliferation rate of ~23% at day 1 and 17% at day 3. This is followed very closely by the substrates C1 (~22% at day 1 and 14% at day 3) and B1 (~16% at day 1 and 10% at day 3). The differences in proliferation between B2 and C1 are moderate at day 1, and gradually increase up to day 7, being P = 0.210 at day 1, P = 0.110 at day 3, P = 0.0070 at day 7. Instead, the differences between C1 and C2 are significant since day 1 (P < 0.001 for all considered days) (see Supplementary Information). Significantly lower is the percentage of proliferating cells on the substrates A2 and A1, with P = 0.01 at day 1 and day 3; differently from this, at day 7 the proliferation among the different substrates is comparable, with P > 0.05 (one way ANOVA, Tukey's multiple comparison test). Finally, C2 identifies the substrate with the lowest percentage of proliferating cells being equal to ~7% at day 1 and 3% at day 3 (P = 0.01 for all the considered days).

The characterization of 3T3 cell behavior on a reference flat silicon substrate is reported in a separated Supplementary Information file. NIH 3T3 cells cultured on flat, unetched wafers show at day 1 and day 3 a constant proliferation rate which suddenly drops at day 7 after the cells have reached confluence.

The surface area covered by the cells at 1 day post seeding was also measured and is shown in Figure 3B for all six substrates. This is calculated by projecting the cell area over a reference, flat plane and dividing the resulting total area by the number of cells. Very interestingly, a small difference is observed for the first five substrates, moving from A1 to C1, with an average covered area of ~0.40 ± 0.20 mm2 (P > 0.05). Conversely, cells tend to be more spread on the substrate C2 with a covered area of 1.0 ± 0.28 mm2, which is approximately 2.5 times larger than for all other substrates (P = 0.001).To determine the size of focal contacts and the number of adhesion clusters, paxillin was detected via indirect immune-fluorescence at 1 day post seeding. Paxillin is a 68 kDa cytoplasmic protein that localizes to discrete sites of cell attachment to the extracellular matrix that are the focal adhesions (FAs). It is involved in the processing of external stimuli that modulate important cellular events including cell adhesion, cell motility and growth control. Its size was here measured and reported in clusters. Per each substrate, a number of cells and regions of interest were considered in determining the size of paxillin clusters, as reported in the Supplementary Information.

The paxillin clusters were categorized by size in transient and mature structures (cluster area < 1.5 μm2 and > 1.5 μm2, respectively). Note that transient adhesion structures are often described as small in size and fail in becoming mature and stable contacts if the spreading signal decreases37,38. It is observed that the number of small clusters exceeds by 2 to 4 times the number of larger clusters, for all six substrates (Figure 3C). But more interestingly, no significant difference in the cluster numberis depicted for the first five substrates, from A1 to C1, returning a value of ~40 and 145 for the large and small clusters, respectively (P > 0.05 for clusters < than 1.5 μm2, P > 0.1 for clusters > than 1.5 μm2). Conversely, the occurrence of paxillin clusters on the C2 substrate is enhanced, reaching values of ~100 and 310 for the large and small clusters, respectively (P < 0.05 for clusters < than 1.5 μm2, P < 0.01 for clusters > than 1.5 μm2). This is consistent with the cell spreading data and again it is observed a characteristic 2 to 2.5 ratio between the values of physical quantities measured for the C2 and all other five substrates. The data presented in Figure 3 are also provided in a tabular form in the Supplementary Table 1, together with the statistical analysis of the data.

The effect of (Ra, Df) on cell adhesion and proliferation

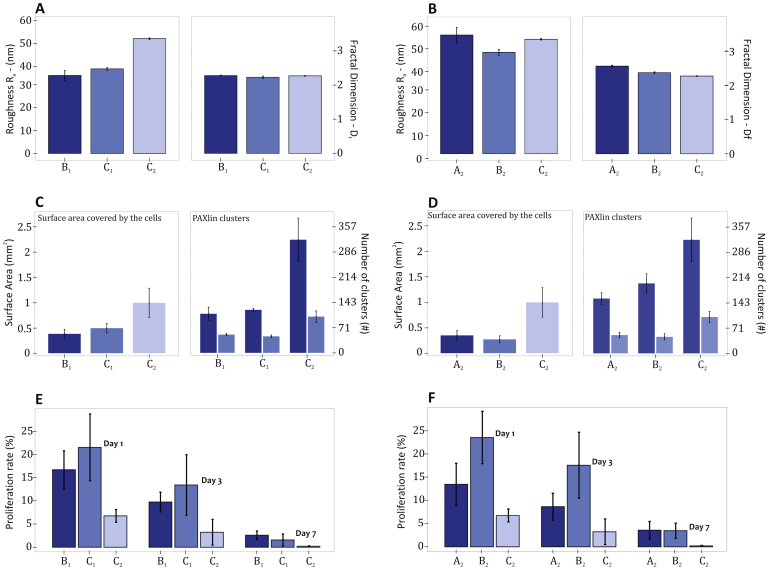
The substrates B1, C1 and C2 are characterized by a similar fractal dimension (Df = 2.26 ± 0.02, P = 0.05) and a different roughness Ra = 34.10, 36.98 and 50.22 nm (P = 0.005) (Figure 4A). The surface adhesion energy γ and the adsorption of bovine fibronectin do not change significantly (Supplementary Information), thus implying that the major difference among the three substrates has to be ascribed to the average surface roughness Ra. The substrate with an intermediate roughness (C1 with Ra = 36.98 ± 0.56 nm) presents the largest cell proliferation rate, at all time points considered. This confirms the notion for which substrates with intermediate roughness provide conditions that favor cell proliferation, as originally noted by the authors36.

Figure 4. Comparative analysis between silicon substrates with similar topographical features.

Figure 4

Open in a new tab

The silicon substrates B1, C1 and C2 present similar Df ( = 2.26 ± 0.02) and a different Ra ( = 34.10, 36.98 and 50.22 nm). For these substrates, the variation in topographical features is shown in the inset (A), the variation in adhesion behavior is shown in the inset (C), and the variation in proliferation rates is shown in the inset (E). The silicon substrates A2, B2 and C2 present similar Ra ( = 48.94 ± 3.96 nm) and a different Df ( = 2.56, 2.37 and 2.27). For these substrates, the variation in topographical features is shown in the inset (B), the variation in adhesion behavior is shown in the inset (D), and the variation in proliferation rates is shown in the inset (F).

On the other hand, the substrates A2, B2 and C2 are characterized by a similar roughness (Ra = 48.94 ± 3.96 nm, P = 0.05) and a different fractal dimension Df = 2.56, 2.37 and 2.27 (P < 0.001) (Figure 4B). The surface adhesion energy γ and the adsorption of bovine fibronectin do not change significantly (Supplementary Information), implying that the major difference among the three substrates has to be ascribed to the fractal dimension Df. In this comparison, substrates with larger fractal dimension (>2.4, B2 and A2) present the higher cell proliferation rates, at all time points considered. Indeed, the substrate B2 (Ra = 44.50 ± 1.31 nm and Df = 2.37 ± 0.02) offers the best combination in terms of roughness and fractal dimension to maximize proliferation over all other substrates. Differently, C2 (Ra = 50.22 ± 0.31 nm and Df = 2.27 ± 0.01) presents the cell largest adhesion and the lowest proliferation rate.

Morphology and organizationof cells attached on nanorough silicon substrates

Despite the remarkably difference in proliferation rates and focal adhesion formation,the 3T3 fibroblasts were observed to spread well onall six silicon substrates. No major differences in cell morphology can be detected by merely observing the fluorescent microscopy images presented in Figure 5A. It should be also noted that at day 1, the number of cells adhering on all the substrates is not significantly different (Figure 5B). To determine if the organization of spread cells would vary on the different substrates, a cluster analysis was performed for cells adhering on the substrates for 24 hr (Figure 5C).The clustering coefficient (cc) is a parameter that gives a measure of the propensity of the nodes of a graph to cluster together. And thus the extent of gathering of a population of cells may be lumped in the sole global metric parameter cc; cc spans from 0 to 1, at the limit of cc going to 0, the cells are poorly or not connected, being uniformly distributed on the substrate, when cc tends to unity, cells form few groups (Supplementary Information). Here, the tendency of forming cell-cell contacts is comparable for all the substrates and it is not correlated to cell proliferation (Supplementary Figure S5.1). Experimental evidence suggests that changes in cell shape and cytoskeleton organization can induce a mechanical distortion of the nucleus and thus lead to variations in overall cell function39,40,41. The cell shape index (CSI) and nuclear shape index (NSI) were quantified by post-processing the fluorescent images shown in Figure 5. These two parameters are presented in the Supplementary Figure S6.1 for all considered six substrates. The NSI is fairly independent on the substrate type, exhibiting an average value slightly lower than 0.9 (Supplementary Figure S6.1A). The small differences observed for the CSI (Supplementary Figure S6.1B, P = 0.01), vary nevertheless over the six substrates consistently with the cell spreading and paxillin cluster size, as from Figure 3. The shape indices analysis demonstrates that the 3T3 fibroblasts tend to elongate (low CSI) keeping a rounded, not deformed nucleus (high NSI) on all six substrates. Therefore, the observed variation in cell proliferation rates and adhesion cannot be directly related to alterations in cell and nuclear morphology. Taken together, these results indicate that fibroblast phenotype is maintained for all the substratesand that the effects on cell proliferation and focal adhesion formation are mediated by interactions at the interface between cells and the specific substrate property.

Figure 5. Cell morphological analysis of mouse 3T3 fibroblasts.

Figure 5

Open in a new tab

(A) A1–C2, Eachline presents fluorescent microscopy images for the 3T3 fibroblasts cultured on the six substrates at day 1 post seeding. The paxillin density and clustering, the nuclear labeling with DAPI, and F-actin staining are shown in the first, second and third column, respectively. The merging of the three images is presented in the fourth column. (B) the number of cells adhering on each substrate 24 hr after seeding was determined by DAPI counting. (C) the clustering coefficient derived from the cells after 24 from seeding.

Discussion

Cells growing on rough substrates would have to generate intimate contact with the local topographical features by wrapping their membranes around peaks and over ridges. Cell adhesion is a process that manifests initially with the formation of transient focal complexes (FX) with a characteristic size smaller than 1.5 μm2 38. If conditions permit, these FX clusterswould mature into more stable focal adhesions (FA) exhibiting a much larger surface area (>1.5 μm2) and generally increase in size during cell spreading. Through these points of anchorage, cells exchange forces with the substrate (the microenvironment) in the range of a few pN per adhesion receptor, i.e. integrin.

The topographical images presented in Figure 2 show for the first five substrates (from A1 to C1) a surface profile characterized by several, densely packed sharp peaks. Differently, the profile of the substrate C2 is characterized by more regular, parallel ridges and a fewer sharp peaks. It could be argued that cells in contact with sharper peaks cannot easily establish stable and mature contacts (FA), whereas the more even ridges observed over C2 could support the formation of larger adhesive structures. Indeed, for cells lying over sharp peaks, the formation of FA would require membrane wrapping around the small peak, somehow similar to an internalization-like process (Supplementary Figure S7.1)42. This could be energetically favorable only under some specific conditions. If the cell membrane is locally approximated as a thin elastic layer with a bending modulus κ, the membrane wrapping around a peak with radius R requires a variation in local elastic energy equal to 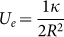Inline graphic which has to be balanced by the change in adhesion energy 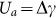Inline graphic. Therefore, local membrane wrapping will only occur if Ua ≥ Ue, or if the peak radius R is larger than 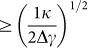Inline graphic. Generally, κ is of the order of 300 kBT (~4 × 10-21 J) and Δγ is of the order of 10−6 – 10−5 J/m2, thus leading to a critical radius Rranging between a few hundreds of nanometers and 1 μm32,43,44. In other words, wrapping around sharp peaks, in the order of a few hundreds of nanometers and smaller, will not be energetically convenient for cells, and thus stable adhesion would be impaired under such conditions.

In several studies on various cell model systems, it has been shown that a spread cell shape is a requirement for cell cycle progression45. Upon adhesion, the process of integrin clustering is important in triggering integrin signaling. Adhesion also turns on the force-dependent organization of the cytoskeleton, which in turn acts in maintaining integrin clusters. The mechanisms whereby cells are capable to adjust their cytoskeletal organization to minute changes in their immediate surroundings have been discussed by Geiger et al46, and are based on the finely tuned crosstalk between the assembly of one type of integrin-based adhesion complex, namely focal adhesions, and the forces that are at work in the associated cytoskeletal network owing to actin polymerization and actomyosin contraction.

Despite this understanding, the relative contribution of the direct effect of cell adhesion versus the adhesion-dependent signaling on cell proliferation is still unsolved and controversial. Davey et al. have shown that cell spreading can be uncoupled from cell proliferation by altering the expression of the integrin α5β147. This study indicates a phenomenological link between the size of the adhesion structures and proliferation, while cell phenotype and organization are maintained. From the energetic analysis above, cells cultured on substrates exhibiting a densedistribution of sharp peaks (i.e. the first five substrates: A1–C1) would less likely generate stable FAs. This could be associated with limitations in the tensile forces transmittable at the adhesion spots (below the pN range per receptor molecules), which could prevent the unfolding of molecules, such as talin, directly involved in the maturation of FX into FAs48.

Consequently, if cells cannot develop stable adhesion spots, the intracellular and intercellular signaling machinery could instead favor increased proliferation. At this stage, this is just an hypothesis that, however, does have some evidence in other natural system always struggling between instability and stability to evolve49.

In summary, aset of randomly rough, self-affine fractal silicon substrates for cell culture can be produced by KOH etching. The surface roughness Ra and fractal dimension Df are controlled independently by modulating the etchant concentration and processing time. Six silicon substrates were produced with Ra ranging from ~30 and 50 nm, and Df varying between 2.2 and 2.6. The adhesion, proliferation and morphology of 3T3 fibroblasts were assessed on these different substrates. Although cells appear well spread and elongated on all substrates with a rounded, non stretched nucleus, adhesion and proliferation rates are selectively enhanced on specific substrates. Proliferation rates are maximized on substrates with moderate roughness (Ra ~ 40 nm) and sufficiently large fractal dimension (Df ~ 2.4) (substrate C1).

Interestingly, independent studies support the finding that proliferation is optimized over substrates exhibiting the larger fractal dimension. For astrocytoma cells growing over pentacene thin films with different morphologies, Tonazzini et al50 demonstrated that cells exhibit optimum viability for pentacene films with larger fractal dimensions, rather than for a specific surface roughness. Moreover, following an approach similar to that of the present study, they explained those observations by means of a conformational adaptation of the cell membrane to the pentacene surface, which implies an elastic deformation of the cell membrane, whereby the energy cost would depend on the local curvature of the surface.

Differently from proliferation, adhesion is optimized on substrates with high roughness (Ra ~ 50 nm) and low fractal dimension (Df ~ 2.2) (substrate C2). The area covered by the cells and the number of paxillin clusters, two parameters related to cell adhesion,are 2 to 2.5 times larger on C2 as compared to all other five substrates, including the highly proliferative C1 substrate. Moreover, the area of the single cells expressed over different substrates have been derived and reported in the Supplementary Figure S8.1, where it is shown that the single cell area is optimized over the C2 sample. These additional data support the notion that the surfaces with small fractal dimension improve adhesion, in a way that is consistent with the data of paxillin clusters distribution, and the total area covered by the cells.

Whilst the surface profile of the substrate C2 shows quite regular ridges, C1 exhibits sharp and densely packed peaks over which the formation of stable adhesion spots is energetically non-favored. It is speculated that cells residing on C1 could be locked in a state of non-equilibrium seeking, without reaching, a stable adhesion configuration. This could continuously stimulate the cell machinery and eventually support cell proliferation over adhesion. Although the regulating mechanisms remains unclear, cell adhesion and proliferation can be selectively singled out with this set of randomly nanorough silicon substrates.

Methods

Preparation of randomly rough silicon substrates

(111)-oriented Si wafers were used as substrates. The superficial natural layer of SiO2 was removed by immersion in HF:H2 = 1:5 v/v solution for 30 sec. The resulting silicon substrates were then wet etched in KOH solution at the constant temperature T = 70°C and at different times and concentrations to obtain surfaces with different roughness (Ra) and fractal dimension (Df). These data are recapitulated in Fig. 1, and range from 29 to about 52 nm as regarding the Ra, and from 2.23 to about 2.56 as regarding the Df. Notice that the untreated Si has a surface roughness of about 2.3 nm. The most interesting characteristic of the data, as reported in Figure 1C, is that the roughness and the fractal dimension of the substrates are controlled separately. This is especially evident from Figure 2A, where the surface roughness Ra is poorly influenced by the dilution of the solution, and thus all the points at constant etching time have approximately the same Ra. On the contrary, the fractal dimension strongly depends upon the concentration of KOH and, on account of this, for instance, the samples A2, B2 and C2 have a fairly constant Ra, with small deviations from an average value of about 48 nm, and instead span the broad Df range 2.27–2.56. The average surface roughness uniformity and reproducibility were assessed by measuring Ra at multiple areas of the wafers. Repeated AFM measurements were used to derive the Raof the substrates. Using standard mathematical procedures, a power spectrum was obtained from each image. The distinguishing fractal dimensions for each roughness were further derived. The surface contact angles, appended in Figure 1C, were measured using an automatic contact angle meter, as explained below.

Atomic Force Microscopy characterization

Atomic force microscopy (VeecoMultiMode with NanoScope V controller) was used for the measurements of the substrates. All the measurements were performed in a dry environment in intermittent contact mode (oscillating frequency ~270 kHz) over a sampling area of 50 × 50 μm2. Room temperature was kept constant (or stable) for all the acquisitions. An anisotropic pyramidal tip with a radius of about 15 nm was used as a probe (TESP, NanoWorldLdt. Co.). The tip was made of silicon and was mounted onto a rectangular shaped cantilever with a typical spring constant comprised between 20 (min) and 80 (max) N/m. Multiple measurements were done in different scan directions to exclude artifacts. At least four images in height mode (trace and retrace) were recorded per sample. The images had a resolution of 512 × 512 pixels and were acquired at a scanning rate of 1 Hz. These were therefore processed with the diSPMLab software (provided by Veeco), using either flattening or plane fit according to the relief characteristics, with the minimal polynomial order needed. The characteristic Rawas thus deconvolved for each substrate. Using conventional mathematical procedures implemented in Mathematica®, a power spectrum (PS) was further derived for each image.

Surface contact angle measurement

Surface hydrophilicity of the samples was determined by measuring the water contact angle with one drop of about 5 μl of D.I. water using an automatic contact angle meter (KSV CAM 101, KSV INSTRUMENTS LTD, Helsinki, Finland) at room temperature. Four measurements were performed on each substrate to evaluate the average contact angleθ, at 5 s.

Fourier analysis and fractal dimension of the substrates

The AFM profiles were thoroughly processed to obtain the corresponding power spectrum density functions C(q), and thus significant information regarding the fractal dimension and microstructure of the substrates at study:

graphic file with name srep01461-m1.jpg

Where χ = (x, y) is the planar coordinate; z(χ) is the surface profile measured from the average surface plane, defined as <z> = 0; and q is the wave number, related to the characteristic wavelength λ as q = 2π/λ. The symbol <…> stands for ensemble averaging over a collection of different surfaces with identicalstatistical properties. Since the 2D power spectrum density introduced above is impractical for comparison purposes, a 1D power spectrum density was conveniently extracted using the FACA (Fractal Analysis by Circular Averaging) approach. Considering the polar variables q and ψ, being q = (qx2 + qy2)1/2 and ψ = arctan(qy/qx) in the plane (x, y) of interest,the power spectrum C(q) is derived as an average taken over every circumference Γ of radius q and origin (qx = 0, qy = 0), that is

graphic file with name srep01461-m2.jpg

In the case of self-affine surfaces, for which a rescale in the planar coordinates x → bx and y → by is accompanied by a rescaling in the normal direction z (bχ) → bHz(χ), the power spectrum C(q) takes the form

graphic file with name srep01461-m3.jpg

Where qo is the lower cut-off wave-number corresponding to an upper cut-off wavelength λo = 2π/qo; and ho is related to the Ra roughness amplitude as ho = π/2 Ra. A self-affine fractal surface can be consequently univocally identified by specifying the surface roughness Ra, the cut-off wavenumberqo and the coefficient H, known as the Hurst coefficient. In a log-log plot, the power spectrum density appears as a line with a slope β for q > qo. The slope β is related to the Hurst parameters as β = 2(H + 1). The fractal dimension Df of the surface can be derived from β or H as Df = (8 − β)/2 or Df = 3 − H. The fractal dimension Df for a surface ranges from 2, representing a perfectly flat surface (Euclidean dimension of a surface), to 3, representing an extremely rough surface. For Df = 2.5, the so-called Brownian surfaces are identified which have totally random and uncorrelated profiles.

Cell culture

Mouse NIH3T3 fibroblasts (ATCC CRL-2795) were cultured, with a concentration of 25000 cells/cm2 for 24 hours, in growth medium, consisting of Dulbecco's modified Eagel medium (DMEM; Gibco BRL, Germany) supplemented with 10% heat inactivated fetal calf serum (FCS; Sigma-Aldrich) and 1% penicillin/streptomycin (Gibco BRL) at 37°C and 5% CO2. 25000 cells/cm2 for 24 hours incubation.

Cell proliferation assay

Cell proliferation was determined by measuring DNA synthesis via the EdU assay Kit according to the manufacturer's protocol (Click-iT® EdU AlexaFluor488 Imaging Kit, Life Technologies). In brief, cells were plated on the different surfaces, with a concentration of 25000 cells/cm2. After 2 h the samples wereincubated in media containing 10 μM of EdU reagent for 22 h. After fixation nuclei were stained with DAPI and the samples embedded in Elvanol. Fluorescence microscopy was carried out with an Olympus IX inverted microscope (Olympus, Hamburg, Germany) using a DeltaVision RT system (Applied Precision Inc., Issaquah, USA). Cells were examined with a 20× air objective lens (UPlanFl 20×/0.5 Ph1, Olympus) and fluorescence detected with a cooled CCD camera (Photometrics, Kew, Australia). Image acquisition was performed with Resolve3D (Applied Precision Inc.). EdU positive nuclei were counted and normalized for total number of DAPI positive nuclei for each image using the particle analysis tool of imageJ1.43 m (http://rsb.info.nih.gov/ij/). All experiments were performed in three technical repeats using three samples per condition and imaging randomly 5–7 different fields of view of each sample.

Indirect Immuno-fluorescence and imaging of adhesion

Cells were plated onto the different substrates under starving conditions (1% FCS and 1% antibiotics in DMEM). After 24 hr, cells were fixed with 3.7% (w/v) paraformaldehyde (PFA, Riedel-de Haën) in PBS for 30 min at RT followed by permeabilization with 0.1% (v/v) Triton-X-100 (Sigma) in PBS for 5 min. Samples were then blocked in 1% (w/v) BSA in PBS for 10 min.

Focal adhesions, actin stress fibers and fibronectin(adsorption of bovine fibronectin from culture medium without the presence of cells)were detected using indirect immunofluorescence. Samples were incubated with mouse anti-paxillinIgG(BD Biosciences) or rabbit anti-bovine fibronectinIgG (Chemicon) both diluted in 1% (w/v) BSA/PBS according to the manufacturer's recommendation for 1 h at RT. Alexa488 goat anti-rabbit IgGor Alexa647 goat anti-mouse IgG (Life Technologies) were used as secondary antibodies, whereas Phalloidin-TRITC (Sigma) was used for the detection of actin stress fibers. All samples were mounted in Elvanol supplemented with 1 μg/ml DAPI (Sigma) for nuclear staining.

Notice that, here, the fibronectin was not stained together with the paxillin. The fibronectin staining was performed in a cell-free experiment, thus eliminating the risk of cross staining.

Wide field microscopy and image acquisition was carried out as described above. Cells were examined with 10× air and 60× oil immersion objective lenses (EC-PlanNeoFluor 10×/0.3 Ph1, Zeiss, and PlanApo 60×/1.4 Oil, Olympus). The experiment was performed in three technical repeats, using two samples from each group and imaging 15–20 different fields of view of each sample. All images were analyzed with ImageJ. In brief, paxillin cluster sizes were analyzed by creating binary images from the raw data (obtained by the 60× lens) by adjusting the threshold individually for each image. Only clusters in the range of 0.35 μm2 to 20 μm2 were considered and counted by using the particle analysis tool. The distribution as well as the count of the different cluster sizes was determined for each condition. Cell area was determined from images obtained with the 10× lens by using the watershed tool and the ‘analyze particles’ tool afterwards. The accordant cell number was determined by counting the nuclei.

Statistical analysis

All the data are reported as the sample mean ± the standard deviation (SD). Pair-wise comparisons between means of different groups were performed using a Student t-test (two tailed, unpaired, unpaired) where, for each couple of normally distributed populations, the null hypothesis that the means are equal were verified. Everywhere in the text the difference between two subsets of data is considered statistically significant if the Student t-test gives a significance level P (P value) smaller than 0.05. Multiple comparisons were performed using an univariate analysis of variance (ANOVA). ANOVA provides a statistical test of whether or not the means of several groups are all equal, and therefore generalizes the Student t-test to more than two groups. ANOVA was used here for comparing more than two means. In some cases, the probability that the means of two populations were equal was evaluated using a Tukey's post test. This post test is used in statistics when one needs to address multiple comparisons, and comes by the fact that even when there is a statistically significant difference between several groups, we can find that this difference may be especially attributed to some inequalities of specific pairs of groups. This post test protects against the fact of rejecting at least one true null hypothesis in the whole set of data.

Author Contributions

F.G. designed the experimental plan, realized the substrates, performed the C.A. measurements, performed the numerical calculations and statistical analysis and helped in writing the manuscript. R.M. performed and analysed the cell experiments. L.C. performed the proliferation experiments. E.B. Performed the AFM measurements. P.E.S. and P.M. developed the protocols and performed the measurements for thenon specific adsorption of serum molecules. E.A.C.-A. designed the experimental plan, supervised theproject for the part on cellresponse and wrote the manuscript. P.D. conceived the idea, designed theexperimental plan, wrote the manuscript and performed the statisticalanalysis.All the authors discussed the results andcommented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep01461-s1.doc (1.7MB, doc)

Acknowledgments

FG and PD acknowledge the support from the European Science Foundation EUROCORES Programme FANAS, through funds by the Consiglio Nazionale delle Ricerche and the EC Sixth Framework Programme under contract N. ERAS-CT-2003-980409FANAS.RM, LC and EACA acknowledge the support from the Max Planck Society and from the Deutsche Forschungsgemeinschaft (DFG SFB/TR79 to EACA).

References

  1. Chen C., Mrksich M., Huang S., Whitesides G. & Ingber D. Geometric control of cell life and death. Science 276, 1425–1428 (1997). [DOI] [PubMed] [Google Scholar]
  2. Kim D., Provenzano P., Smith C. & Levchenko A. Matrix nanotopography as a regulator of cell function. J Cell Biol 197, 351–360 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Stevens M. & George J. Exploring and engineering the cell surface interface. Science 310, 1135–1138 (2005). [DOI] [PubMed] [Google Scholar]
  4. Biggs M., Richards R. & Dalby M. Nanotopographical modification: a regulator of cellular function through focal adhesions. Nanomedicine 6, 619–633 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Nikkhah M., Edalat F., Manoucheri S. & Khademhosseini A. Engineering microscale topographies to control the cell-substrate interface. Biomaterials 33, 5230–5246 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bellail A., Hunter S., Brat D., Tan C. & Van Meir E. Microregional extracellular matrix heterogeneity in brain modulates glioma cell invasion. Int J Biochem Cell Biol 36, 1046–1069 (2004). [DOI] [PubMed] [Google Scholar]
  7. Kim D. et al. Nanoscale cues regulate the structure and function of macroscopic cardiac tissue constructs. Proc Natl Acad Sci U S A 107, 565–570 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bettinger C., Langer R. & Borenstein J. Engineering substrate topography at the micro- and nanoscale to control cell function. Angew Chem Int Ed Engl 48, 5406–5415 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Falconnet D., Csucs G., Grandin H. & Textor M. Surface engineering approaches to micropattern surfaces for cell-based assays. Biomaterials 27, 3044–3063 (2006). [DOI] [PubMed] [Google Scholar]
  10. Weibel D., Diluzio W. & Whitesides G. Microfabrication meets microbiology. Nat Rev Microbiol 5, 209–218 (2007). [DOI] [PubMed] [Google Scholar]
  11. Unadkat H. et al. An algorithm-based topographical biomaterials library to instruct cell fate. Proc Natl Acad Sci U S A 108, 16565–16570 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kim D. et al. Guided Cell Migration on Microtextured Substrates with Variable Local Density and Anisotropy. Adv Funct Mater 19, 1579–1586 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Provenzano P., Inman D., Eliceiri K., Trier S. & Keely P. Contact guidance mediated three-dimensional cell migration is regulated by Rho/ROCK-dependent matrix reorganization. Biophys J 95, 5374–5384 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Biggs M., Richards R., Gadegaard N., Wilkinson C. & Dalby M. The effects of nanoscale pits on primary human osteoblast adhesion formation and cellular spreading. J Mater Sci Mater Med 2007 18, 399–404 (2007). [DOI] [PubMed] [Google Scholar]
  15. Dalby M. et al. The control of human mesenchymal cell differentiation using nanoscale symmetry and disorder. Nat Mater 6, 997–1003 (2007). [DOI] [PubMed] [Google Scholar]
  16. Milner K. & Siedlecki C. Submicron poly(L-lactic acid) pillars affect fibroblast adhesion and proliferation. J Biomed Mater Res A 82, 80–91 (2007). [DOI] [PubMed] [Google Scholar]
  17. Kolind K. et al. A combinatorial screening of human fibroblast responses on micro-structured surfaces. Biomaterials 31, 9182–9191 (2010). [DOI] [PubMed] [Google Scholar]
  18. Liliensiek S., Campbell S., Nealey P. & Murphy C. The scale of substratum topographic features modulates proliferation of corneal epithelial cells and corneal fibroblasts. J Biomed Mater Res A 79, 185–192 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Bosman F. & Stamenkovic I. Functional structure and composition of the extracellular matrix. J Pathol 200, 423–428 (2003). [DOI] [PubMed] [Google Scholar]
  20. Abrams G., Goodman S., Nealey P., Franco M. & Murphy C. Nanoscale topography of the basement membrane underlying the corneal epithelium of the rhesus macaque. Cell Tissue Res 299, 39–46 (2000). [DOI] [PubMed] [Google Scholar]
  21. Bozec L. & Horton M. Skeletal tissues as nanomaterials. J Mater Sci Mater Med 17, 1043–1048 (2006). [DOI] [PubMed] [Google Scholar]
  22. Bozec L., van der Heijden G. & Horton M. Collagen fibrils: nanoscale ropes. Biophys J 92, 70–75 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Brody S. et al. Characterizing nanoscale topography of the aortic heart valve basement membrane for tissue engineering heart valve scaffold design. Tissue Eng 12, 413–421 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Eyden B. Structural variations of collagen in normal and pathological tissues: role of electron microscopy. Micron 32, 287–300 (2001). [DOI] [PubMed] [Google Scholar]
  25. Fratzl P., Gupta H. S., Roschger P. & Klaushofer K. in Nanotechnology - Nanomedicine Vol. 5, (ed Vogel, ed. ) 345–360 (Wiley-VCH Weinheim, 2009). [Google Scholar]
  26. Barabási A.-L. & Stanley H. Fractal concepts in surface growth. (Press Syndicate of the University of Cambridge, 1995). [Google Scholar]
  27. Persson B. Adhesion between an elastic body and a randomly rough hard surface. Eur Phys J E 8, 385–401 (2002). [DOI] [PubMed] [Google Scholar]
  28. Bettinger C., Zhang Z., Gerecht S., Borenstein J. & Langer R. Enhancement of In Vitro Capillary Tube Formation by Substrate Nanotopography. Adv Mater 20, 99–103 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Brunetti V. et al. Neurons sense nanoscale roughness with nanometer sensitivity. Proc Natl Acad Sci U S A 107, 6264–6269 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Chen W., Villa-Diaz L. & Sun Y. Nanotopography influences adhesion, spreading, and self-renewal of human embryonic stem cells. ACS Nano 6, 4094–4103 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Yim E. et al. Nanopattern-induced changes in morphology and motility of smooth muscle cells. Biomaterials 26, 5405–5413 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Webster T. & Ejiofor J. Increased osteoblast adhesion on nanophase metals: Ti, Ti6Al4V, and CoCrMo. Biomaterials 25, 4731–4739 (2004). [DOI] [PubMed] [Google Scholar]
  33. Li B. & Logan B. Bacterial adhesion to glass and metal-oxide surfaces. Colloids Surf B Biointerfaces 36, 81–90 (2004). [DOI] [PubMed] [Google Scholar]
  34. Dalby M., Riehle M., Johnstone H., Affrossman S. & Curtis A. Polymer-demixed nanotopography: control of fibroblast spreading and proliferation. Tissue Eng 8, 1099–1108 (2002). [DOI] [PubMed] [Google Scholar]
  35. Fan Y. et al. Culture of neural cells on silicon wafers with nano-scale surface topograph. J Neurosci Methods 120, 17–23 (2002). [DOI] [PubMed] [Google Scholar]
  36. Gentile F. et al. Cells preferentially grow on rough substrates. Biomaterials 31, 7205–7212 (2010). [DOI] [PubMed] [Google Scholar]
  37. Cavalcanti-Adam E. et al. Cell spreading and focal adhesion dynamics are regulated by spacing of integrin ligands. Biophys J 92, 2964–2974 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zaidel-Bar R., Cohen M., Addadi L. & Geiger B. Hierarchical assembly of cell-matrix adhesion complexes. Biochem Soc Trans 32, 416–420 (2004). [DOI] [PubMed] [Google Scholar]
  39. Khatau S. et al. A perinuclear actin cap regulates nuclear shape. Proc Natl Acad Sci U S A 106, 19017–19022 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Maniotis A., Bojanowski K. & Ingber D. Mechanical continuity and reversible chromosome disassembly within intact genomes removed from living cells. J Cell Biochem 65, 114–130 (1997). [PubMed] [Google Scholar]
  41. Versaevel M., Grevesse T. & Gabriele S. Spatial coordination between cell and nuclear shape within micropatterned endothelial cells. Nat Commun 3, 671 (2012). [DOI] [PubMed] [Google Scholar]
  42. Decuzzi P. & Ferrari M. The receptor-mediated endocytosis of nonspherical particles. Biophys J 94, 3790–3797 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Simson R. et al. Membrane bending modulus and adhesion energy of wild-type and mutant cells of Dictyostelium lacking talin or cortexillins. Biophys J 74, 514–522 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Decuzzi P. & Ferrari M. Modulating cellular adhesion through nanotopography. Biomaterials. Biomaterials 31, 173–179 (2010). [DOI] [PubMed] [Google Scholar]
  45. Assoian R. & Klein E. Growth control by intracellular tension and extracellular stiffness. Trends Cell Biol 18, 347–352 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Geiger B., Spatz J. & Bershadsky A. Environmental sensing through focal adhesions. Nat Rev Mol Cell Biol 10, 21–33 (2009). [DOI] [PubMed] [Google Scholar]
  47. Davey G., Buzzai M. & Assoian R. Reduced expression of (α)5(β)1 integrin prevents spreading-dependent cell proliferation. Journal of Cell Science 112, 4663–4672 (1999). [DOI] [PubMed] [Google Scholar]
  48. DuFort C., Paszek M. & Weaver V. Balancing forces: architectural control of mechanotransduction. Nat Rev Mol Cell Biol 12, 308–319 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Geblinger D., Addadi L. & Geiger B. Nano-topography sensing by osteoclasts. J Cell Sci 123, 1503–1510 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tonazzini I. et al. Multiscale Morphology of Organic Semiconductor Thin Films Controls the Adhesion and Viability of Human Neural Cells. Biophysical Journal 98, 2804–2812 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep01461-s1.doc (1.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES