Spatial extent of an outbreak in animal epidemics

Abstract

Characterizing the spatial extent of epidemics at the outbreak stage is key to controlling the evolution of the disease. At the outbreak, the number of infected individuals is typically small, and therefore, fluctuations around their average are important: then, it is commonly assumed that the susceptible–infected–recovered mechanism can be described by a stochastic birth–death process of Galton–Watson type. The displacements of the infected individuals can be modeled by resorting to Brownian motion, which is applicable when long-range movements and complex network interactions can be safely neglected, like in the case of animal epidemics. In this context, the spatial extent of an epidemic can be assessed by computing the convex hull enclosing the infected individuals at a given time. We derive the exact evolution equations for the mean perimeter and the mean area of the convex hull, and we compare them with Monte Carlo simulations.

Models of epidemics traditionally consider three classes of populations—namely, the susceptible (S), the infected (I), and the recovered (R). This framework provides the basis of the so-called SIR model (1, 2), a fully connected mean-field model where the population sizes of the three species evolve with time t by the coupled nonlinear equations: dS/dt = −βIS, dI/dt = βIS − γI, and dR/dt = γI. Here, γ is the rate at which an infected individual recovers, and β denotes the rate at which it transmits the disease to a susceptible (3–5). In the simplest version of these models, the recovered cannot be infected again. These rate equations conserve the total population size I(t) + S(t) + R(t) = N; one assumes that, initially, there is only one infected individual, and the rest of the population is susceptible: I(0) = 1, S(0) = N − 1, and R(0) = 0. Of particular interest is the outbreak stage (i.e., the early times of the epidemic process), when the susceptible population is much larger than the number of infected or recovered. During this regime, for large N, the susceptible population hardly evolves and stays S(t) ∼ N; therefore, nonlinear effects can be safely neglected, and one can just monitor the evolution of the infected population alone: dI/dt ∼ (βN − γ)I(t). Thus, the ultimate fate of the epidemics depends on the key dimensionless parameter R₀ = βN/γ, which is called the reproduction rate. If R₀ > 1, the epidemic explodes and invades a finite fraction of the population; if R₀ < 1, the epidemic goes to extinction, and in the critical case R₀ = 1 the infected population remains constant (6–8).

This basic deterministic SIR has been generalized to a variety of both deterministic as well as stochastic models, and distinct advantages and shortcomings are discussed at length in refs. 9–11. Generally speaking, stochastic models are more suitable in the presence of a small number of infected individuals, when fluctuations around the average may be relevant (9, 10). During the outbreak of epidemics, the infected population is typically small: in this regime, the evolution can be modeled by resorting to a stochastic birth–death branching process of the Galton–Watson type for the number of infected (9–11), where each infected individual transmits the disease to another individual at rate βN and recovers at rate γ. The epidemic may become endemic for R₀ > 1 and becomes extinct for R₀ < 1, whereas for R₀ = 1 fluctuations are typically long-lived and completely control the time evolution of the infected population (3–5).

How far in space can an epidemic spread? Branching processes alone are not sufficient to describe an outbreak, and spatial effects must necessarily be considered (1, 4, 12–14). Quantifying the geographical spread of an epidemic is closely related to the modeling of the population displacements. Brownian motion is often considered as a paradigm for describing the migration of individuals, despite some well-known shortcomings: for instance, finite speed effects and preferential displacements are neglected. Most importantly, a number of recent studies have clearly shown that individuals geographically far apart can actually be closely related to each other through the so-called small-world connections, such as air traffic, public transportation, and so on; then, the spread of epidemics among humans cannot be realistically modeled without considering these complex networks of interconnections (15–18). Nonetheless, Brownian motion provides a reasonable basis for studying disease propagation in animals and possibly plants (here, pathogen vectors are insects) (5).

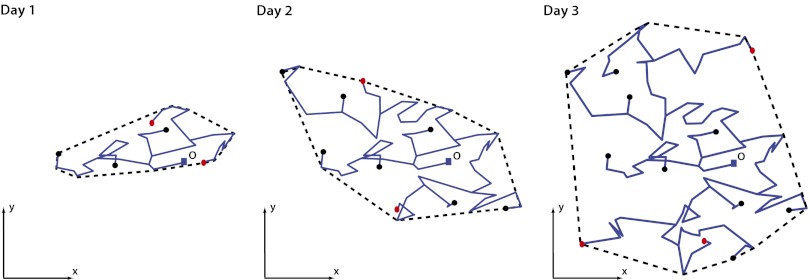
Although theoretical models based on branching Brownian motion have provided important insights on how the population size grows and fluctuates with time in a given domain (1, 4, 13, 14), another fundamental question is how the spatial extension of the infected population evolves with time. Assessing the geographical area traveled by a disease is key to the control of epidemics, which is especially true at the outbreak, when confinement and vaccination could be most effective. One major challenge in this very practical field of disease control is how to quantify the area that needs to be quarantined during the outbreak. For animal epidemics, this issue has been investigated experimentally (for instance, in the case of equine influenza) (19). The most popular and widely used method consists of recording the set of positions of infected animals and, at each time instant, constructing a convex hull (i.e., a minimum convex polygon surrounding the positions; a precise definition of the convex hull is given below) (Fig. 1). The convex hull at time t then provides a rough measure of the area over which the infections have spread up to time t. The convex hull method is also used to estimate the home range of animals (i.e., the territory explored by a herd of animals during their daily search for food) (20, 21).

Fig. 1.

The snapshots of the trajectories of an assembly of infected individuals at the epidemics outbreak at three different times (schematic) starting from a single infected at the origin O at time t = 0.Individuals that are still infected at a given time t are displayed as red dots, whereas individuals already recovered are shown as black dots. The convex hull enclosing the trajectories (shown as a dashed line) is a measure of the geographical area covered by the spreading epidemic. As the epidemic grows in space, the associated convex hull also grows in time.

In this paper, we model the outbreak of an epidemic as a Galton–Watson branching process in presence of Brownian spatial diffusion. Despite infection dynamics being relatively simple, the corresponding convex hull is a rather complex function of the trajectories of the infected individuals up to time t, whose statistical properties seem to be a formidable problem. Our main goal is to characterize the time evolution of the convex hull associated with this process, particularly its mean perimeter and area.

The rest of the paper is organized as follows. We first describe precisely the model and summarize our main results. Then, we provide a derivation of our analytical findings supported by extensive numerical simulations. We conclude with perspectives and discussions. Some details of the computations are relegated to SI Text.

Model and Main Results

Consider a population of N individuals uniformly distributed in a 2D plane, with a single infected at the origin at the initial time. At the outbreak, it is sufficient to keep track of the positions of the infected, which will be marked as particles. The dynamics of the infected individuals are governed by the following stochastic rules. In a small time interval dt, each infected alternatively has three actions.

• i) The infected individual recovers with probability γdt. This event corresponds to the death of a particle with rate γ.

• ii) The infected individual infects, by local contact, a new susceptible individual from the background with probability bdt. This event corresponds to the birth of a new particle that can subsequently diffuse. The originally infected particle still remains infected, which means that the trajectory of the originally infected particle branches into two new trajectories. The rate b replaces the rate βN in the SIR or the Galton–Watson process mentioned before.

• iii) The infected individual diffuses with diffusion constant D with probability 1 − (γ + b)dt. The coordinates {x(t), y(t)} of the particle get updated to the new values {x(t) + η_x(t)dt, y(t) + η_y(t)dt}, where η_x(t) and η_y(t) are independent Gaussian white noises with zero mean and correlators 〈η_x(t)η_x(t′)〉 = 2Dδ(t − t′), 〈η_y(t)η_y(t′)〉 = 2Dδ(t − t′), and 〈η_x(t)η_y(t′)〉 = 0.

The only dimensionless parameter in the model is the ratio R₀ = b/γ (i.e., the basic reproduction number).

Consider now a particular history of the assembly of the trajectories of all of the infected individuals up to time t, starting from a single infected initially at the origin (Fig. 1). For every realization of the process, we construct the associated convex hull C. To visualize the convex hull, imagine stretching a rubber band so that it includes all of the points of the set at time t inside it and then releasing the rubber band. It shrinks and finally gets stuck when it touches some points of the set; therefore, it cannot shrink any more. This final shape is precisely the convex hull associated with this set.

In this paper, we show that the mean perimeter 〈L(t)〉 and the mean area 〈A(t)〉 of the convex hull are ruled by two coupled nonlinear partial differential equations that can be solved numerically for all t (Fig. 2). The asymptotic behavior for large t can be determined analytically for the critical (R₀ = 1), subcritical (R₀ < 1), and supercritical (R₀ > 1) regimes. In particular, in the critical regime, the mean perimeter saturates to a finite value as t → ∞, whereas the mean area diverges logarithmically for large t:

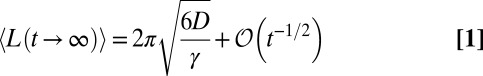and

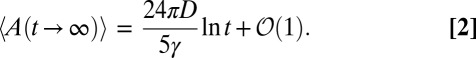This prediction seems rather paradoxical at a first glance. How can the perimeter of a polygon be finite while its area is divergent? The resolution to this paradox owes its origin precisely to statistical fluctuations. The results in Eqs. 1 and 2 are true only on average. Of course, for each sample, the convex hull has a finite perimeter and a finite area. However, as we later show, the probability distributions of these random variables have power-law tails at long time limits. For instance, although Prob(L, t → ∞) ∼ L⁻³ for large L (thus leading to a finite first moment), the area distribution behaves as Prob(A, t → ∞) ∼ A⁻² for large A. Hence, the mean area is divergent as t → ∞ (Fig. 2).

Fig. 2.

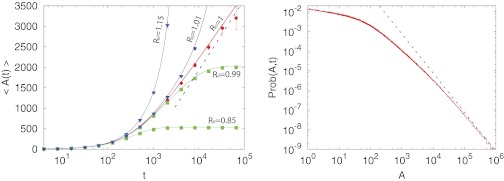
(Left) The average area 〈A(t)〉 of the convex hull as a function of the observation time. For the parameter values, we have chosen D = 1/2 and b = R₀γ = 0.01. We considered five different values of R₀. We have obtained these results by two different methods. (i) One method is by the numerical integration of Eqs. 9 and 14 and using Eq. 15. These results are displayed as solid lines. (ii) The other method is by Monte Carlo simulations of the 2D branching Brownian motion with death with the same parameters averaged over 10⁵ samples. Monte Carlo simulations are displayed as symbols. The dashed lines represent the asymptotic limits as given in Eq. 2 for the critical case R₀ = 1. Additional details of the numerical simulations are provided in SI Text. (Right) Distribution of the area of the convex hull for the critical case R₀ = 1, with γ = 0.01 and D = 1/2, as obtained by Monte Carlo simulations with 2 × 10⁶ realizations. The dashed line corresponds to the power-law (24πD/5γ)A⁻² as predicted by expression 20.

When R₀ ≠ 1, the evolution of the epidemic is controlled by a characteristic time t*, which scales like t* ∼ |R₀ − 1|⁻¹. For times t < t* the epidemic behaves as in the critical regime. In the subcritical regime, for t > t*, the quantities 〈L(t)〉 and 〈A(t)〉 rapidly saturate, and the epidemic goes eventually to extinction. In contrast, in the supercritical regime (which is the most relevant for virulent epidemics that spread fast), a new time-dependent behavior emerges when t > t*, because there exists a finite probability (namely 1 − 1/R₀) that the epidemic never goes to extinction (Fig. 3). More precisely, we later show that

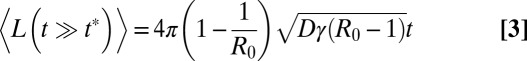and

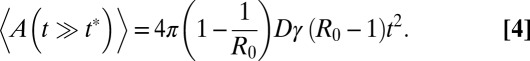The ballistic growth of the convex hull stems from an underlying traveling front solution of the nonlinear equation governing the convex hull behavior. Indeed, the prefactor of the perimeter growth is proportional to the front velocity 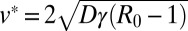. As time increases, the susceptible population decreases because of the growth of the infected individuals: this depletion effect leads to a breakdown of the outbreak regime and a slowing down of the epidemic propagation.

Fig. 3.

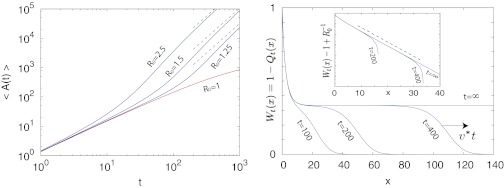
(Left) The time behavior of the average area in the supercritical regime for different values of R₀ > 1. Dashed lines represent the asymptotic scaling as in Eq. 4. The red curve corresponds to the critical regime. (Right) The behavior of W_t(x) = 1 − Q_t(x) for R₀ = 1.5 at different times as in Eq. 21. When t → ∞, 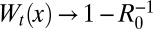, and for large but finite times, the traveling front behavior is clearly visible. Inset displays the exponential convergence of W_t(x) to the asymptotic limit. The dashed line represents .

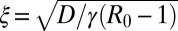Statistics of the Convex Hull

Characterizing the fluctuating geometry of C is a formidable task even in absence of branching (b = 0) and death (γ = 0), i.e., purely for diffusion process in 2Ds. Major recent breakthroughs have, nonetheless, been obtained for diffusion processes (22, 23) by a clever adaptation of the Cauchy integral geometric formulae (24, 25) for the perimeter and area of any closed convex curve in 2Ds. In fact, the problem of computing the mean perimeter and area of the convex hull of any generic 2D stochastic process can be mapped, using Cauchy formulae, to the problem of computing the moments of the maximum and the time at which the maximum occurs for the associated 1D component stochastic process (22, 23). This technique was used for computing the mean perimeter and area of the convex hull of a 2D regular Brownian motion (22, 23) and a 2D random acceleration process (26).

Our main idea here is to extend this method to compute the convex hull statistics for the 2D branching Brownian motion. Using this general mapping and isotropy in space (SI Text), the average perimeter and area of the convex hull are given by

and

where x_m is the maximum displacement of our 2D stochastic process in the x direction up to time t, t_m is the time at which the maximum displacement along x direction occurs, and y(t_m) is the ordinate of the process at t_m (i.e., when the displacement along the x direction is maximal). A schematic representation is provided in Fig. 4, where the global maximum x_m is achieved by one single infected individual, whose path is marked in red. A crucial observation is that the y component of the trajectory connecting O to this red path is a regular 1D Brownian motion. Hence, given t_m and t, clearly 〈y²(t_m)〉 = 2D〈t_m〉. Therefore,

Eqs. 5 and 7 thus show that the mean perimeter and area of the epidemics outbreak are related to the extreme statistics of a 1D branching Brownian motion with death. Indeed, if we can compute the joint distribution P_t(x_m, t_m), we can, in turn, compute the three moments 〈x_m〉, 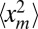, and 〈t_m〉 that are needed in Eqs. 5 and 7. We show below that this calculation can be performed exactly.

Fig. 4.

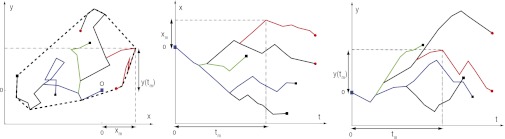
(Left) A branching random walk composed of five individuals. At time t = 0, a single infected individual is at the origin O and starts diffusing (blue line). At later times, this individual branches and gives rise to other infected individuals. Among these individuals, the red path reaches the maximum x_m along the x component up to the final time t. infected individuals at a given time t are displayed as red dots, whereas recovered individuals are displayed as black dots. (Center) The displacement along the x direction as a function of time. The red path reaches the global maximum x_m at time t_m. (Right) The displacement along the y direction as a function of time. When the red path reaches the global maximum x_m at time t_m, its y coordinate attains the value y(t_m). A crucial observation is that the y component of the trajectory connecting O to the red path is a regular Brownian motion. This observation does not apply to the x component, which is constrained to reach the global maximum of the branching process.

Convex Hull Perimeter and Maximum x_m.

For the average perimeter, we just need the first moment 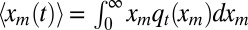, where q_t(x_m) denotes the probability density of the maximum of the 1D component process. It is convenient to consider the cumulative distribution Q_t(x_m) (i.e., the probability that the maximum x displacement stays below a given value x_m up to time t). Then, q_t(x_m) = dQ_t(x_m)/dx_m, and 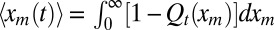. Because the process starts at the origin, its maximum x displacement, for any time t, is necessarily nonnegative (i.e., x_m ≥ 0). We next write down a backward Fokker–Planck equation describing the evolution of Q_t(x_m) by considering the three mutually exclusive stochastic moves in a small time interval dt: starting at the origin at t = 0, the walker during the subsequent interval [0, dt] dies with probability γdt, infects another individual (i.e., branches) with probability bdt = R₀γdt, or diffuses by a random displacement Δx = η_x(0)dt with probability 1 − γ(1 + R₀)dt. In the last case, its new starting position is Δx for the subsequent evolution. Hence, for all x_m ≥ 0, one can write

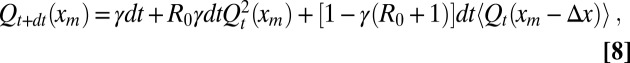where the expectation 〈〉 is taken with respect to the random displacements Δx. The first term means that if the process dies right at the start, its maximum up to t is clearly zero and hence, necessarily less than x_m. The second term denotes the fact that, in case of branching, the maximum of each branch stays below x_m: because the branches are independent, one gets a square. The third term corresponds to diffusion. By using 〈Δx〉 = 0 and 〈Δx²〉 = 2Ddt and expanding Eq. 8 to the first order in dt and second order in Δx, we obtain

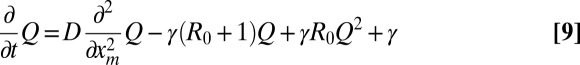for x_m ≥ 0, satisfying the boundary conditions Q_t(0) = 0 and Q_t(∞) = 1 and the initial condition Q₀(x_m) = Θ(x_m), where Θ is the Heaviside step function. Hence, from Eq. 5,

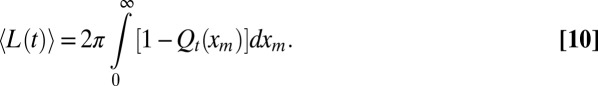Eq. 9 can be solved numerically for all t and all R₀ values, which allows for subsequent computation of 〈L(t)〉 in Eq. 10 (details are provided in SI Text and Figs. S1, S2, and S3).

Convex Hull Area.

To compute the average area in Eq. 7, we need to evaluate 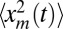as well as 〈t_m〉. After the cumulative distribution Q_t(x_m) is known, the second moment 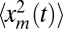can be directly computed by integration, namely 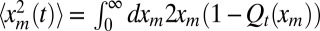. To determine 〈t_m〉, we need to also compute the probability density p_t(t_m) of the random variable t_m. Unfortunately, writing down a closed equation for p_t(t_m) is hardly feasible. Instead, we first define P_t(x_m, t_m) as the joint probability density that the maximum of the x component achieves the value x_m at time t_m, when the full process is observed up to time t. Then, we derive a backward evolution equation for P_t(x_m, t_m) and integrate out x_m to derive the marginal density 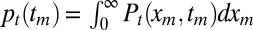. Following the same arguments as for Q_t(x_m) yields a backward equation for P_t(x_m, t_m),

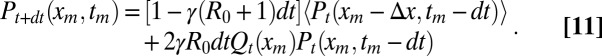The first term at the right-hand side represents the contribution from diffusion. The second term represents the contribution from branching: we require that one of them attains the maximum x_m at the time t_m − dt, whereas the other stays below x_m [Q_t(x_m) being the probability that this condition is satisfied]. The factor 2 comes from the interchangeability of the particles. Developing Eq. 11 to leading order gives

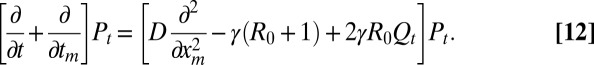This equation describes the time evolution of P_t(x_m, t_m) in the region x_m ≥ 0 and 0 ≤ t_m ≤ t. It starts from the initial condition P₀(x_m, t_m) = δ(x_m)δ(t_m) (because the process begins with a single infected with x component located at x = 0, it implies that, at t = 0, the maximum x_m = 0 and also t_m = 0). For any t > 0 and x_m > 0, we have the condition P_t(x_m, 0) = 0. We need to also specify the boundary conditions at x_m = 0 and x_m → ∞, which read (i) P_t(∞, t_m) = 0 (because for finite t, the maximum is necessarily finite) and (ii) 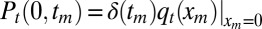. The latter condition comes from the fact that, if x_m = 0, the x component of the entire process, starting at 0 initially, stays below zero in the time interval [0, t], which happens with probability 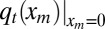: consequently, t_m must necessarily be zero. Furthermore, by integrating P_t(x_m, t_m) with respect to t_m, we recover the marginal density q_t(x_m).

The numerical integration of the full Eq. 12 would be rather cumbersome. Fortunately, we do not need this calculation. Because we are only interested in 〈t_m〉, it is convenient to introduce

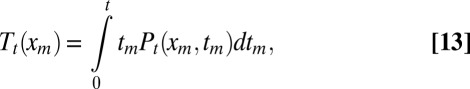from which the average follows as 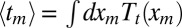. Multiplying Eq. 12 by t_m and integrating by parts, we get

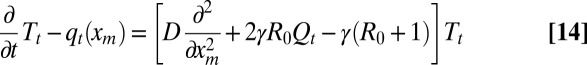with the initial condition T₀(x_m) = 0 and the boundary conditions T_t(0) = 0 and T_t(∞) = 0. Eq. 14 can be integrated numerically together with Eq. 9 (details are provided in SI Text), and the behavior of

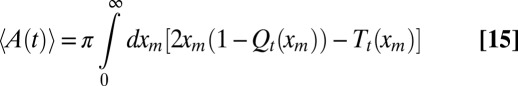as a function of time is illustrated in Fig. 2.

Critical Regime.

We now focus on the critical regime R₀ = 1. We begin with the average perimeter: for R₀ = 1, Eq. 9 admits a stationary solution as t → ∞, which can be obtained by setting ∂Q/∂t = 0 and solving the resulting differential equation. In fact, this stationary solution was already known in the context of the genetic propagation of a mutant allele (27). Taking the derivative of this solution with respect to x_m, we get the stationary probability density of the maximum x_m:

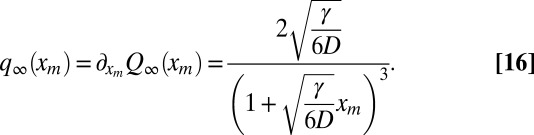The average is 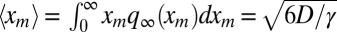, which yields Eq. 1 for the average perimeter of the convex hull at late times.

To compute the average area in Eq. 7, we need to also evaluate the second moment 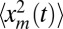, which diverges as t → ∞ because of the power-law tail of the stationary probability density 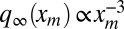for large x_m. Hence, we need to consider large but finite t. In this case, the time-dependent probability density q_t(x_m) displays a scaling form, which can be conveniently written as

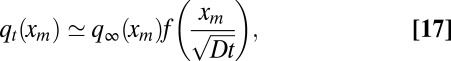where f(z) is a rapidly decaying function with f(z ≪ 1) 1 and f(z ≫ 1) 0. Using the scaling form of expression 17 and Eq. 9, one can derive a differential equation for f(z). However, it turns out that we do not really need the solution of f(z).

From expression 17, we see that the asymptotic power-law decay of q_t(x_m) for large x_m has a cutoff around 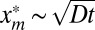and that f(z) is the cutoff function. The second moment at finite but large times t is given by 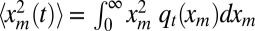. Substituting the scaling form and cutting off the integral over x_m at 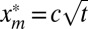[where the constant c depends on the precise form of f(z)], we get to leading order for large t:

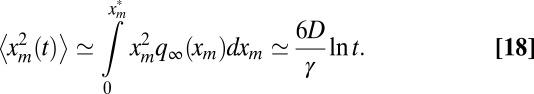Thus, interestingly, the leading order result is universal [i.e., independent of the details of the cutoff function f(z); the c dependence is only in the subleading term]. To complete the characterization of 〈A(t)〉 in Eq. 7, we still need to determine 〈t_m〉: in SI Text, we explicitly determine the stationary solution P_∞(x_m, t_m) for R₀ = 1. By following the same arguments as for 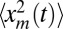, we show that

for large t, which leads again to a logarithmic divergence in time. Finally, substituting expressions 18 and 19 in Eq. 7 gives the result announced in Eq. 2.

A deeper understanding of the statistical properties of the process would demand knowing the full distribution Prob(L, t) and Prob(A, t) of the perimeter and area. These quantities seem rather hard to compute, but one can obtain the asymptotic tails of the distributions by resorting to scaling arguments. Following the lines of the Cauchy formula (SI Text), it is reasonable to assume that, for each sample, the perimeter scales as L(t) ∼ x_m(t). We have seen that the distribution of x_m(t) has a power-law tail for large t: 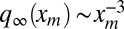for large x_m. Then, assuming the scaling L(t) ∼ x_m(t) and using Prob(L, t → ∞)dL ∼ q_∞(x_m)dx_m, it follows that, at late times, the perimeter distribution also has a power-law tail: Prob(L, t → ∞) ∼ L⁻³ for large L. Similarly, using the Cauchy formula for the area, we can reasonably assume that, for each sample, 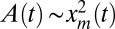in the scaling regime. Once again, using Prob(A, t → ∞)dA = q_∞(x_m)dx_m, we find that the area distribution also converges, for large t, to a stationary distribution with a power-law tail: Prob(A, t → ∞) ∼ A⁻² for large A. Moreover, the logarithmic divergence of the mean area calls for a precise ansatz on the tail of the area distribution, namely

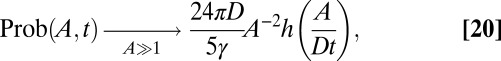where the scaling function h(z) satisfies the conditions h(z ≪ 1) = 1 and h(z ≫ 1) 0. It is not difficult to verify that expression is the only scaling compatible with Eq. 2. These two results are consistent with the fact that, for each sample, typically A(t) ∼ L²(t) at late times in the scaling regime. Our scaling predictions are in agreement with our Monte Carlo simulations (Fig. 2). The power-law behavior of Prob(A, t) implies that the average area is not representative of the typical behavior of the epidemic area, which is actually dominated by fluctuations and rare events, with likelihood given by expression 20.

Supercritical Regime.

When R₀ > 1, it is convenient to rewrite Eq. 9 in terms of W(x_m, t) = 1 − Q(x_m, t):

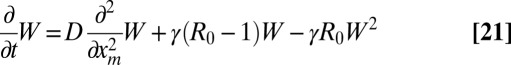starting from the initial condition W(x_m, 0) = 0 for all x_m > 0 (Fig. 3). From Eq. 10, 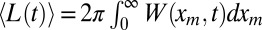is just the area under the curve W(x_m, t) vs. x_m up to a factor 2π. As t → ∞, the system approaches a stationary state for all R₀ ≥ 1, which can be obtained by setting ∂_tW = 0 in Eq. 21. For R₀ > 1, the stationary solution W(x_m, ∞) approaches the constant 1 − 1/R₀ exponentially fast as x_m → ∞, namely 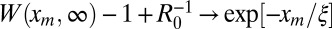, with a characteristic length scale 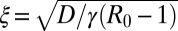. However, for finite but large t, W(x_m, t) as a function of x_m has a two-step form: it first decreases from 1 to its asymptotic stationary value 1 − 1/R₀ over the length scale ξ, and then decreases rather sharply from 1 − 1/R₀ to 0. The frontier between the stationary asymptotic value 1 − 1/R₀ (stable) and 0 (unstable) moves forward with time at constant velocity, thus creating a traveling front at the right end, which separates the stationary value 1 − 1/R₀ to the left of the front and 0 to the right. This front advances with a constant velocity v* that can be estimated using the standard velocity selection principle (28–30). Near the front, where the nonlinear term is negligible, the equation admits a traveling front solution: W(x_m, t) ∼ exp[−λ(x_m − vt)], with a one parameter family of possible velocities v(λ) = Dλ + γ(R₀ −1)/λ, parametrized by λ. This dispersion relation v(λ) has a minimum at 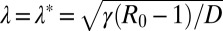, where 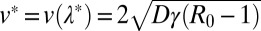. According to the standard velocity selection principle (28–30), for a sufficiently sharp initial condition, the system will choose this minimum velocity v*. The width of the front remains ∼(1) at large t. Thus, because of this sharpness of the front, to leading order for large t, one can approximate W(x_m, t) (1 − 1/R₀)Θ(v*t − x_m) near the front. Hence, to leading order for large t, one gets 〈x_m(t)〉 (1 − 1/R₀)v*t and 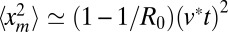. The former gives, from Eq. 5, the result announced in Eq. 3. For the mean area in Eq. 7, the term 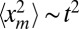for large t dominates over 〈t_m〉 ∼ t (which can be neglected), and we get the result announced in Eq. 3.

Conclusions

In this paper, we have developed a general procedure for assessing the time evolution of the convex hull associated with the outbreak of an epidemic. We find it extremely appealing that one can successfully use mathematical formulae (Cauchy) from 2D integral geometry to describe the spatial extent of an epidemic outbreak in relatively realistic situations. Admittedly, there are many assumptions in this epidemic model that are not quite realistic. For instance, we have ignored the fluctuations of the susceptible populations during the early stages of the epidemic: this hypothesis clearly breaks down at later times, when depletion effects begin to appear because of the epidemic invading a thermodynamical fraction of the total population. In addition, we have assumed that the susceptible individuals are homogeneously distributed in space, which is not the case in reality. Nonetheless, it must be noticed that, in practical applications, whenever strong heterogeneities appear, such as mountains, deserts, or oceans, one can split the analysis of the evolving phenomena by conveniently resorting to several distinct convex hulls—one for each separate region. For analogous reasons, the convex hull approach would not be suitable to characterize birth–death processes with long-range displacements, such as for instance branching Lévy flights.

The model discussed in this paper based on branching Brownian motion is amenable to exact results. More generally, realistic models could be taken into account by resorting to cumbersome Monte Carlo simulations. The approach proposed in this paper paves the way for assessing the spatial dynamics of the epidemic by more conveniently solving two coupled nonlinear equations under the assumption that the underlying process be rotationally invariant.

We conclude with an additional remark. In our computations of the mean perimeter and area, we have averaged over all realizations of the epidemics up to time t, including realizations that are already extinct at time t. It would also be interesting to consider averages only over the ensemble of epidemics that are still active at time t. In this case, we expect different scaling laws for the mean perimeter and the mean area of the convex hull. In particular, in the critical case, we believe that the behavior would be much closer to that of a regular Brownian motion.