Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2013 Feb 25;110(11):4273–4278. doi: 10.1073/pnas.1301814110

Free energy landscape for the binding process of Huperzine A to acetylcholinesterase

Fang Bai a,b, Yechun Xu c, Jing Chen c, Qiufeng Liu c, Junfeng Gu a, Xicheng Wang a, Jianpeng Ma d,e, Honglin Li f,1, José N Onuchic g,1, Hualiang Jiang c,f,1
PMCID: PMC3600462  PMID: 23440190

Abstract

Drug-target residence time (t = 1/koff, where koff is the dissociation rate constant) has become an important index in discovering better- or best-in-class drugs. However, little effort has been dedicated to developing computational methods that can accurately predict this kinetic parameter or related parameters, koff and activation free energy of dissociation (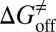Inline graphic). In this paper, energy landscape theory that has been developed to understand protein folding and function is extended to develop a generally applicable computational framework that is able to construct a complete ligand-target binding free energy landscape. This enables both the binding affinity and the binding kinetics to be accurately estimated. We applied this method to simulate the binding event of the anti-Alzheimer’s disease drug (−)−Huperzine A to its target acetylcholinesterase (AChE). The computational results are in excellent agreement with our concurrent experimental measurements. All of the predicted values of binding free energy and activation free energies of association and dissociation deviate from the experimental data only by less than 1 kcal/mol. The method also provides atomic resolution information for the (−)−Huperzine A binding pathway, which may be useful in designing more potent AChE inhibitors. We expect this methodology to be widely applicable to drug discovery and development.

Keywords: thermodynamics, flexible docking, metastable states, transition states

Traditionally, drug discovery is driven by the idea that binders with higher binding affinity to a target should be more efficacious than those with lower binding affinity to the same target (1). It is obvious that the efficacy of a drug is not only associated with thermodynamics but also related to the binding kinetics between the drug and a defined target (2). Numerous examples demonstrated that drug efficacy does not always linearly correlate with binding affinity (3). Therefore, an affinity-based drug discovery approach is less than complete, and an emerging paradigm emphasizing both thermodynamics and kinetics of drug action has been widely recognized and appreciated in drug discovery (1). In particular, ligand–receptor binding kinetics (BK), which have been overlooked in traditional drug discovery approaches, are unprecedentedly emphasized in almost all steps along the drug discovery and development pipeline (1, 4, 5). Indeed, a statistical analysis on existing drugs demonstrated that the BK profile can be a key differentiator between different drugs (6). Drug-target residence time or dissociative half-life (t1/2 = 0.693/koff) has become an important index in lead optimization (4). Thus, the BK-based paradigm will be promising in discovering better- or best-in-class drugs (1).

Like the experimental approaches for drug discovery, the current computational drug design methods mainly emphasize binding affinity (7–11). Nevertheless, despite more than 30 y of effort, predicting binding free energies for ligands interacting to targets with sufficient accuracy is still an unsolved problem (12). The shortages of existing methods for predicting binding affinity—fast but inaccurate or accurate but slow—seem to be turning against the further expansion of the drug design approaches from an affinity-emphasized paradigm to a BK-emphasized paradigm. Recently, energy landscape theory, which was originally used to investigate protein folding problems (13–15), has been extended to study ligand–macromolecule binding (16–21). To extend the ideas from energy landscape theory for protein folding and function to quantitative drug design, it is necessary to develop a computational method that may produce a rigorous and precise binding free energy landscape (BFEL) for a ligand binding to its target protein.

If such a landscape is produced, the binding free energy profile and free energy barriers for association and dissociation may be obtained from the BFEL and kon and koff values could thus be derived according to the Eyring equation if the transmission factors are known. For most ligand–protein interactions, the transmission factors are unknown; therefore it is difficult to directly predict the absolute values of kon and koff (22). Nevertheless, for the drug design case we expect that changes to the ligand will affect barriers much more than the transmission coefficient, which for small molecules should not be large. Therefore, prediction of the activation free energy of dissociation should be sufficient for drug discovery.

Recently, an increasing number of groups have been interested in kinetic simulation and prediction for ligand–protein binding. By performing 495 molecular dynamics simulations, Buch et al. constructed the binding process for zamidine to trypsin and obtained accurate binding free energy with an error of ∼1 kcal/mol compared with the experimental value, although both the predicated kon and koff deviate from the experimental values by at least an order of magnitude (23). Huang and Caflisch investigated the spontaneous dissociation processes of six small ligands from the active site of the FK506 binding protein (24). However, the calculation results seem qualitative rather than quantitative because their constructed BFEL is not complete and accurate (24). Held et al. developed a computational method to analyze the ensemble of association pathways and used this approach to study the binding of a phosphate ion to the Escherichia coli phosphate-binding protein (25). Moreover, the published results for kinetics simulations have not been concerned with pharmacologically important targets and ligands as complex as real drugs. On the other hand, all these predictions need large-scale molecular dynamics simulations, which are too expensive to be applied in drug design.

Here, we present a computational method that could construct a complete free energy landscape for a drug binding to its target, from which the binding free energy (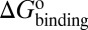Inline graphic) and activation free energies for association (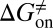Inline graphic) and dissociation (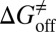Inline graphic) can be quantitatively estimated. We applied this method to simulate the binding process between (−)−Huperzine A (HupA), a marketed natural product drug against Alzheimer’s disease (26), and its target acetylcholinesterase (AChE) (27). The prediction is in excellent agreement with the experimental result we performed in parallel in the present study. 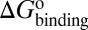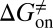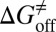The predicted value of Inline graphic is very close to the experimental value, and the predicted values of Inline graphic and Inline graphic deviate from the experimental data only by 2.4 and 1.6 kJ/mol, respectively. Additionally, our method also provided the atomic resolution information of the HupA binding pathway, possible binding transition states, and metastable states, which should be useful in designing more potent AChE inhibitors.

Results

Strategy for Construction of Binding Free Energy Landscape.

The results of this work are based on the analysis of computational and experimental data for the binding process between HupA and Torpedo californica acetylcholinesterase (TcAChE). The detailed procedure for constructing BFEL is described in SI Text and Fig. S1. Briefly, the computational flow is as follows: (i) Analyze the target structure and address the possible binding pockets or gorges for the ligand entering or leaving from the active site. (ii) Construct a lattice model for the target protein by dividing the large cubic box surrounding the protein into a number of small cubic boxes (lattices).(iii) Construct ligand–receptor binding configuration space by docking the ligand molecule into the lattices that enclose the possible binding pockets and the ligand entering and leaving paths. (iv) Calculate the binding free energy for each ligand–receptor binding configuration. (v) Construct the BFEL surface, address the possible binding (unbinding) pathway(s), and estimate the corresponding parameters of thermodynamics and kinetics. To achieve this goal, we improved the molecular mechanic-generalized Born surface area (MM-GBSA) method for free energy calculation and developed a unique multiobjective algorithm-based flexible docking method for binding configuration sampling (details in SI Text).

Binding Free Energy Calculation.

Balancing speed and physical rigorousness, we used a hybrid MM-GBSA method by combining pair-wise–based and grid-based methods (28, 29) to calculate the binding free energy. Furthermore, to enhance the calculation accuracy, we modified the formulation of MM-GBSA (details in SI Text); i.e., the four energy terms of MM-GBSA were weighted by four coefficients (ω1–ω4), respectively,

graphic file with name pnas.1301814110eq1.jpg

where ΔEvdw, ΔEes, ΔGgb, and ΔGsa are, respectively, the Lennard–Jones 6–12 potential, Coulombic potential, and polarization and nonpolarization components of salvation free energy. Weighting coefficients ω1–ω4 are obtained by fitting computational data with experimental data, using the multiple linear regression method (details in SI Text). In the present study, the experimental binding data of eight available AChE inhibitors with TcAChE were used to fit the values of ω1–ω4 (Table S1). The fitted values of ω1–ω4 for TcAChE are 0.2245, −0.4818, −0.6288, and −3.6828, respectively (details in SI Text). The predicted binding free energies for these eight inhibitors to TcAChE correlated well with the experimental data (Fig. S2).

Sampling Binding Configuration Space.

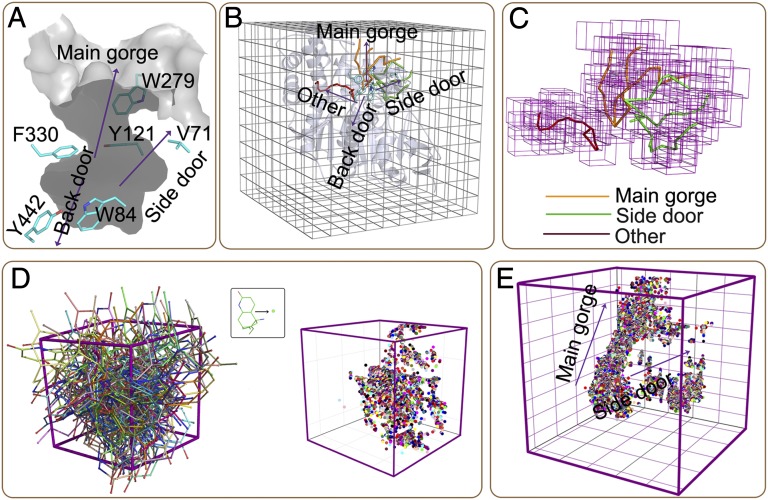
A flexible docking program developed by ourselves was used to construct the binding configuration space between HupA and TcAChE (details in SI Text). To test the reliability of our computational methods for docking and free energy calculation, we used the X-ray crystal structure of apo-TcAChE [Protein Data Bank (PDB) ID: 1EA5] (30) rather than the HupA–TcAChE complex (PDB ID: 1VOT) (26) as the starting point for constructing the HupA–TcAChE BFEL. TcAChE was first surrounded by a box with a dimension of 60 × 60 × 60 Å3, which was further divided into 1,000 cubic lattices. To increase the computational effectiveness, only those lattices around the binding pocket and possible binding and unbinding paths of TcAChE were selected for binding configuration sampling. The main active-site gorge of TcAChE is about 20 Å deep and consists of two separated ligand-binding sites, the acylation (or active) site and the peripheral anionic site (31) (Fig. 1A). The possible existence of a back door and a side door of AChE increases the complexity of ligand binding to this protein (32) (Fig. 1A). We used the MOLE program (an explorer of molecular channels) (33) to locate and characterize the possible binding or unbinding paths on the basis of all of the available X-ray–determined crystal structures of TcAChE (34) (details in SI Text). MOLE is a Voronoi mesh-based explorer that can effectively probe possible channels, pores, and tunnels in a protein for ligands entering into or leaving out a receptor (http://mole.chemi.muni.cz/). For TcAChE, MOLE did not address the path connecting the back door, but captured the main gorge, the path to the side door, and a novel path perpendicular to the main gorge (Fig. 1B). On the basis of the MOLE analysis, we constructed a lattice model for binding configuration sampling (Fig. 1C).

Fig. 1.

Fig. 1.

Open in a new tab

Configuration sampling for HupA–TcAChE Binding. (A) Stereoview of the active-site gorge of TcAChE and three putative ligand exit pathways indicated in the previous study (32). (B) Latticing TcAChE for sampling the binding configuration space. Sticks represent the possible ligand-binding tunnels addressed by using the Voronoi mesh-based MOLE algorithm (33). Orange sticks indicate the direction of the main gorge for ligand binding and unbinding, green sticks stand for the binding and unbinding tunnels connecting the side door, and the red stick denotes a novel tunnel that was not observed in the previous research. (C) Lattice model around the possible binding pathways. (D) Representative ligand configurations sampled in a cubic lattice described by the binding conformations (Left) and the centers of mass (Right) of HupA. (E) The entire binding configuration space represented by the centers of mass of the binding conformations of HupA.

After setting up the lattice model, the HupA–TcAChE binding configuration space was constructed by docking the HupA molecule into the lattices. A multiobjective optimization algorithm developed on the basis of nonsorting genetic algorithm II (NSGAII) (35) was used to optimize the binding poses of HupA and the corresponding conformations of the flexible residues around HupA (details in SI Text). The four energy terms (ΔEvdw, ΔEes, ΔGgb, and ΔGsa) in Eq. 1 were adopted as objective functions for the multiobjective optimizations. The docking simulation produced totally 127,371 binding configurations. Fig. 1D shows the 3D distributions of the sampled binding configurations in one typical lattice. The distributions of all sampled binding configurations in the whole configuration space are shown in Fig. 1E, which indicates that there are no continuous points along the novel path, suggesting that HupA may hardly enter into or leave this path due to its narrow space. Although there are points around the side door, the distribution from the active site to the side door is not continuous, indicating that HupA also could not reach to the active site through this tunnel. The binding configurations contribute continuously along the main gorge, suggesting that the main gorge is an exclusive pathway for HupA entering and leaving.

HupA–TcAChE BFEL.

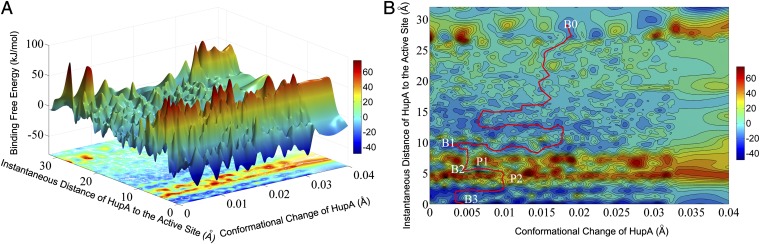
The detailed procedure for BFEL construction is described in SI Text. Binding free energy of each of the 127,371 sampled HupA–TcAChE binding configuration was calculated using Eq. 1. Based on the structural and energetic information of the sampled binding configurations, a BFEL surface was constructed by using the Gridfit algorithm (36) and the nearest-neighbor algorithm encoded in Matlab (37). During the BFEL construction, two parameters were selected as the reaction coordinates; one is the distance between the center of mass of HupA at an instantaneous configuration and that of HupA at the active site, and the other is the minimized root mean SD (RMSD) between the instantaneous conformation of HupA and that at the active site. The constructed 3D surface of the BFEL and its projection on the reaction coordinate plane are also shown in Fig. 2.

Fig. 2.

Fig. 2.

Open in a new tab

(A) Three-dimensional representation of the constructed binding free energy landscape (BFEL) for the HupA–TcAChE binding process. (B) Two-dimensional representation of the binding free energy landscape between HupA and TcAChE. The red line is the lowest-energy binding pathway of HupA binding to TcAChE.

In general, the BFEL is separated into two regions by a high and long energy barrier (like a mountain chain); one side of the energy barrier faces an area with various “hills” and “canyons” with different heights or depths, and the other side of the energy barrier looks like a cliff (Fig. 2A). The physiognomy of the “cliff”-faced area reflects the interaction characteristics of HupA with the active site and that of the hills area characterizes interactions of HupA with the peripheral anionic site and fluctuation of HupA in the bulk solvent. The 2D projection of BFEL on the reaction coordinate plane could clearly demonstrate the energetic properties of the binding and unbinding processes of HupA to TcAChE (Fig. 2B; details in Discussion).

Characterization of Binding Pathway for HupA to TcAChE.

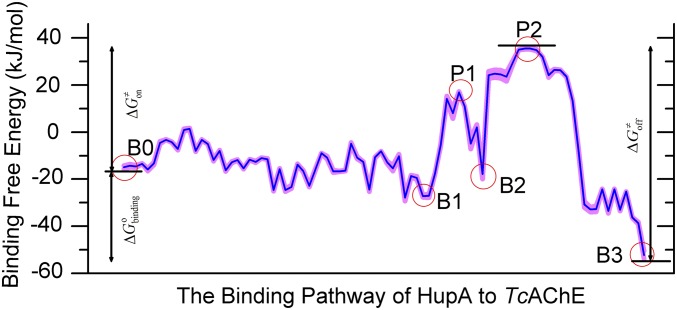
To address the ligand–receptor binding pathway, we developed an algorithm that may search out the lowest-energy binding pathway from the BFEL (Fig. S3A; details in SI Text). The most possible pathways of HupA binding to TcAChE are shown in Fig. 2B, and the corresponding binding free energy profile along this pathway is shown in Fig. 3. Along the binding pathway, there are three low-energy wells corresponding to three metastable states (B0–B2), one stable state (B3), and two energy peaks related to two transition states (P1 and P2). The snapshot of B3 shows the structural binding state of HupA arriving at the active site. Energetically, B3 is the globally lowest-energy state in the overall BFEL (Fig. 3). The docked binding configuration of HupA–TcAChE in the B3 state is extremely close to the X-ray structure of the HupA–TcAChE complex (26); the RMSDs are 0.588 and 0.775 Å for HupA and the flexible residues of TcAChE, respectively (Fig. S3B). This indicates the reliability of our computational method.

Fig. 3.

Fig. 3.

Open in a new tab

Binding free energy profile corresponding to the possible binding pathway in Fig. 2B. The blue curve represents the binding free energy profile along the binding pathway and the pink shadow represents the predictive error of the profile.

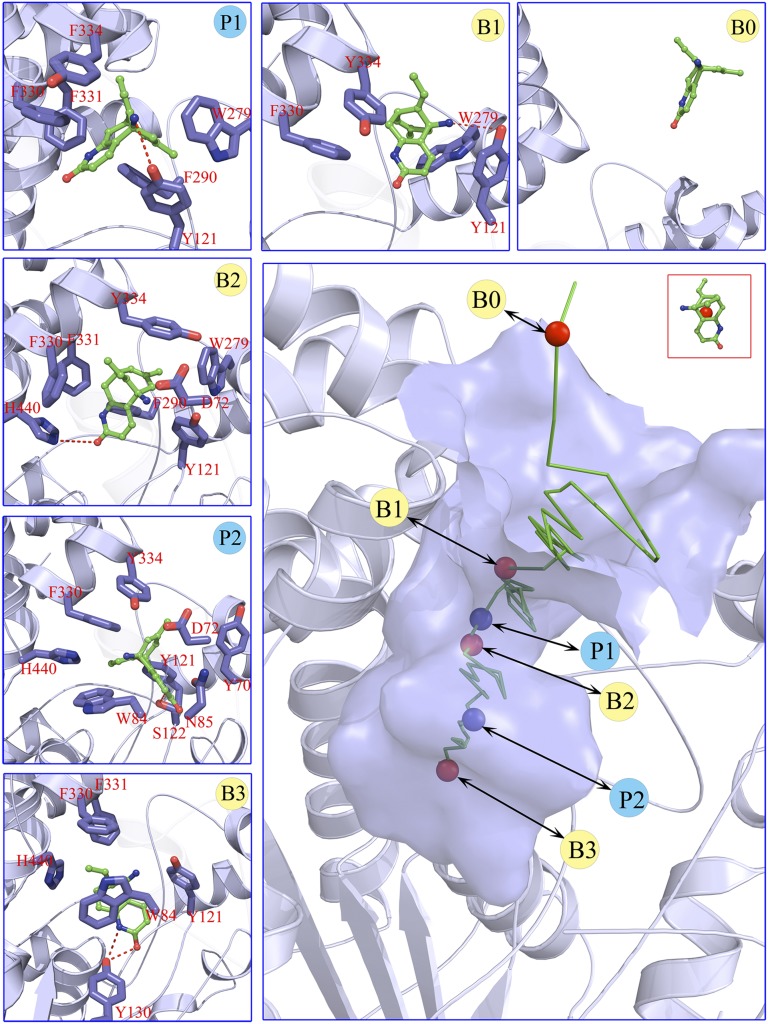
Now we discuss the binding process of HupA from the bulk solvent to the active site (B3). Structural snapshots of the metastable states and transition states in the binding pathway were also isolated from the sampled binding configurations on the basis of their location at the binding configuration space (Fig. 4 and Fig. S4). It is interesting that HupA may enter into the active gorge in two orientations, the carbonyl group stretching into the gorge first and the ethylidene methyl group stepping into the gorge first, thereby producing two equi-energy entering trajectories, designed as path I and path II, respectively (Fig. S5). HupA could arrive at the active site of TcAChE through path I (Fig. 4). Nevertheless, HupA could arrive at the bottom of the peripheral anionic site but could not move farther to reach the active site through path II (Figs. S4 and S5). Therefore, there are two equi-energy binding configurations for B1, P1, and B2, but only one binding configuration for P2 and B3 (Fig. 4 and Fig. S4). Of note, the role of residues in the peripheral site of human AChE (hAChE) in positioning the ligand in a proper orientation before it enters into the active site was also addressed by Branduardi et al. (21) in their metadynamics simulation on the penetration of tetramethylammonium (TMA) into the hAChE gorge. Interestingly, this study revealed that site B1 is also a metastable basin for TMA.

Fig. 4.

Fig. 4.

Open in a new tab

Structural features along the most possible binding pathway of HupA entering the gorge of TcAChE. (Lower Right) The binding pathway of HupA to TcAChE corresponding to the binding free energy profile shown in Fig. 2B. Green stick reflects the lowest-binding free energy pathway portrayed by the centers of mass of the instantaneous configurations of HupA. Circles highlight the (meta)stable states (red) and transition states (blue). Smaller panes (Upper and Left) represent the interaction models for the metastable, stable, and transition states indicated in the binding pathway. Red dashed lines in structural models indicate the hydrogen bonds.

Here, only path I is discussed in more detail and the structural information of path II is shown in Fig. S4. For path I, the snapshot of B0 indicates that, at this state, HupA interacts with the solvent molecules and may translate and rotate freely, adopting appropriate orientations to enter into the active gorge of TcAChE (Fig. 4 and Fig. S4). After crossing a low-energy barrier, HupA arrives at the first metastable state B1, binding to the entrance of the active gorge of TcAChE with a binding free energy of about −27.2 kJ/mol. B1 is stabilized mainly by the hydrophobic interactions between HupA and three hydrophobic residues (W279, Y334, and F330) and a hydrogen bond between the amino group of HupA and the hydroxyl group of Y70. Moving farther and crossing a relatively high-energy barrier of about 16.9 kJ/mol (P1), HupA reaches the second metastable state B2. At the transition state P1, the side chains of F330 and Y121 directly obstruct HupA to move farther, and the extrusion from HupA motion twists the conformations of the side chains of Y334 and W279. These factors result in the energy barrier for HupA in between B1 and B2. In the snapshot of P1, weak hydrophobic interactions between HupA and two hydrophobic residues (F290 and F331) and a hydrogen bond of the amino group of HupA to hydroxyl of Y121 have been observed. By pushing the side chains of F330 and Y121 forward, HupA arrives at the second metastable state B2, which is stabilized by several interactions between HupA and TcAChE, including a hydrogen bond between the carboxyl group of HupA and the imidazole ring of H440; a π-π stacking between the pyridine ring of HupA and the side chain of F330; and hydrophobic interactions of HupA with F290, F331, and F334. At this stage, the side chains of W279 and Y334 recovered to their stable conformations. Before entering into the active site, HupA has to travel over the highest-energy barrier of the second transition state P2 (about 35.5 kJ/mol) by overcoming the strong steric hindrances from N85, Y70, D72, Y121,F330, Y334, H440, and W84. At state B3, HupA is stabilized by several kinds of strong interactions formed between the ligand and protein.

Prediction vs. Experiment for Binding Affinity and Kinetic Parameters.

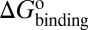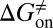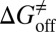Mapping the binding process onto a simple two-state model for the reaction of HupA with TcAChE, we can calculate Inline graphic, Inline graphic, and Inline graphic values for HupA to TcAChE based on the energetic profile (Fig. 3). The binding free energy and kinetic data were estimated as 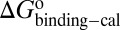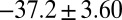Inline graphic = Inline graphic kJ/mol, Inline graphic = Inline graphic 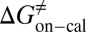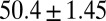kJ/mol, and 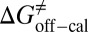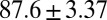Inline graphic = Inline graphic kJ/mol. The predicted data of binding free energy are in excellent agreement with the reported experimental data, −38.6 kJ/mol at 25 °C (25) and −38.2 kJ/mol at 22 °C (38). However, no kinetic data have been reported for HupA–TcAChE binding. To verify the accuracy of our prediction, we determined both the thermodynamic and the kinetic parameters for HupA–TcAChE binding by using surface plasmon resonance (SPR) technology (details in SI Text). To obtain the experimental activation free energies for association and dissociation processes, kon and koff values at five different temperatures in the 10–30 °C range were determined by using SPR technology (Table S2 and Fig. 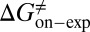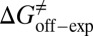S6A), and the values of Inline graphic and Inline graphic were obtained by fitting the linear form of Eyring’s equation (Fig. S6B). Surprisingly, both the determined binding free energy and activation free energies are extremely close to our predicted values: 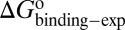Inline graphic = −38.0 kJ/mol, 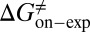Inline graphic = 48.0 kJ/mol, and 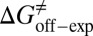Inline graphic = 86.0 kJ/mol (Fig. S6 B and C). The predicted values of binding and activation free energies deviate from the experimental values by 0.8, 2.4, and 1.6 kJ/mol, respectively. This accurate prediction for ligand–receptor binding kinetics again demonstrates the reliability of our computational method.

Discussion

Both the current experimental and computational approaches for drug discovery are binding affinity emphasized (1). Developing a computational method to predict binding kinetic parameters is urgently needed for quantitative drug design. To this end, we have extended the ideas of energy landscape theory for protein folding and function to drug design and developed a computational method to construct a BFEL for a ligand binding to its target protein. Thus, both binding affinity and kinetic parameters can be estimated.

The reliability and practicability of our method have been validated by simulation and computation of the HupA–TcAChE binding process. Our method might construct a reasonable BFEL, containing useful information for deeply understanding the action mechanism of HupA (Figs. 3 and 4). The BFEL not only addressed the possible stable, metastable, and transition states for HupA interacting with TcAChE but also accurately predicted thermodynamic and kinetic data for HupA binding (Fig. 3 and Fig. S3B). Of note, the computational method is also applied to simulate the binding even for E2020, a marketed drug for the treatment of Alzheimer’s disease, to TcAChE. The computational data of both binding affinity and kinetics are in good agreement with the SPR-determined results. This result further strengthens the reliability of our computational method.

During BFEL construction, the binding free energy for each ligand–receptor binding configuration was estimated by an improved MM-GBSA method (details in SI Text). Therefore, our method could improve the accuracy of binding free energy for ligand–receptor interactions. With sufficient sampling of ligand–receptor binding configurations, our method can construct a complete and precise binding free energy landscape, which includes the detailed information about the ligand–receptor binding process. Different from previous attempts for construction of BFEL (23, 24, 39, 40), points assigned onto the landscape surface are standard binding free energies rather than values relative to binding free energies that are derived from binding configuration clustering and probability calculation. In addition, the computational expense of our method is relatively cheap. Accordingly, it is applicable in studying ligand–receptor binding processes and of general interest in biomedical and pharmaceutical research.

As mentioned in the introductory section, drug–target binding kinetic parameters, especially residence time (1/koff) or dissociative half-life (t1/2 = 0.693/koff), have become an important index in discovering better- or best-in-class drugs (4). However, all existing computational drug design strategies and approaches are developed on the basis of the idea of binding affinity; therefore, there is an urgent need to develop binding kinetics-based approaches for drug design. The accurate prediction for HupA–TcAChE binding implies that our method could be used in designing compounds by using both the binding affinity and the kinetic parameters as indexes. The strategy is as follows: (i) Establish a BFEL for an existing drug (active compound) binding to a target of interest. If the target is totally new, one could discover active compounds by using the traditional drug design or screening approaches. (ii) From the BEEL, figure out the binding pathway and isolate the structural snapshots of the possible metastable, transition, and binding states to illustrate the binding mechanism of ligand to protein. (iii) Design or virtually screen compounds targeting both binding site (e.g., B3 in Fig. 4) and transition site (e.g., P2 in Fig. 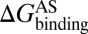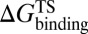4) and evaluate the binding free energies to these two sites for each compound, designated as Inline graphic and Inline graphic, respectively. At the same time calculate the solvation energy of the compound, 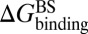Inline graphic. 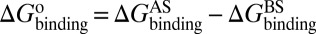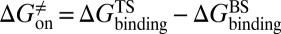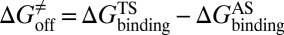Thus, three parameters can be obtained for each compound: binding free energy Inline graphic, activation free energy of the association process Inline graphic, and Inline graphic. (iv) Select compounds with small values of 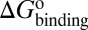Inline graphic but large values of 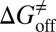Inline graphic for further experimental assay.

Materials and Methods

System Preparation.

The preparation processes of the structural models for protein, inhibitors, and their complexes are provided in SI Text, Table S1, and Fig. S2.

Enzyme and Chemical Samples.

TcAChE was kindly offered by Joel L. Sussman and Israel Silman at the Weizmann Institute of Science, Rehovot, Israel. The chemical sample of HupA was kindly provided by Dayuan Zhu at the Shanghai Institute of Materia Medica, Chinese Academy of Sciences.

SPR Determination.

SPR measurements were performed on a BIAcore T200 instrument (BIAcore GE Healthcare). Details on the experiment procedure and statistical treatment of experimental data are provided in SI Text.

Supplementary Material

Supporting Information
supp_110_11_4273__index.html (7.2KB, html)

Acknowledgments

The authors thank Profs. Joel L. Sussman and Israel Silman for providing the enzyme of TcAChE and Prof. Dayuan Zhu for providing chemical samples of HupA for our experimental validation research. The authors also thank GE Healthcare Life Sciences, Ltd. for supporting the SPR assays. This work was supported by the State Key Program of Basic Research of China (2009CB918500 and 2009CB918502), the National Natural Science Foundation of China (20721003, 20720102040, 21173076, 81222046, and 81230076), the Shanghai Committee of Science and Technology (Grant 11DZ2260600), the 863 Hi-Tech Program of China (Grant 2012AA020308), the National Science and Technology Major Project (2009ZX09501-001), a Scholarship Award for Excellent Doctoral Student granted by the Ministry of Education (to F.B.), the “100 Talents Project” of the Chinese Academy of Sciences (Y.X.), and the Program for New Century Excellent Talents in University [Grant NCET-10-0378 (to H.L.)]. J.N.O.’s work was supported by the Center for Theoretical Biological Physics sponsored by the National Science Foundation (NSF) (Grant PHY-0822283) and by NSF Grant MCB-1214457. J.N.O. is a scholar in Cancer Research sponsored by the Cancer Prevention and Research Institute of Texas. J.M. acknowledges support of grants from the National Institutes of Health (R01-GM067801), the National Science Foundation (MCB-0818353), and the Welch Foundation (Q-1512). Computational resources were supported by the National Supercomputing Center in Tianjin, China (Tianhe-1), the Shanghai Supercomputer Center, and the Computer Network Information Center of the Chinese Academy of Sciences. J.N.O. and J.M. acknowledge support of a grant from the International Workstation for Protein Folding and Drug Design, Shanghai Institute of Materia Medica, Chinese Academy of Sciences.

Footnotes

The authors declare no conflict of interest.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1301814110/-/DCSupplemental.

References

  • 1.Zhang R, Monsma F. Binding kinetics and mechanism of action: Toward the discovery and development of better and best in class drugs. Expert Opin Drug Discov. 2010;5(11):1023–1029. doi: 10.1517/17460441.2010.520700. [DOI] [PubMed] [Google Scholar]
  • 2.Kenakin T, Jenkinson S, Watson C. Determining the potency and molecular mechanism of action of insurmountable antagonists. J Pharmacol Exp Ther. 2006;319(2):710–723. doi: 10.1124/jpet.106.107375. [DOI] [PubMed] [Google Scholar]
  • 3.Swinney DC. Biochemical mechanisms of drug action: What does it take for success? Nat Rev Drug Discov. 2004;3(9):801–808. doi: 10.1038/nrd1500. [DOI] [PubMed] [Google Scholar]
  • 4.Copeland RA, Pompliano DL, Meek TD. Drug-target residence time and its implications for lead optimization. Nat Rev Drug Discov. 2006;5(9):730–739. doi: 10.1038/nrd2082. [DOI] [PubMed] [Google Scholar]
  • 5.Copeland RA. The dynamics of drug-target interactions: Drug-target residence time and its impact on efficacy and safety. Expert Opin Drug Discov. 2010;5(4):305–310. doi: 10.1517/17460441003677725. [DOI] [PubMed] [Google Scholar]
  • 6.Swinney DC. The role of binding kinetics in therapeutically useful drug action. Curr Opin Drug Discov Devel. 2009;12(1):31–39. [PubMed] [Google Scholar]
  • 7.Yan Z, Wang J. Specificity quantification of biomolecular recognition and its implication for drug discovery. Sci Rep. 2012;2:309. doi: 10.1038/srep00309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Taft CA, Da Silva VB, Da Silva CH. Current topics in computer-aided drug design. J Pharm Sci. 2008;97(3):1089–1098. doi: 10.1002/jps.21293. [DOI] [PubMed] [Google Scholar]
  • 9.Tang Y, Zhu WL, Chen KX, Jiang HL. New technologies in computer-aided drug design: Toward target identification and new chemical entity discovery. Drug Discov Today Technol. 2006;3(3):307–313. doi: 10.1016/j.ddtec.2006.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Ou-Yang SS, et al. Computational drug discovery. Acta Pharmacol Sin. 2012;33(9):1131–1140. doi: 10.1038/aps.2012.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Kortagere S, Ekins S. Troubleshooting computational methods in drug discovery. J Pharmacol Toxicol Methods. 2010;61(2):67–75. doi: 10.1016/j.vascn.2010.02.005. [DOI] [PubMed] [Google Scholar]
  • 12.Blaney J. A very short history of structure-based design: How did we get here and where do we need to go? J Comput Aided Mol Des. 2012;26(1):13–14. doi: 10.1007/s10822-011-9518-x. [DOI] [PubMed] [Google Scholar]
  • 13.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
  • 14.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89(18):8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Wang J, Verkhivker GM. Energy landscape theory, funnels, specificity, and optimal criterion of biomolecular binding. Phys Rev Lett. 2003;90(18):188101–188105. doi: 10.1103/PhysRevLett.90.188101. [DOI] [PubMed] [Google Scholar]
  • 17.Schug A, Onuchic JN. From protein folding to protein function and biomolecular binding by energy landscape theory. Curr Opin Pharmacol. 2010;10(6):709–714. doi: 10.1016/j.coph.2010.09.012. [DOI] [PubMed] [Google Scholar]
  • 18.Mobley DL, Dill KA. Binding of small-molecule ligands to proteins: “What you see” is not always “what you get”. Structure. 2009;17(4):489–498. doi: 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Levy Y, Onuchic JN, Wolynes PG. Fly-casting in protein-DNA binding: Frustration between protein folding and electrostatics facilitates target recognition. J Am Chem Soc. 2007;129(4):738–739. doi: 10.1021/ja065531n. [DOI] [PubMed] [Google Scholar]
  • 20.Shoemaker BA, Wang J, Wolynes PG. Structural correlations in protein folding funnels. Proc Natl Acad Sci USA. 2000;97(3):8868–8873. doi: 10.1073/pnas.94.3.777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Branduardi D, Gervasio FL, Cavalli A, Recanatini M, Parrinello M. The role of the peripheral anionic site and cation-π interactions in the ligand penetration of the human AChE gorge. J Am Chem Soc. 2005;127(25):9147–9155. doi: 10.1021/ja0512780. [DOI] [PubMed] [Google Scholar]
  • 22.Winzor DJ, Jackson CM. Interpretation of the temperature dependence of equilibrium and rate constants. J Mol Recognit. 2006;19(5):389–407. doi: 10.1002/jmr.799. [DOI] [PubMed] [Google Scholar]
  • 23.Buch I, Giorgino T, De Fabritiis G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc Natl Acad Sci USA. 2011;108(25):10184–10189. doi: 10.1073/pnas.1103547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Huang D, Caflisch A. The free energy landscape of small molecule unbinding. PLOS Comput Biol. 2011;7(2):e1002002. doi: 10.1371/journal.pcbi.1002002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Held M, Metzner P, Prinz J-H, Noé F. Mechanisms of protein-ligand association and its modulation by protein mutations. Biophys J. 2011;100(3):701–710. doi: 10.1016/j.bpj.2010.12.3699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Raves ML, et al. Structure of acetylcholinesterase complexed with the nootropic alkaloid, (-)-huperzine A. Nat Struct Biol. 1997;4(1):57–63. doi: 10.1038/nsb0197-57. [DOI] [PubMed] [Google Scholar]
  • 27.Kasa P, Papp H, Kasa P, Jr, Torok I. Donepezil dose-dependently inhibits acetylcholinesterase activity in various areas and in the presynaptic cholinergic and the postsynaptic cholinoceptive enzyme-positive structures in the human and rat brain. Neuroscience. 2000;101(1):89–100. doi: 10.1016/s0306-4522(00)00335-3. [DOI] [PubMed] [Google Scholar]
  • 28.Hawkins GD, Cramer CJ, Truhlar DG. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J Phys Chem. 1996;100(51):19824–19839. [Google Scholar]
  • 29.Zou XQ, Sun YX, Kuntz ID. Inclusion of solvation in ligand binding free energy calculations using the generalized-born model. J Am Chem Soc. 1999;121(35):8033–8043. [Google Scholar]
  • 30.Dvir H, et al. X-ray structures of Torpedo californica acetylcholinesterase complexed with (+)-huperzine A and (-)-huperzine B: Structural evidence for an active site rearrangement. Biochemistry. 2002;41(35):10810–10818. doi: 10.1021/bi020151+. [DOI] [PubMed] [Google Scholar]
  • 31.Xu YC, et al. How does huperzine A enter and leave the binding gorge of acetylcholinesterase? Steered molecular dynamics simulations. J Am Chem Soc. 2003;125(37):11340–11349. doi: 10.1021/ja029775t. [DOI] [PubMed] [Google Scholar]
  • 32.Xu YC, et al. Long route or shortcut? A molecular dynamics study of traffic of thiocholine within the active-site gorge of acetylcholinesterase. Biophys J. 2010;99(12):4003–4011. doi: 10.1016/j.bpj.2010.10.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Petřek M, Kosinová P, Koča J, Otyepka M. MOLE: A Voronoi diagram-based explorer of molecular channels, pores, and tunnels. Structure. 2007;15(11):1357–1363. doi: 10.1016/j.str.2007.10.007. [DOI] [PubMed] [Google Scholar]
  • 34.Berman HM, et al. The protein data bank. Nucleic Acids Res. 2000;28(1):235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Kanpur PA, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–197. [Google Scholar]
  • 36.Keim DA, Herrmann A. 1998. The Gridfit algorithm: An efficient and effective approach to visualizing large amounts of spatial data. Proceedings of IEEE Visualization, 1998. International Conference on 24 October 1998, Banissi E, Khosrowshahi F, Sarfraz M (IEEE Computer Society Press, Los Alamitos, CA), pp 181–188.
  • 37.The Mathworks 2009. MATLAB (The Mathworks, St. Natick, MA), Version 7.9.0 (R2009b)
  • 38.Wong DM, et al. Acetylcholinesterase complexed with bivalent ligands related to huperzine a: Experimental evidence for species-dependent protein-ligand complementarity. J Am Chem Soc. 2003;125(2):363–373. doi: 10.1021/ja021111w. [DOI] [PubMed] [Google Scholar]
  • 39.Gong L, Zhou X. Kinetic transition network based on trajectory mapping. J Phys Chem B. 2010;114(32):10266–10276. doi: 10.1021/jp100737g. [DOI] [PubMed] [Google Scholar]
  • 40.Dror RO, et al. Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc Natl Acad Sci USA. 2011;108(32):13118–13123. doi: 10.1073/pnas.1104614108. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_110_11_4273__index.html (7.2KB, html)
1301814110_pnas.201301814SI.pdf (1.8MB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES