Sensory adaptation as optimal resource allocation

Abstract

Visual adaptation is expected to improve visual performance in the new environment. This expectation has been contradicted by evidence that adaptation sometimes decreases sensitivity for the adapting stimuli, and sometimes it changes sensitivity for stimuli very different from the adapting ones. We hypothesize that this pattern of results can be explained by a process that optimizes sensitivity for many stimuli, rather than changing sensitivity only for those stimuli whose statistics have changed. To test this hypothesis, we measured visual sensitivity across a broad range of spatiotemporal modulations of luminance, while varying the distribution of stimulus speeds. The manipulation of stimulus statistics caused a large-scale reorganization of visual sensitivity, forming the orderly pattern of sensitivity gains and losses. This pattern is predicted by a theory of distribution of receptive field characteristics in the visual system.

A basic tenet of sensory biology is that sensory systems adapt to the environment. The adaptation is reflected in static and dynamic characteristics of sensory performance. Viewed statically, sensory systems are highly selective; their sensitivity varies across stimuli as if they favor certain stimuli over others. Dynamically, stimulus selectivity varies across time; it is modified when the environment changes. Thus, stimuli favored in the new environment may be different from those favored in the old environment.

One may view the static and dynamic characteristics of sensory systems as nature’s solutions to the problem of resource allocation. A large but limited number of sensory neurons are divided between many potential stimuli. The division follows the principle of more resources allocated to the more useful stimuli. A striking illustration of this principle is the cortical homunculus (1), a map of the skin and epithelia in the human primary somatosensory cortex (Fig. 1A). Different skin areas have disproportionate representations in the map because of their differential utility: the lips and fingers have much larger neuronal representations than calves and shoulders (2).

Fig. 1.

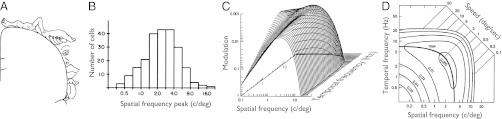
Selectivity of sensory systems. (A) Somatosensory homunculus: a neuronal map of the skin and epithelia in the human cerebral cortex. The size of neuronal representation of skin regions correlates with sensitivity to tactile stimuli (2). (B) Distribution of the peaks of spatial frequency tuning functions for neurons in macaque primary visual cortex. The cell tuning was measured for low temporal frequencies, corresponding to a section of the contrast sensitivity function in C. As in A, the size of neuronal representation of a stimulus correlates with the sensitivity to that stimulus. (C) Human spatiotemporal contrast sensitivity function. The varying height of the surface represents the varying contrast threshold: the amount of luminance contrast (“modulation”) that makes the stimulus just visible; the smaller the modulation at the threshold the higher the sensitivity. (D) A contour plot of the sensitivity function from C. The level curves are the isosensitivity contours, here plotted for five magnitudes of contrast threshold, from 0.005 to 0.08. The ratios of temporal frequency to spatial frequency are stimulus speeds, notated on top right. Stimulus conditions that correspond to the same speed form a diagonal line. Such constant-speed lines for different speeds are parallel to one another in the logarithmic coordinates. The lines are plotted for nine speeds spanning a 500-fold range of speed. The thicker curve labeled “max” connects points of maximal sensitivity across speeds. [A is reproduced from ref. 1; C and D are adapted from ref. 3; B is reprinted from ref. 4: Vision Research, 22/5, De Valois et al., Spatial frequency selectivity of cells in macaque visual cortex. Copyright 1982 with permission from Elsevier.]

A similar picture is found in visual systems. The contrast sensitivity function in Fig. 1 C and D describes the human ability to detect modulations of luminance across a broad range of spatiotemporal stimuli (3). The distribution of neuronal preferences in the primary visual cortex is similar to the distribution of contrast sensitivity, illustrated in Fig. 1B for spatial stimuli (4, 5). It has been argued that the visual stimuli to which we are more sensitive are preferentially useful for perceptual behavior (6–9), similar to how we are more sensitive in the skin regions where high sensitivity is more useful.

Changes in visual stimulation have been widely expected to have the effect of improving visual performance in the new environment (10–12). However, some studies of visual adaptation appear to contradict this expectation. Many procedures have been used to imitate environmental change (13–19). Though some studies found that behavioral and neuronal visual performance improved for stimuli prevailing in the new (“adapting”) environment (20–23), other studies found that performance did not change or it declined where it was expected to improve (16, 20, 23), or the changes occurred for stimuli very different from the adapting ones (20, 23).

We propose that the previous results appear to be inconsistent, because changes of performance have been expected to mirror changes in stimulus statistics. This “stimulus account” of adaptation disregards the notion that visual systems must be prepared for performing multiple tasks, using a broad range of stimuli. As an alternative, we examine a “system account” of adaptation in which adaptive changes are not confined to the stimuli whose statistics have changed. Rather, the adaptive changes are expected to occur for the entire ensemble of potential stimuli. We consider a theory of how the broad allocation of neural resources can be performed optimally, provided that the expected precision of estimating stimulus location and content, spatial and temporal, varies across stimuli (24).

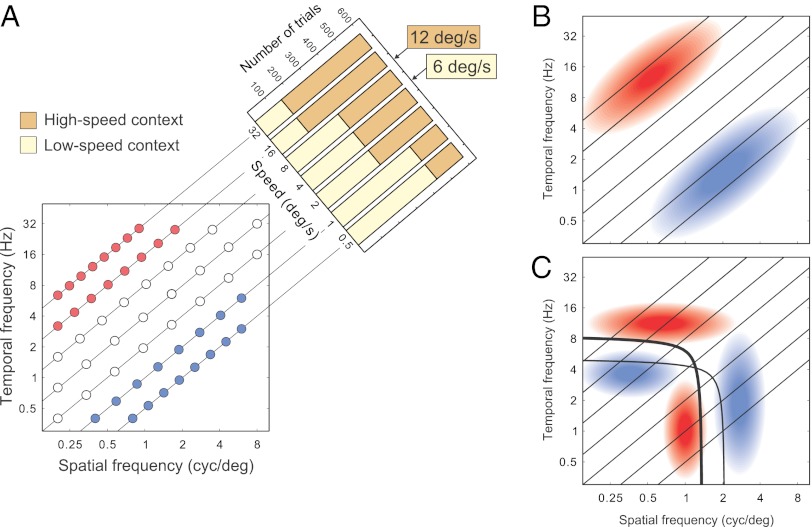
Predictions by the two accounts of adaptation are illustrated schematically in Fig. 2, using the representation of visual performance introduced in Fig. 1. Suppose stimulation has changed as indicated in Fig. 2A and the mean speed of stimuli has increased. By the stimulus account, contrast sensitivity will increase or decrease for the stimuli that became, respectively, more or less common (Fig. 2B). By the system account, adaptive changes will bear upon the entire contrast sensitivity function, rather than the sensitivity for isolated stimuli, leading to the changes of sensitivity illustrated in Fig. 2C.

Fig. 2.

Predictions of sensitivity change. (A) The disks represent stimulus conditions arranged on seven constant-speed lines in the domain of the spatiotemporal sensitivity function (the stimulus space) in Fig. 1D. The histograms on top right illustrate stimulus contexts. In the high-speed context (HS, the dark histogram), high speeds are sampled more often than low speeds. In the low-speed context (LS, light histogram), low speeds are sampled more often. The mean speeds of the contexts are 12 and 6 deg/s. The red and blue disks mark the stimulus conditions for which stimulus frequency increases and decreases across contexts from LS to HS, respectively. (B) Schematic representation of predictions by the stimulus account. Sensitivity is expected to increase (red) or decrease (blue) where stimulation becomes, respectively, more or less frequent. (C) Schematic representation of predictions by the system account (Outline of the System Account of Visual Adaptation). The thick and thin curves represent the theoretical maximal-sensitivity conditions for HS and LS contexts, respectively. The high-speed curve is shifted along the dimension of speed (i.e., up and to the left) relative to the low-speed curve. Because of the shape of the curves, the pattern of expected gains and losses of sensitivity (rendered in red and blue, respectively, as in B) reverses across speed.

According to a theory of efficient allocation of neural resources in the visual system (24), the sensitivity function reflects an optimization with respect to the full range of potential spatiotemporal stimuli, and in view of the fact that small and large receptive fields are not equally suitable for measuring stimulus location and frequency content. The stimuli for which the sensitivity is predicted to be maximal for each speed form a set, whose graphical representation is a curve similar to curve “max” in Fig. 1D. Under changes in stimulus statistics, the shape of the curve is expected to remain largely the same, but the position of the curve is predicted to change as shown in Fig. 2C.

The thick and thin curves in Fig. 2C represent the predictions of the system account for maximal sensitivity in the high-speed and low-speed environments, respectively. Because of the bent shape of the curve, its displacement is expected to entail a pattern of sensitivity changes radically different from the pattern predicted by the stimulus account in Fig. 2A.

In summary, given the same change of stimulation, the stimulus account predicts homogeneous changes of sensitivity within speeds. The system account predicts both gains and losses of sensitivity within speeds, the gains and losses reversed across speeds. At low speeds, gains are expected at lower spatiotemporal frequency conditions than losses. At high speeds, gains are expected at higher frequency conditions than losses.

From the perspective of the system account, effects of adaptation measured in small sets of stimuli can be misleading. Because individual parameters of contrast sensitivity vary from observer to observer, the regions of gains and losses of sensitivity in the stimulus space will vary too. One may accidentally sample the conditions where sensitivity increases or decreases. The results may appear to support the view that sensitivity improves for the more common stimuli, results may appear to oppose that view, or they may add up to a confusing mixture, perhaps of the kind observed in previous studies of visual adaptation. We therefore compared the disparate predictions of Fig. 2 B and C using broad assays of contrast sensitivity.

We generalized a recently developed efficient psychophysical method (25) so we could rapidly measure adaptive sensitivity changes for a large part of the domain of contrast sensitivity function. Using the manipulation of stimulus statistics described in Fig. 2A, we found that adaptive changes of sensitivity did not mirror changes in stimulus statistics. The changes were, however, similar to those predicted by the system account, supporting the view that nature’s solution to the problem of neural resource allocation is similar to an optimal solution (24).

Results

We performed two experiments. First, we confirmed that our estimates of the spatiotemporal contrast sensitivity function were consistent with previous estimates (experiment 1) as a preparation for measuring transformations of this function (experiment 2).

Static Characteristics.

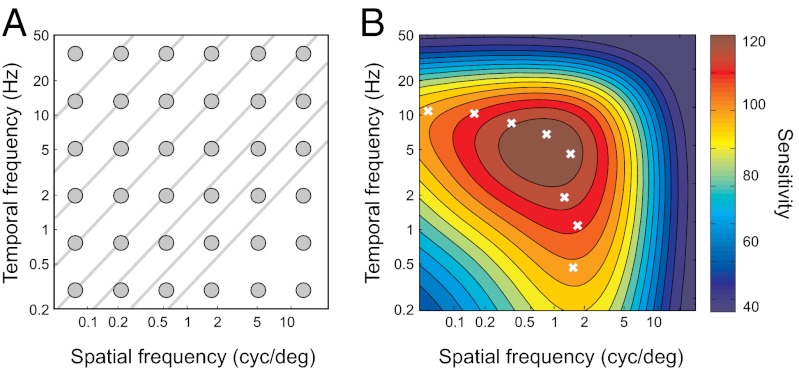
In experiment 1 we used drifting luminance gratings to estimate the amount of luminance contrast that made the gratings just visible at multiple spatial and temporal frequencies of luminance modulation. The stimuli spanned the entire domain of the contrast sensitivity function (Fig. 1D). On every trial, observers reported the direction of motion of drifting luminance gratings at different spatial and temporal frequencies of luminance modulation and luminance contrasts.

Stimulus selection was controlled by a generalized procedure of Lesmes et al. (25). The procedure allowed us to estimate the entire sensitivity function from every observer within one experimental session, repeated several times for each observer. Stimulus conditions were sampled from a broad grid of spatial and temporal frequencies of luminance modulation: the stimulus grid illustrated in Fig. 2A. The stimulus selected from the grid on every trial maximized the increment of information about parameters of the sensitivity function rather than about sensitivities at individual nodes of the grid (Methods).

The results were highly consistent with previous estimates of sensitivity; the distribution of sensitivity across stimuli had the characteristic shape (Fig. 3B), well approximated by the standard model of human spatiotemporal sensitivity: the Kelly function (3) (R² = 84%, P ≪ 0.01; the fitting procedure is described in Methods.) The evidence that our experimental procedure yielded estimates of sensitivity consistent with the standard model allowed us to use the same data-modeling approach in the next experiment.

Fig. 3.

Results of experiment 1. (A) The circles and lines represent the sampled stimulus conditions. We measured “slices” of the spatiotemporal sensitivity function: at one spatial or one temporal frequency (one column or one row of circles), or at one speed (an oblique line). (B) Results of experiment 1 in one observer (O3). The contour plot is an estimate of contrast sensitivity function obtained by fitting a standard model (3) to the estimates of sensitivity at conditions marked by circles in A. The white crosses mark conditions where sensitivity was maximal within the speeds marked by oblique lines in A.

Dynamic Characteristics.

In experiment 2, we studied how the sensitivity function depends on statistics of stimulation. We created two contexts of stimulation by varying how often stimuli were sampled from the same stimulus grid (Fig. 2A). Now the stimulus grid spanned a narrower range of speeds than in experiment 1, ensuring that differences between speeds in the two contexts were sufficiently large. In the low-speed context (Fig. 2A, light-colored bars) stimuli were sampled more often from low-speed than high-speed nodes of the grid, yielding the mean speed of 6 deg/s. In the high-speed context (dark bars), the sampling pattern was reversed, yielding the mean speed of 12 deg/s. The estimates for different contexts were obtained on different days.

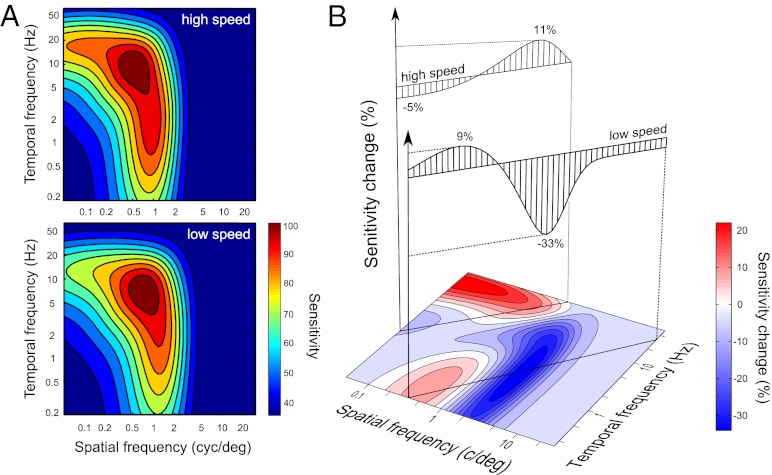
We fitted the estimates of sensitivity from each stimulus context using the Kelly function as in Fig. 3B. As in experiment 1, we found an excellent agreement between the raw and fitted estimates of sensitivity (Fig. S1; lowest R² = 0.85), which allowed us to compute the continuous maps of sensitivity change introduced below. Examples of sensitivity functions obtained this way for the two stimulus contexts are displayed in Fig. 4A. Sensitivity functions for all observers are displayed in Fig. S2. For all observers, the estimates of sensitivity from different stimulus contexts were significantly different from one another (P ≪ 0.01 for both raw and fitted estimates). Notably, both increments and decrements of sensitivity were found within every measured speed, summarized in Fig. S1.

Fig. 4.

Results of experiment 2. (A) Contrast sensitivity functions measured in the two stimulus contexts for one observer (O1). A standard model of contrast sensitivity was fitted to the estimates of sensitivity in high-speed (Upper) and low-speed (Lower) contexts. The warm and cool colors represent high and low sensitivities. Sensitivity functions for all observers are displayed in Fig. S2. (B) The change map on the bottom summarizes how sensitivity changed from the low-speed to high-speed stimulus contexts for all stimulus conditions (Eq. 1). The shades of red and blue represent the gains and losses of sensitivity, and the white regions represent no change. Above the map, samples of sensitivity changes for two speeds demonstrate that the pattern of gains and losses of sensitivity is reversed across speeds, similar to the prediction illustrated in Fig. 2C. Change maps for all observers are displayed in Fig. 5.

In Fig. 4A, sensitivity changes are plotted for two speeds (Fig. 4A Upper) and for the entire domain of the sensitivity function (Fig. 4A Lower). Sensitivity changes were

where h_i and l_i were respective entries in the high-speed and low-speed sensitivity functions. The plots in the upper part of Fig. 4B demonstrate a reversal of sensitivity change across speeds similar to the reversal anticipated by the system account in Fig. 2C. At the low speed, sensitivity decreased for low spatiotemporal frequency conditions and increased for high-frequency conditions. At the high speed, the pattern was reversed.

The seemingly erratic alterations of sensitivity within the narrow samples of stimulus conditions corroborate the notion that changes of sensitivity must be studied over large stimulus sets. As in Fig. 2C, results that appear baffling in narrow stimulus samples may add up to a tractable, predictable picture in large samples. We therefore sought to evaluate patterns of sensitivity change across the full range of tested stimulus conditions.

Analysis of Change Maps.

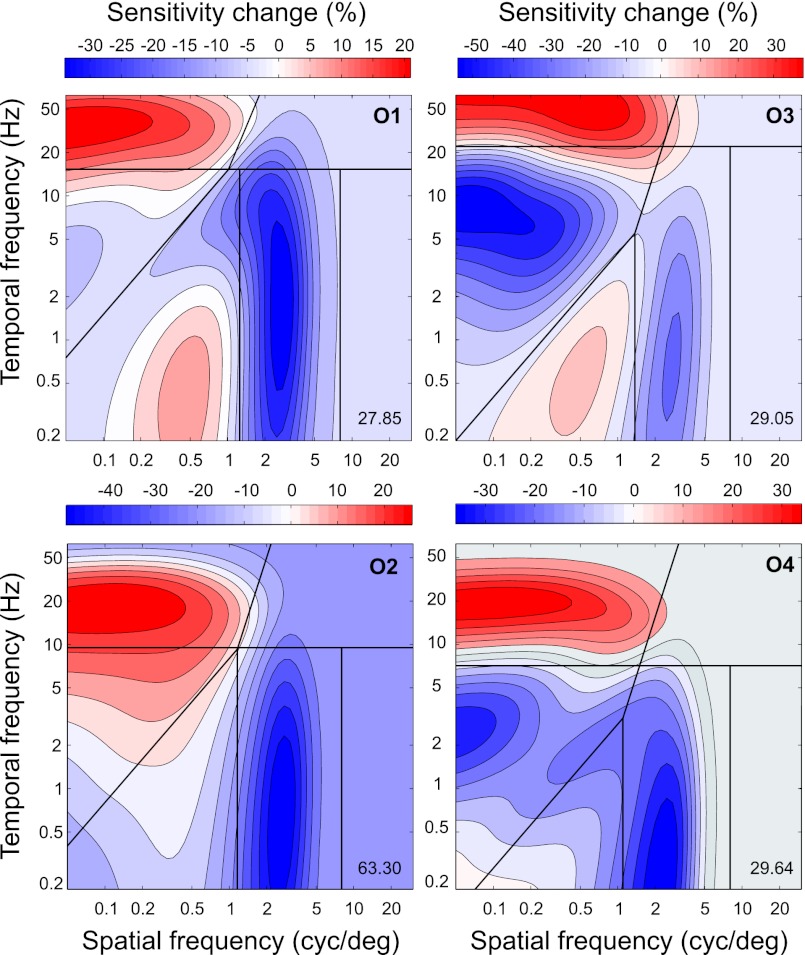
Using permutation analysis of the individual change maps, first we established that the measured changes of sensitivity were unlikely to arise by chance (P < 0.01; Methods). We then evaluated the 2D patterns of sensitivity change captured by the maps in Fig. 5.

Fig. 5.

Change maps. The maps were computed according to Eq. 1. The black lines demarcate regions where gains and losses of sensitivity were expected according to the system account of adaptation introduced in Fig. 2C. Because parameters of individual sensitivity functions varied from across observers, the boundaries between regions of expected gains and losses were derived individually, and template structure remained the same (SI Methods). The numerical display in the bottom right corner of each panel summarizes how well the measured change map was matched by the system template (Eq. S1). The larger the index, the better the match. (The change maps are also displayed in Fig. S2, where changes of sensitivity are scaled by estimation errors, helping to appreciate how effect size varied across stimuli.)

For all observers, the measured patterns of sensitivity change were inconsistent with the stimulus account (Fig. 2B). In every map, sensitivity changes were nonmonotonic within speeds. The nonmonotonicity was predicted by the system account, but the degree to which the measured sensitivity changes were similar to the changes predicted by the system account (Fig. 2C) varied across observers. Two regions of sensitivity gain and two regions of sensitivity loss were found at the expected locations in the change map of observer O3 (map O3); three of the regions were present in maps O1 and O4, and two regions in map O2.

Some diversity of change maps was expected in the system account, however, because regions of sensitivity change were defined relative to the characteristics of sensitivity that varied across observers (Fig. S2). According to the theory underlying the system account (24), the shape of the maximal-sensitivity set ought to be invariant under changes in stimulus statistics, but the position of the set ought to depend on the statistics. We therefore evaluated the change maps using templates of sensitivity change derived relative to the individual maximal-sensitivity sets.

The system template of sensitivity change consisted of four regions where gains and losses of sensitivity were predicted by the system account, as illustrated in Fig. 6A: gains in regions 1 and losses in regions 2. The regions were defined with respect to the individual maximal-sensitivity sets as explained in SI Methods. In Fig. 5, the regions are demarcated by black lines.

Fig. 6.

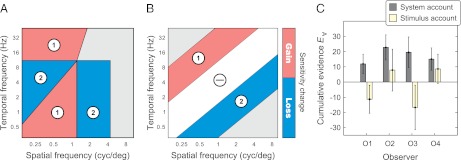
Analysis of change maps. (A and B) Templates of sensitivity change predicted by the system account (A) and stimulus account (B). Sensitivity was expected to change from the low-speed to high-speed stimulus contexts: increase in regions 1 and decrease in regions 2. No change was expected in region ⊖. (C) Results of template matching. The cumulative evidence for both accounts was computed by Eq. 2. The error bars represent 95% confidence intervals. The evidence for the system account is significant for every observer; for the stimulus account it is either negative (observers O1 and O3) or indistinguishable from chance (O2 and O4).

To compare our results with predictions of the two accounts in similar terms, we have also used a stimulus template of sensitivity change. The stimulus template (Fig. 6B) consisted of regions bound to the pattern of stimulus change (Fig. 2A). As shown in Fig. 6B, gains and losses of sensitivity were expected in regions labeled 1 and 2, respectively, and no change of sensitivity was expected in the region labeled ⊖.

The match between the templates of sensitivity change and the measured changes of sensitivity was quantified using cumulative evidence

where E₍₊₎ and E₍₋₎ were the mean changes of sensitivity respectively consistent and inconsistent with the templates (SI Methods). The higher the magnitude of E_∀, the better the match of the data and the template, because the evidence of changes consistent with the template was positive, and the evidence of changes inconsistent with the template was negative.

The stimulus template was the same for all observers because it was defined relative to stimulation, and stimulation did not vary across observers. High evidence E_∀ for the stimulus account would result if the measured changes of sensitivity followed the simple pattern captured by the stimulus template.

The system template had a different manifestation for every observer, because the template was defined relative to observer’s individual sensitivity characteristics. High evidence E_∀ for the system account would result if the measured changes of sensitivity formed a pattern similar to the pattern predicted by the stimulus account, i.e., if the gains and losses of sensitivity were arranged relative to the maximal-sensitivity sets similar to how they were arranged in the system template.

Results of the template-matching analysis are summarized in Fig. 6C. Cumulative evidence E_∀ for the system account is represented by the dark bars. In every case, the cumulative evidence was significantly greater than expected by chance (P < 0.01 for every observer, estimated by resampling; SI Methods). The cumulative evidence E_∀ for the stimulus account is represented by the light bars. Cumulative evidence was against the stimulus account for two observers (O1 and O3): the negative values of E_∀ were significantly more negative than expected by chance (P < 0.05 for both observers). For the two other observers, E_∀ was weakly in favor of the stimulus account, but it was statistically indistinguishable from chance.

Discussion

We found that changes in statistics of speed of visual stimuli caused a large-scale reorganization of spatiotemporal contrast sensitivity. Monotonic changes in stimulus speed induced changes of sensitivity that were highly nonmonotonic across speed, forming distinct regions of gains and losses of sensitivity summarized by the change maps in Fig. 5.

The results were unlikely to arise from changes in attentional or decision strategies by our observers. Had the observers registered the changes in stimulation and dedicated more attention to the more likely stimuli (26), or had they altered their decision biases in accord with stimulation (27, 28), changes of performance would form a pattern portrayed in Fig. 2B. In the high-speed context the sensitivity would increase for high speeds and decrease for low speeds (Fig. 2B), in comparison with the sensitivity in the low-speed context. Instead, the changes of sensitivity formed clusters of gains and losses inconsistent with this stimulus account of adaptation.

The observed changes of sensitivity were consistent with the system account of adaptation (Fig. 2C) in which gains and losses of sensitivity were expected within high speeds and within low speeds. The system account rests on a theory concerned with allocation of limited neural resources in the visual system (24). According to the theory, the spatiotemporal contrast sensitivity function (Fig. 1) reflects an optimal allocation of neurons characterized by receptive fields of different sizes. The allocation optimizes sensory performance with respect to the entire ensemble of potential stimuli. Changes in stimulation are therefore expected to cause changes in characteristics of neurons sensitive to a wide range of stimuli, manifested in a large-scale transformation of the sensitivity function.

For two reasons, the present results are likely to generalize to other stimuli and tasks. First, the differences in visual performance across stimuli revealed by the spatiotemporally contrast sensitivity function were found to generalize to many stimuli and tasks (29, 30). Second, predictions of the theory of optimal resource allocation (24) are not confined to contrast sensitivity as a measure of visual performance.

What mechanisms are likely to control the efficient allocation of receptive fields? Studies of cortical neurons selective for moving stimuli have shown that, just as in the somatosensory homunculus (Fig. 1A), the number of neurons selective for a stimulus correlates with sensitivity to that stimulus. For example, the number of neurons selective for spatial and temporal frequencies of luminance modulation correlates with the contrast sensitivity at those spatial frequencies (5, 31, 32) (Fig. 1B). Therefore, it is likely that effects of adaptation observed in the present study are mediated by changing preferences of many neurons, across a broad range of preferred stimuli, and from different cortical areas where neuronal receptive fields have different sizes (33).

Previous studies of the neural mechanisms of motion adaptation support this expectation. For example, motion-sensitive neurons in cortical visual area middle temporal (MT) of behaving macaque monkeys were found to change their speed selectivity and sensitivity after a short exposure to moving visual patterns (23). These changes occurred in neurons selective for both the adapting conditions and conditions very different from the adapting. Speed sensitivity increased for some stimuli but decreased for others. Similar neuronal changes were found in other visual submodalities (34) and other sensory modalities (35).

Our behavioral results suggest that such neuronal changes should form a lawful pattern across the space of stimulus parameters, as in the change maps displayed in Fig. 5. Previous physiological studies did not allow one to test such predictions because the range of stimuli used was too narrow, or the stimuli were broadband (they had very broad representations in the frequency domain). Future studies can pursue this issue by assaying adaptation-induced changes of sensitivity in neurons with very different stimulus preferences, using stimuli with well-defined frequency content, such as luminance gratings or grating mixtures (36).

Studies of the relationship of single sensory neurons and sensory behavior have often concentrated on how signals from multiple neurons with similar preferences are combined to optimize behavior (37–39). Our results suggest that this question must be approached from a broader perspective, asking how multiple neurons with very different stimulus preferences are allocated to stimuli. Whether an individual neuron ought to increase or decrease its sensitivity to particular stimulus depends on that neuron’s context—i.e., where its selectivity is located in the space of stimulus parameters relative to the preferences of other neurons, and against the entire distribution of system’s sensitivity.

The theme of efficient allocation of neural resources has been long pursued in research of visual attention (40, 41). Numerous studies showed that allocation of attention in the visual system is mediated by rapid changes in preference (gain and selectivity) of individual neurons (42–45). For example, motion-sensitive neurons in cortical visual area MT in macaque monkeys shifted their spatial preferences toward the attended stimulus location, and spatial preferences of many neurons at the attended location sharpened (46). Adaptation, too, was found to induce changes of neuronal preferences in this cortical area (23, 47). It is plausible that effects of adaptation and attention are mediated by the same neural circuits, even though the two processes are presumably governed by different constraints (48, 49). Adaptation and attention can therefore manifest two strategies that nervous systems deploy over different temporal scales to achieve their unmatched versatility with limited resources.

Methods

Apparatus and Stimuli.

The stimuli were displayed on a Sony Trinitron CRT monitor at 120 Hz refresh rate using Psychtoolbox toolkit (50, 51). High gray-scale resolution (14 bits) was attained using a commercially available circuit (52). The stimuli were drifting sinusoidal luminance gratings at different spatial (f_s) and temporal (f_t) frequencies of luminance modulation. Stimulus luminance profile was L = L₀[1 + c sin 2π(f_x + f_tt) + ϕ], where c is luminance contrast, t is time, and ϕ is phase. Mean luminance L₀ was set to the middle of the display’s dynamic range (81 cd/m²). The stimulus was rendered on a 400 × 400 array of pixels, subtending 2.08 × 2.08°. Stimulus luminance was tapered at the edges using a Gaussian window whose SD was 0.5 of the spatial wavelength (1/f_s) of the current stimulus. Stimulus durations were set at one full cycle of the temporal frequency of luminance modulation. Observers received an auditory cue before each trial about the spatial frequency of the upcoming stimulus (small, medium, or large) and a brief auditory signal was presented immediately after the stimulus to reduce temporal uncertainty. The stimuli were viewed binocularly with the natural pupil at the viewing distance of 225 cm in dim light. Direction of movement (up or down) was randomly selected for each trial. The task was direction discrimination. Observers indicated the perceived motion direction (up or down) by pressing a key, and received auditory feedback about the correctness of response.

Psychophysical Procedure.

Stimulus spatial and temporal frequencies f_s and f_t were arranged on a grid in the stimulus parameter space as illustrated in Fig. 2A for experiment 1 and Fig. 3A for experiment 2. Stimulus parameters for every trial were sampled from the stimulus grid using an efficient Bayesian procedure that was a generalization of the quick CSF procedure (25) to stimulus dimensions f_s and f_t. This procedure greatly accelerated measurement of sensitivity using an information gain algorithm (53, 54) that estimated parameters of sensitivity functions directly, rather than estimating sensitivities at individual stimulus conditions. In experiment 1, the procedure sampled stimulus parameters either from the rectangular grid represented by the disks in Fig. 3A, or from the oblique grid represented by the diagonal lines in the same figure. In experiment 2, only the latter procedure was used for the seven speeds indicated in Fig. 2A. In every experimental session, the seven procedures were run independently and concurrently, their trials interleaved, with 50 trials per procedure. Each procedure used the same prior distribution defined as in equation A1 in ref. 25. Sessions were repeated three times for every observer. Each session (350 trials) lasted no longer than 40 min. Estimates of contrast sensitivity were averaged across sessions for every node of stimulus grid and fitted by the Kelly model (3) as described in Modeling Spatiotemporal Sensitivity.

Observers.

Four human observers took part in the experiment (three males and one female): two of the authors and two naive. The observers had normal or corrected-to-normal vision. All participants provided informed consent to participate in the experiment. The experiments followed a protocol approved by the Salk Institute's Institutional Research Board.

Modeling Spatiotemporal Sensitivity.

Analysis of contrast sensitivity was performed both using the raw estimates of sensitivity produced by our psychophysical procedure for nodes of the stimulus grid, and using fitted functions of spatiotemporal contrast sensitivity. The fits were derived using the Kelly function (i.e., equation 5 in ref. 3): G(α, υ) = kυα²exp(−2α/α_max), where υ is speed, α is a constant inferred by Kelly from spatial frequency characteristics of receptive fields, and k and α_max are speed-dependent coefficients. The raw estimates were obtained for 36 stimulus conditions in experiment 1 (Fig. 2A) and for 56 conditions in experiment 2 (Fig. 2A).

Kelly function was fitted to the raw estimates of sensitivity on a grid of 60 spatial and 80 temporal frequency conditions, the same in experiments 1 and 2. The fits accounted for the average of 84% of the variability (R²) of raw sensitivity estimates (SD 8%). Using permutation analysis, we found that the probability to obtain such a fit by chance was smaller than 0.01, for all observers. (The individual coefficients of determination R² were 0.81, 0.91, 0.75, and 0.92 for observers O1–O4, respectively.) Maximal-sensitivity sets 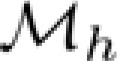and 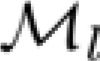were estimated for the high-speed and low-speed stimulus contexts, respectively, by finding the stimulus conditions at which the Kelly models had maximal values on multiple constant-speed lines. Parameters of 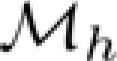and 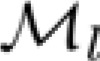were used to derive the templates of sensitivity change described below.

Permutation Analysis of Sensitivity.

We evaluated differences between contrast sensitivity estimates from different stimulus contexts using standard randomization methods. Sensitivity estimates in each stimulus context were randomly and repeatedly permuted, and root mean square differences D_k between the permuted estimates were computed on each iteration K, forming distribution 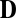of such differences. Fraction p of D that was smaller than zero was an estimate of the probability that the measured difference between sensitivities in the two stimulus contexts occurred by chance.