Estimation of Stratified Mark-Specific Proportional Hazards Models with Missing Marks

Abstract

An objective of randomized placebo-controlled preventive HIV vaccine efficacy trials is to assess the relationship between the vaccine effect to prevent infection and the genetic distance of the exposing HIV to the HIV strain represented in the vaccine construct. Motivated by this objective, recently a mark-specific proportional hazards model with a continuum of competing risks has been studied, where the genetic distance of the transmitting strain is the continuous `mark' defined and observable only in failures. A high percentage of genetic marks of interest may be missing for a variety of reasons, predominantly due to rapid evolution of HIV sequences after transmission before a blood sample is drawn from which HIV sequences are measured. This research investigates the stratified mark-specific proportional hazards model with missing marks where the baseline functions may vary with strata. We develop two consistent estimation approaches, the first based on the inverse probability weighted complete-case (IPW) technique, and the second based on augmenting the IPW estimator by incorporating auxiliary information predictive of the mark. We investigate the asymptotic properties and finite-sample performance of the two estimators, and show that the augmented IPW estimator, which satisfies a double robustness property, is more efficient.

1 Introduction

In many medical studies, evaluation of treatment efficacy is based on comparison of survival times between two treatment groups. This is often done through the ratio of two hazard functions of an endpoint. In a preventive HIV vaccine efficacy trial, the usual primary objective is to assess vaccine efficacy (V E) to prevent HIV infection, where typically V E is defined as one minus the hazard ratio (vaccine/placebo) of the failure event. However, it may be quite difficult to achieve an efficacious vaccine due to genetic variation of HIV (Fauci et al., 2008). The study population is exposed to many genetic types of circulating HIVs but the vaccine only contains antigens based on one or a few strains, and the vaccine protection is likely to be lower against strains that are not in the vaccine or that have greater genetic distance from the strain(s) in the vaccine (Gilbert et al., 1999). Assessment of this problem can be formulated with a competing risks failure time model where the endpoint is HIV infection and the mark variable is the genetic type or distance of the transmitting strain(s) from the strain(s) represented in the vaccine (A `mark' by definition is only meaningful/observable in failures). The goal is to evaluate mark-specific vaccine efficacy defined as one minus the mark-specific hazard ratio (vaccine/placebo) of infection.

In HIV vaccine efficacy trials, the mark variable of interest is some measure of genetic distance between an HIV sequence measured from an infected subject and an HIV sequence represented in the vaccine. For example, if the two HIV sequences are aligned, then the genetic distance may be defined as the weighted percent mismatch of amino acids (e.g., Wu et al., 2001), with weights selected to make the distance scientifically/immunologically meaningful. Definitions of genetic distance between unaligned sequences are also possible, for example based on the difference in total counts of amino acids that possess certain physico-chemical properties. For many definitions of genetic distances of interest, the value of the distance may be unique for almost all infected subjects, making it natural to consider it as a continuous mark variable. Gilbert et al. (2004, 2008) developed procedures for estimation and testing of continuous mark-specific hazards rates and relative risks, and Sun et al. (2009) studied the continuous mark-specific proportional hazards model, which allows evaluating mark-specific vaccine efficacy with adjustment for covariate effects.

However, the previous work for a continuous mark did not account for missingness of the mark variable in failures, so that its valid implementation relies on a dubious missing completely at random assumption (MCAR). While these methods will perform satisfactorily for mark variables measured in almost all failures, for which violations of MCAR are inconsequential, they may be invalid and misleading under moderate-to-high rates of missingness. Moreover, arguably the marks of greatest scientific interest in HIV vaccine trials are subject to high rates of missingness. In particular, ideally the mark would be defined based on the HIV strain that is actually transmitted. However, because vaccine trials only periodically test for HIV infection, the earliest observable HIV genotype is measured using a subjects' earliest available blood sample, which is drawn days, weeks, or several months after the actual transmission event. Therefore the ideal mark definition is unachievable, and we must consider knowledge of HIV evolution and the HIV testing algorithm to develop a workable definition.

HIV vaccine trials test volunteers for anti-HIV antibodies at periodic intervals (e.g., every 3 or 6 months); these antibody-based tests have near-perfect sensitivity to detect infections that occurred at least 4 weeks ago but otherwise may miss the infection. For all subjects with an HIV antibody positive (Ab+) test, a “look-back” procedure is applied wherein earlier available blood samples are tested for HIV infection using a more sensitive antigen-based HIV-specific PCR assay, which has near-perfect sensitivity if the infection occurred at least one week ago; thus for example if blood samples are drawn 2 weeks and 6 weeks after HIV acquisition, and the Ab and PCR tests are applied to both samples, then with very high probability the 2-week sample will be Ab−, PCR+ and the 6-week sample will be Ab+, PCR+. Therefore, each infected subject is classified into one of two groups, defined by whether the earliest sample is Ab− and PCR+ (an `early' sample) or is Ab+ and PCR+ (a `later' sample). These groups approximately correspond to the first available sample being drawn less than or greater than 4 weeks after HIV acquisition. Extensive analysis of early viruses suggests that these viruses well-approximate the transmitting strain, whereas later viruses tend to have undergone significant evolution, with many genetic mutations (Keele et al., 2008). If the mark is defined based on the earliest sampled virus from each infected subject, then the fact that it is often significantly mutated relative to the transmitted virus may make the analysis misleading about the relationship between vaccine efficacy and the exposing virus. One remedy to this problem defines the mark as the early virus in the Ab− and PCR+ phase, which will likely be missing from many infected subjects, with missingness rate depending on the frequency of HIV testing. For the recent Step HIV vaccine trial with genetic data on 87 diagnosed HIV infections, with 6-monthly HIV antibody testing, 41 were Ab−/PCR+ viruses, for a missingness rate of 53% (unpublished data). The sequel trial that is ongoing (named HVTN 505), with 3-monthly HIV antibody testing, is expected to give a missingness rate of less than 50%. The `early' mark of interest may be missing for other reasons besides HIV evolution, for example because of a missing blood sample or a technical problem in measuring the HIV sequence; the developed methods accommodate this issue by allowing separate models of the different missingness types.

To analyze data with the mark defined as the genetic distance from the early virus, a `complete-case' application of the previously developed methods, which excludes infected subjects without a measured mark, may be highly biased and inefficient. Accordingly, this article develops valid and more efficient estimation methods for data-sets with missing at random continuous marks. The new methods restrict attention to a univariate mark variable, albeit if the vaccine contains multiple HIV sequences and/or if multiple sequences are transmitted to a study participant (which happens in a minority of cases, Keele et al., 2008), then it would be of interest to study a multivariate mark variable defined as the set of genetic distances to the vaccine sequences. The current methods can accommodate multiple genetic distances by defining the univariate mark as the minimum of the multiple distances.

Early work in nonparametric estimation for failure time data with missingness of a discrete mark (failure type) include Dinse (1986), Racine-Poon & Hoel (1984) and Lagakos & Louis (1988). Goetghebeur & Ryan (1990) and Dewanji (1992) derived modified logrank tests to compare survival experience between two groups. Goetghebeur & Ryan (1995) and Lu & Tsiatis (2001) studied proportional cause-specific hazards models for one particular failure cause. Gao & Tsiatis (2005) studied linear transformation models of cause-specific hazard functions and Lu & Liang (2008) studied semiparametric additive models of cause-specific hazard functions.

We develop two estimation approaches for the stratified mark-specific proportional hazards model. The first uses inverse probability weighting (IPW) of the complete-case estimator, which leverages auxiliary predictors of whether the mark is observed. The second approach, adapting the theory of Robins et al. (1994), augments the IPW complete-case estimator with auxiliary predictors of the missing marks.

The article is organized as follows. Notation, assumptions, and the stratified mark-specific proportional hazards model are introduced in Section 2. The estimation procedures are proposed in Section 3. The asymptotic properties of the proposed estimators are derived in Section 4. Procedures for constructing confidence intervals for mark-specific vaccine efficacies are also given in Section 4. The finite-sample performance and robustness analysis of the estimators are studied in simulations in Section 5. Proofs of the main results are placed in the web Appendices.

2 Stratified mark-specific proportional hazards models and missing marks

Let T be the failure time, V a continuous mark variable, and Z(t) a possibly time-dependent p-dimensional covariate. Under the competing risks model, the mark V is only defined and observable when T is observed, whereas if T is right-censored, the mark is undefined and meaningless. Suppose that the conditional mark-specific hazard function at time t given the covariate history Z(s), for s ≤ t, defined below only depends on the current value Z(t). The conditional mark-specific hazard function given Z(t) = z is defined as

$$\lambda (t,v\mid z)=\underset{h_1,h_2\to 0}{\lim }P\{T\in [t,t+h_1),V\in [v,v+h_2)\mid T\ge t,Z(t)=z\}∕h_1{h}_2$$ (1)

with t ranging over a fixed interval [0, τ]. Assume that V is continuous and has a known bounded support; rescaling V if necessary, this support is taken to be [0, 1]. The function given in (1) is the natural analog of its discrete counterpart, with similar interpretation.

Gilbert et al. (2008) defined mark-specific vaccine efficacy as VE(t, v) = 1−λ(t, v|z = 1)/λ(t, v|z = 0), with z the indicator of assignment to the vaccine group; they developed several nonparametric and semiparametric tests concerning VE(t, v) as well as a nonparametric estimation method. Sun et al. (2009) studied the mark-specific proportional hazards (PH) model, λ(t, v|z(t)) = λ₀(t, v)exp {β(v)^T z(t)}, where λ₀(·, v) is the unspecified baseline hazard function and β(v) is the p-dimensional unknown regression coefficient function of v. For the HIV vaccine trial application, the covariate is partitioned as z(t) = (z₁, z₂(t))^T, where z₁ is the treatment (vaccine) group indicator and z₂(t) is a vector of possibly time-dependent covariates. Then the covariate-adjusted mark-specific vaccine efficacy defined above takes the simpler form VE(v) = 1 − exp(β₁(v)), without any dependence on t. Assuming the vaccine and placebo groups have the same distribution of the number of exposures to viruses with genetic distance marks in a neighborhood of v (by randomization and double-blinding), VE(v) approximates the multiplicative effect of the vaccine to reduce the instantaneous rate of infection with this virus type (Gilbert et al., 2008; Sun et al., 2009). The statistical procedures developed by Sun et al. (2009) are based on observations of the random variables (X, Z(·), V) for δ = 1 and (X, Z(·)) for δ = 0, where X = min{T, C}, δ = I(T ≤ C), and C is a censoring random variable. Whereas the earlier work assumed V was observed whenever T is observed, here we allow V to be missing, and incorporate in the estimation procedures auxiliary covariates and/or auxiliary mark variables that inform about the probability V is observed and about the distribution of V. For our motivating example discussed above, genetic data for the `later' virus measured in almost all infected subjects is a natural auxiliary mark to help predict the genetic distance V for an `early' virus that is frequently missing.

In practice, different key subgroups (e.g., men and women; subjects living in different geographic regions) typically have different baseline mark-specific hazards of HIV infection. The stratified mark-specific PH model postulates that the conditional mark-specific hazard function given covariate z(t) for an individual in the kth stratum equals

$${\lambda }_k(t,v\mid z(t\left)\right)={\lambda }_{0k}(t,v)\text{exp}\left\{\beta {\left(v\right)}^{T}z\right(t\left)\right\},k=1,\dots ,K,$$ (2)

where β(v) is the p-dimensional unknown regression coefficient function of v, λ_0k(·, v) is the unspecified baseline hazard function for the kth stratum and K is the number of strata. Model (2) allows different baseline functions for different strata. Similar generalizations of the Cox model was studied by Dabrowska (1997).

Next we introduce some notation and assumptions that are used throughout the article. Let n_k be the number of subjects in the kth stratum; the total sample size is $n={\sum }_{k=1}^K{n}_k$. As above, the right-censored mark-specific failure time is represented by (X, δ, V) and Z(·) is the covariate process. Let R be the indicator of whether all possible data are observed for a subject; R = 1 if either δ = 0 (right-censored) or if δ = 1 and V is observed; and R = 0 otherwise. Auxiliary variables A may be helpful for predicting missing marks. Since the mark can only be missing for failures, supplemental information is potentially useful only for failures, for predicting missingness and for informing about the distribution of missing marks. For example, the `later' HIV virus V* can be considered a subset of A. In general, A could include multiple viral sequences per infected subject at multiple time-points along with the time points at which the viruses are sequenced, giving a picture of the intra-subject evolution of a subject's HIV infection. The relationship between A and V can be modelled to help predict V (see Section 5 for a simulation example).

We assume that the censoring time C is conditionally independent of (T, V) given Z(·) for an individual in the kth stratum. We also assume the mark V is missing at random (Rubin, 1976); that is, given δ = 1 and W = (T, Z(T), A) of an individual in the kth stratum, the probability that the mark V is missing depends only on the observed W, not on the value of V; this assumption is expressed as

$$r_k\left(W\right)\equiv P(R=1\mid \delta =1,W)=P(R=1\mid V,\delta =1,W).$$ (3)

Let π_k(Q) = P (R = 1|Q) where Q = (δ, W). Then π_k(Q) = δr_k(W) + (1 − δ). The missing at random assumption (3) also implies that V is independent of R given Q:

$${\rho }_k(v,W)\equiv P(V\le v\mid \delta =1,W)=P(V\le v\mid R=1,\delta =1,W).$$ (4)

For an observed value w of W of an individual in the kth stratum, we write r_k(w) = P (R = 1|δ = 1, W = w) and ρ_k(v, w) = P (V ≤ v|δ = 1, W = w). The stratum-specific definitions of r_k(w) and ρ_k(v, w) leave the options for the models of the probability of complete-case and mark distribution to be different for different strata.

Let for each k, {X_ki, Z_ki(·), δ_ki, R_ki, V_ki, A_ki; i = 1, …, n_k} be iid replicates of {X, Z(·), δ, R, V, A} from that stratum. The observed data is denoted by {O_ki; i = 1 …, n_k, k = 1, …, K}, where O_ki = {X_ki, Z_ki(·), R_ki, R_kiV_ki, A_ki} for δ_ki = 1 and O_ki = {X_ki, Z_ki(·), R_ki = 1} for δ_ki = 0. We assume that {O_ki; i = 1 …, n_k, k = 1, …, K} are independent for all subjects. Similarly, we denote W_ki = (T_ki, Z_ki(T_ki), A_ki) and Q_ki = (δ_ki, W_ki).

We consider a parametric model r_k(W_ki, ψ_k) for r_k(W_ki), where ψ_k is an unknown vector of parameters to be further discussed in the next section. Let π_k(Q_ki, ψ_k) = δ_kir_k(W_ki, ψ_k) + (1 − δ_ki). Additional notation is introduced in the following. For $\beta \in {\mathbb{R}}^p$, t ≥ 0, let Y_ki(t) = I(X_ki ≥ t),

$$S_k^{\left(j\right)}(t,\beta )=n_k^{-1}\sum _{i=1}^{n_k}{Y}_{ki}\left(t\right)\exp \left\{{\beta }^T{Z}_{ki}\right(t\left)\right\}{Z}_{ki}{\left(t\right)}^{\otimes j},$$

$${\tilde{S}}_k^{\left(j\right)}(t,\beta ,{\psi }_k)=n_k^{-1}\sum _{i=1}^{n_k}{R}_{ki}{\left({\pi }_k\right(Q_{ki},{\psi }_k\left)\right)}^{-1}{Y}_{ki}\left(t\right)\exp \left\{{\beta }^T{Z}_{ki}\right(t\left)\right\}{Z}_{ki}{\left(t\right)}^{\otimes j},$$

where for any $z\in {\mathbb{R}}^p$, z^⊗0 = 1, z^⊗1 = z and z^⊗2 = zz^T. Define $s_k^{\left(j\right)}(t,\beta )=E{S}_k^{\left(j\right)}(t,\beta )$ and ${\tilde{s}}_k^{\left(j\right)}(t,\beta ,{\psi }_k)=E{\tilde{S}}_k^{\left(j\right)}(t,\beta ,{\psi }_k)$. Under the missing at random assumption (3), $s_k^{\left(j\right)}(t,\beta )={\tilde{s}}_k^{\left(j\right)}(t,\beta ,{\psi }_k)$ if the model r_k(W_ki, ψ_k) is correctly specified. Let

$$J_k(t,\beta )=\frac{S_k^{\left(2\right)}(t,\beta )}{S_k^{\left(0\right)}(t,\beta )}-{\left(\frac{S_k^{\left(1\right)}(t,\beta )}{S_k^{\left(0\right)}(t,\beta )}\right)}^{\otimes 2},$$

$${\tilde{J}}_k(t,\beta ,{\psi }_k)=\frac{{\tilde{S}}_k^{\left(2\right)}(t,\beta ,{\psi }_k)}{{\tilde{S}}_k^{\left(0\right)}(t,\beta ,{\psi }_k)}-{\left(\frac{{\tilde{S}}_k^{\left(1\right)}(t,\beta ,{\psi }_k)}{{\tilde{S}}_k^{\left(0\right)}(t,\beta ,{\psi }_k)}\right)}^{\otimes 2},$$

$${\stackrel{‒}{Z}}_k(t,\beta )=\frac{S_k^{\left(1\right)}(t,\beta )}{S_k^{\left(0\right)}(t,\beta )},{\tilde{Z}}_k(t,\beta ,{\psi }_k)=\frac{{\tilde{S}}_k^{\left(1\right)}(t,\beta ,{\psi }_k)}{{\tilde{S}}_k^{\left(0\right)}(t,\beta ,{\psi }_k)}.$$

Let ${\stackrel{‒}{z}}_k(t,\beta )=s_k^{\left(1\right)}(t,\beta )∕s_k^{\left(0\right)}(t,\beta )$ and $I_k(t,\beta )=s_k^{\left(2\right)}(t,\beta )∕s_k^{\left(0\right)}(t,\beta )-{\left({\stackrel{‒}{z}}_k\right(t,\beta \left)\right)}^{\otimes 2}$.

3 Estimation procedures

When there are no missing marks, β(v) in model (2) can be estimated by maximizing the following local log-partial likelihood function for β = β(v) at a fixed v:

$$l(v,\beta )=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left[{\beta }^T{Z}_{ki}\left(t\right)-\log \left(\sum _{j=1}^{n_k}{Y}_{kj}\left(t\right)e^{{\beta }^T{Z}_{kj}\left(t\right)}\right)\right]N_{ki}(dt,du),$$ (5)

where K_h(x) = K(x/h)/h, K(·) is a kernel function with support [−1, 1], τ is the end of the follow-up period and h = h_n is a bandwidth. Here N_ki(t, v) = I(X_ki ≤ t, δ_ki = 1, V_ki ≤ v) is the marked counting process with a jump at the uncensored failure time X_ki and the associated mark V_ki. The log partial likelihood function (5) resembles that of Kalbfleisch & Prentice (1980) in the case of discrete marks, except that it borrows strength from observations having marks in the neighborhood of v. The kernel function is designed to give greater weight to observations with marks near v than those further away. As discussed by Silverman (1986, p.43), the choice of kernel function has little to do with the performance of the estimators. For example, the asymptotic relative efficiency of the Tukey kernel compared to the optimal Epanechnikov kernel is 0.9897 and the Gaussian kernel has a relative efficiency of 0.9512. It is common to assume compact support for technical simplicity. The bandwidth, on the other hand, is an important parameter in the estimation of β(v). The cross-validation method is often used for bandwidth selection. This is further discussed in Section 5.

Taking the derivative of l(v, β) with respect to β gives the score function

$$U(v,\beta )=l_{\beta }^{\prime }(v,\beta )=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{ki}\left(t\right)-\frac{S_k^{\left(1\right)}(t,\beta )}{S_k^{\left(0\right)}(t,\beta )}\right)N_{ki}(dt,du).$$ (6)

The maximum partial likelihood estimator is a solution to U(v, β) = 0. This estimator was studied by Sun et al. (2009) when there is no stratification, i.e. K = 1.

In the presence of missing marks, (5) can only be applied directly to estimate β(v) through a complete-case analysis (e.g., excluding failures with a missing mark), which may be biased and inefficient. Our first approach to remedying this problem, following the idea of Horvitz & Thompson (1952), uses inverse probability weighting of complete-cases. However, this approach has been shown to be inefficient in several situations (Gao & Tsiatis, 2005; Lu & Liang, 2008); also see Scharfstein et al. (1999). Our second approach, adapting the idea of Robins et al. (1994), augments the inverse probability weighted complete-case estimation equation with a consistent estimator of the conditional distribution of the mark that uses the estimator from the first approach and auxiliary data from subjects with missing marks.

Our model formulation is different from those in the existing literature on the discrete competing risks model, where only the cause-specific hazard function for one particular cause is modeled while the cause-specific hazard functions for the other causes are left unspecified. To evaluate mark-specific vaccine effects, model (2) specifies a proportional mark-specific hazards model for each mark v, 0 ≤ v ≤ 1. This model induces restrictions on the conditional mark distribution ρ_k(v, W_k) given in (4), so that arbitrary modeling may run into conflicts with the mark-specific PH model (2) and result in inconsistent estimation. This modeling restriction requires a different approach, as described below.

3.1 Inverse probability weighted complete-case estimator

Following Horvitz & Thompson (1952), inverse probability weighting of complete-cases has been commonly used in missing data problems. Let r_k(W_ki, ψ_k) be the parametric model for the probability of complete-case r_k(W_ki) defined in (3), where ψ_k is a q-dimensional parameter. For example, one can assume the logistic model with logit$\left(r_k\right(W_{\mathit{ki}},{\psi }_k\left)\right)={\psi }_k^T{W}_{\mathit{ki}}$ for those with δ_ki = 1. By (3), the maximum likelihood estimator $\widehat{\psi }=({\widehat{\psi }}_1,\dots ,{\widehat{\psi }}_K)$ of ψ = (ψ₁,…,ψ_K) is obtained by maximizing the observed data likelihood,

$$\prod _{k,i}{\left\{r_k\right(W_{ki},{\psi }_k\left)\right\}}^{R_{ki}{\delta }_{ki}}{\{1-r_k(W_{ki},{\psi }_k\left)\right\}}^{(1-R_{ki}){\delta }_{ki}}.$$ (7)

We propose the following inverse probability weighted (IPW) estimating equation for β:

$$U_{ipw}(v,\beta ,\widehat{\psi })=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{ki}\right(t)-{\tilde{Z}}_k(t,\beta ,{\widehat{\psi }}_k\left)\right)\frac{R_{ki}}{{\pi }_k(Q_{ki},{\widehat{\psi }}_k)}{N}_{ki}(dt,du).$$ (8)

The IPW estimator of β(v) solves the above equation and is denoted by ${\widehat{\beta }}^{\mathit{ipw}}\left(v\right)$.

The baseline function λ_0k(t, v) can be estimated by ${\widehat{\lambda }}_{0k}^{\mathit{ipw}}(t,v)$, obtained by smoothing the increments of the following estimator of the doubly cumulative baseline function ${\Lambda }_{0k}(t,v)={\int }_0^t{\int }_0^v{\lambda }_{0k}(s,u)$ dsdu:

$${\widehat{\Lambda }}_{0k}^{ipw}(t,v)=\sum _{i=1}^{n_k}{\int }_0^t{\int }_0^v\frac{R_{ki}}{{\pi }_k(Q_{ki},{\widehat{\psi }}_k)}\frac{N_{ki}(ds,du)}{n_k{\tilde{S}}_k^{\left(0\right)}(s,{\widehat{\beta }}^{ipw}(u),{\widehat{\psi }}_k)}.$$ (9)

For example, one can use kernel smoothing,

$${\widehat{\lambda }}_{0k}^{ipw}(t,v)={\int }_0^{\tau }{\int }_0^1{K}_{b_1}^{\left(1\right)}(t-s)K_{b_2}^{\left(2\right)}(v-u){\widehat{\Lambda }}_{0k}^{ipw}(ds,du),$$ (10)

where $K_{b_1}^{\left(1\right)}\left(x\right)=K^{\left(1\right)}(x∕b_1)∕b_1$ and $K_{b_2}^{\left(2\right)}\left(x\right)=K^{\left(2\right)}(x∕b_2)∕b_2$, with K⁽¹⁾(·) and K⁽²⁾(·) the kernel functions and b₁ and b₂ the bandwidths.

3.2 Augmented inverse probability weighted complete-case estimator

The IPW estimator ${\widehat{\beta }}^{\mathit{ipw}}\left(v\right)$ uses only complete cases and is inefficient. Following Robins et al. (1994), Gao & Tsiatis (2005) proposed augmented inverse probability weighted complete-case estimators for the linear transformation model of cause-specific functions subject to missing failure types. Lu & Liang (2008) studied a semiparametric additive model for cause-specific functions with missing failure types. In both papers, an additional model is supplied for the conditional probability of the failure type of interest P(J = 2|W) to utilize the data from the failures with missing types as well as from the complete cases when there is only one stratum, where J is the type of failure in a typical competing risks set-up. Whereas Gao & Tsiatis (2005) and Lu & Liang (2008) had the flexibility to model P(J = 2|W), our conditional distribution of the mark, ρ_k(v, w), being specified for each v ∈ [0, 1], has a built-in structure that must be considered. Nevertheless, we will show that the idea of Robins et al. (1994) can still be used for model (2) to improve efficiency. Specifically, more efficient estimation of (2) can be achieved by incorporating knowledge of ρ_k(v, w) into the estimation procedure. Let g_k(a|t, v, z) = P(A_ki = a|T_ki = t, V_ki = v, Z_ki = z, δ_ki = 1). Then

$${\rho }_k(v,w)={\int }_0^v{\lambda }_k(t,u\mid z)g_k(a\mid t,u,z)du∕{\int }_0^1{\lambda }_k(t,u\mid z)g_k(a\mid t,u,z)du,$$ (11)

where w = (t, z, a). If A_ki is independent of V_ki given (T_ki, Z_ki, δ_ki), then ${\rho }_k(v,w)={\int }_0^v{\lambda }_k(t,u\mid z)\mathit{du}∕{\int }_0^1{\lambda }_k(t,u\mid z)\mathit{du}$. In this case, ρ_k(v, w) can be estimated by ${\widehat{\rho }}_k^{\mathit{ipw}}(v,w)={\int }_0^v{\widehat{\lambda }}_k^{\mathit{ipw}}(t,u\mid z)\mathit{du}∕{\int }_0^1{\widehat{\lambda }}_k^{\mathit{ipw}}(t,u\mid z)\mathit{du}$, where ${\widehat{\lambda }}_k^{\mathit{ipw}}(t,u\mid z)={\widehat{\lambda }}_{0k}^{\mathit{ipw}}(t,u)\exp \left\{{\left({\widehat{\beta }}^{\mathit{ipw}}\right(u\left)\right)}^{T}z\right\}$. Routine kernel methods can be used to show that ${\widehat{\rho }}_k^{\mathit{ipw}}(v,W_{\mathit{ki}})\underrightarrow{P}{\rho }_k^{\mathit{ipw}}(v,W_{\mathit{ki}})$ at the rate of (nh)^−1/2 when b₁ ≍ b₂ ≍ h, where ≍ means convergence to zero at the same rate.

When the auxiliary marks A_ki are correlated with V_ki, the conditional distribution ρ_k(v, w) involves the function g_k(a|t, u, z), which can be modeled to capture the correlation. The stronger the correlation, the greater potential to improve efficiency. As considered in Section 1, if V_ki is the genetic distance of an early virus, then an auxiliary mark A_ki that is expected to predict V_ki is the genetic distances of all available later viruses and their sampling times.

Consider a parametric model g_k(a|t, u, z, θ_k) for g_k(a|t, u, z). Let ${\widehat{g}}_k(a\mid t,u,z)$ be an estimator of g_k(a|t, u, z). Then ρ_k(v, w) can be estimated by

$${\widehat{\rho }}_k^{ipw}(v,w)={\int }_0^v{\widehat{\lambda }}_k^{ipw}(t,u\mid z){\widehat{g}}_k(a\mid t,u,z)du∕{\int }_0^1{\widehat{\lambda }}_k^{ipw}(t,u\mid z){\widehat{g}}_k(a\mid t,u,z)du.$$ (12)

Taking b₁ ≍ b₂ ≍ h, it is easy to show that ${\widehat{\rho }}_k^{\mathit{ipw}}(v,W_{\mathit{ki}})\underrightarrow{P}{\rho }_k(v,W_{\mathit{ki}})$ at the rate of (nh)^−1/2.

Let $N_{\mathit{ki}}^x\left(t\right)=I(X_{\mathit{ki}}\le t,{\delta }_{\mathit{ki}}=1)$, $N_{\mathit{ki}}^v\left(v\right)=I(V_{\mathit{ki}}\le v)$ and ${\widehat{\rho }}^{\mathit{ipw}}(\cdot )=\left({\widehat{\rho }}_1^{\mathit{ipw}}\right(\cdot ),\dots ,{\widehat{\rho }}_K^{\mathit{ipw}}(\cdot \left)\right)$. Following Robins et al. (1994), we obtain the following augmented (AUG) inverse probability weighted estimating equation for β:

$$U_{aug}(v,\beta ,\widehat{\psi },{\widehat{\rho }}^{ipw}(\cdot \left)\right)=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{ki}\right(t)-{\stackrel{‒}{Z}}_k(t,\beta \left)\right)\left\{\frac{R_{ki}}{{\pi }_k(Q_{ki},{\widehat{\psi }}_k)}{N}_{ki}(dt,du)+\left(1-\frac{R_{ki}}{{\pi }_k(Q_{ki},{\widehat{\psi }}_k)}\right)N_{ki}^x\left(dt\right)d\left({\widehat{\rho }}_k^{ipw}\right(u,W_{ki}\left)\right)\right\}.$$ (13)

The AUG estimator of β(v) solves the above equation and is denoted by ${\widehat{\beta }}^{\mathit{aug}}\left(v\right)$.

The doubly cumulative baseline function ${\Lambda }_{0k}(t,v)={\int }_0^t{\int }_0^v{\lambda }_{0k}(s,u)\mathit{dsdu}$ is estimated by

$${\widehat{\Lambda }}_{0k}^{aug}(t,v)=\sum _{i=1}^{n_k}{\int }_0^t{\int }_0^v\frac{R_{ki}}{{\pi }_k(Q_{ki},{\widehat{\psi }}_k)}\frac{N_{ki}(ds,du)}{n_k{S}_k^{\left(0\right)}(s,{\widehat{\beta }}^{aug}(u\left)\right)}+\left(1-\frac{R_{ki}}{{\pi }_k(Q_{ki},{\widehat{\psi }}_k)}\right)\frac{N_{ki}^x\left(ds\right)d\left({\widehat{\rho }}_k^{ipw}\right(u,W_{ki}\left)\right)}{n_k{S}_k^{\left(0\right)}(s,{\widehat{\beta }}^{aug}(u\left)\right)}.$$ (14)

The baseline hazard function λ_0k(t, v) can be estimated by the kernel estimator

$${\widehat{\lambda }}_{0k}^{\mathit{aug}}(t,v)={\int }_0^{\tau }{\int }_0^1{K}_{b1}^{\left(1\right)}(t-s)K_{k2}^{\left(2\right)}(v-u){\widehat{\Lambda }}_{0k}^{\mathit{aug}}(\mathit{ds},\mathit{du}).$$ (15)

4 Asymptotic properties

Let ${\mathcal{F}}_t=\sigma \left\{I\right(X_{\mathit{ki}}\le s,{\delta }_{\mathit{ki}}=1),I(X_{\mathit{ki}}\le s,{\delta }_{\mathit{ki}}=0),V_{\mathit{ki}}I(X_{\mathit{ki}}\le s,{\delta }_{\mathit{ki}}=1),Z_{\mathit{ki}}(s);0\le s\le t,i=1,\dots ,n_k,k=1,\dots ,K\}$, be the (right-continuous) filtration generated by the full data processes {N_ki(s, v), Y_ki(s), Z_ki(s); 0 ≤ s ≤ t, 0 ≤ v ≤ 1, i = 1, …, n_k, k = 1, …, K}. Assume $E\left(N_{\mathit{ki}}\right(\mathit{dt},\mathit{dv})\mid {\mathcal{F}}_{t-})=E\left(N_{\mathit{ki}}\right(\mathit{dt},\mathit{dv})\mid Y_{\mathit{ki}}(t),Z_{\mathit{ki}}(t\left)\right)$, that is, the mark-specific instantaneous failure rate at time t given the observed information up to time t only depends on the failure status and the current covariate value. By the definition (1), $E\left(N_{\mathit{ki}}\right(\mathit{dt},\mathit{dv})\mid {\mathcal{F}}_{t-})=Y_{\mathit{ki}}\left(t\right){\lambda }_k(t,v\mid Z_{\mathit{ki}}(t\left)\right)\mathit{dtdv}$. Hence, the mark-specific intensity of N_ki(t, v) with respect to ${\mathcal{F}}_t$ equals Y_ki(t)λ_ki(t, v|Z_ki(t)). Let $M_{\mathit{ki}}(t,u)={\int }_0^t{\int }_0^u\left[N_{\mathit{ki}}\right(\mathit{ds},\mathit{dx})-Y_{\mathit{ki}}(s\left){\lambda }_k\right(s,x\mid Z_{\mathit{ki}}\left(s\right)\left)\mathit{dsdx}\right]$. By Aalen & Johansen (1978), M_ki(·, v₁) and M_ki(·, v₂) − M_ki(·, v₁) are orthogonal square integrable martingales with respect to ${\mathcal{F}}_t$ for any 0 ≤ v₁ ≤ v₂ ≤ 1.

Let ${\mathcal{F}}_t^{\ast }={\mathcal{F}}_t\cup \{R_{\mathit{ki}},{\delta }_{\mathit{ki}}{A}_{\mathit{ki}};i=1,\dots ,n_k,k=1,\dots ,K\}$ be the right continuous filtration obtained by adding R_ki and δ_kiA_ki to ${\mathcal{F}}_t$. Let ${\lambda }_{\mathit{ki}}^{\ast }(t,v)=P(T_{\mathit{ki}}=t,V_{\mathit{ki}}=v\mid X_{\mathit{ki}}\ge t,Z_{\mathit{ki}}(t),R_{\mathit{ki}},{\delta }_{\mathit{ki}}{A}_{\mathit{ki}})$. Then

$$E\left(N_{\mathit{ki}}\right(\mathit{dt},\mathit{dv})\mid {\mathcal{F}}_{t-}^{\ast })=Y_{\mathit{ki}}\left(t\right){\lambda }_{\mathit{ki}}^{\ast }(t,v)\mathit{dtdu},$$ (16)

where $Y_{\mathit{ki}}\left(t\right){\lambda }_{\mathit{ki}}^{\ast }(t,v)$ is the intensity of N_ki(t, v) with respect to ${\mathcal{F}}_t^{\ast }$. Assume that ${\lambda }_{\mathit{ki}}^{\ast }(t,v)$ is continuous in (t, v). Let $M_{\mathit{ki}}^{\ast }(t,v)=N_{\mathit{ki}}(t,v)-{\int }_0^t{\int }_0^v{\lambda }_{\mathit{ki}}^{\ast }(s,u)Y_{\mathit{ki}}\left(s\right)\mathit{dsdu}$. By Aalen & Johansen (1978), for any 0 ≤ v₁ ≤ v₂ ≤ 1, the processes $M_{\mathit{ki}}^{\ast }(t,v_1)$ and $M_{\mathit{ki}}^{\ast }(t,v_2)-M_{\mathit{ki}}^{\ast }(t,v_1)$, 0 ≤ t ≤ τ are orthogonal square integrable martingales.

The following regularity conditions are assumed throughout the rest of the paper. Most of the notation can be found at the end of Section 2.

Condition A

• (A.1)β(v) has componentwise continuous second derivatives on [0, 1]. For each k = 1, …, K, the second partial derivative of λ_0k(t, v) with respect to v exists and is continuous on [0, τ] × [0, 1]. The covariate process Z_ki(t) has paths that are left continuous and of bounded variation, and satisfies the moment condition E[∥Z_ki(t)∥⁴ exp(2M∥Z_ki(t)∥)] < ∞, where M is a constant such that (v, β(v)) ∈ [0, 1] × (−M, M)^p for all v and ∥A∥ = max_k,l |a_kl| for a matrix A = (a_kl).
• (A.2)Each component of $s_k^{\left(j\right)}(t,\theta )$ is continuous on [0, τ]×[−M, M]^p,${\tilde{s}}_k^{\left(j\right)}(t,\theta {\psi }_k)$ is continuous on [0, τ]×[−M, M]^p×[−L, L]^q for some M, L > 0 and j = 0, 1, 2. ${\text{sup}}_{t\in [0,\tau ],\theta \in {[-M,M]}^p}\Vert S_k^{\left(j\right)}(t,\theta )-s_k^{\left(j\right)}(t,\theta )\Vert =O_p\left(n^{-1∕2}\right)$, and ${\text{sup}}_{t\in [0,\tau ],\theta \in {[-M,M]}^p,{\psi }_k\in {[-L,L]}^q}\Vert {\tilde{S}}_k^{\left(j\right)}(t,\theta ,{\psi }_k)-{\tilde{s}}_k^{\left(j\right)}(t,\theta ,{\psi }_k)\Vert =O_p\left(n^{-1∕2}\right)$.
• (A.3)The limit p_k = lim_n→∞ n_k/n exists and 0 < p_k < 1. $s_k^{\left(0\right)}(t,\theta )\rangle 0$ on [0, τ] ×[−M, M]^p and the matrix $\Sigma \left(v\right)={\sum }_{k=1}^K{p}_k{\Sigma }_k\left(v\right)$ is positive definite, where ${\Sigma }_k\left(v\right)={\sum }_{k=1}^K{\int }_0^{\tau }{I}_k(t,\beta (v\left)\right){\lambda }_{0k}(t,v)s_k^{\left(0\right)}(t,\beta (v\left)\right)\mathit{dt}$.
• (A.4)The kernel functions K(·), K⁽¹⁾(·) and K⁽²⁾(·) are symmetric with support [−1, 1] and have bounded variation. The bandwidths satisfy b₁ ≍ b₂ ≍ h and nh² → ∞ and nh⁵ = O(1) as n → ∞.
• (A.5)There is a ε > 0 such that r_k(W_ki) ≥ ε for all k, i with δ_ki = 1.

Discussion of some of these conditions can be found in Sun et al. (2009). To avoid the problems at the boundaries v = 0, 1, we study the asymptotic properties of $\widehat{\beta }\left(v\right)$ for interior values of v ∈ [a, b] ⊂ (0, 1).

4.1 Asymptotic results of inverse probability weighted complete-case estimator

The consistency and asymptotic normality of ${\widehat{\beta }}^{\mathit{ipw}}\left(v\right)$ are established in the next two theorems.

Theorem 1. Under Condition A, if the model for r_k(W_ki) is correctly specified, then ${\widehat{\beta }}^{\mathit{ipw}}\left(v\right)\underrightarrow{P}\beta \left(v\right)$ uniformly in v ∈ [a, b] ⊂ (0, 1) as n → ∞.

Let ν₀ = ʃ K²(x) dx, μ₂ = ʃ x²K(x)dx,

$$\vartheta \left(v\right)=\sum _{k=1}^K{p}_{k}E\left\{{\int }_0^{\tau }\left[Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{z}}_k(t,\beta \left)\right]\frac{{\partial }^2{\lambda }_k(t,v\mid Z_{\mathit{ki}}(t\left)\right)}{\partial v^2}{Y}_{\mathit{ki}}\left(t\right)\mathit{dt}\right\},$$

$${\Sigma }_k^{\ast }\left(v\right)=E\left\{{\int }_0^{\tau }{\left[Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{z}}_k(t,\beta \left)\right]}^{\otimes 2}\frac{R_{\mathit{ki}}}{{\left({\pi }_k\right(t,Z_{\mathit{ki}},{\delta }_{\mathit{ki}}{A}_{\mathit{ki}}\left)\right)}^2}{\lambda }_{\mathit{ki}}^{\ast }(t,v)Y_{\mathit{ki}}\left(t\right)\mathit{dt}\right\}.$$

Theorem 2. Under Condition A, if the model for r_k(W_ki) is correctly specified, then ${\left(\mathit{nh}\right)}^{1∕2}\left[{\widehat{\beta }}^{\mathit{ipw}}\right(v)-\beta (v)+\frac{1}{2}{\mu }_2{h}^2{\Sigma }^{-1}(v\left)\vartheta \right(v\left)\right]\underrightarrow{\mathcal{D}}N(0,{\nu }_0{\Sigma }^{-1}(v\left){\Sigma }^{\ast }\right(v\left){\Sigma }^{-1}\right(v\left)\right)$ for v ∈ [a, b] as n → ∞, where ${\Sigma }^{\ast }\left(v\right)={\sum }_{k=1}^K{p}_k{\Sigma }_k^{\ast }\left(v\right)$ and Σ(v) is given in condition (A.3).

By (16) and by the property of expectation that E(·) = E{E(·|W_ki),

$${\int }_0^v{\Sigma }^{\ast }\left(u\right)\mathit{du}=\sum _{k=1}^K{p}_{k}E\left\{{\int }_0^v{\int }_0^{\tau }{\left[Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{z}}_k(t,\beta \left(u\right)\left)\right]}^{\otimes 2}\frac{1}{{\pi }_k\left(W_{\mathit{ki}}\right)}{N}_{\mathit{ki}}(\mathit{dt},\mathit{du})\right\}.$$

ν₀Σ*(v) can be consistently estimated by

$${\tilde{\Sigma }}_{\mathit{ipw}}^{\ast }\left(v\right)=n^{-1}h\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{\left(K_h\right(u-v\left)\right)}^2{\left[Z_{\mathit{ki}}\right(t)-{\tilde{Z}}_k(t,\widehat{\beta }\left(u\right),{\widehat{\psi }}_k\left)\right]}^{2\otimes }\frac{R_{\mathit{ki}}}{{\left({\pi }_k\right(Q_{\mathit{ki}},{\widehat{\psi }}_k\left)\right)}^2}{N}_{\mathit{ki}}(\mathit{dt},\mathit{du}).$$

The proof of Theorem 2 uses a Taylor expansion of the score function, leading to ${\widehat{\beta }}^{\mathit{ipw}}\left(v\right)-\beta \left(v\right)=-{\left(U_{\mathit{ipw}}^{\prime }\right(v,{\beta }^{\ast }\left(v\right),\widehat{\psi }\left)\right)}^{-1}{U}_{\mathit{ipw}}(v,\beta (v),\widehat{\psi })$, where β*(v) is on the line segment between ${\widehat{\beta }}^{\mathit{ipw}}\left(v\right)$ and β(v), and

$$U_{\mathit{ipw}}^{\prime }(v,\beta ,\widehat{\psi })=-\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\frac{R_{\mathit{ki}}}{{\pi }_k(Q_{\mathit{ki}},{\widehat{\psi }}_k)}{\tilde{J}}_k(t,\beta ,{\widehat{\psi }}_k)N_{\mathit{ki}}(\mathit{dt},\mathit{dt})$$

is the derivative of $U_{\mathit{ipw}}(v,\beta ,\widehat{\psi })$ with respect to β. Here ${\tilde{J}}_k(t,\beta ,{\widehat{\psi }}_k)$ is defined at the end of Section 2. It can be shown that ${\widehat{\Sigma }}_{\mathit{ipw}}\left(v\right)\equiv -n^{-1}{U}_{\mathit{ipw}}^{\prime }(v,\widehat{\beta }(v),\widehat{\psi })\underrightarrow{P}\Sigma \left(v\right)$ as n → ∞. Thus, the asymptotic variance ν₀Σ⁻¹(v)Σ*(v)Σ⁻¹(v) can be estimated by ${\left({\widehat{\Sigma }}_{\mathit{ipw}}\right(v\left)\right)}^{-1}{\tilde{\Sigma }}_{\mathit{ipw}}^{\ast }\left(v\right){\left({\widehat{\Sigma }}_{\mathit{ipw}}\right(v\left)\right)}^{-1}$.

4.2 Asymptotic results of augmented inverse probability weighted complete-case estimator

Let $S_{\mathit{ki}}^{\psi }$ and $I_k^{\psi }$ be the score vector and information matrix for ${\widehat{\psi }}_k$ under (7). Then

$$S_{\mathit{ki}}^{\psi }=\frac{{\delta }_{\mathit{ki}}(R_{\mathit{ki}}-r_k(W_{\mathit{ki}},{\psi }_{k0}\left)\right)}{r_k(W_{\mathit{ki}},{\psi }_{k0})(1-r_k(W_{\mathit{ki}},{\psi }_{k0}\left)\right)}\frac{\partial r_k(W_{\mathit{ki}},{\psi }_{k0})}{\partial {\psi }_k},$$ (17)

$$I_{\mathit{ki}}^{\psi }=E\left\{\frac{{\delta }_{ki}}{r_k(W_{\mathit{ki}},{\psi }_{k0})(1-r_k(W_{\mathit{ki}},{\psi }_{k0}\left)\right)}\frac{\partial r_k(W_{\mathit{ki}},{\psi }_{k0})}{\partial {\psi }_k}{\left(\frac{\partial r_k(W_{\mathit{ki}},{\psi }_{k0})}{\partial {\psi }_k}\right)}^T\right\},$$ (18)

and ${\widehat{\psi }}_k-{\psi }_{k0}=n_k^{-1}{\sum }_{i=1}^{n_k}{\left(I_k^{\psi }\right)}^{-1}{S}_{\mathit{ki}}^{\psi }+o_p\left(n_k^{-1∕2}\right)$.

We also introduce the following notation:

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\mathit{ki}}& ={\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{z}}_k(t,\beta \left(u\right)\left)\right)\frac{R_{\mathit{ki}}}{{\pi }_k(Q_{\mathit{ki}},{\psi }_{k0})}{M}_{\mathit{ki}}(\mathit{dt},\mathit{du}),\hfill \\ \hfill {\mathcal{B}}_{\mathit{ki}}& ={\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{z}}_k(t,\beta \left(u\right)\left)\right)\left(1-\frac{R_{\mathit{ki}}}{{\pi }_k(Q_{\mathit{ki}},{\psi }_{k0})}\right)E\left\{M_{\mathit{ki}}\right(\mathit{dt},\mathit{du})\mid Q_{\mathit{ki}}\},\hfill \\ \hfill {\mathcal{D}}_k& =n_k^{-1}\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{z}}_k(t,\beta \left(u\right)\left)\right)\otimes \left\{\frac{-R_{\mathit{ki}}}{{\left({\pi }_k\right(Q_{\mathit{ki}},{\psi }_{k0}\left)\right)}^2}\frac{\partial {\pi }_k(Q_{\mathit{ki}},{\psi }_{k0})}{\partial {\psi }_k}{M}_{\mathit{ki}}(\mathit{dt},\mathit{du})\right\},\hfill \\ \hfill {\mathcal{O}}_{\mathit{ki}}& ={\mathcal{D}}_k{\left(I_k^{\psi }\right)}^{-1}{S}_{\mathit{ki}}^{\psi }.\hfill \end{array}$$ (19)

The next theorem shows that the AUG estimator ${\widehat{\beta }}^{\mathit{aug}}(t,v)$ is consistent if either r_k(w, ψ_k) or g_k(a|t, v, z, θ_k) is correctly specified, a double robustness property.

Theorem 3. Assuming Condition A, ${\widehat{\beta }}^{\mathit{aug}}\left(v\right)\underrightarrow{P}\beta \left(v\right)$ uniformly in v ∈ [a, b] ⊂ (0, 1) as n → ∞. This consistency holds if either rk(w; ψ_k) or g_k(a|t, v, z, θ_k) is correctly specified.

Following the proofs of Theorem 2 and 3, it is easy to show that ${\left(\mathit{nh}\right)}^{1∕2}\left[{\widehat{\beta }}^{\mathit{aug}}\right(v)-\beta (v)+\frac{1}{2}{\mu }_2{h}^2{\Sigma }^{-1}(v\left){\vartheta }^{\ast }\right(v\left)\right]$ is asymptotically normal for v ∈ [a, b] ⊂ (0, 1) for some function ϑ*(v) if either r_k(w, ψ_k) or g_k(a|t, v, z, θ_k) is correctly specified. When both r_k(w, ψ_k) and g_k(a|t, v, z, θ_k) are correctly specified, Theorem 4 below shows that ${\widehat{\beta }}^{\mathit{aug}\left(v\right)}$ is more efficient than ${\widehat{\beta }}^{\mathit{ipw}\left(v\right)}$.

Theorem 4. Assuming Condition A, if both r_k(w, ψ_k) and g_k(a|t, v, z, θ_k) are correctly specified, we have${\left(\mathit{nh}\right)}^{1∕2}\left[{\widehat{\beta }}^{\mathit{aug}}\right(v)-\beta (v)+\frac{1}{2}{\mu }_2{h}^2{\Sigma }^{-1}(v\left)\vartheta \right(v\left)\right]\underrightarrow{\mathcal{D}}N(0,{\nu }_0{\Sigma }^{-1}(v\left){\Sigma }^{\ast }\right(v\left){\Sigma }^{-1}\right(v\left)\right)$ for v ∈ [a, b] as n → ∞ where ${\Sigma }^{\ast }\left(v\right)={\sum }_{k=1}^K\mathit{pk}{\Sigma }_k^{\ast }\left(v\right)$ and Σ(v) is given in the condition (A.3). The estimator ${\widehat{\beta }}^{\mathit{aug}\left(v\right)}$ is more efficient than ${\widehat{\beta }}^{\mathit{ipw}\left(v\right)}$ in the sense that

$$\mathit{Cov}\left\{{\left(\mathit{nh}\right)}^{1∕2}\right[{\widehat{\beta }}^{\mathit{ipw}}\left(v\right)-\beta \left(v\right)+(1∕2){\mu }_2{h}^2{\Sigma }^{-1}\left(v\right)\vartheta \left(v\right)\left]\right\}=\mathit{Cov}\left\{{\left(\mathit{nh}\right)}^{1∕2}\right[{\widehat{\beta }}^{\mathit{aug}}\left(v\right)-\beta \left(v\right)+(1∕2){\mu }_2{h}^2{\Sigma }^{-1}\left(v\right)\vartheta \left(v\right)\left]\right\}+h{\Sigma }^{-1}\left(v\right)\left(\sum _{k=1}^K(n_k∕n)\mathit{Cov}\{{\mathcal{O}}_{k1}-{\mathcal{B}}_{k1}\}\right){\Sigma }^{-1}\left(v\right)+o_p\left(h\right).$$ (20)

Equation (20) shows that the asymptotic covariance $\mathit{Cov}\left\{{\left(\mathit{nh}\right)}^{1∕2}\right[{\widehat{\beta }}^{\mathit{aug}}\left(v\right)-\beta \left(v\right)+{(1∕2)}_{{\mu }_2}{h}^2{\Sigma }^{-1}\left(v\right)\vartheta \left(v\right)\left]\right\}$ is smaller than $\mathit{Cov}\left\{{\left(\mathit{nh}\right)}^{1∕2}\right[{\widehat{\beta }}^{\mathit{ipw}}\left(v\right)-\beta \left(v\right)+{(1∕2)}_{{\mu }_2}{h}^2{\Sigma }^{-1}\left(v\right)\vartheta \left(v\right)\left]\right\}$ and the difference between the two covariances is at the order of h. The demonstrated efficiency gain for ${\widehat{\beta }}^{\mathit{aug}}\left(v\right)$ is reasonable since the estimation procedures for both ${\widehat{\beta }}^{aug}\left(v\right)$ and ${\widehat{\beta }}^{ipw}\left(v\right)$ are based on the local partial likelihood with h as its bandwidth.

Let ${\widehat{\rho }}_k^{\mathit{aug}}(\cdot )$ be defined similarly to ${\widehat{\rho }}_k^{\mathit{ipw}}(\cdot )$ given in (12) with the AUG estimator ${\widehat{\lambda }}_k^{\mathit{aug}}(t,u\mid z)={\widehat{\lambda }}_{0k}^{\mathit{aug}}(t,u)\exp \left\{{\left({\widehat{\beta }}^{\mathit{aug}}\right(u\left)\right)}^{T}z\right\}$. Let ${\widehat{\rho }}^{\mathit{aug}}(\cdot )=\left({\widehat{\rho }}_1^{\mathit{aug}}\right(\cdot ),\dots ,{\widehat{\rho }}_K^{\mathit{aug}}(\cdot \left)\right)$, ${\widehat{\Sigma }}_{\mathit{aug}}\left(v\right)=-n^{-1}{U}_{\mathit{aug}}^{\prime }(v,{\widehat{\beta }}^{\mathit{aug}}(v),\widehat{\Psi },\widehat{\rho }(\cdot \left)\right)$ and

$${\tilde{\Sigma }}_{\mathit{aug}}^{\ast }\left(v\right)=n^{-1}h\sum _{k=1}^K\sum _{i=1}^{n_k}{\left\{{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)\left(Z_{\mathit{ki}}\right(t)-{\stackrel{‒}{Z}}_k(t,{\widehat{\beta }}^{\mathit{aug}}\left(u\right)\left)\right)\left[\frac{R_{\mathit{ki}}}{{\pi }_k(Q_{\mathit{ki}},{\widehat{\psi }}_k)}{N}_{\mathit{ki}}(\mathit{dt},\mathit{du})+\left(1-\frac{R_{\mathit{ki}}}{{\pi }_k(Q_{\mathit{ki}},{\widehat{\psi }}_k)}\right)N_{\mathit{ki}}^x\left(\mathit{dt}\right)d\left({\widehat{\rho }}_k^{\mathit{aug}}\right(u,W_{\mathit{ki}}\left)\right)\right]\right\}}^{\otimes 2}.$$

The asymptotic variance of ${\left(\mathit{nh}\right)}^{1∕2}\left({\widehat{\beta }}^{\mathit{aug}}\right(v)-\beta (v\left)\right)$ can be consistently estimated by ${\left({\widehat{\Sigma }}_{\mathit{aug}}\right(v\left)\right)}^{-1}{\tilde{\Sigma }}_{\mathit{aug}}^{\ast }\left(v\right){\left({\widehat{\Sigma }}_{\mathit{aug}}\right(v\left)\right)}^{-1}$.

Let $\beta \left(v\right)={\left({\beta }_1\right(v),{\beta }_2^T(v\left)\right)}^T$ where β₁(v) is the coefficient for vaccination status and β₂(v) for other covariates. Let ${\sigma }_1^2\left(v\right)$ be the first element on the diagonal of the matrix ν₀Σ⁻¹(v)Σ*(v)Σ⁻¹(v) and ${\widehat{\sigma }}_1^2\left(v\right)$ its consistent estimator, which is the first element on the diagonal of ${\left({\widehat{\Sigma }}_{\mathit{aug}}\right(v\left)\right)}^{-1}{\tilde{\Sigma }}_{\mathit{aug}}^{\ast }\left(v\right){\left({\widehat{\beta }}_{\mathit{aug}}\right(v\left)\right)}^{-1}$. By Theorem 4, a large sample 100(1−α% pointwise confidence interval for β₁(v) is given by ${\widehat{\beta }}_1^{\mathit{aug}}\left(v\right)\pm {\left(\mathit{nh}\right)}^{1∕2}{z}_{\alpha ∕2}{\widehat{\sigma }}_1\left(v\right)$, 0 < v < 1, where z_α/2 is the upper α/2 quantile of the standard normal distribution. The confidence intervals for the other coefficient functions can be constructed similarly.

The mark-specific vaccine efficacy V E(v) = 1−exp(β₁(v)) can be estimated by $\widehat{\mathit{VE}}\left(v\right)=1-\exp \left({\widehat{\beta }}_1^{\mathit{aug}}\right(v\left)\right)$. By Theorem 4 and the delta method, ${\left(\mathit{nh}\right)}^{1∕2}\left(\widehat{VE}\right(v)-\mathrm{VE}(v\left)\right)\underrightarrow{\mathcal{D}}N(0,{\sigma }_1^2(v\left)\exp \right(2{\beta }_1\left(v\right)\left)\right)$ for v ∈ (0,1). A large sample 100(1 − α)% pointwise confidence interval for VE(v) is then given by $\widehat{\mathrm{VE}}\left(v\right)\pm {\left(\mathit{nh}\right)}^{1∕2}{z}_{\alpha ∕2}{\widehat{\sigma }}_1\left(v\right)\exp \left({\widehat{\beta }}_1^{\mathit{aug}}\right(v\left)\right)$, o < v < 1.

5 Simulation study

5.1 Assessment of estimation procedures under correctly specified models

First, we conduct a simulation study to check the finite sample performance of the two proposed estimation procedures when both r_k(w) and g_k(a|t, v, z) are correctly specified. The augmented inverse probability weighted complete-case estimator (AUG) for (2) with missing marks is compared to the complete-case estimator (CC) wherein the failures with missing marks are deleted for the analysis, and to the inverse probability weighted complete-case estimator (IPW). These estimators are compared to the unachievable benchmark, the full data likelihood estimator (Full), which analyzes the full data-set before some simulated marks are deleted. We consider the case with K = 1 stratum, in which case the CC and Full methods are that of Sun et al. (2009).

With k = 1 throughout this section, let Z_ki be the treatment indicator taking value 0 or 1 with probability of 0.5 for each value. The (T_ki, V_ki) are generated from the following mark-specific proportional hazards model:

$$\lambda (t,v\mid z)=\text{exp}\{\gamma v+(\alpha +\beta v\left)z\right\},t\ge 0,0\le v\le 1,$$ (21)

where α, β and γ are constants. Under model (21), the mark-specific baseline function is λ₀(t, v) = exp(γv) and the mark-specific vaccine efficacy is VE(v) = 1 − exp(α + βv). The vaccine efficacy VE(v) = 0 for α = 0 and β = 0, indicating no vaccine efficacy. The vaccine efficacy does not depend on the type of infecting strain if β = 0, while the VE(v) decreases in v if β > 0. We examine the estimation procedures for the following specific models:

• (M1)(α, β, γ) = (0, 0, 0.3), where VE(v) = 0;
• (M2)(α, β, γ) = (−0.69, 0, 0.3), where VE(v) does not depend on v;
• (M3)(α, β, γ) = (−0.6, 0.6, 0.3), where VE(v) decreases;
• (M4)(α, β, γ) = (−1.2, 1.2, 0.3), where VE(v) decreases.

All failure times greater than τ = 2.0 are considered as censored. In addition, we generate random censoring times from an exponential distribution, independent of (T, V), with parameter adjusted so that the overall censoring rates range from 25% to 35%. The complete-case indicator R_ki is generated with conditional probability r_k(W_ki) = P(R_ki = 1|δ_ki = 1, W_ki), where

$$\text{logit}\left(r_k\right(W_{\mathit{ki}}\left)\right)={\psi }_{k0}+{\psi }_{k1}{Z}_{\mathit{ki}},i=1,\dots ,n_k.$$ (22)

Here ψ_k0 = 0.2 and ψ_k1 = −0.2. The proportion of missing marks is about 50%, similar to the rate observed in current HIV vaccine efficacy trials.

For the proposed AUG estimator, conditional on (T_ki, Z_ki, V_ki), we assume that a single auxiliary mark follows the model

$$A_{\mathit{ki}}={(\theta +1)}^{-1}(V_{\mathit{ki}}+\theta U_{\mathit{ki}}),\theta >0,$$ (23)

for i = 1, …, n_k, where V_ki is the possibly missing mark generated from model (21), U_ki is uniformly distributed on [0, 1] independent of V_ki, and θ > 0 measures the association between A_ki and V_ki. The correlation coefficient ρ between A_ki and V_ki is 1 for θ = 0. Since A_ki is observed for all observed failure times, the AUG estimator in this case is the Full estimator. The A_ki and V_ki are independent for θ = ∞(ρ = 0), in which case the AUG estimator is denoted by AUG-A0. The AUG estimator is denoted by AUG-A1 for θ = 0.8 yielding ρ ∞ 0.78, by AUG-A2 for θ = 0.4 with ρ ∞ 0.92 and by AUG-A3 for θ = 0.2 with ρ ∞ 0.98. Thus the simulation compares the AUG estimators at four levels of association between A_ki and V_ki.

We study settings with relatively high correlations because these occur for real data-sets due to the fact that inter-subject HIV sequence diversity is considerably larger than intra-subject HIV sequence diversity (Keele et al., 2008). We have found linear correlations between early and later sequence distances as high as 0.98.

Under model (23), the conditional density of A_ki given (T_ki, Z_ki, V_ki) is

$$g_k(a\mid t,v,z;\theta )=\frac{1+\theta }{\theta }I\left\{\frac{v}{1+\theta }\le a\le \frac{v+\theta }{1+\theta }\right\},0\le a\le 1,0\le v\le 1.$$ (24)

The likelihood for θ is

$$L\left(\theta \right)=\prod _{{\delta }_{\mathit{ki}}=1,R_{\mathit{ki}}=1}\left(\frac{1+\theta }{\theta }I\left\{\frac{V_{\mathit{ki}}}{1+\theta }\le A_{\mathit{ki}}\le \frac{V_{\mathit{ki}}+\theta }{1+\theta }\right\}\right)\text{for}\theta >0.$$

It is easy to show that the maximum likelihood estimator is $\widehat{\theta }={\max }_{{\delta }_{\mathit{ki}}}=1,R_{\mathit{ki}}=1\{V_{\mathit{ki}}∕A_{\mathit{ki}},(1-V_{\mathit{ki}})∕(1-A_{\mathit{ki}}\left)\right\}-1$. Plugging in the density estimator $g_k(a\mid t,v,z;\widehat{\theta })$ into (12) yields ${\widehat{\rho }}_k^{\mathit{ipw}}(v,w)$, which is used to construct the AUG estimator of β in (13).

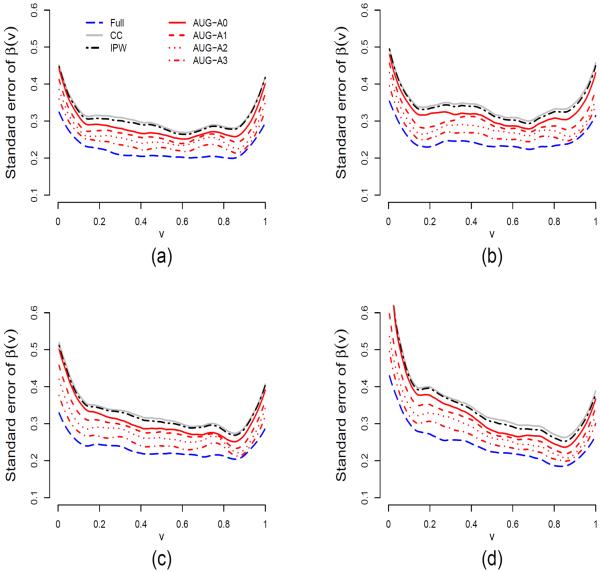
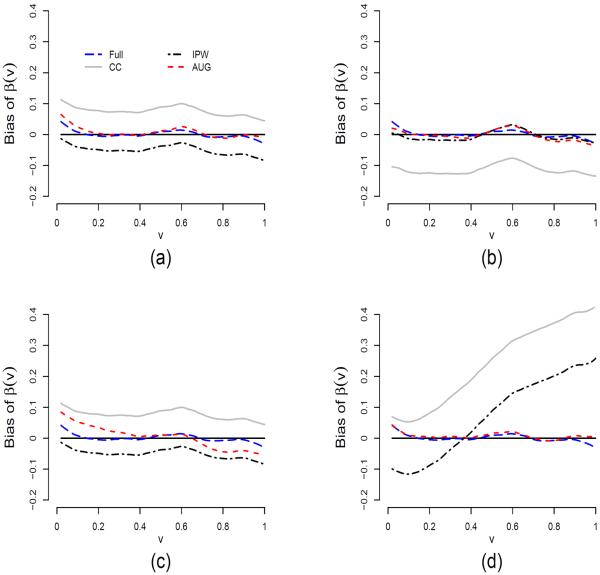
Performance of the proposed estimation procedures is evaluated for the models described in (21), (22) and (24) through simulations. We use the Epanechnikov kernel K(x) = .75(1 − x²)I{|x| ≤ 1}. The same kernel is also used for K⁽¹⁾(x) and K⁽²⁾(x). For sample size n = 500 and bandwidths b₁ = 0.1 and h = b₂ = 0.15, Figure 1 shows the average estimates of β(v) under the models (M1)–(M4) based on 500 simulations for four different procedures: Full, CC, IPW and AUG. Figure 2 shows the standard errors of these estimates and Figure 3 shows the pointwise coverage probabilities of 95% confidence intervals for β(v) constructed using the AUG estimators based on 500 simulations.

Figure 1.

Bias of estimation for β(v) under four procedures: Full, CC, IPW and AUG based on 500 simulations for n = 500, b₁ = 0.1 and h = b₂ = 0.15; (a) for model (M1), (b) for model (M2), (c) for model (M3) and (d) for model (M4). AUG-A0 is the AUG estimator corresponding to ρ = 0, AUG-A1 for ρ ≈ 0.78, AUG-A2 for ρ ≈ 0.92 and AUG-A3 for ρ ≈ 0.98, where ρ is the correlation coefficient between A_ki and V_ki.

Figure 2.

Average standard errors of the estimates for β(v) under four procedures: Full, CC, IPW and AUG based on 500 simulations for n = 500, b₁ = 0.1 and h = b₂ = 0.15; (a) for model (M1), (b) for model (M2), (c) for model (M3) and (d) for model (M4). AUG-A0 is the AUG estimator corresponding to ρ = 0, AUG-A1 for ρ ≈ 0.78, AUG-A2 for ρ ≈ 0.92 and AUG-A3 for ρ ≈ 0.98, where ρ is the correlation coefficient between A_ki and V_ki.

Figure 3.

Estimated pointwise coverage probabilities of 95% confidence intervals for β(v) constructed using the AUG estimator based on 500 simulations for n = 500, b₁ = 0.1 and h = b₂ = 0.15; (a) for model (M1), (b) for model (M2), (c) for model (M3) and (d) for model (M4). AUG-A0 is the AUG estimator corresponding to ρ = 0, AUG-A1 for ρ ≈ 0.78, AUG-A2 for ρ ≈ 0.92 and AUG-A3 for ρ ≈ 0.98, where ρ is the correlation coefficient between A_ki and V_ki.

The simulation results show that the bias of both estimators is very small at a level comparable to that of the full data likelihood estimator (Figure 1). However, the complete-case estimator yields large bias especially for models (M2)–(M4). The simulations also validate that the AUG estimator is more efficient than the IPW estimator (Figure 2). In particular, the AUG estimator without auxiliary marks (AUG-A0) has smaller standard errors than the IPW estimator, and the AUG estimator with the auxiliary mark has smaller standard errors than the AUG estimator without auxiliary marks. Moreover, the standard errors of the AUG estimator decrease as the correlation between the auxiliary mark and the mark of interest increases, with the standard errors for AUG-A1, AUG-A2 and AUG-A3 getting closer to that of the Full estimator. The pointwise coverage probabilities displayed in Figures 3 are almost all in the range of 92.5% and 97.5% for v ∈ (0, 1), indicating adequate performance of the proposed variance estimator for the AUG estimator. The deviation from the 95% nominal level is attributed to both the limited sample size (at n = 500) and the limited number of simulation runs (also at 500). The pointwise coverage probabilities are expected to be closer to 95% when both the sample size and the number of simulation runs increase.

The bandwidth selection is important in nonparametric smoothing procedures. The bias tends to be larger and the standard errors smaller for larger bandwidths. A reasonable bandwidth choice trades-off between bias and standard error. We have tried simulations with different bandwidths, taking bandwidth b₂ equal to 0.05 and 0.1 and b₁ equal to 0.15, and found our procedures relatively insensitive to the choice. The standard errors are larger at the boundary points than at the inner points, v ∈ (b₂, 1 − b₂). In practice, the appropriate bandwidth selection can be based on a $\mathcal{K}$-fold cross-validation method. This approach is widely used in the nonparametric function estimation literature and has been investigated by Efron & Tibshirani (1993) and Tian et al. (2005) among others. The simulations also show satisfactory performance of the AUG estimator of V E(v); see Figures 1–3 in the web Appendices.

5.2 Robustness analysis of the estimation procedures under mis-specified models

This subsection considers robustness of the proposed estimators to mis-specifications of r_k(w) and/or g_k(a|t, v, z), and to violation of the missing at random assumption. As above Z_ki is a binary random variable taking value 0 or 1 with probability 0.5 for each value. The (T_ki, V_ki) are generated from the mark-specific proportional hazards model (21) with (α, β, γ) given in (M3). The censoring times C_ki for model (M3) remain the same as before yielding approximately 30% censoring and X_ki = min(T_ki, C_ki).

Robustness of the estimators to mis-specification of r_k(w) is examined by assuming model (22) while the actual complete-case indicator R_ki is generated with the conditional probability r_k(W_ki) = P(R_ki = 1|δ_ki = 1, W_ki), where

$$\text{logit}\left(r_k\right(W_{\mathit{ki}}\left)\right)=1.1+Z_{\mathit{ki}}-X_{\mathit{ki}},i=1,\dots ,n_k.$$ (25)

Robustness of the AUG estimator is also examined when g_k(a|t, v, z) is mis-specified. This is carried out by assuming the model (23) for the auxiliary mark or equivalently model (24) for g_k(a|t, v, z) while the actual mark is generated from

$$A_{\mathit{ki}}={(1.2+2\tau )}^{-1}(V_{\mathit{ki}}+0.2U_{\mathit{ki}}+2X_{\mathit{ki}}),$$ (26)

for i = 1, …, n_k, where U_ki is uniformly distributed on [0, 1] independent of V_ki.

Robustness of the estimators to violation of the missing at random assumption (3) is examined by assuming model (22) while the actual R_ki depends on V_ki through the model

$$\text{logit}\left(r_k\right(W_{\mathit{ki}}\left)\right)=0.6+Z_{\mathit{ki}}-2V_{\mathit{ki}},i=1,\dots ,n_k.$$ (27)

The proportion of missing marks among the observed failure times is kept around 50% in all of the cases.

For sample size n = 500 and bandwidths b₁ = 0.1 and h = b₂ = 0.15, Figure 4 shows the bias of the estimators of β(v) under model (M3) based on 500 simulations for four different procedures: Full, CC, IPW and AUG. Figure 5 shows the standard errors of these estimators. In both figures, panel (a) shows the plots when r_k(w) is mis-specified following (25) and g_k(a|t, v, z) is correctly specified by (24) with θ = 0.2; panel (b) shows the plots when g_k(a|t, v, z) is mis-specified following (26) and r_k(w) is correctly specified by (22) with ψ_k1 = 0.2 and ψ_k1 = −0.2; and panel (c) shows the plots when r_k(w) is mis-specified following (25) and g_k(a|t, v, z) is mis-specified following (26); and panel (d) shows the plots when r_k(w) depends on V_ki following (27) and g_k(a|t, v, z) is correctly specified by (24) with θ = 0.2.

Figure 4.

Bias of estimation for β(v) with the estimators, Full, CC, IPW and AUG, under model (M3) with n = 500, b₁ = 0.1 and h = b₂ = 0.15 based on 500 simulations. (a) shows the plots when r_k(w) is mis-specified following (25) and g_k(a|t, v, z) is correctly specified by (24) with θ = 0.2. (b) shows the plots when g_k(a|t, v, z) is mis-specified following (26) and r_k(w) is correctly specified by (22) with ψ_k1 = 0.2 and ψ_k1 = −0.2. (c) shows the plots when r_k(w) is mis-specified following (25) and g_k(a|t, v, z) is mis-specified following (26). (d) shows the plots when r_k(w) depends on V_ki following (27) and g_k(a|t, v, z) is correctly specified by (24) with θ = 0.2.

Figure 5.

Standard errors of the estimators, Full, CC, IPW and AUG, for β(v) under model (M3) with n = 500, b₁ = 0.1 and h = b₂ = 0.15 based on 500 simulations. (a) shows the plots when r_k(w) is mis-specified following (25) and g_k(a|t, v, z) is correctly specified by (24) with θ = 0.2. (b) shows the plots when g_k(a|t, v, z) is mis-specified following (26) and r_k(w) is correctly specified by (22) with ψ_k1 = 0.2 and ψ_k1 = −0.2. (c) shows the plots when r_k(w) is mis-specified following (25) and g_k(a|t, v, z) is mis-specified following (26). (d) shows the plots when r_k(w) depends on V_ki following (27) and g_k(a|t, v, z) is correctly specified by (24) with θ = 0.2.

The bias of the IPW estimator is large as seen in Figure 4(a) when r_k(w) is mis-specified. Figures 4(a) and (b) show that the AUG estimator has very little bias tracking closely the full data likelihood estimator when one of r_k(w) and g_k(a|t, v, z) is mis-specified, reflecting the double robustness property of the AUG estimator. When both r_k(w) and g_k(a|t, v, z) are mis-specified, the AUG estimator still has smaller bias compared to the IPW estimator, as seen in Figure 4(c). Surprisingly, the AUG estimator yields as little bias as the full data likelihood estimator when the missing at random assumption is violated in Figure 4(d) while the IPW estimator shows very large bias. In all the scenarios, the complete-case estimator has largest bias. Figure 5 shows that the AUG estimator is more efficient than the IPW estimator with smaller standard error when both r_k(w) and g_k(a|t, v, z) are correctly specified, and this efficiency gain diminishes when one of them is mis-specified. Again the AUG estimator seems to have smaller standard error when the missing at random assumption is violated as shown in Figure 5(d).

6 Discussion

To address the fact that mark variables are subject to missingness in HIV vaccine efficacy trials and other applications, this article extends previous work on the continuous mark-specific proportional hazards model to accommodate marks missing at random. We developed two approaches based on inverse probability weighting (IPW) of complete-cases, wherein failures in the score equation are weighted by the reciprocal of the probability the mark is observed. As always for IPW-based methods, the methods provide unstable estimation if some failures have outlying estimated probabilities near zero; therefore effective implementation in practice requires careful definition of the mark and covariates in the missingness model. Moreover, performance of the IPW-based methods depends on the ability to build a good model for the probability of observing the mark in failures. For HIV vaccine efficacy trials with the mark defined as the genetic distance of an `early' virus (i.e., measured on an HIV antibody negative blood sample), subject characteristics that could help predict whether the `early' virus is observed include viral load (very high viral load predicts the virus is early, and very low/undetectable viral load makes the sequencing technology prone to fail to measure the sequence), the timing of the subject's HIV tests including any extra tests beyond those scheduled, whether the infection was diagnosed during the series of injections (when HIV testing is more frequent), and whether any antiretroviral pre-exposure prophylaxis was received.

Following Robins et al. (1994), our second approach augments the IPW estimating equation with a term for failures with a missing mark, which recovers information through modeling and estimation of the mark distribution. The simulation study showed that this approach effectively gains back efficiency compared to the IPW approach, and that the quality of predictive modeling heavily influences the extent of efficiency improvement. In our formulation the conditional density of the auxiliaries given the mark of interest is modeled and estimated. Therefore in practice a one-dimensional (or at most two-dimensional) auxiliary may be all that the data can support, given the need to either use nonparametric density estimation or to specify a reasonable parametric model. Fortunately for HIV vaccine efficacy trials with mark the genetic distance of the `early' virus, the genetic distance of a `later' virus may be a well-predicting univariate mark, as supported by examination of HIV sequence databases. Recently completed and ongoing efficacy trials are measuring distances from early and later viruses, and it will be of interest to apply the new methods to the forthcoming data-sets.

This article focused on point and interval estimation, leaving the problem of inference for future work.