pH-dependent dynamics of complex RNA macromolecules

Abstract

The role of pH-dependent protonation equilibrium in modulating RNA dynamics and function is one of the key unanswered questions in RNA biology. Molecular dynamics (MD) simulations can provide insight into the mechanistic roles of protonated nucleotides, but it is only capable of modeling fixed protonation states and requires prior knowledge of the key residue’s protonation state. Recently, we developed a framework for constant pH molecular dynamics simulations (CPHMD^MSλD) of nucleic acids, where the nucleotides’ protonation states are modeled as dynamic variables that are coupled to the structural dynamics of the RNA. In the present study, we demonstrate the application of CPHMD^MSλD to the lead-dependent ribozyme; establishing the validity of this approach for modeling complex RNA structures. We show that CPHMD^MSλD accurately predicts the direction of the pK_a shifts and reproduces experimentally-measured microscopic pK_a values with an average unsigned error of 1.3 pK_a units. The effects of coupled titration states in RNA structures are modeled, and the importance of conformation sampling is highlighted. The general accuracy of CPHMD^MSλD simulations in reproducing pH-dependent observables reported in this work demonstrates that constant pH simulations provides a powerful tool to investigate pH-dependent processes in nucleic acids.

INTRODUCTION

The role of protonated nucleotides in modulating RNA dynamics and function has recently emerged as one of the key unanswered questions in the study of RNA biology.¹ These nucleotides, which typically have elevated pK_a values, can be protonated at physiological pH and have been implicated in structural roles,^2–6 such as in the formation of non-canonical A⁺•C base pairs that are known to stabilize RNA loop structures.^7,8 Protonated adenine and cytosine residues also play a significant role in ribozyme catalysis, serving as general acid-base catalysts, which is analogous to the catalytic role of histidine residues in enzymes.^9–13 Some examples include the hepatitis delta virus ribozyme^14–18 and the hairpin ribozyme,^19–24 where experimental studies have demonstrated that a significant drop in catalytic activity arises from the mutation of key adenine and cytosine residues that have elevated pK_a values. pH-dependent dynamics have also been reported in a number of RNA systems, such as the pH-dependent RNA tertiary structure of a retrovirus pseudoknot,²⁵ the base-flipping conformation change of the U6 RNA intramolecular stem-loop of the spliceosome complex,²⁶ conformational changes in the peptidyl-transferase center of the ribosome,^27–32 and structural changes of helix 69 of the 50S ribosomal subunit.^33,34

Information on the microscopic pK_a value of each residue is invaluable in narrowing the list of nucleotides that titrate at physiological pH and are responsible for these pH-dependent properties. To achieve this goal, experimental techniques used to study pH-dependent behavior in RNA have made significant progress over the last decade. Early work by Pardi and co-workers demonstrated the utility of NMR spectroscopy to measure microscopic pK_a values.³⁵ More recent approaches include the use of nucleobase analogs that serve as pH-dependent fluorescent sensors,^24,36,37 and the use of Raman spectroscopy to measure microscopic pK_a values of specific residues.^17,23 Despite the copious amounts of biochemical and structural data emerging from these studies, there still remains some ambiguity as to the specific function of these protonated residues. In such situations, in silico modeling of RNA structures in the form of molecular dynamics (MD) simulations, which have the ability to provide detailed atomistic insight, can be used to shed light on existing ambiguities.^22,38–43 However, traditional MD simulations are only capable of modeling fixed protonation states, and are limited by the fact that substantial prior knowledge about the identity of the key residues and their corresponding protonation states is required. In terms of in silico prediction of pK_a values, Honig, Pyle, and co-workers have explored the calculation of pK_a values of nucleic acids using numerical solutions to the nonlinear Poisson–Boltzmann (NLPB) equation on a series of NMR structures.⁴⁴ While these calculated pK_a values may identify the correct protonation state to be assigned in a traditional MD simulation, they lack the ability to incorporate protonation state information that is directly coupled to changes in the local electrostatic environment.

The ability to perform pH-coupled molecular dynamics is clearly desirable since it would yield more realistic pH-dependent responses to structural fluctuations and provide deeper mechanistic insight into RNA catalyzed reactions. Such a computational method has been developed for use with proteins.^45–56 One approach, known as continuous constant pH molecular dynamics (CPHMD), uses the λ dynamics formalism^57–59 to describe the protonation state coordinates. In this formalism, the protonation states of nucleotides change dynamically throughout the simulation that is set according to the external pH simulated, and further adjusted according to the changes in the electrostatic microenvironment around the titrating residue. This method was developed by Brooks, Shen, and co-workers,^60–65 and CPHMD simulations have been successfully applied to investigate numerous pH-dependent properties in proteins.^66–75 The recent extension of λ dynamics, known as Multi-Site λ-Dynamics (MSλD)^76,77 was used to expand the framework of constant pH molecular dynamics (CPHMD^MSλD) to encompass nucleic acids, which has been applied to model nucleotide compounds to yield pK_a values with a high level of accuracy.⁷⁸ Unlike the pK_a values calculated from traditional computational methods like NLPB, the CPHMD^MSλD framework has the added advantage of including dynamical information to its free energy calculations, making it more suitable for modeling pH-dependent properties that correlates to structural fluctuations or local conformation changes.

In this article, we describe the first application of CPHMD^MSλD to study the titration behavior of an RNA structure. We focus our analysis on the lead-dependent ribozyme, which is perhaps the best-characterized RNA macromolecule as it has experimentally measured microscopic pK_a values for almost half of its adenine and cytosine residues. We demonstrate the practical utility of CPHMD^MSλD simulations by showing its ability to accurately reproduce experimental pK_a and predict the correct direction of shifted pK_a values without any a priori input about the protonation states of the system. Lastly, using the flexible GAAA tetraloop and the A⁺•C base pair of the lead-dependent ribozyme as model examples, we explore the coupling between protonation states and conformational dynamics, and the effect they have on the protonation equilibria of nucleic acids.

MATERIALS AND METHODS

Structure Preparation

The input structure for lead-dependent ribozyme was generated from the PDB file (Accession code: 1LDZ), using the lowest energy NMR structure reported.⁷⁹ Hydrogen atoms were added using the HBUILD facility in CHARMM.⁸⁰ The RNA structure was solvated in a cubic box of explicit TIP3P⁸¹ water molecules of length ~70 Å using the convpdb.pl tool from the MMTSB toolset.⁸² The ionic strength was simulated by adding, using convpdb.pl, the appropriate number of Na⁺ and Cl^– ions to match experimentally reported salt concentrations, which was 100mM unless otherwise specified.⁸³ The terminal ends of the RNA were hydroxylated using CHARMM’s 5TER and 3TER patches. Additional patches were constructed to represent the protonated forms of adenine and cytosine. All of the associated bonds, angles and dihedrals were explicitly defined in the patch. Each titratable residue was simulated as a hybrid model that explicitly included atomic components of both the protonated and unprotonated forms. The titratable fragment included the nitrogen atom that is protonated, the protonated hydrogen and adjacent atoms whose partial charge differed according to the protonation state as reported previously by Goh et. al.⁷⁸ The environment atoms were defined as all atoms that were not included in the titratable fragments.

Molecular Dynamics Simulation

MD simulations were performed within the CHARMM macromolecular modeling program (version c36a6) using the CHARMM36 all-atom force field for RNA⁸⁴ and TIP3P water.⁸¹ The SHAKE algorithm⁸⁵ was used to constrain the hydrogen-heavy atom bond lengths. The Leapfrog Verlet integrator was used with an integration time step of 2 fs. A non-bonded cutoff of 12 Å was used with an electrostatic force shifting function and a van der Waals switching function between 10 Å and 12 Å. The CPHMD^MSλD simulations are performed using an extended Hamiltonian approach where the protonation state of the residue is described by a continuous variable, λ, which is propagated simultaneously with the spatial coordinates at a specified external pH via multi-site λ-dynamics (MSλD).⁷⁶ λ dynamics was performed within the BLOCK facility using the MSλD framework (MSLD) and selecting the λ^Nexp functional form for λ (FNEX). Linear scaling by λ was applied to all energy terms except bond, angle and dihedral terms, which were treated at full strength regardless of λ value to retain physically reasonable geometries. Each θ_α was assigned a fictitious mass of 12 amu•Å² and λ values were saved every 10 steps. Variable biases (F_var) were added to the hybrid potential energy function to enhance transition rates between the two protonation states, and the associated force constant (k_bias) used were identical to the optimized values reported by by Goh et. al.⁷⁸ The temperature was maintained at 298K by coupling to a Langevin heatbath using a frictional coefficient of 10ps^–1. After an initial minimization, the system was heated for 4 ps and equilibrated for 4 ps before a production run of 5 ns was performed. Each simulation run was repeated 9 times, beginning with different initial velocities. Each group of 9 simulation runs was then repeated at a different external pH, and we simulated the system from pH 1 to 7 at every integer pH interval, resulting in cumulative simulation time of 315 nanoseconds (ns).

Calculation of pK_a values

The populations of unprotonated (N^unprot) and protonated (N^prot) states are defined as the total number of times in the trajectory where conditions λ_α,1 > 0.8 and λ_α,2 > 0.8 are satisfied, respectively, and are used to derive the unprotonated fraction (S^unprot):

$$S^{\mathit{unprot}}(\text{pH})=\frac{N^{\mathit{unprot}}(\text{pH})}{N^{\mathit{unprot}}(\text{pH})+N^{\mathit{prot}}(\text{pH})}$$ (1)

In our protocol, each single S^unprot value was calculated by combining the populations of N^prot and N^unprot from 3 independent simulations at the same pH. These combined S^unprot values were then collected over the entire pH range (typically from pH 1 to 7) and were fitted to a generalized version of the Henderson-Hasselbalch formula:

$$S^{\mathit{unprot}}(\text{pH})=\frac{1}{1+{10}^{-n(pH-\mathit{pKa})}}$$ (2)

The pK_a values and the Hill coefficients (n) were calculated using equation (2). In this formalism, n has a theoretical value of one and deviations from this value indicate the degree of cooperativity (n > 1) or anti-cooperativity (n < 1) between strongly interacting titratable groups.^86,87 As we have performed 9 independent simulations, we have 3 different titration curves and their corresponding pK_a value and Hill coefficient. In this article, the reported values and its uncertainty correspond to the mean and standard deviation of the 3 sets of pK_a calculations.

RESULTS & DISCUSSION

pK_a calculations using CPHMD^MSλD simulations

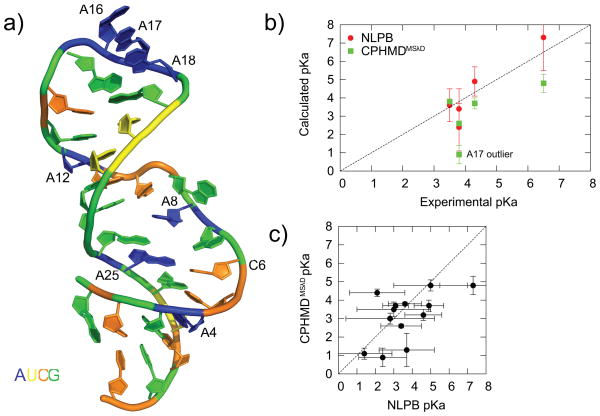
pH-dependent experimental observables, such as microscopic pK_a values, may be used as an indicator of how accurately CPHMD^MSλD simulations reproduce pH-dependent properties. Unlike protein systems, where the microscopic pK_a value of multiple ionizable residues for many proteins are readily available,⁸⁸ the literature of nucleic acid pK_a research is much sparser with only a single pK_a value measured for a handful of RNA systems. The lead-dependent ribozyme is, to the best of our knowledge, the most thoroughly-studied RNA system that has the largest number of experimentally-measured microscopic pK_a values (Fig. 1a).⁸³ As such, we have used it as a model system for benchmarking the performance of CPHMD^MSλD simulations in this paper. Results from our calculations, as well as the appropriate comparisons with existing pK_a values calculated using the NLPB equation⁴⁴ are summarized in Fig. 1.

Fig. 1.

Comparison of pK_a values for lead-dependent ribozyme. (a) The lead-dependent ribozyme and the residues with experimentally measured pK_a values. (b) Correlation plot of calculated pK_a values from computational approaches (NLPB and CPHMD^MSλD) and experimental pK_a values. (c) Correlation plot of pK_a values calculated from NLPB compared to CPHMD^MSλD. The error bars denote the standard deviation of calculated pK_a values. All NLPB calculations were obtained from Honig, Pyle and co-workers.⁴⁴

One of the key advantages of the CPHMD^MSλD framework is that no a priori information about the protonation states or the identity of the residues-of-interest of the system under investigation is required. In CPHMD simulations of proteins,⁶² one typically titrates all ionizable residues simultaneously and allows the local electrostatic microenvironment around each residue to determine the protonation state at a given external pH. In an analogous setup, we simultaneously titrated all ionizable residues (cytosine and adenine) of the lead-dependent ribozyme. As summarized in Fig. 1b and Table 1, we demonstrate good agreement with experimental pK_a values. Relative to experiments, our calculated pK_a values have an unsigned average error (AUE) of 1.3 pK_a units. With the exception of residue A16, the rank ordering of our calculated pK_a values also agree with experimentally measured values. The correlation coefficient between calculated and experimental pK_a value was 0.76 which is statistically significant at the 95% level. The precision of our calculated pK_a values, defined as the standard deviation of 3 independent sets of pK_a calculations (see Materials and Methods) was 0.3 pK_a units, which compares favorably to the average experimental uncertainty of 0.4 pK_a units. Our precision of 0.3 pK_a units translates to 0.4 kcal/mol, which is comparable to the precision of previous calculations on hydration free energy of benzene derivatives performed using MSλD.⁷⁷ The corresponding Hill coefficient of the calculated pK_a values were also generally below 1 (Table 1), suggesting that anti-cooperative interactions are the dominant mode in which titrating residues interact with one another.

Table 1.

Comparison between experimental pK_a values with the calculated pK_a values obtained from CPHMD^MSλD simulations.

Residue	Exp. pKa	CPHMDMSλD Simulations
		n	pKa	Error
A4	< 3.0	0.4 ± 0.1	0.6 ± 0.1	-
A8	4.3 ± 0.3	0.7 ± 0.3	3.7 ± 0.3	−0.6
A12	< 3.0	1.1 ± 0.3	0.7 ± 0.3	-
A16	3.8 ± 0.4	0.7 ± 0.1	2.6 ± 0.1	−1.2
A17	3.8 ± 0.4	0.4 ± 0.0	0.9 ± 0.5	−2.9
A18	3.5 ± 0.6	0.6 ± 0.0	3.8 ± 0.1	0.3
A25	6.5 ± 0.1	0.4 ± 0.1	4.8 ± 0.5	−1.7
AUE Precision			± 0.3	1.3

Comparing pK_a values between CPHMD^MSλD simulations and NLPB calculations

All experimentally-measured microscopic pK_a values for the lead-dependent ribozyme have been discussed in the preceding section, and the only data for the other adenine and cytosine residues are those obtained from NLPB calculations reported by Honig, Pyle and co-workers.⁴⁴ As summarized in Table 2, the average unsigned difference of the pK_a values calculated by both computational methods for all 13 residues is 1.1 pK_a units, which is smaller than the average standard deviation of 1.5 pK_a units for the NLPB pK_a values. We performed a paired t-test on the two sets of pK_a values and the two-tailed P-value was 0.19, which indicates that the difference between CPHMD^MSλD and NLPB pK_a values were not statistically significant at the 95% level. As illustrated in Fig. 1c, within the reported precision, we conclude that the calculated pK_a from both methods are consistent with each other.

Table 2.

Calculated pK_a values of all adenine and cytosine residues in lead-dependent ribozyme obtained from NLPB calculations⁴⁴ and CPHMD^MSλD simulations indicate that both models produce consistent results and reasonable pK_a shifts given structural considerations.

Residue	Structure	NLPB		CPHMDMSλD		Abs Difference (NLPB vs CPHMDMSλD)	pKa shift (wrt to ref pKa)
		pKa	stdev	pKa	stdev
C2	wc	2.1 ±	1.5	4.4 ±	0.2	2.3	+
A4	wc	< 3.0		0.6 ±	0.1		−
C5	wc	3.0 ±	2.0	3.5 ±	0.4	0.5	−
C6	A+C	2.8 ±	2.4	3.0 ±	0.3	0.2	−
A8		4.9 ±	0.8	3.7 ±	0.3	1.2	0
C10	wc	1.4 ±	1.5	1.1 ±	0.3	0.3	−
C11	wc	3.7 ±	1.5	1.3 ±	0.9	2.4	−
A12	wc	< 3.0		0.7 ±	0.3		−
C14	wc	4.6 ±	1.0	3.2 ±	0.3	1.4	−
A16		3.4 ±	1.1	2.6 ±	0.1	0.8	−
A17		2.4 ±	1.3	0.9 ±	0.5	1.5	−
A18		3.6 ±	0.9	3.8 ±	0.1	0.2	0
A25	A+C	7.3 ±	1.8	4.8 ±	0.5	2.5	+
C28	wc	3.1 ±	0.7	3.7 ±	0.1	0.5	−
C30	wc	5.0 ±	2.0	4.8 ±	0.3	0.2	+
Average Unsigned Values			1.5		0.3	1.1

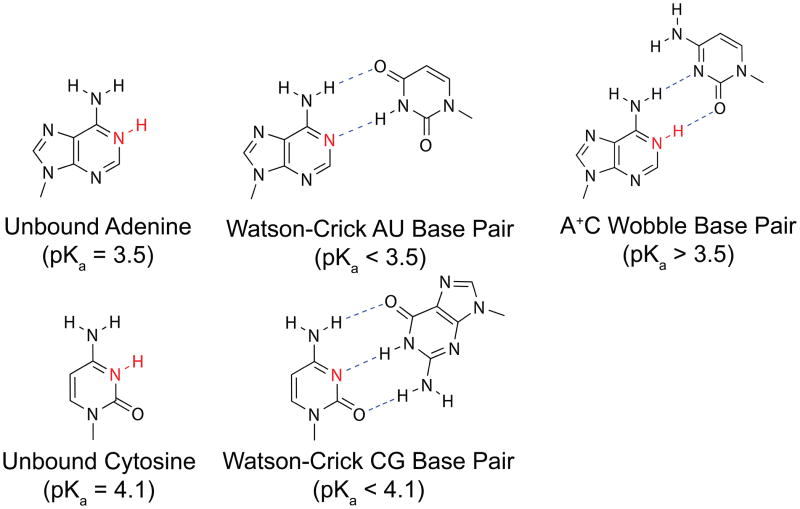
Next, we ask if the shift in calculated pK_a values relative to the reference pK_a of the free unbound nucleobase is reasonable based on the structural considerations. A number of residues have been determined by experimental studies to be involved in Watson-Crick base pairing (indicated as “wc” in the structure column in Table 2). When adenine or cytosine participates in canonical base pairing as illustrated in Fig. 2, their pK_a will be shifted lower relative to the reference value. This is because the nitrogen atoms (N1 for adenine, N3 for cytosine) that can be protonated serve as hydrogen bond acceptors, which make it energetically unfavorable for the base to be protonated. For all 9 residues in the lead-dependent ribozyme that are known to be base paired, CPHMD^MSλD predicted a lower pK_a relative to the reference compound. The exceptions are residues C2 and C30, which are located at the ends of the helix and are subject to fraying motions that weakens their base pairing interactions and increases their exposure to solvent. There is also a protonated A25⁺•C6 base pair in the lead-dependent ribozyme, which is a configuration that raises the pK_a of the adenine base, as the protonated hydrogen on the N1 atom of adenine serves as a hydrogen bond donor to the N3 acceptor on cytosine (Fig. 2). The calculated pK_a value of residue A25 was 4.8, which is shifted upwards from the reference value of 3.5 (Table 2). The calculated pK_a value of residue C6 was 1.8, which is shifted downwards from the reference value of 4.1 (Table 2). Thus, the direction of pK_a shifts of both residues in the A25⁺•C6 base pair was correctly predicted. Lastly, based on the NMR data from Legault and Pardi, they reported that no cytosine residue in the lead-dependent ribozyme had an abnormally high pK_a value,⁸³ and our CPHMD^MSλD based calculations are consistent with their observations.

Fig. 2.

Illustration of adenine and cytosine and their hydrogen-bonding configuration in a canonical Watson-Crick base pair, and the protonated A⁺•C base pair.

Comparison of Constant pH MD Simulations between Proteins and Nucleic Acids

The accuracy of our pK_a calculations compares favorably with established work on CPHMD simulations of proteins, which has a reported RMSE of 1.0 pK_a units for surface-exposed residues and 1.5 pK_a units for buried residues.⁶² The similar level of accuracy relative to established work on protein CPHMD simulation is encouraging, considering that constant pH simulations of nucleic acid systems are met with several unique challenges. In nucleic acids, almost 50% of the residues present are titrating in unison and base-base interactions are extremely common given that they are the fundamental interactions that give rise to secondary and tertiary structure in RNA, analogous to how interactions between the amide backbone of protein contribute to protein secondary structure. This means that the probability of having coupled titrating interactions (i.e., when the protonation state of a nucleotide affects an adjacent residue and vice-versa) is high, which would increase the requirements for convergence.

The challenging nature of converging nucleic acid titrations is partially reflected in our longer 15 ns explicit solvent simulations, which is almost an order of magnitude longer than the shorter ~2ns simulations reported for protein CPHMD simulations.⁶² However, the longer simulation time should be considered in the context that previous pK_a calculations on proteins which were performed in implicit solvent with temperature-replica exchange enhanced sampling,⁶² where it is expected that more rapid sampling in both conformation space and titration coordinates would result in faster convergence. By contrast, our simulations were performed in explicit solvent and sampling of titration coordinates is slower due to the fact that the solvent needs to reorganize whenever the protonation state changes.⁷⁸ Despite the fact that implicit solvent models confer sampling advantages, there have been a number of unresolved issues based on earlier CPHMD work. For example, it has been reported that the Generalized-Born (GB) implicit solvent model underestimates the desolvation and buried charge-charge interactions which increases the error of predicted pK_a values of buried residues.⁶² In addition, the approximations made in modeling hydrophobic interactions are known to cause structural compaction and possible distortion of the overall structure, which can be another source of error in pK_a calculations.^65,73 The above-mentioned sources of errors that are still unresolved in implicit solvent CPHMD are corrected with an explicit solvent representation of the protein’s conformational dynamics,⁶⁵ highlighting the advantages of using an explicit solvent framework as we have done in our CPHMD^MSλD simulations. In addition, some RNA systems like the HDV ribozyme rely on specific Mg²⁺ ions to tune the local electrostatic environment around certain residues and consequently their pK_a values,⁸⁹ and the use of an explicit solvent model is needed to model this effect. Finally, it is worthwhile to consider that existing GB models used in earlier CPHMD simulations have been parameterized primarily against proteins,^90,91 and the naive application to nucleic acid systems is likely to introduce more errors if no re-paramaterization against nucleic acids is performed. Indeed, this expectation is consistent with earlier implicit solvent CPHMD simulations performed on the glmS ribozyme by Šponer, Otyepka and coworkers,⁹² which demonstrated that implicit solvent models were unable to generate stable trajectories, and the simple Debye-Hückel screening function that is used to simulate the salt concentration appeared to have contributed to the inaccurate pK_a predictions.

Conformational Dynamics and Coupled Titrating Interactions

The interplay between conformational dynamics and protonation states, the process of how local structural changes modify the electrostatic microenvironment around residues to cause a change in protonation state, is well documented in many RNA systems. Some examples include retrovirus pseudoknot structures,²⁵ the intramolecular stem-loop of the spliceosome complex,²⁶ the peptidyl-transferase center of the ribosome,^27–32 and helix 69 of the 50S ribosomal subunit,^33,34 where the pH-dependent dynamics of these RNA complexes are known to alter their structure and function. Similar observations have also been reported in proteins as well.^52,74,93 Thus, the importance of conformational dynamics in RNA systems in influencing protonation states, together with the high possibility of coupled titrating interactions due to the ubiquitous nature of base-base interactions, is going to be of emerging interest in the field of CPHMD simulations of nucleic acids.

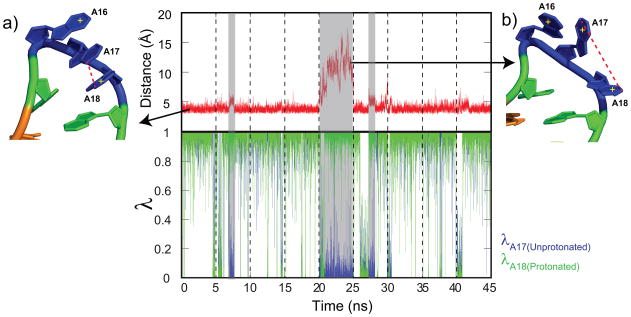
The GAAA tetraloop of the lead-dependent ribozyme is a conformationally dynamic motif common to many RNA structures.⁹⁴ It contains three titratable adenine residues. It serves as an excellent model for examining the interplay between conformational dynamics and coupled titrating interactions in our CPHMD^MSλD simulations. The lowest energy conformation as determined by NMR spectroscopy is one where the three adenine residues (A16, A17, A18) adopt a triply stacked conformation as shown in Fig. 3a. Considering the close proximity of these residues, it is likely that their protonation states are coupled. Examination of the distance between the N1 atoms at pH 2 indicates that A17 and A18 remain stacked on top of each other and they do not move more than 4 Å away for most of the simulation as indicated in Fig. 3. This distance is much lower than the 6 Å distance that we previously reported in dinucleotides, which is the range where only weak interactions between adjacent nucleotides were observed.⁷⁸ This suggests that there may be anti-cooperative interactions between the two residues, which was confirmed by the near perfect correlation between the unprotonated state of A17 and the protonated state of A18 when the N1-N1 interatomic distance is less than 4 Å (Fig. 3). In one of the MD runs (highlighted in grey), this distance increased to 15 Å, which was concomitant with A17 transitioning to and maintaining a predominantly protonated state (λ_{A17,unprotonated} = 0). In this run, the lead-dependent ribozyme sampled and remained trapped in an alternative unstacked conformation as illustrated in Fig. 3b, which altered the electrostatic microenvironment around each residue and consequently their protonation states. At the same time, we observed a loss in correlation between the protonation states of A17 and A18 whenever their distance exceeded 6 Å. The results presented here are the first example of a microscopic examination of the interplay between local conformational dynamics and coupled titrating interactions in nucleic acid literature.

Fig. 3.

Concatenated trajectories from 9 independent 5 ns runs that describe (top) the distance between N1 atoms of A17/A18 at pH 2 and (bottom) the corresponding λ_unprot state of A17 and λ_prot state of A18. (a) A typical triply-stacked lowest energy conformation maintained throughout most of the simulations, (b) an alternative unstacked conformation that resulted in a decoupling of A17-A18 interactions.

This physically realistic model of coupled titrating interactions that respond to conformational dynamics in our CPHMD^MSλD simulations helps account for the calculated pK_a value of 0.9 of residue A17 (Table 1). Since A17 and A18 remain stacked for most of the simulation, the positive electrostatic environment generated by A18 would artificially depress the tendency of A17 to achieve protonation. In addition, apart from the strong correlations between the protonation states of these 2 residues (Fig. 3), the pK_a value calculated from titrating residue A17 only, with A18 permanently assigned to its protonated state was less than 1, confirming that the coupled A17-A18 interactions are responsible for the shifted pK_a value of residue A17.

To reconcile the difference between calculated and experimental pK_a values of A17, we suggest that the coupled titrating interactions observed in our simulations become decoupled on the longer NMR timescale, when the loop undergoes multiple excursions between various alternate conformations. This would be consistent with the work of Pardi and co-workers which indicated that the GAAA tetraloop of the lead-dependent ribozyme adopts at least one other low energy conformation.^95,96 The existence of alternative conformations sampled by such GNRA tetraloops has been suggested by fluorescence spectroscopy experiments,⁹⁷ and possible alternative conformations was suggested by temperature replica exchange MD simulations.⁹⁸ A visual inspection of these alternate conformations indicate that more than half of them are different from the triply-stacked conformation, which suggests that the sampling limitations in straightforward MD simulations that prevents us from accessing the other alternative conformations sampled may be responsible for the reduced accuracy of residue A17’s pK_a value.

Coupled Titrating Interactions of Protonated Base Pairs

The A25⁺•C6 base pair in the lead-dependent ribozyme is another interesting case where we can examine the effects of coupled titrating interactions in our CPHMD^MSλD simulations. Examination of the hydrogen bonding distances indicates that the system oscillates between closed (Fig. 4b) and semi-open (Fig. 4a) conformations. The closed conformation is consistent with the NMR structure of the A25⁺•C6 base pair, and it promotes the protonation of A25. The semi-open state on the other hand exposes A25 to the solvent and is therefore expected to have a protonation equilibrium that is similar to the reference adenosine compound. When we reprocessed the concatenated trajectory from all simulation runs and extracted the segments that maintained a proper A25⁺•C6 geometry, the resulting pK_a was 6.0 as shown in Fig. 4. Conversely, the pK_a calculated from segments of the trajectory that did not maintain the base-paired geometry was 3.9, which is close to the reference pK_a of 3.5 for a solvent-exposed adenosine. Thus, the excursions between these two conformations accounts for the calculated pK_a value of 4.8 for residue A25, which is lower than the experimental pK_a of 6.5. The A25⁺•C6 base pair as we have seen, has similar conformational sampling challenges as the GAAA tetraloop. The larger underprediction of 1.7 pK_a units that corresponds to a free energy difference of 2.3 kcal/mol, is thus consistent with observations in the literature for free energy calculations in systems with higher demands in terms of conformational sampling usually have a lower accuracy as compared to systems that exhibit lesser conformational dynamics.^99,100

Fig. 4.

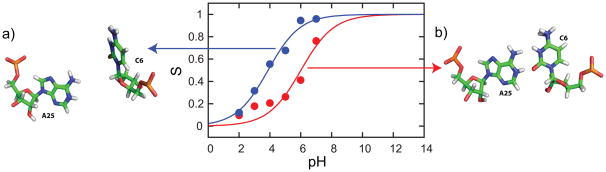
Titration curves from reprocessed trajectory that maintained a (red) closed conformation and (blue) semi-open conformation resulted in distinct pK_a values of 6.0 and 3.9 respectively. (a) A sample snapshot of a semi-open conformation and (b) a typical closed conformation.

Using CPHMD^MSλD Simulations to Investigate Localized pH-dependent Properties

The conventional approach in CPHMD simulations to investigate pH-dependent properties is to titrate the entire system. While this represents the most rigorously accurate approach, if one is investigating pH-dependent properties at a local site and the identity of titrating residues-of-interest are known, an informed choice to restrict the titration to a specific set of residues may be prudent. Such an approach would be justified, especially if available experimental data indicates that there are no other titrating residues in the vicinity of the local site within the pH range of interest that is being simulated. As an illustration of such informed CPHMD^MSλD simulations, we performed a single-site titration of the lead-dependent ribozyme to investigate the A25⁺•C6 base pair. In this single-site titration simulation, residue A25 is allowed to change its protonation state, but all other residues were assigned a protonation state that is consistent with their reference pK_a values (i.e., adenine and cytosine are unprotonated, guanine and uracil are protonated). From structural considerations (Fig. 2), we know that the cytosine in the A25⁺•C6 base pair will have a pK_a that is lower relative to its reference value. Thus, assigning it as constitutively deprotonated residue (i.e., not titrating it in CPHMD^MSλD simulations) is a well-justified approximation. The resulting pK_a value from single-site CPHMD^MSλD simulations is 6.1, which is close to the experimental value of 6.5. Lastly, from NMR studies we know that the pK_a value of residue A25 decreases from 6.5 to 5.9 when the salt concentration was increased from 100mM and 500mM NaCl, due to the additional screening effect in a higher ionic strength environment.¹⁰¹ Using single-site CPHMD^MSλD simulations, our calculated pK_a values decreased from 6.1 to 5.0 when the simulated salt concentration was increased from 100mM to 500mM. The pK_a calculations agree well with experiment, highlighting that CPHMD^MSλD simulations can be used to model the effects that ionic strength has on the protonation state of residues in RNA structures. Interestingly, the pK_a calculations from the single-site titration of the A25⁺•C6 base pair were more accurate than our multi-site simulations when all titratable residues were titrating. This is because the “semi-open” conformation that was sampled in the multi-site titration was not as frequently visited in our single-site titration. Given the increased extent of available conformational space to explore in the multi-site titrations, it is possible that insufficient conformational sampling may be causing the less accurate pK_a results.

Addressing Future Challenges of CPHMD^MSλD Simulations of complex RNA Systems

Our analysis of coupled titrating interactions and conformational dynamics of the lead-dependent ribozyme has led to the conclusion that CPHMD simulations will have to adequately sample local conformational changes in order to accurately reproduce experimentally-measured pH-dependent properties, particularly for residues that are situated in flexible regions. The need for better conformational sampling is well documented in the literature of free energy calculations,^99,100 which we suggest may be particularly pertinent to RNA systems that are inherently more dynamic than most protein systems. Existing literature on CPHMD simulations in proteins have shown that improved accuracy of calculated pK_a values and faster convergence can be achieved through enhanced sampling methods, namely replica-exchange MD.^55,65 We anticipate that other sampling strategies, such as self-guided Langevin dynamics¹⁰² and orthogonal space random walk,^93,103,104 may also be effective in addressing the conformation sampling challenges in the study of pH-dependent properties of RNA, because most systems only involve a local conformation change around the titrating residue. Another avenue of improvement for our CPHMD^MSλD framework may be the CHARMM force field itself, which has been shown to inaccurately simulate certain RNA motifs.¹⁰⁵ However, the recent reparamterization efforts that led to the development of the CHARMM36 nucleic acid force field⁸⁴ on which this work is based, have to some extent addressed the deficiencies reported in earlier work. Nevertheless, we acknowledge that the existing parameters for charged nucleobases may need to be optimized for better consistency with the latest CHARMM36 nucleic acid force field, especially in the context of the charged nucleobases, such as the A⁺•C base pair where we observed that more accurate results were obtained in our single-site titration simulations. Ongoing work to enhance CPHMD^MSλD with enhanced sampling methods and to ensure consistent parameterization of charged nucleobases in the CHARMM force field will be reported in due course.

Lastly, it has been suggested that the use of spherical cutoffs in our CPHMD^MSλD framework, without any long-range electrostatic treatment, such as PME, may introduce errors to the simulated dynamics of the ribozyme, which could potentially affect the resulting pK_a values. While earlier work has suggested that PME provides a more accurate simulation of nucleic acid dynamics than group-based cutoff methods,¹⁰⁶ later publications have shown that an atom-based cutoff method using an appropriate force shifting function, such as that employed in this paper, is just as capable as PME in simulating accurate dynamics of charged nucleic acid systems.¹⁰⁷

CONCLUSION

We have provided the first demonstration of constant pH MD (CPHMD^MSλD) simulations of a complex RNA structure, the lead-dependent ribozyme. pK_a values calculated from CPHMD^MSλD simulations agree well with experimental pK_a values with an average unsigned error of 1.3 pK_a units. The accuracy of our pK_a calculations is comparable to established CPHMD work in proteins and the direction of the pK_a shifts for all residues in the lead-dependent ribozyme are also accurately predicted when compared to experimental data or structural considerations. Using the GAAA tetraloop and the A⁺•C base pair of the lead-dependent ribozyme as model systems, we demonstrated that CPHMD^MSλD simulations are able to model the effects that conformational dynamics and coupled titrating interactions have on the protonation equilibria of titrating residues. Using CPHMD^MSλD simulations to reproduce pH-dependent observables, in this case microscopic pK_a values of an RNA structure, validates the underlying physical basis of our model. The promising results from this study open the door to investigate pH-dependent dynamical processes of other RNA structures with confidence. Given that the role of protonated nucleotides is being increasingly recognized in regulating RNA structure and function, we anticipate that CPHMD^MSλD will be a powerful tool used in tandem with existing experimental techniques to investigate pH-dependent dynamics of RNA structures to improve on our fundamental understanding of RNA biology.