Towards Accurate Prediction of Protonation Equilibrium of Nucleic Acids

Abstract

The role of protonated nucleotides in modulating the pH-dependent properties of nucleic acids is one of the emerging frontiers in the field of nucleic acid biology. The recent development of a constant pH molecular dynamics simulation (CPHMD^MSλD) framework for simulating nucleic acids has provided a tool for realistic simulations of pH-dependent dynamics. We enhanced the CPHMD^MSλD framework with pH-based replica exchange (pH-REX), which significantly improves the sampling of both titration and spatial coordinates. The results from our pK_a calculations for the GAAA tetraloop, which was predicted with lower accuracy previously due to sampling challenges, demonstrates that pH-REX reduces the average unsigned error (AUE) to 0.7 pK_a units, and the error of the most poorly predicted residue A17 was drastically reduced from 2.9 to 1.2 pK_a unit. Lastly, we show that pH-REX CPHMD^MSλD simulations can be used to identify the dominant conformation of nucleic acid structures in alternate pH environments. This work suggests that pH-REX CPHMD^MSλD simulations provide a practical tool for predicting nucleic acid protonation equilibrium from first-principles, and offering structural and mechanistic insight into the study of pH-dependent properties of nucleic acids.

The role of protonated nucleotides in modulating the pH-dependent properties of nucleic acids is at the frontier of questions in the field of nucleic acid biology.^1,2 Protonated nucleotides serve as key catalytic residues in many ribozymes,^3–10 and protonated base pairs are known to stabilize RNA loop structures.^11,12 They also control the pH-dependent dynamics of numerous RNA systems, such as the retrovirus pseudoknot,¹³ peptidyl-transferance center of the ribosome,^14–19 helix 69 of the 50S ribosomal subunit,^20,21 and the U6 intramolecular stem-loop of the spliceosome complex.²² In DNA systems, the presence of protonated A⁺•C base pairs are known to cause mutagenic and carcinogenic effects.^23,24 Measuring the pH-dependence of such properties allows one to infer a macroscopic pK_a of the overall nucleic acid system, but limited information can be obtained about the specific residues that control its activity. Given the ubiquity of protonated nucleotides in regulating pH-dependent activity, the ability to measure the microscopic pK_a value associated with the protonation event at a specific residue is invaluable in identifying key nucleotides of interest, which is often necessary to obtain a deeper mechanistic insight into these pH-dependent processes.

Recently, Al-Hashimi and co-workers discovered the existence of low population transient state conformations that are functionally important in both RNA and DNA systems, some of which are known to exhibit pH-dependent behavior.^25,26 Conventional experimental techniques such as NMR spectroscopy,^27–29 pH-dependent fluorescent nucleobase analogs^30–32 and Raman spectroscopy^33,34 have not been able to directly characterize such pH-dependent transient states, although progress has been made through the development of novel NMR techniques.³⁵ Computational methods such as molecular dynamics (MD) simulations that have been traditionally used to provide mechanistic insight to the role of protonated residues,^36–38 do not model realistic pH-dependent dynamics because the protonation states are fixed throughout the simulation. Therefore, there is a need for pH-coupled MD simulations, where the protonation state of titrating residues changes dynamically in response to their microenvironment. In addition, since no a priori information on the pK_a value of key titrating residues is required, pH-coupled MD simulations are uniquely suited to investigate pH-dependent transient states and other systems where there is limited experimental data.

One form of pH-coupled MD simulations, known as constant pH MD simulations has been developed for proteins,^39–43 and successfully applied to investigate numerous pH-dependent properties.^44–50 However, it was only recently that a newer framework of constant pH MD simulations based on multi-site λ-dynamics (CPHMD^MSλD) was established to address questions related to the pH-dependent properties of nucleic acids.⁵¹ Blind pK_a prediction on the lead-dependent ribozyme has shown that the direction of pK_a shifts were accurately predicted, with an average unsigned error of 1.3 pK_a units relative to experimental pK_a values.⁵² However, for residues in a GAAA tetraloop, which presents significant sampling challenges because of conformation-dependent pK_a behavior and coupled titrating interactions, the calculated pK_a values were predicted with lower accuracy,⁵² hampering the usefulness of CPHMD^MSλD simulations for predictive studies. In this article, we describe the application of pH-based replica exchange (pH-REX) to augment the sampling capabilities of CPHMD^MSλD simulations. Using pH-REX significantly improves sampling of titration and spatial coordinates of the residues in the GAAA tetraloop, reducing the error of A17, the most poorly predicted residue, from −2.9 to −1.2 pK_a units. Our work provides evidence that pH-REX CPHMD^MSλD simulations allow one to achieve accurate pK_a predictions, to around 1 pK_a unit, even for residues that are problematic in conventional CPHMD^MSλD simulations.

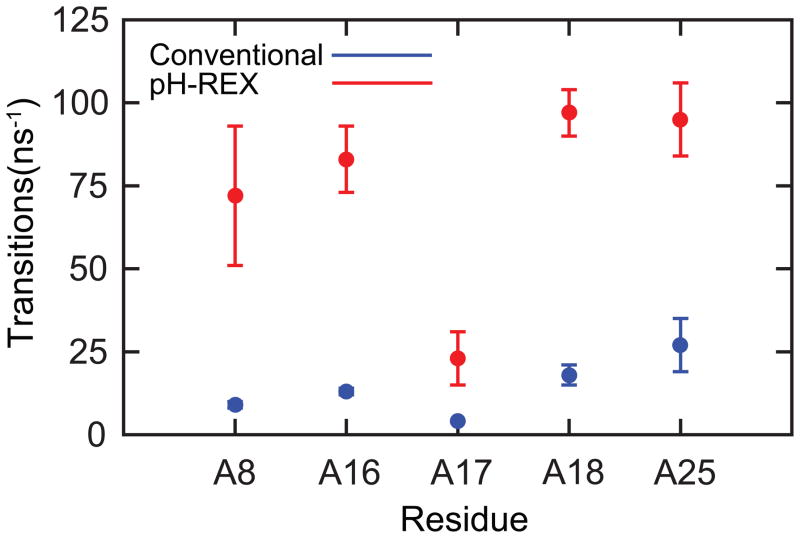
We first present our results on the performance of pH-REX CPHMD^MSλD simulations on the lead-dependent ribozyme. To judge the quality of a computational model, pH-dependent experimental observables, such as microscopic pK_a values, may be used as an indicator of how accurately the CPHMD^MSλD simulation reproduces pH-dependent properties. Unlike proteins, where the microscopic pK_a value of multiple ionizable residues for numerous proteins have been measured,⁵³ the literature of nucleic acid pK_a research is much sparser, with only a single pK_a value measured for a handful of RNA systems. The lead-dependent ribozyme is, to the best of our knowledge, the most thoroughly-studied RNA system from the standpoint of experimentally-measured microscopic pK_a values.⁵⁴ Therefore, we use it as a model system for benchmarking the performance of pH-REX CPHMD^MSλD simulations. The microscopic pK_a values calculated from pH-REX simulations, as summarized in Table 1, are consistent with previous work that utilized CPHMD^MSλD with conventional MD simulations.⁵² As illustrated in Fig. 1, up to an 8-fold improvement in the transition rates in λ-space is observed in our pH-REX simulations. The sampling improvement of titration coordinates results in faster convergence, which is demonstrated by fact that pH-REX sampling achieves the same level of accuracy using a total simulation time that is 5-fold shorter than conventional CPHMD^MSλD simulations. In addition, we also observe that the improvement in λ-space sampling for the residues of the lead-dependent ribozyme is higher than that of the 3-fold improvement in single nucleotide compounds (see Fig. S1).

Table 1.

Calculated pK_a values from conventional and pH-REX CPHMD^MSλD simulations of the lead-dependent ribozyme demonstrate a similar level of accuracy.

Residue	Exp pKa	Conventional CPHMDMSλD (3×5ns)			pH-REX CPHMDMSλD (3ns)
		n	pKa	Error	n	pKa	Error
A4	<3.1	0.4 ± 0.1	0.6 ± 0.1		1.3 ± 0.5	0.9 ± 0.4
A8	4.3 ± 0.3	0.7 ± 0.3	3.7 ± 0.3	−0.6	0.9 ± 0.4	3.8 ± 0.6	−0.5
A12	<3.1	1.1 ± 0.3	0.7 ± 0.3		1.0 ± 0.3	0.6 ± 0.2
A16	3.8 ± 0.4	0.7 ± 0.1	2.6 ± 0.1	−1.2	0.7 ± 0.1	2.6 ± 0.0	−1.2
A17	3.8 ± 0.4	0.4 ± 0.0	0.9 ± 0.5	−2.9	1.0 ± 0.6	1.1 ± 0.5	−2.7
A18	3.5 ± 0.6	0.6 ± 0.0	3.8 ± 0.1	0.3	0.8 ± 0.1	3.6 ± 0.0	0.1
A25	6.5 ± 0.1	0.4 ± 0.1	4.8 ± 0.5	−1.7	0.5 ± 0.1	4.5 ± 0.2	−2.0
AUE				1.3			1.3

Figure 1.

pH-REX CPHMD^MSλD simulations accelerates sampling of titration coordinates by up to 8-fold in the lead-dependent ribozyme.

In complex RNA structures, where multiple residues are titrated simultaneously, the coupled interactions between these titrating groups lead to slower convergence, because the sampling of titration coordinates is hindered by the protonation states of adjacent interacting titrating groups.⁵² The variable biases applied in conventional CPHMD^MSλD simulations only serve to flatten the potential energy surface of each λ variable, but the orthogonal barriers that arise from these coupled titrating interactions are not addressed. Unlike the recent methodological advances in enhanced sampling strategies reported by Yang and co-workers,^55,56 pH-REX sampling does not directly address these orthogonal barriers per se. However, it does periodically shuffle conformations to a higher or lower pH where all residues adopt a uniform protonation state. We suggest that this process effectively decouples the protonation states of interacting residues, allowing one to ameliorate the sampling issues related to these orthogonal barriers.

Having demonstrated that pH-REX accelerates sampling of titration coordinates, we now explore the apparent underprediction of the pK_a value of residue A17, which is situated in the GAAA tetraloop of the lead-dependent ribozyme. We performed an initial 15 ns simulation of the excised GAAA tetraloop for pH values between 1 to 4, and compared the results to conventional CPHMD^MSλD simulations. As summarized in Table 2 and Table S1, the calculated pK_a of residue A17 from the conventional simulations is 1.4, compared to the pK_a of 2.3 obtained using pH-REX sampling. Extending our simulations for an additional 15 ns confirmed that the pK_a value has converged (Fig. S2). On the whole, pH-REX sampling yields systematic improvement of the predicted pK_a values of the GAAA tetraloop, where the average unsigned error (AUE) was reduced to 0.7 pK_a units, which is 50% lower than our previous work.⁵²

Table 2.

pH-REX CPHMD^MSλD simulations of the GAAA tetraloop of lead-dependent ribozyme improved the accuracy of calculated pK_a values compared to straightforward MD simulations.

Residue	GAAA				AAA
	Exp pKa	Conventional CPHMDMSλD (0–15ns)	pH-REX CPHMDMSλD (0–15ns)	pH-REX CPHMDMSλD (16–30ns)	pH-REX CPHMDMSλD (0–15ns)
A16	3.8±0.4	3.2 ± 0.2	3.1 ± 0.1	3.3 ± 0.1	3.5 ± 0.1
A17	3.8±0.4	1.4 ± 0.3	2.3 ± 0.6	2.6 ± 0.4	3.5 ± 0.1
A18	3.5±0.6	3.9 ± 0.1	3.9 ± 0.1	4.0 ± 0.1	3.9 ± 0.1
AUE		1.1	0.9	0.7

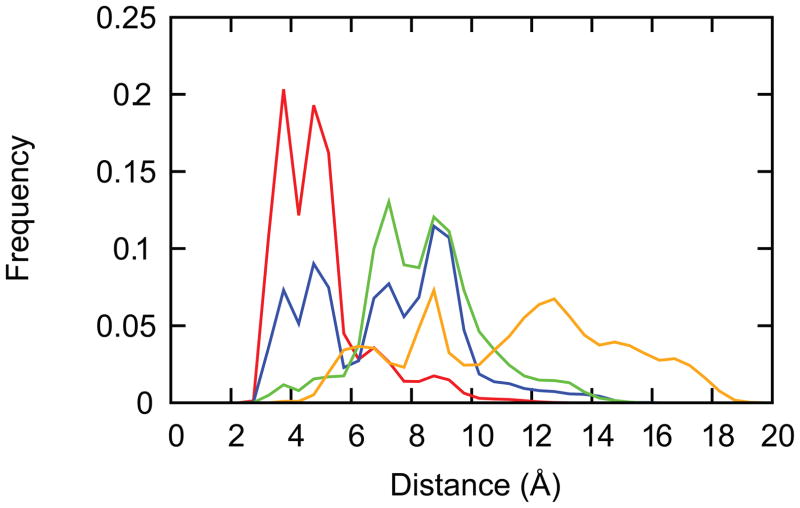
The apparent underprediction of the pK_a value of residue A17 originates from the anti-cooperative interactions between residues A17 and A18, which artificially suppresses the ability of A17 to adopt the protonated state at low pH conditions.⁵² This arises from the triply stacked conformation of the GAAA tetraloop, which is characterized by short interatomic distances between the N1 atoms of the two residues. We analyzed this interatomic distance in our simulations of the GAAA tetraloop at pH 1, in the context of another reference simulation of the AAA trinucleotide sequence, which has no structural elements imposing conformational restrictions on it. As shown in Fig. 2, the N1-N1 distances sampled in our pH-REX simulations of the GAAA tetraloop ranged from 2 to 10 Å, which are intermediate between the conventional GAAA tetraloop simulations ( 2 to 6 Å ) and the AAA trinucleotide simulations ( 6 to 18 Å ). The conformational space sampled using pH-REX is reasonable as it does not exhibit more dynamical behavior than the free AAA trinucleotide, but it also samples more conformations than conventional CPHMD^MSλD simulations of the GAAA tetraloop. This trend of exploring progressively larger N1-N1 distances results in more weakly coupled interactions that is reflected in the pK_a value of the central adenine residue, which increases from 1.4 to 2.3 to 3.5 (Table 2). In addition, we also observed a slight difference in the distribution of the N1-N1 distances between the first 15 ns and the subsequent 15 ns trajectory of the excised GAAA tetraloop. Specifically, the “close contact” region of 3 to 6 Å that describes the initial stacked conformation was partially populated in the first 15 ns, which suggests that the system was still equilibrating. This suggests that sufficient equilibration on the order of a few ns may be required, and metrics such as RMSD relative to the initial structure may be used to determine when equilibration is complete, particularly if one is expecting a significant conformational change in an alternate pH environment.

Figure 2.

Distribution of the interatomic distance of the N1 atoms of residue A17 and A18 of the GAAA tetraloop at pH 1 for a conventional 15ns MD simulation (red trace), the first 15 ns pH-REX simulation (blue trace) and the next 15 ns pH-REX simulation (green trace), compared to a 15 ns pH-REX simulation of the AAA trinucleotide (orange trace).

The experimentally measured pK_a values are a superposition of the microscopic pK_a values of the various conformations visited by the GAAA tetraloop on the timescale accessible to NMR measurements,⁵² and the various pH values at which such measurements were recorded. We clustered the conformations sampled by pH-REX simulations at pH 1 (low pH) and 4 (high pH), and the representative structures are illustrated in Fig. 3 The initial triply-stacked conformation (Fig. 3b), which is representative of the NMR structure solved at physiological pH is known to lower the pK_a value of residue A17. While it may be the dominant conformation sampled at high pH, this conformation is populated only 20% of the time at low pH. We observe that the dominant conformation sampled at low pH is partially unstacked, where the N1-N1 distance is increased to 9.3 Å (Fig. 3a), and a fully unstacked conformation is observed 10% of the time (Fig. 3c). Interestingly, these unstacked conformations are populated 21% of the time at higher pH. The significant improvement in our pK_a predictions for residues in the GAAA tetraloop correspond to the sampling of these alternative conformations, suggesting that sampling using pH-REX provides a more accurate model of the tetraloop’s pH-dependent dynamics. Lastly, our results also indicate that pH-REX CPHMD^MSλD simulations can be used to identify the dominant conformation of nucleic acid systems in different pH environments or low population conformations at physiological pH. With the discovery of pH-dependent transient states in both RNA and DNA systems that have been suggested to be functionally important,^25,26 we anticipate that pH-REX CPHMD^MSλD simulations will provide further structural and mechanistic insight into the findings gleaned from experimental studies, especially in situations where direct experimental characterization of such transient states are challenging.

Figure 3.

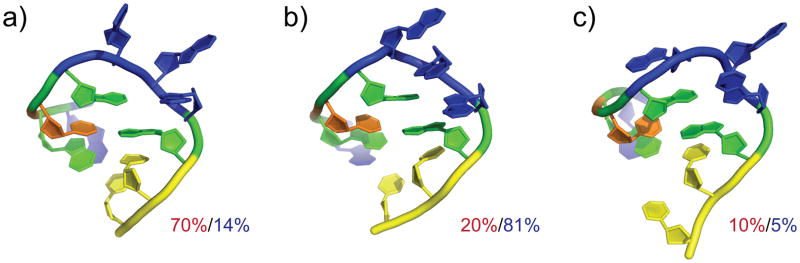
Representative conformations from a cluster analysis of the pH-REX trajectory of the GAAA tetraloop and their relative populations sampled at pH 1 (in red) and pH 4 (in blue).

Thus far, we have shown that pH-REX CPHMD^MSλD simulations are effective in modeling accurate pH-dependent dynamics of small nucleic acid motifs like the GAAA tetraloop. In this final section, we demonstrate the scalability of pH-REX CPHMD^MSλD simulations to larger systems. Our initial pK_a calculations on the full-length ribozyme (Table 1) yielded similar results to conventional CPHMD^MSλD simulations, which suggest that the sampling efficiency is not as high as in our simulations of the excised GAAA tetraloop. Since conformational diffusion across pH space is responsible for enhancing sampling, increasing the total number of accepted Monte Carlo (MC) moves should improve the accuracy of calculated pK_a values. In the full-length ribozyme, the majority (i.e., 10 out of 15) of the residues are base paired and have pKa values of less than 3.⁵² Thus, unlike high pH conditions where most of the titrating residues adopt a uniform protonation state, at low pH conditions the majority of residues would be titrating. This implies that there would be more pronounced potential energy difference between adjacent replicas, and consequently a lower MC exchange rate is expected at low pH. Under low pH conditions, the MC exchange rate of the excised tetraloop was at least 30%, which is 3 times higher than that of the full-length ribozyme (SI Fig S3). This lower exchange rate in the full-length ribozyme is correlated with a reduction in the sampling of titration coordinates, particularly for residue A17 (Fig. 4). As shown in Fig. 4a, increasing the frequency of MC attempts from every 1.0 ps to 0.1 ps significantly increased λ-transitions to ~350–650 ns⁻¹. Prior work by Baptista and co-workers has shown that re-equilibration of the solvent induced by the introduction of a charged protonation state requires 1 to 3 ps,³⁹ and we have observed a similar solvent reorganization triggered by a protonation state change in explicit solvent CPHMD^MSλD simulation.⁵¹ Using the mean solvent relaxation time of 2 ps, one arrives at a transition rate of ~500 ns⁻¹, which balances the need for titration coordinates sampling and solvent relaxation. In some instances, such as residue A8, the transition rate was above this value. We acknowledge that the pH-REX metropolis criterion maintains detailed balance and the results should in principle be unaffected by the MC exchange frequency. However, we observed significant variation in transition rates between the 3 independent runs, which could cause issues in reproducibility and convergence. Therefore, in practice it may be useful to allow for sufficient solvent relaxation occur.

Figure 4.

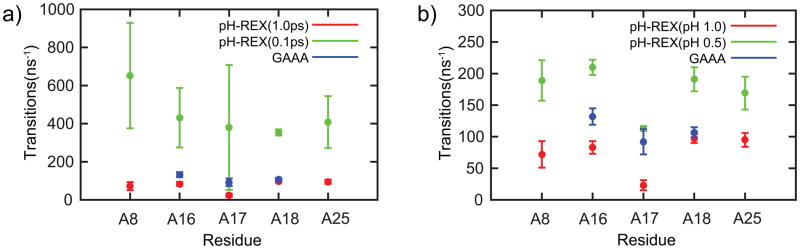
Effects on titration coordinates sampling by (a) increasing the MC attempt frequency and (b) reducing pH window spacing from 1.0 to 0.5.

Our observations on increasing the MC exchange frequency differs with the findings reported by Roitberg and co-workers, where no performance degradation was observed at higher MC exchange frequencies.⁵⁷ This difference is likely due to the fact that our model uses an explicit solvent representation where solvent reorganization needs to be accounted for, whereas the work of Roitberg and co-workers was performed in implicit solvent, which adiabatically adjusts to the protein conformation. Instead of attempting to increase the MC exchange frequency, one may also increase the probability of exchange by reducing the potential energy difference between adjacent windows (i.e. reduce the pH-spacing). In simulations using a smaller spacing of 0.5 pH units the exchange rate for the full-length ribozyme was increased to 40% as shown in SI Fig. S4. As illustrated in Fig. 4b, reducing the pH-spacing more than doubled the transition rate in λ-space. We observed the most significant improvement in the transition rate of residue A17, which increased from 23ns⁻¹ to 113 ns⁻¹. This is on par with the transition rate of 92 ns⁻¹ observed in the GAAA tetraloop. The transition rate was also uniformly consistent across the 3 independent simulation runs, which ensures the robustness of the calculations. Qualitatively, the titration curves obtained across 3 independent runs also demonstrated better convergence for pH-REX simulations with smaller pH spacing (Fig. S5). Finally, using this smaller pH spacing of 0.5, we reran pH-REX CPHMD^MSλD simulations on the full-length ribozyme. After an initial ~10 ns of equilibration, the calculated pK_a values started to converge and results comparable to the GAAA tetraloop were achieved within 13 ns (Table 3, Table S2 and Fig. S6), demonstrating that pH-REX CPHMD^MSλD simulation scales well to simulate pH-dependent properties of full-sized nucleic acid systems.

Table 3.

pH-REX CPHMD^MSλD simulations of the full-length lead-dependent ribozyme at 0.5 pH window spacing demonstrate comparable results to the GAAA tetraloop within 13 ns.

Residue	Exp pKa	pH-REX CPHMDMSλD
		(0–3ns)	(3–8ns)	(8–13ns)	(13–18ns)	(18–23ns)
A16	3.8±0.4	2.6 ± 0.1	2.7 ± 0.2	2.9 ± 0.2	2.9 ± 0.1	2.8 ± 0.1
A17	3.8±0.4	1.4 ± 0.3	1.5 ± 0.6	1.8 ± 0.6	2.4 ± 0.1	2.4 ± 0.1
A18	3.5±0.6	3.8 ± 0.1	3.8 ± 0.1	3.9 ± 0.1	3.8 ± 0.1	3.7 ± 0.0

In conclusion, we have enhanced the framework of constant pH molecular dynamics (CPHMD^MSλD) for nucleic acids with pH-based replica exchange (pH-REX) sampling. Using pH-REX significantly improves sampling of titration and spatial coordinates, and the shuffling of conformations across pH space has the effect of decoupling interactions between titrating residues. This allows us to ameliorate some of the sampling issues related to orthogonal barriers that originate from coupled protonation equilibrium and conformational-dependent pK_a behavior, as illustrated in our example of the GAAA tetraloop motif. Our pK_a calculations on the GAAA tetraloop indicate that pH-REX reduced the average unsigned error (AUE) to 0.7 pK_a units, which is 50% lower than previous work,⁵² and the error of the most poorly predicted residue was drastically reduced from −2.9 to −1.2 pK_a unit. The scalability of pH-REX sampling was also demonstrated by showing that similarly accurate pK_a values could be achieved when simulating full-sized nucleic acid systems, such as the lead-dependent ribozyme. Our results affirm that pH-REX CPHMD^MSλD simulation is maturing into a practical tool for accurate first-principles prediction of nucleic acid protonation equilibrium, where accurate modeling of pH-dependent properties is achieved, even for residues that have hampered convergence due to sampling issues (e.g., slow dynamics and/or coupled titration behavior). Finally, we highlighted that pH-REX CPHMD^MSλD simulations can be used to identify the dominant conformation of nucleic acid structures in alternate pH environments or to provide structural characterization of pH-dependent transient states, making it a useful tool to provide structural and mechanistic insight in the study of pH-dependent properties of nucleic acids.

METHODS

Structure Preparation

Input structures of the nucleotide compounds were generated from the CHARMM topology files using the IC facility in CHARMM. The input structure for lead-dependent ribozyme was generated from the PDB file (Accession code: 1LDZ).⁵⁸ Hydrogen atoms were added using the HBUILD facility in CHARMM.⁵⁹ The systems were solvated in a cubic box of explicit TIP3P water⁶⁰ using the convpdb.pl tool from the MMTSB toolset,⁶¹ and the ionic strength was simulated by adding the appropriate number of Na⁺ and Cl⁻ counterions to match experimental salt concentration (100–150mM NaCl). The two isomers of the test nucleotides were constructed using the patch keywords 5PHO and 3PHO. All other nucleic acid structures were hydroxylated using the 5TER and 3TER patches in CHARMM. The excised GAAA tetraloop was constructed by extracting residues 12 to 21 from the lead-dependent ribozyme, and harmonic distance restraints were applied to enforce base pairing between residues A12 and U21. Patches for the protonated forms of adenine and cytosine were constructed as previously reported (see SI Methods).⁵¹

Simulation Details

MD simulations were performed within the CHARMM macromolecular modeling program (version c36a6) using the CHARMM36 all-atom force field for RNA⁶² and TIP3P water.⁶⁰ The SHAKE algorithm⁶³ was used to constrain the hydrogen-heavy atom bond lengths. The Leapfrog Verlet integrator was used with an integration time step of 2 fs. A non-bonded cutoff of 12 Å was used with an electrostatic force shifting function and a van der Waals switching function between 10 Å and 12 Å. The distance cutoff in generating the list of pairwise interactions was 15 Å. CPHMD simulations utilize an extended Hamiltonian approach, where the protonation state of the residue is described by a continuous variable, λ, which is propagated simultaneously with the spatial coordinates at a specified external pH using multi-site λ-dynamics (see SI Methods).^64,65 After an initial minimization, the system was heated for 100 ps and equilibrated for 100ps (for nucleotide compounds) or 400 ps (for RNA structures), followed by a production run of 3 ns, unless otherwise stated. A pH-REX sampling protocol for CPHMD simulations in hybrid and implicit solvent have been previously reported by Wallace and Shen,⁶⁶ and we have implemented their formalism with our explicit solvent CPHMD^MSλD simulations. Replicas were that were simulated at various pH conditions are exchanged based on the following Metropolis criterion:

$$P=\{\begin{array}{cc}1;& \text{if}\mathrm{\Delta }\le 0\\ exp(-\mathrm{\Delta });& \text{otherwise}\end{array}\text{where}\mathrm{\Delta }=\beta \left[\begin{array}{l}{U}^{\text{pH}}\left(\left\{{\lambda }_i\right\};\text{p}{\text{H}}^{\prime }\right)+U^{\text{pH}}\left(\left\{{{\lambda }_i}^{\prime }\right\};\text{pH}\right)\hfill \\ -U^{\text{pH}}\left(\left\{{\lambda }_i\right\};\text{pH}\right)-U^{\text{pH}}\left(\left\{{{\lambda }_i}^{\prime }\right\};\text{p}{\text{H}}^{\prime }\right)\hfill \end{array}\right]$$ (1)

Exchange attempts were made at every 1 ps unless otherwise stated. CPHMD^MSλD simulations were performed from pH 1 to 4 for the GAAA tetraloop and pH 1 to 8 for the full length lead-dependent ribozyme, with integer value pH spacing (unless otherwise specified). All CPHMD^MSλD simulations were performed in triplicate.

Calculating pK_a values

The populations of unprotonated (N^unprot) and protonated (N^prot) states are defined as the total number of times in the trajectory where conditions λ_α,1 > 0.8 and λ_α,2 > 0.8 are satisfied respectively, and are used to derive the unprotonated fraction (S^unprot):

$$S^{\mathit{unprot}}(\text{pH})=\frac{N^{\mathit{unprot}}(\text{pH})}{N^{\mathit{unprot}}(\text{pH})+N^{\mathit{prot}}(\text{pH})}$$ (2)

These S^unprot ratios that were computed across the entire pH range were then fitted to a generalized version of the Henderson-Hasselbalch formula to obtain a single pK_a value:

$$S^{\mathit{unprot}}(\text{pH})=\frac{1}{1+{10}^{-n(pH-\mathit{pKa})}}$$ (3)

The reported pK_a value and its error correspond to the mean and standard deviation calculated from 3 sets of independent runs. In the calculation of transition rates, a transition is defined as a move in λ space between physical protonation states using the same definitions for calculating N^unprot and N^prot (i.e., moving between λ_α,1 > 0.8 and λ_α,1 < 0.2 constitutes a valid transition). The transition rate statistics reported for each residue was calculated from the simulation where the external pH was closest to the pKa value of the residue.