Abstract
The eukaryotic cell cycle is characterized by alternating oscillations in the activities of cyclin-dependent kinase (Cdk) and the anaphase-promoting complex (APC). Successful completion of the cell cycle is dependent on the precise, temporally ordered appearance of these activities. A modest level of Cdk activity is sufficient to initiate DNA replication, but mitosis and APC activation require an elevated Cdk activity. In present-day eukaryotes, this temporal order is provided by a complex network of regulatory proteins that control both Cdk and APC activities via sharp thresholds, bistability, and time delays. Using simple computational models, we show here that these dynamical features of cell-cycle organization could emerge in a control system driven by a single Cdk/cyclin complex and APC wired in a negative-feedback loop. We show that ordered phosphorylation of cellular proteins could be explained by multisite phosphorylation/dephosphorylation and competition of substrates for interconverting kinase (Cdk) and phosphatase. In addition, the competition of APC substrates for ubiquitylation can create and maintain sustained oscillations in cyclin levels. We propose a sequence of models that gets closer and closer to a realistic model of cell-cycle control in yeast. Since these models lack the elaborate control mechanisms characteristic of modern eukaryotes, they suggest that bistability and time delay may have characterized eukaryotic cell divisions before the current cell-cycle control network evolved in all its complexity.
Introduction
Progression through the eukaryotic cell cycle is a classic example of temporal and spatial organization in the perpetuation of life. In one stage of the cell cycle, called the S phase, the cell replicates its genetic material and packs the two identical sister chromatids into chromosomes. At a later stage, these replicated sister chromatids are segregated to opposite poles of the predivisional cell, in a spatially organized process called mitosis. A new round of DNA replication should only take place in the next cycle, after completion of the previous mitosis (M phase). Strict alternation of S and M phases is essential for successful cell proliferation; therefore, the molecular mechanisms responsible for temporal ordering of these two events are fundamental for all eukaryotic life.
Both S and M phases are triggered by the phosphorylation of cellular proteins required for DNA replication and mitosis by cyclin-dependent kinases (Cdks). A Cdk is active as a protein kinase only in complex with a regulatory subunit, called cyclin. In present-day eukaryotes, different Cdk/cyclin complexes are responsible for initiation of the S and M phases, which suggests a qualitative model of cell-cycle control. According to the qualitative model, the temporal order of the S and M phases is a consequence of alternating oscillations of at least two Cdk/cyclin complexes with different substrate specificities. This might be true, but it is difficult to reconcile with the fact that a single Cdk/cyclin complex (Cdk/cyclin-B) can provide perfect temporal order in the eukaryotic cell cycle (1–3). This observation led to the proposal of a quantitative model of cell-cycle control according to which the oscillation of a single Cdk activity between low and high values is the only fundamental requirement for ordered cell-cycle progression provided that small Cdk activity is sufficient to trigger DNA replication but higher activity is required to bring about the M phase (1–5). Since phosphorylation of S- and M-phase substrates is a reversible process counteracted by protein phosphatases (PPases), there are two (possibly overlapping) explanations for the quantitative model: S-phase substrates may have higher affinities for Cdk than do M-phase substrates, or they may be less susceptible to counteracting PPase activities. The presence of large amounts of S and M substrates of the interconverting enzymes (Cdk and PPase) could create a competition among the substrates, and this competition for Cdk and PPase could be the underlying mechanism responsible for temporal ordering of the S and M phases (in the quantitative model). This competition is further amplified by the fact that several Cdk target proteins are phosphorylated on more than one site (multisite phosphorylation) (6,7). Hence, the several hundred Cdk targets with multiple phosphorylation sites can easily account for an overall concentration of Cdk phosphosites in the millimolar range (6).
Although Cdk activity is dominant from the start of DNA replication until the meta/anaphase transition of mitosis, the ubiquitin-ligase activity of the anaphase-promoting complex (APC) is dominant for the rest of the cell cycle (from mitosis through G1 until the next S phase). The APC is a molecular machine that drives chromosome segregation and exit from mitosis by targeting securin and mitotic cyclins for degradation (8). Similar to Cdks, the APC also modifies many cellular proteins and targets them for proteasome-dependent degradation. In addition, ubiquitylation by the APC is also a multistep process, because the substrates must be polyubiquitylated (in more than four places) to be recognized by the proteasome. Therefore, competition for substrates can also significantly influence the dynamics of APC-dependent protein degradation (9).
In this work, we explore the role of substrate competition with respect to these two fundamental cell-cycle regulators, Cdk and APC. We ask the question, what are the emergent properties of a dynamical network when the substrates of Cdk and APC compete with each other? Our work is strongly influenced by theoretical work on substrate competition in specific signal-transduction pathways (10) and in more general settings (11,12).
Results
Competition between two groups of substrates for Cdk and its counteracting PPase
Case 1: singly phosphorylated substrates
We categorize the numerous substrates of Cdk and its counteracting PPase into two groups, S substrates and M substrates, and we assume that with respect to their interconverting enzymes, substrates in one group have similar kinetic properties, which are different from the properties of the other group. S represents substrates that must be phosphorylated (or dephosphorylated) for S-phase progression, whereas M indicates the group of substrates whose phosphorylation state is crucial for progression through mitosis (Fig. 1). Our grouping is independent of whether phosphorylation activates or inhibits the substrates. For example, we imagine that both DNA-replication licensing factors (e.g., Cdc18 and Cdt1), which are inhibited by Cdk phosphorylation, and replication initiator proteins (e.g., Sld1), which are activated, belong to the S group of substrates. Initially, we consider the case where both pools of substrates are singly phosphorylated and dephosphorylated by Cdk and PPase, according to Michaelis-Menten kinetics. The unphosphorylated forms (S and M) and the phosphorylated forms (SP and MP) mutually inhibit each other’s interconversion in a competitive manner (Fig. 1).
Figure 1.

Scheme of a minimal model for the ordered progression of DNA replication and mitosis. (A) Model containing two groups of substrates (S and M) that can each be phosphorylated once by a Cdk/cyclin complex. Phosphorylation of S promotes progression into DNA replication, whereas phosphorylation of M brings about the entry into mitosis. The dynamics of the model is based on substrate competition between S and M for phosphorylation by Cdk and between SP and MP for dephosphorylation by PPase. In this version of the model, as well as in all models of this study, the kinetics of phosphorylation/dephosphorylation are described by a Goldbeter-Koshland switch (13). (B and C) Bifurcation diagrams of the phosphorylated substrates for DNA replication, SP (B), and mitosis, MP (C), as functions of Cdk activity. In both cases, low Cdk activity results in low levels of SP and MP (the G1 state), whereas high Cdk activity promotes full phosphorylation of S and M (the S/G2/M state). For intermediate Cdk activity, the model exhibits bistability in the phosphorylation of S and M. As Cdk activity rises from 0.1 to 0.25 along the lower branch of the bistable switch, the S substrates become significantly phosphorylated (B), whereas the M substrates remain unphosphorylated (C), which suggests that cells enter the S phase (DNA synthesis) before they commit to mitosis. However, as soon as Cdk activity exceeds ∼0.26, M substrates are abruptly phosphorylated and the cell enters mitosis. Parameter values for the simulations are given in Section 1 of Supplement 1 in the Supporting Material.
Note that the letters S and M refer to several different ideas, depending on context. The S phase and M phase are temporally separate phases of the cell cycle, in which DNA is synthesized and mitotic division is carried out, respectively. S substrates and M substrates refer to proteins that are phosphorylated and/or dephosphorylated during the S phase and M phase of the cell cycle. The letters S and M (SP and MP) are the names of generic representatives of S substrates and M substrates (or their phosphorylated forms). In equations, S and M (SP and MP) represent the concentrations (real numbers) of these proteins.
The kinetic equations describing the time evolution of the concentrations of the phosphorylated forms of S and M are given by
| (1) |
| (2) |
where S = ST – SP, M = MT – MP, and ST and MT are constants (total concentrations of S and M substrates). In these equations, Cdk is the activity of Cdk/cyclin complex.
The definitions of the kinetic parameters used in our calculations, together with their numerical values, are listed in Supplement 1 of the Supporting Material. Since we consider the PPase activity to be constant, we have included it in the corresponding rate constants as maximal rates (V). We scale the concentrations of both substrates (S and M) and their Michaelis constants to the total concentration of phosphoacceptor sites in the cell (substrate concentration multiplied by the average number of phosphorylation sites/substrate). Therefore, our total substrate concentrations (ST and MT) are equal to 1, whereas the Michaelis constants are ≪1. Because the Michaelis constants are all ≪1, the phosphorylation and dephosphorylation reactions in our models behave as Goldbeter-Koshland switches (13). As a consequence, the extent of phosphorylation of S and M substrates is an ultrasensitive function of the ratio of activities of Cdk and PPase. In all the models proposed here, the phosphatase activity is considered to be constant. Thus, the extent of phosphorylation of S and M substrates is only a function of Cdk activity. We assume a constant activity of the phosphatase for the sake of simplicity, to keep the models as minimal as possible. However, it is known that phosphatase activities are regulated in present-day eukaryotic cell cycles. For example, the activity of PP2A-B55 plays a key role in the Greatwall pathway regulating mitosis in higher eukaryotes (14,15), and the activity of Cdc14 phosphatase is critical for mitotic exit in budding yeast (16).
We find that competitive inhibitions among substrates of two Goldbeter-Koshland switches create a bistable response in terms of substrate phosphorylations (Fig. 1). We illustrate the bistable behavior on one-parameter bifurcation diagrams for both SP (Fig. 1 B) and MP (Fig. 1 C) as functions of Cdk (the bifurcation parameter). Both Cdk substrates stay unphosphorylated at small values of Cdk, whereas both of them get fully phosphorylated at high values. However, the phosphorylation threshold is much sharper for M substrates than for S substrates. Both types of substrate get dephosphorylated below a certain Cdk activity threshold, which is smaller than the phosphorylation threshold. Observe that the dephosphorylation threshold is sharper for S substrates than for M substrates. Between the two thresholds, both low- and high-phosphorylation steady states coexist and the system is said to be bistable. The difference in the sharpness of the two thresholds influences the dynamics of phosphorylation and dephosphorylation of the two types of substrate. Indeed, when Cdk activity rises, S substrates get phosphorylated earlier than M substrates, whereas when Cdk activity falls, the opposite is true.
Using a model for the double phosphorylations of MAP kinases, Kholodenko and colleagues predicted a similar bistable response (10,17). The difference between our model and that of Kholodenko is that we consider two different substrates phosphorylated at one site each, whereas they studied double phosphorylation of a single substrate (MAP kinases).
In summary, two groups of competitive monophosphorylated Cdk substrates can create a bistable switch with coexisting barely and fully phosphorylated states, but the fully phosphorylated states of S and M substrates are mostly overlapping, as functions of Cdk activity.
The minimal model proposed in Fig. 1 might be sufficient to explain the ordered progression of the S and M phases, if phosphorylation of only a fraction of S substrates is sufficient to trigger DNA replication, whereas most M-phase substrates must be phosphorylated to enter mitosis. However, in the next section, we will see that, under more realistic assumptions, it is possible to achieve more robust, ordered progression from DNA replication to mitosis.
Case 2: doubly phosphorylated substrates
Allowing for double phosphorylation of S and M substrates, we construct a network (Fig. 2) of coupled Kholodenko-type bistable switches. Unphosphorylated and monophosphorylated substrates are competing for phosphorylation by the kinase Cdk, whereas the monophosphorylated and doubly phosphorylated substrates are competing for dephosphorylation by the counteracting PPase.
Figure 2.
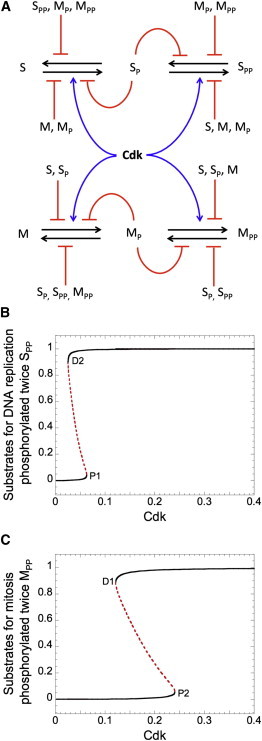
A model for the ordered progression of DNA replication and mitosis based on double phosphorylation of S and M substrates. (A) A kinase, Cdk, can phosphorylate twice the substrates required for DNA replication, S, and mitosis, M. The unphosphorylated (S and M) or monophosphorylated (SP and MP) substrates compete for phosphorylation by the kinase, while the monophosphorylated and twice-phosphorylated (SPP and MPP) substrates compete for dephosphorylation by the counteracting PPase. (B and C) Bifurcation diagrams of SPP and MPP as functions of Cdk activity. As Cdk activity increases from 0, the system passes through two domains of bistability. At the edge of the first domain (Cdk ≈ 0.06), the S substrates become fully phosphorylated and the cell commences DNA replication. Only later, when Cdk activity increases beyond the edge of the second bistability domain (Cdk ≈ 0.24) do the M substrates become fully phosphorylated, at which point the cell enters mitosis. Parameter values for these simulations are given in Section 2 of Supplement 1 in the Supporting Material.
The kinetic equations describing the time evolution of the unphosphorylated forms of S and M, and the doubly phosphorylated forms (SPP and MPP) are given by Eqs. 3–6.
| (3) |
| (4) |
| (5) |
| (6) |
The monophosphorylated forms are calculated from the conservation equations
Supplement 1 of the Supporting Material provides the numerical values of the kinetic parameters used in our calculations. As before, the steady-state responses of SPP and MPP are illustrated on bifurcation diagrams (Fig. 2, B and C), using Cdk as the bifurcation parameter (assuming constant activity of PPase). Competition between the two substrates for Cdk and PPase creates bistability, as in the monophosphorylated case. However, in this case, the thresholds for phosphorylation and dephosphorylation of S and M substrates are different, which creates two domains of bistability with four saddle-node bifurcation points (P1, P2, D1, and D2). Therefore, when Cdk activity is rising, the DNA replication substrates (S) get doubly phosphorylated above P1, whereas the mitotic substrates stay unphosphorylated. Double phosphorylation of M substrates requires Cdk activity to pass a higher threshold (P2). This difference in the phosphorylation thresholds could explain why cells initiate DNA replication earlier than they enter into mitosis.
In Fig. 3, we show that whereas the singly-phosphorylated-substrates model (Fig. 1 A) exhibits a single domain of bistability (see Supplement 2 of the Supporting Material: Domain of bistability for the singly phosphorylated substrates model), the doubly-phosphorylated-substrates model (Fig. 2 A) exhibits two domains of bistability. The single domain of bistability in Fig. 3 A separates a region where the substrates for DNA replication and mitosis are mainly unphosphorylated (for low Cdk activity) from a region where they are mainly phosphorylated (for high Cdk activity). The two domains of bistability in Fig. 3 B provide a more robust separation of the phosphorylation of S-phase substrates from M-phase substrates. Starting from a low level of Cdk, the first domain of bistability delimits a region of low SPP from a region of high SPP, whereas M stays mainly in an unphosphorylated state. The second domain of bistability separates regions of low and high MPP. By allowing a separation in the thresholds for S and M phosphorylation, the two steps of substrate phosphorylation and dephosphorylation improve the separation between the phases of DNA replication and mitosis. Moreover, the model shows that the bistability domains are enlarged, with two steps of phosphorylation and dephosphorylation of S and M substrates as compared to a single step (compare Fig. 3, A and B).
Figure 3.

Two-parameter bifurcation diagrams (k1M versus Cdk) for the models in Figs. 1 and 2. (A) The model with singly phosphorylated substrates has a single domain of bistability. (B) The model with doubly phosphorylated substrates has two domains of bistability. Regions where the steady-state levels of phosphorylated substrates (SP and MP in A and SPP and MPP in B) are high or low are indicated. Other parameter values used in these calculations are given in Supplement 1 of the Supporting Material.
Returning to Fig. 2, B and C, we observe that when Cdk activity is dropping, the two groups of substrates get dephosphorylated at different Cdk activities: M substrates get dephosphorylated first (below D1), whereas SPP disappears later (below D2). Because replication licensing factors belong to the S-group of substrates, this temporal difference in dephosphorylation can explain why cells license replication origins only after they exit from mitosis. Indeed, the relicensing of replication origins only after Cdk activity drops below a low threshold is critical for the subsequent rise in activity to trigger S-phase onset and hence for the proper alternation of the S and M phases.
This temporal ordering of phosphorylation and dephosphorylation of S and M substrates requires an oscillation of Cdk activity, which we discuss in the next section.
Competition between APC substrates can create an important time delay
Case 1: competition-dependent oscillations
APC gets activated during mitosis, because it is one of the M-phase substrates of Cdk (18). Active APC polyubiquitylates many proteins, which targets them to proteasome-dependent degradation and thereby drives the cell out of mitosis. However, successful exit from mitosis requires the degradation of only two proteins in budding yeast cells (19) and fruit fly cells (20). One of these proteins is cyclin B (CycB), which is required for Cdk activity in mitosis. CycB degradation destabilizes the mitotic state by inactivating Cdk, which results in APC inactivation as well. The other protein is securin, an inhibitor of anaphase separation of sister chromatids. Securin degradation releases separase, a protease that cleaves a component of the cohesin complex that holds together the sister-chromatid pairs. In this section, we develop a model assuming that securin and CycB competitively inhibit each other for APC-dependent degradation (Fig. 4 A). That securin and CycB compete with each other for APC-dependent ubiquitylation has been demonstrated experimentally in mouse oocytes (21).
Figure 4.
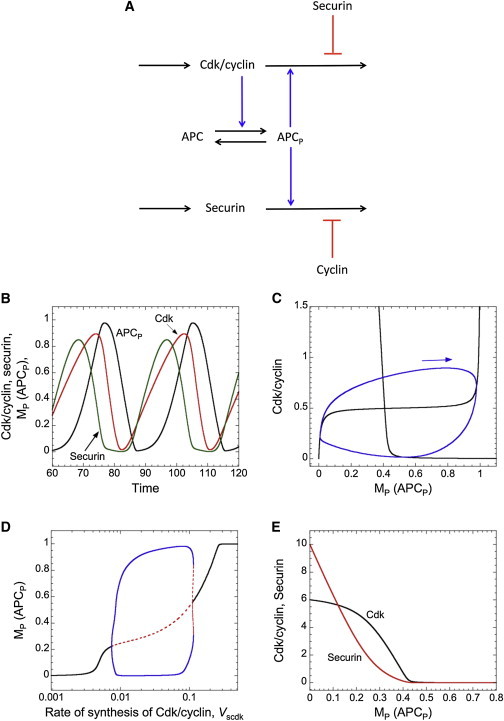
A minimal, embryonic-type cell-cycle oscillator. (A) Scheme of a three-variable oscillator based on negative feedback between Cdk/cyclin and APC. Cdk ensures the phosphorylation of APC, which then promotes the degradation of Cdk/cyclin. A time delay is introduced by competitive inhibition between Cdk/cyclin and securin for polyubiquitylation by APC. (B) Time course of sustained oscillations of Cdk/cyclin, securin, and the phosphorylated form of APC. (C) The limit cycle (closed curve) is projected onto the Cdk/cyclin versus APCP plane. The arrow indicates the direction of motion along the limit cycle. Black curves are the Cdk/cyclin and APCP nullclines. (D) Bifurcation diagram. APCP as a function of the rate of synthesis of Cdk/cyclin, Vscdk. Solid curves indicate stable steady states (for low and high values of Vscdk) and stable limit cycles (for intermediate values of Vscdk); dashed curves indicate unstable steady states and unstable oscillations. (E) Cdk/cyclin and securin nullclines when APCP is considered as a parameter. Parameter values for the simulations are given in Section 3 of Supplement 1 in the Supporting Material.
The kinetic equations describing the time evolution of the Cdk/CycB complex (Cdk), of the phosphorylated form of APC (APCP), and of securin (Sec) are given by Eqs. 7 to 9:
| (7) |
| (8) |
| (9) |
with the conservation equation
Supplement 1 in the Supporting Material shows the list of parameters together with their numerical values used in our simulations in Fig. 4. Since (we assume) securin is a better APC substrate than CycB, securin delays CycB degradation (Fig. 4 B), which creates a time delay in the negative-feedback loop between Cdk/CycB and the APC. This time-delayed negative-feedback loop generates oscillations in CycB and securin levels and in APC activity (Fig. 4 B). In the absence of securin the two-component negative-feedback loop cannot show sustained oscillations (not shown).
A projection of the limit cycle on the Cdk-versus-APCP phase plane is illustrated in Fig. 4 C. The APCP nullcline is sigmoidal, because the APC is regulated by a Goldbeter-Koshland switch. A threshold characterizes the Cdk nullcline, because securin is the preferential APC substrate (Fig. 4 E). Indeed, securin is degraded more rapidly than Cdk when the level of APCP increases. Sustained oscillatory behavior, corresponding to cell-cycle progression, appears only in a certain range of CycB synthesis rate (Vscdk), as illustrated by the one-parameter bifurcation diagram in Fig. 4 D. A similar dynamical behavior is observed with the rate of synthesis of securin, Vssec (not shown). The fact that the model oscillates only in a particular window of Vscdk or Vssec values suggests that appropriate levels of Cdk/cyclin and securin are needed to ensure that the time delay in the negative-feedback loop is consistent with sustained oscillations.
Case 2: competition-independent oscillations
So far, we have a minimal cell-cycle oscillator, based on competitive inhibition between CycB and securin for APC-dependent degradation. Next, we extend the minimal model by including double phosphorylation of APC. In this case, there is competitive inhibition between the different phosphoforms of APC for phosphorylation by Cdk/cyclin and dephosphorylation by PPase (Fig. 5 A). This extended model also exhibits sustained oscillations (Fig. 5 B). In the extended model, securin degradation is no longer necessary for sustained oscillation (Fig. 5 C), because APC behaves as a bistable switch in response to changing Cdk activity (Fig. 5, D and E). Indeed, bistability generates a hysteretic response, which creates a time delay in the dynamic network that can compensate for the absence of securin (22). Superimposed on the bistable switch are the limit-cycle oscillations (closed curves) of the model in the presence (Fig. 5 D) or absence (Fig. 5 E) of securin. We observe that the limit cycle surrounds completely the bistable switch in the presence of securin, whereas it does not reach the upper branch of the bistable switch in the absence of securin. The fact that securin is not needed for sustained oscillations and repetitive cycling is in agreement with experimental observations that securin is not necessary for cell-cycle progression in yeasts (23) or mammalian cells (24).
Figure 5.

Minimal oscillator with two steps of phosphorylation and dephosphorylation of M substrates (namely, APC). (A) Schematic diagram. Cdk/cyclin phosphorylates M and MP, and the doubly phosphorylated form of M (MPP) promotes the degradation of Cdk/cyclin. The different phosphoforms of M compete for phosphorylation by Cdk and dephosphorylation by PPase. (B and C) Time evolution of Cdk/cyclin, securin, and MPP in the presence or absence, respectively, of securin. (D and E) For the cases with and without securin, the limit cycle (closed curve) is projected onto the APCPP-versus-Cdk/cyclin phase plane. The S-shaped curve is the APCPP nullcline. For intermediate values of Cdk/cyclin, a region of bistability is present in the phosphorylation state of APC, whether or not securin is present. Arrows indicate the direction of motion along the limit cycle. (F and G) Bifurcation diagrams for MPP versus Vscdk in the presence or absence, respectively, of securin. Solid curves indicate stable steady states or maxima and minima of the sustained oscillations, and dashed curves indicate unstable states. With securin present, the limit-cycle region is bounded by a SNIC bifurcation at Vscdk ≈ 0.005 and a Hopf bifurcation at Vscdk ≈ 0.15. In the absence of securin, sustained oscillations are still possible, and in this case, the limit-cycle region is bounded by two Hopf bifurcations. Parameter values for the simulations are given in Section 4 of Supplement 1 in the Supporting Material.
The role of securin in the dynamics of the negative-feedback oscillator model with double phosphorylation of APC is illustrated in one-parameter bifurcation diagrams (Fig. 5, F and G). Although securin is not needed for the limit-cycle oscillations, securin increases the amplitude of oscillations because it extends the time delay. To our knowledge, there is no experimental evidence that securin influences the amplitude of CycB oscillations.
In conclusion, a minimal model of cell-cycle regulation, based on the Cdk-APC negative-feedback loop, can exhibit sustained oscillations due to time delays that come from three different sources:
-
1.
competitive inhibition between securin and cyclin for APC-dependent degradation;
-
2.
a bistable switch in the phosphorylation state of APC;
-
3.
inhibitory phosphorylation of Cdk/CycB complexes, a mechanism that is not discussed here, but see Novak and Tyson (25).
A substrate competition model for eukaryotic cell-cycle oscillations
Combining our models for ordered progression through DNA replication and mitosis (Fig. 2) and for a minimal cell-cycle oscillator (Figs. 4 and 5), we now propose a simple model for cell-cycle regulation based on competition of substrates for phosphorylation by Cdk and ubiquitylation by APC (see Fig. 6 A). This model incorporates two groups of substrates, one required for DNA replication (S) and one for mitosis (M), and a resetting mechanism for inactivation of Cdk/CycB at the end of mitosis due to the aforementioned negative-feedback loop. To this end, we assume that APC is one of the M-phase substrates of Cdk and PPase.
Figure 6.
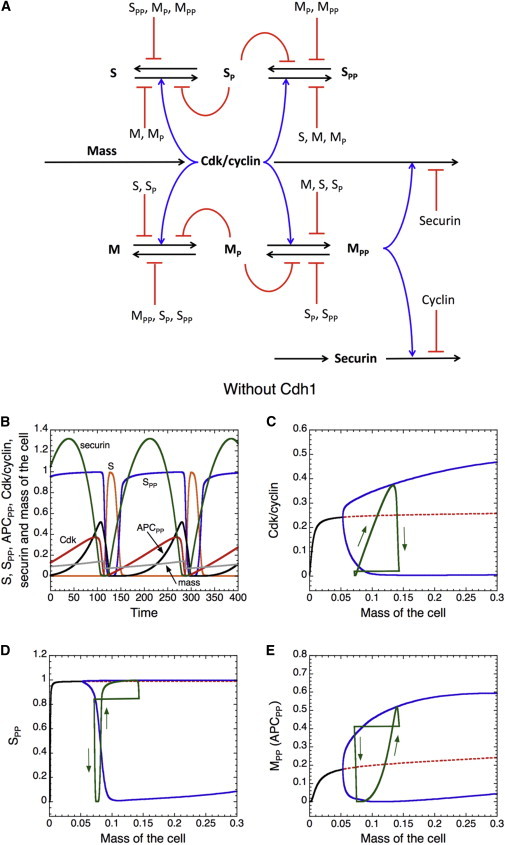
A model of Cdk oscillations with sequential activation of DNA replication and mitosis. (A) Schematic diagram, combining the basic features of Figs. 2A and 4A. Two types of substrate competition are present in this model: 1), competitive inhibition between the different phosphoforms of S and M substrates for Cdk and its counteracting PPase; and 2), competitive inhibition between Cdk/cyclin and securin for ubiquitylation by active APC (APCPP). Growth control of the cell cycle is incorporated by assuming that the rate of synthesis of Cdk/cyclin is proportional to the mass of the cell. (B) Time courses of Cdk/cyclin, S, SPP, APCPP, securin, and cell mass. In these simulations, mass increases exponentially with a doubling time of 190 time units. The rate of cyclin synthesis, Vscdk in Eq. 7, is multiplied by mass to couple cyclin accumulation to cell growth. Binary cell division is assumed to occur when Cdk drops below a chosen threshold (0.02) at the end of mitosis. Phosphorylation of S, i.e., initiation of DNA replication, precedes phosphorylation of APC, i.e., entry into mitosis. (C–E) Bifurcation diagrams of Cdk/cyclin, SPP, and APCPP are shown as functions of cell mass, considered as a parameter. Solid curves indicate stable steady states or maxima and minima of the sustained oscillations, dashed curves indicate unstable states, and closed curves indicate cell-cycle trajectory from B. Parameter values for the simulations are given in section 5 of Supplement 1 in the Supporting Material.
A characteristic feature of cell division in growing cells is that they divide as often as they double their cytoplasmic mass (balanced growth and division). To capture this feature of cell-cycle control, we make the rate of cyclin synthesis proportional to cell mass, which (we assume) is increasing exponentially. We also assume that cell mass is halved when Cdk activity drops below a certain threshold at the end of mitosis. Observe that in this model, in addition to the negative feedback between Cdk/cyclin and APC, there is a second negative-feedback loop between cell mass and Cdk activity, because cell growth drives increased CycB synthesis, whereas Cdk activation in mitosis eventually leads to a reduction in cell mass at division.
Time courses of S, SPP, APCPP, Cdk, Sec, and cell mass are shown in Fig. 6 B. Although this model generates growth-controlled oscillations in cell-cycle regulators and their substrates (Fig. 6 B), the duration of the G1 phase, when Cdk activity is low, is much too short. To understand the dynamical basis of these oscillations, we performed bifurcation analysis of the regulatory proteins as functions of cell mass (Fig. 6, C–E). The bifurcation diagrams reveal stable limit cycles arising at a supercritical Hopf bifurcation and growing quickly to large amplitude just beyond the bifurcation point. For small cell mass, the model is characterized by a stable steady state corresponding to cell-cycle arrest. Superimposing the cell-cycle trajectories (Fig. 6 B) on the bifurcation diagrams (Fig. 6, C–E, closed curves) indicates that cells are cycling in the limit-cycle domain above the bifurcation point. Since the cycle time is identical to the mass doubling time, these cycles are growth-controlled, but they lack a bona fide size-control checkpoint. A size-control checkpoint represents a steady state that blocks cell-cycle oscillations until a critical size is reached (see below). In this network, the period of the oscillation is cell-mass dependent, which allows balanced growth and division.
Nongrowing, quiescent cells usually arrest in the G1 phase of the cell cycle without any Cdk activity, but this model has a stable steady state of low Cdk activity only at vanishingly small cell mass, because after exiting from mitosis, APC turns off in response to the drop in Cdk activity, and the inactivation of APC allows cyclin to rise again. However, in present-day eukaryotes, an APC regulator, called Cdh1, gets activated by dephosphorylation at mitotic exit. Active Cdh1 promotes the degradation of cyclin and securin (see Fig. 7 A), whereas Cdk/cyclin inhibits Cdh1 by phosphorylation. This double-negative-feedback loop (Cdh1 degrades cyclin, Cdk/cyclin inhibits Cdh1) gives rise to a stable G1-like steady state (Fig. 7 B) characterized by a high level of dephosphorylated, active Cdh1 (S substrate) and a low level of Cdk/cyclin. In effect, Cdh1 is as an amplifier of APC function. Once APC becomes active, Cdk activity falls due to the degradation of cyclin by APC. The reduction in Cdk activity allows dephosphorylation and activation of Cdh1, which takes over the APC’s role of degrading cyclin and securin.
Figure 7.

Dynamical behavior of the final model with Cdh1 as an S substrate. (A) Schematic diagram. (B) Time courses of Cdk/cyclin, S (Cdh1), SPP (Cdh1PP), APCPP, securin, and cell mass. Notice that Cdh1 allows an extended G1 phase where S is unphosphorylated (compare Fig. 7B with Fig. 6B). In this case, terms for Cdk degradation by Cdh1, , and for securin degradation by Cdh1, , are added to Eqs. 7 and 9, respectively. (C–E) Bifurcation diagrams of Cdk/cyclin, SPP, and APCPP are plotted as functions of cell mass, considered as a parameter. Superimposed on these bifurcation diagrams are the limit-cycle oscillations (closed curve) in B. Parameter values for the simulations are given in section 5 of Supplement 1 in the Supporting Material.
This G1-like steady state is evident in the bifurcation diagrams (Fig. 7, C–E) for the network in Fig. 7 A. The G1-like steady state gives way to large-amplitude limit-cycle oscillations at a saddle node bifurcation point on an invariant circle (SNIC) at cell mass ≈ 0.21. Superimposing the cell-cycle trajectories of Fig. 7 B on the bifurcation diagrams indicates that in each cycle, the cell oscillates back and forth across the SNIC bifurcation. As cell mass increases during the G1 phase, the cell crosses this bifurcation point and enters transiently into a domain of sustained oscillations. The level of Cdk/cyclin increases during S/G2/M, eventually activating the APC. Once activated, the APC promotes degradation of Cdk/CycB, which triggers cell division and resetting of the cell cycle back to the G1-like steady state. In our experience, a SNIC bifurcation provides more reliable growth control of the cell-division cycle than does a Hopf bifurcation (26).
Discussion
The eukaryotic cell cycle is controlled by alternating activities of Cdks and the APC. Cdk/cyclin complexes phosphorylate proteins required for DNA replication (S phase) and mitosis (M phase). APC-dependent ubiquitylation targets proteins for degradation by the proteasome. Since both Cdk and APC have numerous substrates in eukaryotic cells and modify those substrates at multiple sites, it is reasonable to assume competition among these substrates for their catalysts. Numerous theoretical studies have stressed the role of phosphorylation/dephosphorylation cycles and substrate competition in cell signaling to promote bistable behavior and ultrasensitive response (10,17,27–29). A study based on both theoretical and experimental approaches also showed that ultrasensitivity in the inactivation of the kinase Wee1, a critical G2/M regulator of the cell cycle, could emerge as a result of substrate competition (30). Inspired by these studies, we have analyzed here the potential role of substrate competition and/or multisite modification of Cdk and APC substrates in the regulation of the eukaryotic cell cycle.
First, we show that competition between two groups of Cdk substrates, whose phosphorylations are required for DNA replication (S) and mitosis (M), generates bistable behavior (Figs. 1 and 2). In these models, the substrates are competing for both of their interconverting enzymes, Cdk and its counteracting PPase. We show that the number of bistable domains is dependent on the number of phosphorylation sites on the substrates. With single-site phosphorylation of both S and M substrates, only one domain of bistability is generated, with sharp kinase/phosphatase thresholds. Hence, as Cdk activity rises and falls, both S and M substrates are phosphorylated and dephosphorylated simultaneously (Fig. 1). Therefore, a single competitive phosphorylation/dephosphorylation cycle of S and M substrates cannot explain the temporal separation of DNA replication and mitosis during cell-cycle progression. However, double phosphorylation of S and M substrates can provide two domains of bistability with separate phosphorylation/dephosphorylation thresholds of S and M substrates (Figs. 2 and 3). The different thresholds could explain why S and M substrates get phosphorylated at different levels of rising Cdk activity, and hence why DNA replication precedes mitosis. Furthermore, S-phase substrates are dephosphorylated at a lower kinase/phosphatase ratio than mitotic substrates, which could explain why the block of rereplication is released only after cells exit from mitosis.
These observations suggest that multisite phosphorylation of competitive S and M substrates is a possible theoretical foundation of the so called quantitative model for cell-cycle progression (2–5). The quantitative model is supported by experimental observations showing that oscillation of a single Cdk/cyclin fusion protein in fission yeast is sufficient to trigger the major cell-cycle events in proper sequence (3). These authors showed that DNA replication commences in response to a low activity of Cdk/cyclin, whereas mitosis requires Cdk/cyclin to cross a much higher activity threshold (3).
We have also analyzed the dynamical consequences of substrate competition and multisite phosphorylation in case of APC-catalyzed polyubiquitylation of proteins, which leads to their degradation by proteasomes. APC is activated by Cdk/cyclin-dependent phosphorylation, and one of its targets is cyclin itself, which creates a negative-feedback loop. We show that this negative feedback can drive sustained limit-cycle oscillations if
-
1.
another APC substrate competitively inhibits cyclin degradation (Fig. 4), or
-
2.
the APC is activated by Cdk/cyclin-dependent multisite phosphorylation (Fig. 5).
Since cyclin and securin are the only essential APC substrates in yeast and Drosophila, we assume that securin is delaying cyclin degradation. However, securin is not an essential protein for cell cycle oscillations in yeast. Perhaps some APC substrate other than securin is ubiquitylated faster than cyclin and accounts for the time delay, but more likely, the time delay is attributable to the fact that APC activation requires Cdk-dependent phosphorylation at numerous sites. If at least two of these sites are competing for Cdk and PPase, then a bistable switch is created that generates the required time delay for the negative feedback to oscillate. We show that a combination of these two time-delay mechanisms (competition of APC substrates and APC multisite phosphorylation) creates a robust, periodic fluctuation of Cdk/cyclin activity that could be the heart of the eukaryotic cell-cycle clock.
By combining this clock model with the model for ordered phosphorylation of Cdk substrates, we create a simple, effective model for the eukaryotic cell cycle. In this model, the clock mechanism guarantees the fluctuation of Cdk/cyclin activity between low and high values by periodic activation of APC (Fig. 6). Rising Cdk activity phosphorylates DNA-replication substrates (S) first and mitotic substrates (M) later. Assuming that the rate of cyclin synthesis is proportional to the size of the cell, the oscillator adjusts its period to the mass doubling time. Therefore, cell mass is doubled during the cell cycle and halved at cell division.
To account for the extended G1 phase in most eukaryotic cell cycles, we have supplemented the model with a role for Cdh1-dependent activation of the APC after exit from mitosis. At the G1/S transition, Cdh1 gets inhibited by Cdk-dependent phosphorylation and stays inactive until mitotic exit, when PPase activity prevails over Cdk. Since the temporal profile of Cdh1 phosphorylation is identical to that of S substrates, we identify active Cdh1 with unphosphorylated S substrates. With this simple extension, the model describes G1 size-controlled cell cycles of eukaryotes (Fig. 7).
Many experimental and theoretical studies have emphasized the importance of these molecular regulatory mechanisms for correct progression through the eukaryotic cell cycle. These studies, pertaining to embryos (25,31–33), yeast cells (34,35), and mammalian cells (36–44), have amply demonstrated that cell-cycle progression is driven by interlaced positive and negative-feedback loops in the regulation of cyclin-dependent kinases. The model proposed here suggests that cell-cycle regulation depends on at least two levels of bistability, the first from positive-feedback loops embedded in the molecular regulatory network itself, and the second from the intrinsic kinetics of competition between different substrates for protein kinases or for ubiquitin ligases. From an evolutionary point of view, because many of the sophisticated positive-feedback loops in the regulatory mechanism were probably missing in primitive cells, the second source of bistability might have been of great importance for the ordered progression of DNA replication and mitosis in the earliest eukaryotes.
Acknowledgments
C.G. holds a postdoctoral research fellowship from the Foundation Philippe Wiener–Maurice Anspach. J.J.T. is supported by grants from the National Institutes of Health (5R01-GM078989-07 and 1U54-CA149147-03). The work in B.N.’s group was supported by Biotechnology and Biological Sciences Research Council and by the European Community's Seventh Framework Programmes UniCellSys/201142 and MitoSys/241548.
Supporting Material
References
- 1.Fisher D.L., Nurse P. A single fission yeast mitotic cyclin B p34cdc2 kinase promotes both S-phase and mitosis in the absence of G1 cyclins. EMBO J. 1996;15:850–860. [PMC free article] [PubMed] [Google Scholar]
- 2.Stern B., Nurse P. A quantitative model for the cdc2 control of S phase and mitosis in fission yeast. Trends Genet. 1996;12:345–350. [PubMed] [Google Scholar]
- 3.Coudreuse D., Nurse P. Driving the cell cycle with a minimal CDK control network. Nature. 2010;468:1074–1079. doi: 10.1038/nature09543. [DOI] [PubMed] [Google Scholar]
- 4.Uhlmann F., Bouchoux C., López-Avilés S. A quantitative model for cyclin-dependent kinase control of the cell cycle: revisited. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2011;366:3572–3583. doi: 10.1098/rstb.2011.0082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Oikonomou C., Cross F.R. Rising cyclin-CDK levels order cell cycle events. PLoS ONE. 2011;6:e20788. doi: 10.1371/journal.pone.0020788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kõivomägi M., Valk E., Loog M. Dynamics of Cdk1 substrate specificity during the cell cycle. Mol. Cell. 2011;42:610–623. doi: 10.1016/j.molcel.2011.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Holt L.J., Tuch B.B., Morgan D.O. Global analysis of Cdk1 substrate phosphorylation sites provides insights into evolution. Science. 2009;325:1682–1686. doi: 10.1126/science.1172867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murray A.W. Recycling the cell cycle: cyclins revisited. Cell. 2004;116:221–234. doi: 10.1016/s0092-8674(03)01080-8. [DOI] [PubMed] [Google Scholar]
- 9.Rape M., Reddy S.K., Kirschner M.W. The processivity of multiubiquitination by the APC determines the order of substrate degradation. Cell. 2006;124:89–103. doi: 10.1016/j.cell.2005.10.032. [DOI] [PubMed] [Google Scholar]
- 10.Ortega F., Garcés J.L., Cascante M. Bistability from double phosphorylation in signal transduction. Kinetic and structural requirements. FEBS J. 2006;273:3915–3926. doi: 10.1111/j.1742-4658.2006.05394.x. [DOI] [PubMed] [Google Scholar]
- 11.Qiao L., Nachbar R.B., Shvartsman S.Y. Bistability and oscillations in the Huang-Ferrell model of MAPK signaling. PLOS Comput. Biol. 2007;3:1819–1826. doi: 10.1371/journal.pcbi.0030184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ventura A.C., Sepulchre J.A., Merajver S.D. A hidden feedback in signaling cascades is revealed. PLOS Comput. Biol. 2008;4:e1000041. doi: 10.1371/journal.pcbi.1000041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goldbeter A., Koshland D.E., Jr. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA. 1981;78:6840–6844. doi: 10.1073/pnas.78.11.6840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vigneron S., Brioudes E., Castro A. Greatwall maintains mitosis through regulation of PP2A. EMBO J. 2009;28:2786–2793. doi: 10.1038/emboj.2009.228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Castilho P.V., Williams B.C., Goldberg M.L. The M phase kinase Greatwall (Gwl) promotes inactivation of PP2A/B55δ, a phosphatase directed against CDK phosphosites. Mol. Biol. Cell. 2009;20:4777–4789. doi: 10.1091/mbc.E09-07-0643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Queralt E., Uhlmann F. Cdk-counteracting phosphatases unlock mitotic exit. Curr. Opin. Cell Biol. 2008;20:661–668. doi: 10.1016/j.ceb.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Markevich N.I., Hoek J.B., Kholodenko B.N. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 2004;164:353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pines J. Cubism and the cell cycle: the many faces of the APC/C. Nat. Rev. Mol. Cell Biol. 2011;12:427–438. doi: 10.1038/nrm3132. [DOI] [PubMed] [Google Scholar]
- 19.Thornton B.R., Toczyski D.P. Securin and B-cyclin/CDK are the only essential targets of the APC. Nat. Cell Biol. 2003;5:1090–1094. doi: 10.1038/ncb1066. [DOI] [PubMed] [Google Scholar]
- 20.Oliveira R.A., Hamilton R.S., Nasmyth K. Cohesin cleavage and Cdk inhibition trigger formation of daughter nuclei. Nat. Cell Biol. 2010;12:185–192. doi: 10.1038/ncb2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Marangos P., Carroll J. Securin regulates entry into M-phase by modulating the stability of cyclin B. Nat. Cell Biol. 2008;10:445–451. doi: 10.1038/ncb1707. [DOI] [PubMed] [Google Scholar]
- 22.Novak B., Tyson J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008;9:981–991. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Alexandru G., Uhlmann F., Nasmyth K. Phosphorylation of the cohesin subunit Scc1 by Polo/Cdc5 kinase regulates sister chromatid separation in yeast. Cell. 2001;105:459–472. doi: 10.1016/s0092-8674(01)00362-2. [DOI] [PubMed] [Google Scholar]
- 24.Mei J., Huang X., Zhang P. Securin is not required for cellular viability, but is required for normal growth of mouse embryonic fibroblasts. Curr. Biol. 2001;11:1197–1201. doi: 10.1016/s0960-9822(01)00325-6. [DOI] [PubMed] [Google Scholar]
- 25.Novak B., Tyson J.J. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J. Cell Sci. 1993;106:1153–1168. doi: 10.1242/jcs.106.4.1153. [DOI] [PubMed] [Google Scholar]
- 26.Tyson J.J., Csikasz-Nagy A., Novak B. The dynamics of cell cycle regulation. Bioessays. 2002;24:1095–1109. doi: 10.1002/bies.10191. [DOI] [PubMed] [Google Scholar]
- 27.Salazar C., Höfer T. Competition effects shape the response sensitivity and kinetics of phosphorylation cycles in cell signaling. Ann. N. Y. Acad. Sci. 2006;1091:517–530. doi: 10.1196/annals.1378.093. [DOI] [PubMed] [Google Scholar]
- 28.Salazar C., Brümmer A., Höfer T. Timing control in regulatory networks by multisite protein modifications. Trends Cell Biol. 2010;20:634–641. doi: 10.1016/j.tcb.2010.08.012. [DOI] [PubMed] [Google Scholar]
- 29.Thomson M., Gunawardena J. Unlimited multistability in multisite phosphorylation systems. Nature. 2009;460:274–277. doi: 10.1038/nature08102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kim S.Y., Ferrell J.E., Jr. Substrate competition as a source of ultrasensitivity in the inactivation of Wee1. Cell. 2007;128:1133–1145. doi: 10.1016/j.cell.2007.01.039. [DOI] [PubMed] [Google Scholar]
- 31.Tyson J.J. Modeling the cell division cycle: cdc2 and cyclin interactions. Proc. Natl. Acad. Sci. USA. 1991;88:7328–7332. doi: 10.1073/pnas.88.16.7328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Goldbeter A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc. Natl. Acad. Sci. USA. 1991;88:9107–9111. doi: 10.1073/pnas.88.20.9107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ferrell J.E., Jr., Machleder E.M. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science. 1998;280:895–898. doi: 10.1126/science.280.5365.895. [DOI] [PubMed] [Google Scholar]
- 34.Chen K.C., Calzone L., Tyson J.J. Integrative analysis of cell cycle control in budding yeast. Mol. Biol. Cell. 2004;15:3841–3862. doi: 10.1091/mbc.E03-11-0794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Barik D., Baumann W.T., Tyson J.J. A model of yeast cell-cycle regulation based on multisite phosphorylation. Mol. Syst. Biol. 2010;6:405. doi: 10.1038/msb.2010.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Aguda B.D. A quantitative analysis of the kinetics of the G(2) DNA damage checkpoint system. Proc. Natl. Acad. Sci. USA. 1999;96:11352–11357. doi: 10.1073/pnas.96.20.11352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Qu Z., Weiss J.N., MacLellan W.R. Regulation of the mammalian cell cycle: a model of the G1-to-S transition. Am. J. Physiol. Cell Physiol. 2003;284:C349–C364. doi: 10.1152/ajpcell.00066.2002. [DOI] [PubMed] [Google Scholar]
- 38.Yang L., MacLellan W.R., Qu Z. Multisite phosphorylation and network dynamics of cyclin-dependent kinase signaling in the eukaryotic cell cycle. Biophys. J. 2004;86:3432–3443. doi: 10.1529/biophysj.103.036558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Swat M., Kel A., Herzel H. Bifurcation analysis of the regulatory modules of the mammalian G1/S transition. Bioinformatics. 2004;20:1506–1511. doi: 10.1093/bioinformatics/bth110. [DOI] [PubMed] [Google Scholar]
- 40.Novák B., Tyson J.J. A model for restriction point control of the mammalian cell cycle. J. Theor. Biol. 2004;230:563–579. doi: 10.1016/j.jtbi.2004.04.039. [DOI] [PubMed] [Google Scholar]
- 41.Pfeuty B., Kaneko K. The combination of positive and negative feedback loops confers exquisite flexibility to biochemical switches. Phys. Biol. 2009;6:046013. doi: 10.1088/1478-3975/6/4/046013. [DOI] [PubMed] [Google Scholar]
- 42.Gérard C., Goldbeter A. Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle. Proc. Natl. Acad. Sci. USA. 2009;106:21643–21648. doi: 10.1073/pnas.0903827106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chauhan A., Lorenzen S., Bernard S. Regulation of mammalian cell cycle progression in the regenerating liver. J. Theor. Biol. 2011;283:103–112. doi: 10.1016/j.jtbi.2011.05.026. [DOI] [PubMed] [Google Scholar]
- 44.Gérard C., Gonze D., Goldbeter A. Effect of positive feedback loops on the robustness of oscillations in the network of cyclin-dependent kinases driving the mammalian cell cycle. FEBS J. 2012;279:3411–3431. doi: 10.1111/j.1742-4658.2012.08585.x. [DOI] [PubMed] [Google Scholar]
- 45.Bouchoux C., Uhlmann F. A quantitative model for ordered Cdk substrate dephosphorylation during mitotic exit. Cell. 2011;147:803–814. doi: 10.1016/j.cell.2011.09.047. [DOI] [PubMed] [Google Scholar]
- 46.Loog M., Morgan D.O. Cyclin specificity in the phosphorylation of cyclin-dependent kinase substrates. Nature. 2005;434:104–108. doi: 10.1038/nature03329. [DOI] [PubMed] [Google Scholar]
- 47.Schweiger R., Linial M. Cooperativity within proximal phosphorylation sites is revealed from large-scale proteomics data. Biol. Direct. 2010;5:6. doi: 10.1186/1745-6150-5-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Weinman E.J., Steplock D., Shenolikar S. Cooperativity between the phosphorylation of Thr95 and Ser77 of NHERF-1 in the hormonal regulation of renal phosphate transport. J. Biol. Chem. 2010;285:25134–25138. doi: 10.1074/jbc.M110.132423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pullen N., Brown N.G., Akhtar M. Cooperativity during multiple phosphorylations catalyzed by rhodopsin kinase: supporting evidence using synthetic phosphopeptides. Biochemistry. 1993;32:3958–3964. doi: 10.1021/bi00066a016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


