The Energy Costs of Insulators in Biochemical Networks

Abstract

Complex networks of biochemical reactions, such as intracellular protein signaling pathways and genetic networks, are often conceptualized in terms of modules—semiindependent collections of components that perform a well-defined function and which may be incorporated in multiple pathways. However, due to sequestration of molecular messengers during interactions and other effects, collectively referred to as retroactivity, real biochemical systems do not exhibit perfect modularity. Biochemical signaling pathways can be insulated from impedance and competition effects, which inhibit modularity, through enzymatic futile cycles that consume energy, typically in the form of ATP. We hypothesize that better insulation necessarily requires higher energy consumption. We test this hypothesis through a combined theoretical and computational analysis of a simplified physical model of covalent cycles, using two innovative measures of insulation, as well as a possible new way to characterize optimal insulation through the balancing of these two measures in a Pareto sense. Our results indicate that indeed better insulation requires more energy. While insulation may facilitate evolution by enabling a modular plug-and-play interconnection architecture, allowing for the creation of new behaviors by adding targets to existing pathways, our work suggests that this potential benefit must be balanced against the metabolic costs of insulation necessarily incurred in not affecting the behavior of existing processes.

Introduction

A ubiquitous motif in signaling pathways responsible for a cell’s response to environmental stimuli is the ATP-consuming phosphorylation-dephosphorylation (PD) enzymatic cycle, in which a substrate is converted into product in an activation reaction triggered or facilitated by an enzyme, and subsequently the product is transformed back (or deactivated) into the original substrate, helped on by the action of a second enzyme. For example, a large variety of eukaryotic cell signal transduction processes (1–4) rely upon Mitogen-activated protein kinase cascades for some of the most fundamental processes of life (cell proliferation and growth, responses to hormones, apoptosis), and these are built upon cascades of PD cycles. More generally, this type of reaction, often called a futile, substrate, or enzymatic cycle (5), shows up in many other prokaryotic and eukaryotic systems, including, for example, bacterial two-component systems and phosphorelays (6,7), GTPase cycles (8), actin treadmilling (9), glucose mobilization (10), metabolic control (11), cell division and apoptosis (12), and cell-cycle checkpoint control (13). Many reasons have been proposed for the existence of these futile cycles. In some cases, their function is dictated by the underlying physical chemistry; this may be the case in transmembrane signal transduction, or in metabolic processes that drive energetically unfavorable transformations. In other contexts, and particularly in signaling pathways, there has been speculation that futile cycles play a role ranging from signal amplification to analog-to-digital conversion that triggers decision-making such as cell division (1). An alternative view is that futile cycles can act as insulators that minimize retroactivity impedance effects arising from interconnections. In that role, enzymatic cycles might help enable a plug-and-play interconnection architecture that facilitates evolution (14–16).

An important theme in contemporary molecular biology literature is the attempt to understand cell behavior in terms of cascades and feedback interconnections of more elementary modules, which may be reused in different pathways (17–19). Modular thinking plays a fundamental role in the prediction of the behavior of a system from the behavior of its components, guaranteeing that the properties of individual components do not change upon interconnection. Intracellular signal transduction networks are often thought of as modular interconnections, passing along information while also amplifying or performing other signal-processing tasks. It is assumed that their operation does not depend upon the presence or absence of downstream targets to which they convey information. However, just as electrical, hydraulic, and other physical systems often do not display true modularity, one may expect that biochemical systems, and specifically, intracellular protein signaling pathways and genetic networks, do not always connect in an ideal modular fashion.

Motivated by this observation, the article (14) dealt with a systematic study of the effect of interconnections on the input/output dynamic characteristics of signaling cascades. Following Saez-Rodriguez et al. (20), the term “retroactivity” was introduced for generic reference to such effects, which constitute an analog of nonzero output impedance in electrical and mechanical systems, and retroactivity in several simple models was quantified. It was shown how downstream targets of a signaling system (loads) can produce changes in signaling, thus propagating backward (and sideways) information about targets. Further theoretical work along these lines was reported in Ossareh et al. (15), Kim and Sauro (16), Del Vecchio and Sontag (21), and Sontag (22). Experimental verifications were reported in Ventura et al. (23) and in Jiang et al. (24), using a covalent modification cycle based on a reconstituted uridylyltransferase/uridylyl-removing enzyme PII cycle, which is a model system derived from the nitrogen assimilation control network of Escherichia coli.

The key reason for retroactivity is that signal transmission in biological systems involves chemical reactions between signaling molecules. These reactions take a finite time to occur, and during the process, while reactants are bound together, they generally cannot take part in the other dynamical processes that they would typically be involved in when unbound. One consequence of this sequestering effect is that the influences are also indirectly transmitted laterally, in that for a single input-multiple output system, the output to a given downstream system is influenced by other outputs.

To attenuate the effect of retroactivity, Del Vecchio et al. (14) proposed a negative feedback mechanism inspired by the design of operational amplifiers in electronics, employing a mechanism implemented through a covalent modification cycle based on phosphorylation-dephosphorylation reactions. For appropriate parameter ranges, this mechanism enjoys a remarkable insulation property, having an inherent capacity to shield upstream components from the influence of downstream systems and hence to increase the modularity of the system in which it is placed. One may speculate whether this is indeed one reason that such mechanisms are so ubiquitous in cell signaling pathways. Leaving aside speculation, however, one major potential disadvantage of insulating systems based on operational amplifier ideas is that they impose a metabolic load, ultimately because amplification requires energy expenditure.

Thus, a natural question to ask from a purely physical standpoint: Does better insulation require more energy consumption? This is the article’s subject. We provide a qualified positive answer: for a specific (but generic) model of covalent cycles, natural notions of insulation and energy consumption, and a Pareto-like view of multiobjective optimization, we find, using a numerical parameter sweep in our models, that better insulation indeed requires more energy.

In addition to this positive answer in itself, two major contributions of this work are:

• 1.Introduction of the innovative measures of retroactivity combined with insulation, in terms of two competing goals: minimization of the difference between the output of the insulator and the ideal behavior, and attenuation of the competition effect (the change in output when a new downstream target is added).
• 2.Introduction of a possible new way to characterize optimality through balancing of these goals in a Pareto sense.

These contributions should be of interest even in other studies of insulation that do not involve energy use.

The relationship between energy use and optimal biological function is an active theme of contemporary research that has been explored in several different contexts. Recent studies have examined the need for energy dissipation when improving adaptation speed and accuracy, in the context of perfect adaptation (25), and when performing computation, such as sensing the concentration of a chemical ligand in the environment (26). The tradeoff between the energy expenditure necessary for chemotaxis and the payoff of finding nutrients has also been considered (27), yielding insights into the costs and benefits of chemotactic motility in different environments. Such studies are important in characterizing the practical constraints guiding evolutionary adaptation.

Our work contributes to this research by relating the metabolic costs of enzymatic futile cycles with their capacity to act as insulators, facilitating modular interconnections in biochemical networks. While energy use in PD cycles has been related to noise filtering properties (28) and switch stability (29), to our knowledge our work is the first to explore the connection between energy use and insulation. Recent work demonstrates that enzymatic futile cycles can be key components in providing amplification of input signals, while linearizing input-output response curves (30,31). We show that these properties come at a cost: better performance of the PD cycle as an insulator requires more energy use.

Mathematical Model of the Basic System

We are interested in biological pathways that transmit a single, time-dependent input signal to one or more downstream targets. A prototypical example is a transcription factor Z, which regulates the production of one or more proteins by binding directly to their promoters, forming a protein-promoter complex. Assuming a single promoter target for simplicity, this system is represented by the set of reactions

$$\begin{array}{c}\varnothing \stackrel{k\left(t\right)}{\to }Z\stackrel{\delta }{\to }\varnothing ,\\ Z+p\underset{k_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftharpoons }}C,\end{array}$$ (1)

where p stands for the promoter and C denotes the protein-promoter complex. For our analysis, the particular interpretation of Z, p, and C will not be important. One thinks of Z as describing an upstream system that regulates the downstream target C. Although mathematically the distinction between upstream and downstream is somewhat artificial, the roles of transcription factors as controllers of gene expression, or of enzymes on substrate conversions, and not the opposite, are biologically natural and accepted.

We adopt the convention that the (generally time-dependent) concentration of each species is denoted by the respective italics symbol; for example, X = X(t) is the concentration of X at time t. We assume that the transcription factor Z is produced or otherwise activated at a time-dependent rate k(t), and decays at a rate proportional to a constant δ, and that the total concentration of the promoter p_tot is fixed. This leads to a set of ordinary differential equations (ODEs) describing the dynamics of the system,

$$\begin{array}{l}\frac{dZ}{dt}=k\left(t\right)-\delta Z-k_{\text{on}}Z\left(p_{\text{tot}}-C\right)+k_{\text{off}}C,\\ \frac{dC}{dt}=k_{\text{on}}\left(p_{\text{tot}}-C\right)Z-k_{\text{off}}C.\end{array}$$ (2)

The generalization of these equations to the case of multiple output targets is straightforward. Protein synthesis and degradation take place on timescales that are orders of magnitude larger than the typical timescales of small molecules binding to proteins, or of transcription factors binding to DNA (32). Thus, we will take the rates k(t) and δ to be much smaller than other interaction rates such as k_on and k_off. In Eq. 1, Z represents the input, and C the output.

The ideal system and the distortion measure

Sequestration of the input Z by its target p affects the dynamics of the system as a whole, distorting the output to C as well as to other potential downstream targets. In an ideal version of Eq. 2, where sequestration effects could be ignored, the dynamics would instead be given by

$$\begin{array}{l}\frac{dZ}{dt}=k\left(t\right)-\delta Z,\\ \frac{dC}{dt}=k_{\text{on}}\left(p_{\text{tot}}-C\right)Z-k_{\text{off}}C.\end{array}$$ (3)

The term $-k_{\text{on}}Z\left(p_{\text{tot}}-C\right)+k_{\text{off}}C$ that was removed from the first equation represents a “retroactivity” term, expressed in the language of Del Vecchio et al. (14). This is the term that quantifies how the dynamics of the upstream species Z is affected by its downstream target C. In the ideal system presented in Eq. 3, the transmission of the signal from input to output is undisturbed by retroactivity effects. We thus use the relative difference between the output signal in a system with realistic dynamics and the ideal output, as given by the solution of Eq. 3, as a measure of the output signal distortion, and define the distortion $\mathcal{D}$ to be

$$\mathcal{D}=\frac{1}{{\sigma }_{C_{\text{ideal}}}}\langle \left|C_{\text{ideal}}\left(t\right)-C_{\text{real}}\left(t\right)\right|\rangle ,$$ (4)

where 〈|·|〉 denotes a long time average. Here we normalize by dividing by the standard deviation of the ideal signal,

$${\sigma }_{C_{\text{ideal}}}=\sqrt{\langle {\left(C_{\text{ideal}}\left(t\right)-\langle C_{\text{ideal}}\left(t\right)\rangle \right)}^2\rangle }.$$ (5)

Thus, Eq. 4 measures the difference between the output in the real and ideal systems, in units of the typical size of the time-dependent fluctuations in the ideal output signal.

Fan-out: multiple targets

Another consequence of sequestration effects is the interdependence of the output signals to different downstream targets connected in parallel (33). Each molecule of Z may only bind to a single promoter at a time, thus introducing a competition between the promoters to bind with the limited amount of Z in the system. This is a question of practical interest, as transcription factors typically control a large number of target genes. For example, the tumor suppressor protein p53 has well over a hundred targets (34). A similar issue appears in biochemistry, where promiscuous enzymes may affect even hundreds of substrates. For example, alcohol dehydrogenases target ∼100 different substrates to break down toxic alcohols and to generate useful aldehyde, ketone, or alcohol groups during biosynthesis of various metabolites (35).

We quantify the size of the competition effect by the change in an output signal to a given target in response to an infinitesimal change in the abundance of another parallel target. For definiteness, consider Eq. 1 with an additional promoter p′, which bonds to Z to form a complex C′ with the same on/off rates as p,

$$Z+p^{\prime }\stackrel{k_{\text{on}}}{\underset{k_{\text{off}}}{\rightleftharpoons }}{C}^{\prime },$$

and the corresponding equation added to Eq. 2,

$$\frac{d{C}^{\prime }}{dt}=k_{\text{on}}\left(p_{\text{tot}}^{\prime }-C^{\prime }\right)Z-k_{\text{off}}{C}^{\prime }.$$

We then define the competition effect of the system Eq. 2 as

$$\mathcal{C}=\frac{1}{{\sigma }_C}\langle \left|{\left(\frac{\partial C\left(t\right)}{\partial p_{\text{tot}}^{\prime }}\right)|}_{p_{\text{tot}}^{\prime }=0}\right|\rangle .$$ (6)

Again, we normalize by the standard deviation of the output signal C(t),

$${\sigma }_C=\sqrt{\langle {\left(C\left(t\right)-\langle C\left(t\right)\rangle \right)}^2\rangle },$$ (7)

computed with p′_tot = 0, so that Eq. 6 measures the change in the output signal when an additional target is introduced relative to the size of the fluctuations of the output in the unperturbed system.

Mathematical Model of an Insulator

As shown in Fig. 1, typical performance of the simple direct coupling system defined by Eq. 2 is poor, assuming, as in Del Vecchio et al. (14), that we test the system with a simple sinusoidally varying production rate

$$k\left(t\right)=k\left(1+\text{sin}\omega t\right),$$ (8)

whose frequency ω is similar in magnitude to k and δ. Oscillation of the output signal in response to the time-varying input is strongly damped relative to the ideal. The output is also sensitive to other targets connected in parallel: as the total load increases, the output signal is noticeably damped in both the transient and steady state. Here the flux of Z into and out of the system is too slow to drive large changes in the output C as the rate of production k(t) varies.

Figure 1.

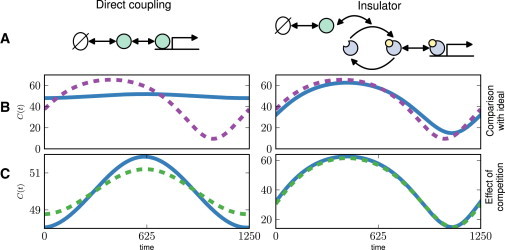
Retroactivity effects lead to signal distortion, and attenuation of output signals when additional targets are added. Comparison of retroactivity effects on a signaling system with a direct coupling (DC) architecture (left) and one with an insulator, represented by a phosphorylation-dephosphorylation cycle (right). (A) Cartoon schematic of the signaling system. In the DC system (Eq. 1), the input binds directly to the target. With an insulator (Eq. 9), the input drives phosphorylation of an intermediate signaling molecule, whose phosphorylated form binds to the target. (B) Illustration of distortion. The ideal output signal (dashed, and see Eq. 3 in text) with retroactivity effects neglected, is plotted against the output for each system with nonlinear dynamics (solid), given by Eq. 2 for the DC system and Eq. 10 for the insulator. (C) Illustration of competition effect. The output signal in a system with a single target (solid) is compared with the output signal when multiple targets are present (dashed). Note the greatly reduced amplitude of variation of the output in the DC system. Plots of the output signals in each system are shown in the steady state, over a single period of k(t). This plot was made using the parameters k(t) = 0.01(1 + sin(0.005t)); δ = 0.01; α₁ = β₁ = 0.01; α₂ = β₂ = k₁ = k₂ = 10; k_on = k_off = 10; p_tot = 100; and X_tot = 800, Y_tot = 800 for the insulator. Parameters specifying the interaction with the new promoter p^′ in the perturbed system are k^′_on = k^′_off = 10, and p^′_tot = 60.

As suggested in Del Vecchio et al. (14), the retroactivity effects in this system can be ameliorated by using an intermediate signal processing system, specifically one based on a phosphorylation-dephosphorylation (PD) futile cycle, between the input and output. Such systems appear often in signaling pathways that mediate gene expression responses to the environment (32). In this system, the input signal Z plays the role of a kinase, facilitating the phosphorylation of a protein X. The phosphorylated version of the protein X^∗ then binds to the target p to transmit the signal. Dephosphorylation of X^∗ is driven by a phosphatase Y. Assuming a two-step model of the phosphorylation-dephosphorylation reactions, the full set of reactions is

$$\begin{array}{c}Ø\stackrel{k\left(t\right)}{\to }Z\stackrel{\delta }{\to }Ø,\\ Z+X\underset{{\beta }_2}{\overset{{\beta }_1}{\rightleftharpoons }}{C}_1\stackrel{k_1}{\to }{X}^{\ast }+Z,\\ Y+X^{\ast }\underset{{\alpha }_2}{\overset{{\alpha }_1}{\rightleftharpoons }}{C}_2\stackrel{k_2}{\to }X+Y,\\ X^{\ast }+p\underset{k_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftharpoons }}C.\end{array}$$ (9)

The total protein concentrations X_tot and Y_tot are fixed.

The forward and reverse rates of the phosphorylation-dephosphorylation reaction depend implicitly on the concentrations of phosphate donors and acceptors, such as ATP and ADP. Metabolic processes ensure that these concentrations are held far away from equilibrium, biasing the reaction rates and driving the phosphorylation-dephosphorylation cycle out of equilibrium. As routinely done in enzymatic biochemistry analysis, we have made the simplifying assumption of setting the small rates of the reverse processes X^∗ + Z → C₁ and X + Y → C₂ to zero. The ODEs governing the dynamics of the system are then

$$\begin{array}{l}\frac{dZ}{dt}=k\left(t\right)-\delta Z-{\beta }_{1}Z\left(X_{\text{tot}}-C_1-C_2-C-X^{\ast }\right)+\left({\beta }_2+k_1\right)C_1,\\ \frac{d{C}_1}{dt}={\beta }_{1}Z\left(X_{\text{tot}}-C_1-C_2-C-X^{\ast }\right)-\left({\beta }_2+k_1\right)C_1,\\ \frac{d{C}_2}{dt}={\alpha }_1{X}^{\ast }\left(Y_{\text{tot}}-C_2\right)-\left({\alpha }_2+k_2\right)C_2,\\ \frac{d{X}^{\ast }}{dt}=k_1{C}_1-{\alpha }_1{X}^{\ast }\left(Y_{\text{tot}}-C_2\right)+{\alpha }_2{C}_2-k_{\text{on}}{X}^{\ast }\left(p_{\text{tot}}-C\right)+k_{\text{off}}C,\\ \frac{dC}{dt}=k_{\text{on}}{X}^{\ast }\left(p_{\text{tot}}-C\right)-k_{\text{off}}C.\end{array}$$ (10)

In an Appendix, we provide mathematical results regarding the stability of this system of ODEs in response to the periodic rate k(t), justifying our focus on long-time steady-state behavior.

As shown in Fig. 1, for suitable choices of parameters the output signal in the system including the PD cycle is able to match the ideal output much more closely than in the direct coupling system. The output signal is also much less sensitive to changes in other targets connected in parallel than in the system where the input couples directly to the promoter. One can think of this system with the insulator as equivalent to the direct coupling system, but with effective production and degradation rates

$$\begin{array}{l}{k}_{\text{eff}}\left(t\right)=k_1{C}_1+{\alpha }_2{C}_2,\\ {\delta }_{\text{eff}}={\alpha }_1\left(Y_{\text{tot}}-C_2\right),\end{array}$$ (11)

which may be much larger than the original k(t) and δ, thus allowing the system with the insulator to adapt much more rapidly to varying input.

The fact that the PD cycle is driven out of equilibrium, therefore consuming energy, is critical for its signal processing effectiveness. Our focus will be on how the performance of the PD cycle as an insulator depends upon its rate of energy consumption.

Our hypothesis is that better insulation requires more energy consumption. To formulate a more precise question, we need to find a proxy for energy consumption in our simple model.

Energy use and insulation

The free energy consumed in the PD cycle can be expressed in terms of the change in the free energy of the system ΔG resulting from the phosphorylation and subsequent dephosphorylation of a single molecule of X. One can also measure the amount of ATP which is converted to ADP, which is proportional to the current through the phosphorylation reaction C₁ → X^∗ + Z. In the steady state, because the phosphorylation and dephosphorylation reactions are assumed to be irreversible and the total concentration X_tot is fixed, the time averages of these two measures are directly proportional. The average free energy consumed per unit time in the steady state is then proportional to the average current

$$J=\langle k_1{C}_1\rangle .$$ (12)

Different choices of the parameters appearing in the phosphorylation and dephosphorylation reactions, such as k₁, k₂, and X_tot, will lead to different rates of energy use and also different levels of performance in terms of the competition effect and distortion.

We focus our attention on the concentrations X_tot and Y_tot as tunable parameters. While the reaction rates such as k₁ and k₂ depend upon the details of the molecular structure and are harder to directly manipulate, concentrations of stable molecules like X and Y can be experimentally adjusted, and hence the behavior of the PD cycle as a function of X_tot and Y_tot is of great practical interest. When building synthetic circuits in living cells, for example, X_tot and Y_tot can be tuned by placing the genes that express these proteins under the control of constitutive promoters of adjustable strengths, or through the action of inducers (36).

Comparing different parameters in the insulator: Pareto optimality

In measuring the overall quality of our signaling system, the relative importance of faithful signal transmission, as measured by small distortion, and a small competition effect, will vary. This means that quality is intrinsically a multiobjective optimization problem, with competing objectives. Rather than applying arbitrary weights to each quantity, we will instead approach the problem of finding ideal parameters for the PD cycle from the point of view of Pareto optimality, a standard approach to optimization problems with multiple competing objectives that was originally introduced in economics (37). In this view, one seeks to determine the set of parameters of the system for which any improvement in one of the objectives necessitates a sacrifice in one of the others. Here, the competing objectives are the minimization of $\mathcal{D}$ and $\mathcal{C}$.

A Pareto optimal choice of the parameters is one for which there is no other choice of parameters that gives a smaller value of both $\mathcal{D}$ and $\mathcal{C}$. Pareto optimal choices, also called Pareto efficient points, give generically optimum points with respect to arbitrary positive linear combinations α$\mathcal{D}$ + β$\mathcal{C}$, thus eliminating the need to make an artificial choice of weights.

An informal analysis

A full mathematical analysis of the system of nonlinear ODEs in Eq. 10 is difficult. In biologically plausible parameter ranges, however, certain simplifications allow one to develop intuition about its behavior. We discuss now this approximate analysis, to set the stage for, and to help interpret the results of, our numerical computations with the full nonlinear model.

We make the following Ansatz: the variables Z(t) and X^∗(t) evolve more slowly than C₁(t), C₂(t), and C(t). Biochemically, this is justified because phosphorylation and dephosphorylation reactions tend to occur on the timescale of seconds (38,39), as do transcription factor promoter binding and unbinding events (32), while protein production and decay takes place on the timescale of minutes (32). In addition, we analyze the behavior of the system under the assumption that the total concentrations of enzyme and phosphatase, X_tot and Y_tot, are large. In terms of the constants appearing in Eq. 10, we assume

$$\begin{array}{l}{K}_1=\frac{{\beta }_2+k_1}{{\beta }_1}\gg X_{\text{tot}}\gg 1,\\ K_2=\frac{{\alpha }_2+k_2}{{\alpha }_1}\gg Y_{\text{tot}}\gg 1,\\ \left\{k\left(t\right),\delta \right\}\ll k_{\text{on}}\approx k_{\text{off}}.\end{array}$$ (13)

Thus, on the timescale of Z(t) and X^∗(t), we can make the quasi-steady-state (Michaelis-Menten) assumption that C₁(t), C₂(t), and C(t) are at equilibrium. Setting the right-hand sides of $d{C}_1/dt$, $d{C}_2/dt$, and $dC/dt$ to zero, and substituting in the remaining two equations of Eq. 10, we obtain the following system:

$$\begin{array}{c}\frac{dZ}{dt}\approx k\left(t\right)-\delta Z,\\ \frac{d{X}^{\ast }}{dt}\approx k_1{C}_1-k_2{C}_2.\end{array}$$

The lack of additional terms in the equation for Z(t) is a consequence of the assumption that K₁ >> X_tot, which amounts to a low binding affinity of Z to its target X (relative to the concentration of the latter); this follows from a total quasi-steady-state approximation as in Ciliberto et al. (40) and Borghans et al. (41). Observe that such an approximation is not generally possible for the original system Eq. 1, and indeed this is the key reason for the retroactivity effect (14).

With the above assumptions, in the system with the insulator, Z(t) evolves approximately as in the ideal system Eq. 3. In this quasi-steady-state approximation

$$C_1\approx \left(\frac{1}{K_1}\right)\left(X_{\text{tot}}-C_1-C_2-C\right)Z\approx \left(\frac{1}{K_1}\right)X_{\text{tot}}Z$$

and

$$C_2\approx \left(\frac{1}{K_2}\right)\left(Y_{\text{tot}}-C_2\right)X^{\ast }\approx \left(\frac{1}{K_2}\right)Y_{\text{tot}}{X}^{\ast },$$

and thus we have

$$\frac{d{X}^{\ast }}{dt}\approx \left(\frac{k_1}{K_1}\right)X_{\text{tot}}Z-\left(\frac{k_2}{K_2}\right)Y_{\text{tot}}{X}^{\ast }.$$

Finally, let us consider the effect of the following condition:

$$\left(\frac{k_1}{K_1}\right)X_{\text{tot}}\approx \left(\frac{k_2}{K_2}\right)Y_{\text{tot}}\gg 1.$$ (14)

If this condition is satisfied, then

$$\frac{d{X}^{\ast }}{dt}\approx K\left(Z-X^{\ast }\right),$$

with K >> 1, which means that X^∗(t) ≈ Z(t), and thus the equation for $dC/dt$ in Eq. 10 reduces to that for the ideal system in Eq. 3. In summary, if Eq. 14 holds, we argue that the system with the insulator will reproduce the behavior of the ideal system, instead of the real system in Eq. 2. Moreover, the energy consumption rate in Eq. 12 is proportional to k₁C₁ ≈ (k₁/K₁)X_totZ, and hence will be large if Eq. 14 holds, which intuitively leads us to expect high energy costs for insulation.

These informal arguments (or more formal ones based on singular perturbation theory (14)) justify the sufficiency, but not the necessity, of Eq. 14. Our numerical results will show that this condition is indeed satisfied for a wide range of parameters that lead to good insulation.

Numerical Results on Pareto Optimality

We have explored the performance of the insulating PD cycle over an extensive range of parameters to test our hypothesis that better insulation requires more energy consumption. In Fig. 2 we show a plot of $\mathcal{C}$ and $\mathcal{D}$ for systems with a range of X_tot and Y_tot, obtained by numerical integration of the differential equations expressed in Eq. 10 (see also Fig. 3 for a three-dimensional view). Pareto optimal choices of parameters on the tested parameter space are indicated by solid points.

Figure 2.

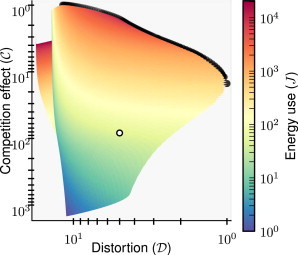
Performance of the insulator measured by the competition effect $\mathcal{C}$ and distortion $\mathcal{D}$ of the output in the system with an insulator (Eq. 10), tested over a range of X_tot and Y_tot varied independently from 10 to 10,000 in logarithmic steps. For simplicity, $\mathcal{C}$ and $\mathcal{D}$ are rescaled such that the smallest (best) values are equal to one. Points are shaded according to the logarithm of the rate of energy consumption of the PD cycle. (Solid dots) Pareto efficient parameter points. Rates of energy consumption increase as one approaches the Pareto front; obtaining small values of the competition effect is particularly costly. (Open dot) For comparison, $\mathcal{C}$ and $\mathcal{D}$ positions for the direct coupling system are marked. See Numerical Results on Pareto Optimality for details. This plot was made using the parameters k(t) = 0.01(1 + sin(0.005t)), δ = 0.01, α₁ = β₁ = 0.01, α₂ = β₂ = k₁ = k₂ = 10, k_on = k_off = 10, and p_tot = 100.

Figure 3.

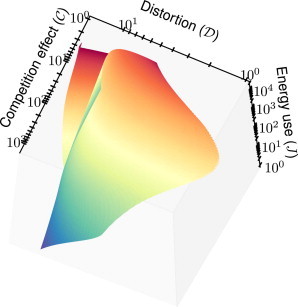
Three-dimensional plot of competition effect $\mathcal{C}$ and distortion $\mathcal{D}$, along with the rate of energy consumption J, in the system including an insulator (Eq. 10). Note the fold in the plot; it is possible for two different values of the parameters to yield the same measures of insulation $\mathcal{C}$ and $\mathcal{D}$, but with different rates of energy consumption.

Superior performance of the insulator is clearly associated with higher rates of energy consumption, as shown in the figure. Typically the rate of energy consumption increases as one approaches the set of Pareto optimal points, referred to as the Pareto front. Indeed, choices of parameters on or near the Pareto front have some of the highest rates of energy expenditure. Conversely, the parameter choices that have the poorest performance also consume the least energy. As shown above, this phenomenon can be understood by noting that the energy consumption rate from Eq. 12 will be large when the conditions for optimal insulation from Eq. 14 are met.

Note that it is possible for two different choices of the parameters X_tot and Y_tot to yield the same measures of insulation $\mathcal{C}$ and $\mathcal{D}$, but with different rates of energy consumption. This results in a fold in the sheet in Fig. 2, most clearly observed near $\mathcal{D}$ = 10 and $\mathcal{C}$ = 4. We see then that while better insulation generally requires larger amounts of energy consumption, it is not necessarily true that systems with high rates of energy consumption always make better insulators. See also the three-dimensional plot of $\mathcal{C}$, $\mathcal{D}$, and J shown in Fig. 3 for a clearer picture.

In addition to the general trend of increasing energy consumption as competition effect or distortion decrease, we find that a strong local energy optimality property is satisfied. We observe numerically that any small change in the parameters X_tot and Y_tot, which leads to a decrease in both the competition effect and distortion, must be accompanied by an increase in the rate of energy consumption, excluding jumps from one side of the fold to the other. This local property complements the global observation that Pareto optimal points are associated with the regions of parameter space with the highest rates of energy consumption.

While we find Pareto optimal choices of the concentrations X_tot and Y_tot span several orders of magnitude, the ratio of X_tot to Y_tot is close to unity for nearly all Pareto optima (see Fig. 4). A small number of Pareto optimal points are found with very different total concentrations of X and Y, but these points appear to be due to boundary effects from the sampling of a finite region of the parameter space. Indeed, we have argued that the insulator should perform best when Eq. 14 is satisfied. For the choice of parameters considered here, this gives X_tot/Y_tot = (k₂K₁)/(k₁K₂) = 1. Tests with randomized parameters confirm that Eq. 14 gives a good estimate of the relationship between X_tot and Y_tot for Pareto optimal points (see Fig. 5 for an example).

Figure 4.

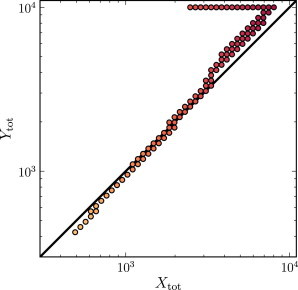
Scatter plot of the Pareto optimal sets of parameters X_tot and Y_tot corresponding to those in Figs. 2 and 3. Pareto optimal points are typically those which strike a balance between the total concentrations of X and Y, as suggested by the analysis of Mathematical Model of an Insulator. We predict that Pareto optima will lie along the line (k₁/K₁)X_tot = (k₂/K₂)Y_tot (shown in background, prediction from Eq. 14), in good agreement with the simulation results. Each point is shaded according to the rate of energy consumption for that choice of parameters. Increases in either X_tot or Y_tot result in increased energy expenditure. Due to the limited range of parameters that could be tested, some Pareto optima lie along the boundaries of the parameter space (see the elbow in the scatter points, top of the plot).

Figure 5.

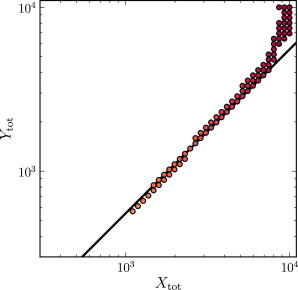
Scatter plot of the Pareto optimal sets of parameters X_tot and Y_tot for an insulator using the randomly shifted parameters. Based on Eq. 14, we predict that Pareto optima will lie along the line (k₁/K₁)X_tot = (k₂/K₂)Y_tot (shown in background). Parameters used are k(t) = 0.0137(1 + sin(0.005t)); δ = 0.0188; α₁ = 0.0107; β₁ = 0.0102; α₂ = 5.31; β₂ = 16.42; k₁ = k₂ = 10; k_on = 5.19; k_off = 12.49; and p_tot = 100. Each point is shaded according to the rate of energy consumption for that choice of parameters (scale analogous to that of Figs. 2–4).

We also observe that there is a lower bound on the concentration of X_tot and Y_tot for optimal insulation. Though we tested ranges of concentrations from 10 to 10,000, the first optimal points only appear when the concentrations are ∼500, several times larger than the concentration of the target (p_tot = 100) and much larger than the concentration of the signal protein (Z_max ≈ 2 in our simulations). Interestingly, the insulator consumes less energy for these first Pareto optimal parameter choices than at higher concentrations, and achieves the best measures of distortion with relatively low competition effect as well. This suggests that smaller concentrations may be generically favored, particularly when energy constraints are important.

We conclude that the specification of Pareto optimality places few constraints on the absolute concentrations X_tot and Y_tot in the model, save for a finite lower bound, but the performance of the insulator depends strongly on the ratio of the two concentrations. This observation connects with the work of Gutenkunst et al. (42), who noted sloppy parameter sensitivity for many variables in systems biology models, excepting some stiff combinations of variables that determine a model’s behavior.

For comparison, we indicate the values of $\mathcal{D}$ and $\mathcal{C}$ of the simpler direct coupling architecture, with no insulator, by an open dot in Fig. 2. While many choices of parameters for the insulating PD cycle, including most Pareto optimal points, lead to improvements in the distortion relative to that of the direct coupling system, the most dramatic improvement is in fact in the competition effect. Roughly $85\%$ of the parameter values tested for the insulator have a lower value of the competition effect than that found for the direct coupling system. This suggests that insulating PD cycles may be functionally favored over simple direct binding interactions, particularly when there is strong pressure for stable output to multiple downstream systems.

Finally, we note that the analysis performed here has not factored in the potential metabolic costs of production for X and Y. Such costs would depend on the structure of these components, as well as their rates of production and degradation, which we have not addressed and which may be difficult to estimate in great generality. However, as the rate of energy consumption increases with increasing X_tot and Y_tot (see Fig. 4), we would expect to find similar qualitative results regarding rates of energy consumption even when factoring in production costs.

Discussion

A very common motif in cell signaling is that in which a substrate is ultimately converted into a product, in an activation reaction triggered or facilitated by an enzyme, and, conversely, the product is transformed back (or deactivated) into the original substrate, helped on by the action of a second enzyme. This type of reaction, often called a futile, substrate, or enzymatic cycle, appears in many signaling pathways: GTPase cycles (8); bacterial two-component systems and phosphorelays (6,7); actin treadmilling (9); glucose mobilization (10); metabolic control (11); cell division and apoptosis (12); and cell-cycle checkpoint control (13). See Samoilov et al. (5) for many more references and a discussion. While phosphorelay systems do not consume energy, most of these futile cycles consume energy, in the form of ATP or GTP use.

In this work we explored the connection between the ability of energy consuming enzymatic futile cycles to insulate biochemical signaling pathways from impedance and competition effects, and their rate of energy consumption. Our hypothesis was that better insulation requires more energy consumption. We tested this hypothesis through the computational analysis of a simplified physical model of covalent cycles, using two innovative measures of insulation, referred to as competition effect and distortion, as well as a possible new way to characterize optimal insulation through the balancing of these two measures in a Pareto sense. Our results indicate that indeed better insulation requires more energy.

Testing a wide range of parameters, we identified Pareto optimal choices that represent the best possible ways to compromise two competing objectives: the minimization of distortion and of the competition effect. The Pareto optimal points share two interesting features: First, they consume large amounts of energy, consistent with our hypothesis that better insulation requires greater energy consumption. Second, the total substrate and phosphatase concentrations X_tot and Y_tot typically satisfy Eq. 14. Assuming that rates for phosphorylation and dephosphorylation are similar, this implies X_tot ∼ Y_tot. There is also a minimum concentration required to achieve a Pareto optimal solution; arbitrarily low concentrations do not yield optimal solutions. Interestingly, insulators with Pareto optimal choices of parameters close to the minimum concentration also expend the least amount of energy, compared to other parameter choices on the Pareto front, and have the least distortion while still achieving low competition effect. This suggests that these points near the minimum concentration might be generically favored, particularly when energy constraints are important.

Many reasons have been proposed for the existence of futile cycles in nature, such as signal amplification, increased sensitivity, or analog-to-digital conversion for help in decision-making. An alternative, or at least complementary, possible explanation (14) lies in the capabilities of such cycles to provide insulation, thus enabling a plug-and-play interconnection architecture that might facilitate evolution. Our results suggest that better insulation requires a higher energy cost, so that a delicate balance may exist between, on the one hand, the ease of adaptation through creation of new behaviors by adding targets to existing pathways, and on the other hand, the metabolic costs necessarily incurred in not affecting the behavior of existing processes.

Our results were formulated for a model in which the input signal is a transcription factor Z that regulates the production of one or more proteins by promoter binding, as described by Eq. 1. We have analyzed (details not given here) another model, and derived a similar qualitative conclusion: namely, that higher energy is required to attain better insulation and is also required for chemical reactions that describe signaling systems in which Z denotes the active form of a kinase; and that p is a protein target which can be reversibly phosphorylated to give a modified form C.

Appendix

In this article we have studied numerical solutions of the set of ODEs given in Eq. 10. For the values of parameters we tested, solutions of Eq. 10 are well behaved, and after long times approach a periodic steady-state solution, where the period T is the same as that of the sinusoidal time-varying production rate k(t) given in Eq. 8. We present analytical results that verify that solutions of Eq. 10 are well behaved for more general choices of parameters. In particular, we prove that:

• 1.For an approximate one-step enzymatic model, a unique and globally attracting solution exists in response to any periodic input.
• 2.There is always a periodic solution of Eq. 10 in response to any periodic input k(t).
• 3.Given some very general physical assumptions for the parameters, solutions of Eq. 10 are linearly stable around an equilibrium point when the input is constant. When the input is time-varying with small amplitude oscillations, a periodic solution exists that is close to each asymptotically stable equilibrium point.

The first proof is shown below, and proofs for the second and third results are given in the Supporting Material.

Globally attracting periodic solutions for a one-step model

We now provide a theoretical analysis showing that there is a unique and globally attracting response to any periodic input, under the assumption that the phosphorylation and dephosphorylation reactions are well approximated by the one-step enzymatic model (43):

$$\begin{array}{l}Ø\stackrel{k\left(t\right)}{\to }Z\stackrel{\delta }{\to }Ø,\\ Z+X\stackrel{k_1}{\to }{X}^{\ast }+Z,\\ Y+X^{\ast }\stackrel{k_2}{\to }X+Y,\\ X^{\ast }+p\underset{k_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftharpoons }}C.\end{array}$$ (15)

(A similar simplified system was used in Del Vecchio et al. (14) to study the sensitivity of retroactivity to parameters.) Such a model can be obtained in the limit that k₁,k₂ → ∞ in Eq. 10, as considered previously, where now the rates k₁ and k₂ in Eq. 15 are equivalent to β₁ and α₁, respectively, in Eq. 10.

The conservation of X and p give the conservation equations X + X^∗ + C = X_tot and p + C = p_tot. We thus obtain the following set of nonlinear differential equations, where k(t) is a positive and time-varying input function:

$$\begin{array}{c}\frac{dZ}{dt}=k\left(t\right)-\delta Z,\\ \frac{d{X}^{\ast }}{dt}=k_{1}Z\left(X_{\text{tot}}-X^{\ast }-C\right)-k_{2}Y{X}^{\ast }+k_{\text{off}}C-k_{\text{on}}{X}^{\ast }\left(p_{\text{tot}}-C\right),\\ \frac{dC}{dt}=-k_{\text{off}}C+k_{\text{on}}{X}^{\ast }\left(p_{\text{tot}}-C\right).\end{array}$$

Observe that the amount of phosphatase Y is constant. Because X = X_tot – X^∗ − C ≥ 0 and p = p_tot – C ≥ 0, physically meaningful solutions are those that lie in the set $\mathcal{S}$ of vectors (Z(t), X^∗(t), and C(t)), which satisfy the constraints

$$Z\left(t\right)\ge 0,X^{\ast }\left(t\right)\ge 0,0\le C\left(t\right)\le p_{\text{tot}},X^{\ast }\left(t\right)+C\left(t\right)\le X_{\text{tot}}.$$

Observe that any solution that starts in the set $\mathcal{S}$ at time t = 0 stays in $\mathcal{S}$ for all t > 0, because dZ/dt ≥ 0 when Z = 0; dX^∗/dt ≥ 0 when X^∗ = 0; dC/dt ≥ 0 when C = 0; d(X^∗ + C)/dt ≤ 0 when X^∗ + C = X_tot; and dC/dt ≤ 0 when C = p_tot. We will now prove that, for any given but arbitrary input k(t) ≥ 0, there is a unique periodic solution $\hat{\xi }\left(t\right)=\left(\hat{Z}\left(t\right),{\hat{X}}^{\ast }\left(t\right),\text{and}\hat{C}\left(t\right)\right)$ in $\mathcal{S}$ of the above system, and this solution is also a global attractor, in the sense that, for every initial condition ${\xi }_0=\left(Z\left(0\right),X^{\ast }\left(0\right),C\left(0\right)\right)\in \mathcal{S}$, the solution ξ(t) with ξ(0) = ξ₀ satisfies that $\left|\xi \left(t\right)-\hat{\xi }\left(t\right)\right|\to 0$ as t → ∞.

It is convenient to make the change of variables W(t) = X^∗(t) + C(t) so that the equations become

$$\begin{array}{c}\frac{dZ}{dt}=k\left(t\right)-\delta Z,\\ \frac{dW}{dt}=k_{1}Z\left(X_{\text{tot}}-W\right)-k_{2}Y\left(W-C\right),\\ \frac{dC}{dt}=-k_{\text{off}}C+k_{\text{on}}\left(W-C\right)\left(p_{\text{tot}}-C\right).\end{array}$$

To prove the existence of a globally attracting periodic orbit, we can equivalently study the system in these new variables, where $\mathcal{S}$ is now the set defined by

$$\begin{array}{l}Z\left(t\right)\ge 0,0\le C\left(t\right)\le p_{\text{tot}},\\ C\left(t\right)\le W\left(t\right)\le X_{\text{tot}}.\end{array}$$

To show the existence and global attractivity of a periodic solution, we appeal to the theory of contractive systems (44–46). The key result that we use is as follows. Consider a system of ODEs,

$$\frac{dx}{dt}=f\left(t,x\left(t\right)\right),$$ (16)

defined for t ∈ [0, ∞] and x ∈ C, where $\mathcal{S}$ is a closed and convex subset of ${\mathbb{R}}^n$; f(t,x) is differentiable on x; and f(t,x), as well as the Jacobian of f with respect to x, denoted as $J=J\left(t,x\right)=\partial f/\partial x\left(t,x\right)$, are continuous in (t,x). Furthermore, suppose that f is periodic with period T, $f\left(t+T,x\right)=f\left(t,x\right)$ for all t ≥ 0, x ∈ $\mathcal{S}$. In our system, n = 3, (x,t) is the vector consisting of (Z(t), W(t), and C(t)), and the periodicity arises from k(t + T) = k(t) for all t ≥ 0. We recall that, given a vector norm on Euclidean space (|·|), with its induced matrix norm ||A||, the associated matrix measure or logarithmic norm μ is defined (47,48) as the directional derivative of this matrix norm in the direction of A and evaluated at the identity matrix:

$$\mu \left(A\right):=\underset{h\searrow 0}{\text{lim}}\frac{1}{h}\left(\Vert I+hA\Vert -1\right).$$

The key result in our context is as follows. Suppose that, for some matrix measure μ,

$$\underset{x\in \mathcal{S},t\ge 0}{\text{sup}}\mu \left(J\left(x,t\right)\right)<0.$$

Then, there is a unique periodic solution $\hat{\xi }\left(t\right):\left(0,\infty \right)\to C$ of Eq. 16 of period T and, moreover, for every solution x(t), it holds that $\left|\xi \left(t\right)-\hat{\xi }\left(t\right)\right|\to 0$ as t → ∞. A self-contained exposition, with simple proofs, of this and several other basic results on contraction theory, is given in Sontag (49). As matrix measure, we will use the measure μ_P,∞ induced by the vector norm |Px|_∞, where P is a suitable nonsingular matrix and ${\left|x\right|}_{\infty }={\text{max}}_{1\le i\le \infty }\left|x_i\right|$. For this norm, Michel et al. (50) has that ${\mu }_{P,\infty }\left(A\right)={\mu }_{\infty }\left(PA{P}^{-1}\right)$, and, in general, ${\mu }_{\infty }\left(B\right)={\text{max}}_i\left(b_{ii}+{\sum }_{i\ne j}\left|b_{ij}\right|\right)$. Computing with our example, we have, denoting $\overline{J}:=PJ{P}^{-1}$,

$${\mu }_{P,\infty }\left(J\right)={\mu }_{\infty }\left(\overline{J}\right)=\underset{i}{\text{max}}\left(J_{ii}+\sum _{j\ne i}\left|J_{ij}\right|\right).$$

With the weighting matrix P = diag(α,1,β), for our system we have

$$\overline{J}=\left(\begin{array}{ccc}-\delta & 0& 0\\ \frac{k_1\left(X_{\text{tot}}-W\right)}{\alpha }& -k_{1}Z-k_{2}Y& \frac{k_{2}Y}{\beta }\\ 0& k_{\text{on}}\beta \left(p_{\text{tot}}-C\right)& -k_{\text{off}}-k_{\text{on}}\left(W-C\right)-k_{\text{on}}\left(p_{\text{tot}}-C\right)\end{array}\right)$$

(which is independent of t), and

$${\mu }_{P,\infty }\left(J\right)=\text{max}\left\{A_1,A_2,A_3\right\},$$

where

$$\begin{array}{l}{A}_1=-\delta <0,\\ A_2=\frac{k_1\left(X_{\text{tot}}-W\right)}{\alpha -k_{1}Z-k_{2}Y\left(1-1/\beta \right)}\le \frac{k_1{X}_{\text{tot}}}{\alpha -k_{2}Y\left(1-1/\beta \right)},\\ A_3=k_{\text{on}}\left(\beta -1\right)\left(p_{\text{tot}}-C\right)-k_{\text{off}}-k_{\text{on}}\left(W-C\right)\le k_{\text{on}}\left(\beta -1\right)p_{\text{tot}}-k_{\text{off}}.\end{array}$$

It will be enough to show that there is a choice of α and β such that ${\text{sup}}_{\xi \in \mathcal{S}}$ A_i < 0 for i = 2, 3. Picking any number

$$1<\beta <1+\frac{k_{\text{off}}}{2k_{\text{on}}{p}_{\text{tot}}},$$

we guarantee that A₃ ≤ −k_off/2 < 0, and also 1 – 1/β > 0. Finally, picking any number,

$$\alpha \ge \frac{2k_1{X}_{\text{tot}}}{k_{2}Y\left(1-1/\beta \right)},$$

we guarantee that A₂ ≤ −k₂Y(1−1/β)/2 < 0.