Magnetic Resonance Fingerprinting

Summary

Magnetic Resonance (MR) is an exceptionally powerful and versatile measurement technique. The basic structure of an MR experiment has remained nearly constant for almost 50 years. Here we introduce a novel paradigm, Magnetic Resonance Fingerprinting (MRF) that permits the non-invasive quantification of multiple important properties of a material or tissue simultaneously through a new approach to data acquisition, post-processing and visualization. MRF provides a new mechanism to quantitatively detect and analyze complex changes that can represent physical alterations of a substance or early indicators of disease. MRF can also be used to specifically identify the presence of a target material or tissue, which will increase the sensitivity, specificity, and speed of an MR study, and potentially lead to new diagnostic testing methodologies. When paired with an appropriate pattern recognition algorithm, MRF inherently suppresses measurement errors and thus can improve accuracy compared to previous approaches.

Introduction

Magnetic Resonance (MR) techniques such as NMR spectroscopy and Magnetic Resonance Imaging (MRI) are widely used throughout physics, biology and medicine because of their ability to generate exquisite information about numerous important material or tissue properties, including those reflective of many common disease states^1-4. However, in practice MR acquisitions are often restricted to a qualitative or “weighted” measurement of a limited set of these properties; the MR signal intensity is almost never quantitative by itself. The same material can have different intensities in different data sets depending on many factors, including the type and setup of the scanner, the detectors used, and so on. Because of this, the quantitative analysis of MR results typically focuses on differences between spectral peaks, spatial locations or different points in time. Even in clinical MRI today, one typically refers to a tissue or material as being “hyperintense” or “hypointense” compared to another area, which may not provide a quantitative indication of the severity of the differences, and may have reduced sensitivity to global changes. Thus robust, fully quantitative multiparametric acquisition has long been the goal of research in MR^5-8. However the quantitative methods developed to date typically provide information on a single parameter at a time, require significant scan time, and are often highly sensitive to system imperfections. Simultaneous, multiparametric measurements are almost always impractical due to scan time limits and a high sensitivity to the measurement setup and experimental conditions. Thus purely qualitative MR measurements remain the standard today, particularly in clinical MRI.

Here we introduce a novel paradigm, Magnetic Resonance Fingerprinting (MRF) that may overcome these constraints by taking a completely different approach to data acquisition, post-processing and visualization. Instead of using a repeated, serial acquisition of data for the characterization of individual parameters of interest, MRF uses a pseudorandomized acquisition that causes the signals from different materials or tissues to have a unique signal evolution or “fingerprint” that is simultaneously a function of the multiple material properties under investigation. The processing after acquisition involves a pattern recognition algorithm to match the fingerprints to a predefined dictionary of predicted signal evolutions. These can then be translated into quantitative maps of the MR parameters of interest.

MRF is related to the concept of compressed sensing (CS)^9-12, and shares many of its predicted benefits. For example, preliminary results show that MRF could acquire fully quantitative results in a time comparable to a traditional qualitative MR scan, without the high sensitivity to measurement errors found in many other fast methods. Most importantly, MRF has the potential to quantitatively examine many MR parameters simultaneously given enough scan time, while current MR techniques can only examine a limited set of parameters at once. Thus MRF opens the door to computer-aided multiparametric MR analyses, similar to genomic or proteomic analyses, that could detect important but complex changes across a large number of MR parameters simultaneously. When an appropriate pattern recognition algorithm is used, MRF also provides a new and more robust behavior in the presence of noise or other acquisition errors that may lead to the near complete suppression of deleterious effects stemming from these factors. While we focus on demonstrating the feasibility for MRI in this study, it is rather straightforward to translate these results to other MR fields, such as multiparametric NMR spectroscopy, dynamic contrast enhanced MRI (DCE-MRI) and dynamic susceptibility contrast MRI(DSC-MRI)¹³.

Generation and Recognition of MRF Signals

The key assumption underlying the MRF concept is that one can generate unique signal evolutions, or fingerprints, for different materials or tissues using an appropriate acquisition scheme. Here we demonstrate that this is possible through the continuous variation of the acquisition parameters throughout the data collection. Variations in the pulse sequence parameters during acquisition have been used previously in MRI and MR spectroscopy to reduce the signal oscillations¹⁴ and to improve the spectral response^15-17. However, these variations were primarily used in a preparation phase or to make the signal more constant. Randomized sampling patterns have also been used previously to aid in the separation of spatiotemporal signals in moving objects or substances with different resonance frequencies^18-20. Here we demonstrate that temporal and spatial incoherence required in MRF can be achieved by varying acquisition parameters such as the flip angle (FA) and phase of RF pulses, the repetition time (TR), echo time (TE), and sampling patterns in a pseudorandom manner.

After the data are acquired, the separation of the signal into different material or tissue types can be achieved through pattern recognition. In its simplest form, this process is analogous to matching a person’s real fingerprint to a database. Once a match is made, a host of additional information about the person such as name, address and phone number can be obtained simultaneously once the fingerprint sample is identified. In MRF, this pattern recognition can take place through many means. In the current implementation, we construct a dictionary that contains signal evolutions from all foreseeable combinations of materials and system-related parameters. For example, T₁, T₂, off-resonance frequency are included in this study, or other properties such as diffusion and magnetization transfer (MT) using the well-established Bloch equation formalism of MR^21,22. Once this dictionary of possible signal evolutions is generated, a matching or pattern recognition algorithm^23,24 is then used to select a signal vector or a weighted set of signal vectors from the dictionary that best correspond to the observed signal evolution. All the parameters that were used to build this signal vector in the dictionary can then be retrieved simultaneously. At present, the calculation of a complete dictionary containing the realistic range of T₁, T₂ and off-resonance requires only a few minutes on a modern desktop computer.

It should be noted that there are near infinite possibilities for MRF-compatible pulse sequences. Other MR parameters of interest can be investigated by identifying pulse sequence components that impart differential sensitivity to the parameters of interest. Moreover, different components can be varied simultaneously, adding the potential for a highly efficient experimental design that allows almost any material characteristic visible using MR to be analyzed in a quantitative way using MRF.

Validation of the Concept

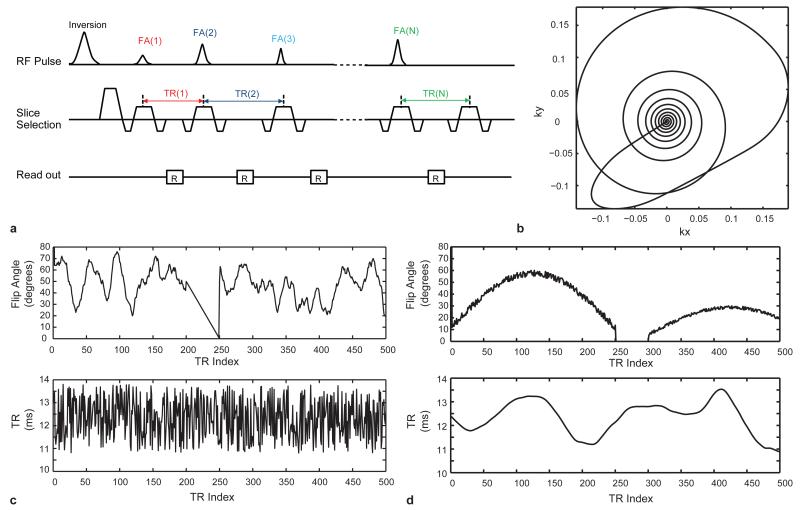
For a proof of principle implementation, an MRF acquisition based on an inversion-recovery balanced steady state free-precession (IR-bSSFP) sequence was employed (Figure1a). This choice of this basic pulse sequence for this initial implementation was based on the extensive existing knowledge about the evolution of the IR-bSSFP signal evolution, and its sensitivity to T₁, T₂ and off-resonance²⁵. After each RF pulse, one interleaf of a variable density spiral (VDS) read out²⁶ was acquired, as shown in Figure 1b. Such a VDS trajectory has been used in fast imaging²⁷ and for the reduction of undersampling errors²⁸. Two MRF acquisition patterns with randomized FA and TR were used as shown in Figure 1c and d in separate scans to demonstrate the flexibility of the choice of the acquisition parameters.

Figure 1. MRF sequence pattern.

a, Acquisition sequence diagram. In each TR, various sequence components are varied in a pseudorandom pattern. b, Here, one variable density spiral trajectory was used per TR. The trajectory rotated from one TR to the next. c and d are examples of the first 500 points of FA and TR patterns that were used in this study.

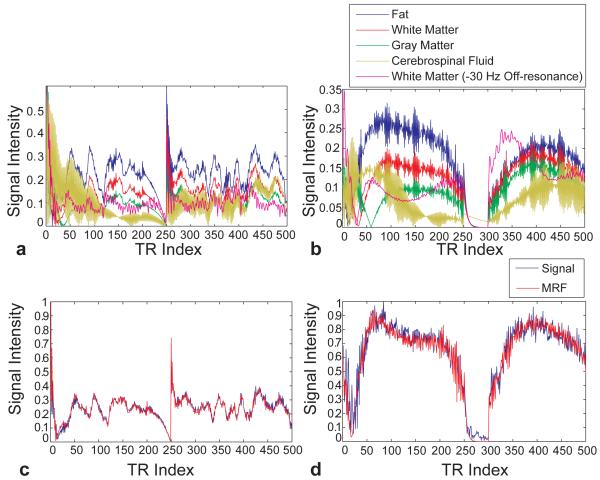
Figure 2a and b show the simulated signal evolution curves that would be expected from four commonly encountered tissues of the brain (fat, White Matter (WM), Gray Matter (GM) and Cerebral Spinal Fluid (CSF)) using the schematic implementation shown in Figure 1c and d, respectively. Each tissue type has characteristic T₁ and T₂ values and thus each signal evolution has a different shape, which confirms that it is possible to satisfy this fundamental assumption in MRF. Note also that the signal levels in these evolutions represent a large fraction of the equilibrium magnetization (which is normalized to 1 in these figures.) Conventional spoiled steady-state sequences typically generate signal levels corresponding to 1-10% of the equilibrium magnetization. Figure 2c and 2d show an acquired signal evolution curve from fully sampled phantom experiments and its match to the dictionary by using the acquisition pattern shown in Figure 1c and 1d, along with the recovered T₁, T₂, proton density (M₀) and off-resonance frequency values. MRF was able to match the signal to the corresponding dictionary entry and obtain the same T₁ and T₂ values from both sequence patterns. A video of the signal evolution from a fully sampled in vivo scan is also included (Supplementary Movie1), demonstrating the oscillating nature of the MRF signal observed in vivo.

Figure 2. Signal properties and matching results from phantom study.

(a and b) Simulated signal evolution curves corresponding to four normal brain tissues using the sequence patterns in Figure 1c and 1d, respectively as a fraction of the equilibrium magnetization. The curve from white matter with off-resonance is also plotted. (c and d) Measured signal evolutions from one of eight phantoms using different sequence patterns and their dictionary match. The estimated T₁, T₂, and off-resonance are (340 ms, 50 ms, −4 Hz) and (340 ms, 50 ms, −13 Hz) in (c) and (d), respectively. The plots are normalized to their maximum value.

Accelerated MRF Acquisitions

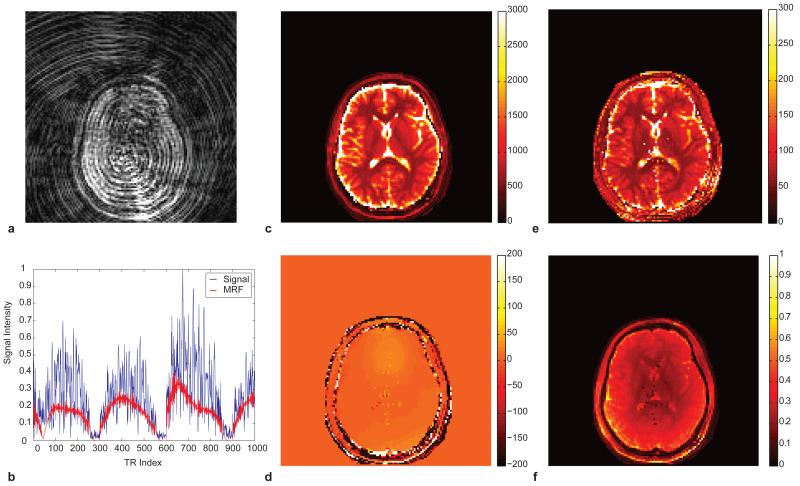
In addition to simultaneously quantifying multiple parameters, the error tolerance of MRF can be significantly better than conventional MRI. Because MRF is based on pattern recognition in a setting where the form of all predicted signal evolutions is known, MRF should be less sensitive to errors during the measurement. This is similar to conventional fingerprint recognition techniques which often contend with smudges and partial fingerprint information. In particular, the interaction of the temporal and spatial incoherence possible in MRF provides new opportunities to accelerate image acquisition through rejection of spatial undersampling errors. In order to test the limits of this acceleration, the same MRF sequence as shown in Figure 1a-c was modified to use only one spiral readout in each acquisition block. Therefore, the data collected are only 1/48^th of the normally required data at each time point, resulting in a total acquisition time of 12.3 seconds corresponding to 1000 sampled time points. (See Figure 3a and Supplementary Movie 2.) The signal evolutions from all 1000 undersampled time points were used directly to match one entry from the dictionary to quantify T₁, T₂, M₀ and off-resonance simultaneously, as shown in Figure 3b. Because these errors are incoherent with the expected MRF signals, they are largely ignored by the following processing steps. Figures 3c-f show that high quality estimates of the MR parameters are generated even with this significant level of undersampling. WM, GM and CSF regions were then selected from the resultant maps. The mean T₁ and T₂ values obtained from each region were listed in the Table 1 and are within the range of previously reported literature values ^29-32. The shortened T₂ value in CSF is likely due to out-of-plane flow in this 2D experiment. A similar effect can be observed in conventional T₂ mapping techniques as well³³. Also note that the roughly −220 Hz chemical shift of fat protons is clearly visualized in the off-resonance map.

Figure 3. MRF results from highly undersampled data.

a. An image at the 5^th TR out of 1000 was reconstructed from only 1 spiral readout demonstrating the significant errors from undersampling. b, one example of acquired single evolution and its match to the dictionary. Note the significant interference resulting from the undersampling. The reconstructed parameter maps show a near complete rejection of these errors based solely on the incoherence between the underlying MRF signals and the undersampling errors. (c), T₁ map (e) T₂ map (d) off-resonance frequency and (f) spin-density (M₀) map. These data required 12.3 seconds to acquire.

Table 1.

In vivo data: Comparison of MRF results and reference values in different brain regions

	T1 (ms)	T2 (ms)
White Matter	685 ± 33	65 ± 4
Previously Reported	608 - 756	54 - 81
Gray Matter	1180 ± 104	97 ± 5.9
Previously Reported	998 - 1304	78 - 98
Cerebrospinal Fluid	4880 ± 379	550 ± 251
Previously Reported	4103 - 5400	1800 - 2460

Motion Error Tolerance in MRF

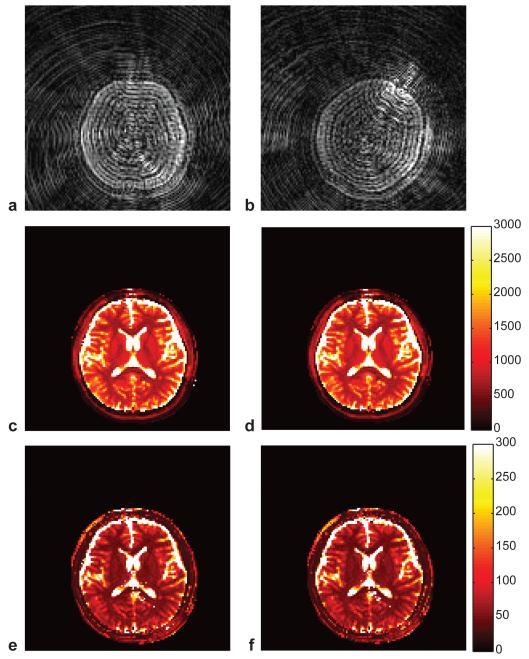
Since motion is one of the most common sources of error in an MRI scan, a motion corrupted scan was performed using the accelerated MRF acquisition described in the prior section. The subject was instructed to randomly move his head for the last 3 s of a total 15 s scan. Supplementary movie 3 shows the random motion as well as severe undersampling artifacts in the reconstructed images. Figure 4 compares the quantitative maps from the data with and without the motion corrupted data. The maps acquired during motion show almost no sensitivity to the motion and show nearly the same quality and anatomy as the maps from the motion-free data, thus indicating that the signal changes resulting from motion were uncorrelated with the evolutions included in the dictionary, and were largely ignored by the pattern recognition algorithm.

Figure 4. Demonstration of error tolerance in the presence of motion.

Reconstructed images acquired at the 12^th second (a) and at the 15^th second (b) demonstrate the large shift in the head position. The resulting MRF maps are nearly identical, demonstrating a rejection of both undersampling and motion errors that are uncorrelated with the expected signal evolution. (T₁ map (c) and T₂ map (e) from the first 12 seconds that has no motion, T₁ map (d) and T₂ map (f) from entire 15 seconds that includes the motion).

Accuracy and Efficiency of MRF

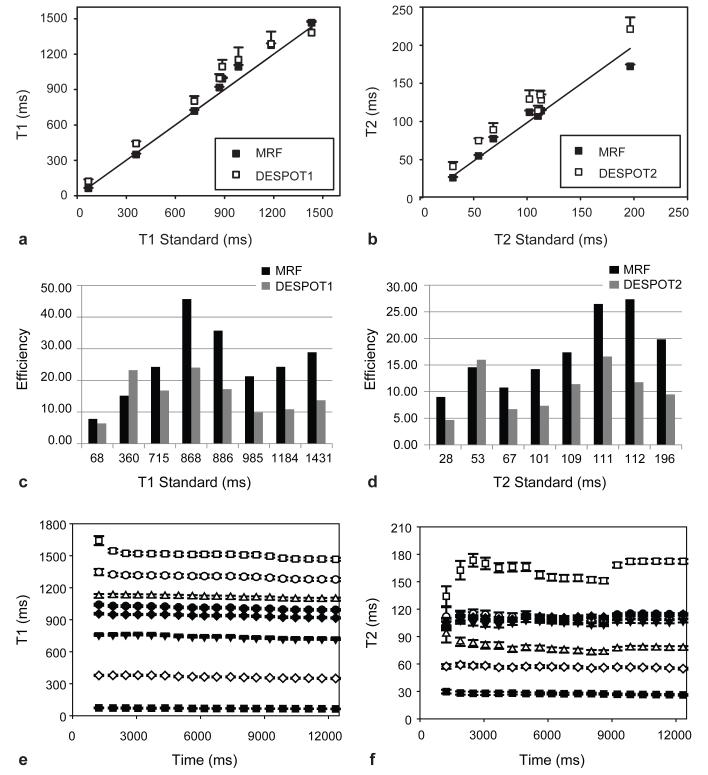
The accuracy and efficiency of the MRF acquisitions were compared with alternative mapping strategies: standard spin echo sequences (SE)³⁴ as well as modern rapid combined T₁ and T₂ mapping methods DESPOT1 and DESPOT2 (Driven Equilibrium Single Pulse Observation of T₁ and T₂, respectively)³⁰ using manufactured agar phantoms. Figure 5a compares the phantom T₁ and T₂ values from these methods. The concordance coefficient correlations for T₁ and T₂ between MRF and spin-echo sequence were 0.988 and 0.974, respectively. The concordance coefficient correlations for T₁ and T₂ between DESPOT and spin-echo sequence were 0.956 and 0.914, respectively. The high concordance correlation coefficients indicate that both methods are in good agreement with standard spin echo measurements and that MRF shows a better accuracy than DESPOT1 and DESPOT2.

Figure 5. Accuracy, Efficiency and Error estimation for MRF and DESPOT.

The T₁ and T₂ values retrieved from MRF from eight phantoms were compared with those acquired from DESPOT1(a), DESPOT2(b) and a standard spin-echo sequence. The efficiency of MRF was compared to DESPOT1(c) and DESPOT2(d) at different T₁ and T₂ values. MRF has an average of 1.87 and 1.85 times higher efficiency than DESPOT1 and DESPOT2, respectively. (e) and (f) show the means and standard deviations of T₁ and T₂ as a function of acquisition time. Error bars represent the standard deviations of the results over a 25-pixel region in the center of each phantom, which are smaller than the symbols for most MRF results.

The theoretical comparison of the efficiency from various mapping methods has been presented by Grawley³⁵ and Deoni³⁶ and is based on a measure of precision per square root of scan time. In those publications, DESPOT1 and DESPOT2 were shown to have greater efficiency than all previously known conventional and accelerated mapping strategies³⁶. As can be seen in Figure 5b, MRF outperforms both DESPOT1 and DESPOT2 by an average factor of 1.87 and 1.85, respectively. For example, at a T₁ of ~1280 ms, MRF shows an average efficiency for estimation of T₁ of 24.2, while DESPOT1 has an average efficiency of 10.89. This means that for this T₁ value, MRF achieves a precision of +/− 15.2 ms (or 1.2%) in 12 seconds of scan time, while the precision in DESPOT1 would be +/−33.9 ms (or 2.6%) for the same scan time. The DESPOT methods apparently display higher efficiency from the single phantom with T₁ of 360 ms and T₂ of 53 ms. However, in this one particular phantom, DESPOT overestimated the values of T₁ and T₂ by 23% and 42% respectively compared to the standard values, as can be seen in Figure 5a, thus causing an erroneous increase in the apparent efficiency. Note that these efficiency estimates do not include the waiting times between the acquisition of the different sub-sequences in DESPOT, nor do they include the time required to reach steady state during each acquisition, and thus should be viewed as conservative estimates of MRF’s performance when compared to DESPOT1 or 2.

Because there is no steady state in the signal evolution from MRF, new information will be continuously added by longer acquisitions. Figure 5c and d illustrates the changes of mean and standard deviation as different acquisition times were used to quantify T₁ and T₂, with a clear trend towards lower error at longer acquisition times. Thus one can select a tradeoff between precision and scan time.

Discussion and Conclusions

The MRF concept presented here is a new approach to MR and provides many opportunities to extend MR measurements beyond their current limits. This originates from the unique pulse sequence design concept in MRF, where the goal is to generate unique signal evolutions that can be matched to theoretical signal evolutions and subsequently yield underlying quantitative information about the material, tissue, or pathology of interest. Since there is no a priori requirement on the shape of the signal evolution curves, there are more degrees of freedom in designing an MRF acquisition, where parameters such as TR, TE, RF pulses and sampling trajectories (among others) can be varied together to produce the simultaneous sensitivity to numerous tissue properties. The ability to analyze oscillating signals in MRF also provides the opportunity to use larger fractions of the available magnetization than methods that rely on a steady-state signal, which is a significant factor contributing to the higher efficiency in MRF. In addition, the oscillatory signal in MRF allows one to sample more informative points along a longer signal evolution as compared to conventional methods which always reach a steady state level after some finite amount of time. Specifically, our initial results here demonstrate that the efficiency of MRF is approximately 1.8 times higher than the DESPOT methods, which were previously the most efficient methods for the measurement of relaxation parameters. Thus the direct prediction of the oscillating, incoherent signal evolutions through the Bloch simulation provides us the potential to obtain new quantitative information that is impractical today because of the prohibitively long scan times required, especially in biological samples and patients.

As demonstrated by the results shown here, MRF has the potential to significantly reduce the effects of errors during acquisition through its basis in pattern recognition. Acquisition errors may globally reduce the probability of a match of an observed signal to any given fingerprint, but as long as the errors do not cause another fingerprint to become the most likely match, the correct quantitative identification will still be made. Ideally, the sequence pattern will be designed so that the various fingerprints from different tissues and materials are as independent as possible, thus ensuring this robustness against motion and other practical errors.

Commercial MR scanners include methods to minimize the effects of unavoidable system imperfections. However, these inaccuracies are becoming increasingly important as MR technology is pushed to its limits, such as the use of very high magnetic fields or physically larger systems. MRF provides a route to model and account for system imperfections such as B₀ and B₁ field inhomogeneities by adding these parameters into the dictionary simulation. Since both MRF and DESPOT2 are based on a bSSFP sequence, which is known to be sensitive to field inhomogeneities^30,37, Supplementary Figure 2 compares the T₂ maps acquired from MRF and DESPOT2 from an in vivo scan. Since off-resonance is not taken into account in the DESPOT2 model, the T₂ map from DESPOT2 shows areas of signal voids resulting from susceptibility effects at the air-tissue interfaces. MRF naturally incorporates these effects into the fingerprints, and thus the maps generated by MRF do not show these errors. Thus MRF could, for example, provide higher quality results using the current generation of MR scanners. Alternatively MRF could also allow the design of lower cost MR scanners that can provide the same quality as today’s high end systems through application of MRF models.

Because of its ability to provide quantitative results across many parameters simultaneously, MRF could lead to the direct identification of a material, tissue or pathology based solely on its fingerprint. For example, many cancer cells show changes in multiple MR parameters (e.g. T₁, T₂, self-diffusion tensor, etc), a combination (though no single parameter) of which could potentially characterize them as different from all surrounding normal tissue types, and thus potentially separable. In an ideal situation, each given material, tissue, or pathology would have its own signal evolution which would be orthogonal to all other signal evolutions. The MRF concept also implies that completely different acquisition schemes are possible in cases where one is only interested in the presence or absence of a particular material or disease state. For example, one could do a very rapid MRF scan of a bulk area of material or tissue and compare the measured signal evolutions against the set of known states of interest. This measurement could either indicate the presence of the material or disease of interest, or indicate its absence within a margin of error. This feature could result in very rapid and accurate screening procedures. In particular, this feature may help to relax the required spatial resolution of an MRI exam, thus increasing the speed, and potentially reducing the cost of an MRI exam. A preliminary example of this kind of visualization is shown in the Supplemental Material Section 3. Using the MRF concept, the operation of the MR unit will also be greatly simplified, since the ‘all in one’ scan concept of MRF has the potential to reduce the dozens of parameters currently presented to the MR operator to a simple ‘scan’ button.

It is important to note that the proof-of-principle implementation of MRF shown here is but one of the many possibilities that could be employed for this technique and both the sequence design/implementation and post-processing methods will continue to be a significant open area of research just as sequence design has advanced over the decades since the conventional methods have been introduced. Other, more advanced pattern recognition algorithms^38-42 will likely improve the performance of MRF. For spatially encoded MRI applications, the parameters retrieved from MRF are far fewer than the number of pixels in the images, and since the signals generated are largely incoherent, MRF has the additional potential to be highly accelerated through combination with other compressed sensing methods for accelerated spatial encoding, in addition to the now standard parallel imaging methods^43-45, neither of which were included in Figure 5. Any of these methods would reduce the undersampling errors seeing in Figure 3a even before the pattern recognition step, which should result in higher quality results. We have recently published data indicating that we can achieve ~10× reduction in imaging time for a 2D slice using parallel imaging alone^43,45,46. Also, it should be noted that the proof-of-principle results shown here only take advantage of two spatial dimensions for undersampling, while it is well known that taking full advantage of undersampling in all three spatial dimensions gives higher performance than a 2D acquisition due to the reduced power of the resulting errors at any given undersampling factor⁴⁷. Thus a combination of an optimized 3D MRF pulse sequence with parallel imaging and more advanced pattern matching algorithms will allow realization MRF in very short scan times.

Methods

1. Sequence Design

After an initial inversion pulse, the first sequence pattern shown in Figure 1c used a pseudorandomized series (Perlin Noise⁴⁸) of flip angle (FA) and a random repetition time (TR) between 10.5 ms and 14 ms based on a uniform random number generator. A linear ramp was added to the FA train since we have seen that this can increase differential sensitivity to both T₁ and T₂.

The second FA pattern in Figure 1d used a series of repeating sinusoidal curves with a period of 250 TRs and alternating maximum flip angles. In the odd periods, the flip angle is calculated as $F{A}_t=10+\sin \left(\frac{2\pi }{500}t\right)\times 50+random\left(5\right)$, where t is from 1 to 250, random(5) is a function to generate uniformly distributed values with a standard deviation of 5. In the even periods, we divide the previous period’s flip angle by 2. A 600 ms delay was added between each of the periods to allow for both differential magnetization recovery according to T₁ and differential signal decay according to T₂. In this case, the TR was a Perlin noise pattern. The RF phase for both of the patterns in Figure 1 alternated between 0 and 180° on successive RF pulses.

The variable density spiral-out trajectory was designed to have 5.8 ms readout time in each TR and to have zero and first moment gradient compensation using minimum-time gradient design⁴⁹. This trajectory required one interleaf to sample the inner 10×10 region, while 48 interleaves were required to fully sample the outer portions of k-space. During acquisition, the spiral trajectory rotated 7.5° from one time point to the next, so that each time point had a slightly different spatial encoding.

2. Dictionary Design

The dictionary used in the matching algorithm was simulated using MATLAB (The MathWorks, Natick, MA). Signal time courses with different sets of characteristic parameters (T₁, T₂ and off-resonance) were simulated. The ranges of T₁ and T₂ for the in vivo study were chosen according to the typical physiological limits of tissues in the brain: T₁ values were taken to be between 100 and 5000 ms (in increments of 20 ms below a T₁ of 2000 ms and in an increment of 300 ms above.) The T₂ values included the range between 20 and 3000 ms (with an increment of 5 ms below a T₂ of 100 ms, an increment of 10 ms between 100 ms and 200 ms and an increment of 200 ms above a T₂ of 200 ms.) Since MR is sensitive to parts per million (ppm) level deviations in the B0 field, different off-resonance frequencies (1 Hz increment between ±40 Hz, 2 Hz between ±40 to ±80 Hz, 10 Hz between ±90 to ±250 Hz and 20 Hz between ±270 to ±400 Hz) were simulated for each combination of T₁ and T₂ parameters to incorporate the effects of signal evolutions in different B₀ fields. A total of 563,784 dictionary entries, each with 1000 time points, were generated in 399 seconds on a standard desktop computer. One dictionary entry was selected for each measured pixel location using template matching. In this case, the vector dot-product was calculated between the measured time course and all dictionary entries (appropriately normalized to each having the same sum squared magnitude) using the complex data for both. The dictionary entry with the highest dot-product was then selected as most likely to represent the true signal evolution. The proton density (M₀) of each pixel was calculated as the scaling factor between the measured signal and the simulated time course from the dictionary. For this experiment, four parameters were retrieved simultaneously from each of the 128×128 pixels using MRF. This calculation required about 3 minutes on a standard desktop computer.

3. Data Acquisition

All MRI and MRF data were acquired on a 1.5T whole body scanner (Siemens Espree, Siemens Healthcare, Erlangen, Germany) with a 32 channel head receiver coil (Siemens Healthcare, Erlangen, Germany). A square field of view of 300 × 300 mm² was covered with a matrix of 128×128 pixels. The slice thickness was 5 mm. Images from each acquisition block were reconstructed separately using non-uniform Fourier transform (NUFFT)⁵⁰. The resultant time series of images was used to determine the value for the parameters (T₁, T₂, M₀ and off-resonance) as described above.

In vivo experiments were performed with IRB guidelines, including written informed consent. For the fully sampled spiral acquisition shown in Supplementary Movie1, 48 repetitions were acquired, each with a different interleaf of the total acquisition. A recovery time of 5 seconds was used in between various acquisitions and this was taken into account in the simulated dictionary.

For the phantom study shown in Figure 2 and 4, eight cylindrical phantoms were constructed with varying concentrations of GdCl3 (Aldrich) and agarose (Sigma) to yield different T₁ and T₂ values ranging from 67 to 1700 ms and 30 to 200 ms, respectively. Standard Spin Echo (SE) sequences were used to quantify T₁ and T₂ separately (T₁ quantification: 13 TRs ranging from 50 to 5000 ms, TE = 8.5 ms, total acquisition time = 33.4 minutes; T₂ quantification: Spin Echo sequences with TEs = [15 30 45 60 90 150 200 300 400] ms, TR = 10000 ms, total acquisition time = 3.2 hours.). T₁ values were calculated pixel-wise using a standard three-parameter nonlinear least squares fitting routine to solve the equation: S(TR) = a + be^{T R/T1}. T₂ values were determined in a pixel-wise fashion using a two-parameter nonlinear least squares fitting routine to solve the equation S(TE) = ae^{−T E/T2}, DESPOT1 and DESPOT2 sequences using a fully sampled spiral readout were implemented based on the acquisition values from Deoni et al³⁰: DESPOT1: FA: 4° and 15°, TR:13.6 ms, DESPOT2: FA: 15° and 55°, TR=10.8 ms. The T₁ and T₂ values were calculated from the equations provided by Deoni et al ³⁰. A 20 s waiting period was used in between the different acquisitions. The initial 10 s of data acquisition was not used in order to ensure that the signal was in steady-state for each of the DESPOT acquisitions. In the following analysis of efficiency, only the pure time of data acquisition for the steady-state DESPOT images is used. For DESPOT1 this was 1.27 s and for DESPOT2 it was 2.29 s (which includes the time for the required DESPOT1 acquisition.)

Statistical Analysis

Quantitative estimates of the errors and efficiencies of MRF, DESPOT1 and DESPOT2 were calculated pixel-wise using a bootstrapped Monte Carlo method as in Riffe et al ⁵¹. Two sets of raw data were acquired for each sequence: the encoded signal and a separate acquisition that only contained noise. Fifty reconstructions were then calculated by randomly resampling the acquired noise and adding it to the raw data prior to reconstruction and quantification. The means and standard deviations of T₁ and T₂ along the 50 repetitions were calculated, and both were averaged within a 5×5 pixels square region of interest for each phantom. The concordance correlation coefficients (ρ_c) were calculated using the equation⁵²:

$${\rho }_c=\frac{2S_{12}}{S_2^1+S_2^2+{({\overline{Y}}_2-{\overline{Y}}_1)}^2},$$

where Y₁ and Y₂ denotes the T₁ or T₂ values from two different methods, n is the number of phantoms, ${\overline{Y}}_j=\frac{1}{n}{\sum }_{i=1}^n{Y}_{ij}$, $S_j^2=\frac{1}{n}{\sum }_{i=1}^n{(Y_{ij}-{\overline{Y}}_j)}^2$, j=1,2 and $S_{12}=\frac{1}{n}{\sum }_{i=1}^n(Y_{i1}-{\overline{Y}}_1)(Y_{i2}-{\overline{Y}}_2)$. The efficiency of the methods was calculated using:

$$Efficiency=\frac{T_{n}NR}{\sqrt{T_{seq}}},n=1,2$$

where T_nNR is the T₁ or T₂ to noise ratio (defined as the T₁ or T₂ value divided by the estimated error). T_seq is the total acquisition time for MRF, and the relevant acquisition times for DESPOT1 and DESPOT2 (where the waiting times required for the approach to steady state and the time between each of the DESPOT1 and DESPOT2 scans to allow for complete recovery of magnetization were ignored.)