Motif discovery and transcription factor binding sites before and after the next-generation sequencing era

Abstract

Motif discovery has been one of the most widely studied problems in bioinformatics ever since genomic and protein sequences have been available. In particular, its application to the de novo prediction of putative over-represented transcription factor binding sites in nucleotide sequences has been, and still is, one of the most challenging flavors of the problem. Recently, novel experimental techniques like chromatin immunoprecipitation (ChIP) have been introduced, permitting the genome-wide identification of protein–DNA interactions. ChIP, applied to transcription factors and coupled with genome tiling arrays (ChIP on Chip) or next-generation sequencing technologies (ChIP-Seq) has opened new avenues in research, as well as posed new challenges to bioinformaticians developing algorithms and methods for motif discovery.

INTRODUCTION

‘Motif discovery’ (or ‘motif finding’) in biological sequences can be defined as the problem of finding short similar sequence elements (building the ‘motif’) shared by a set of nucleotide or protein sequences with a common biological function. The identification of regulatory elements in nucleotide sequences, like transcription factor binding sites (TFBSs), has been one of the most widely studied flavors of the problem, both for its biological significance and for its bioinformatic hardness [1, 2].

This first step of gene expression, ‘transcription’, is finely regulated by a number of different factors, among which ‘transcription factors’ (TFs) play a key role binding DNA near the transcription start site of genes (in the ‘promoter’ region), but often also within the region to be transcribed or in distal elements like ‘enhancers’ or ‘silencers’ [3, 4]. The actual DNA region interacting with and bound by a single TF (called TFBS) usually ranges in size from 8–10 to 16–20 bp. TFs bind the DNA in a sequence-specific fashion, that is, they recognize sequences that are similar but not identical, differing in a few nucleotides from one another.

The introduction of technologies like oligonucleotide microarrays [5, 6] has given the possibility of measuring simultaneously the mRNA expression levels of thousands of genes at the same time. Thus, since TFs activate or block the transcription of genes by binding DNA, and genes showing similar expression patterns should be regulated by the same TFs, the genomic regions essential for the regulation of coexpressed genes (e.g. their promoters) should contain short and similar sequence elements, corresponding to binding sites for the common regulators [7, 8]. Promoters from clusters of coexpressed genes (usually a few dozens) have been thus the most typical input to algorithms for finding overrepresented sequence motifs, even though regulatory elements could be located elsewhere in the genome.

On the other hand, the recent introduction of technologies like chromatin immunoprecipitation (ChIP [9]), coupled with tiling arrays (ChIP on Chip [10]) or next-generation sequencing (ChIP-Seq [11]), has permitted the direct genome-wide identification of regions bound in vivo by a given TF. In other words, ChIP permits to single out a set of genomic regions whose binding sites from the same TF are experimentally supported. These regions usually range in size from a few dozen base pairs to a few hundred base pairs. Thus, ChIP experiments are another perfect case study for motif finding, since the regions obtained from ChIPs are larger than the actual TFBSs themselves, which still have to be discovered within the regions. The actual binding specificity of the TF investigated can be thus identified and modeled. ChIP-Seq has rapidly become the de facto standard in this field, posing, as we will discuss in the following, new challenges to the developers of algorithms and tools.

DESCRIBING TRANSCRIPTION FACTOR BINDING SITES

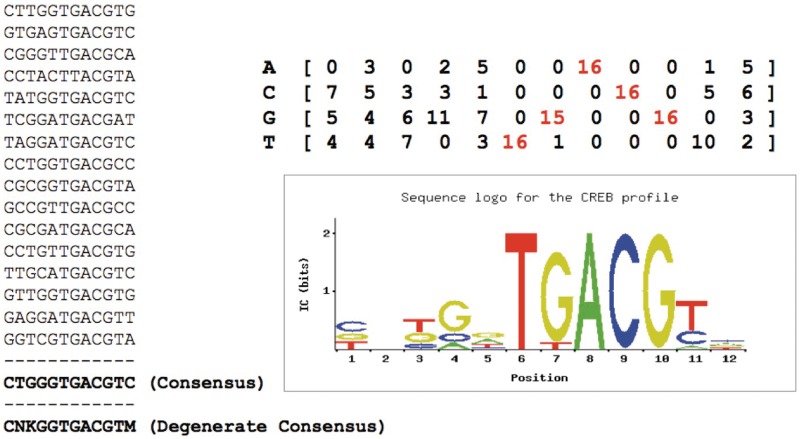
An example of a set of binding sites recognized by the same TF (CREB) is shown in Figure 1. We can summarize them by building their ‘consensus’, denoting for each position what seems to be the nucleotide preferred by the TF. Since approximation is tolerated by TF binding, all oligos that differ from the consensus up to a maximum number of nucleotide substitutions can be considered valid instances of binding sites for the same TF. On the other hand, the observation of a collection of TFBSs like the example of Figure 1 shows how specific positions are strongly conserved throughout all the sites, i.e. the TF does not seem to tolerate variation in those places, while differences seem to be confined to some other positions. Accordingly, one could employ ‘degenerate consensuses’, which can use symbols denoting not only a single nucleotide, but different nucleotides at the same position, e.g. by using IUPAC codes [12], in which different letters denote a set of nucleotides (e.g. W = A or T, S = C or G, U = A,C, or G, N = any nucleotide and so on). All oligos which respect the definition given by the degenerate consensus are again assumed to be recognized by the TF.

Figure 1:

Describing a ‘motif’ representing the binding specificity of a transcription factor (CREB). Given a set of oligos known to be bound by the same TF, we can represent the motif they form by a ‘consensus’ (bottom left) with the most frequent nucleotide in each position; a ‘degenerate’ consensus, which includes ambiguous positions where there is no nucleotide clearly preferred (N = any nucleotide; K = G or T; M = A or C, according to IUPAC codes [12]); an alignment profile (right) that can be converted into a nucleotide frequency matrix by dividing each column by the number of sites used, as well as into a ‘sequence logo’ [13] showing the conservation of nucleotides and the respective information content contribution at each position.

Finally, the most flexible and widely used way of building descriptors for TF binding is to align the available sites, and to build an (ungapped) alignment ‘profile’ with the count or the frequency with which each nucleotide appears at each position in the sites. Once the profile has been built, any candidate oligo can be compared to it, by using the corresponding nucleotide frequencies to assess how well it fits the descriptor. The result is a score ranging from 0 to 1 (rather than a yes/no decision like with consensuses), expressing the ‘likelihood’ of the oligo to fit the profile with respect to a random background nucleotide distribution [14].

DISCOVERING TRANSCRIPTION FACTOR BINDING SITES

Regardless of the representation used, and of the experiment performed to select the sequences to be analyzed, the problem of motif discovery of TFBSs in nucleotide sequences can be informally defined as follows. The input is a set of DNA sequences, typically a few hundred base pairs long. The goal is to find one or more motifs, that is, one or more sets of oligos (10–16 bp long) appearing in a large fraction of the sequences (thus allowing for experimental errors and the presence of false positives in the set). Oligos belonging to the same motif should be similar to one another enough to be likely to be binding sites recognized by the same TF. The motif size is usually assumed to be known a priori. To assess the actual significance of the motif, and to discriminate it against random similarities, the motif should not appear with the same frequency and/or the same degree of oligo similarity in a set of sequences selected at random or built at random with some model generating ‘biologically feasible’ DNA sequences. Since the binding specificity of several TFs is already known, the motifs discovered can be then compared to already known motifs with tools like STAMP [15] or TOMTOM [16].

This problem has been widely studied, and the various approaches introduced so far mainly differ in two points. The first is how similar oligos forming a candidate motif are chosen, and the motif they form is built and described. Then, in how the statistical significance (overrepresentation) of the motifs is assessed, and which ‘background’ or ‘random’ model is employed.

Given k input DNA sequences of length n, and a motif size m, by assuming that a motif instance should appear in each sequence we have (n − m + 1)^k candidate solutions that can be built by combining all the m-mers in all the possible ways, that is, an overall number that is exponential in the number of input sequences. Therefore, the exhaustive enumeration of the solution space (all possible oligo combinations) is computationally unfeasible [17]. The choice of how to model motifs has thus straightforward implications in the heuristics that can be applied to solve the problem.

USING PROFILES

Since profiles provide a description of the binding specificity of a TF more powerful and flexible than consensuses, they have been very often the method of choice in the modeling of the solutions of motif discovery. In general, the rationale is to select some oligos from the input sequences, align them and score the resulting profile according to its conservation with a suitable measure of significance. The problem can be formalized as one of ‘combinatorial optimization’, that is, finding the combination of oligos that build the highest-scoring profile by exploring the search space of all possible combinations with some heuristic and avoiding exhaustive enumeration. Nearly all the combinatorial optimization techniques (i.e. greedy, local search, stochastic search, genetic algorithms and so on) have been tried and applied over the years.

For example, a greedy heuristic was introduced in refs [18, 19], in which solutions are build incrementally by first solving the problem on two sequences, then by adding the third one and so on, saving at each step only the highest scoring profiles. When the last sequence of the set has been processed, the resulting profiles, output by the program, will contain one oligo for each input sequence.

Another way of exploring the solution space is to start from a given profile and refine it by substituting some oligos of the profile with others likely to produce better solutions. Given a profile, the Multiple Expectation Maximisation for Motif Elicitation (MEME) algorithm [20, 21] evaluates the likelihood of each oligo of given length to fit the profile with respect to the rest of the sequences, while the rest of the sequences should fit a ‘background model’ better than the profile. According to this principle, a likelihood normalized value is computed for each m-mer of each input sequence in the E (Expectation) step. Then, the algorithm builds a new profile by aligning all the sequence oligos of length m weighted by the corresponding likelihood value, in the M (Maximisation) step. At the beginning, the algorithm builds a profile from each m-mer in the input sequences, then it performs on each one a single E and a single M step. The highest scoring profile obtained in this way is further optimized with more EM steps. If MEME can be seen as the implementation of a local search strategy, the heuristic employed in the Gibbs sampling strategy [22, 23] can be seen as its stochastic counterpart. Indeed, the initial motivation was to improve a EM local search strategy similar to the one employed by MEME [24], avoiding possible premature convergence to local maxima. The basic idea, assuming again that one site appears in each input sequence, is to build an initial profile by choosing an m-mer at random in each of the k input sequences. Then, the oligo coming from a given sequence S is removed from the profile; a likelihood value is computed for each oligo in S, representing how well it fits the model induced by the profile with respect to some background distribution; then an oligo is chosen from sequence S with probability proportional to the likelihood values computed. The oligo is added to the profile, replacing the one that was removed before. These steps are iterated a number of times, or until convergence (no oligo replacement is made) is reached. This variant of the algorithm is also known as the ‘site sampler’. The main difference with local search is that in the latter the best oligos are always selected deterministically according to how well they fit the current solution, while the Gibbs sampler chooses how to modify the current solution in a stochastic way. Further improvements were introduced [23] for allowing multiple occurrences (or no occurrence) of a motif within the same sequence (algorithm known as ‘motif sampler’). Modifications of the basic Gibbs sampling technique were also described for example in AlignACE [25] and ANN-Spec [26].

The function used to assess profile significance should simultaneously take into account both how much each column of the profile is conserved and how the nucleotide frequencies in the profile differ from a ‘background’ distribution that should correspond to the frequencies that would be obtained by aligning oligos chosen at random. If we assume that nucleotides in genomic sequences are independent, the overall conservation of the motif and its distance from a ‘background’ random distribution can be measured by computing the ‘information content’ (IC) or ‘relative entropy’ of the profile:

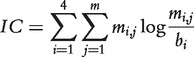where m_i,j is entry in row i and column j of the profile and b_i is the expected frequency of nucleotide i in the input sequences (which can be derived from the genomic sequence of the organism studied or from the input sequences themselves). This measure, expressed in ‘bits’, accounts for how much each column is conserved and how much the nucleotide frequencies obtained in the profile differ from what would have been obtained by aligning oligos chosen at random. In case of uniform background frequencies, this measure equals Shannon's entropy. Relative entropy is also the measure employed to design sequence logos, with the height of each nucleotide in each position proportional to its entropy contribution. For example, in the logo shown in Figure 1, uniform background frequencies are assumed, and the most conserved nucleotides have an entropy of 2 bits (derived from an observed frequency of 1.0 compared to the expected frequency of 0.25).

The weakest point of this type of model is that the ‘background’ probability of finding a nucleotide in the input sequences is not influenced by its neighbors, an assumption that can be easily proven to be too unrealistic in natural sequences. A straightforward improvement, introduced in different tools, has been thus to model the background with a higher order Markov model [27]. Intuitively, when a j-th order Markov model is employed, the probability of finding a nucleotide in a given position of a sequence depends on the j nucleotides preceding it in the sequence itself. The model parameters can be estimated from the analysis of a number of regulatory regions, e.g. by taking all the promoters of all the genes annotated in a given species and producing organism-specific probability distributions and expected oligo frequencies [28]. In turn, any significance score can be augmented by terms indicating not only how much the profile itself is conserved, but also how (un)likely it is to find the oligos composing it in the sequences analyzed according to the background model employed [29].

For example, the performance of MEME has been shown to be significantly improved by the introduction of a higher-order background [30]. Different flavors of Gibbs samplers are presented in refs [31–33], where the background is described with a third order Markov model.

In the GLAM [34] software the sampling procedure as well as the IC score have been modified in order to compare profiles of different size, sparing the user the visual inspection and comparison of the results obtained trying different motif lengths. The optimal length is computed with a simulated annealing strategy. In ref. [35], the idea presented is to use position-specific frequencies: the expected frequency of an oligo is estimated by analyzing the oligos that appear at approximately the same distance from the genes transcription start site with a Bayesian segmentation algorithm.

NestedMICA [36] introduced mosaic background modeling. The idea is to use four different higher order background models according to the overall nucleotide composition of the input sequences, and in particular to the content of C and G nucleotides (corresponding to the presence or absence of CpG islands in promoters). The profile optimization strategy adopted in this algorithm is also novel, based on a sequential Monte Carlo Expectation Maximization approach.

Research has also focused on employing different optimization strategies. Genetic algorithms are combined with expectation maximization in GADEM [37]. Also, in all the algorithms we described so far optimization steps are performed only by selecting oligos to build a solution according to their respective similarity or their similarity to the profile, but the scores to be optimized are considered only a posteriori to compare different candidate solutions. A straightforward approach could be then to consider directly the scoring function in the optimization, as in ref. [38] where evolutionary computation is employed. In ref. [39], Gibbs sampling has been applied directly to the optimization of the IC score associated with profiles, reporting performance improvements over traditional a posteriori methods.

USING CONSENSUSES

If consensuses are employed, the problem can be formalized in a completely different way: for each of the 4^m nucleotide sequences of length m (8–16 bp for TFBSs), collect from the input sequences all its approximate occurrences with up to e mismatches, and compute the significance of finding a given match count number. In other words, it becomes an exhaustive approximate pattern matching problem. Typically, pattern matching is performed allowing from two (for 8-mers) to four (on 16 nt) substitutions. Indeed, this has been the earliest approach to the problem [40–42], although considered to be too time-consuming. The application of indexing structures to the input sequence set, however, made it feasible on real case studies, reducing also its theoretical complexity from 4^m to 4^e (exponential in the number of mismatches allowed instead of on motif length [43, 44]).

If no substitutions in instances of the same motif are allowed, the problem becomes simpler and this strategy can be employed in genome-wide analyses of overrepresented oligos, as for example in refs [45–47]. That is, oligos can be counted in a subset of the genomic regions (e.g. promoters, or regions accessible to TFs including enhancers), and their count compared to an expected value based on their genome-wide frequency. Similar overrepresented oligos can be clustered in a post-processing stage, and considered instances of binding sites for the same TF. Exhaustive pattern matching can be also accelerated significantly by using ‘degenerate consensuses’, which allow for variation only in the degenerate or ambiguous positions [48, 49].

Exhaustive matching with no restrictions on the position of substitutions was introduced in the SMILE [43] and Weeder [44] algorithms, where the exhaustive search for the exponential number of candidate consensuses was implemented with the preliminary indexing of the sequences with a suffix tree [50]. SMILE then compares the number of occurrences of a given motif with its occurrences in a ‘negative’ or ‘random’ sequence set, while in Weeder the observed number of occurrences of a motif is compared with expected oligo frequencies derived from all the promoter regions of the same organism of the input sequences, with a measure similar to IC applied to whole oligos instead of single nucleotides [51]. To overcome the coarseness of the consensus representation, the best instances of each motif can be extracted from the sequences by using a profile built with the oligos selected by the consensus-based algorithm, in order to have a more fine-grained ranking of predicted motif instances and to detect oligos fitting the motif but exceeding the predefined substitution thresholds used.

A further refinement of consensus associated significance measures is presented in ref. [52], where given a Markov model of some order a P-value is computed with a compound Poisson approximation for the null distribution of the number of motif occurrences both in terms of overall number of occurrences and of number of sequences containing a motif instance. The monotonicity properties of the compound Poisson approximation are exploited to avoid exhaustive enumeration of candidate consensuses.

OTHER METHODS

While the model employed is fundamental to predict candidate sites that fit a descriptor [14], or compare different motifs [15], it is much less so when the aim is to extract from the sequences a set of oligos sharing some level of pairwise similarity. For example, a straightforward way of modeling the problem is to employ a graph, whose nodes correspond to oligos of the input sequences and edges connect nodes corresponding to similar oligos. The problem can be thus recast in graph–theory terms, and motifs can be found for example by detecting cliques [53, 54] or maximum density subgraphs [55]. However, the same argument concerning the complexity of the solution space of profile-based optimization methods holds for graph-based approaches, making the introduction of optimization heuristics mandatory to obtain solutions in reasonable time. Alternatively, the motif discovery problem can be recast as a clustering one, in which oligos forming the motif should cluster together, and the rest should belong to a ‘background’ cluster. Suitable clustering strategies like ‘self organizing maps’ can be then applied to solve the problem [56, 57].

PERFORMANCE EVALUATION BEFORE NEXT-GENERATION SEQUENCING

Assessing the merits and shortcomings of different algorithms for motif finding has always been far from being straightforward. When experimental data were scarce, algorithms were often tested on synthetic data sets, in which simulated binding sites were planted into simulated sequences [53, 58, 59]. Some benchmark sequence sets derived from experimental data have been introduced over the last few years [60–62].

All in all, the overall picture that emerged was that, starting from gene expression data and promoter sequences, motif finding algorithms could provide reliable results in simple organisms like bacteria or yeast, but in higher eukaryotes like human the performance was still far from being satisfactory. Consensus-based methods showed in different tests a slightly better performance [61], probably due to the possibility of performing an exhaustive search and thus of finding optimal solutions, or suboptimal candidate solutions to be further refined with profile-based optimization methods.

The poor performance usually reported for motif finding in promoter analysis is due to several reasons. First of all, similarity shared by sites recognized by the same TF is often very subtle, and when just a few sequences are investigated the motif they would form is not conserved enough to be discriminated against random similarities. Then, the complexity of the regulation of every level of gene expression seems to grow in parallel with organism complexity, and coexpression does not mean coregulation. The functional activity of a promoter depends on the nature and the spatial organization of several TFBSs. Therefore, what yields a set of coexpressed genes in human, mouse or Drosophila can be the combined activity of several different cooperating or competing factors each one acting on a subset of genes. Third, TFBSs are not confined to the promoter region, since transcription can be regulated by distal elements like enhancer or silencers, and can be located thousands or even millions of base pairs away from the genes they regulate. On the other hand, the statistical methods usually employed to assess motif significance and enrichment cannot produce feasible results on whole intergenic regions. Finally, traditional motif finding algorithms usually ignored chromatin structure and epigenetic information, assuming that all regions of DNA are accessible to TFs in the same way, and thus TF binding depends on sequence only.

The main issue is however not the lack of motif prediction, but, vice versa, typically motif finding algorithms report as significant motifs that can be considered as false positives. This has led to the establishment of ‘meta-predictors’ [63–65] that pool together the output of different algorithms, with the idea that motifs on which different tools agree on are more likely to possess some biological function.

Other additional considerations are usually employed when performing analyses aimed at finding common regulators of the genes and their sites in the sequences. One can limit the search to already known motifs, by matching the sequences to the TFBSs profiles available in specialized databases (see, e.g. [66] and references therein). Also, a widely used technique has been ‘phylogenetic footprinting’ [67–69], that is, to compare a given sequence with its orthologous counterparts in evolutionary close enough species. Indeed, a strikingly high level of sequence conservation can be found across different genomes in noncoding regions [70], as well as in conserved short sequence elements within promoters likely to be single conserved TFBSs. This type of analysis can be performed prior to motif finding, by masking out the less conserved parts of the sequences investigated, but also simultaneously, by designing algorithms aimed at finding motifs both overrepresented in a sequence set, and at the same time significantly conserved with respect to homologous sequences in other species (see, e.g. [71, 72], which are enhancements of the Gibbs sampler and MEME to this case). The drawback is clearly that every single functional site in an organism like human cannot be expected to be conserved in other species [73].

Improvements in motif finding reliability have also been reported when nucleosome occupancy of sequences has been added to a Gibbs sampling algorithm [74], by modifying the a priori probabilities, as also introduced in ref. [75] for MEME or in ref. [76], where a sampling method (parallel tempering) similar to NestedMICA is employed with better convergence properties than standard Gibbs sampling. The idea is that while in general at the beginning all the oligos of the input sequences have the same probability of being part of a conserved motif, these probabilities can be modified according to any given criterion, e.g. conservation in orthologous sequences or nucleosome occupancy, thus associating with some oligos higher a priori probabilities of being selected during the optimization iterations [77].

THE CHROMATIN IMMUNOPRECIPITATION ERA

In the last few years novel experimental methodologies have been introduced, opening to researchers in the field novel avenues of unprecedented power. A typical example is ChIP [9], that allows for the extraction from the cell nucleus of a specific protein–DNA chromatin complex, like TFs together with the DNA they bound in vivo. The introduction of ‘tiling arrays’ has permitted for the first time the analysis of the DNA extracted on a whole-genome scale (ChIP on Chip [10]) by using probes designed to cover a whole genome or at least its promoter regions. DNA regions bound by the TF are those whose corresponding probes show the greater enrichment over a control experiment. The recent introduction of novel and efficient sequencing technologies collectively known as ‘next-generation sequencing’ [78] has permitted taking this approach one step further, and in order to identify the DNA regions extracted by the cell, the DNA can be sequenced (ChIP Sequencing, or ChIP-Seq [11]). Once again, the regions bound by the TF investigated are the ones showing enrichment over a control sample, expressed as the difference between the number of times each base pair of the genome has appeared in the sequenced IP sample versus the control [79].

The typical output of experiments of this kind consists of a list of thousands of genomic regions, whose size seldom exceeds a few hundred base pairs. Although the TF binding the regions is already known, motif discovery methods apply also to this case, for finding the actual binding sites for the TF within the regions and for modeling its binding specificity in vivo. Also, ‘secondary motifs’ less conserved than the main one could be associated with other TFs cooperating with the TF investigated. Indeed, when applied to sequences from ChIP experiments motif discovery methods become more reliable than in promoter analysis, for different reasons. The most important one is that the frequency with which binding sites for the same TF appear is much higher in regions coming from a ChIP, where they should appear a very high percentage of the sequences examined, even more than once in a single sequence, while in promoters from coexpressed genes there is no guarantee for this. Thus, ChIP experiments produce sequence sets which are ‘cleaner’ and more importantly much more redundant, since in thousands of sequences we can expect to find several instances of binding sites highly similar to one another. In gene promoter analysis the input set is much less cleaner, the sequence set is much smaller (and thus the different sites in the sequences can be very different from one another) and the sequences are longer. Indeed, the performance of traditional motif finding methods on ChIP sequence sets managed to redeem their bad reputation in several cases, by actually ‘discovering’ the sites bound by the TF (see among many others [80–83]).

The main drawback is that the size of the input is significantly larger. In promoter analysis it rarely exceeds a few hundred sequences, while in genome-wide ChIPs a typical input is made of thousands of sequences. Hence, the (n − m + 1)^k candidate solutions constitute a search space too large for profile-based methods, which even with heuristics become too slow taking days or weeks to complete a computation. Indeed, ChIP-tailored versions of MEME [84] and the Gibbs sampler [85] overcome this issue by preselecting a subset of the sequences and performing the motif optimization only on them. STEME [86] is a speed up of MEME in which sequences are indexed with a suffix tree for accelerating the EM steps in which sequences have to be scanned with the profile currently being optimized, and feasible time requirements also for ChIP-Seq data are reported. ChIPMunk [87] combines EM with a greedy approach similar to Consensus, again to speed up the profile optimization.

On the other hand, the number of candidate solutions for consensus based methods (4^m) remains constant regardless of the size of the input, and computation time is expected to increase only linearly in the matching stage. However, even the more widely applied tools of this kind, like Weeder, can be significantly slow, taking several hours on typical case studies, because they were devised for finding subtle similarities in small sequence sets, rather than large similarities in large ones. For example, when looking for motifs 10-bp long in promoter analysis Weeder collects from the sequences the occurrences of 10-mers up to three substitutions: but in ChIP studies it often suffices to allow one or two substitutions to capture the main motif bound by the TF investigated, thus reducing time complexity both in theory and in practice.

All these considerations have thus led to the introduction of consensus-based methods tailored for working on large scale ChIP studies, like MDScan [88], Trawler [89], Amadeus [90] (introduced for ChIP on Chip), and DREME [91], CisFinder [92], cERMIT [93], HMS [85], and RSAT Peak-motifs [94] (introduced for ChIP-Seq). All these tools report significant reduction of computational resources required over methods that were devised for promoter analysis. The general ideas underlying these tools are somewhat similar. Initial candidate solutions are built by matching consensuses (as e.g. MDScan and RSAT) or degenerate consensuses (Trawler, Amadeus, DREME, cERMIT) on the input sequences—which can be indexed with a suffix tree as in Trawler to speed up the search. Exact or degenerate consensuses are in fact powerful enough to capture significant motifs given the much higher redundancy of motif instances in the sequences. Significance can be then assessed for example with a third-order background model (MDScan), or more simply by comparing the match counts in the input to randomly selected background sequence sets, e.g. with z-scores (Trawler) or a hypergeometric test (Amadeus and DREME), or the overall match count across the whole genome. Finally, similar motifs are merged, and motifs are modeled with a profile which can be further optimized on the input sequences.

Also, since probe or sequence enrichment defining a bound region in ChIP is reported to be an indicator of the affinity of the TF for the region [95], higher priority or weight can be given to those regions that are more enriched in the experiment. This is something that can be trivially done by analyzing only a selected subset of ‘best’ sequences [84, 85], but can be taken into account directly by the algorithms, as in MDScan on ChIP on Chip and ChIPMunk, cERMIT for ChIP-Seq, similarly to what has been done by correlating sequence motifs in promoters with gene expression [96, 97].

In the last couple of years ChIP-Seq has become the method of choice for the genome-wide characterization of TF binding, as well as polymerase binding and histone modifications. Next-generation sequencing can be used also for building genomic maps of DNA methylation (ME-DIPseq), open chromatin accessible to TFs (DNase I hypersensitive sites—DNase-Seq, Formaldehyde-Assisted Isolation of Regulatory Elements—FAIRE-Seq [98]), and other genetic or epigenetic factors involved in the regulation and activation of gene transcription.

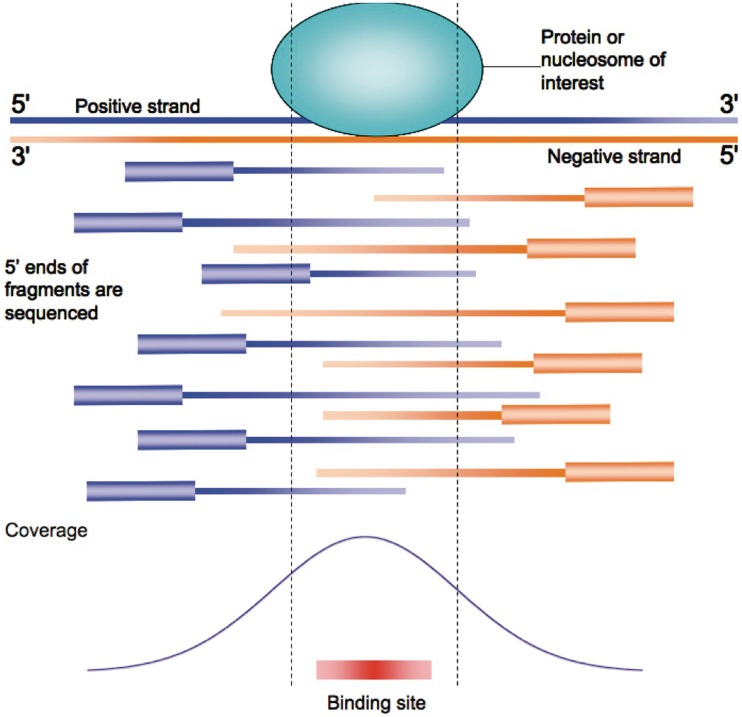
ChIP-Seq can provide maps of the binding of the TF studied with a much higher resolution than ChIP on Chip [99], as shown in Figure 2: the sites bound by the TF are more likely to be located near the center of the region extracted [95] or within a few base pairs from the point of maximum enrichment within the ‘peak’ region itself. Thus, input sequences can be made shorter, confining the analysis on the 100–200 bp around the point of ‘peak’. Positional bias within the input sequences becomes then another key factor for assessing the significance of a motif, as in ref. [100] where IC is applied also to the position where motifs appear with respect to a background uniform distribution, or in the HMS tool. In case, however, of TFs binding DNA as homo- or hetero-multimers, hence with multiple sites in the same ChIP region, the picture is less clear and positional bias much less evident (see e.g. Figure 4 from [79]). In this case, however, different motifs should be located at preferred distances from one another, and thus positional bias should be detected by comparing motifs’ relative distances.

Figure 2:

Schematic view of the results of ChIP-Seq performed on a genomic region bound by a TF [79]. DNA is fragmented at random, and thus the ends of each sequenced DNA fragment map on different positions on the genome. Each fragment is assumed to be the 5′ of a 200- to 300-bp region. The ‘peak’, corresponding to the point of maximum enrichment (‘coverage’) within the region (that is, appearing in the highest number of sequenced fragments) should be located in correspondence of the actual binding site for the TF (bottom).

ChIP-Seq or similar experiments providing genome-wide epigenetic profiles can be also a support of great importance in motif discovery itself. For example, as with nucleosome occupancy, the analysis can be confined only to regions of open chromatin accessible to the TFs (identified by DNase-Seq or FAIRE-Seq [101, 102]), or corresponding to specific histone modification profiles, or on nonmethylated DNA. Indeed, several whole genome maps of these latter elements are becoming available, e.g. within the ENCODE project, and data can be retrieved from databases like the UCSC Genome Browser [103]. It should be kept in mind, however, that these maps are strongly cell-line or even allele specific: hence reliable results can be obtained if TF binding is investigated in the same cell line for which epigenetic information is available.

PERFORMANCE EVALUATION IN THE ChIP-Seq ERA

Genome-wide ChIP experiments for TFs can also be a source of great value for building feasible benchmark sequence sets for the testing of motif finding algorithms, like the ‘Harbison data set’ derived from 203 DNA binding proteins in yeast presented in ref. [104] or the ‘metazoan data set’ introduced in ref. [90], composed of several promoter sets mostly derived from genome-wide ChIP on Chip experiments. These data sets can be considered as an ‘hybrid’ benchmark, composed of promoter sequences (like in an expression study) in which however the TF binding has been identified through ChIP. Indeed, the performance of motif finding algorithms improves significantly with respect to promoter analysis.

On the other hand, as of today there is still no reference benchmark set derived from ChIP-Seq, and in the respective articles the different methods are usually compared only on a few data sets, that change according to the authors’ expertise or taste. Overall, binding sites from the main TF investigated in each experiment are nearly always correctly recovered also by ‘first generation’ methods like MEME or Weeder, as shown by the myriad articles presenting the results of genome-wide ChIP-Seq experiments now published. The main difference lies in computational resources needed, as discussed before, with newest methods being much faster, and, indeed, special emphasis is often put on the execution time needed by the algorithms that often differ very little in the overall design and significance measure adopted. Also, older methods tend to produce a more redundant output, with highest scoring motifs highly similar to one another. Some tools have then been introduced to ‘clean’ the output and for clustering redundant motifs [105]. We can expect finding the binding motif for the TF investigated to become even easier in the future, with the introduction of novel experimental techniques like ChIP-exo [106, 107], which by using exonuclease trims the DNA regions at a precise distance from the binding site.

The focus of more recent motif discovery methods has anyway further moved on, that is, not only by assessing the performance of motif-finding algorithms in recovering the sites for the TF studied, but also in identifying, as mentioned before, sites for secondary TFs binding DNA in the neighborhood of the main one [108, 109], and positional correlations among different motifs. Meta-servers pooling the output of different methods can be applied also for this task, each one detecting a different set of secondary motifs [64, 65]. However, we still lack a unique benchmark data set, and often the assessment of the merits of a method in finding correlated motifs is left to the speculation of the authors, e.g. ‘motifs A and B are both found to be enriched, and indeed from literature we know cases in which TFs A and B co-operate’. Also with ChIP-Exo data the focus can move to finding functionally distinct motifs for the same TF, clustering of different motifs, secondary interactions and combinatorial modules within a compound motif.

As with gene expression experiments, in which the selection of the set of genes to be studied influences the result of motif discovery, also the selection of the ChIP enriched regions is an essential step for the feasibility of the results. ‘Peak finding’, that is, identifying enriched regions in a ChIP-Seq experiment is a very hot topic of research nowadays, with novel methods appearing on a regular basis: the up and downsides of the different strategies have yet to be fully appreciated [110]. In this case, however, it has been shown how sequence analysis can be also applied in parallel to peak finding to support the results: in other words, since the regions actually bound by the TF should be enriched for the TF binding sites, the presence/absence of the motif within a putative binding region can be used as a further indicator of the reliability of a given prediction. Thus, peak finders can be integrated with peak finding tools to provide a comprehensive pipeline for ChIP-Seq analysis, as with GADEM [109].

A great amount of data have been recently produced, e.g. by the ENCODE project [103], including ChIP-Seq experiments for dozens of TFs in several cell lines as well as histone modifications, DNA methylation and so on. Other than being an invaluable source of information, we suggest this data could be used also to build exhaustive benchmark sets for motif discovery algorithms. One could choose the binding regions (‘peaks’) for a given TF, and check which methods correctly identify the corresponding binding motif (usually, this is the case for all the methods). Then, secondary motifs found to be enriched in the peaks analyzed can be checked against peaks from other ChIP-Seq experiments performed in the same cell line, to determine whether the subset of regions in which they are predicted are indeed also peaks for the corresponding TFs. In other words, one could validate a predicted secondary motif coming from a ChIP-Seq peak set against the ChIP-Seq peaks of the corresponding TF. Finally, the influence of epigenetic information on the results could be studied and assessed, by including in the predictions data on histone modifications or DNA methylation, and determine whether it correlates with the presence or absence of motifs.

Key Points.

• Motif discovery (motif finding) has been one of the most widely studied problems in bioinformatics.

• A typical case study for motif discovery has been the analysis of sequences (e.g. promoters) from genes showing similar expression patterns and likely to be bound by the same set of transcription factors, in order to identify their putative binding sites that should appear to be overrepresented in the sequences.

• Different algorithmic strategies and significance measures for assessing overrepresentation have been applied to the problem, however with limited success in higher eukaryotes.

• The recent introduction of ChIP coupled with tiling arrays or next-generation sequencing (ChIP on Chip and ChIP-Seq) has permitted the genome-wide identification of the regions bound by transcription factors.

• Regions derived from a ChIP experiment are a perfect case study for the computational discovery of TFBSs, leading on one hand to better results, but on the other posing new computational challenges for developers of motif discovery algorithms and tools.

SUPPLEMENTARY DATA

A Table summarizing the most widely used tools for motif finding as of today is available as Supplementary data online at http://bib.oxfordjournals.org/.

FUNDING

‘Ministero dell’Istruzione, Università e Ricerca’ (MIUR, Italy): ‘Laboratorio Internazionale di Bioinformatica’, ‘Laboratorio di Bioinformatica per la Biodiversità Molecolare’ (Project DM19410), ‘PRIN 2009’; Consiglio Nazionale delle Ricerche: Flagship Project ‘Epigen’ and by the Center of Excellence in Genomics (CEGBA, Italy)’.

Biographies

Federico Zambelli is a post-doc at the University of Milan. His research interests are focused on bioinformatics tools for investigating transcriptional and post-transcriptional regulation of gene expression.

Graziano Pesole is a full professor of Molecular Biology at the University of Bari (Italy) and Director of the Institute of Biomembranes and Bioenergetics of the National Research Council. He leads a multidisciplinary research team in ‘Bioinformatics, Comparative Genomics and Molecular Biodiversity’ and his research interests include bioinformatics, development of tools for genome annotation, comparative genomics and molecular evolution.

Giulio Pavesi is an associate professor of Computer Science at the University of Milan (Italy). His research interests are mainly focused on bioinformatics in general, and regulatory motif discovery in particular. He also works on discrete models of complex systems.