Protein Structure Refinement through Structure Selection and Averaging from Molecular Dynamics Ensembles

Abstract

A molecular dynamics (MD) simulation based protocol for structure refinement of template-based model predictions is described. The protocol involves the application of restraints, ensemble averaging of selected subsets, interpolation between initial and refined structures, and assessment of refinement success. It is found that sub-microsecond MD-based sampling when combined with ensemble averaging can produce moderate but consistent refinement for most systems in the CASP targets considered here.

Introduction

Much progress has been made towards predicting the tertiary structure of proteins from their amino-acid sequence.^1–3 By far the most success has been found with template-based modeling (TBM) methods^4–6 where information from known experimental structures is utilized. Traditionally, TBM would use a single homologous protein for which a structure is available, but the best methods combine structural information from multiple templates in a variety of different algorithms.^1,7–11 Using such methods, structures for most soluble proteins can be obtained today with high accuracy as long as sufficiently close structural templates can be found in the Protein Data Bank.¹² Nevertheless, the resulting models for non-trivial cases often retain structural errors with respect to experimental structures that limit the use of such models in further studies. For example, TBM-derived structures are often problematic as drug design targets^13,14 or as starting structures for detailed mechanistic studies via molecular dynamics simulations and other computational methods.¹⁵

Structure refinement methods aim at the further improvement of TBM-based models towards experimental accuracy.^16–18 Because TBM-based models already utilize knowledge from related structures, most refinement algorithms that have been proposed rely on physics-based techniques, in particular molecular dynamics (MD) simulations.^16,19–21 Although successful examples of MD-based refinement have been reported in the past,^2,11,19–26 consistent success appears to be hindered by a combination of insufficient sampling,^11,27,28 force field inaccuracies,^20,29 and an inability to reliably identify refined structures that may be generated during the course of an MD simulation.^{11,23,29–32} To address these issues, statistical potentials^21,33–35 and optimized force fields^20,36,37 have been used as well as effective sampling techniques such as replica-exchange^19,24,25,33 and self-guided Langevin dynamics³⁸ simulations. In some studies it was possible to generate improved structures by as much as 0.5 Å in root-mean-square deviation (RMSD) in one out of five models,^25,33 but reliable identification of a single refined structure remained difficult. Recently, Fan et al.²⁴ have shown that by mimicking the electrostatic effects with chaperone Hamiltonian replica-exchange MD simulation can generate refined structures for 10 out of 15 targets with improvements of more than 1 Å RMSD for the secondary structure elements, but again reliable selection of refined structures without knowledge of the native state remained challenging. However, on average models selected based on a statistical potential function, Distance-scaled Finite Ideal gas REference (DFIRE),^39,40 could be improved by 0.25 Å from the initial models.²⁴

A common observation is that unrestrained MD simulations of template-based models almost invariably end up drifting away from the native structure.^19,23 Refinement is more likely to occur when structures are restrained,^19,23 but the drawback of using restraints is that the degree to which structures can be refined is limited. The most extensive test of MD-based refinement published so far involved simulations up to 100 µs for CASP8 (Critical Assessment of techniques for protein Structure Prediction) and CASP9 refinement targets.²³ In that work from the Shaw group, the final structures were not improved on average but refinement could be achieved by using a cluster-based selection method to reach 1% in terms of GDT-TS (Global Distance Test-Total Score)⁴¹ for conformations extracted from simulations exceeding 10 µs in length. Better structures with sometimes much more significantly improved GDT-TS scores were generated in these simulations but could not be identified reliably.²³

Finally, Zhang et al.³⁶ used a fragment-guided MD technique, in which different fragments of target proteins were restrained to their homologous templates. Using this technique, improvements in GDT-HA (GDT-High Accuracy) scores were possible for targets with initial GDT-HA scores of greater than 50. However, for CASP8 and CASP9 targets average improvement was limited to only 0.6% in terms of GDT-HA and the improvement in RMSD was insignificant.

Here, we are presenting a structure refinement protocol that combines MD-based sampling in explicit solvent using the latest CHARMM (Chemistry at HARvard Molecular Mechanics) force field⁴², a scoring protocol that identifies the most native-like structures, and ensemble averaging to mimic the conditions under which experimental structures are obtained. Using this protocol, we are able to consistently refine CASP8 and CASP9 targets with relatively modest computational resources.

In the following, the computational methods are described before results are presented and discussed.

Methods

We have performed all-atom molecular dynamics (MD) simulations for 26 refinement targets from CASP8 and CASP9. The targets used here as test sets are listed in Table 1. The initial structures were provided by the CASP organizers and represent predicted models of high accuracy for the respective targets that were submitted during CASP. Along with the initial coordinates, the CASP organizers also provided information for many targets about regions that refinement should focus on. This information was used here to apply restraints on the remaining parts of the structure considered to be accurate. For targets where a refinement residue range was not provided during CASP we determined a residue restraint list during the respective CASP rounds when knowledge of the experimental structures was not yet available under the assumption that the core secondary structure elements are likely to be more correct than other parts of the structure. The resulting list of restraints for each target is given in Table 1. For 16 targets the restraint regions were selected based on CASP suggestions, and for the remaining 10 targets restraints were based on core secondary structure elements.

Table 1.

CASP8 and CASP9 refinement targets used here as test cases with the total number of residues and C_α-RMSD of the initial models from the respective native structures. Restraint regions denote residues for which harmonic restraints were applied to maintain structures near their initial structures. The targets were sorted according to increasing RMSD values. The regions suggested by CASP are shown in bold.

Target	# of res.	RMSD (Å)	GDT- HA	Restraint regions
TR592	105	1.26	72.9	17–29;36–46;58–67;76–121
TR453	87	1.47	71.3	5–34;45–91
TR432	130	1.65	77.5	1–84;93–130
TR462a	75	1.76	57.7	1–5;10–16;21–30;35–42;50–53;57–60;64–75
TR594	140	1.82	67.0	1–71;82–101;114–140
TR614	121	1.87	71.5	11–33;53–64;75–109
TR435	137	1.89	67.9	15–19;26–27;38–66;75–87;92–94;98–103;113–133;137–151
TR530	80	1.99	69.1	36–44;56–74;80–115
TR488	95	2.11	75.0	1–11;17–95
TR469	63	2.18	63.5	3–7;11–28;33–50;54–65
TR462b	68	2.42	48.9	76–83;88–91;97–106;114–124;127–129;133–136;140–143
TR389	135	2.64	63.3	10–15;22–34;49–55;68–73;81–82;100–109;116–126
TR464	69	2.73	59.8	18–37;44–56;61–86
TR569	79	3.01	52.2	1–25;44–49;62–79
TR454	192	3.24	42.3	5–24;29–34;40–44;50–71;77–107;113–138;147–167;176–196
TR567	142	3.44	58.3	4–21;28–47;55–59;67–74;90–101;109–145
TR574	102	3.58	40.0	28–35;49–57;71–73;79–81;85–91;97–106
TR557	125	4.06	46.8	1–11;21–40;49–52;73–100;107–125
TR429a	79	4.31	54.8	22–37;44–57;68–80;89–93;98–100
TR517	159	4.64	53.6	1–62;89–159
TR606	123	4.85	52.6	56–144
TR429b	76	4.98	30.3	101–104;108–111;115–122;128–154;162–176
TR624	69	5.19	35.9	5–11;16–20;34–51;57–73
TR568	97	6.15	35.8	62–77;91–94;107–108;124–158
TR622	122	6.47	51.9	1–96
TR576	138	6.85	45.3	25–56;66–119

For each initial structure, missing hydrogens were built using the HBUILD module in CHARMM.^43,44 The protein structures were then solvated in a cubic box of water with a minimum distance of 10 Å between any protein atom and the edge of the box. The systems were neutralized by adding Na⁺ or Cl⁻ as counterions to balance the overall charge. All of the systems were equilibrated by minimization followed by heating through short simulations over 1 ps at 50 K, 100 K, 150 K, 200 K, 250 K, and 298 K. Subsequent production simulations were carried out at 298 K and 1 bar pressure in the NTP (constant number of particles, temperature, and pressure) ensemble over different simulation lengths up to 200 ns.

The CHARMM36 force field⁴² was used in combination with the TIP3 water model⁴⁵. The CHARMM36 force field was recently introduced as an improved version of the previous CHARMM22/CMAP force field^46,47. The main differences are improved sampling of backbone propensities in better agreement with experimental data, in particular NMR J-coupling data, and improved side chain torsions, also to improve agreement with experimental data.⁴² In all simulations, periodic boundaries were applied and particle-mesh Ewald summation was used to calculate electrostatic interactions using a grid spacing of 1 Å. Direct-space electrostatic and Lennard-Jones interactions were truncated using a switching function between 8.5 Å and 10 Å. All simulations used holonomic constraints on bonds involving hydrogens so that a 2 fs integration time step could be used. Simulations were carried out with and without restraints according to Table 1. Restraints were applied through a harmonic force on C_α atoms with a force constant of 1 kcal/mol/Ų.

Because part of our refinement protocol involves averaging over structural ensembles, a second set of simulations was carried out to allow side chains in the averaged structures to relax while maintaining the backbone geometries. This was accomplished by resolvation of the refined structures followed by minimization over 5000 steps and two short MD simulations at 10 K and 100 K, each for 40 ps. During these minimization and MD simulations, all C_α atoms were restrained with a force constant of 100 kcal/mol/Ų. The quality of the structures before and after the final refinement simulations was assessed using the MolProbity structure validation web service⁴⁸

All of the systems were initially setup using CHARMM^43,44 and the MMTSB (Multiscale Modeling Tools for Structural Biology) Tool Set⁴⁹. Production simulations were carried out using NAMD⁵⁰. Analysis was carried out using a combination of CHARMM, the MMTSB Tool Set, and custom scripts and programs.

Results

Molecular dynamics simulations were carried out for the CASP8 and CASP9 refinement targets starting from the template-based models provided during the respective CASP rounds for the CASPR refinement competition. Simulations were run with and without restraints and over different lengths of 24 ns, 200 ns, or eight times 3 ns to compare the effect of different amounts of sampling. The conformations sampled for each target during these simulations were then subjected to different selection and averaging protocols with the goal to obtain refined structures. Each protocol and the corresponding results are described in more detail in the following.

Final and Best Structures

The most straightforward MD-based refinement protocol would consist of simply considering the final structure at the end of a given MD run. Tables 2 and 3 show the change in RMSD and GDT-HA, respectively, relative to the native structures for the final structures under different conditions. We show here changes in both RMSD and GDT-HA⁵¹ values because they emphasize different aspects. GDT-HA represents the fraction of residues in the model that are within a short RMSD cutoff from a reference structure. Improvements in GDT-HA characterize to what extent the fraction of high-quality parts of a given structure is increased while ignoring parts of a structure that are of poor quality. RMSD changes capture the entire structure including bad parts of the structure. Often, GDT-HA and RMSD are highly correlated but in some cases, we find refinement in one measure but not in the other and vice versa. The first observation from the results in Tables 2 and 3 is that without restraints most of the structures move away from the native structure, some significantly, despite the relatively short simulation length of 24 ns. However, for the few cases where the final structure is refined, the improvement can also be quite significant, by about 1 Å for two targets. The occasional success but overall failure with unrestrained MD simulations is consistent with similar findings by other groups.²³ When restraints are applied during simulations of the same length, the number of refined targets increases from 5 to 9 (out of total of 26 cases considered here) but while the restraints prevent large deviations away from the native they also limit to what extent structures can be improved.

Table 2.

Changes in RMSD (Å) from the experimental structure relative to the RMSDs of the initial models during MD simulations with and without restraints over different simulation lengths. For all cases, the ΔRMSD for the final conformation and the overall lowest RMSD are given. Improved cases with negative ΔRMSD values are highlighted in bold.

Target	NO RESTRAINTS		WITH RESTRAINTS
	24 ns		24 ns		8 × 3 ns		200 ns
	Final	Best	Final	Best	Final	Best	Final	Best
TR592	0.42	−0.05	−0.07	−0.18	−0.12	−0.16	−0.12	−0.20
TR453	0.34	0.08	0.16	−0.09	0.17	−0.10	0.44	−0.09
TR432	1.39	−0.12	−0.13	−0.30	−0.26	−0.34	−0.18	−0.31
TR462a	0.53	0.04	0.44	0.04	−0.04	−0.26	0.42	−0.07
TR594	1.37	0.13	0.75	0.00	0.05	−0.12	0.34	0.00
TR614	1.11	0.03	0.40	−0.13	0.25	−0.11	0.08	−0.13
TR435	0.13	−0.31	0.30	0.03	0.07	−0.08	0.78	0.03
TR530	−0.27	−0.64	0.18	−0.27	−0.22	−0.40	0.26	−0.35
TR488	1.29	−0.08	0.00	−0.25	−0.16	−0.23	−0.13	−0.26
TR469	0.72	−0.14	−0.02	−0.19	−0.09	−0.20	0.15	−0.19
TR462b	0.23	−0.16	0.10	−0.11	−0.02	−0.14	0.17	−0.11
TR389	0.81	0.01	−0.27	−0.62	−0.11	−0.51	0.31	−0.62
TR464	0.89	−0.14	−0.02	−0.16	0.03	−0.15	−0.12	−0.23
TR569	0.46	−0.03	−0.24	−0.50	−0.26	−0.47	−0.28	−0.69
TR454	0.89	−0.31	0.06	−0.15	−0.10	−0.19	−0.12	−0.20
TR567	−1.00	−1.46	0.02	−0.18	−0.03	−0.11	−0.06	−0.20
TR574	1.82	0.15	1.07	0.07	0.09	−0.50	1.16	−0.40
TR557	−0.01	−0.75	−0.58	−0.67	−0.35	−0.57	−0.61	−0.84
TR429a	2.32	−1.19	0.20	−0.20	−0.08	−0.21	−0.03	−0.26
TR517	3.05	0.03	0.50	−0.12	0.15	−0.17	0.46	−0.12
TR606	1.76	0.01	1.63	−0.28	0.58	−0.93	−0.80	−1.51
TR429b	−0.35	−0.59	−0.02	−0.17	−0.04	−0.25	0.01	−0.23
TR624	−0.90	−1.83	−0.21	−0.68	−0.03	−0.37	−0.63	−0.89
TR568	0.59	0.13	0.07	−0.31	0.32	−0.10	0.29	−0.43
TR622	0.20	0.03	0.23	−0.05	0.06	−0.72	1.63	−0.32
TR576	1.01	0.51	0.74	0.49	0.70	0.37	0.28	0.00
Avg.	0.72	−0.26	0.20	−0.19	0.02	−0.27	0.14	−0.33
#better	5	15	9	21	15	25	11	23

Table 3.

Changes in GDT-HA from the experimental structure relative to the GDT-HA values of the initial models during MD simulations as in Table 2. Improved cases with positive ΔGDT-HA values are highlighted in bold.

Target	NO RESTRAINTS		WITH RESTRAINTS
	24 ns		24 ns		8 × 3 ns		200 ns
	Final	Best	Final	Best	Final	Best	Final	Best
TR592	−10.5	6.2	4.5	8.3	4.1	6.4	5.7	9.1
TR453	−5.5	4.0	−4.0	5.8	1.7	4.0	0.9	5.8
TR432	−22.7	1.4	−2.5	5.0	3.9	4.8	2.5	6.4
TR462a	−6.0	1.3	−1.3	5.7	−0.3	7.3	−1.0	7.3
TR594	−23.8	−4.5	−0.7	3.8	0.9	2.1	−0.7	4.1
TR614	−16.2	−1.1	0.0	4.6	0.4	2.8	−1.4	6.3
TR435	−6.2	0.2	−4.9	0.2	−1.6	1.3	−3.5	1.8
TR530	−1.6	2.8	−0.9	3.1	1.3	4.4	−2.8	3.1
TR488	−1.3	6.6	2.4	6.6	5.0	5.8	5.3	7.1
TR469	−16.7	−4.8	−2.4	2.0	−1.6	2.8	−5.6	3.2
TR462b	1.5	8.5	−1.1	2.2	0.7	4.0	−1.5	2.6
TR389	−18.9	−7.3	−6.9	−1.9	−5.8	−0.6	−7.3	−1.9
TR464	−4.7	3.3	0.0	5.4	−0.4	3.6	1.5	6.2
TR569	−7.0	3.2	0.0	6.0	1.3	5.7	−0.6	7.6
TR454	−11.6	1.3	−1.3	2.3	1.3	3.0	0.3	4.0
TR567	−3.0	1.6	−0.4	4.8	2.5	4.2	2.8	5.3
TR574	−7.9	−2.5	1.7	4.2	3.2	3.7	0.7	6.4
TR557	1.0	7.2	2.2	7.4	3.8	6.6	5.2	9.0
TR429a	0.4	10.5	2.8	12.1	5.6	11.7	8.9	14.5
TR517	−1.6	2.4	−1.9	3.0	2.0	3.6	−2.4	3.0
TR606	−7.9	−2.2	1.8	4.7	−0.4	3.5	−1.4	5.7
TR429b	2.6	7.9	−0.7	2.6	0.0	4.6	−1.0	4.3
TR624	6.9	11.2	4.4	6.2	0.4	4.0	2.2	6.2
TR568	−8.0	3.9	1.0	3.9	0.3	3.4	0.3	4.6
TR622	−14.1	0.0	2.7	6.0	4.8	6.0	2.5	7.4
TR576	−11.6	−4.2	−1.1	2.0	−0.7	0.5	−1.3	2.9
Avg.	−7.5	2.2	−0.3	4.5	1.2	4.2	0.3	5.5
#better	5	18	9	25	18	25	13	25

Extending the sampling to 200 ns further increases the number of structures that were refined at the end to 11 (according to RMSD) or 13 (according to GDT-HA). However, even better results were found when the average final structures from many short simulations (8 × 3 ns) were considered with now more than half of the structures being refined. The use of multiple short simulations is expected to improve sampling over a single long simulation^33,52 and our results suggest that increased sampling does lead to improved success with refinement. This is in agreement with previous findings.²³ It is interesting to note that when selecting the average final structure from the 8 × 3 ns simulations, we already find an average improvement in GDT-HA score by 1.2, comparable to the results reported by the Shaw group after much longer simulations.

As shown in Figures S1 and S2 (supplementary material), the RMSD and GDT-HA scores fluctuate significantly during the simulations and while the final structures are often not improved, there are improved structures at other times during the simulation for many targets. Tables 2 and 3 also show the improvement in RMSD and GDT-HA for the best structures (in terms of RMSD or GDT-HA) that were sampled during the simulations. Without restraints, only about half of the targets are refined at some point during the trajectory, but with restraints refined structures are found for almost all of the targets, in particular during the longer 200 ns simulation and during the multiple short simulations. The average maximum improvement in terms of GDT-HA is again similar to the values for the simulations from the Shaw group after about 10 µs. This finding raises the possibility that such long simulations may not be necessary to achieve refinement and that other methodological factors may be more critical.

Lowest-scoring Structures

Since refined structures were generated during most of the simulations, the next question we investigated was whether application of a scoring function to an ensemble of structures extracted from the MD runs would allow us to identify the most native-like, and therefore refined structures. Table 4 shows the change in RMSD and GDT-HA with respect to the experimental structures when selecting the conformation with the lowest DFIRE score. We chose DFIRE as one of the best-performing scoring functions that has been widely applied in structure prediction applications.^39,40 The results indicate that selecting structures based on the lowest DFIRE score has similar performance or is even slightly worse than simply taking the final structures. This is not entirely surprising when considering the correlation coefficients between RMSD or GDT-HA and the DFIRE score. Although the correlation coefficients largely have the correct sign (positive for RMSD, negative for GDT-HA), their small magnitude – with a few exceptions – suggests that it would be difficult to reliably select a single structure. We also considered other scoring functions (data not shown) and found similar results.

Table 4.

Changes in RMSD (Å) and GDT-HA upon selecting structures with the lowest DFIRE score and correlation coefficients of RMSD or GDT-HA vs. iRMSD or DFIRE. Correlation coefficients larger than 0.30 (RMSD) or less than −0.30 (GDT-HA) are highlighted in bold.

Target	200 ns				8 × 3 ns
	Δ RMSD	Δ GDT- HA	Correlation RMSD/GDT-HA		Δ RMSD	Δ GDT- HA	Correlation RMSD/GDT-HA
			vs iRMSD	vs DFIRE			vs iRMSD	vs DFIRE
TR592	−0.06	0.5	0.10/0.02	0.04/−0.10	−0.06	0.2	0.16/−0.09	0.35/−0.27
TR453	0.16	0.3	0.95/−0.33	0.19/−0.17	0.30	−1.4	0.89/−0.43	0.35/−0.30
TR432	−0.12	2.1	−0.03/0.02	0.06/−0.11	−0.04	0.4	−0.25/0.24	−0.01/−0.17
TR462a	0.21	4.7	0.51/−0.43	0.25/−0.51	0.31	−0.7	−0.11/−0.21	−0.16/−0.14
TR594	0.18	2.0	0.61/0.07	0.30/−0.25	0.07	−1.4	0.50/−0.06	0.17/−0.15
TR614	0.38	−4.2	0.05/−0.02	0.22/−0.32	0.29	0.7	−0.03/−0.01	0.06/−0.33
TR435	0.20	−2.7	0.95/0.15	0.57/0.03	0.08	−3.1	0.71/−0.37	0.34/−0.21
TR530	0.96	−3.4	0.93/−0.55	−0.02/−0.03	0.03	0.3	0.16/−0.14	0.15/−0.27
TR488	−0.13	2.9	−0.20/0.23	0.01/−0.14	−0.10	0.3	−0.24/0.24	0.06/−0.11
TR469	0.09	−3.2	0.46/−0.27	0.11/−0.22	−0.04	−0.8	−0.10/−0.12	0.22/−0.26
TR462b	0.30	−3.3	0.57/−0.43	−0.15/0.04	0.02	−1.5	0.43/−0.48	0.24/−0.23
TR389	0.30	−7.1	0.71/−0.22	0.27/−0.15	−0.51	−5.8	0.08/−0.49	0.62/−0.28
TR464	−0.13	0.4	−0.37/0.18	0.12/−0.03	0.04	−2.2	−0.14/0.00	−0.06/0.07
TR569	−0.37	3.8	−0.45/0.21	0.01/−0.13	−0.03	0.0	−0.70/0.08	0.18/0.00
TR454	−0.09	0.1	0.37/−0.16	0.35/−0.37	− 0.19	0.8	0.13/−0.07	0.09/−0.16
TR567	−0.05	0.7	−0.10/−0.11	−0.07/−0.08	−0.02	0.7	0.05/−0.20	0.05/0.03
TR574	1.08	2.0	0.64/−0.03	0.15/−0.25	−0.09	−2.0	0.32/0.22	0.48/−0.18
TR557	−0.56	6.0	−0.30/0.36	−0.16/0.00	−0.03	1.6	−0.66/0.34	−0.20/0.06
TR429a	−0.14	9.7	0.20/−0.09	0.32/−0.32	0.06	6.5	0.36/−0.04	0.04/−0.23
TR517	0.03	−1.3	0.48/0.00	0.43/0.01	0.01	1.1	0.51/−0.12	0.45/−0.15
TR606	−0.96	0.4	−0.04/0.08	0.80/−0.14	−0.26	−2.2	0.43/−0.02	0.55/−0.01
TR429b	−0.09	1.0	0.19/−0.06	0.41/−0.27	−0.10	0.3	0.71/−0.50	0.48/−0.44
TR624	−0.44	1.8	−0.46/−0.05	0.06/−0.05	0.32	−2.2	0.16/−0.03	−0.12/0.05
TR568	0.03	2.6	−0.14/0.15	0.02/−0.20	0.14	1.6	0.36/−0.20	0.29/−0.26
TR622	0.04	3.9	0.82/−0.23	0.77/−0.28	0.27	0.8	−0.23/−0.06	0.09/0.05
TR576	0.29	−2.5	−0.22/0.04	0.40/−0.10	0.84	−4.9	0.47/0.03	0.07/−0.08
Avg.	0.04	0.7	0.24/−0.06	0.21/−0.16	0.05	−0.5	0.15/−0.10	0.18/−0.15

Ensemble-averaged Structures

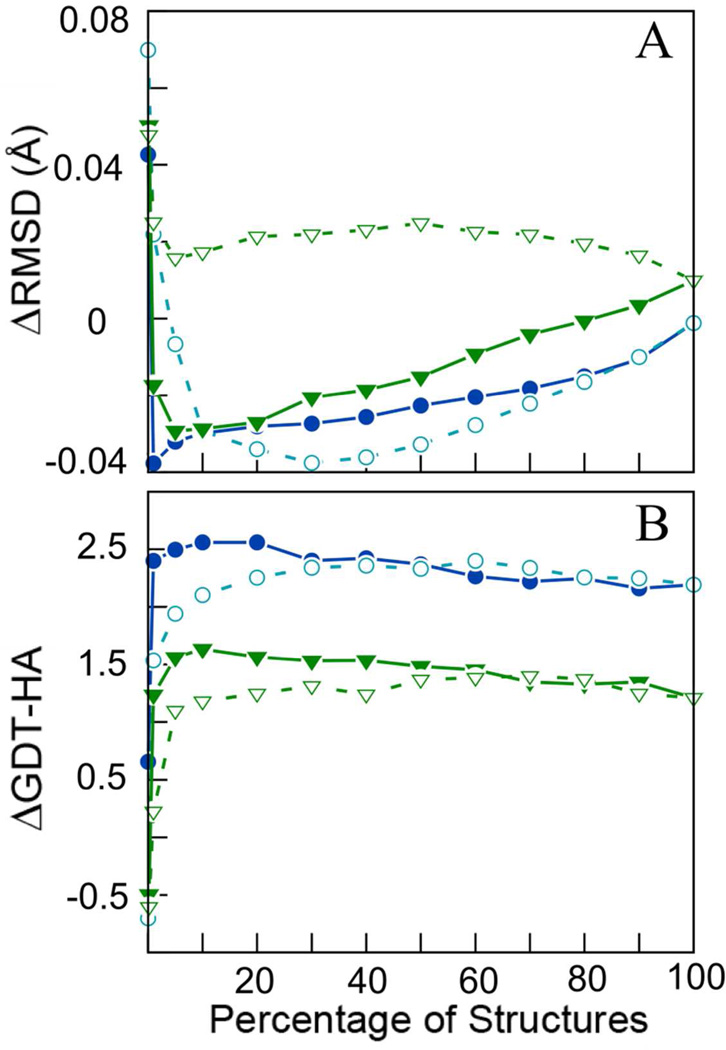
Next, we considered that experimental structures are the product of conformational averaging rather than representing single snapshots. Consequently, we obtained average structures from the MD-generated structure ensembles. Figure 1 shows the effect of averaging different percentages of the MD-generated structures that were sorted either according to their DFIRE score or based on their distance from the initial structure (iRMSD). We find that averaging generally outperforms selecting a single structure, while averaging over the 10% of structures with the lowest DFIRE scores results in a maximum improvement in GDT-HA by 2.6, which is about half of what could be achieved theoretically if the best conformation could be selected from each trajectory. However, when considering RMSD, an even smaller ensemble of only the 1% best-scoring structures results in a maximum improvement by 0.04 Å. Interestingly, selecting structures according to low iRMSD values, i.e. averaging over structures that have moved the least from the initial structure, also results in refinement. The rationale for that finding is that when structures start to deviate significantly from the initial template-based model, they are much more likely to move away from the native structure than towards it.

Figure 1.

Change in RMSD with respect to native structure (A) and in GDT-HA (B) upon averaging different subsets of structures sorted by either DFIRE scores or iRMSD. Results from the 200 ns MD runs are shown in blue (circles) and from 8×3 ns sampling in green (triangles). Open symbols denote iRMSD-based selection; closed symbols refer to DFIRE-based selection.

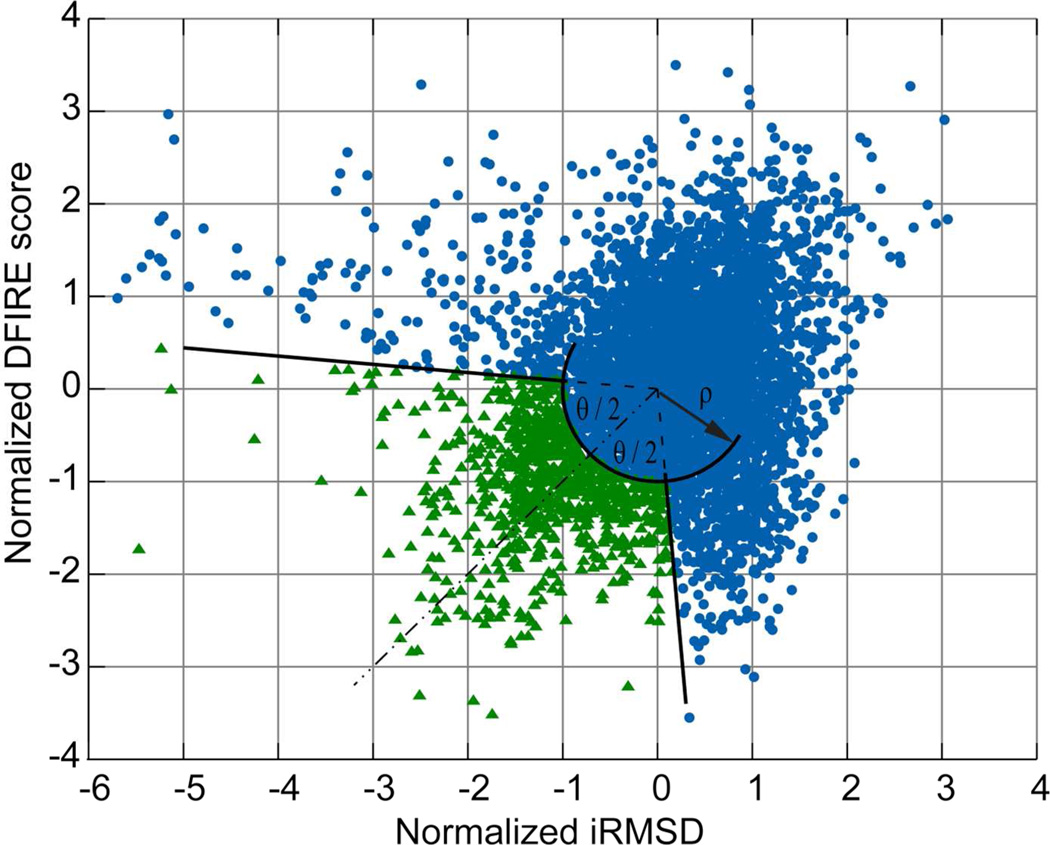
The observation that both DFIRE and iRMSD appear to be suitable metrics to identify ensembles of structures that when averaged provide structures that are likely closer to the native state, prompted us to consider a combination of both scores for selecting a subset of structures to be averaged. Since the range of these two scores is different, we first normalized the values by subtracting the mean and dividing by their respective standard deviations for a given set of structures. We then chose values in an open arc segment as illustrated in Fig. 2. Given the identity line through the origin (dashed line in Fig. 2), structures were chosen within a given angle θ/2, around the line to the origin and at a minimum radial distance ρ from the center of the distribution.

Figure 2.

Subset selection based on combination of DFIRE and iRMSD scores (normalized by their respective standard deviations). Selected structures (green triangles) are outside the circle with radius (ρ) and within the segment with angle (θ).

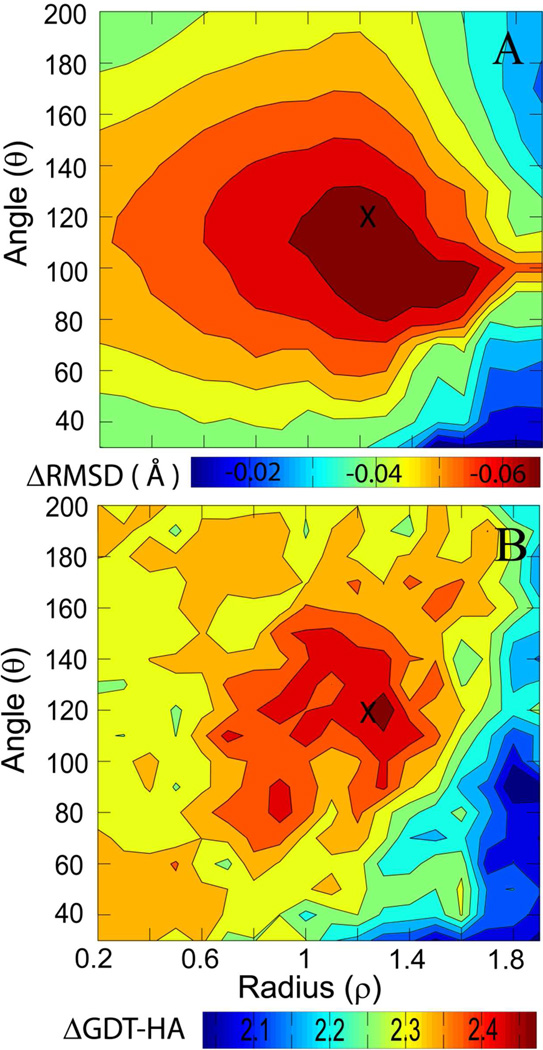
To find optimal values of (ρ, θ), we varied ρ from 0.2 to 1.9 with increments of 0.1, and changed the angle θ from 30 to 200 degrees at increments of 10. For each target, we extracted the structures that lie in the aforementioned region, and then calculated the average structure. Figure 3 shows the average improvements in RMSD and GDT-HA as functions of ρ and θ. As optimal values that maximize both RMSD and GDT-HA we chose ρ=1.2 and θ=120°. Using these values, the RMSD is improved by 0.07 Å and GDT-HA scores by 2.6. The improvements in RMSD and GDT-HA for individual targets using this criterion are given in Table 5. We find that GDT-HA is not further improved over simply selecting the 10% of the structures with the lowest DFIRE score but the improvement in RMSD appears to be more significant.

Figure 3.

Change in RMSD with respect to native structure (A) and GDT-HA (B) as a function of radius (ρ), and angle (θ). Parameters considered to be optimal and used subsequently for subset averaging are indicated by ‘X’.

Table 5.

Change in RMSD (Å) and GDT-HA upon averaging over selected subsets (see text) with and without additional structure interpolation.

Target	200 ns					8 × 3 ns
	Corr. iRMSD vs. DFIRE	Subset Average		Structure Interpolation		Corr. iRMSD vs. DFIRE	Subset Average		Structure Interpolation
		Δ RMSD	Δ GDT -HA	Δ RMSD	Δ GDT- HA		Δ RMSD	Δ GDT- HA	Δ RMSD	Δ GDT -HA
TR592	0.01	−0.14	6.2	−0.13	4.3	0.14	−0.12	3.1	−0.11	1.9
TR453	0.14	0.09	2.9	0.04	2.9	0.20	0.03	2.3	0.00	2.9
TR432	−0.03	−0.19	4.4	−0.19	3.7	0.18	−0.14	3.5	−0.12	3.7
TR462a	0.49*	0.20	4.0	0.13	3.0	0.68*	0.08	0.7	0.03	0.3
TR594	−0.05	0.15	2.0	0.09	1.3	0.13	0.01	0.7	−0.01	0.7
TR614	0.45*	0.24	3.9	0.08	4.2	0.54*	0.33	−0.4	0.22	0.7
TR435	0.59*	0.23	−1.8	0.14	−0.9	0.36	−0.01	−0.9	−0.02	−0.2
TR530	−0.07	−0.16	0.9	−0.16	0.6	0.11	−0.17	2.2	−0.15	1.6
TR488	0.04	−0.12	5.0	−0.11	4.5	−0.06	−0.13	4.2	−0.12	4.5
TR469	−0.16	−0.02	−0.8	−0.03	0.0	0.06	−0.06	−2.4	−0.06	−0.8
TR462b	−0.28	0.07	0.7	0.00	2.6	0.37	−0.03	2.2	−0.06	3.3
TR389	0.17	−0.43	−2.6	−0.48	−1.5	0.27	−0.14	−2.2	−0.16	−0.8
TR464	0.09	−0.01	1.1	−0.01	0.7	0.14	0.03	0.4	0.02	0.0
TR569	0.06	−0.29	1.0	−0.27	1.0	−0.19	−0.07	0.3	−0.06	1.0
TR454	0.23	−0.09	1.7	−0.09	1.8	0.14	−0.08	1.3	−0.07	2.1
TR567	0.23	−0.06	3.3	−0.06	2.5	−0.04	−0.02	3.3	−0.02	2.6
TR574	−0.01	0.24	3.9	0.10	2.7	0.12	−0.04	1.5	−0.06	1.2
TR557	0.12	−0.56	4.2	−0.49	3.6	0.33	−0.18	3.8	−0.15	3.0
TR429a	0.18	−0.09	9.3	−0.10	8.5	0.10	−0.08	6.1	−0.08	6.9
TR517	0.28	0.22	1.3	0.12	1.4	0.50*	0.03	2.4	0.02	2.0
TR606	−0.19	−1.04	2.6	−1.00	3.3	0.32	−0.01	0.2	−0.03	0.4
TR429b	0.28	−0.12	0.3	−0.13	0.0	0.49*	−0.15	1.7	−0.13	1.3
TR624	−0.09	−0.33	4.0	−0.29	3.6	−0.07	0.00	0.4	−0.01	0.0
TR568	−0.09	0.02	3.1	−0.02	2.8	0.48*	0.18	1.0	0.14	1.0
TR622	0.84*	0.14	5.8	0.07	5.4	0.26	0.17	4.3	0.12	3.9
TR576	0.31	0.31	0.4	0.21	0.4	0.52*	0.68	−1.3	0.52	−0.9
Avg.	--	−0.07	2.6	−0.10	2.4	--	0.00	1.5	−0.01	1.6
Avg.*	--	−0.12	2.5	−0.14	2.3	--	−0.05	1.7	−0.06	1.9
#better	--	15	23	16	23	--	16	21	18	20

Averages were calculated for all targets and for those where the correlation coefficient of iRMSD vs. DFIRE is larger than 0.4 (indicated by^*)

A drawback of structure averaging is that further refinement is necessary afterwards to generate stereochemically good models. As an alternative protocol, we also selected the ensemble structure closest to the subset averages. The data given in Table S1 shows that on average there is no improvement in RMSD and there is only a small improvement in GDT-HA for structures taken from the 200 ns simulation. This suggests that averaging rather than selecting a single structure is a key to the success of the refinement protocol described here.

Structure Interpolation

As a result of subset averaging described above we can generate refined structures for a majority of cases (15–16 out of 26 in terms of RMSD and 21–23 in terms of GDT-HA, see Table 5). The idea we followed next was that whether it would be possible to refine structures further by extrapolating the 3N-dimensional vector between the initial model and the refined structures. More specifically, we consider the vector difference between the C_α coordinates in the initial model, ${\overrightarrow{R}}_{C_{\alpha }}^{(\mathit{\text{init}})}$, and the ones obtained from the ensemble-averaged structures ${\overrightarrow{R}}_{C_{\alpha }}^{(\mathit{\text{avg}})}$, most of which are refined relative to the initial model. Note, that the average structure is already superimposed to the initial model as a result of how the ensemble average was generated. We then tested whether a new set of coordinates obtained according to Eq. 1 would increase the degree of refinement:

$${\overrightarrow{R}}_{C_{\alpha }}^{(\mathit{\text{new}})}=(1-\mathrm{\alpha }){\overrightarrow{R}}_{C_{\alpha }}^{(\mathit{\text{init}})}+\mathrm{\alpha }{\overrightarrow{R}}_{C_{\alpha }}^{(\mathit{\text{avg}})}$$ Eq. 1

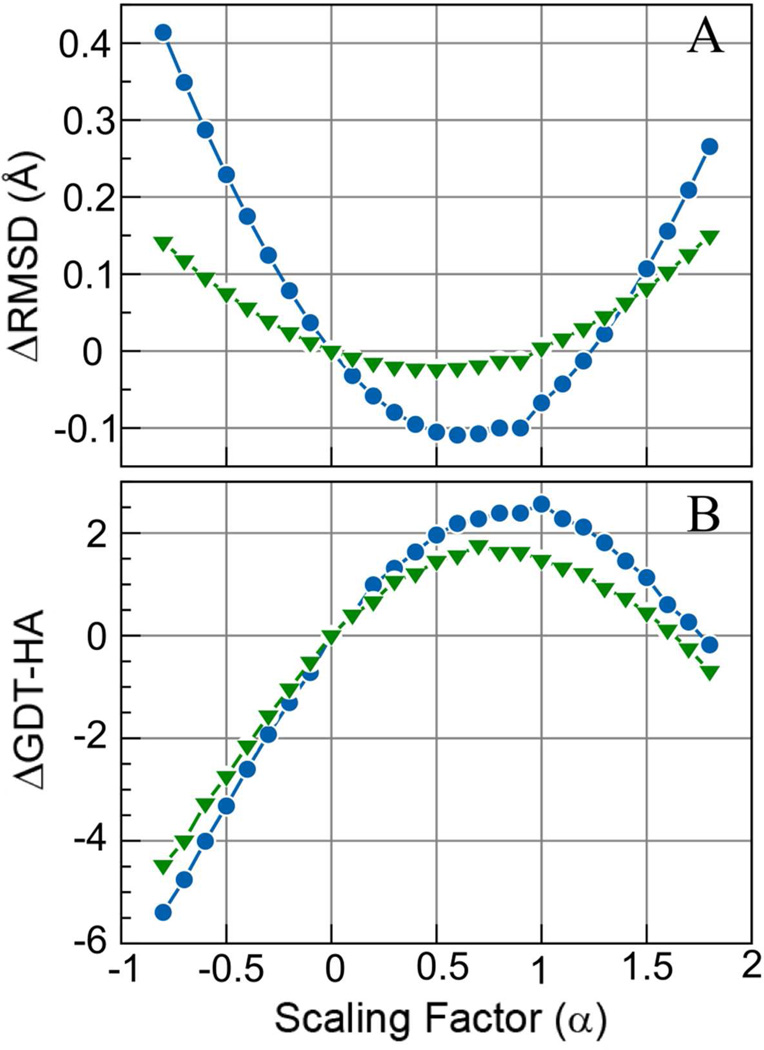
where α is a scaling factor. Here, α=0 corresponds to the initial model, and α=1 corresponds to the ensemble-averaged structure. Values of α between 0 and 1 would correspond to interpolation between the initial and refined structures, values beyond 1 would be extrapolation beyond the refined structures. Figure 4 shows the effect of applying Eq. 1 on the overall change in GDT-HA and RMSD. We find the optimum value of α to be α=0.6 for maximizing improvements in RMSD, and α=1 for GDT-HA. This result was surprising as we expected that values of α>1 may improve structures further. However, closer inspection of which targets are most affected by the structure interpolation approach suggests that scaling coordinates according to Eq. 1 has a stronger effect on the RMSD of targets where the RMSD increased during the refinement stage (see Fig. 5), i.e. structures that were made worse during the refinement. On the other hand, there was less of an impact on the structures that could be refined. Hence, the overall effect is an average improvement. It is unclear to what extent this is a general finding but as a result of applying the structure interpolation method (with α=0.8) we find further improvement in terms of RMSD. However, GDT-HA becomes slightly worse when the structure interpolation method is applied.

Figure 4.

Change in RMSD with respect to native structure (A) and GDT-HA (B) upon structure interpolation between the initial (α=0.0) and the subset-averaged structures (at α=1.0). Results from 200 ns MD runs are shown in blue (circles) and from 8×3 ns sampling in green (triangles).

Figure 5.

Change in RMSD with respect to native structure as a function of correlation between iRMSD and DFIRE scores with (green triangles) and without (red squares) structure interpolation.

The restraints applied during the MD simulations were either given by the CASP organizers or determined by us (see Table 1). An interesting question is whether the origin of the restraint list had an impact on the refinement success. The changes in RMSD and GDT-HA after refinement for the targets with CASP-suggested restraints were −1.4 Å and 2.6, respectively, but somewhat less, −0.04 Å and 2.0, respectively, for the targets where we selected the restraints. Hence, refinement is most successful if sampling can be targeted to the regions known to be deviating most from the native.

Quality Assessment

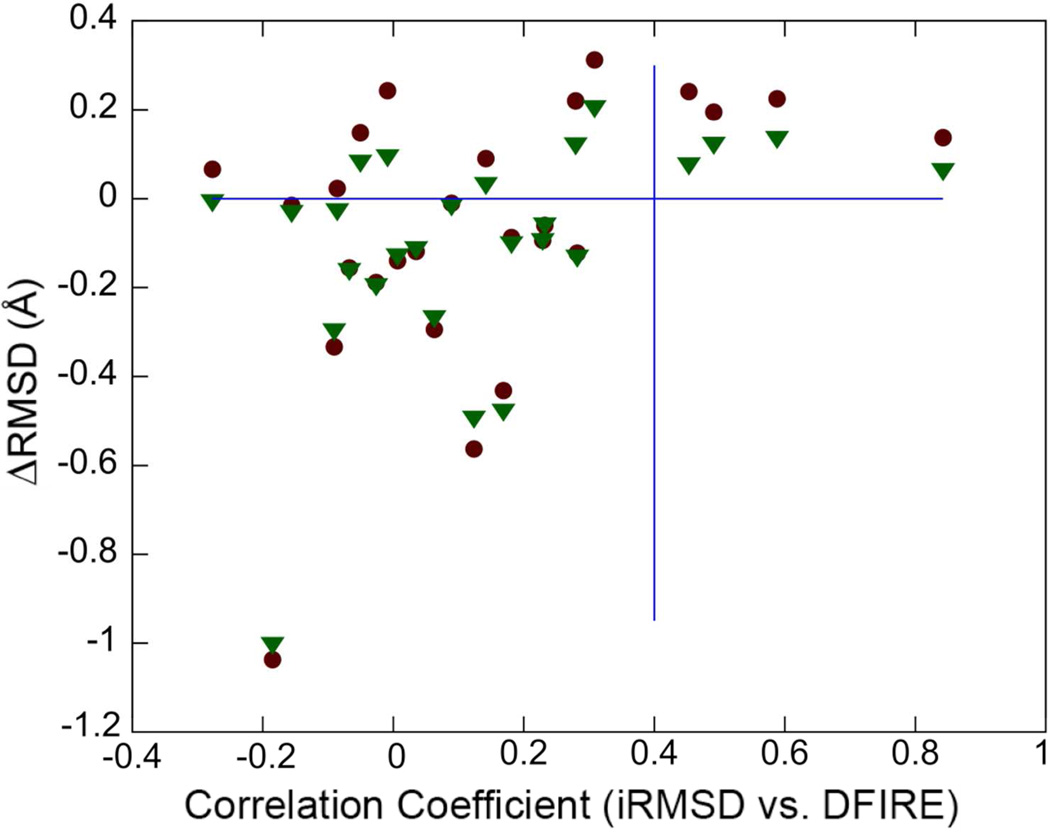
Finally, we considered whether it is possible to predict in which cases refinement is successful and when structures become worse as a result of refinement. Motivated by a previous analysis using a correlation-based metric,^53,54 we considered the correlation between the two scores iRMSD and DFIRE, both of which are available without knowledge of the native structure. The rationale for using this score is that because iRMSD is often correlated with RMSD (see Table 4), a correlation between DFIRE and iRMSD is indicative of a correlation between DFIRE and RMSD. Figure 5 shows the change in RMSD after refinement as a function of this correlation coefficient. It can be seen that all of the significantly refined structures have a correlation coefficient between −0.4 and 0.4 while higher correlation coefficients larger than 0.4 correlate with a lack of refinement. Significant correlation between DFIRE and RMSD (and by proxy with iRMSD) most likely occurs when structures move by a significant extent. It appears from this analysis that in those cases the motion is likely to be away from the native structure rather than towards it. Using a DFIRE/iRMSD correlation coefficient of <0.4 as a criterion that refinement has been successful, we identify four cases, TR435, TR462A, TR614, and TR622, that are outside this range and for which refinement was therefore assumed not to be successful. If we use the initial model (ΔRMSD=0) for these targets instead of the ‘refined’ structures, the average change in RMSD from the native improves further, to −0.12 (without structure interpolation) and to −0.14 (with structure interpolation). The effect on GDT-HA is less clear, because the improvement is actually slightly decreased for the 200 ns set but it improves for the 8 × 3 ns sampling set.

Final Refinement of Averaged Structures

So far, the structural analysis has focused on the C_α coordinates. As a result of the averaging and structure interpolation procedures, the generated structures are of poor quality in terms of bond geometries, clashes, etc. which is readily apparent when submitting those models to structural analysis tools (see Table 6). In order to generate overall high quality structures, we performed additional short MD simulations where the C_α atoms were constrained to maintain the overall improvement in structure but where other atoms were allowed to relax. The quality of the final models was improved dramatically (see Table 7) to result in high-quality refined structures. After the final step, the average change in RMSD was still −0.0.8 Å, and the change in GDT-HA was 2.3. For comparison with other studies, we also calculated the average improvement in GDT-TS for the final structures to be 1.6.

Table 6.

Quality measures of averaged structures before (Avg) and after (MD) refinement via restrained MD simulations.

Target	Clash score		% poor rotamers		% Ramach. outliers		Cβ dev.		% bad bonds		% bad angles		MolProbity score
	Avg	MD	Avg	MD	Avg	MD	Avg	MD	Avg	MD	Avg	MD	Avg	MD
TR592	147.8	3.0	5.6	4.2	8.8	0.0	64	2	82.7	0.0	41.4	0.0	3.9	2.0
TR453	435.8	2.2	11.4	5.7	8.4	0.0	77	3	92.9	0.0	75.0	0.0	4.6	1.9
TR432	295.0	0.9	5.5	4.6	7.2	0.8	112	2	85.8	0.0	76.4	0.0	4.2	1.3
TR462a	445.7	0.0	14.3	0.0	15.3	4.2	63	3	94.6	0.0	93.2	0.0	4.7	1.0
TR594	253.2	3.1	9.7	5.3	14.2	6.0	116	5	91.2	0.0	74.3	0.7	4.4	2.3
TR614	722.7	8.2	45.7	10.6	31.0	10.6	119	15	100	0.0	100	6.1	5.6	2.9
TR435	382.9	1.4	13.0	4.6	7.6	0.8	114	3	88.7	0.0	75.2	0.8	4.6	1.8
TR530	219.0	3.9	9.1	3.0	10.4	2.6	63	1	80.8	0.0	65.4	0.0	4.2	2.0
TR488	314.1	0.7	9.0	7.5	4.4	3.3	72	3	89.3	0.0	61.3	0.0	4.3	1.8
TR469	366.8	1.1	2.3	4.6	3.4	1.7	49	0	78.7	0.0	75.4	0.0	3.9	1.5
TR462b	686.6	1.8	20.4	6.1	19.7	4.6	58	2	98.5	0.0	92.7	1.5	5.2	2.1
TR389	537.0	4.2	17.4	10.1	14.0	5.4	124	11	96.2	0.0	92.4	3.8	5.0	2.6
TR464	126.5	0.0	0.0	2.0	1.5	0.0	44	0	79.4	0.0	50.0	0.0	2.7	0.7
TR569	320.3	2.7	8.6	1.7	6.7	1.3	57	3	85.7	0.0	75.3	1.3	4.3	1.6
TR454	243.4	1.0	4.4	1.5	5.9	0.5	149	0	86.7	0.0	56.9	0.5	4.0	1.0
TR567	168.4	2.2	6.7	1.0	4.5	0.8	101	3	75.0	0.0	46.3	0.7	3.9	1.3
TR574	515.8	3.9	28.2	6.4	23.2	5.1	94	6	97.0	0.0	90.1	4.0	5.2	2.5
TR557	336.6	2.6	11.1	2.0	9.0	2.5	111	5	91.9	0.0	83.9	0.8	4.5	1.8
TR429a	656.0	1.6	26.5	4.4	34.2	7.9	76	6	10	0.0	98.7	3.9	5.3	2.1
TR517	363.7	2.7	11.5	5.3	8.9	3.8	148	8	96.9	0.0	87.4	0.6	4.5	2.1
TR606	590.1	6.3	38.4	6.1	30.6	5.0	118	15	95.9	0.0	100	4.9	5.4	2.6
TR429b	551.9	3.2	14.3	6.4	28.4	8.1	71	8	92.1	0.0	96.1	4.0	5.0	2.4
TR624	330.1	3.6	15.5	5.2	9.1	0.0	58	2	95.6	0.0	88.2	0.0	4.6	2.1
TR568	455.5	2.6	11.0	2.4	17.2	4.3	87	4	97.9	0.0	96.8	1.1	4.8	1.8
TR622	472.8	5.5	37.4	7.7	29.3	3.5	110	7	97.5	0.0	96.6	0.9	5.3	2.5
TR576	702.3	5.5	38.2	11.8	24.8	6.8	127	13	98.5	0.0	99.3	1.5	5.4	2.8
Avg:	409.2	2.8	16.0	5.0	14.5	3.4	92	5	91.1	0.0	80.3	1.4	4.6	1.9

Table 7.

Summary of the average improvements in RMSD (Å) and GDT-HA for all the attempted methods for structure selection out of 8×3 ns and 200 ns simulation sets; Best in trajectory is given as a reference for the maximum possible improvement.

Method:	Δ RMSD (Å)		Δ GDT-HA
	8 × 3 ns	200 ns	8 × 3 ns	200 ns
Best in trajectory	−0.27	−0.33	4.2	5.5
Final Structure	0.02	0.14	1.2	0.3
Lowest DFIRE	0.05	0.04	−0.5	0.7
Average over 10% lowest DFIRE	−0.03	−0.04	1.6	2.6
Average over 1% lowest iRMSD	0.01	−0.04	1.4	2.4
Subset average from combined DFIRE/iRMSD scores	0.00	−0.07	1.5	2.6
Closest structure to subset average	0.07	0.01	−0.6	0.6
Subset average and structure interpolation	−0.01	−0.10	1.6	2.4
Subset average/interpolation with correlation-based filtering	−0.06	−0.14	1.9	2.3

Discussion and Conclusion

We are presenting here a new protocol for structure refinement that is based on MD simulations, but adds a new scoring and averaging protocol. A summary of the performance with different structure selection methods is presented in Table 7. Overall, the refinement results reported here are moderate, but what we consider most important is that we are able to consistently refine the large majority of structures rather than making a significant fraction worse as in earlier attempts at structure refinement. The overall refinement results are better than those reported recently by the Shaw group despite the much shorter simulations used here which may be due to a number of different reasons. The force field that was used here is a recently updated version of the CHARMM force field that appears to outperform most other available force fields in other tests.⁴² Furthermore, the use of ensemble averages instead of single structures appears to lead to significant improvements that may compensate for the much more limited sampling compared to the work by Shaw et al. With respect to the sampling, we find that nearly equivalent refinement can be achieved with multiple short simulations rather than a single long simulation. This is consistent with previous findings,^33,52 but is a point that merits further investigation since it is generally much easier to run many short simulations than one very long simulation on commonly available computer platforms. We also attempted here to employ an extrapolation scheme to further refine structures –which was not successful so far – and an assessment criterion to determine whether structure refinement is successful –which does appear to have merit.

Another question is whether the refinement success is biased by how the starting structures were generated. The targets considered here were selected by the CASP organizers from the best predictions during the CASP competition. While this limits the methods by which the models were generated to a few top groups, an effort was made to avoid selecting models from only one participating group. Hence, the models used as starting structures here represent some degree of diversity in terms of how they were created. Since we see consistent refinement across most of the targets we assume that refinement success is independent of the exact way the structures were initially prepared. Furthermore, similar results for sampling from 200 ns simulations vs. 8 × 3 ns simulations suggests that just a few nanoseconds were enough to equilibrate the structures sufficiently.

Finally, it would be interesting to see whether repeated application of the protocol presented here can be used in an iterative protocol to achieve more significant refinement. These are areas that we will focus on in more detail in future studies.