Microfluidic oscillators with widely tunable periods

Abstract

We present experiments and theory of a constant flow-driven microfluidic oscillator with widely tunable oscillation periods. This oscillator converts two constant input-flows from a syringe pump into an alternating, periodic output-flow with oscillation periods that can be adjusted to between 0.3 s to 4.1 h by tuning an external membrane capacitor. This capacitor allows multiple adjustable periods at a given input flow-rate, thus providing great flexibility in device operation. Also, we show that a sufficiently large external capacitance, relative to the internal capacitance of the microfluidic valve itself, is a critical requirement for oscillation. These widely tunable microfluidic oscillators are envisioned to be broadly useful for the study of biological rhythms, as on-chip timing sources for microfluidic logic circuits, and other applications that require variation in timed flow switching.

1. Introduction

Oscillation is not only ubiquitous but also crucial in biological,^1–4 chemical,^{5, 6} and electronic⁷ systems. For instance, electronic oscillators are widely used to make clock signals for the coordination of circuit functions. Biological oscillators are also prevalent and essential: neurons generate periodic action potentials, and hormonal cells periodically secret biochemicals to alter cell metabolism. Due to the distinctive functions of each biological oscillator, each biological oscillation has remarkably different period, ranging from sub second to a month.¹

Less developed but intriguing for biochemical applications and fluidic device development are microfluidic oscillators.^8–12 With a function analogous to electronic DC to AC conversion, the output of the microfluidic oscillator can be used as on-chip timing sources for microfluidic logic gates^12–16 and as a periodic, biochemical stimulator for biological samples.^17–21 A major limitation of previously reported microfluidic oscillators, however, is that they have one pre-defined oscillation period for a given flow rate. To adjust oscillation periods, the input flow rates has to be altered and even then the previously reported oscillators operate within a moderate periodic range of a second to few minutes^8,9 or exclusively at very fast periods (< sec).^10–12

Here, this paper develops a theoretical understanding and performs experimental validation of a novel constant flow-driven microfluidic oscillator, where external capacitors are used to enable a broad range of oscillation periods without changing input flow rates (Fig. 1). We show theoretically that arbitrarily long oscillation periods are possible by simply increasing the external capacitance. In contrast, short oscillation periods are limited by the condition where the external capacitance must be larger than that of the internal capacitance of the fluidic valve components. We then experimentally demonstrate the ability to drive an oscillator at different periods that span 4 orders of magnitude by using a combination of different capacitance and flow rates.

Fig. 1.

Microfluidic oscillator with a wide range of period tunability. (A) An external membrane capacitor and a microfluidic valve having an internal membrane capacitor. The valve has a top-side, a bottom actuation chamber, and a membrane. P_T and P_B are pressures at the valve's top-side inlet and bottom actuation chamber, respectively. (B) Schematic of the oscillator system consisting of two valves. It illustrates the three dimensional structure of the system and shows how the two valves are connected to each other. As illustrated in (A), the system has external and internal capacitances (C_e and C_i). A syringe pump provides a constant inflow rate, Q_i. (C) Circuit diagram of the microfluidic oscillator. The diagram depicts the connection of the valve's top inlet (Ti), top outlet (To), bottom inlet (Bi), and bottom outlet (Bo). Fluidic resistances (R₁ to R₅) are 5.94×10¹¹, 1.38×10¹², 1.62×10¹², 2.44×10¹³, 2.27×10¹¹ N s m⁻⁵, respectively.

2. Experimental

2.1. Device fabrication and its structure

Device fabrication and experimental setups are explained in our previous study.⁹ Each device consists of three layers of poly(dimethylsiloxane) (PDMS): top and bottom slab for channel and valve features, and a thin membrane middle layer (Right panel of Fig. 1A). The height of channels and valves were 75 μm. External membrane capacitors also consist of three layers of PDMS (Left panel of Fig. 1A), and the diameter and the thickness of the external membrane capacitor were varied in the range of 2–11 mm and 10–40 μm, respectively. Two pressure sensors were connected at the inlets to measure the pressures of microfluidic valves' top side, and a syringe pump was used to provide a constant flow. The working solution was deionized water.

2.2. Device parameters

The pressure change of a fluidic system is converted to an elastic energy by a mechanical capacitor having a flexible solid layer. The larger the capacitance is, the slower the pressure change is. The capacitances in our oscillator system can be separated into “external” capacitances (C_e) and “internal” capacitances (C_i); see Fig. 1A and 1B. C_e is determined by the combined effects of connection tubes, pressure sensors, and the tunable membrane-capacitors which are all external to the core oscillator circuits comprised of two inter-connected switching valves (Fig. 1B). On the other hand, C_i arises mainly from the flexibility of the switching valve's membrane.

Difference between the pressure of the valve's bottom actuation chamber (P_B, right panel of Fig. 1A) and that of the valve's top-side inlet (P_T) determines open and close state of the valve. Specifically, the valve-open condition is given by

$$P_{\mathrm{T}}-P_{\mathrm{B}}>P_{\text{th-open}},$$ (1)

where P_th-open is open threshold pressure. The valve-close condition is given by

$$P_{\mathrm{T}}-P_{\mathrm{B}}<P_{\text{th-open}},$$ (2)

where P_th-close is close threshold pressure. The meaning of equations 1 and 2 are as follows: Once the valve is open, it is not closed until P_T − P_B < P_th-close is satisfied. Also, once the valve is closed, it does not open until P_T − P_B > P_th-open.

P_th-open is defined as the difference between P_T and P_B as a valve opens. This P_th-open is also approximately the difference between valve 1 and 2's P_T (P_T1 and P_T2) as each valve opens because the fluidic resistance R₄ (Fig. 1C) is one order of magnitude higher than the fluidic resistances R₂ and R₃ (Supplementary Fig. S1). As a result, the fluidic resistance condition enables the following approximation:

$$P_{\mathrm{B}1}\approx P_{\mathrm{T}2}\text{when valve}2\text{opens}$$ (3)

$$P_{\mathrm{B}2}\approx P_{\mathrm{T}1}\text{when valve}1\text{opens}$$ (4)

This approximation is practically useful as it eliminated the needs to measure the pressures of the bottom actuation chamber (P_B1 and P_B2). In our oscillators, we measured a P_th-close of − 1 ± 0.2 kPa.²² Commercial software (PLECS, Plexim GmbH, Switzerland) was used for the numerical simulation of the microfluidic oscillator. For the simulation, we used theoretical value of C_i and measured values of C_e, P_th-close, and P_th-close.

3. Results and Discussion

3.1. Influence of C_e plus C_i on oscillation period

Understanding the effect of capacitances in the context of valve operation is key to designing functional period-adjustable oscillators. The minimalistic oscillator has two microfluidic valves connected to each other, where the output of one valve's top inlet connects to the bottom actuation chamber of the other and vice versa. This inter-connectedness leads to the two valves alternating with each other in terms of when each valve is open or closed.

This process is illustrated in Fig. 2, where a red and a clear solution are infused at a constant flow rate. When valve 2 is open (Top panel of Fig. 2A), the red solution flows through the bottom actuation chamber of valve 1, closing it off, then exiting through the outlet. During this process, P_B1 as well as the interconnected P_T2 decreases (equation 3). On the other hand, because valve 1 is closed P_T1 increases as the clear solution continues to be infused but with no place to exit. Thus, P_T1 − P_B1 gradually increases and when P_T1 − P_B1 eventually surpasses P_th-open (equation 1), valve 1 opens (Bottom panel of Fig. 2A). As valve 1 opens, the clear solution flows through the bottom actuation chamber of valve 2, closing it off then exiting through the outlet (equation 2). Now, because valve 2 is closed, P_T2 increases as the red solution continues to be infused but with no place to exit. This process cycles repeatedly resulting in an oscillatory output.

Fig. 2.

The two valve self-switching mechanism of the oscillator. (A) Alternating opening and closing of the two valves. Arrows having solid black and dotted gray lines depict the flow directions in the top and the bottom layer of the device, respectively. Note that open and close state of each valve is opposite for oscillation. (B) Measured representative pressure profiles of the two valves' top-side inlets (P_T) in the oscillator. (C) Corresponding outflow rate (Q_o). In (B) and (C), gray region is valve 2-open and 1-close, and the white region is the opposite.

The oscillatory outflow of fluids is accompanied by repeated accumulation and release of P_T1 and P_T2 (Figs. 2B and 2C). The accumulation-rate of the closed valve's P_T (dP_T/dt) is approximated to be Q_i /(C_e + C_i), where Q_i is inflow rate. Thus as illustrated in Fig. 2B, the duration of a closed-valve state is expressed as

$$(C_{\mathrm{e}}+C_{\mathrm{i}})P_{\text{th-open}}∕Q_{\mathrm{i}}$$ (5)

The oscillation period of a symmetric two valve system is twice this single valve closure duration.

3.2. Limits of C_e, C_i, and Q_i where oscillation is achieved

While equation 5 provides a useful guide for estimating oscillation periods, it only provides a partial picture of oscillator function as not all values of C_e, C_i, and Q_i support oscillation. Let us first look at how the pressures P_T1 and P_B1 of valve 1 changes over time when C_e > C_i. Under this condition, P_B1 becomes sufficiently high upon opening of valve 2; see the second white region of Fig. 3A. As a result, valve 1 can be shut off (P_T1 − P_B1 < P_th-close). On the other hand, when C_e is ~ C_i or < C_i, flow-change created by the opening of valve 2 is buffered by the relatively large internal capacitance leading to insufficient increases in P_B1 (Gray region of Fig. 3B), and no valve 1 closure. As a result, both valves stay open resulting in a non-oscillatory outflow.

Fig. 3.

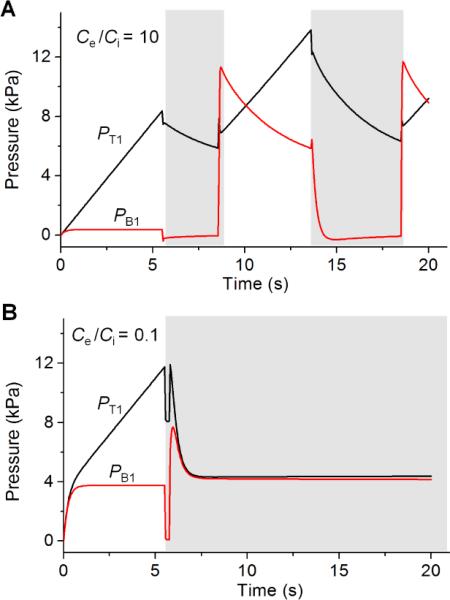
Pressure profiles of valve 1. Results are from computational simulations. C_e+C_i is constant at 10.1×10⁻¹³ m⁵/N. C_e/C_i is 10 in (A), which shows oscillations; and 0.1 in (B),which does not oscillate. Gray region is valve 1-open state. Q_i and P_th-open are 10 μL/min and 8 kPa, respectively.

Computational predictions, along with a few experimental examples, of what values of C_e, C_i, and Q_i support oscillation are summarized in Fig. 4. In our experiment, the valve opening threshold pressures were measured to be between 9 and 40 kPa depending on the valve type. Importantly, when we used large valves having deep trenches (~ 2 mm) to make C_i (Fig. S2) constantly larger than C_e, we eliminated oscillations (unfilled circles of Fig. 4).

Fig. 4.

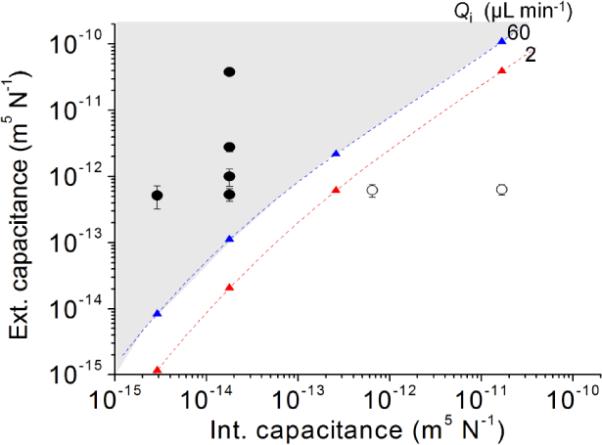
Computational predictions of what C_e and C_i values will support oscillations for two different values of Q_i. Filled circles (•) are experimentally confirmed points within this graph where oscillations are observed, whereas unfilled circles (∘) are experimentally confirmed points where oscillations are not observed. Critical points (▴) and lines are obtained by simulation and cubic polynomial curve fitting, respectively. Thus, the gray region represents the theoretical oscillation region. At the critical points, C_e/C_i values are in the range of 0.5–11 for the given conditions.

The critical values of C_e/C_i are in the range of 0.5–11 for the range of capacitances and Q_i's noted. Interestingly, the critical line shifted up as Q_i increased (Fig. 4). That is, for a given C_i, the critical value of C_e required for oscillation increases with increasing Q_i. Thus, to realize oscillations over a wide range of Q_i, an important condition is that C_e/C_i >>1 be maintained. There are two important take away messages: (i) very fast oscillation is possible through small C_i+C_e but under the condition of C_e/C_i >>1. The result implies that, to achieve extremely fast oscillations, connection tubes and syringes as well as other connected components should be rigid to have small C_e; furthermore, the membrane of the device should be even more rigid or have less C_i. (ii) Extremely slow oscillation is enabled by large C_e, not by large C_i. It should be noted that the change of C_e does not alter the maximum outflow rate or other operational conditions with respect to P_th-open and fluidic resistances. In other words, the change of C_e should only affect oscillation period. Thus adjusting oscillation periods using an external capacitor is not only convenient but is a great advantage in the design and operation of oscillators.

P_th-open and Q_i can also be adjusted to change oscillation periods (see equation 5). However, altering P_th-open affects outflow rate and other device operation parameters as well. For example, a higher P_th-open (Fig. 2B) would result not only in slow oscillation periods but higher maximum flow rates as well. A low P_th-open should theoretically lead to faster oscillation periods at lower maximum flow rates. Higher Q_i can also give faster oscillations accompanied by higher outflow rates. However, when Q_i surpasses a critical value, oscillation stops because the oscillator cannot respond to pressure changes fast enough.²² Lower Q_i will lead to slow oscillations with no lower limits.

3.3. Widely tunable oscillation period

With theoretical predictions in hand, we experimentally tested how changing C_e, through external membrane capacitors, would alter oscillation behavior. External membrane capacitors with different radius (r) and the thickness (h) of the external membrane are readily prepared. Because capacitance scales as r⁶/h³ (ref. 23), small changes in r and h can drastically alter capacitance. Figure 5A shows that, through tuning external membrane capacitors, the oscillation period of the same base oscillator circuit can span more than 4 orders of magnitude, from 0.3 s to 4.1 h. Compared to previous oscillators^8–12 that have < 10 times difference between the maximum and minimum oscillation periods, the current scheme provides at least a 10³ times wider range. This range covers the period of the many biological oscillations such as neuronal (~ms to ~s), cardiac (~s), and hormonal oscillations (~min to ~hr).¹ Also, our scheme allows multiple adjustable periods at a given input flow-rate whereas previous oscillators have only one period at a given input. Thus, the use of external membrane capacitors provide great flexibility for oscillator operation, expanding their usefulness as an on-chip timing source for microfluidic logic gates^12–16 and as a periodic, biochemical stimulator for biological samples.^17–21

Fig. 5.

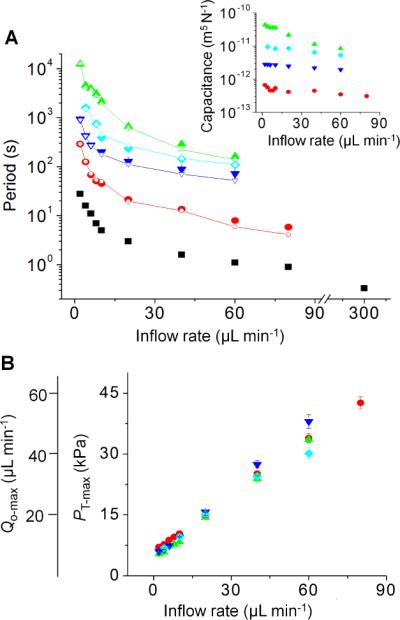
Widely tunable oscillation periods. Filled and unfilled points are the experimental and simulation results, respectively, and C_i is 1.8×10⁻¹⁴ m⁵ N⁻¹. (A) The oscillation period for the same base oscillator circuit can be widely tuned by use of different external capacitors. The actual C_e values of the capacitors that result in each oscillation period are shown in the inset. Note that the same capacitor gives slightly different effective capacitance values depending on inflow rate. (B) Different inflow rates also change maximum pressures (P_T-max) and maximum outflow rates (Q_o-max). Note that these values do not depend much on capacitor values.

The inset of Fig. 5A shows that the effective external capacitance decreases at high Q_i. This is because the membrane of the external capacitor becomes stiffer as the membrane deflects more at the high Q_i's. The moment at which a valve opens is that moment at which the valve's top-side inlet pressure is at a maximum value (P_T-max) (defined in Fig. 2B) and accordingly the moment at which the outflow rate is also at a maximum (Q_o-max) (defined in Fig. 2C). Thus, Fig. 5B simultaneously presents P_T-max and Q_o-max with respect to Q_i. Note that although some of the oscillators are not identical, P_T-max (or Q_o-max) values are very similar regardless of different C_e because they are the same oscillator type.

Conclusions

We have explored the role of valve intrinsic and extrinsic capacitance in determining whether a two-valve fluidic circuit will produce oscillatory outflows or not. We found that the use of a sufficiently large external capacitance, relative to the non-negligible intrinsic valve capacitance was critical for oscillation to be supported. Furthermore, within this constraint, we showed that for a given input flow rate, larger external capacitors would lead to slower oscillation periods with minimal effects on the maximum outflow rates. Since external capacitors can be easily exchanged, this provides a practical way for a single base oscillator circuit that is being operated at a constant input flow rate to generate outflows with a wide range of oscillation periods. Although we only showed oscillation periods of up to 4.1 h for the specific base oscillator circuit described, the oscillation period can be further increased by using larger external membrane capacitors or slower inflow rates. Because of the requirement for external capacitance to be larger than the internal valve capacitance, however, obtaining oscillation periods significantly shorter than the demonstrated 0.3 s will require redesign of the valve components.