Effects of Jamming on Nonequilibrium Transport Times in Nanochannels

Abstract

Many biological channels perform highly selective transport without direct input of metabolic energy and without transitions from a “closed” to an “open” state during transport. Mechanisms of selectivity of such channels serve as an inspiration for creation of artificial nanomolecular sorting devices and biosensors. To elucidate the transport mechanisms, it is important to understand the transport on the single molecule level in the experimentally relevant regime when multiple particles are crowded in the channel. In this Letter we analyze the effects of interparticle crowding on the nonequilibrium transport times through a finite-length channel by means of analytical theory and computer simulations.

The functioning of living cells depends critically on molecular transport through various transport channels [1]. Many of them function without a direct input of metabolic energy and without a movable “gate” that would involve transitions from an “open” to a “closed” state during transport. Nevertheless, such channels are selective, efficient, and fast. Examples include porins, nuclear pore complex, and others [2,3]. The functioning of such channels has served as an inspiration for the creation of artificial biosensors and nanomolecular filters [4–8] that promise to play an ever increasing role in nanotechnological and nanomedical applications, such as single-mismatch DNA detection [7], enantiomer separation [8], pathogen detection [9], and design of antibiotic drugs optimized for penetrating the cell [10]. Such manmade channels also serve as test beds for examining models of biological transport [5,6].

Biological and artificial transport channels, such as those mentioned above, usually contain a passageway through which the molecules translocate by diffusion. From recent experimental and theoretical work, it has become increasingly clear that in many cases the transport selectivity of such channels is not dictated merely by molecule size, but is controlled by transient binding of the transported molecules inside the passageway [2–18]. The crucial insight into understanding the transport selectivity of such channels is that even in the absence of any physical barrier for the entrance to the channel, the probability of a particle to translocate through it is low (of an order of the aspect ratio of the channel) [13]. Transient trapping (due to binding) inside the channel overcomes this “dimensionality barrier” [13,14]. However, if the molecules are trapped in the channel for too long, the channel becomes crowded and transport is diminished. The interplay of these two effects provides a basis for selective transport, whereby only the molecules that are trapped in the channel for an optimal time transit through the channel with a high flux [12–16]. Related mechanisms have been known in the context of carrier-assisted membrane transport as “facilitated diffusion” [11]. Theoretical models that include the transient trapping combined with the effects of confinement [11–15] provide a good explanation of the behavior of the mean flux through nanochannels and show a good agreement with the experimental data [12].

However, from a biological perspective, transport of a single molecule can constitute a significant signalling effect [1]. Thus, it is important to understand the transport through such channels on the single molecule level. Advances in fluorescent microscopy and other methods allow one to follow the transport of individual molecules through a channel [7,16]. Single molecule tracking experiments provide a wealth of information about the transport mechanisms, which is not accessible from the measurements of the bulk flux through the channel. The kinetics of transport of a single particle through the channel in the absence of other particles is well understood [13,14,17]. In this Letter, we analyze the effects of crowding of the particles inside the channel on the transport times of individual particles in the experimentally relevant regime when a nonequilibrium steady state flux passes through the channel.

Single particle

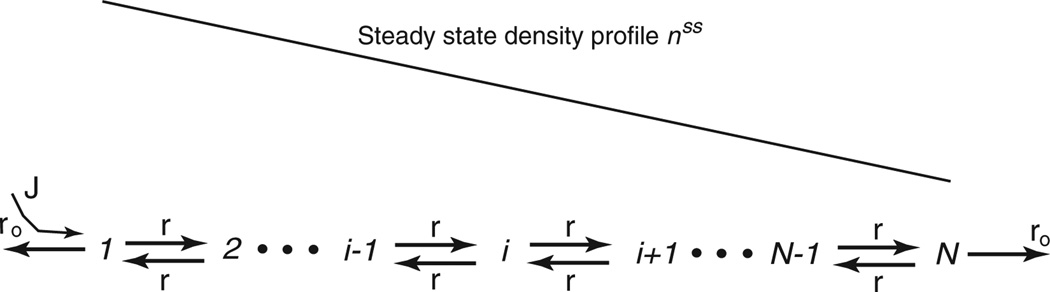
Here, we briefly review the kinetics of a single particle passing through the channel in order to explain the methods employed herein. The channel is represented as a sequence of “sites”1, …, N. Inside, the particle performs diffusionlike random walk starting at the “entrance” site 1 and hopping between the internal sites 1 ≤ i ≤ N at an average rate r (for simplicity, we assume that the channel is uniform). The particle can leave the channel from the terminal sites 1 and N with an average rate r_o. Transient trapping in the channel is described by choosing r_o < r. This hopping process is illustrated in Fig. 1. At any time t, the position of the particle in the channel is described by the vector of probabilities p_i(t) to be at a particular site i: |p(t)〉 = ((p₁(t),…, p_i(t),…, p_N(t)). We also define the vector |i〉 as a vector with the ith element equal to 1 and all other elements equal to 0, so that 〈i|p(t)〉 = p_i(t) (where 〈x|y〉 is the scalar product of the vectors |x〉 and |y〉). The master equation for the probability vector, describing the hopping through and out of the channel ends, can be written as $\frac{d}{dt}|p(t)\rangle =\mathrm{M̂}·|p(t)\rangle$ [18]. The formal solution of the master equation can be written as |p(t)〉 = e^M̂t|p(0)〉, where |p(0)〉 is the initial condition [17]; for a particle starting at site 1, |p(0)〉 = |1〉 = (1, 0, …, 0) The instantaneous probability flux to the right out of the channel is r_op_N(t), and the probability that the particle had exited the channel from the right side by time t is $P_{\to }^t={\int }_0^t{r}_o{p}_N(t\prime )dt\prime$ [14(d),17].

FIG. 1.

The channel is represented by a sequence of sites 1, …, N between which the particles can hop with rate r. The rate of hopping out of the channel from its ends is r_o. In the single-particle case, a particle starts at site 1 and hops inside the channel until it exits from either end. In the multiparticle case, the particles enter at site 1 with rate J(1 – n₁/m) where m is the maximal occupancy allowed. The line shows the steady-state concentration profile.

The total probability to exit to the right $P_{\to }\equiv P_{\to }^{\infty }$ is

$$P_{\to }={\int }_0^{\infty }{r}_o\langle N|e^{\mathrm{M̂}t}|1\rangle dt\prime =-r_o\langle N|{\mathrm{M̂}}^{-1}|1\rangle ,$$ (1)

where 〈i|X̂|j〉 ≡ X̂_ij. After some algebra [18], Eq. (1) gives for the total probability to exit from the channel on the right (the translocation probability): $P_{\to }=\frac{1}{2+(N-1)r_o/r}$, in accord with previous works [12,14]. Note that P_→ increases as r_o diminishes. That is, trapping of the particle in the channel increases the translocation probability [11,14].

We now calculate the directional mean exit times. The probability distribution of the exit times to the right f_→(t) is $f_{\to }(t)=-\frac{1}{P_{\to }}\frac{d}{dt}(1-P_{\to }^t)=r_o{p}_N(t)/P_{\to }$ [14(d),17]. Thus, the mean time to exit the right is

$${\mathrm{T̄}}_{\to }={\int }_0^{\infty }t\prime f_{\to }(t\prime )dt\prime =r_o\langle N|{({\mathrm{M̂}}^{-1})}^2|1\rangle /P_{\to }.$$ (2)

Similarly, the mean first passage time to the left is ${\mathrm{T̄}}_{\leftarrow }={\int }_0^{\infty }t\prime f_{\leftarrow }(t\prime )=r_o\langle 1|{({\mathrm{M̂}}^{-1})}^2|1\rangle /P_{\leftarrow }$. The mean time to exit from any of the ends is

$$\mathrm{T̄}=r_o{\int }_0^{\infty }t(p_N(t)+p_1(t))dt={\mathrm{T̄}}_{\leftarrow }{P}_{\leftarrow }+{\mathrm{T̄}}_{\to }{P}_{\to }.$$ (3)

Using the equations above, we obtain explicit expressions for the mean times:

$${\mathrm{T̄}}_{\to }=\frac{N[6P_{\leftarrow }+P_{\to }(N(N-3)+2){(r_o/r)}^2]}{6r_o},\mathrm{T̄}=\frac{N}{2r_o},{\mathrm{T̄}}_{\leftarrow }=\frac{N[6P_{\leftarrow }{P}_{\to }+P_{\to }^2(N(2N-3)+1){(r_o/r)}^2]}{6r_o{P}_{\leftarrow }},$$ (4)

in agreement with previous results obtained in the continuum limit [14(d)]. Note that the mean trapping time T̄ is linearly proportional to the channel length N. Surprisingly, the mean time for the particle to exit to the left T̄_← also scales like N for N ≫ 1, due to the possibility of large excursions into the channel before it returns to the left end. By contrast, the mean exit time to the right has two distinct regimes. For short channels, or strong trapping (Nr_o/r ≪ 1), ${\mathrm{T̄}}_{\to }\sim \frac{N}{2r_o}$, while for long channels, or weak trapping, (Nr_o/r ≫ 1), ${\mathrm{T̄}}_{\to }~\frac{N^2}{2r}$ (see also Fig. 3). Physically, for strong trapping, the bottleneck for the exit to the right is the release from the channel end, while for long channels and weak trapping the exit time is dominated by the time it takes to diffuse through the channel from left to right.

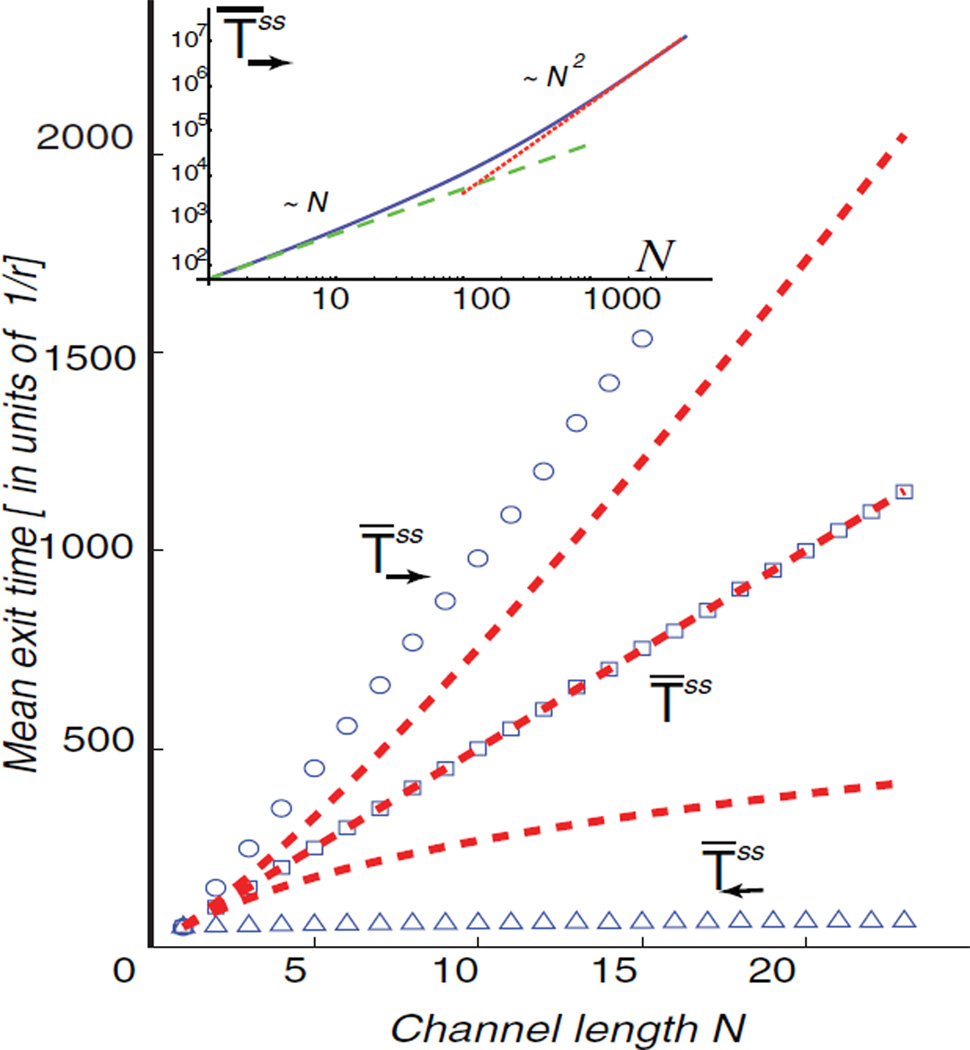
FIG. 3.

(color online) Dependence of the transport time in the crowded regime on the channel length N. Dashed red lines—- mean-field results; symbols—corresponding simulations; r = 1, r_o = 0.01, J = 0:5. The dependence on N is qualitatively similar to the single-particle case—see text. Inset: The transition between small N (linear dependence) and large N (quadratic dependence) regimes (logarithmic scale); r = 1, r_o = 0.01, J = 0.1.

Single particle on the background of the steady-state flux

When a finite flux J impinges onto the channel entrance, at any moment there can be many particles in the channel that might interfere with each other’s passage and prevent the entrance of new ones. The particles in the channel obey the same kinetics as the single particles, with a condition that a site can contain up to a maximal number of particles m. For constant J, a nonequilibrium steady state is established and the system can be described in terms of site occupancies $n_i=|{n\rangle }_i^{ss}$. The steady-state profile of a uniform channel can be solved exactly: $n_i^{ss}=\frac{{JP}_{\to }(1+(N-i)r_o/r)}{r_o+{JP}_{\leftarrow }/m}$ [12,18–20].

We now turn to the main results of this Letter—how does the crowding, when many particles are present in the channel, affect the transport times of individual particles within the nonequilibrium steady-state flux. To the best of our knowledge, no exact analytical solution exists in this case. The transport of an individual particle can be viewed as occurring on the background of the steady-state density profile|n〉^ss. In the mean-field approximation, the probability p_i(t) of a particle to be present at a given site is described by the following equations [18–21]:

$$\frac{{dp}_i}{dt}={rp}_{i-1}(1-\frac{n_i^{ss}}{m})+{rp}_{i+1}(1-\frac{n_i^{ss}}{m})-{rp}_i(1-\frac{n_{i-1}^{ss}}{m})-{rp}_i(1-\frac{n_{i+1}^{ss}}{m}),$$ (5)

with the appropriate boundary conditions [18]. Using matrix notations: $\frac{d}{dt}|p(t)\rangle ={\mathrm{M̂}}^{ss}·|p(t)\rangle$ Explicit matrix elements of M̂^ssare given in [18]. As in the single-particle case above, these linear equations can be solved analytically.

To test the feasibility of the mean-field approximation, we compared the probability of a particle to exit to the right, computed using the exact solution for the steady-state density with the mean-field result (see below). First, the average exit flux to the right is $J_{\to }=r_o{n}_N^{ss}$, which yields for the probability of an individual particle within this steady-state flux to exit to the right [12,18]:

$$P_{\to }^{ss}=\frac{J_{\to }}{J(1-n_1/m)}=\frac{1}{2+(N-1)r_o/r.}$$ (6)

On the other hand, from the mean-field approximation of Eq. (5) $P_{\to }^{ss}=-r_o\langle N|{({\mathrm{M̂}}^{ss})}^{-1}|1\rangle$ [see Eq. (1)]. Using the expressions for $n_i^{ss}$, after some algebra we get the same result as the exact expression, Eq. (6). Thus, the mean-field approximation yields an exact result: the probability of an individual particle to exit to the right is not affected by crowding and is the same as in the single-particle case (at least for uniform channels) [19,20]. The directional mean exit times can be calculated by repeating the same algebra as for the case of a single particle, but with M^ss instead of M. We find that the mean trapping time is ${\mathrm{T̄}}^{ss}=\frac{N}{2r_o}$ — surprisingly, like the translocation probability, the mean trapping time is also not affected by the crowding. By contrast, the directional times to exit to the right and to the left, ${\mathrm{T̄}}_{\to }^{ss},{\mathrm{T̄}}_{\leftarrow }^{ss}$ respectively, do change due to interparticle interactions, compared to the single-particle case. After some algebra [18], one gets for the mean time to exit to the left, ${\mathrm{T̄}}_{\leftarrow }^{ss}=r_o\langle 1|{(M^{ss})}^{-2}|1\rangle /P_{\leftarrow }$,

$${\mathrm{T̄}}_{\leftarrow }^{ss}=-\frac{Nm}{J^2{P}_{\leftarrow }}[{mr}_o+{JP}_{\leftarrow }+\frac{J}{2}]+\frac{rm{({JP}_{\leftarrow }+{mr}_o)}^2}{J^3{r}_o{P}_{\leftarrow }{P}_{\to }}\times \left[\psi \right(N+\frac{rm}{{JP}_{\to }})-\psi (\frac{rm}{{JP}_{\to }}\left)\right],$$ (7)

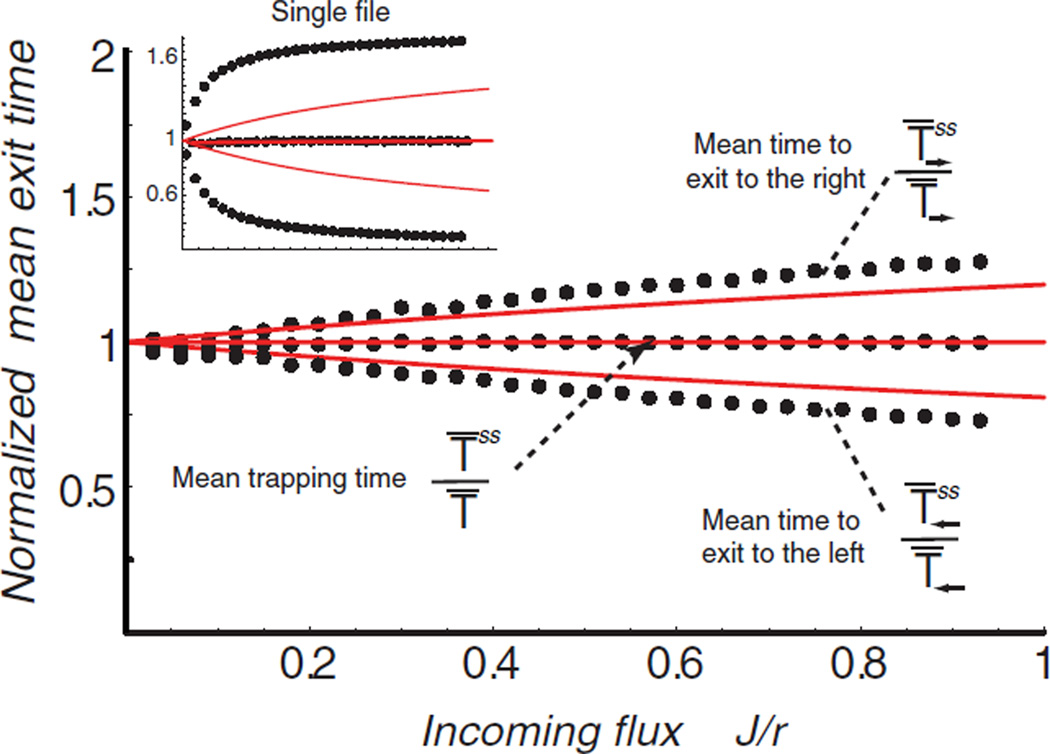
where $\psi (x)=\frac{d}{dx}\mathrm{\Gamma }(x);\mathrm{\Gamma }(x)$ is a γ function. The mean exit time to the right can be obtained in a similar fashion. The dependence of the exit times on the impinging flux J is illustrated in Fig. 2. Unlike the exit probabilities, crowding increases the mean time to exit to the rightT̄_→, and decreases the mean time to exit to the leftT̄_←. Interestingly, however, the qualitative dependence on the channel length N is similar to the single-particle case (J = 0), as shown in Fig. 3. Importantly, the transport times remain finite even in the fully jammed regime (J → ∞), when the flux through the channel saturates to its maximal value. In particular, the mean time to exit to the right tends to $\frac{N-2P_{\leftarrow }^2}{2P_{\to }{r}_o}$, while the mean time to exit to the left tends to $\frac{P_{\leftarrow }}{r_o}$ [18].

FIG. 2.

(color online) Ratios of the mean exit times in the jammed regime to the single-particle times. Upper lines—${\mathrm{T̄}}_{\to }^{ss}/{\mathrm{T̄}}_{\to }$. Lower lines—${\mathrm{T̄}}_{\leftarrow }^{ss}/{\mathrm{T̄}}_{\leftarrow }$. Solid red lines—analytical solution, dotted lines—simulations; N = 6, r = 1, r_o = 0.1, m = 3 for all lines. Inset: Same for single-file transport (m = 1).

In order to corroborate the results of the mean-field approximation and to investigate the limits of its validity, we performed computer simulations of the transport through the channel using a variant of the Kinetic Monte Carlo algorithm [22]. Both the simulations and the mean-field results show that the forward times are increased due to the jamming while the backward times are decreased. The increase in forward exit times is easily understood considering the reduction in hopping rates inside the channel due to crowding. The origin of the decrease in the backward exit time is more subtle: the crowding increases the number of particles which hop backwards out of the channel immediately after their entrance For wide channels that can accommodate more than one particle at each site, the mean-field results for the directional transport times ${\mathrm{T̄}}_{\to }^{ss}\text{and}{\mathrm{T̄}}_{\leftarrow }^{ss}$ agree closely with the simulations. For strictly single file channels (m = 1), the mean field approximation underestimates the actual value of the exit time to the right ${\mathrm{T̅}}_{\to }^{ss}$ and overestimates the exit time to the left ${\mathrm{T̅}}_{\leftarrow }^{ss}$, but still reproduces the right qualitative dependence of the times on the flux J and other parameters. The reason for the underestimation of the time to exit to the right is that the mean-field approximation neglects the correlation between successive jumps (a particle hopping to one of its neighbor sites leaves behind it a vacancy and thus has a higher probability to hop back to the same site in the next jump). Interestingly, the simulations show that the mean field result for the mean trapping time T̅^ss is exact (at least for a uniform channel). Corrections to the mean-field diffusion rate of a tracer particle in equilibrium conditions were calculated in [21] using effective medium theory. Such corrections improve the approximation also in our case; however, their systematic analysis lies outside the scope of the present Letter.

Discussion

To summarize, we have analyzed the effects of crowding and interparticle competition for space on the transport times through narrow channels of finite length under a nonequilibrium steady-state condition. The results of the mean-field analysis are corroborated by computer simulations. We have shown that in uniform channels the jamming increases the forward exit time, while decreasing the backward exit time. Surprisingly, jamming does not affect the mean dwelling time in uniform channels. The situation might be different in nonuniform channels; however, the mean-field approximation should provide a qualitatively correct picture even in this case [19,20], full discussion of which lies beyond the scope of the present work. The model provides a theoretical framework for analysis of single molecule transport through biological and artificial nanochannels. The parameters of the model, the rates r_o and r, can be related to the experimentally controlled factors such as diffusion coefficients inside and outside the channel and the binding affinity of the molecule in the channel. We emphasize the difference between the results of this Letter and the well-studied case of tracer diffusion in infinite single-file channels [23]. Finally, we note that the methods of this Letter can be extended to treat arbitrary molecular signalling pathways and other systems [24].