Abstract
Despite research spanning several decades, the exact value of the shear modulus Gs of the erythrocyte membrane is still ambiguous, and a wealth of studies, using measurements based on micropipette aspirations, ektacytometry systems and other flow chambers, and optical tweezers as well as application of several models have found different average values in the range 2–10 µN/m. Our study shows that different methodologies have predicted the correct shear modulus for the specific membrane modeling employed, i.e. the variation in the shear modulus determination results from the specific membrane modeling. Available experimental findings from ektacytometry systems and optical tweezers suggest that the dynamics of the erythrocyte membrane is strain-hardening at both moderate and large deformations. Thus the erythrocyte shear modulus cannot be determined accurately using strain-softening models (such as the neo-Hookean and Evans laws) or strain-softening/strain-hardening models (such as the Yeoh law) which overestimate the erythrocyte shear modulus. According to our analysis, the only available strain-hardening constitutive law, the Skalak et al. law, is able to match well both deformation-shear rate data from ektacytometry and force-extension data from optical tweezers at moderate and large strains, using an average value of the shear modulus of Gs = 2.4–2.75 µN/m, i.e. very close to that found in the linear regime of deformations via force-extension data from optical tweezers, Gs = 2.5±0.4 µN/m. In addition, our analysis suggests that a standard deviation in Gs of 0.4–0.5 µN/m (owing to the inherent differences between erythrocytes within a large population) describes well the findings from optical tweezers at small and large strains as well as from micro-pipette aspirations.
1. INTRODUCTION
A human erythrocyte is essentially a capsule (i.e. a membrane-enclosed fluid volume) where the liquid interior (cytoplasm) is a concentrated hemoglobin solution that behaves as a Newtonian fluid with viscosity µc ≈ 6–10 mPa s [1, 2]. In healthy blood and in the absence of flow, the average human erythrocyte assumes a biconcave discoid shape of surface area Sc = 135 µm2, with a diameter of 7.8 µm and a thickness varying from 0.8 − 2.6 µm at physiological osmolarity, resulting in a volume of Vc = 94 µm3 [3, 4]. The erythrocyte membrane is a complex multi-layered object consisting of a 4-nm-thick lipid bilayer (which is essentially a two-dimensional incompressible fluid with no shear resistance) and an underlying elastic network of spectrin (which exhibits shear resistance like a two-dimensional elastic solid) [4].
Despite research spanning several decades, the exact value of the shear modulus Gs of the erythrocyte membrane is still ambiguous, and a wealth of studies, using measurements based on micro-pipette aspirations, ektacytometry systems and other flow chambers, and optical tweezers as well as application of different models have found different average values in the range 2–10 µN/m. Early experimental studies using micro-pipette aspiration reported an average shear modulus of Gs = 4–10 µN/m [5–7] while models proposed a strain-dependent shear modulus with a value near Gs = 2 µN/m at low strains, e.g. see [8]. In 1999, Hénon et al. [9], utilizing optical tweezers at small strains, found the membrane shear modulus to be Gs = 2.5 ± 0.4 µN/m. Later studies, using force-extension data from optical tweezers and matching them with continuum and molecular models, found a shear modulus in the high range, Gs = 8.3 µN/m [10–12]. In our recent work [13], we compared our computational results with ektacytometry findings [14] and found a very good match for a shear modulus very close to the average value found by optical tweezers at low strains, Gs = 2.5 µN/m [9]. (To facilitate the subsequent discussion, in several places only the shear modulus value will be presented with the implicit assumption that its units are always µN/m.)
The significant discrepancies between these values suggest a need to examine the methodologies employed. Our review of published studies on the determination of the erythrocyte shear modulus reveals the following conclusions (as also discussed in sections 3 and 4). (i) Several studies are approximate since they utilize simple (or even crude) models and thus, at best, they find the order of magnitude of the shear modulus rather than its exact value. (ii) From the rest of the studies which rely on accurate models, many utilize identical or very similar methodologies and thus it is not surprising that they predict a similar value for the shear modulus. Therefore, from the available large number of studies employing accurate models, only a much smaller set is truly independent. (iii) This small set of independent methodologies still predict different values of the shear modulus. Thus a question naturally arises as to the reasons for this variation on the shear modulus determination.
Based on the above, the present paper has two main goals: (a) to explain why different methodologies predict different values of the erythrocyte shear modulus; and (b) to predict accurately the value of the shear modulus and, in particular, its average value and the range of its possible variation (owing to the inherent differences between erythrocytes within a large population).
In section 2 we review several constitutive laws that have been used for the continuum description of the erythrocyte membrane since they are the basis to relate the available experimental measurements to the erythrocyte shear modulus. Based on the nature of these constitutive laws and their relationship, in section 3 we discuss the determination of the shear modulus via four distinct methodologies: force-extension data from optical tweezers at small and large strains, deformation-shear rate data from ektacytometry, and data from micro-pipette aspirations. A review of additional methodologies on the shear modulus of the erythrocyte membrane has been included in section 4.
We emphasize that our review of the existing studies on the determination of the erythrocyte shear modulus included in this paper cannot be all-inclusive owing to the difficulty in finding all papers published and, most important, to the limited space commonly available for the references in a given publication. Thus, in this work, we include and discuss a few representative publications for several methodologies employed on shear modulus determination. Our comparisons and comments on earlier studies do not intend, by any mean, to discount any previous study; all of them have provided invaluable information on the challenging problem of the physics of erythrocyte dynamics and its modeling.
2. MEMBRANE DYNAMICS
A. Common constitutive laws
Several constitutive laws have been used for the continuum description of thin elastic membranes such as that of the erythrocyte and many artificial capsules, e.g. [10, 13, 15–17]. These laws describe the principal elastic tensions τi (i = 1, 2) on the membrane as a function of the principal stretch ratios λi. Note that λi = dsi/dSi, where dSi and dsi denote line elements in the reference and the deformed shapes, while the principal strain components are given by [15]. Below we present the elastic tension τ1 for five constitutive laws; to calculate τ2 reverse the λi subscripts.
The Hooke (H) law (physically valid for small deformations) assumes that the membrane tensions depend linearly on the surface strain [15]
| (1) |
where is the shear modulus associated with this law and νs the surface Poisson ratio (νs ≠ 1).
The neo-Hookean (NH) law, a special case of the Mooney-Rivlin law, results from the application of the corresponding three-dimensional law to a very thin membrane [15, 18]
| (2) |
where is the associated shear modulus. This law does not contain a parameter associated with area dilatation which is implicitly embodied into the law.
The Yeoh law (YE) [19] is a higher-order extension of the neo-Hookean law; its application to a very thin membrane gives the corresponding two-dimensional law [18]
| (3) |
where is the associated shear modulus, and and dimensionless parameters.
The Skalak et al. (SK) law [20] adds non-linearly the area dilatation to the shear deformation
| (4) |
In the equation above, is the shear modulus associated with this law while the dimensionless parameter C is associated with the area-dilatation modulus of the membrane (scaled with its shear modulus). In particular, analysis in the limit of small deformations shows that the area-dilatation modulus is [15].
The Evans (EV) law [17, 21] adds linearly the area dilatation to the shear deformation,
| (5) |
where is the shear modulus associated with this law while the dimensionless parameter CEV represents the area-dilatation modulus of the membrane (scaled with its shear modulus). Note that this law is also called Evans-Skalak law in some papers, e.g. [18, 22], probably because it appeared later in the book of Evans and Skalak [23].
It is of interest to know that the Skalak et al. and Evans laws are two-dimensional laws, derived to represent thin elastic membranes. On the other hand, the (original) Hooke, neo-Hookean and Yeoh laws are three-dimensional laws, derived to represent elastic materials. One may apply these laws to thin elastic membranes by either using the three-dimensional laws with a very small membrane thickness and volume incompressibility (i.e. λ1λ2λ3 = 1) or utilizing the corresponding two-dimensional laws presented above. (The derivation of the two-dimensional laws from the original three-dimensional laws has been described in earlier papers, e.g. see section 3.3 in Ref.[18] and section 4.7 in Ref.[24].)
Under (mechanically) uniaxial extension or isotropic dilatation of capsules with finite surface area-dilatation resistance, it was found that the neo-Hookean and Evans laws are strain-softening (i.e. their tensions increase sub-linearly with the strain) while the Skalak et al. law is strain-hardening (i.e. its tensions grow super-linearly with the strain) [15, 18]. (Note that the linear increase used in these comparisons refers to the common slope of all laws in the linear regime of deformations.) The same behavior is observed in the steady-state dynamics of these capsules in planar extensional flows [25]. The behavior of the Yeoh law is more complicated; while at small deformations it behaves like the neo-Hookean law, due to the higher-order correction included in the Yeoh law, its nature (strain-softening or strain-hardening) and its degree of strain-softening vary with deformation at moderate and large deformations and depends on the particular choice of its two parameters, and [19].
B. Constitutive laws and local area-incompressibility
Erythrocyte continuum models (such as the ones used to determine the membrane’s shear modulus) commonly treat the erythrocyte membrane as a locally area–incompressible elastic solid by either employing a large area-dilatation modulus or imposing directly the local area-incompressibility constraint λ1λ2 = 1, e.g. [6, 10, 16].
By imposing locally the constraint λ1λ2 = 1, the constitutive laws described earlier are simplified to the following equations
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
It is interesting to note that several studies, e.g. [5, 6, 10, 12, 26], referred to and/or employed the Evans law under local area-incompressibility in the form
| (11) |
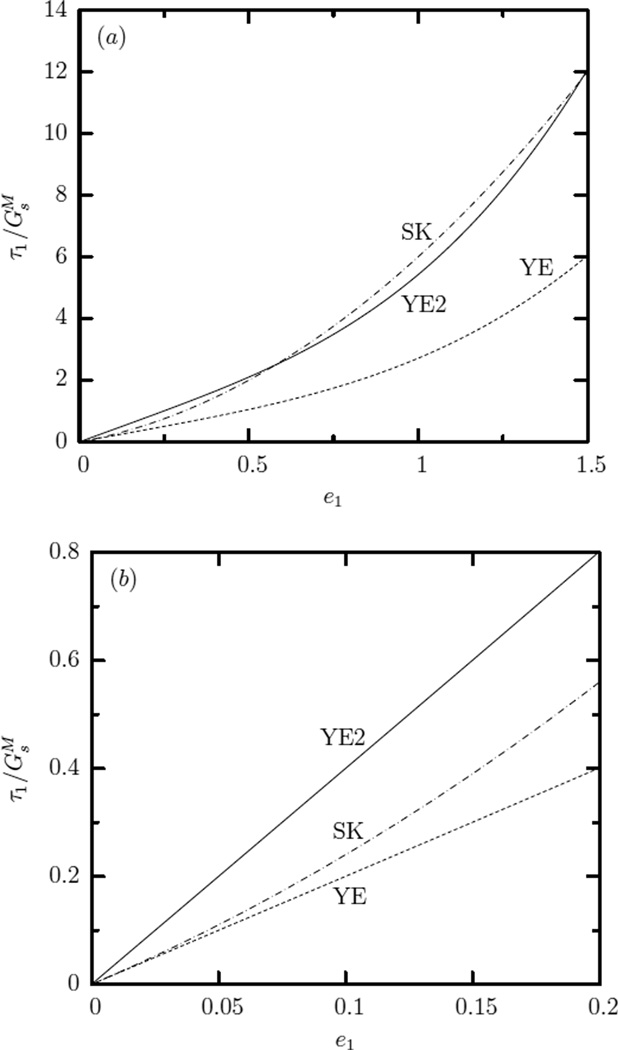
In figure 1 we plot the principal tension τ1 (scaled with its associated shear modulus) as a function of the principal strain for all of the laws studied in this paper. Note that for the Hooke law we used νs = 1/3 which produces a practically linear tension-strain dependence up to e1 = 1.5 (or λ1 = 2) included in this figure with a slope very close to the common slope of all laws at small deformations. For the Yeoh law we used and , i.e. the value of these two parameters (according to our notation and definition) employed in Ref.[10] to match erythrocyte’s force-extension data from optical tweezers at large strains.
FIG. 1.
Principal tension τ1 (scaled with its associated shear modulus) as a function of the principal strain e1 for the Hooke (HO), neo-Hookean (NH), Yeoh (YE), Skalak et al. (SK) and Evans (EV) laws under local area-incompressibility λ1λ2 = 1. For the Hooke law we used νs = 1/3 while for the Yeoh law we used and .
Figure 1 shows that, even under local area-incompressibility, the Skalak et al. law is strain-hardening, the neo-Hookean and Evans laws are strain-softening while the Evans law is more strain-softening than the neo-Hookean law. For the particular choice of the parameters and , after the initial strain-softening behavior at low deformations, the Yeoh law becomes strain-hardening at large strains.
Small deformation behavior
When local area-incompressibility is enforced and the deformation is very small, i.e. , where |ε| ≪ 1, all aforementioned constitutive laws result into the same equation, i.e.
| (12) |
as simple perturbation algebra shows. Thus, under local area-incompressibility and in the small-deformation regime all laws produce identical tension-extension behavior for the same shear modulus, i.e.
| (13) |
In essence, all constitutive laws behave as the Hooke law due to the linearization inherent in the regime of small deformations.
Non-small-deformation behavior
In moderate and large deformations, the different constitutive laws produce different behavior. Based on the strain-hardening or strain-softening nature of each law, we expect that, for a given deformation, the more strain-softening law should produce the same tensions as a less strain-softening law but for a higher shear modulus.
This behavior has been identified for the deformation of capsules with moderate area-dilatation resistance. For example, by matching the force-deformation curves derived from (mechanical) compression experiments, Carin et al. [27] showed that the strain-softening Evans law produces an almost 40% higher shear modulus than the Skalak et al. law [27].
In addition, if the matching is not valid over the entire deformation range, we expect the difference in the predicted shear moduli to increase with the deformation of matching. Thus, at small deformations all laws predict the same shear modulus; by matching at moderate deformations the more strain-softening law should predict a higher shear modulus, while by matching at large deformations the more strain-softening law should predict a much higher shear modulus.
This was shown in figure 21(b) of our earlier work [25] where we plot the steady-state maximum principal tensions as a function of the capsule extension/ length Lc, for a neo-Hookean and a Skalak capsule with C = 1 in a planar extensional flow. (Note that in our earlier work, the tensions were scaled with the shear modulus of each law while the capsule length was scaled with its equilibrium length.) When Lc = 1.5 (extension 50%), matching the maximum tensions of these laws requires ; the moduli ratio increases to , 3.4 for lengths Lc = 2, 2.5 (or extension 100%, 150%).
To estimate the difference in the predicted shear modulus of these constitutive laws under local area-incompressibility, we match the local tensions given by each law for the same stretch ratio. Based on this, the following relationships are derived
| (14) |
To derive an estimation of the relative magnitude for the shear modulus of these laws, we can approximate the stretch ratio λ1 with the ratio of the extension of the deformed erythrocyte to its extension at the reference (i.e. equilibrium) shape which occurs in a given experimental system. For example, if we assume that at moderate deformations in ektacytometry systems or optical tweezers (or λ1 ≈ 1.41), then the equations above predict
| (15) |
At large deformations (such as in optical tweezer experiments at large strains), the erythrocyte axial diameter is increased to almost 100%; in this case, our prediction for λ1 = 2 gives
| (16) |
The predictions above verify our earlier discussion in this subsection that, for matching in a specific deformation range, the more strain-softening law should produce the same tensions as a less strain-softening law but for a higher shear modulus while the difference in the predicted shear moduli should increase with the deformation range of matching.
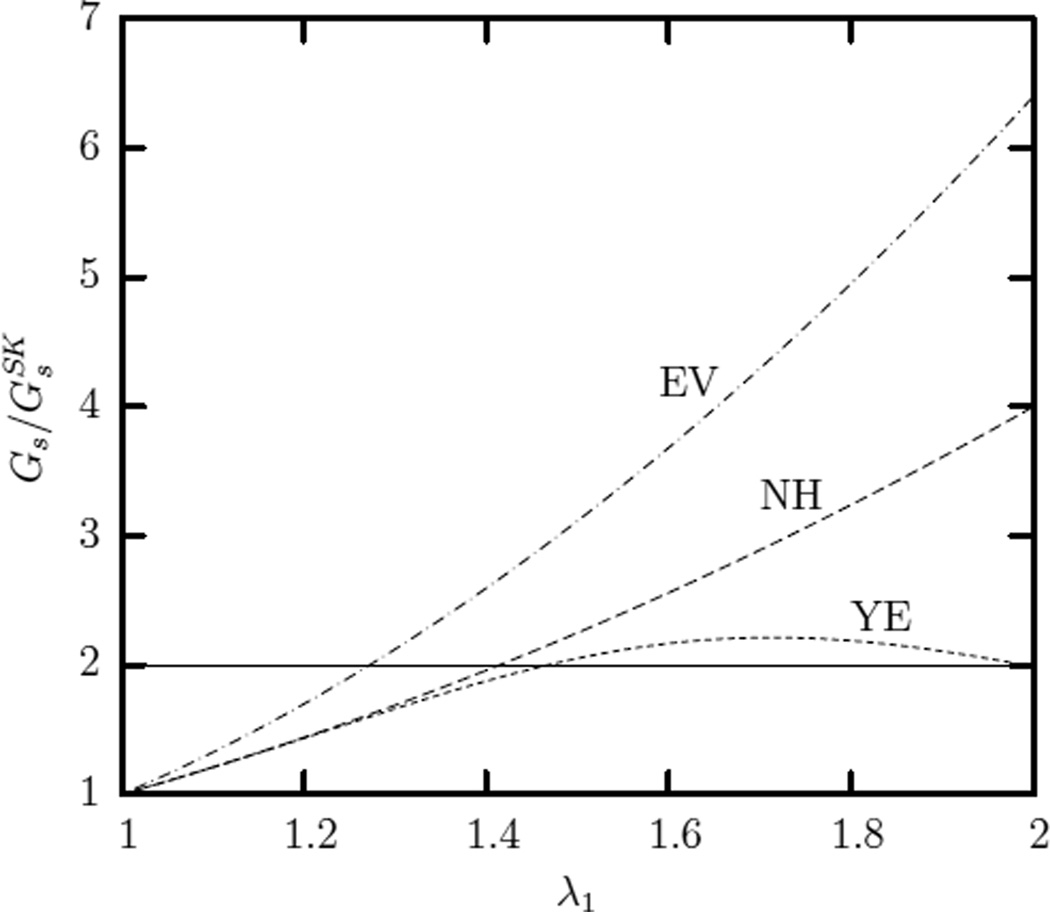
In figure 2 we plot the shear modulus of the neo-Hookean, Yeoh and Evans laws (scaled with the shear modulus of Skalak et al. law) as a function of the stretch ratio λ1. This figure shows clearly that, owing to its strain-hardening at large strains for the specific choice of the parameters and , the Yeoh law should produce a good match at large strains for membranes following the Skalak et al. law. It is of interest to note that for a stretch ratio λ1 in the range [1.35, 2] (which almost covers the extensions used in optical tweezer experiments at large strains [10]), the Yeoh’s shear modulus is with en error of only ±10%.
FIG. 2.
Variation of the shear modulus of the neo-Hookean (NH), Yeoh (YE) and Evans (EV) laws (scaled with the shear modulus of Skalak et al. (SK) law) with the stretch ratio λ1 so that all laws produce the same principal tension τ1.
It is of interest to note that the shear resistance of the erythrocyte membrane results from its spectrin cytoskeleton which may undergo local area changes under the constraint of fixed total area being enclosed beneath the lipid bilayer in the erythrocyte membrane [13, 28, 29]. In our present work, we utilize the assumption of local area-incompressibility (so that we are able to determine the relationship between different constitutive laws), because this assumption has been employed by earlier shear modulus finding methodologies, e.g. via force-extension data from optical tweezers at moderate and large strains [10, 11, 30], via micro-pipette aspiration [6, 7, 26], and from electrically induced deformation experiments [16], as discussed in more detail in sections 3 and 4.
C. Finding the shear modulus of a membrane
In section 2B we discussed that different constitutive laws should predict different estimations of the shear modulus of the erythrocyte membrane, depending on the degree of strain-softening of each law and the deformation range of matching. Thus, a question naturally arises as to how to determine accurately the shear modulus of a given membrane and in particular of the erythrocyte. To help answer this question (which actually constitutes a research interest spanning several decades), two major statements can be made.
First, if the dynamics of a membrane is known to follow a given constitutive law in a range of deformations, then the shear modulus predicted by this law in this deformation range represents an accurate determination of the shear modulus of this membrane.
The statement above does not imply that if a constitutive law matches some experimental findings in a given range (e.g. the force-deformation curve from compression experiments or the deformation-shear rate curve from ektacytometry systems or the force-extension relationship from optical tweezers at large strains), then this means that the dynamics of this membrane follows this law. Due to the bulk (and thus simplistic) nature of some experimental findings, these can be matched in a given range or even in the entire range of available deformations via one or several laws without the membrane to follow one or any of these laws.
For example, obviously the biocompatible alginate capsule used in the compression experiments of Carin et al. [27] mentioned earlier, cannot be at the same time strain-hardening and strain-softening since it was found that the strain-hardening Skalak et al. law as well as the strain-softening Evans law describe well the capsule’s force-deformation compression curves. In reality, this capsule may follow one of these two laws or even none of them. Again this points to the simplistic nature of some available experimental findings.
Therefore, to find the constitutive law which truly describes the dynamics of a certain capsule (and thus its real shear modulus) more detailed (or complicated) experimental data are needed, i.e. using different experimental data (e.g. force-deformation but also deformation-shear rate data) and probably including information about local properties describing the capsule dynamics as opposed to the commonly available bulk-type experimental data (e.g. force-deformation or deformation-shear rate data).
For example, Lefebvre and Barthès-Biesel [31] proposed to flow capsules into a microchannel of comparable dimensions and observe local details of its interfacial shape as a function of the flow rate (including the curvature along the capsule profile) as a way to deduce the membrane shear modulus. Based on this, alginate capsules were found to show a strain-hardening dynamics best modeled by the Skalak et al. law with a small pre-stress.
The second major conclusion which can be drawn on this subject is that, to avoid the complications arising from the fact that different laws predict different values of the membrane shear modulus based on experimental findings at moderate and large deformations, one may consider the membrane dynamics at small deformations where all laws predict identical value of the shear modulus. Thus, the membrane moduli are formally defined by basic deformations in the linear regime of deformations. In particular, the (surface) Young modulus Es (which is associated with the shear modulus Gs) is measured by the membrane response to a uniaxial extension while the area-dilatation modulus Ga is measured by the membrane response to an isotropic tension [15, 20].
The small-deformation regime offers an additional advantage to the shear-modulus finding methodologies which employ an analytical equation to relate the membrane shear modulus with the experimental measurements; due to the linearization inherent in this deformation regime, the required relationship is, in general, easier to derive than in the (non-linear) regime of large deformations.
3. NATURE AND SHEAR MODULUS OF THE ERYTHROCYTE MEMBRANE
Nature of erythrocyte membrane under strain
Measurements in ektacytometry systems have long shown that the erythrocyte’s (ektacytometry) deformation increases logarithmically with the shear stress in both moderate and large deformations. (See for example figure 3 in Ref.[14].) This finding reveals two conclusions: (a) the cell membrane has a single nature under both moderate and large strains, i.e. it is either strain-hardening or strain-softening, and (b) this single nature is strain-hardening since the deformation-shear stress dependence is logarithmic. In addition, force-extension data from optical tweezers show clearly a hard-straining behavior at large strains, as has been identified in earlier studies, e.g. see figure 8 in Ref.[10]. The shear resistance of the erythrocyte membrane results from its elastic network of spectrin [4] while the strain-hardening nature of the spectrin cytoskeleton with deformation has also been identified via computational modeling [11, 32].
Our reasoning based on the experimental findings suggests that the erythrocyte membrane is strain-hardening for non-small deformations, i.e. for both moderate and large strains. In this case, the erythrocyte shear modulus cannot be determined accurately using strain-softening models (such as the neo-Hookean and Evans laws) or strain-softening/strain-hardening models (such as the Yeoh law). In particular, both types of laws are expected to produce a higher value of the shear modulus as discussed in section 2B.
Determination of shear modulus at small strains via force-extension data from optical tweezers
In 1999, Hénon et al. [9], utilizing optical tweezers at small strains (stretching force < 15 pN), determined the membrane shear modulus to be Gs = 2.5 ± 0.4 µN/m. The discotic cell at rest was modeled by two parallel discs submitted to zero stress at their border. Owing to the linear regime of deformations, the early study employed constitutive laws from linear elasticity to relate the cell’s transverse diameter with the applied force and the shear modulus.
To support their high value of the membrane shear modulus found by optical tweezers at large strains, Dao, Suresh and coworkers [10] discussed several possible reasons for the low shear modulus found by Hénon et al. [9], including “idealization of a biconcave cell as a two-dimensional planar disc” and “neglecting the effects of the relatively large contact region between the cell and the beads”. In our opinion, these possible reasons do not constitute proofs while so far no study has actually challenged the findings of Hénon et al. [9] at low strains, e.g. by proving that either the experiments or the employed analytical model are erroneous.
It is of interest to note that the earlier theoretical model of Fischer et al. [8] also suggested a low value of Gs = 2 µN/m at small strains to explain experiments on red cells whose membrane shear modulus has been increased by treatment with diamide. To match the higher value of the shear modulus at large strains known from micro-pipette aspiration studies, the authors proposed a strain-dependent shear modulus [8].
Determination of shear modulus at moderate strains via deformation-shear rate data from ektacytometry
In our recent work [13], we developed a cytoskeleton-based continuum erythrocyte algorithm based on the Skalak et al. law. In addition, we compared our computational results with the ektacytometry deformation-shear rate findings reported in figure 3 of Hardeman et al. [14]. Our computational results capture two important aspects of the relationship between cell deformation and capillary number (or wall shear stress): (i) the dependence is logarithmic for the employed range of shear rates, and (ii) while using a log-scale for the capillary number, our method produces a slope consistent with experimental results. (See figure 3 in our earlier paper [13].) In addition, for Gs = 2.4 µN/m the experimental and computational curves coincide suggesting that the sample used in the experimental measurement had a shear modulus very close to the average value found by optical tweezers at low strains, Gs = 2.5 µN/m [9].
We emphasize that additional comparisons of our computational results reported in Ref.[13] with ektacytometry findings from different studies show that the matching shear modulus falls inside the range for Gs valid for most red blood cells at low strains, i.e. 1.7–3.3 µN/m [9], and rather close to the average value. In particular, the ektacytometry’s deformation-shear stress data included in table 1 of Wang et al. [33] from the LORCA ektacytometer correspond to a shear modulus Gs = 2.3; the ektacytometry data for the control (i.e. normal erythrocytes) included in figure 1 of Alexy et al. [34] correspond to Gs = 2; while new ektacytometry data received from Hardeman (personal communication) correspond to Gs = 2.1. Therefore, our four comparisons reveal an average value of the shear modulus Gs = 2.2.
Note that our comparisons involve experimental findings via the LORCA ektacytometer which works at the human body temperature of 37° and its measurements show negligible standard deviation. Since all the remaining methodologies discussed in this paper determine the shear modulus at room temperature (near 25°), we can apply a temperature correction to our shear modulus determination. In their micro-pipette aspiration study, Waugh and Evans [6] reported a 9% decrease in the shear modulus from 24.8° to 35.3° in their table 1; using this correction our average value of the shear modulus becomes Gs = 2.4. The slightly higher value of Gs = 2.64 is obtained if we use the 20% decrease from 25° to 35° reported in figure 11 in the electrically induced deformation methodology of Engelhardt and Sackmann [16].
Determination of shear modulus at moderate and large strains via force-extension data from optical tweezers
In a series of papers, Dao, Suresh and coworkers determined the shear modulus of the erythrocyte membrane by matching computational results from continuum and molecular models with their optical tweezer force-extension data at moderate and large strains (stretching force 20 to 198 pN), e.g. [10–12]. The results based on their continuum modeling were summarized in Ref. [10]. In particular, the authors utilized a finite-element program to solve for the cell shape deforming as in the optical tweezer experiments, assuming that the erythrocyte membrane follows either the neo-Hookean law (with or without enforcing local area incompressibility) or the Yeoh law (without enforcing local area incompressibility). During the deformation, the flow inside the erythrocyte was not considered; the cytoplasm was treated as an inviscid fluid which acts to keep the interior volume constant. (Similar continuum modeling was employed in later studies from other groups with similar predictions, e.g. [36].)
As reported in figure 7 of the earlier study [10], the neo-Hookean law is able to describe adequately the cell’s axial diameter at moderate strains only (stretching force 20 to 88 pN) but fails at higher strains since it cannot describe the erythrocyte’s hard-straining behavior in this range of deformations. Without enforcing local area incompressibility, the shear modulus was found to vary in the range [5.3, 11.3] due to the variation in the experimental data with an average value of . The shear modulus under local area incompressibility is 75% of that without, i.e. it varies in the range [4, 8.5] with an average value of [10].
According to our estimation discussed in section 2B, the corresponding shear modulus for a membrane following the Skalak et al. law is expected to be about half that of the neo-Hookean law, i.e. under local area incompressibility it is expected to vary in the range [2, 4.25] with an average value of . This is very close to that found in the linear regime of deformations, i.e. average value Gs = 2.5 and range [1.7, 3.3] [9].
When the Yeoh law was used to described the erythrocyte membrane, the computations of Dao, Suresh and coworkers were able to describe adequate the cell’s axial diameter at both moderate and large strains (stretching force 20 to 198 pN) as seen in figure 8 of the earlier study [10], due to the hard-straining nature of the Yeoh law at large strains (as also shown in our figure 1). Without enforcing local area incompressibility, they found the same range and average value as for their neo-Hookean law at moderate strains. (We note that the model was unable to match the transverse diameter; an optical matching for the average value of the experimental data suggests an average value for the shear modulus below 3.)
By using the shear modulus of the Yeoh law which best matches the erythrocyte axial diameter, and converting it to the corresponding shear modulus under local area incompressibility by multiplying with 0.75 as suggested by the authors (see Ref.[10] and table 1 in Ref.[12]), we obtain the same values as for the neo-Hookean law. As shown clearly in our figure 2, for almost the entire range of the strains used in the work of Dao, Suresh and coworkers, the Yeoh’s shear modulus is with an error of only ±10%. Thus, again we obtain the same determination for the shear modulus of the Skalak et al. law: range [2, 4.25] and average value of .
It is of interest to note that the recent study of Le et al. [36] which considered the same membrane modeling with that of Dao and coworkers [10] but also solved the inner viscous flow utilizing their implicit immersed boundary method, reported a shear modulus range of [4.8, 10] and an average value of , based on matching with the optical tweezer data for the axial diameter as shown in their figure 13. If we account for the missing local area-incompressibility (by multiplying by 0.75) and convert to the Skalak et al. law (by dividing by 2), we get the range [1.8, 3.75] which is very close to the range [1.7, 3.3] found in the linear regime [9].
Therefore, the Skalak et al. law is the only employed law which is able to match well both deformation-shear rate data from ektacytometry and force-extension data from optical tweezers at moderate and large strains using a value of the shear modulus very close to that found in the linear regime of deformations, i.e. Gs = 2.5 µN/m [9]. This reinforces further our earlier conclusion that the nature of the erythrocyte membrane is strain-hardening at both moderate and large deformations.
An important conclusion here is that the shear modulus found by matching a constitutive law with experimental data in a specific range of deformations is not necessarily the same as that found in the linear regime of deformations, i.e. the true shear modulus of the membrane. For example, if the erythrocyte membrane follows the Skalak et al. law, then our understanding is that Dao, Suresh and coworkers [10–12] as well as other groups [36] found the shear modulus that represents the Yeoh law at large strains but not the true shear modulus of the erythrocyte membrane, as shown optically in figure 3 and explained in its caption.
FIG. 3.
Principal tension τ1 (scaled with the membrane’s shear modulus ) as a function of the principal strain e1 for the Yeoh (YE) and the Skalak et al. (SK) laws having the membrane’s shear modulus, i.e. . Also plotted is the tension-strain dependence YE2 for the Yeoh law having a shear modulus twice that of the membrane, . (a) Curve YE2 appears to match adequately the SK curve in moderate and large strains while optically it also appears to produce a good matching at small strains owing to the large x-axis scale. (b) Working in the linear regime (e.g. plotting the data only for small strains) it is obvious that curve YE2 cannot match the common slope (i.e. the membrane’s shear modulus ) of the other two curves.
Determination of shear modulus from micro-pipette aspiration
Different research groups have long used micro-pipette aspiration experiments to determine the mechanical properties of the erythrocyte membrane, e.g. [5–7, 26, 37]. These studies utilized the incompressible Evans law, given by Eq.(11), and an analytical equation to relate the pipette suction pressure with the aspiration length. Based on this methodology the shear modulus was found to vary in the range 4–10 with a typical value of Gs = 6–7 at room temperature [5].
Hénon et al. [9] discussed several possible reasons to explain the difference between their low shear modulus value at the linear regime and the high value from the micro-pipette aspiration. According to their summary"the shear modulus is expected to increase from the small to the finite deformation regime, and because the elastic modulus measured with micro-pipettes is a combination of the shear modulus and area compressibility” [9].
Our analysis suggests that this difference results from the constitutive law employed in the micro-pipette aspiration studies. Based on our discussion in section 2B, the Evans incompressible law should overestimate the erythrocyte shear modulus (based on the Skalak et al. law) by a factor of 2–3 at moderate deformations and much more at larger deformations. To show further the correspondence between the two laws, in the Appendix we employ Evans analysis for the statics of the micro-pipette aspiration but utilize the incompressible Skalak et al. law, and show that the moduli ratio should vary in the range [1.5, 3.6] for the aspiration lengths usually employed in the micro-pipette studies. Thus the typical value of Gs = 6.5 found by micro-pipette aspirations corresponds to a moduli ratio of which is rather well representative of the overestimation of the Evans law (with respect to the Skalak et al. law) in these experiments.
It is of interest to note that the values of the standard deviation found in micro-pipette aspiration studies are consistent with the standard deviation of 0.4 found by Hénon et al. [9], if we scale them with the corresponding moduli ratio. For example, Waugh and Evans found Gs = 6.61 ± 1.24; scaling this standard deviation with 2.5/6.61 we obtain 0.47. We also obtain the same scaled standard deviation from the study of Evans et al. [26] who found Gs = 9 ± 1.7. Lelièvre et al. [37] found Gs = 4.5 ± 0.8 and thus their scaled standard deviation is 0.44.
In essence, we believe that the (very) strain-softening Evans law cannot represent well the strain-hardening behavior of the erythrocyte membrane at non-linear deformations, and thus methodologies which employ this law should always overestimate the shear modulus of the erythrocyte membrane.
4. REVIEW OF ADDITIONAL METHODOLOGIES ON THE SHEAR MODULUS OF THE ERYTHROCYTE MEMBRANE
Cytoskeleton molecular models
A series of papers utilized spectrin-based molecular algorithms and compared their results with force-extension measurements via optical tweezers at moderate and large strains, e.g. [11, 12, 38]. These studies are based on the molecular algorithm of Dao, Suresh and coworkers and thus it is not surprising that they predicted a shear modulus in the high-range, Gs = 8.3 µNm [11, 12, 38], since this spectrin algorithm employs specific values for the associated molecular parameters that match the Yeoh continuum law, as discussed in Ref.[12]. Further, the shear modulus of the molecular algorithms originally results from the particular choice of the employed molecular parameters and not via matching with optical tweezer measurements that is used only for verification (see section 2.4 in Ref. [12] and section 4.3 in Ref. [38]).
It is of interest to note that the molecular algorithms of Dao et al. [11, 12] and Hartmann [38], which do not account for the local area-incompressibility forces of the lipid bilayer, produce a practically linear force-extension relationship which does not match well the hard-straining nature of the erythrocyte shown in the experimental measurements (e.g. see figure 8 in Ref.[12] and figure 7 in Ref.[38]). By incorporating the constraint of local area-incompressibility in the spectrin description, Karniadakis and coworkers [30] produced a very good match with the hard-straining force-dependence for the axial diameter of the erythrocyte.
As discussed in our cytoskeleton-based continuum erythrocyte algorithm [13], the local area-incompressibility forces (i.e. locally isotropic forces) of the lipid bilayer should be accounted for in any spectrin modeling either continuum or molecular. However, in our opinion enforcing a local area-incompressibility on the spectrin membrane appears to be stricter than necessary since the cytoskeleton can undergo local area changes under the constraint of fixed total area being enclosed beneath the lipid bilayer in the erythrocyte membrane [13, 28, 29]. (The main issue here is that the local area-incompressibility forces of the lipid bilayer produce incompressibility of the local area on the lipid bilayer but not necessarily on the spectrin cytoskeleton.)
The incorporation of the local area-incompressibility constraint in the spectrin description [30] reduced the predicted shear modulus from Gs = 8.3 to Gs = 6.3. This reduction is in agreement with the correction factor of 0.75 suggested in the earlier studies of Dao, Suresh and coworkers [10, 11] since 8.3 × 0.75 = 6.2, i.e. in essence the methodology of Karniadakis and coworkers [30] corresponds to an incompressible Yeoh law. Therefore, based on the analysis of this paper, if the parameters of Karniadakis’ methodology are modified to match the Skalak et al. law, then we expect the prediction of the shear modulus to be within the range found by Hénon et al. [9].
Low-viscosity ektacytometry
Alternative ektacytometry systems have been developed by Wen and coworkers [39, 40] that involve erythrocytes in the “wheel” orientation in low-viscosity surrounding liquids at moderate shear rates. Based on a simple analytical model (which assumes that the incompressible Evans law applies to the maximum elongation of the cell), the authors predicted a shear modulus of Gs = 6.1 via measurements through changes in laser-diffraction patterns, and a shear modulus of Gs = 4.3 via direct observations of erythrocyte deformation in a flow chamber.
Recently, MacMeccan et al. [41], utilizing a coupled lattice-Boltzmann/finite-element method, found good agreement with the experimental data on deformation versus flow rate in the flow chamber [39, 40]. The numerical method utilizes the physiological conditions of the human erythrocyte with Gs = 5.7 but it does not enforce local area-incompressibility. Observation of their figure 12 shows that a (computational) line with a smaller slope (i.e. a smaller Gs) matches better the experimental results while the shear modulus is further reduced (by a factor of 0.75) if we enforce the local area-incompressibility constraint.
However, the experimental work of Wen and coworkers [39, 40] used red blood cells from rabbits which are smaller than human erythrocytes (i.e. mean diameter 6.5 µm) and thus probably have different properties including equilibrium shape, inner viscosity and shear modulus, while the effects of osmotic pressure and temperature are unclear for these cells. Until these issues are clarified, further discussion on these experimental measurements seems redundant.
Methodologies based on electrically induced deformation experiments
Engelhardt and Sackmann [16] developed a method to measure the shear modulus of the erythrocyte membrane based on the fixation and transient deformation of cells in a high-frequency electric field. The cell were subjected to both moderate and large deformations while the shear modulus determination was based on moderate deformations (i.e. elongations less then 3 µm). Owing to the non-linear deformations, the authors had to utilize an approximate sphere-to-ellipsoid deformation model that appears to be accurate at moderate deformations based on numerical tests via finite elements that the authors performed [16]. In addition, Engelhardt and Sackmann employed the incompressible Evans law and found an average value of the shear modulus of all cells of Gs = 6.1. Our analysis in section 2B suggests that the incompressible Evans law should overestimate the erythrocyte shear modulus based on the Skalak et al. law by a factor of 2–3 at moderate deformations. Thus their shear modulus corresponds to a Skalak et al. shear modulus of about which is in excellent agreement with that found in the linear regime [9].
Additional methods
Korin et al. [22] utilized observations of erythrocytes flowing in microchannels at moderate deformations (relative cell extensions between 10% and 60%) and determined a shear modulus of Gs = 3.7. However, the earlier study used the incompressible Evans law which, based on our discussion in section 2B, should overestimate the erythrocyte shear modulus based on the Skalak et al. law by a factor of 2-3 at these deformations. Most important, to solve the flow dynamics the Keller and Skalak model was employed which is an approximate model that predicts only qualitatively the erythrocyte motion [42]. A major source of error in this model results from the omission of the shape-memory effects owing to the non-spherical quiescent erythrocyte shape; this is a phenomenon which has been identified only recently [43, 44]. Thus, the Keller and Skalak model predicts with a small error the erythrocyte inclination but overpredicts by a factor of 5–6 its tank-treading frequency [45] which is used in the model of Korin et al. [22] to determine the membrane shear modulus.
Therefore, the theoretical model of Korin et al. [22] is very approximate and the fact that its prediction of Gs = 3.7 appears to be realistic is because the model contains counter-balanced approximations, i.e. combined significant overprediction with significant underprediction of the true erythrocyte dynamics.
5. CONCLUSIONS
Despite research spanning several decades, the exact value of the shear modulus Gs of the erythrocyte membrane is still ambiguous, and a wealth of studies, using measurements based on micro-pipette aspirations, ektacytometry systems and other flow chambers, and optical tweezers as well as application of different models have found different average values in the range 2–10 µN/m.
Our work shows that different methodologies have predicted the correct shear modulus for the specific membrane modeling employed, i.e. the variation in the shear modulus determination results from the specific membrane modeling. Available experimental findings from ektacytometry systems and optical tweezers suggest that the dynamics of the erythrocyte membrane is strain-hardening at both moderate and large deformations. Thus the erythrocyte shear modulus cannot be determined accurately using strain-softening models (such as the neo-Hookean and Evans laws) or strain-softening/strain-hardening models (such as the Yeoh law) which overestimate the erythrocyte shear modulus. According to our analysis, the only available strain-hardening constitutive law, the Skalak et al. law, is able to match well both deformation-shear rate data from ektacytometry and force-extension data from optical tweezers at moderate and large strains, using a value of the shear modulus of Gs = 2.4–2.75 µN/m, i.e. very close to that found in the linear regime of deformations via force-extension data from optical tweezers, Gs = 2.5 ± 0.4 µN/m [9]. Finally, our work suggests that this is the accurate value of the erythrocyte shear modulus and does not vary with strain. The range of the shear modulus variation (owing to the inherent differences between erythrocytes within a large population) appears to be well described with that found by Hénon et al. [9]; in particular our analysis suggests that a standard deviation in Gs of 0.4–0.5 µN/m describes well the findings from optical tweezers at small and large strains as well as from micro-pipette aspirations.
We emphasize that the strain-hardening nature and the true value of the shear modulus are necessary for the understanding of experimental findings on erythrocytes dynamics, e.g. [8, 14], including their circulation in the blood system. In addition, the shear modulus is used in the determination of other properties of the erythrocyte membrane such as its bending resistance and surface viscosity [8, 17, 26, 30]. Thus we believe that it may be necessary to reconsider the determination of the bending modulus and the viscosity of the erythrocyte membrane from earlier studies, which utilized strain-softening models and high values for the shear modulus.
To improve the understanding of the erythrocyte dynamics, it would be very useful if experimental groups provide non-bulk-type data on erythrocyte deformation such as local details of the interfacial shape of individual cells in basic flows (e.g. simple shear flow or planar extensional flow) or in confined solid geometries (e.g. microfluidic channels). In this case, the experimental studies should also provide information on the properties of the individual cells studied, including equilibrium shape and cytoplasm viscosity.
ACKNOWLEDGMENTS
This work was supported in part by the National Science Foundation and the National Institutes of Health.
Appendix: Micro-pipette aspiration analysis based on the Skalak et al. law
In this appendix, we employ Evans analysis for the statics of the micro-pipette aspiration [46] but utilizing the Skalak et al. law instead of the Evans law so that we can determine the shear modulus of the Skalak et al. law applicable to micro-pipette analysis.
As discussed in pages 122–124 in the work of Waugh and Evans [6], the principal stretch ratio along the meridian direction at a point outside the pipette entrance is given by
| (17) |
where Rp is the pipette internal radius and Lp the aspiration length. The pipette suction pressure is determined by integrating in the plane of the membrane from the pipette tip outward
| (18) |
where τs = (τ1 − τ2)/2. Utilizing the incompressible Evans law for the principal tensions τ1 and τ2 and thus for τs given by Eq.(11), the authors found the pipette suction pressure to be
| (19) |
(Note that the same result for ΔP was also found by Chien et al. [7] who applied the Evans law but considered the statics inside the pipette using a spherical cap model.)
Following the same analysis but for the incompressible Skalak et al. law, given by Eq.(9), we can easily show that
| (20) |
while the pipette suction pressure is now given by
| (21) |
Combining Eqs.(19) and (21), we find the moduli ratio for the two laws
| (22) |
Different micro-pipette aspiration studies have utilized aspiration lengths of about Lp/Rp = 1.5–4, e.g. see [6, 7, 26, 37]. In this range of Lp/Rp, the moduli ratio increases practically linearly with the aspiration length and takes on values of 1.5–3.6. Thus, even based on Evans micro-pipette analysis, if one uses Evans law to describe the tensions of a strain-hardening membrane following the Skalak et al. law, then this will result in a significant overestimation of the shear modulus.
It is of interest to note that Lelièvre et al. [37] reported that they used the Skalak et al. law and the Evans analysis in their micro-pipette aspiration study. However, Lelièvre et al. neglected the last factor for shown in our Eq.(20) and thus found τs for the Evans law given by our Eq.(11) while they used the pipette suction pressure valid for the Evans law, i.e. Eq.(19) above. (See Eqs.(5) and (6) in the earlier study [37]). We note that the factor cannot be neglected in the non-linear regime of deformations such as those used in the micropipette systems. Thus, in essence Lelièvre et al. [37] utilized the Evans law with Evans micro-pipette analysis similarly to earlier studies, e.g. [6, 46].
References
- 1.Skalak R, Özkaya N, Skalak TC. Biofluid Mechanics. Annu. Rev. Fluid Mech. 1989;21:167–204. [Google Scholar]
- 2.Mohandas N, Chasis JA. Red blood cell deformability, membrane material properties and shape: regulation by transmembrane, skeletal and cytosolic proteins and lipids. Sem. Hem. 1993;30:171–192. [PubMed] [Google Scholar]
- 3.Evans EA, Fung Y-C. Improved measurements of the erythrocyte geometry. Microvasc. Res. 1972;4:335–347. doi: 10.1016/0026-2862(72)90069-6. [DOI] [PubMed] [Google Scholar]
- 4.Baskurt OK, Meiselman HJ. Blood rheology and hemodynamics. Sem. Thromb. Hem. 2003;29:435–450. doi: 10.1055/s-2003-44551. [DOI] [PubMed] [Google Scholar]
- 5.Hochmuth RM, Waugh RE. Erythrocyte membrane elasticity and viscosity. Annu. Rev. Physiol. 1987;49:209–219. doi: 10.1146/annurev.ph.49.030187.001233. [DOI] [PubMed] [Google Scholar]
- 6.Waugh R, Evans EA. Thermoelasticity of red blood cell membrane. Biophys. J. 1979;26:115–132. doi: 10.1016/S0006-3495(79)85239-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chien S, Sung K-LP, Skalak R, Usami S, Tözeren A. Theoretical and experimental studies on viscoelastic properties of erythrocyte membrane. Biophys. J. 1978;24:463–487. doi: 10.1016/S0006-3495(78)85395-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fischer TM, Haest CWM, Stöhr-Liesen M, Schmid-Schönbein H, Skalak R. The stress-free shape of the red blood cell membrane. Biophys. J. 1981;34:409–422. doi: 10.1016/S0006-3495(81)84859-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hénon S, Lenormand G, Richert A, Gallet F. A new determination of the shear modulus of the human erythrocyte membrane using optical tweezers. Biophys. J. 1999;76:1145–1151. doi: 10.1016/S0006-3495(99)77279-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mills JP, Qie L, Dao M, Lim CT, Suresh S. Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers. Mech. Chem. Biosys. 2004;1:169–180. [PubMed] [Google Scholar]
- 11.Li J, Dao M, Lim CT, Suresh S. Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Biophys. J. 2005;88:3707–3719. doi: 10.1529/biophysj.104.047332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dao M, Li J, Suresh S. Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mater. Sci. Eng. C. 2006;26:1232–1244. [Google Scholar]
- 13.Dodson WR, III, Dimitrakopoulos P. Tank-treading of erythrocytes in strong shear flows via a non-stiff cytoskeleton-based continuum computational modeling. Biophys. J. 2010;99:2906–2916. doi: 10.1016/j.bpj.2010.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hardeman MR, Goedhart PT, Dobbe JGG, Lettinga KP. Laser-assisted optical rotational cell analyser (LORCA): I. A new instrument for measurement of various structural hemorheological parameters. Clin. Hemorheol. 1994;14:605–618. [Google Scholar]
- 15.Barthès-Biesel D, Diaz A, Dhenin E. Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech. 2002;460:211–222. [Google Scholar]
- 16.Engelhardt H, Sackmann E. On the measurement of shear elastic moduli and viscosities of erythrocyte plasma membranes by transient deformation in high frequency electric fields. Biophys. J. 1988;54:495–508. doi: 10.1016/S0006-3495(88)82982-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Evans EA, Hochmuth RM. Membrane viscoelasticity. Biophys. J. 1976;16:1–11. doi: 10.1016/S0006-3495(76)85658-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rachik M, Barthès-Biesel D, Carin M, Edwards-Levy F. Identification of the elastic properties of an artificial capsule membrane with the compression test: Effect of thickness. J. Colloid Interface Sci. 2006;301:217–226. doi: 10.1016/j.jcis.2006.04.062. [DOI] [PubMed] [Google Scholar]
- 19.Yeoh OH. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993;66:754–771. [Google Scholar]
- 20.Skalak R, Tözeren A, Zarda RP, Chien S. Strain energy function of red blood cell membranes. Biophys. J. 1973;13:245–264. doi: 10.1016/S0006-3495(73)85983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Evans EA. A new material concept for the red cell membrane. Biophys. J. 1973;13:926–940. doi: 10.1016/S0006-3495(73)86035-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Korin N, Bransky A, Dinnar U. Theoretical model and experimental study of red blood cell (RBC) deformation in microchannels. J. Biomech. 2007;40:2088–2095. doi: 10.1016/j.jbiomech.2006.10.004. [DOI] [PubMed] [Google Scholar]
- 23.Evans EA, Skalak R. Mechanics and Thermodynamics of Biomembranes. Boca Raton, FL: CRC; 1980. [Google Scholar]
- 24.Pozrikidis C. Interfacial Dynamics for Stokes Flow. J. Comp. Phys. 2001;169:250–301. [Google Scholar]
- 25.Dodson III WR, Dimitrakopoulos P. Dynamics of strain-hardening and strain-softening capsules in strong planar extensional flows via an interfacial spectral boundary element algorithm for elastic membranes. J. Fluid Mech. 2009;641:263–296. [Google Scholar]
- 26.Evans EA, Mohandas N, Leung A. Static and dynamic rigidities of normal and sickle erythrocytes. J. Clin. Invest. 1984;73:447–488. doi: 10.1172/JCI111234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carin M, Barthès-Biesel D, Edwards-Lévy F, Postel C, Andrei DC. Compression of biocompatible liquid-filled HSA-alginate capsules: determination of the membrane mechanical properties. Biotech. Bioeng. 2003;82:207–212. doi: 10.1002/bit.10559. [DOI] [PubMed] [Google Scholar]
- 28.Fischer TM. Is the surface area of the red cell membrane skeleton locally conserved? Biophys. J. 1992;61:298–305. doi: 10.1016/S0006-3495(92)81837-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Discher DE, Mohandas N, Evans EA. Molecular maps of red cell deformation: hidden elasticity and in situ connectivity. Science. 1994;266:1032–1035. doi: 10.1126/science.7973655. [DOI] [PubMed] [Google Scholar]
- 30.Fedosov DA, Caswell B, Karniadakis GE. A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 2010;98:2215–2225. doi: 10.1016/j.bpj.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lefebvre Y, Barthès-Biesel D. Motion of a capsule in a cylindrical tube: effect of membrane pre-stress. J. Fluid Mech. 2007;589:1570–181. [Google Scholar]
- 32.Mukhopadhyay R, G Lim HW, Wortis M. Echinocyte shapes: bending, stretching, and shear determine spicule shape and spacing. Biophys. J. 2002;82:1756–1772. doi: 10.1016/s0006-3495(02)75527-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang X, Zhao H, Zhuang FY, Stoltz JF. Measurement of erythrocyte deformability by two laser diffraction methods. Clin. Hemo. Microcirc. 1999;21:291–295. [PubMed] [Google Scholar]
- 34.Alexy T, Nemeth N, Wenby RB, Bauersachs RM, Baskurt OK, Meiselman HJ. Effect of lanthanum on red blood cell deformability. Biorheology. 2007;44:361–373. [PubMed] [Google Scholar]
- 35.Hardeman MR. (private communication) [Google Scholar]
- 36.Le DV, White J, Peraire J, Lim KM. and B.C. Khoo, An implicit immersed boundary method for three-dimensional fluid-membrane interactions. J. Comp. Phys. 2010;228:8427–8445. [Google Scholar]
- 37.Lelièvre JC, Bucherer C, Geiger S, Lacombe C, Vereycken V. Blood cell biomechanics evaluated by the single-cell micromanipulation. J. Phys. III France. 1995;5:1689–1706. [Google Scholar]
- 38.Hartmann D. A multiscale model for red blood cell mechanics. Biomech. Model Mechanobiol. 2010;9:1–17. doi: 10.1007/s10237-009-0154-5. [DOI] [PubMed] [Google Scholar]
- 39.Yao W, Wen Z, Yan Z, Sun D, Ka W, Xie L, Chien S. Low viscosity ektacytometry and its validation tested by flow chamber. J. Biomech. 2001;34:1501–1509. doi: 10.1016/s0021-9290(01)00109-9. [DOI] [PubMed] [Google Scholar]
- 40.Liu X, Tang Z, Zeng Z, Chen X, Yao W, Yan Z, Shi Y, Shan H, Sun D, He D, Wen Z. The measurement of shear modulus and membrane surface viscosity of RBC membrane with Ektacytometry: A new technique. Math. Biosci. 2007;209:190–204. doi: 10.1016/j.mbs.2006.09.026. [DOI] [PubMed] [Google Scholar]
- 41.MacMeccan RM, Clausen JR, Neitzel GP, Aidun CK. Simulating deformable particle suspensions using a coupled lattice-Boltzmann and finite-element method. J. Fluid Mech. 2009;618:13–39. [Google Scholar]
- 42.Keller SR, Skalak R. Motion of a tank-treading ellipsoidal particle in a shear flow. J. Fluid Mech. 1982;120:27–47. [Google Scholar]
- 43.Abkarian M, Faivre M, Viallat A. Swinging of red blood cells under shear flow. Phys. Rev. Lett. 2007;98:188302. doi: 10.1103/PhysRevLett.98.188302. [DOI] [PubMed] [Google Scholar]
- 44.Skotheim JM, Secomb TW. Red blood cells and other nonspherical capsules in shear flow: oscillatory dynamics and the tank-treading-to-tumbling transition. Phys. Rev. Lett. 2007;98:078301. doi: 10.1103/PhysRevLett.98.078301. [DOI] [PubMed] [Google Scholar]
- 45.Dodson WR, III, Dimitrakopoulos P. Oscillatory tank-treading motion of erythrocytes in strong shear flows. Phys. Rev. E. 2011;84:011913. doi: 10.1103/PhysRevE.84.011913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Evans EA. New membrane concept applied to the analysis of fluid shear- and micropipette-deformed red blood cells. Biophys. J. 1973;13:941–954. doi: 10.1016/S0006-3495(73)86036-9. [DOI] [PMC free article] [PubMed] [Google Scholar]